Đề học sinh giỏi tỉnh Toán 12 năm 2022 – 2023 sở GD&ĐT Bà Rịa – Vũng Tàu

NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12
TỈNH BÀ RỊA – VŨNG TÀU
NĂM HỌC 2022 – 2023 MÔN TOÁN
Thời gian làm bài: 180 phút (không kể thời gian giao đề) Ngày thi: 13/12/2022
Câu 1: (1.5 điểm) Giải phương trình 2 x 2  3π 4sin
3 cos 2x 1 2cos  x  − = + − . 2 4   
Câu 2: (1.5 điểm) n
Tìm số hạng không chứa x trong khai triển của  1 2 x  − 
với x > 0 biết rằng n là số 2 x    nguyên dương thỏa mãn 0 1 2
C + C + C +.... n + C = . n n n n 1024
Câu 3: (1.5 điểm) 2
2y −3x + 6y +1= 2 x − 2y − 4x −5y −3
Giải hệ phương trình 
(1− y) x − y + x = 2 + (x − y −1) y
Câu 4: (3.5 điểm)
Giải các phương trình sau: + a) + − = ( ) 2 2 2 9 3 2.27 9 3 x x x x x ; b) 3 3 2
x − x + 2ln x − ln (x + 2ln x) = 0. 3
Câu 5: (4.0 điểm) a) Cho hàm số mx + 4 y =
với m là tham số. Tìm tất cả các giá trị nguyên của tham số m x + m thuộc khoảng ( 2023 −
;2023) để hàm số đồng biến trên khoảng (1;+ ∞). b) Cho hàm số 3
y = x − (m + ) 2 2 1 x + (3m + )
1 x + 2m − 2 có đồ thị là (C . Tìm tất cả các giá trị m )
tham số m để (C cắt trục hoành tại 3 điểm phân biệt A(2;0) , m )
B và C sao cho trong hai
điểm B , C có một điểm nằm trong và một điểm nằm ngoài đường tròn (C) 2 2 : x + y =1.
Câu 6: (1.5 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , biết AC vuông góc
với mặt phẳng (SBD) và AB = SD = a, AD = SB = 2a . Tính khoảng cách giữa hai đường thẳng SA và BD .
Câu 7: (2.0 điểm)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , tam giác SAC cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Gọi M , N lần lượt là trung điểm của SA và BC .
Biết AB = a và MN tạo với mặt đáy một góc 60°. Tính thể tích khối chóp S.ABC theo a . TOANMATH.com Trang 1
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
Câu 8: (1.5 điểm)
Cho hàm số f (x) xác định, liên tục trên  và thoả mãn f (cot x) = sin 2x + cos 2x . Tìm giá trị
lớn nhất và giá trị nhỏ nhất của hàm số g (x) = f (x) f (1− x) trên đoạn [ 1; − ] 1 .
Câu 9: (1.5 điểm)
Cho hình lăng trụ đều ABC.A′B C
′ ′ có AB = 2 3 và AA′ = 2 . Gọi M , N, P lần lượt là trung điểm
của các cạnh A′B ,′ A′C ,′ BC và hai điểm F, E lần lượt là giao điểm của mặt phẳng (MNP) với
AB ,′ AC′. Tính thể tích của khối đa diện MFENC B ′ ′ .
Câu 10: (1.5 điểm)
Cho các số thực dương x, y thỏa mãn điều kiện xy ≤ y −1. Tìm giá trị lớn nhất của biểu thức x + y x − 2y P = − . 2 2
x − xy + 3y 6(x + y)
----------- HẾT ---------- Trang 2
TOANMATH.com
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 HƯỚNG DẪN GIẢI
Câu 1: (1.5 điểm) Giải phương trình 2 x 2  3π 4sin
3 cos 2x 1 2cos  x  − = + − . 2 4    Lời giải Ta có: 2 x 2  3π 4sin
3 cos 2x 1 2cos  x  − = + − 2 4    (  π x) 3 2 1 cos
3 cos 2x 2 cos 2x  ⇔ − − = + −  2   
⇔ sin 2x − 3 cos 2x = 2cos x 1 3  π   π sin 2x cos 2x cos x sin 2x  sin  x ⇔ − = ⇔ − = − 2 2 3 2       π π
2x − = − x + k2π  3 2 ⇔  ,k ∈  π  π 2x − = π − − x +    k2π  3  2   5π 2π x = + k  18 3 ⇔  ,k ∈  5π x = + k2π  6 π π π
Kết luận: Phương trình có họ nghiệm là 5 2 5 x = + k ; x =
+ k2π;k ∈ . 18 3 6
Câu 2: (1.5 điểm) n
Tìm số hạng không chứa x trong khai triển của  1 2 x  − 
với x > 0 biết rằng n là số 2 x    nguyên dương thỏa mãn 0 1 2
C + C + C +.... n + C = . n n n n 1024 Lời giải Ta có: ( )n 0 1 2
1+1 = C + C + C +.... n
+ C ⇔ 2n =1024 ⇔ n =10. n n n n 10 10 10 k k
Với n =10 ta có  1  k 2( 10) − 2 x = ∑C x 2 k − x = ∑C 2 k k k −   x − + − . 2 ( ) ( ) 2( 10) 2 10 10  x  k =0 k =0
Số hạng không chứa x trong khai triển ứng với k thỏa mãn: 2.( −10) k k + = 0 ⇔ k = 8. 2
Vậy số hạng không chứa x trong khai triển ứng là: 8 C 2 − = 11520. 10 ( )8
Câu 3: (1.5 điểm) 2
2y −3x + 6y +1= 2 x − 2y − 4x −5y −3
Giải hệ phương trình 
(1− y) x − y + x = 2 + (x − y −1) y Lời giải TOANMATH.com Trang 3
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
x − 2y ≥ 0 
4x − 5y − 3 ≥ 0
Điều kiện của hệ phương trình  . x − y ≥ 0  y ≥ 0
Xét phương trình (1− y) x − y + x = 2 + (x − y −1) y 2
a = x − y a = x − y Đặt  ⇒ 
. Điều kiện a ≥ 0,b ≥ 0. 2 b  =  y b  = y Ta được phương trình 2 2 2 2
(1− b )a + a + b = 2 + (a −1)b ⇔ (1−b)(a − )
1 (a + b + 2) = 0 b =1
(1 b)(a )1(a b 2) 0  ⇔ − − + + = ⇔ a =1  . a + b + 2 =  0
Do a ≥ 0,b ≥ 0 nên a + b + 2 = 0 vô nghiệm.
+ Với b =1ta được y =1thay vào phương trình 3
− x + 9 = 0 ⇔ x = 3.
+ Với a =1ta được x − y =1⇒ x =1+ y thay vào phương trình 2
2y − 3x + 6y +1 = 2 x − 2y − 4x − 5y − 3 ta được phương trinh 2 2y − 3( y + )
1 + 6y +1 = 2 1− y − 1− y 2
⇔ 2y + 3y − 2 = 1− y .
Đặt t = 1− y (0 ≤ t ≤ ) 1 ta được phương trình
 t − t − =
2t − 7t − t + 3 = 0 ⇔ (2t − 2t −3)(t + t − ) 2 2 2 3 0 4 2 2 2 1 = 0 ⇔  2
t + t −1 = 0  1− 7 t = ≈ 0.822 − (loai) 2   1+ 7 t = ≈1.822(loai) 2 1 − + 5 ⇔  ⇔ t = .  1 − − 5 t = ≈ 1.61 − (loai) 2  2  1 − + 5 t = ≈ 0.61  2 1 5 t − + − + − + = hay 1 5 5 1 5 1 = 1− y ⇔ y = ⇒ x = . 2 2 2 2  + − 
Vậy hệ phương trình có 2 nghiệm là (x y) = ( ) (x y) 5 1 5 1 ; 3;1 , ; =  ; . 2 2      Trong S
∆ AB vuông tại A , ta có 2 2
SA = SB − AB = 36 − 9 = 3 3 .
Vậy thể tích khối chóp S.ABCD là 1 1 V = . . SA S = = (đvtt). ABCD .3 3.3.6 18 3 3 3
Câu 4: (3.5 điểm)
Giải các phương trình sau: + a) + − = ( ) 2 2 2 9 3 2.27 9 3 x x x x x ; b) 3 3 2
x − x + 2ln x − ln (x + 2ln x) = 0. 3 Trang 4
TOANMATH.com
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 Lời giải 9 + a) +3 − = ( ) 2 2 2 2x 9x 2 3 2 +6 x + x x x x x x x 2 2.27 9 3 ⇔ 2.3 − 3 = 3 2 3  x + x x = 0 2 3 2  = 2 3 1 2 3 x x x x + + 3 2 ⇔ 3 + 3 − 2 = 0 2 x x 0  ⇔ ⇔ + = ⇔  3 . 2 3 x + x 2 x = −  2 3 = 2 − (loai)   2
Vậy tập nghiệm của phương trình là 3 S 0;  = − . 2   x > 0 b) Điều kiện:  .
x + ln x > 0 3 3 2
x − x + 2ln x − ln (x + 2ln x) 3 3
= 0 ⇔ x = x + 2ln x + 2ln ( 3 x + 2ln x) 3 Đặt 3
t = x + 2ln x (t > 0), kết hợp phương trình ta có hệ: 3 3 t
 = x + 2ln x t  =  x + 2ln x ( ) 1  ⇔  3 3
x = t + 2ln t
x = t + 2ln t  (2) 3 3
⇒ t − x = x + 2ln x − t − 2ln t 3 3
⇒ t + t + 2ln t = x + x + 2ln x (3)
Xét hàm đặc trưng f (u) 3
= u + u + 2ln u , (u > 0) Ta có f ′(u) 2 2
= 3u +1+ > 0, u
∀ > 0 ⇒ f (u) đồng biến trên (u;+∞) u
(3) ⇔ f (t) = f (x) 3
⇔ t = x ⇔ x = x + 2ln x 3
⇔ x − x − 2ln x = 0 . Xét g (x) 3
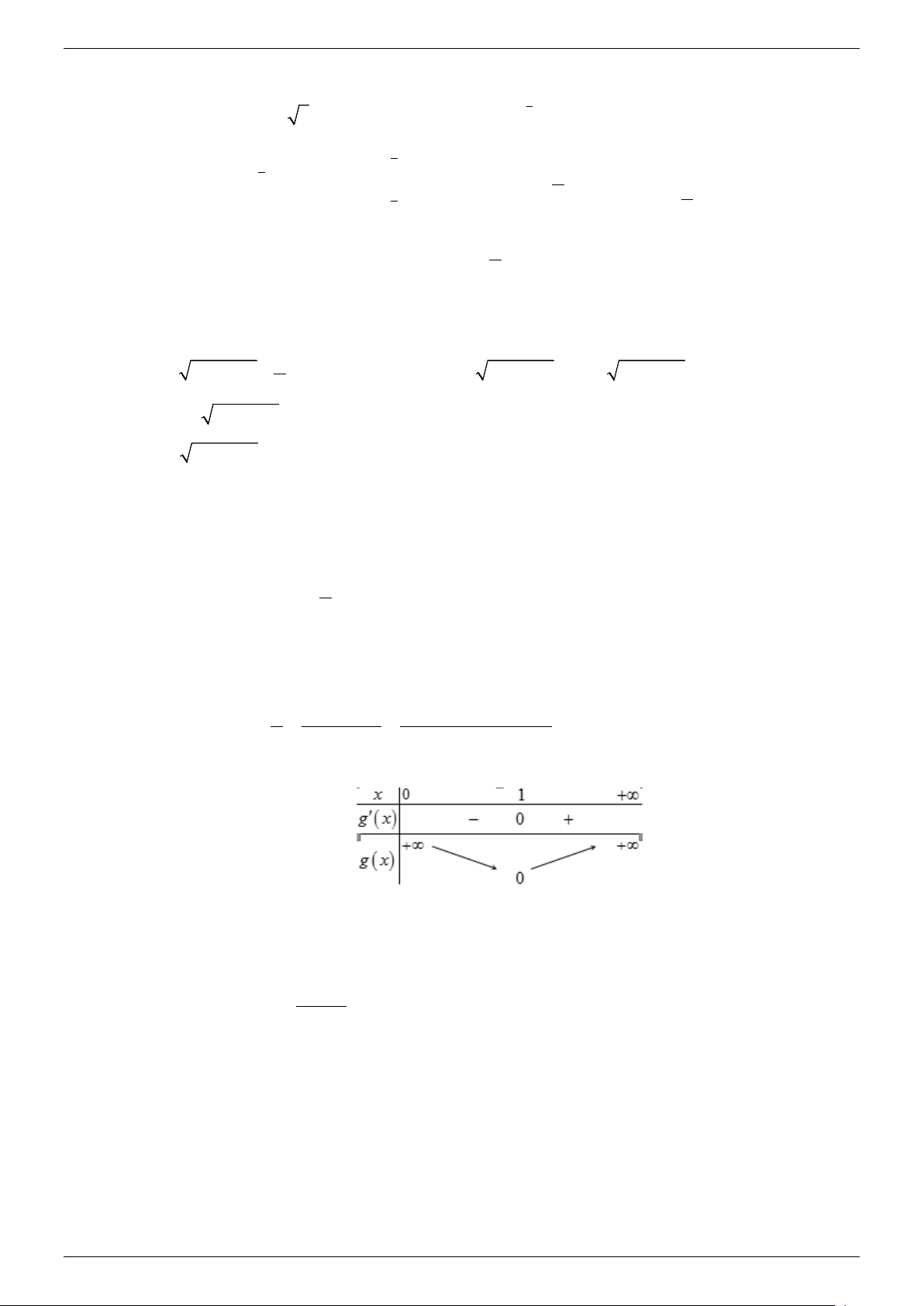
= x − x − 2ln x (x > 0) .
2 3x − x − 2 (x − ) 1 ( 2 3 3x + 3x + 2 2 )
g′(x) = 3x −1− = = x x x
g′(x) = 0 ⇔ x =1
Từ bảng biến thiên x =1 là nghiệm duy nhất của g (x) = 0
Thử lại, ta nhận nghiệm x =1.
Câu 5: (4.0 điểm) a) Cho hàm số mx + 4 y =
với m là tham số. Tìm tất cả các giá trị nguyên của tham số m x + m thuộc khoảng ( 2023 −
;2023) để hàm số đồng biến trên khoảng (1;+ ∞). b) Cho hàm số 3
y = x − (m + ) 2 2 1 x + (3m + )
1 x + 2m − 2 có đồ thị là (C . Tìm tất cả các giá trị m )
tham số m để (C cắt trục hoành tại 3 điểm phân biệt A(2;0) , m )
B và C sao cho trong hai
điểm B , C có một điểm nằm trong và một điểm nằm ngoài đường tròn (C) 2 2 : x + y =1. Lời giải
a) Tập xác định: D =  \{− } m TOANMATH.com Trang 5
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 2 − YCBT m 4 ⇔ y′ = > 0 , x ∀ ∈(1;+ ∞) (x + m)2 2 m − 4 > 0 ⇔  ⇒ m > 2 . −m ∉  (1;+ ∞) Vì m∈( 2023 −
;2023) và m∈ nên ta có m = {3;4;5;.......;2021; } 2022 .
Vậy có 2020 giá trị nguyên của tham số m .
b) Phương trình hoành độ giao điểm: 3 x − (m + ) 2 2 1 x + (3m + )
1 x + 2m − 2 = 0 x = 2 ⇔  . 2
x − 2mx − m +1 = 0 Yêu cầu bài toán 2
⇔ x − 2mx − m +1 = 0 ( )
1 có hai nghiệm phân biệt x , x và 1 2  1
− < x <1< x 1 2  x < 1 − < x <  1 1 2  1+ 5 m < −
+ Điều kiện để phương trình có 2 nghiệm phân biệt: 2
∆′ = m + m −1 > 0 2 ⇔  (2)  1 − + 5 m >  2 + Xét phương trình ( ) 1 - Nếu 1 x = − thì ( )
1 có dạng: 1 + m − m +1 = 0 (vô lý). Suy ra 1
x = − không là nghiệm. 2 4 2 2 - Khi 1 x ≠ − thì ( ) x +1 1 ⇔ m = . 2 2x +1 2
Xét hàm số f (x) x +1 = . 2x +1  1+ 5 2 x = −
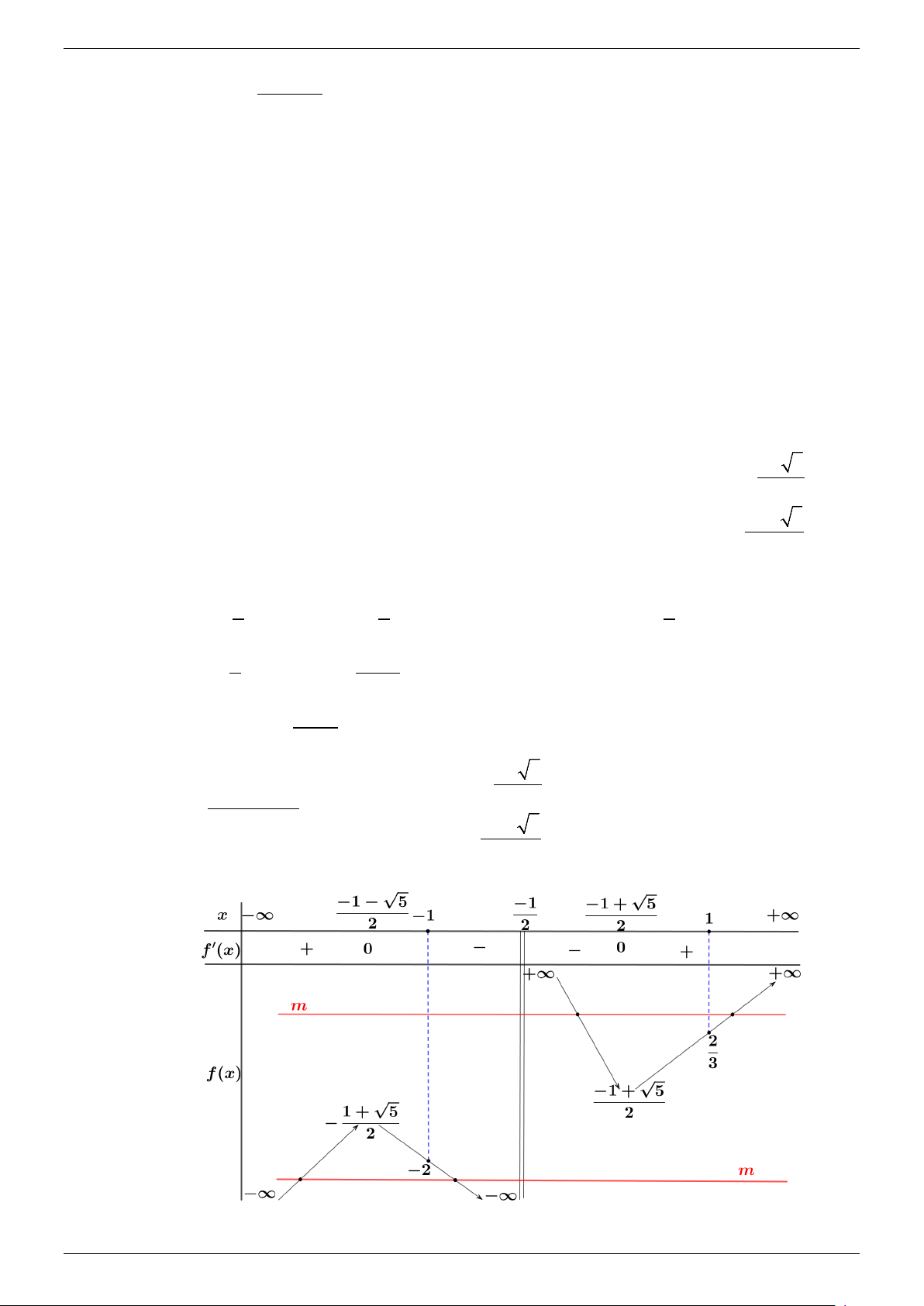
f ′(x) 2x + 2x − 2 = , cho f ′(x) 2 = 0 ⇒  (2x + )2 1  1 − + 5 x =  2 Bảng biến thiên Trang 6
TOANMATH.com
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 m < 2 −  1
− < x <1< x Từ BBT, ta nhận xét 1 2  thì 
thỏa mãn điều kiện (2) . x < 1 − < x < 2  1  > 1 2 m  3 Vậy m ( )  2 ; 2 ;  ∈ −∞ − ∪ + ∞ 
thỏa mãn yêu cầu bài toán. 3   
Câu 6. (1.5 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B , biết AC vuông góc
với mặt phẳng (SBD) và AB = SD = a, AD = SB = 2a . Tính khoảng cách giữa hai đường thẳng SA và BD . Lời giải
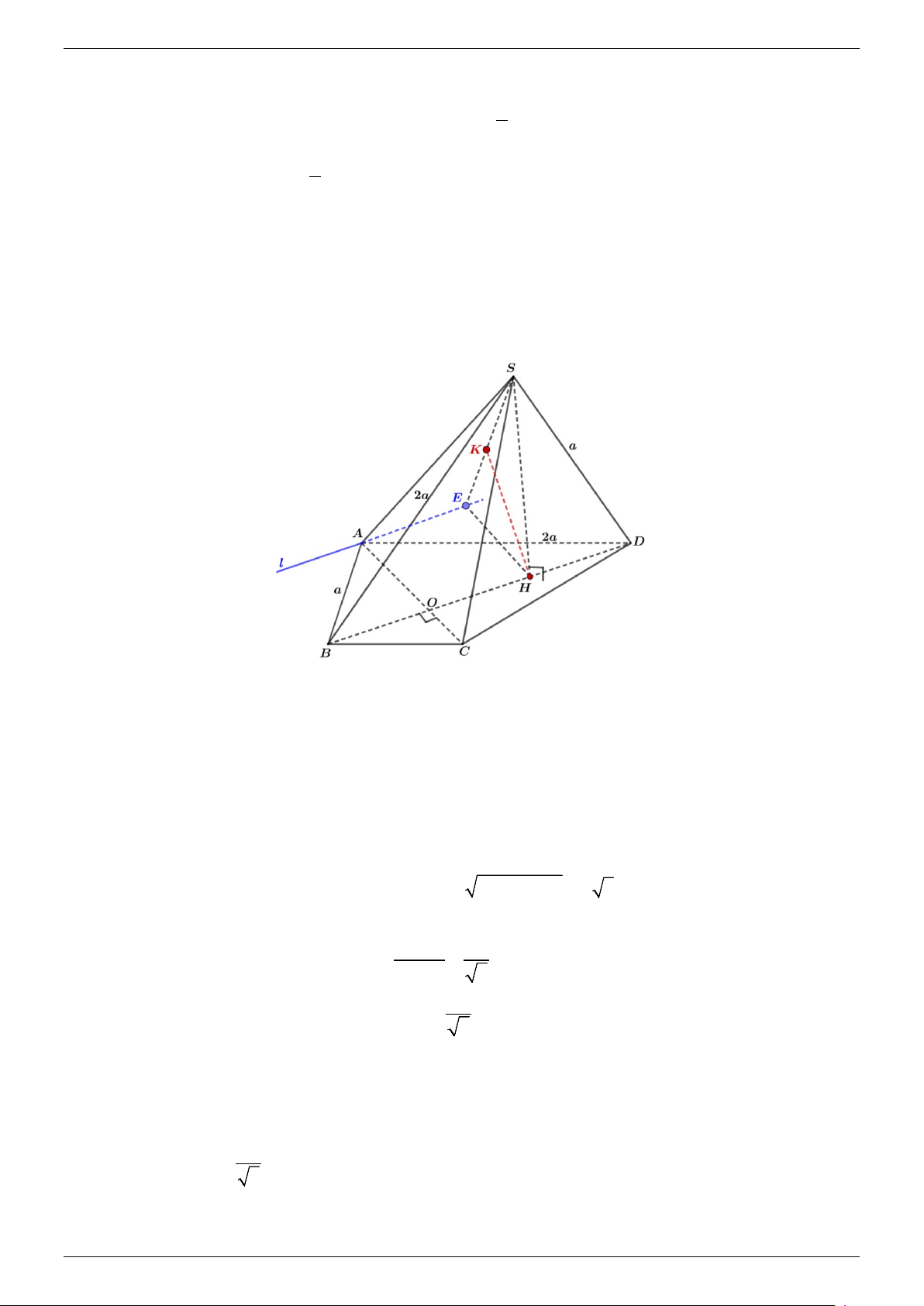
AC ⊥ (SBD) ⬥ Theo đề 
⇒ ( ABCD) ⊥ (SBD). AC ⊂  ( ABCD)
Trong mặt phẳng (SBD) gọi H là hình chiếu của S lên BD (1). (
 ABCD) ⊥ (SBD) Vì ( (2).  ABCD  )∩(SBD) = SD
Từ (1) và (2) suy ra SH ⊥ ( ABCD).
⬥ Trong mặt phẳng ( ABCD) ta có: 2 2
BD = AB + AD = a 5 .
Từ đó suy ra tam giác SBD vuông tại S . Khi đó . SB SD 2 . = . a
SH BD SB SD ⇒ SH = = . BD 5 Mặt khác 2a S ∆ BD = A
∆ DB⇒ AO = SH =
, với O = AC ∩ BD . 5
⬥ Trong mặt phẳng ( ABCD) , gọi l là đường thẳng qua A và song song với BD .
Ta có BD / / (S,l) ⇒ d (BD, AC) = d (BD,(S,l)) = d (H,(S,l)).
Gọi E là hình chiếu của H lên đường thẳng l , vì tứ giác AEHO là hình chữ nhật nên 2a AO = HE = . 5
K là hình chiếu của H lên SE . Khi đó d (H,(S,l)) = HK . TOANMATH.com Trang 7
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
⬥ Xét tam giác SHE vuông cân tại H ( K là trung điểm của HE ): SE 2SH 10a HK = = = . 2 2 5
Vậy d (BD AC) a 10 , = . 5
Câu 7. (2.0 điểm)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , tam giác SAC cân tại S và
nằm trong mặt phẳng vuông góc với đáy. Gọi M , N lần lượt là trung điểm của SA và BC .
Biết AB = a và MN tạo với mặt đáy một góc 60°. Tính thể tích khối chóp S.ABC theo a . Lời giải
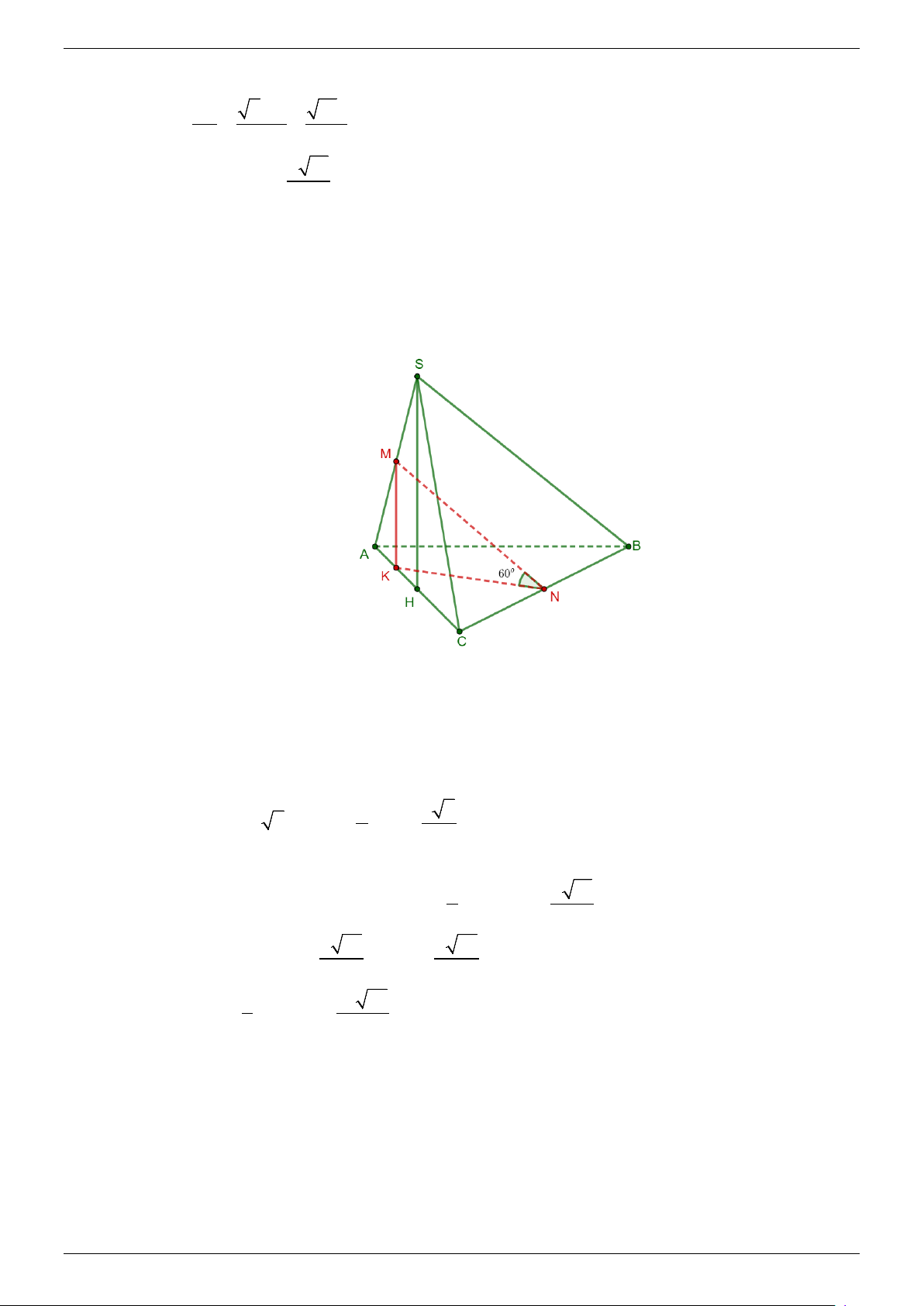
Gọi H, K lần lượt là trung điểm của AC và AH khi đó: SH ⊥ ( ABC) và MK / /SH nên MK ⊥ ( ABC) . ⇒ MN ( ABC)  ( )=  , MNK = 60° . Do tam giác ABC vuông cân tại B và AB = a nên a 3 2
BC = a, AC = a 2 ⇒ CN = ,CK = a . 2 4
Áp dụng định lí cô – sin vào tam giác CKN ta có: 2 2 2 5 2 a 10
KN = CN + CK − 2.CN.CK.cos 45° = a ⇒ KN = 8 4 a 30 a 30
⇒ MK = KN.tan 60° = ⇒ SH = . 4 2 3 Vậy 1 a 30 V = SH S = . S ABC . . 3 ABC 12
Câu 8. (1.5 điểm)
Cho hàm số f (x) xác định, liên tục trên  và thoả mãn f (cot x) = sin 2x + cos 2x . Tìm giá trị
lớn nhất và giá trị nhỏ nhất của hàm số g (x) = f (x) f (1− x) trên đoạn [ 1; − ] 1 . Lời giải Trang 8
TOANMATH.com
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 2 2 Ta có: f ( x) 2cot x
cot x −1 cot x + 2cot x −1
cot = sin 2x + cos 2x = + = , x ∀ ∈ 0;π . 2 2 2 ( )
cot x +1 cot x +1 cot x +1
Đặt t = cot x , điều kiện cho t là t ∈ , tương ứng với điều kiện x∈(0;π ). 2
f (t) t + 2t −1 = , t ∀ ∈  . 2 t +1 2 2
x 1− x + 8x 1− x − 2
Ta có: g (x) = f (x). f (1− x) ( ) ( ) = , x ∀ ∈  . 2
x (1− x)2 − 2x(1− x) + 2
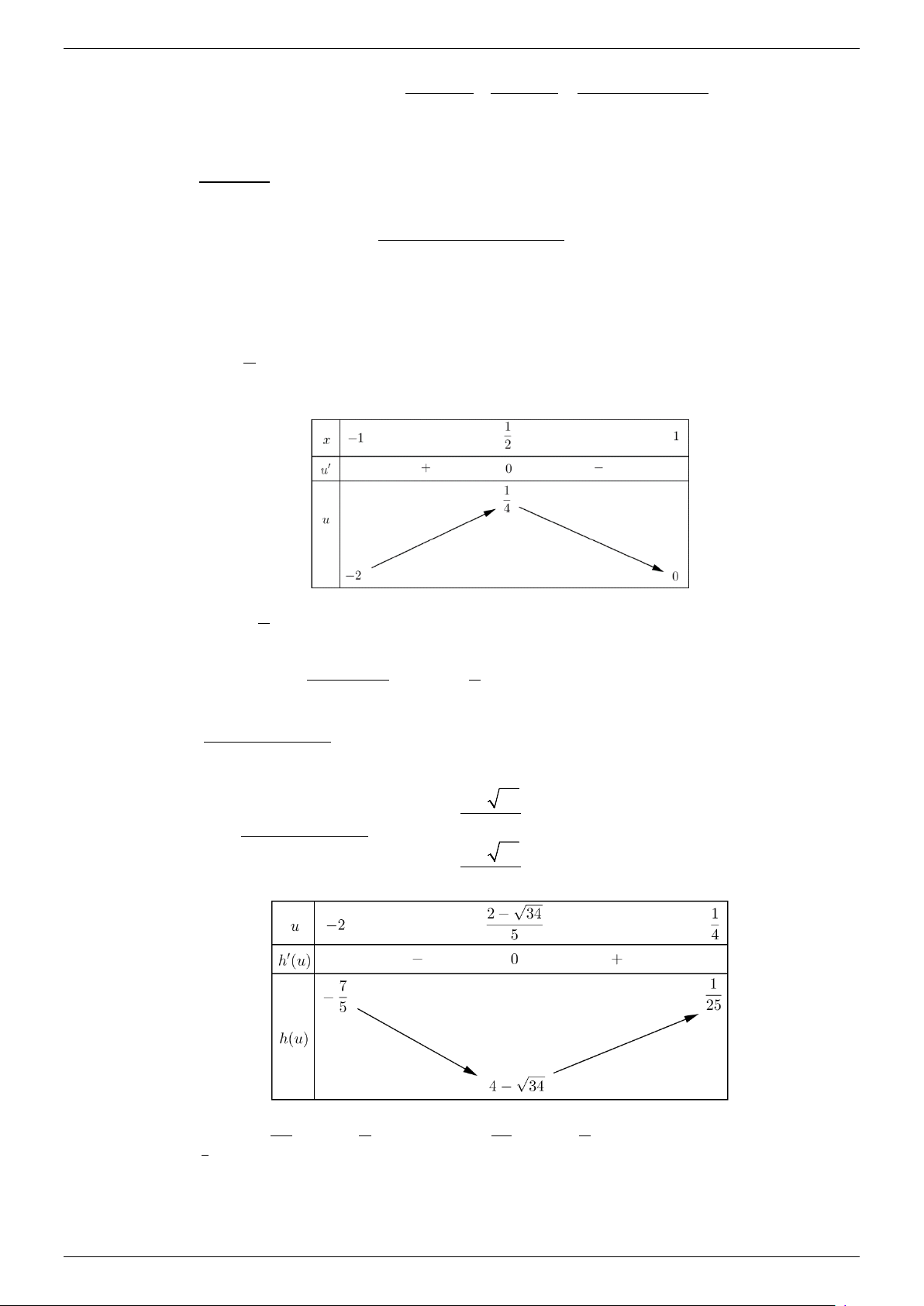
Đặt u = x(1− x). u′ =1− 2x 1 .
u′ = 0 ⇔ x = 2 Ta có bảng biến thiên Do đó 1 u  2;  ∈ −  . 4   2
Khảo sát hàm h(u) u +8u − 2 = trên  1 2;  − . 2 u − 2u + 2  4   2( 2 5 − u + 4u + 6) h′(u) = ( . u − 2u + 2)2 2  − 2( 2 34 2 5 − u + 4u + 6) u = h′(u) 2 = 0 ⇔ = ⇔  ( . u − 2u + 2) 0 2 2  2 + 34 u = (l)  2 Vậy h(u) 1 max = khi 1 u = 1 ⇒ max g (x) = khi 1 x = .  1 2;  − 25 4 [ 1 − ] ;1 25 2  4   TOANMATH.com Trang 9
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
min h(u) = 4 − 34 khi 2 34 u − =
⇒ min g (x) = 4 − 34 khi 1 2 34 3 x − − = .  1 [ 1 − ] 2;  − 5 ;1 2  4  
Câu 9. (1.5 điểm)
Cho hình lăng trụ đều ABC.A′B C
′ ′ có AB = 2 3 và AA′ = 2 . Gọi M , N, P lần lượt là trung điểm
của các cạnh A′B ,′ A′C ,′ BC và hai điểm F, E lần lượt là giao điểm của mặt phẳng (MNP) với
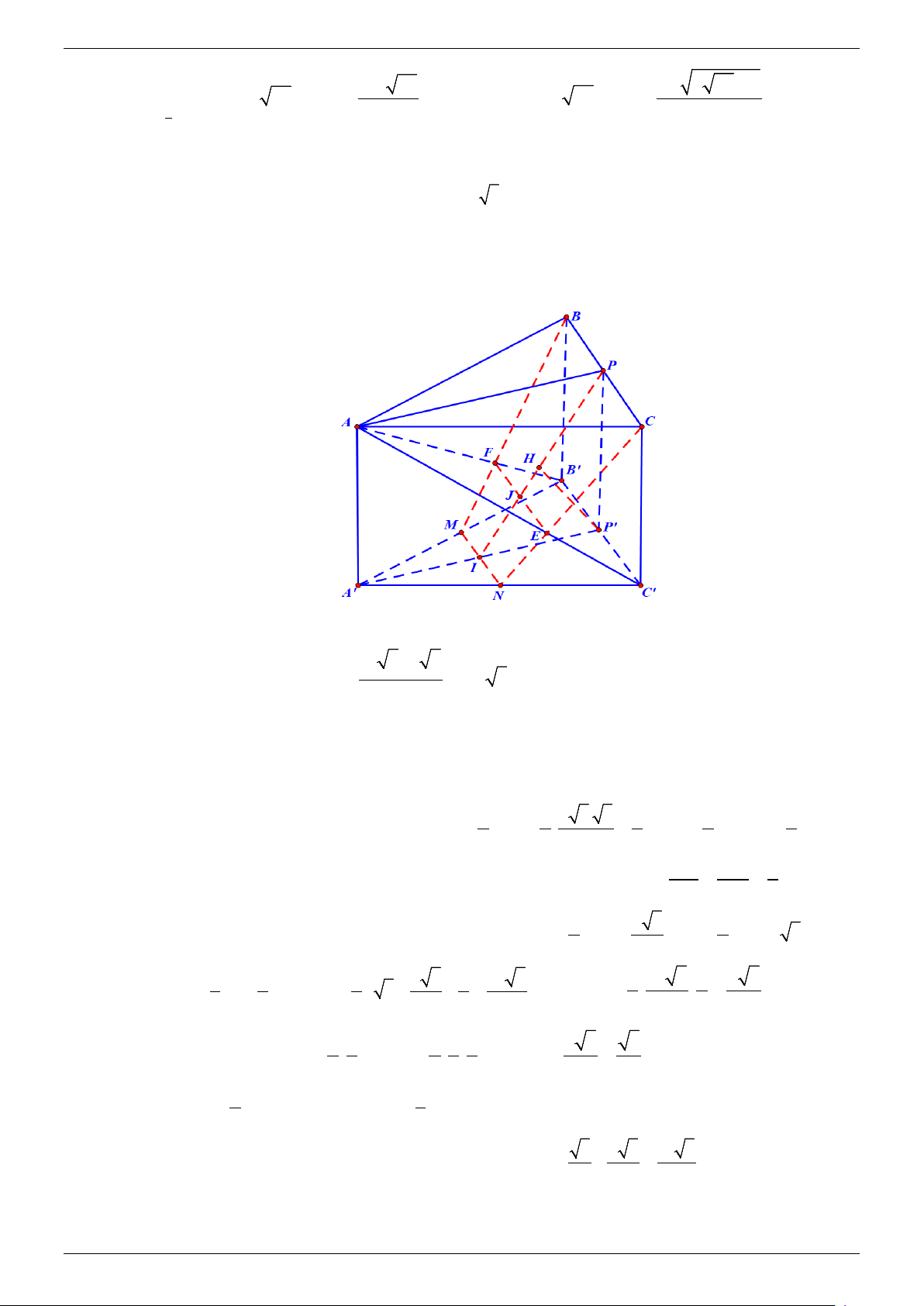
AB ,′ AC′. Tính thể tích của khối đa diện MFENC B ′ ′ . Lời giải
Ta có (MNP) ≡ (MBCN ) . ( )2 2 3 . 3
Thể tích khối ABC.A′B C ′ ′ = .2 = 6 3 . 4
Gọi P′ là trung điểm của B C
′ ′, I = MN ∩ A′P ,′ J = PI ∩ EF .
Vì PP′ ⊥ MN, A′P′ ⊥ MN ⇒ ( APP A
′ ′) ⊥ (MBCN ) và ( APP A
′ ′)∩(MBCN ) = IP .
Gọi H là hình chiếu vuông góc của P′ trên IP ⇒ P H
′ = d (P ,′(FBCE)).
Trong tam giác vuông IPP′ có 1 1 2 3. 3 3 5 6
PP′ = 2, IP′ = A′P′ = .
= ⇒ IP = ⇒ P H ′ = . 2 2 2 2 2 5 Ta có NE MF
E, F là trọng tâm của hai tam giác CA′C′ và BA′B′ nên suy ra 1 = = . NC MB 3
Vì BM = CN ⇒ MFEN là hình thang cân có 2 4 3 1 EF / / = B C ′ ′ = ,MN = B C ′ ′ = 3 , chiều 3 3 2   cao 1 5 1 4 3 5 35 3 1 35 3 6 7 3
IJ = IP = ⇒ S =  +  = ⇒ V = = . P′ MFEN . . MFEN 3 . 3 6 2  3  6 36 .   3 36 5 18 Ta có 1 1 1 1 1 6 3 3 V = = = = = ′ ′ V ′ ′ V ′ ′ ′ V E NC P F MB P . A ABC . . . . . ABC. 4 3 4 3 3 A′B C ′ ′ 36 6 ( vì 1 1 S = ′ ′ = ′ ′ ) ′ ′
S ′ ′ d E A B C d A A B C NP C A B C , , ' , ' ' ( ( )) ( ( )) 4 3
Vậy ta có thể tích khối 3 7 3 13 3 MFENC B ′ ′ = 2V + = + = . ′ ′ V E NC P P′ MFEN 2. . . 6 18 18
Câu 10. (1.5 điểm) Trang 10
TOANMATH.com
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
Cho các số thực dương x, y thỏa mãn điều kiện xy ≤ y −1. Tìm giá trị lớn nhất của biểu thức x + y x − 2y P = − 2 2
x − xy + 3y 6(x + y) Lời giải
Ta có x > 0, y > 0 nên 2 x   1 1 1 1 1 1
xy ≤ y −1 ⇔ ≤ − = − − + ≤   2 y y y  y 2  4 4 x +1 x −2 x + y x − 2 = − y = y − y P 2 2 2
x − xy + 3y 6(x + y)  x  x 6 x + − +  1   3   y   y  y Đặt 1 = x t
, điều kiện 0 < t ≤ ta có t +1 t − 2 P = − y 2 4
t − t + 3 6(t +1) Xét 1 f (t) t +1 t − 2 = − với 0 < t ≤ 2
t − t + 3 6(t +1) 4 3 − t + 7 1 f (′t) = − (t t ) 2(t + − + )2 3 2 1 2 3  1 t 0;  ∀ ∈ ta có 2
:t − t + 3 = t(t −1) + 3 < 3; 3
− t + 7 > 6 và t +1 >1 4    1  3 − t + 7 3 − t + 7 1 1 1 ∀t ∈ 0; : > >  1   và −
> − ⇒ f '(t) > 0, ∀t ∈0; 4   (  t − t + )3 2 6 3 3 2 3 2(t + )2 1 2  4
⇒ f (t) đồng biến trên  1 0;   4  
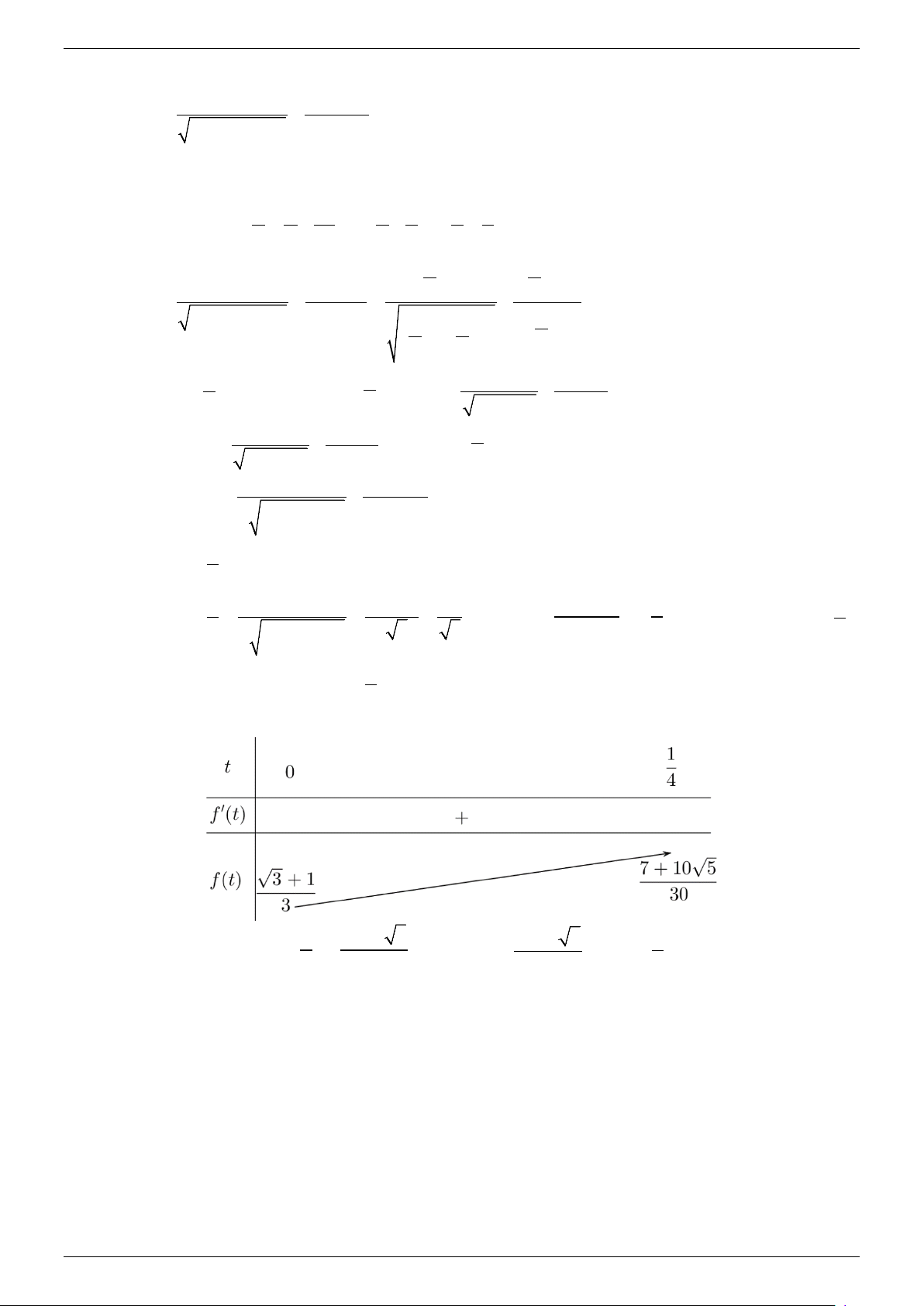
Ta có bảng biến thiên như sau  1  7 +10 5
⇒ f (t) ≤ f = 7 +10 5  . Vậy P = khi 1 x = , y = 2 4    30 max 30 2
----------- HẾT ---------- TOANMATH.com
Trang 11