Đề học sinh giỏi tỉnh Toán 12 năm 2023 – 2024 sở GD&ĐT Hà Tĩnh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 12 THPT HÀ TĨNH NĂM HỌC 2023 - 2024 Môn thi: TOÁN
ĐỀ THI C HÍNH THỨC
Thời gian làm bài: 180 phút (không kể thời gian giao đề)
(Đề thi có 01 trang, gồm 10 câu)
Câu 1. (2.0 điểm) Cho hàm số 2x +1 y =
có đồ thị (C). Gọi I là giao điểm của hai đường tiệm x −1
cận của (C). Tìm tọa độ điểm M sao cho khoảng cách từ I đến tiếp tuyến của (C) tại M đạt giá trị lớn nhất.
Câu 2. (2.0 điểm) Tìm tất cả các tham số m để hàm số 3 2
y = x − x − ( 2 3
m − 6m + 2) x + m − 2 đồng biến trên khoảng (0;3).
Câu 3. (2.0 điểm) Cho hàm số f (x) 1 4 3 9 2
= x − x − x + (16 − m) x với m là tham số. Có bao nhiêu 4 2
giá trị nguyên của m để hàm số g (x) = f ( x ) có đúng 5 điểm cực trị.
Câu 4. (2.0 điểm) Tìm tất cả các giá trị của tham số m để phương trình sau có nghiệm 4 2
x −1 + 2 x −1 = m( 4 2
x +1 + 2 x −1).
Câu 5. (2.0 điểm) Gọi A là tập hợp các số tự nhiên có 5 chữ số. Lấy ngẫu nhiên một số thuộc tập
hợp A, tính xác suất sao cho số được lấy chia hết cho 13 và có chữ số hàng đơn vị là 1.
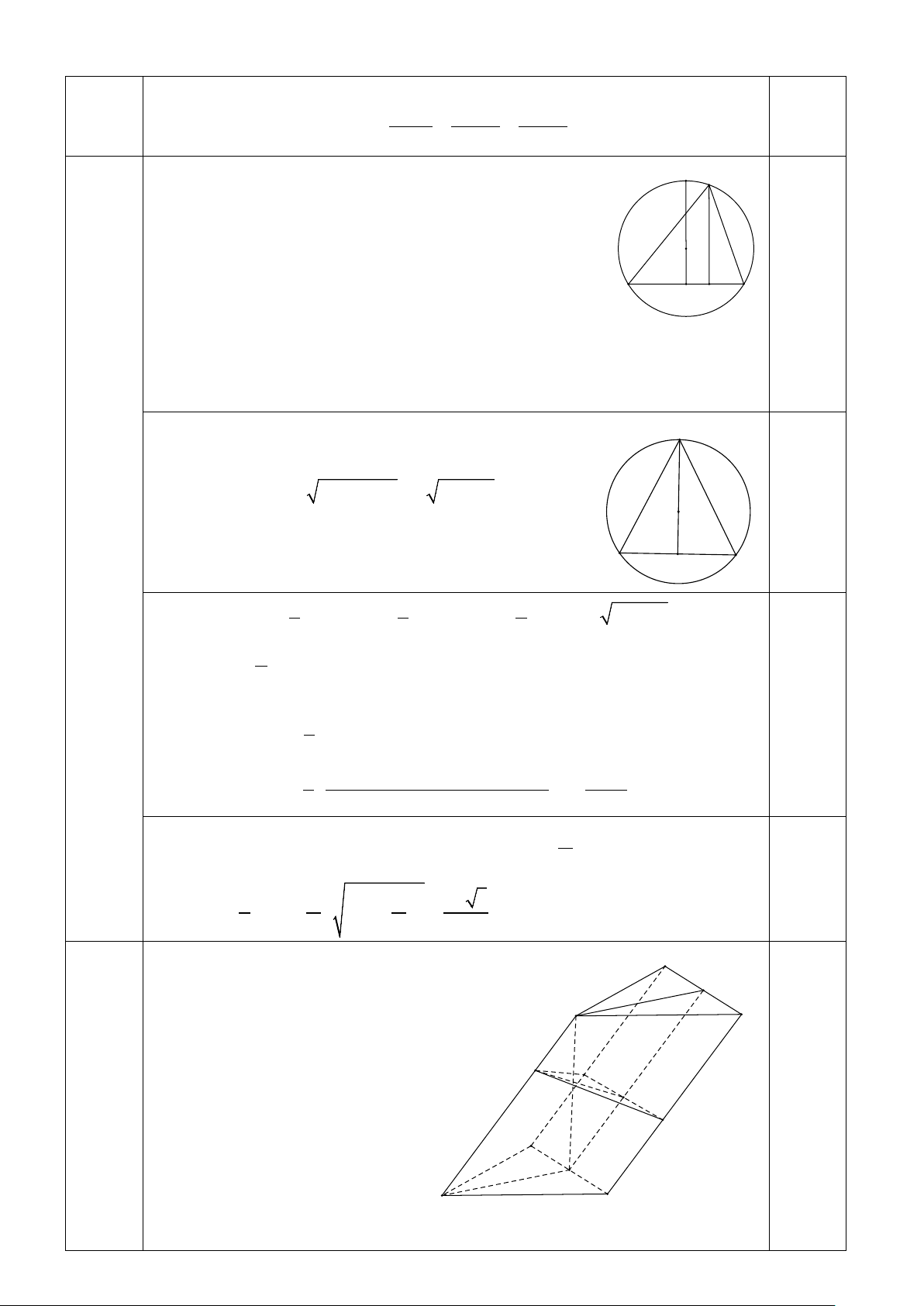
Câu 6. (2,0 điểm) Cho hình trụ (T ) có bán kính đáy và chiều cao đều bằng R , hai đáy là hai hình
tròn (O) và (O') . Gọi AA' và BB' là hai đường sinh bất kì của hình trụ, trong đó ,
A B ∈(O); A', B '∈(O'), M là một điểm di động trên đường tròn (O) . Tính thể tích lớn nhất của
khối chóp M.AA'B'B .
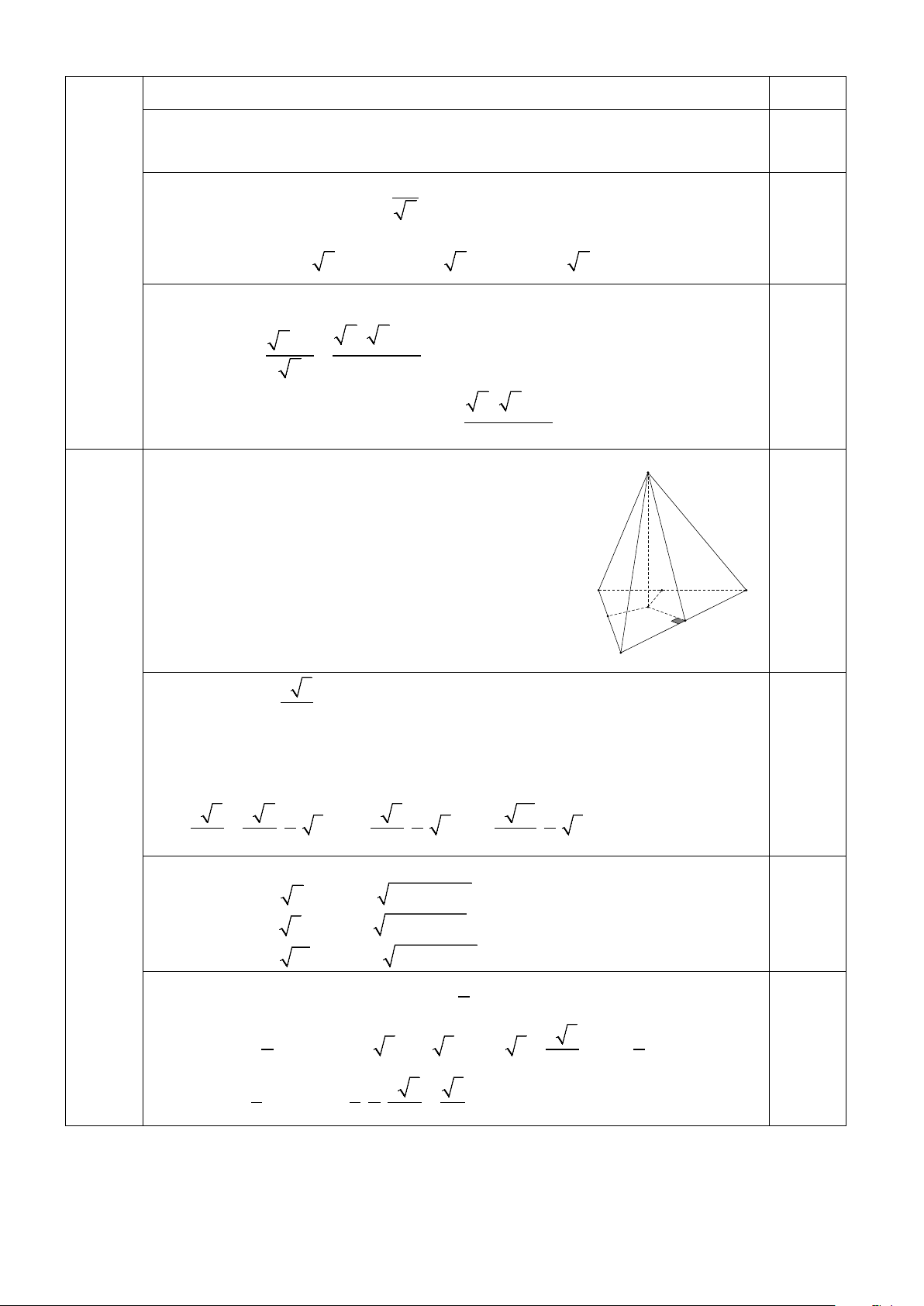
Câu 7. (2,0 điểm) Cho hình lăng trụ ABC.A'B'C ' có đáy là tam giác đều. Hình chiếu vuông góc
của A' lên ( ABC) là trung điểm của BC . Mặt phẳng (P) vuông góc với cạnh AA' và cắt các cạnh
bên AA', BB',CC ' của hình lăng trụ lần lượt tại I, J, K . Biết mặt phẳng ( ABB' A') vuông góc với
mặt phẳng ( ACC ' A') và chu vi của tam giác IJK bằng 1. Tính khoảng cách giữa CC ' và AB .
Câu 8. (2.0 điểm) Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 3 . Biết
d ( A (SBC)) 3 2 , =
, d (B (SCA)) 3 5 , =
và d (C (SAB)) 3 10 , =
; hình chiếu vuông góc của S lên 4 10 20
(ABC) nằm trong tam giác ABC . Tính thể tích khối chóp S.ABC .
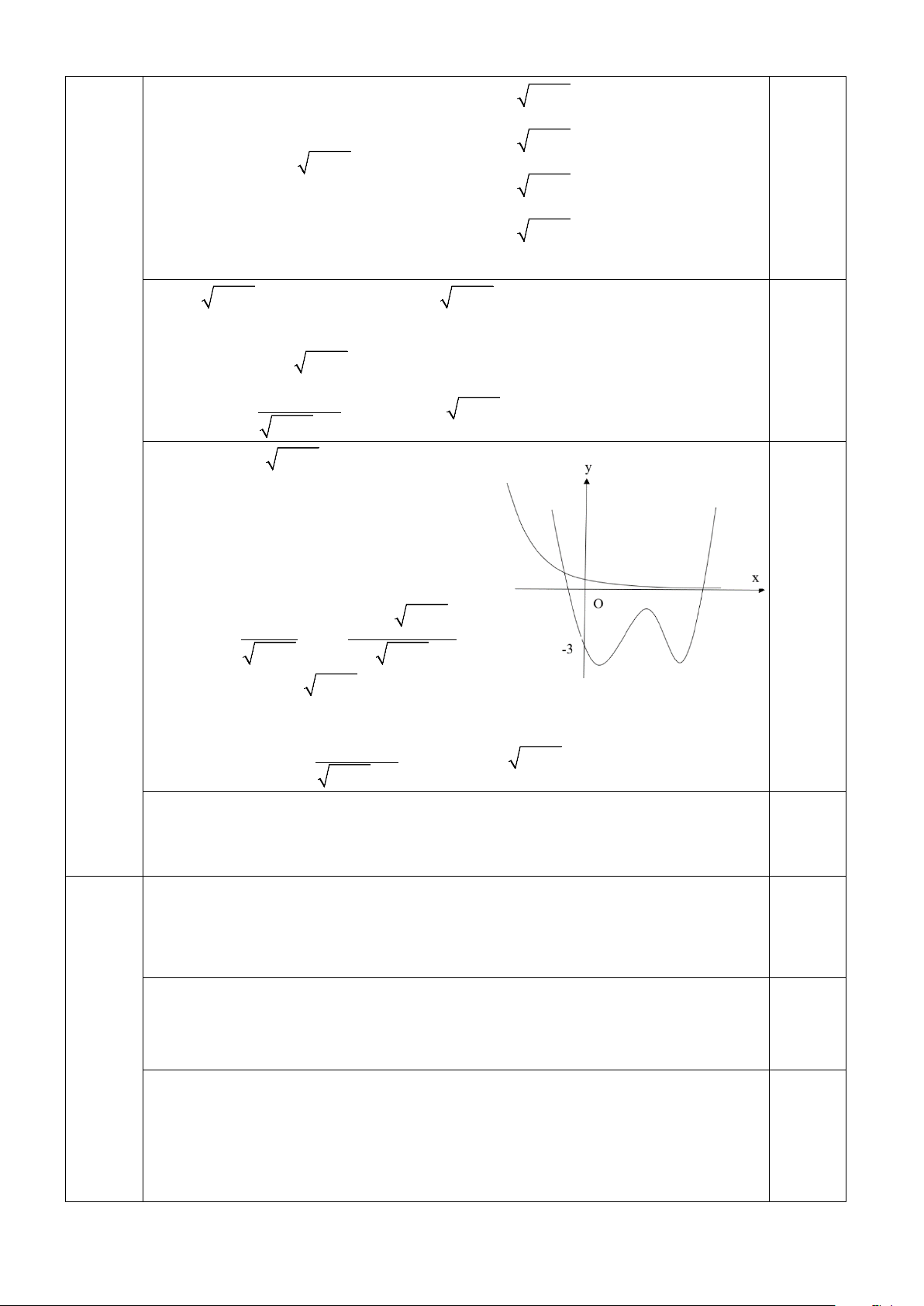
Câu 9. (2.0 điểm) Cho hàm số đa thức bậc bốn có đồ thị như
hình vẽ. Tìm số nghiệm của phương trình:
f ( 2x +1+ x).f (x))+3= 0.
Câu 10. (2.0 điểm) Tìm tất cả các số nguyên x sao cho ứng với mỗi x có không quá 2 số nguyên
y thỏa mãn 2x−5y 19 + − x− y+8 2 + 4
≥ 2048 và x + y > 0.
−−−−−−−−−−−−HẾT−−−−−−−−−−−−
- Thí sinh không được sử dụng tài liệu và máy tính cầm tay;
- Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………….……..… Số báo danh:………………………… 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 12 THPT HÀ TĨNH NĂM HỌC 2023-2024 Môn: TOÁN HƯỚNG DẪN CHẤM
(Hướng dẫn chấm gồm có 06 trang)
Lưu ý: Mọi cách giải khác đáp án mà đúng đều cho điểm tối đa. CÂU ĐÁP ÁN ĐIỂM
Đồ thị (C) có giao điểm hai đường tiệm cận là I (1;2). Gọi  2m +1 M ; m ,(m ≠   )
1 , ta có phương trình tiếp tuyến của (C)tại M là  m −1  0,5 3 − 2m +1 y = x − m +
⇔ 3x + m −1 y − 2m − 2m +1 = 0 2 ( ) ( )2 2 (m − ) 1 m −1 6 m −1
Khoảng cách từ I đến tiếp tuyến của (C) tại M là d = Câu 1 0,5 9 + (m − )4 1 (2,0 đ) Ta có 6 d = ≤ 6 , 9 + m −1 2 ( )2 (m − ) 1 0,5 dấu " = "xảy ra khi 9
= m −1 ⇔ m =1± 3 2 ( )2 (m − )1
Do đó, ta có hai điểm M thỏa mãn là M (1+ 3;2+ 3) và M (1− 3;2− 3). 0,5 Xét f (x) 3 2
= x − x − ( 2 3
m − 6m + 2) x + m − 2 ⇒ f '(x) 2
= 3x − 6x − ( 2 m − 6m + 2) 0,5
Hàm số y = f (x) đồng biến trên khoảng(0;3), xảy ra một trong hai trường hợp sau
Trường hợp 1: Hàm số f (x) đồng biến trên khoảng (0;3) và f (0) ≥ 0 0,5
Trường hợp 2: Hàm số f (x) nghịch biến trên khoảng (0;3) và f (0) ≤ 0
Trường hợp 1: Hàm số f (x) đồng biến trên khoảng (0;3) và f (0) ≥ 0, ta có 2 3
 x − 6x −( 2
m − 6m + 2) ≥ ,0 x ∀ ∈(0;3) 2 2 3
 x − 6x ≥ m − 6m + 2, x ∀ ∈(0;3)  ⇔  m − 2 ≥ 0 m ≥ 2 0,5 Câu 2 2 (2,0 đ)
m − 6m + 2 ≤ 3 − 1  ≤ m ≤ 5 ⇔  ⇔  ⇔ 2 ≤ m ≤ 5. m ≥ 2 m ≥ 2
Trường hợp 2: Hàm số f (x) nghịch biến trên khoảng (0;3) và f (0) ≤ 0, ta có 2 3
 x − 6x −( 2
m − 6m + 2) ≤ 0, x ∀ ∈(0;3) 2 2 3
 x − 6x ≤ m − 6m + 2, x ∀ ∈(0;3)  ⇔  m − 2 ≤ 0 m ≤ 2 m ≥ 7 0,5 2
m − 6m + 2 ≥ 9  ⇔ 
⇔ m ≤ −1⇔ m ≤ −1. m ≤ 2  m ≤ 2
Vậy, ta có 2 ≤ m ≤ 5 hoặc m ≤ 1 − .
Câu 3 Ta có y = f ( x ) là hàm số chẵn trên  nên đồ thị nhận trục Oy làm trục đối (2,0 đ) 0,5
xứng. Từ cách xác định hàm số y = f ( x ) , ta có số điểm cực trị của y = f ( x ) 2
là 2a +1, trong đó a là số điểm cực trị dương của đồ thị hàm số y = f (x). Ta có f (x) 3 2 '
= x − 3x − 9x +16 − m, để hàm số y = f ( x ) có 5 điểm cực trị thì
hàm số y = f (x) có đúng 2 điểm cực trị dương, hay ta có phương trình 0,5
f ′(x) = 0 có đúng 2 nghiệm dương phân biệt, tương đương với phương trình 3 2
x − 3x − 9x +16 = m có đúng 2 nghiệm dương phân biệt.
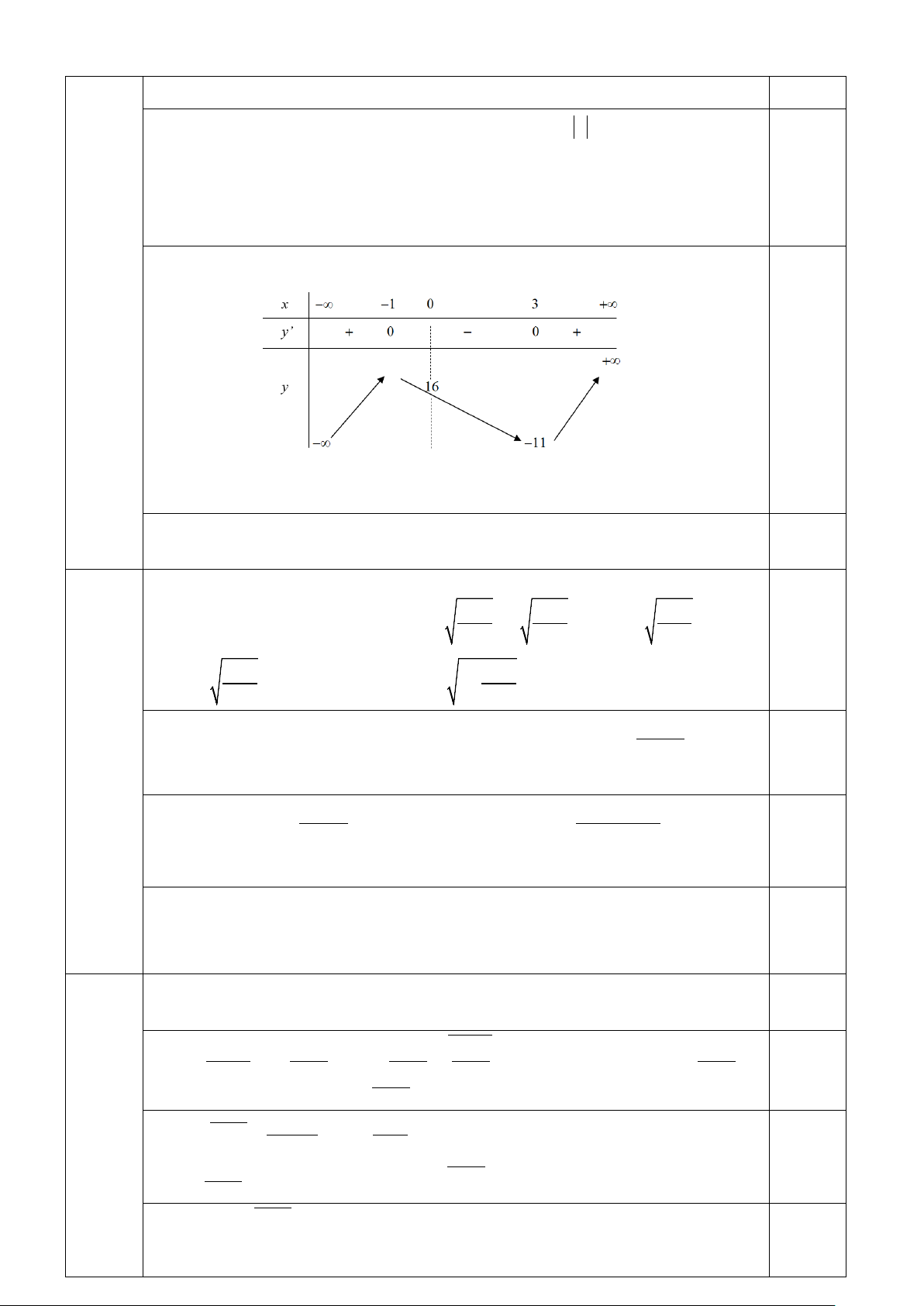
Lập BBT của hàm số h(x) 3 2
= x − 3x − 9x +16 trên khoảng (0;+∞). 0,5
Dựa vào BBT, ta có với 11
− < m < 16 phương trình 3 2
x − 3x − 9x +16 = m có
đúng 2 nghiệm dương phân biệt.
Kết hợp m∈ , ta có m∈{ 10 − ; 9 − ;...; } 15 . 0,5
Vậy, ta có 26 số nguyên m thỏa mãn yêu cầu bài toán.
Điều kiện: x ≥1. − −  − 
Phương trình đã cho tương đương với x 1 x 1 x 1 + 4 =  + 4 2 m 1 2  x 1 x 1  x 1  + + +   0,5 Đặt x −1 = 2 4 t
với 0 ≤ t <1, vì ≤ = 4 0 t 1−
< 1 với mọi x ≥1. x +1 x +1 2
Khi đó, phương trình đã cho trở thành 2t +
+ 2t = m(1+ 2t) t 2t ⇔ m = (1) Câu 4 1+ 2t 0,5
(2,0 đ) Phương trình đã cho có nghiệm khi và chỉ khi phương trình (1) có nghiệm t ∈[0; ) 1 2 2
Xét hàm số ( ) t + 2t f t + + = với t ∈[0; )
1 , ta có f (t) 2t 2t 2 ' = > 0 với mọi 1+ 2t (1+ 2t)2 0,5 t ∈[0; )
1 , do đó hàm số f (t) đồng biến trên [0; ) 1 .
Suy ra phương trình m = f (t) có nghiệm t ∈[0; ) 1 khi và chỉ khi
f (0) ≤ m < f ( ) 1 ⇔ 0 ≤ m <1. 0,5 Vậy 0 ≤ m <1.
Số các số tự nhiên có năm chữ số là: 4
9.10 = 90000 số. Do đó, số phần tử của
không gian mẫu là n(Ω) = 90000. 0,5
Giả sử số tự nhiên thỏa mãn yêu cầu là abcd1.
Ta có abcd1 =10.abcd +1 =13.abcd − 3abcd +1 chia hết cho 13 nên 3abcd −1 0,5
cũng chia hết cho 13, tức là 3abcd −1 =13k với k ∈ . Câu 5 k + k + (2,0 đ) Khi đó 13 1 1 abcd = = 4k + ∈  . 3 3 0,5
Do đó k +1 = t ∈ ⇒ k = 3t −1, nên abcd =13t − 4 3
Ta có 1000 ≤ abcd =13t − 4 ≤ 9999 ⇔ 77,23 ≤ t ≤ 769,46 .
Do t ∈ nên 78 ≤ t ≤ 769 , hay có 692 số t , ứng với mỗi t có 692 số thỏa mãn 0,5 yêu cầu bài toán. 3
Gọi A là biến cố: “Chọn được số chia hết cho 13 và có chữ số hàng đơn vị là 1”, n A
ta có n( A) = 692. Vậy P( A) ( ) 692 173 = = = . n(Ω) 90000 22500
Ta có mặt phẳng đáy (MAB) vuông góc với mặt phẳng E M
( AA'B'B) , hạ MH ⊥ AB suy ra MH là đường cao của
hình chóp M.AA'B 'B
Ta có MH ≤ EI , với E, I là giao điểm của đường thẳng đi O
qua tâm O và vuông góc với dây cung AB ( E,O cùng 0,5 A B phía với AB ). I H
Do đó, để tìm giá trị lớn nhất của thể tích của các khối
chóp M.AA'B 'B ta chỉ cần xét các loại hình chóp M.AA'B 'B , trong đó M là
giao điểm của đường tròn (O) và đường trung trực của đoạn AB , đồng thời
M ,O cùng phía với AB .
Với I là trung điểm AB , ta có MI ⊥ ( ABB' A') . M
Đặt OI = x (0 < x < R), ta có MI = R + x suy ra 2 2 2 2
AB = 2AI = 2 OA −OI = 2 R − x . 0,5 O Câu 6 (2,0 đ) A I B Khi đó 1 1 2 V = S
MI = AA′ AB MI = R R + x R − x M AA B B . ABB A . . . . ( ) 2 2. . ' ' ' ' 3 3 3 2 4 2 ⇒ V = R R + x R − x M AA B B ( )2 ( 2 2 . . ' ' ) 9
Áp dụng bất đẳng thức AM-GM, ta có 0,5 (R + x)2 ( 2 2 R − x ) 1
= (R + x)(R + x)(R + x)(3R − 3x) 3 4 4
1  R + x + R + x + R + x + 3R − 3x  27R ≤ = . 3  4    16
R + x = 3R −3x Dấu “ R
=” xảy ra khi và chỉ khi  .  ∈  ( ⇔ x = x 0; R) 2 0,5 2 3 Vậy 2  R  2  R  R 3
V = R R +  R − = . max 3 2  2      2
Mặt phẳng (IJK ) vuông góc với C'
AA' nên vuông góc với hai cạnh H'
bên còn lại. Gọi H, H ' lần lượt A' B'
là trung điểm của BC, B 'C ' .
BC ⊥ A′H Ta có 
⇒ BC ⊥ AA′ , K I Câu 7 BC ⊥ AH E 0,5
(2,0 đ) Do đó BC ⊥ BB', suy ra tứ giác
BCC 'B ' là hình chữ nhật. J C
Gọi BC = x , do (IJK ) ⊥ BB' , H
nên JK ⊥ BB ' , suy ra JK B  C A
và JK = BC = x . B
Lại có (IJK ) ⊥ AA' và 4
( ABB' A') ⊥ ( ACC ' A') nên IJ ⊥ IK , hay tam giác IJK vuông tại I .
Gọi E = JK ∩ HH ' , ta thấy E là trung điểm của JK . Do BC ⊥ ( AHH ' A') nên 0,5
JK ⊥ ( AHH ' A') ⇒ JK ⊥ IE . Từ đó I
∆ JK vuông cân tại I .
Ta có JK = x , suy ra x IJ = IK = . 2
Theo giả thiết chu vi tam giác IJK bằng 1, nên ta có 0,5
IJ + JK + KI =1 ⇔ x 2 + x =1 ⇔ (1+ 2) x =1⇔ x = 2 −1
Ta có CC '( ABB' A') và IK ⊥ ( ABB' A') , suy ra khoảng cách giữa CC ' và 2 2 1 ( 2 − − )1 AB bằng IK = = . 2 2 0,5 2 ( 2 − )1
Vậy khoảng cách giữa CC ' và AB bằng . 2
Gọi H là hình chiếu vuông góc của S xuống mặt S phẳng ( ABC).
Đặt SH = x . Gọi D, E, F lần lượt là hình chiếu của
H trên BC, C , A AB . 0,5 BC ⊥ SH +) Ta có E 
⇒ BC ⊥ (SHD) ⇒ BC ⊥ SD . A C BC ⊥ HD F H
Tương tự có CA ⊥ SE, AB ⊥ SF D B +) Ta có 3 3 S = , và ABC ∆ 4 SH.S = = = ∆ d A SBC S∆ d B SCA S∆ d C SAB S ABC ( ,( )). SBC ( ,( )). SCA ( ,( )). S∆AB 0,5
Câu 8 (vì cùng bằng 3V ). (2,0 đ) S.ABC 3 3 3 2 1 ⇒ . x = . . 3.SD 3 5 1 3 10 1 = . . 3.SE = . . 3.SF 4 4 2 10 2 20 2 Khi đó 2 2
SD = x 2 ⇒ HD = SD − SH = x 2 2
SE = x 5 ⇒ HE = SE − SH = 2x 0,5 2 2
SF = x 10 ⇒ HF = SF − SH = 3x +) Lại có S = + + 1 = ( .
HD BC + HE.CA + HF.AB) ∆ S∆ S∆ S ABC OBC OAC O ∆ AB 2 1
= (x + 2x + 3x) 3 = 3x 3 3 3 1 ⇒ 3x 3 = ⇒ x = 0,5 2 4 4 Vậy 1 1 1 3 3 3 V = SH S = = . S ABC . . ABC . . . 3 3 4 4 16 5  ( 2
x +1 + x).f (x) = 0 
( 2x +1+ x).f (x) = a
Từ đồ thị ta có f ( 2x +1+ x).f (x)) = 3 − ⇔   0,5 ( 2
x +1 + x).f (x) = b 
( 2x +1+ x).f (x) = c
Với 0 < a < b < c . Ta có 2
x +1 + x > 0, x
∀ ∈  , do đó ( 2x +1+ x) f (x) = 0 ⇔ f (x) = 0, phương
trình này có hai nghiệm phân biệt.
Xét phương trình ( 2x +1+ x) f (x) = k với k > 0 0,5 Ta có ( ) k f x =
⇔ f (x) = k ( 2x +1− x 1 2 ) ( ) x +1 + x
Câu 9 Đặt g (x) = k ( 2x +1− x) ,
(2,0 đ) ta có g(x) > 0 với x ∀ ∈ , k ∀ > 0 .
Số nghiệm của phương trình ( ) 1 là số giao
điểm của hai đồ thị y = f (x) và y = g (x) . Ta có k 0,5 x ( 2 x − x +   1)
g '(x) = k  −1 = < 0 2 2  x +1  x +1 với x ∀ ∈  (do 2
x < x +1, x ∀ ∈  ),
suy ra hàm số y = g (x) là nghịch biến trên  .   Mặt khác, ta có 1 lim   = 0 và + − = +∞ . →−∞ ( 2 lim x 1 x x ) x→+∞ 2  x +1 + x 
Từ đó với mỗi giá trị k > 0 , phương trình ( )
1 luôn có hai nghiệm phân biệt và
các nghiệm này đều khác nhau và khác nghiệm của phương trình f (x) = 0 . 0,5
Vậy phương trình ban đầu có 8 nghiệm phân biệt.
Xét hàm số f ( y) 2 x −5 y 19 + − x− y+8 = 2 + 4
− 2048 là hàm số biến y , tham số x .
Khi đó bất phương trình f ( y) ≥ 0 phải có không quá 2 nghiệm nguyên 0,5 y ∈(− ; x +∞) . Ta có f '( y) 2 x −5 y 19 + − x− y+8 = 5.2 − .ln 2 − 4 ln 4 < 0 với y
∀ ∈  , suy ra hàm số f ( y)
Câu 10 nghịch biến trên  . 0,5
(2,0 đ) Giả sử y = −x + k ,( k ∈ N ) là nghiệm bất phương trình, tức là f (−x + k) ≥ 0
Ta có −x +1< −x + 2 < −x + 3 < ... < −x + k , mà hàm số f ( y) nghịch biến trên  nên f (−x + )
1 > f (−x + 2) > f (−x + 3) > ... > f (−x + k) ≥ 0 0,5
Khi đó bất phương trình f ( y) ≥ 0 có không quá 2 nghiệm nguyên y ∈(− ; x +∞)
khi và chỉ khi f (−x + 3) < 0 . 6 f (−x + 3) 2 2 x +5x+4 5 x +5x+4 < 0 ⇔ 2 + 4 − 2048 < 0 ⇔ 2 < 4 102 2 2
⇔ x + 5x + 4 <10 ⇔ x + 5x − 6 < 0 ⇔ 6 − < x <1 0,5
Do x∈, nên x∈{ 5 − , 4 − , 3 − , 2 − , 1 − , } 0 . …….HẾT……