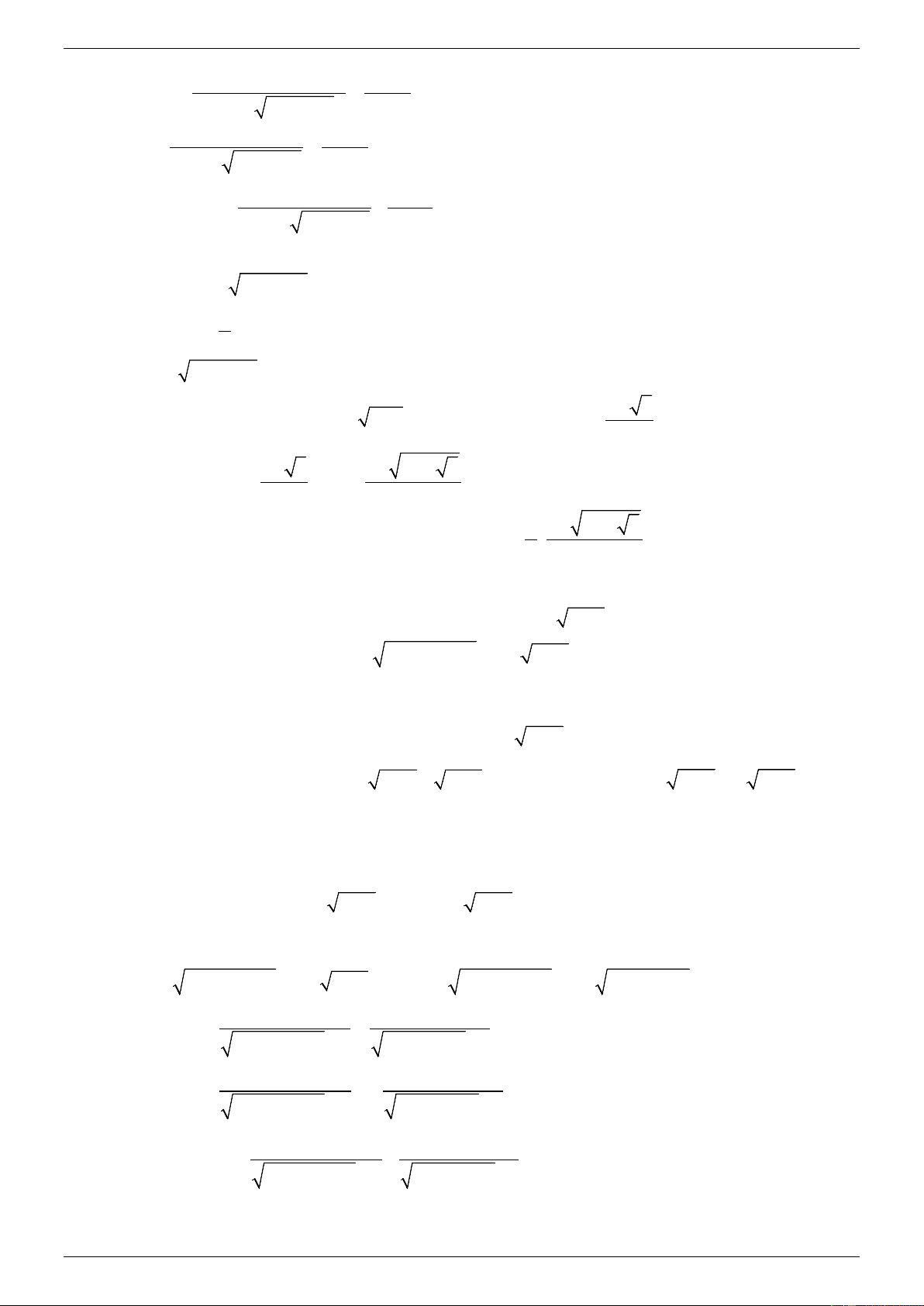

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI HẢI DƯƠNG
LỚP 12 THPT CẤP TỈNH NĂM HỌC 2022 - 2023 TOANMATH.com Môn thi: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 19/10/2022
Thời gian làm bài: 180 phút (không tính thời gian phát đề)
Đề thi gồm 05 câu & 01 trang
Câu I. (2,0 điểm) 2x + 2 1) Cho hàm số y =
C và đường thẳng (d ) có phương trình y = 2
− x + m với m là tham số. x − có đồ thị ( ) 1
Tìm m để đường thẳng (d ) cắt đồ thị (C ) tại hai điểm A và B phân biệt sao cho AB = 5 . 2) Cho hàm số 4 2
y = x − 2mx + m −1 có đồ thị (C
với m là tham số. Tìm m để đồ thị (C có 3 điểm cực m ) m )
trị là 3 đỉnh của tam giác vuông cân.
Câu II. (2,0 điểm)
1) Một nhóm 15 học sinh gồm 6 học sinh lớp A, 5 học sinh lớp B, 4 học sinh lớp C. Lấy ngẫu nhiên 7 học
sinh trong nhóm trên. Tính xác suất để 7 học sinh lấy ra có đủ cả 3 lớp và số học sinh lớp B bằng số học sinh lớp C. 3 2
x + 3x − 4x +1 2) Giải phương trình: 2 = x − x +1 . 2 x + 3
Câu III. (2,0 điểm) 3 2
2y + 6y + 7y + 3+
(3− 2x) x − 2 = 0
1) Giải hệ phương trình: . 2
y + 2y + 4y + 3 = 3+ 7 − x
2) Cho tam giác ABC vuông cân tại A có trọng tâm G; gọi E, H lần lượt là trung điểm của AB, BC. D là điểm
đối xứng với H qua A, I là giao điểm của đường thẳng AB và đường thẳng CD. Biết D( 1 − ;− ) 1 , đường thẳng
IG có phương trình 6x − 3y − 7 = 0 và điểm E có hoành độ bằng 1. Tìm tọa độ các đỉnh của tam giác ABC.
Câu IV. (3,0 điểm)
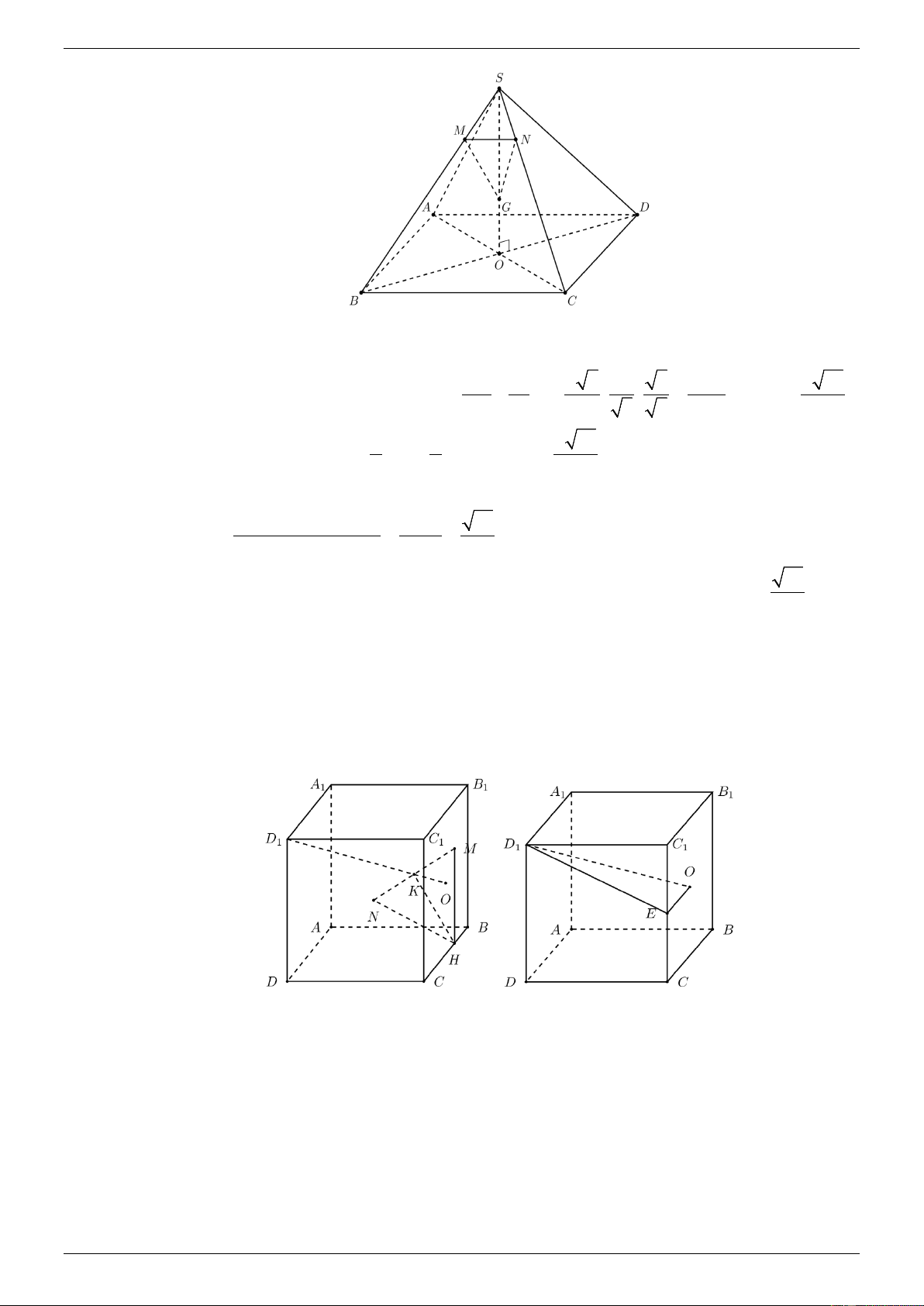
1) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa mặt phẳng (SAB) và mặt phẳng ( ABCD) bằng 60°.
a) Tính thể tích khối chóp S.ABCD theo a. 1
b) Gọi G là trọng tâm của tam giác SAC, M là điểm thuộc cạnh SB sao cho SM =
SB . Tính góc giữa hai 4
đường thẳng GM và BC.
2) Cho hình lập phương ABC .
D A B C D có cạnh bằng a . Đường thẳng d đi qua D và tâm O của hình vuông 1 1 1 1 1
BCC B . Đoạn thẳng MN có trung điểm K thuộc đường thẳng d, biết M thuộc mặt phẳng (BCC B , N thuộc 1 1 ) 1 1
mặt phẳng ( ABCD) . Tìm giá trị nhỏ nhất của độ dài đoạn thẳng MN.
Câu V. (1,0 điểm) 2 2 3 a b 4c
Cho a, b, c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức: P = + + ( . a + b)2
(b + c)2 3(c + a)3
--------------- HẾT ---------------
Giám thị coi thi không giải thích gì thêm./.
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HSG NĂM HỌC 2022-2023 ĐÁP ÁN CHI TIẾT
Câu 1. (2 điểm) + 1) Cho hàm số 2x 2 y =
có đồ thị (C) và đường thẳng (d ) có phương trình y = 2 − x + m x −1
với m là tham số. Tìm m để đường thẳng (d ) cắt đồ thị (C) tại hai điểm A và B phân biệt sao cho AB = 5 . Lời giải
Điều kiện x ≠ 1. +
Xét phương trình hoành độ giao điểm 2x 2 2 = 2
− x + m ⇔ 2x − mx + m + 2 = 0(x ≠ ) 1 ( ) 1 . x −1
Để đường thẳng (d ) cắt đồ thị (C) tại hai điểm A và B phân biệt thì ( ) 1 phải có hai nghiệm 2
m −8m −16 > 0 m > 4 + 4 2 phân biệt khác 1 ⇔ ⇔ (2).
2.1− m + m + 2 = 4 ≠ 0 m < 4 − 4 2
Với điều kiện (2) thì (d ) cắt đồ thị (C) tại hai điểm A(x − x + m và B(x − x + m B ; 2 B ) A; 2 A ) m x + x = A B phân biệt thỏa mãn 2 . m + 2 x x = A. B 2 2 Vì độ dài = ⇔ ( m AB x − x = ⇔ x + x − x x = ⇔ − m + = B A )2 ( A B )2 5 5 5 2 A. B 1 ( 2) 1 4 m = 2 − 2
⇔ m − 4m −12 = 0 ⇔ . m = 6
Kết hợp với điều kiện (2) ta thấy m = 2 − thỏa mãn.
2) Cho hàm số f (x) 4 2
= x − 2mx + m −1 có đồ thị (C với m là tham số. Tìm m để đồ thị m )
(C có 3 cực trị là 3 đỉnh của tam giác vuông cân. m ) Lời giải Ta có: 3
y′ = 4x − 4mx . x = 0 x = 0 y′ = 0 ⇔ ⇔ 2 x = m x = ± m
Để đồ thị (C có 3 cực trị ⇔ y′ = 0 có 3 nghiệm phân biệt ⇔ m > 0 . m )
Với m > 0 thì đồ thị (C có 3 điểm cực trị lần lượt là A(0;m − ) 1 ; B( 2
− m;−m + m − ) 1 ; m ) C ( 2
m;−m + m − ) 1 .
TÀI LIỆU ÔN THI HSG Trang 3
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HSG NĂM HỌC 2022-2023 Ta có: AB = ( 2
− m −m ) AC = ( 2 ; ; m;−m ) 2 4 A . B AC = 0
−m + m = 0
Để tam giác ABC vuông cân tại A ⇔ ⇔ ⇔ m =1 2 4 2 4 AB = AC
m + m = m + m
Kết luận: m =1 thỏa mãn yêu cầu bài toán.
Câu 2. (2.0 điểm)
1) Một nhóm 15 học sinh gồm 6 học sinh lớp A, 5 học sinh lớp B, 4 học sinh lớp C. Lấy ngẫu
nhiên 7 học sinh trong nhóm trên. Tính xác suất để 7 học sinh lấy ra có đủ cả 3 lớp và số học
sinh lớp B bằng số học sinh lớp C. Lời giải
Số phần tử không gian mẫu: n(Ω) 7 = C = 6435 15
Gọi A là biến cố : “ 7 học sinh lấy ra có đủ cả 3 lớp và số học sinh lớp B bằng số học sinh lớp C” .
TH1: 3 học sinh lớp B, 3 học sinh lớp C, 1 học sinh lớp A: 3 3 1
C .C .C = 240 (cách chọn) 5 4 6
TH2: 2 học sinh lớp B, 2 học sinh lớp C, 3 học sinh lớp A: 2 2 3
C .C .C =1200 (cách chọn) 5 4 6
TH3: 1 học sinh lớp B, 1 học sinh lớp C, 5 học sinh lớp A: 1 1 5
C .C .C =120 (cách chọn) 5 4 6
n( A) = 240 +1200 +120 =1560
Xác suất của biến cố A là: P( A) 1560 8 = = . 6435 33 3 2
2) Giải phương trình x + 3x − 4x +1 2 = x − x +1 . 2 x + 3 Lời giải Điều kiện 2
x − x +1≥ 0 ⇔ x ∈ . Ta có 3 2
x + 3x − 4x +1 2 = x − x +1 2 x + 37x+8 2 ⇔ x + 3− = x − x +1 2 x + 3 2 7x + 8
⇔ x + 3− x − x +1 = (1) 2 x + 3 Xét phương trình 2
x + 3+ x − x +1 = 0 2
⇔ x − x +1 = −x − 3 −x − 3 ≥ 0 ⇔ 2 2
x − x +1 = x + 6x + 9 x ≤ 3 − ⇔ 7x = 8 − x ≤ 3 − ⇔ 8 x = − (l) 7 Do đó 2
x + 3+ x − x +1 ≠ 0 với mọi x∈ . Suy ra Trang 4
TÀI LIỆU ÔN THI HSG
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HSG NĂM HỌC 2022-2023 2 2
(x + 3) − (x − x +1) 7x + 8 (1) ⇔ = 2 2
x + 3+ x − x +1 x + 3 7x + 8 7x + 8 ⇔ = 2 2
x + 3+ x − x +1 x + 3 1 1 ⇔ (7x + 8) − = 0 2 2
x + 3 + x − x +1 x + 3 7x + 8 = 0 ⇔ 2 2
x + 3+ x − x +1 = x + 3 8 x = − ⇔ 7 2 2
x − x +1 = x − .x (*) u ≥ 0 Đặt 2
u = x − x . Ta có (*) ⇒ u +1 = u ⇔ 1 5 u + ⇔ = . 2 u +1 = u 2 Suy ra 2 1+ 5 1± 3+ 2 5 x − x = ⇔ x = . 2 2
Vậy tập nghiệm của phương trình đã cho là 8 1± 3+ 2 5 S ; = − . 7 2
Câu 3. (2.0 điểm) 3 2
2y + 6y + 7y + 3+ (3− 2x) x − 2 = 0 (1)
1) Giải hệ phương trình: . 2
y + 2y + 4y + 3 = 3+ 7 − x (2) Lời giải
Điều kiện : 2 ≤ x ≤ 7 . Ta có ( ) ⇔ ( 3 2 1
2 y + 3y + 3y + )
1 + y +1 = (2x −3) x − 2 ⇔ ( y + )3 2
1 + y +1 = 2(x − 2) x − 2 + x − 2 ⇔ ( y + ) + y + = ( x − )3 3 2 1 1 2 2 + x − 2 (3) .
Xét hàm số f (t) 3
= 2t + t với t ∈ . Ta có: f ′(t) 2
= 6t +1 > 0, t
∀ ∈ nên f (t) đồng biến trên . 2
x = y + 2y + 3 *
Do (3) ⇔ f ( y + ) 1 = f ( x − 2) ( )
⇔ y +1 = x − 2 ⇔ . y ≥ 1 −
Thay (*) vào (2), ta được 2
y + 2y + 4y + 3 = 3+ 7 − x 2 2
⇔ y −1+ 2y + 4y + 3 − 3 = 4 − y − 2y −1 2 2 2y + 4y − 6 3− y − 2 ⇔ −1 y y + = 2 2 2y + 4y + 3 + 3
4 − y − 2y +1 ( y − ) 1 (2y + 6) ( y − ) 1 ( y + 3) ⇔ y −1+ = − 2 2 2y + 4y + 3 + 3
4 − y − 2y +1 ⇔ ( y − ) 2y + 6 y + 3 1 1+ +
= 0 ⇔ y =1⇒ x = 6 . 2 2 2y 4y 3 3 4 y 2y 1 + + + − − +
TÀI LIỆU ÔN THI HSG Trang 5
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HSG NĂM HỌC 2022-2023 Vì với y ≥ 1 − ta có 2y + 6 y + 3 1+ + > 0 2 2 2y + 4y + 3 + 3
4 − y − 2y +1
Vậy nghiệm của hệ phương trình là ( ; x y) = (6; ) 1 .
2) Cho tam giác ABC vuông cân tại A có trọng tâm G ; gọi E, H lần lượt là trung điểm của
AB, BC . D là điềm đối xứng với H qua A , I là giao điểm của đường thẳng AB và đường
thẳng CD . Biết D( 1; − 1
− ) , đường thẳng IG có phương trình 6x − 3y − 7 = 0 và điểm E có
hoành độ bằng 1. Tìm tọa độ các đỉnh của tam giác ABC . Lời giải
Gọi N là điểm đối xứng với E qua A , M là điểm đối xứng của A qua D .Khi đó I là trọng
tâm của tam giác ACM . Ta có CG CI 2 =
= ⇒ IG / /DE . IG có véc tơ chỉ phương u = (1;2) . CE CD 3
Giả sử E (1; y +
⇒ DE = 2; y +1 . Mà y 1 2 0 IG / /DE ⇒
= ⇒ y = 3 ⇒ E 1;3 . 0 ( ) 0 ) ( 0 ) 2 1
B(2 − a ;6 −b 1 1 ) Giả sử tọa + + A(a b ) C ( 5a 2 5b 2 ; 5a ;5b 4 G ; ⇒ ⇒ − ⇒ . 1 1 ) 1 1 1 1 H (2a 1;2b 1 3 3 + + 1 1 )
Do G ∈GI ⇒ 2a − b −1 = 0 ⇒ b = 2a −1 1 .Ta có AE = (1− a ;3−b , AC = 4a ;4b − 4 . 1 1 ) ( 1 1 ) 1 1 1 1 ( )
Do tam giác ABC vuông tại A nên ta có
AE.AC = 0 ⇒ 4a 1− a + 4b − 4 3− b = 0 ⇔ a 1− a + b −1 3− b = 0 2 . 1 ( 1 ) ( 1 )( 1 ) 1 ( 1 ) ( 1 )( 1 ) ( ) a = 1 1
Từ (1) và (2) ta được a 1 a 2a 2 4 2a 0 a 1 8 5a 0 − + − − = ⇔ − − = ⇔ . 1 ( 1 ) ( 1 )( 1 ) ( 1 )( 1 ) 8 a = 1 5
Với a =1⇒ b =1⇒ A 1;1 , B 1;5 ,C 5;1 . 1 1 ( ) ( ) ( ) Với 8 11 8 11 2 19 a b A ; , B ; = ⇒ = ⇒ ,C 8;7 . 1 1 ( ) 5 5 5 5 5 5 Trang 6
TÀI LIỆU ÔN THI HSG
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HSG NĂM HỌC 2022-2023
Câu 4. (3.0 điểm)
1) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , góc giữa mặt phẳng (SAB) và
mặt phẳng (ABCD) bằng 60° .
a) Tính thể tích khối chóp S.ABCD theo a .
b) Gọi G là trọng tâm của tam giác SAC , M là điểm thuộc cạnh SB sao cho 1 SM = SB . 4
Tính góc giữa hai đường thẳng GM và BC . Lời giải
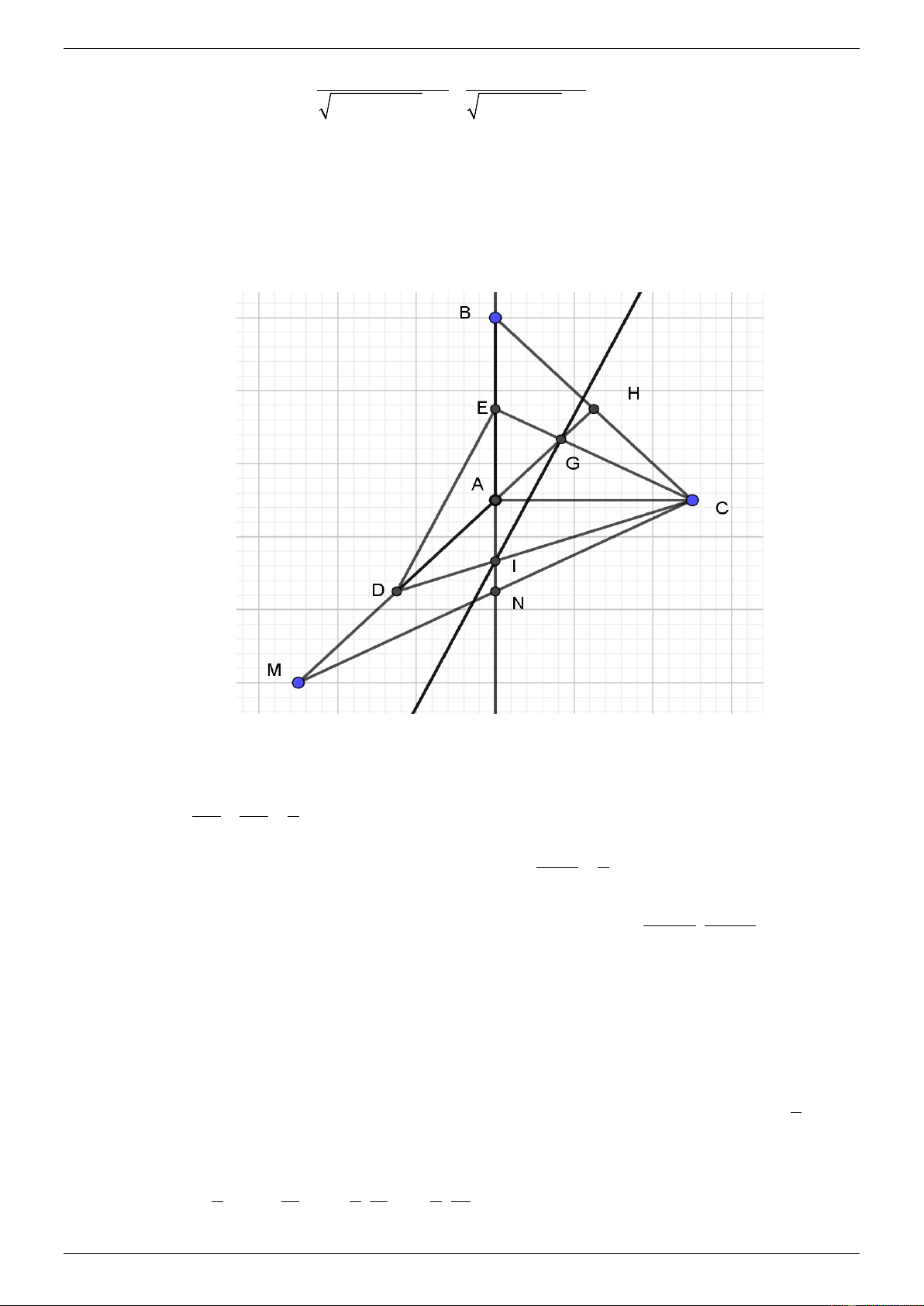
a) Tính thể tích khối chóp S.ABCD theo a .
Gọi O là tâm của hình vuông ABCD , theo giả thiết ta có SO ⊥ (ABCD) ⇒ SO ⊥ A . B (1)
Gọi I là trung điểm của AB . Suy ra 1 a
OI = AD = và OI ⊥ A . B (2) 2 2
Từ (1) và (2) ta có AB ⊥ SIO ⇒ ( SAB ABCD ) = ( ) ( ),( ) SIO . Từ giả thiết ta có SIO 60° ° a = , do đó 3
SO = IO ⋅ tan 60 = . 2 3
Vậy thể tích khối chóp 1 1 a 3 a 3 S.ABCD bằng 2
V = ⋅ SO ⋅ S = ⋅ ⋅ a = ABCD . 3 3 2 6
b) Gọi G là trọng tâm của tam giác SAC , M là điểm thuộc cạnh SB sao cho 1 SM = SB . 4
Tính góc giữa hai đường thẳng GM và BC .
Qua M vẽ đường thẳng song song với BC , cắt SC tại N , khi đó ta có 1 SN = SC. 4 Ta có 2 2 3a a a 5 1 a 5 SB a = + = ⇒ SM = SB = và 2 3 SG = SO = , do đó 4 2 2 4 8 3 3 SO 3 cosGSM = = . SB 5
TÀI LIỆU ÔN THI HSG Trang 7
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HSG NĂM HỌC 2022-2023
Áp dụng định lý côsin trong tam giác GMN ta có = + − ⋅ 2 2 2 2 2 2 5a a a 5 a 3 31a a 93 MG SM SG 2SM SG cosGSM = + − 2⋅ ⋅ ⋅ = ⇒ MG = . 64 3 8 3 5 192 24 Xét tam giác a a GMN có 1 MN = BC = , 93 GM = GN = . 4 4 24
Áp dụng định lý côsin ta có 2 2 2
MG + MN − GN MN 93 cosGMN = = = > 0 2MG ⋅ MN 2MG 31
Vì MN BC và góc GMN nhọn nên (GM BC) = (GM MN ) = 93 cos , cos , cosGMN = . 31
2) Cho hình lập phương ABC .
D A B C D có cạnh bằng D và tâm 1 1 1 1
a . Đường thẳng d đi qua 1
O của hình vuông BCC B . Đoạn thẳng 1 1
MN có trung điểm K thuộc đường thẳng d , biết M
thuộc mặt phẳng (BCC B ),
ABCD . Tìm giá trị nhỏ nhất của độ dài 1 1
N thuộc mặt phẳng ( ) đoạn thẳng MN . Lời giải
Gọi H là hình chiếu vuông góc của M trên BC .
Vì hai mặt phẳng (ABCD) và (BCC B ) vuông góc với nhau và cắt nhau theo giao tuyến 1 1 BC
nên ta có MH ⊥ (ABCD) ⇒ MH ⊥ HN.
Tam giác MHN vuông tại H , K là trung điểm cạnh huyền MN nên ta có MN = 2KH.
Do đó MN nhỏ nhất khi và chỉ khi KH nhỏ nhất, tức là khi KH là đoạn vuông góc chung của
hai đường thẳng d và BC .
Gọi E là trung điểm CC , khi đó BC OE cho nên 1
d(D O, BC = d BC,(D OE) = d C,(D OE) . 1 ) ( 1 ) ( 1 ) Trang 8
TÀI LIỆU ÔN THI HSG
NHÓM TOÁN VDC&HSG THPT
ĐỀ THI HSG NĂM HỌC 2022-2023
Vì OE BC và BC ⊥ (CDD C ) nên (CDD C ) ⊥ (D OE) , do đó 1 1 1 1 1 d( ⋅
C,(D OE)) = d(C, D E) = d(C , D E) C D C E a 1 1 1 = = . 1 1 1 1 2 2 C D + C E 5 1 1 1
Khi KH là đoạn vuông góc chung của D O và
M ∈(BCC B ) thoả mãn 1 BC , khi đó với 1 1
MH ⊥ BC và KH = KM , ta lấy N sao cho K là trung điểm MN . Suy ra tam giác MHN vuông tại N .
Vì MH ⊥ (ABCD) và MH ⊥ HN nên N ∈(ABCD) .
Vậy giá trị nhỏ nhất của độ dài đoạn thẳng a MN bằng 2 . 5
Câu 5. (1.0 điểm)
Cho a,b,c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức: 2 2 3 a b 4c P = + + .
(a +b)2 (b + c)2 3(c + a)3 Lời giải 2 2 3 a b 4c 1 1 4 Ta có P = + + = + + .
(a +b)2 (b + c)2 3(c + a)3 2 2 3 1 b 1 c 31 a + + + a b c b c a
Đặt x = , y = , z = ; x, y, z > 0; xyz =1. a b c 2 1 b 4 Khi đó P = + + ( .
1+ x)2 (1+ y)2 3(1+ z)3 1 1 1
Ta đi chứng minh bất đẳng thức phụ: + ≥ .
(1+ x)2 (1+ y)2 1+ xy Thật vậy:
Theo bất đẳng thức Bunhiacopxki cho 2 số ta có: ( + )2 ≤ ( 2 2 + )( 2 2 ax by a b x + y ). 2 + Từ đó( + )2 1 = 1.1+ . x ≤ (1+ ) 1 x + = (1+ ) x y x xy xy xy . y y y Hay 1 y ≥ . Tương tự 1 x ≥ .
(1+ x)2 (1+ xy)(x + y)
(1+ y)2 (1+ xy)(x + y)
Cộng hai bất đẳng thức cùng chiều ta được: 1 1 1 + ≥
(1+ x)2 (1+ y)2 1+ xy
Dấu đẳng thức xảy ra khi x = y =1.
Áp dụng bất đẳng thức trên ta có: 3z (1+ z)2 + 4 1 4 z 4 P ≥ + = + = .
1+ xy 3(1+ z)3 1+ z 3(1+ z)3 3(1+ z)3 2 3z (1+ z)2 + 4 2
Ta đi chứng minh P ≥ ⇔ ≥ ⇔ (z − )2
1 z + 2 ≥ 0 luôn đúng. 3 ( ) 3 3(1+ z) 3
---------- TOANMATH.com ----------
TÀI LIỆU ÔN THI HSG Trang 9
Document Outline
- de-hoc-sinh-gioi-toan-12-cap-tinh-nam-2022-2023-so-gddt-hai-duong
- Đợt-07-HSG-LỚP-12-SỞ-HẢI-DƯƠNG-NĂM-2022-2023