
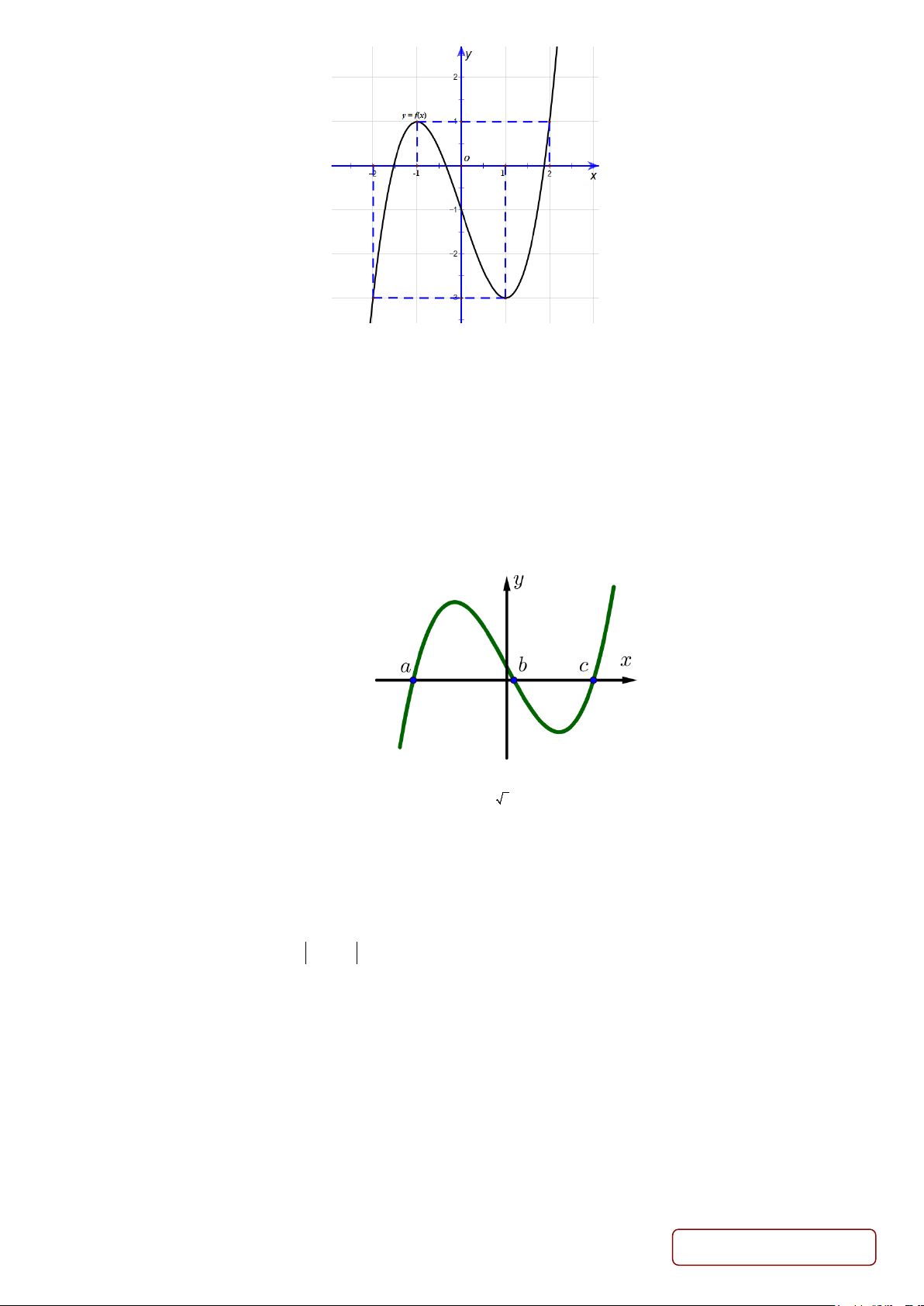











Preview text:
SỞ GD & ĐT THANH HÓA
ĐỀ THI KSCL VÀ CHỌN ĐỘI TUYỂN HSG
TRƯỜNG THCS&THPT THỐNG NHẤT NĂM HỌC 2022 - 2023
Môn: Toán – Lớp 12 Đề chính thức
Thời gian: 90 phút (Không kể thời gian giao đề) Gồm có 6 trang Mã đề thi 235
Câu 1. Tập xác định của hàm số 1 y = là sin x − cos x A. π π π \{k , π k ∈ } . B. \ k2 ,k +
π ∈ . C. \ + k ,
π k ∈ . D. \ + k , π k ∈ 4 2 4
Câu 2. Tìm tập giá trị của hàm số y = 3 sin x − cos x − 2 A. 2; − 3 − − − . B. 3 3; 3 1 . C. [ 4; − 0]. D. [ 2; − 0].
Câu 3. Cho khai triển nhị thức Newton của ( − )2 2 3 n
x , biết rằng n là số nguyên dương thỏa mãn 1 3 5 2n 1 C + + + + = . Hệ số của 7 x + C + C + C + n n n ........ n+ 1024 2 1 2 1 2 1 2 1 bằng A. 2099520 − . B. 414720 − . C. 2099520 . D. 414720 .
Câu 4. Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác đều và có một góc lớn hơn 100° . A. 2 2018C . B. 3 2018C . C. 3 C . D. 3 2018C 896 896 1009 897
Câu 5. Một tổ có 5 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh để làm trực
nhật.Tính xác suất để 3 học sinh được chọn có cả nam và nữ A. 3 . B. 24 . C. 9 . D. 3 . 8 25 11 4 Câu 6. Câu 3.Biết ( 2 lim + 3 + 2 − + )1 a n n n
= , trong đó a là một phân số tối giản. Tính T =3a −b . b b A. T =−13. B. T =13. C. T =1. D. T = −1 u = 1, − u = 3
Câu 7. Cho dãy số (u xác định bởi: 1 2
. Số hạng thứ 7 của dãy là: n ) u = − ∀ ≥ + u u − n n 5 n 6 n , 2 1 1 A. 1023. B. 3261. C. 309. D. 4284
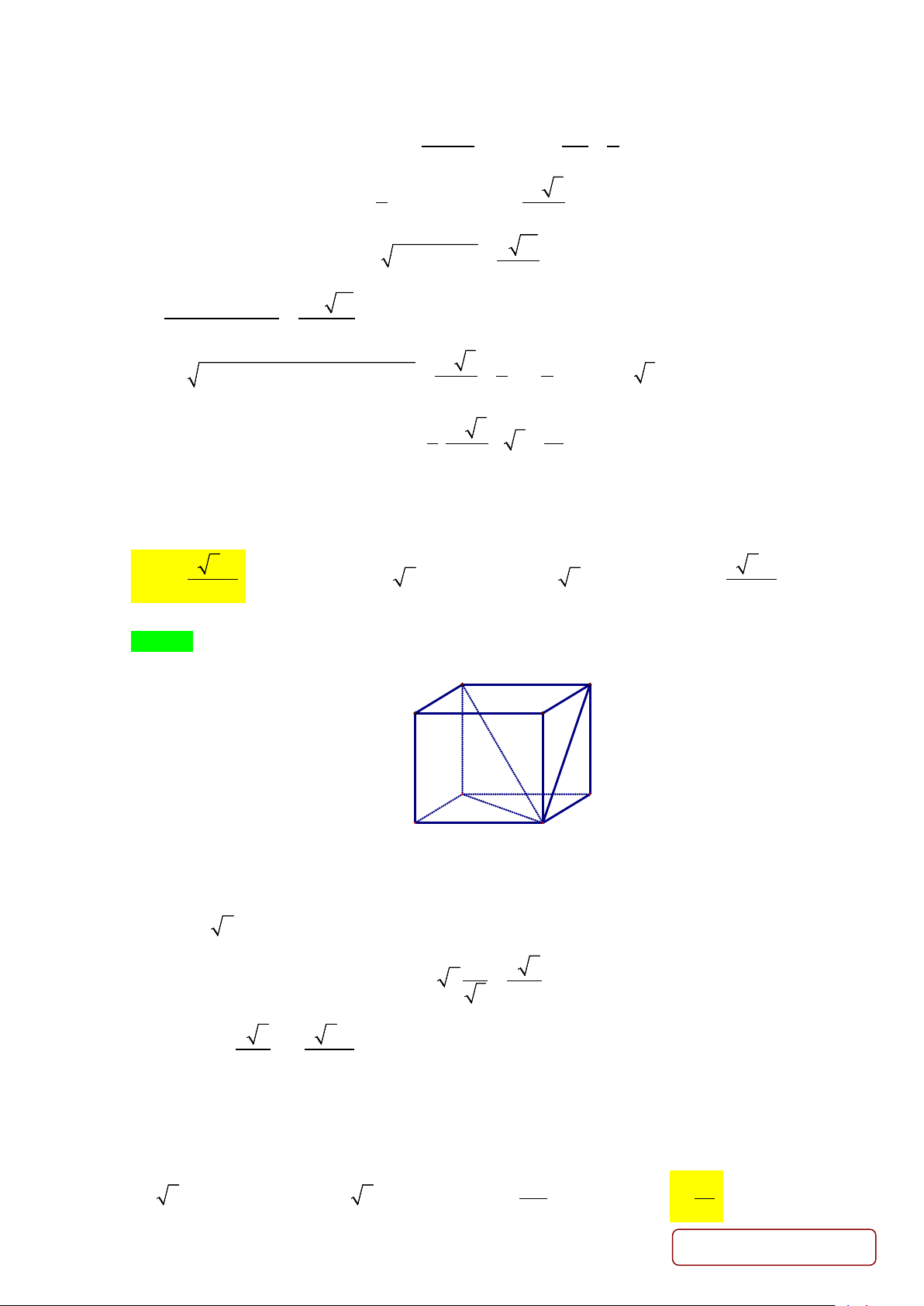
Câu 8. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , SA = SB = a , SC = SD = a 3 . Gọi
E, F lần lượt là trung điểm các cạnh ,
SA SB . Trên cạnh BC lấy M sao cho BM = x ? Tính diện
tích thiết diện của hình chóp với mặt phẳng (MEF ) theo x và a ? A. a 2 2
16x + 8a + a . B. 3a (4x + a 3).C. 3a 2 2
16x + 8a + 3a . D. a 2 2
x −8ax + a . 4 16 16 16
Câu 9. Cho hình chóp tứ giác đều S.ABCD có AB = ,
a SA = a 3 . Gọi G là trọng tâm tam giác SCD .
Góc giữa đường thẳng BG với mặt phẳng ( ABCD) bằng A. 85 arctan . B. 10 arctan . C. 85 arcsin . D. 85 arccos . 17 17 17 17
Câu 10. Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa đường thẳng SA và mặt phẳng
(ABC) bằng 60°. Gọi G là trọng tâm tam giác ABC , tính khoảng cách giữa hai đường thẳng GC và SA . A. a 5 . B. a 5 . C. a 2 . D. a . 10 5 5 5
Câu 11. Cho hàm số 1 3 2
y = − x + 4x − 5x −17 . Phương trình y′ = 0 có hai nghiệm x ; x . Khi đó tổng 3 1 2
x + x bằng: 1 2 A. 8 − . B. 5. C. 5 − . D. 8 . Trang 1/29 - Mã đề 235 2
ax + bx +1, x ≥ 0
Câu 12. Cho hàm số f (x) =
. Khi hàm số có đạo hàm tại x = 0 , hãy tính T = a + 2b . 0
ax − b −1. x < 0 A. T = 4 − .
B. T = 0 . C. T = 6 − . D. T = 4 .
Câu 13. Cho hàm số y = f (x) có đạo hàm là f ′(x) = (x − )2
1 +1. Xét hàm số g (x) f f (x) 1 2 x 2x = − − . 2
Số các nghiệm nguyên của bất phương trình g′(x) ≤ 0 là: A. 1. B. 2 . C. 3. D. 4 − +
Câu 14. Cho đồ thị hàm số (C) 2x 3 : y =
. Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của x −1
(C) với đường thẳng y = x −3.
A. y = −x + 3 và y = −x −1.
B. y = −x − 3 và y = −x +1.
C. y = x − 3 và y = x +1.
D. y = −x + 2 và y = −x +1. Câu 15. Cho hàm số 4
y = x − ( m + ) 2 2 3
4 x + m có đồ thị là (C . Tìm m để đồ thị (C cắt trục hoành tại m ) m )
bốn điểm phân biệt có hoành độ lập thành một cấp số cộng. A. 12 m 12;m − = = . B. m =12. C. 12 m − = . D. 12 m = . 9 9 9 Câu 16. Cho hàm số x −1 y =
. Tính đạo hàm cấp n của hàm số. 2 x − 5x + 6 n n n n A. (n) ( 1) − .n! ( 1) − .n! y − − = 2. − B. (n) ( 1) .n! ( 1) .n! y = 2. + n 1 + n 1 (x − 3) (x − 2) + n 1 + n 1 (x − 3) (x − 2) + n n n n C. (n) ( 1) − .n! ( 1) − .n! y − − = 2. − D. (n) ( 1) .n! ( 1) .n! y = 2. −
(x − 3)n (x − 2)n n 1 + n 1 (x − 2) (x − 3) +
Câu 17. Cho hàm số y = f (x) có đạo hàm trên . Gọi (C , (C , (C lần lượt là đồ thị của các hàm số 3 ) 2 ) 1 )
y = f (x) , y = g (x) = f f (x)
, y = h( x) = f ( 2 x + )
1 . Biết rằng f (2) = 5, f ′(2) = 2, g′(2) = 4 . Hãy tính h′(2). A. h′(2) = 2. B. h′(2) = 4.
C. h′(2) = 6 . D. h′(2) = 8. 3 Câu 18. Hàm số x 2 y = −
+ x − mx +1 nghịch biến trên khoảng (0;+∞) khi và chỉ khi 3
A. m∈[1;+∞) .
B. m∈(1;+∞) .
C. m∈[0;+∞) .
D. m∈(0;+∞) .
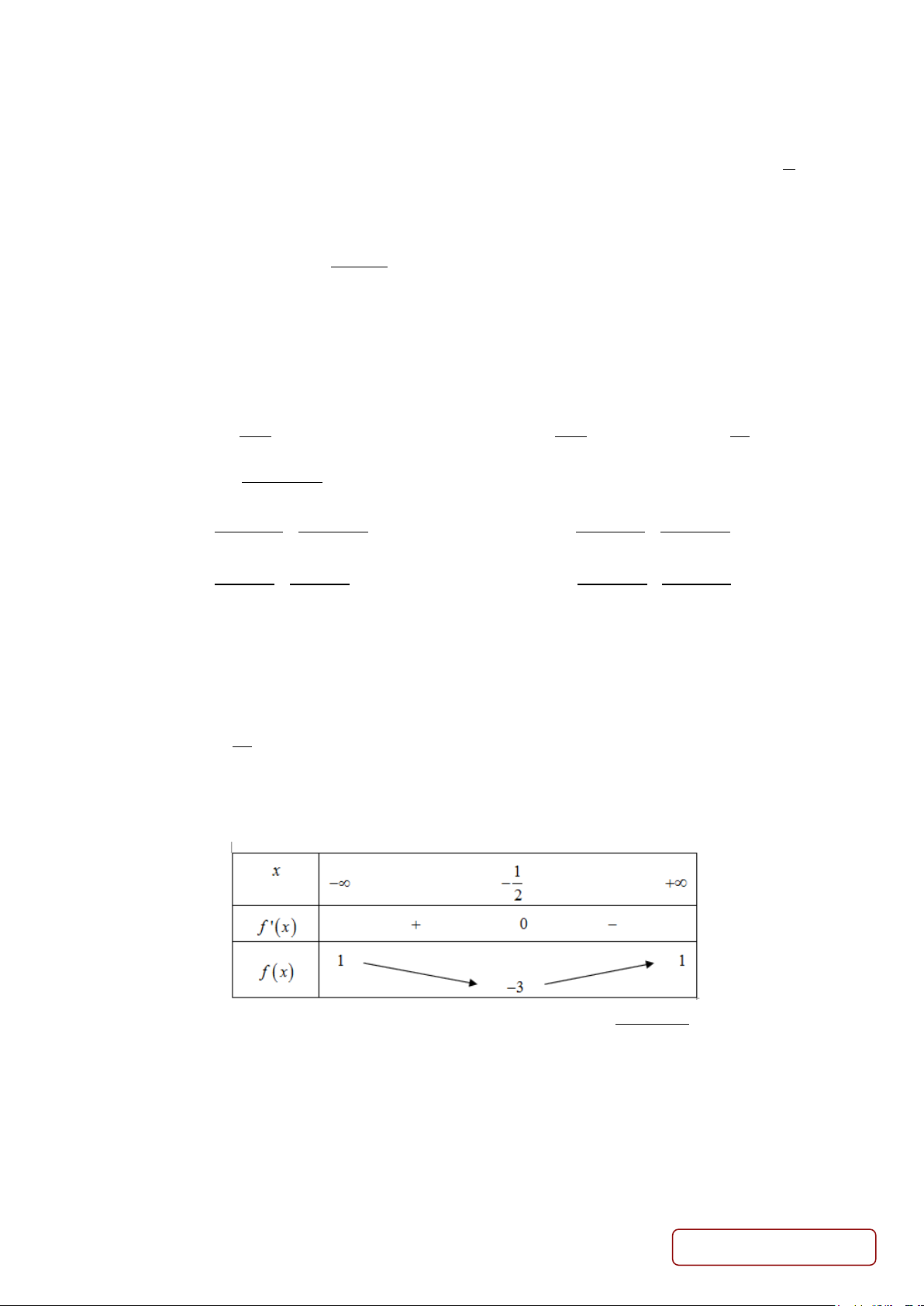
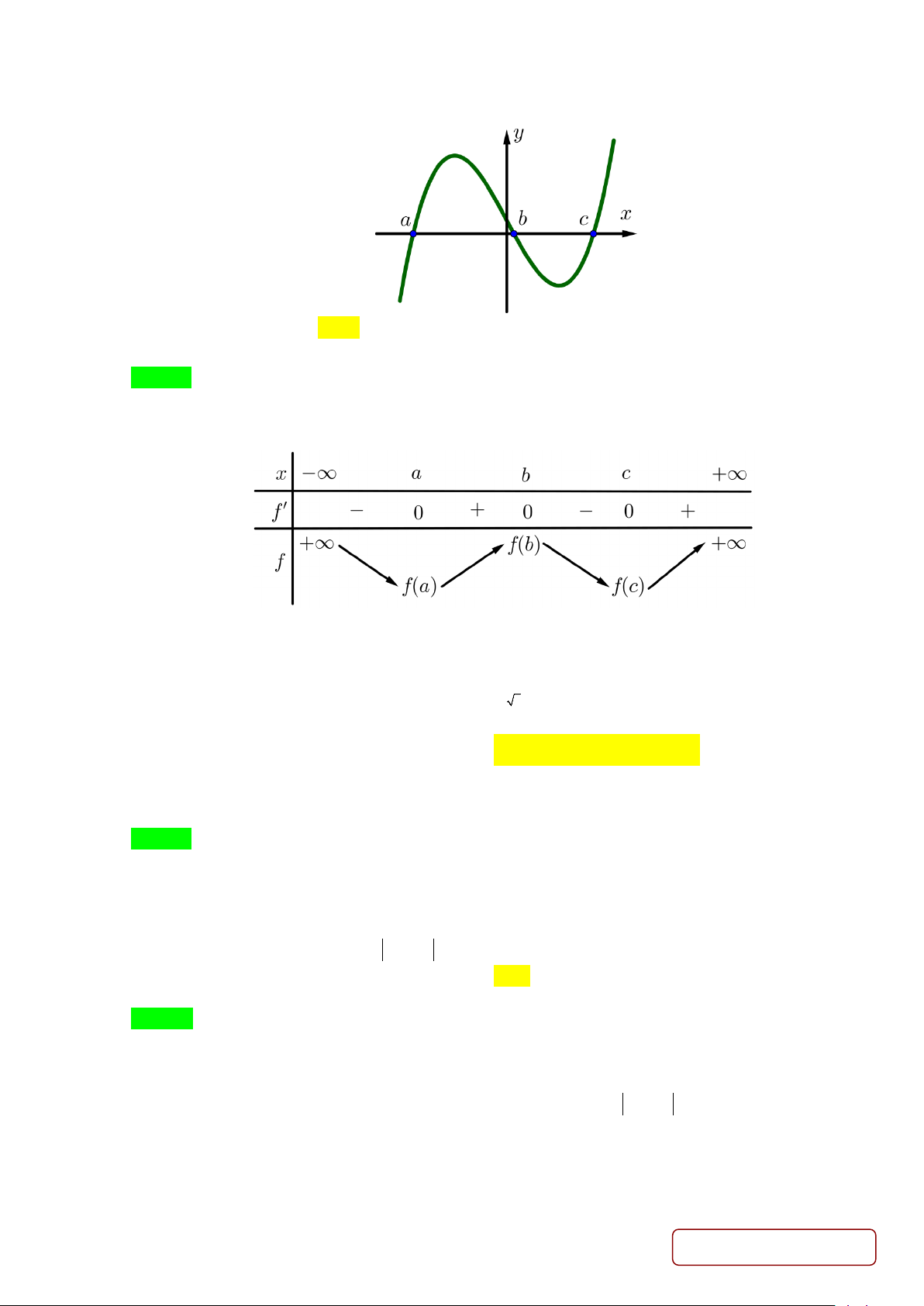
Câu 19. Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là 2 f (x) −1 A. 0 . B. 1. C. 2 . D. 3.
Câu 20. Cho hàm số y = f (x) liên tục trên R và có đồ thị như hình bên. Trang 2/29 - Mã đề 235
Phương trình f (2sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn [ π
− ;π ] khi và chỉ khi A. m∈{ 3 − ; } 1 . B. m∈( 3 − ; ) 1 . C. m∈[ 3 − ; ) 1 . D. m∈( 3 − ; ] 1 .
Câu 21. Cho hàm số f (x) = ( − x )2019 2 1
. Khẳng định nào sau đây là đúng?.
A. Hàm số đồng biến trên .
B. Hàm số đồng biến trên ( ;0 −∞ ).
C. Hàm số nghịch biến trên ( ;0 −∞ ).
D. Hàm số nghịch biến trên .
Câu 22. Cho hàm số = ( ) 4 3 2
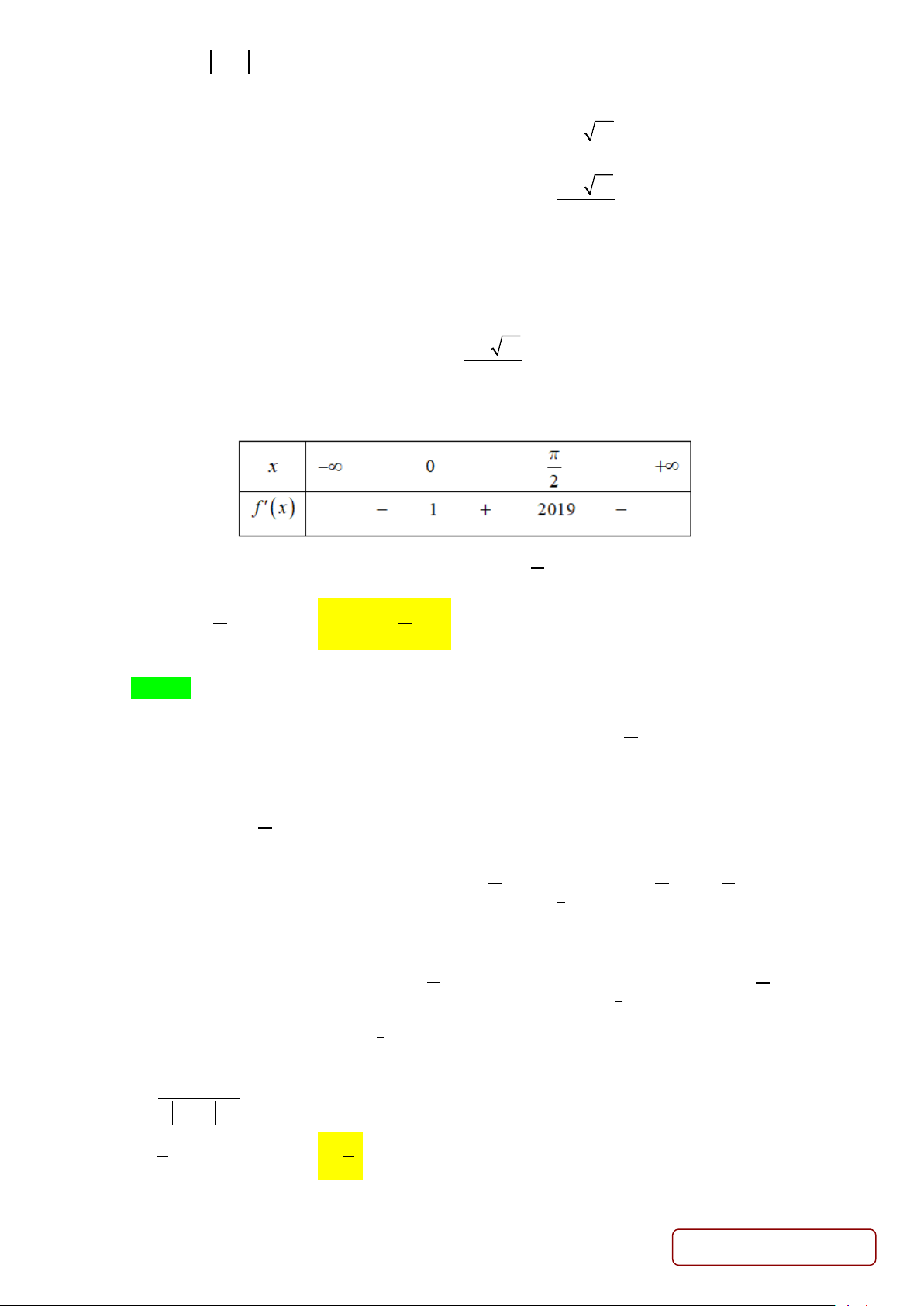
y f x = mx + nx + px + qx + r và hàm số y = f ′(x) có đồ thị như hình vẽ bên. Biết
f (a) > 0 , hỏi đồ thị hàm số y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm? A. 1. B. 2 . C. 3. D. 4 .
Câu 23. Tìm tập xác định D của hàm số y = (x − x − ) 2 4 2 3 4 ?
A. D = (−∞;− ) 1 ∪(4;+∞) .
B. D = (−∞; 2 − ) ∪(2;+∞) .
C. D = (−∞; 2 − ]∪[2;+∞) .
D. D = (−∞;+∞) .
Câu 24. Giả sử phương trình 2
log x − m + 2 log x + 2m = 0 có hai nghiệm thực phân biệt x , x thỏa mãn 2 ( ) 2 1 2
x + x = 6 . Giá trị của biểu thức − là 1 2 x x 1 2 A. 3. B. 8. C. 2. D. 4
Câu 25. Một người nhận hợp đồng dài hạn làm việc cho một công ty với mức lương khởi điểm của mỗi
tháng trong 3 năm đầu tiên là 6 triệu đồng /tháng. Tính từ ngày đầu tiên làm việc, cứ sau đúng 3 năm liên
tiếp thì tăng lương 10% so với mức lương một tháng người đó đang hưởng . Nếu tính theo hợp đồng thì tháng
đầu tiên của năm thứ 16 người đó nhận được mức lương là bao nhiêu ? A. ( )4
6. 1,1 triệu đồng. B. ( )6
6. 1,1 triệu đồng. C. ( )5
6. 1,1 triệu đồng. D. ( )16 6. 1,1 triệu đồng.
Câu 26. Cho ba số a + log 3, a + log 3, a + log 3 theo thứ tự lập thành một cấp số nhân. Công bội của cấp 2 4 8 số nhân đó bằng Trang 3/29 - Mã đề 235 A. 1. B. 1 . C. 1 . D. 1 . 4 2 3
Câu 27. Tích các nghiệm của phương trình log (x + 2) + log (x − 5)2 + log 8 = 0 2 4 1 là 2 A. 12 − . B. 18 − . C. 36. D. 2 − .
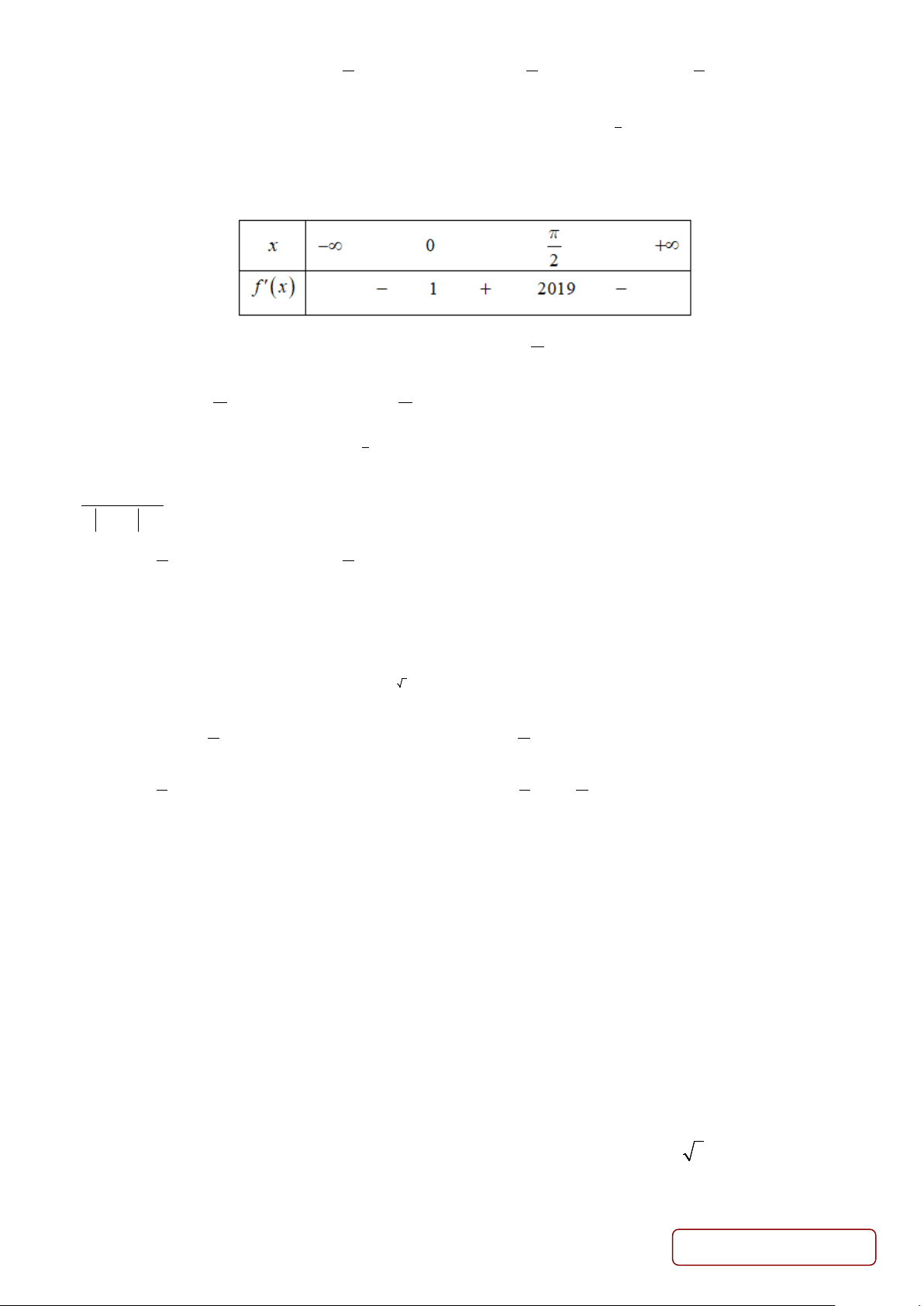
Câu 28. Cho hàm số y = f (x) liên tục và có đạo hàm trên . Hàm số y = f ′(x) có bảng xét dấu như sau Bất phương trình ( ) cos x f x > e
+ m có nghiệm x 0; ∈ khi và chỉ khi 2
A. m f ≤ − 1.
B. m < f − 1.
C. m ≥ f (0) − e .
D. m ≤ f (0) − e . 2 2 1
Câu 29. Cho hàm số ( ) = log + 3x −3x f x x
. Tính tổng bình phương các giá trị của tham số m để phương trình 1 f + f ( 2
x − 2x + 2) = 0
có đúng 3nghiệm phân biệt bằng 2 x m 1 − + A. 5 . B. 7 . C. 3. D. 2 . 2 2
Câu 30. Hàm số = ( 2 − + ) 1 x y x x e có đạp hàm A. ′ = (2 − ) 1 x y x e .
B. ′ = ( 2 − ) x y x x e .
C. ′ = ( 2 + ) x y x x e . D. ′ = ( 2 + ) 1 x y x e .
Câu 31. Tìm nghiệm của bất phương trình 2 log x 2 2log2 2 x + x − 20 ≤ 0 A. 1 0 < x ≤
B. 1 ≤ x ≤ 2 2 2
C. 1 ≤ x ≤ 2 D. 1 1 ≤ x ≤ . 3 3 2
Câu 32. Xét các số nguyên dương a,b sao cho phương trình 2
a ln x + bln x + 5 = 0 có hai nghiệm phân biệt
x , x và phương trình 2
5log x + blog x + a = 0 có hai nghiệm phân biệt x , x thỏa mãn x x > x x . Tìm giá 1 2 3 4 1 2 3 4
trị nhỏ nhất S của S = 2a + 3b min A. S = 30. B. S = 25. C. S = 33. D. S =17 . min min min min
Câu 33. Khối đa diện nào sau đây có các mặt không phải là tam giác đều?
A. Khối bát diện đều.
B. Khối mười hai mặt đều.
C. Khối tứ diện đều.
D. Khối hai mươi mặt đều.
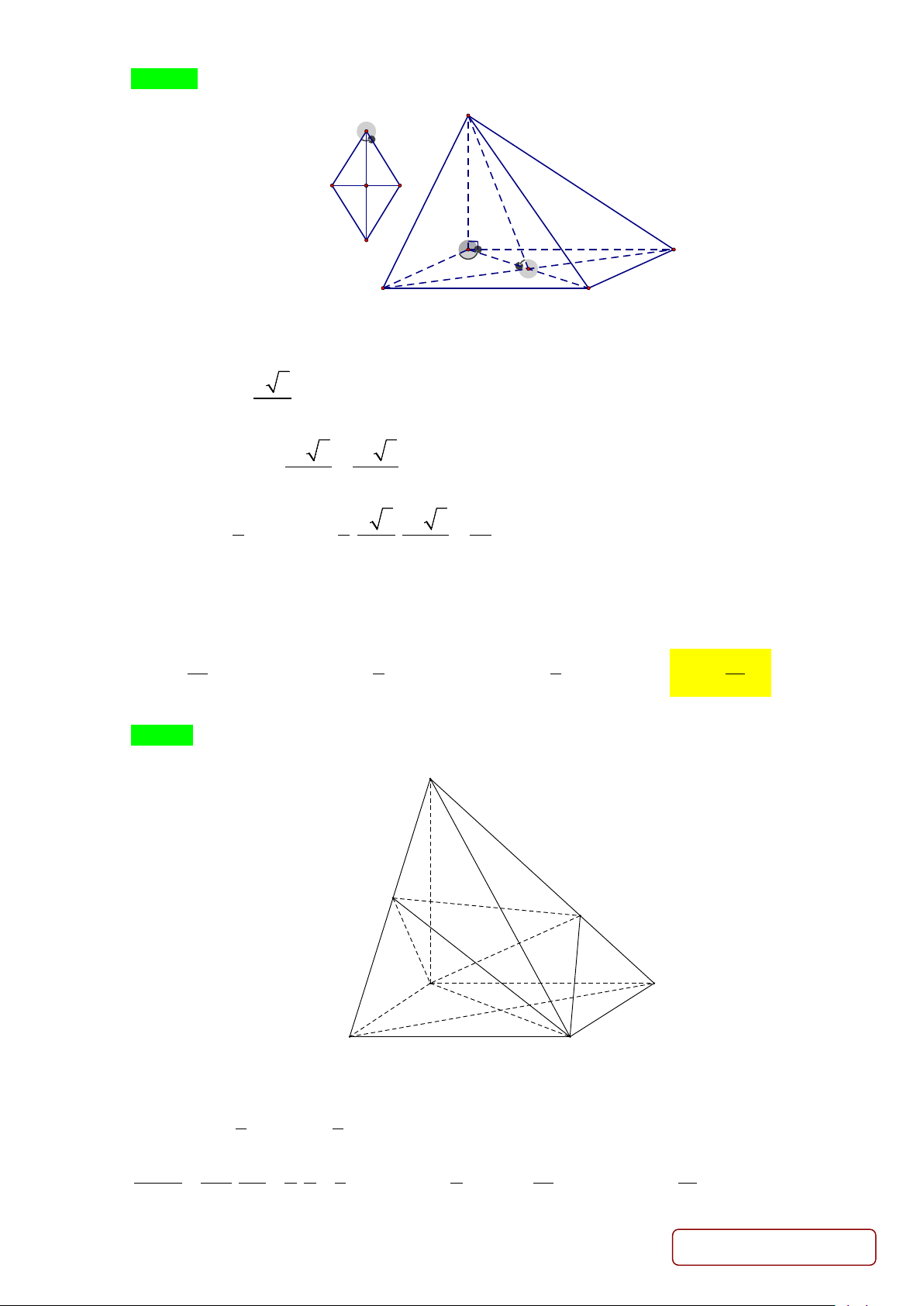
Câu 34. Mệnh đề nào sao đây đúng?
A. Hình bát diện đều có 8 đỉnh, 12 cạnh và 6 mặt.
B. Hình bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
C. Hình bát diện đều có 6 đỉnh, 8 cạnh và 8 mặt.
D. Hình bát diện đều có 8 đỉnh, 12 cạnh và 8 mặt.
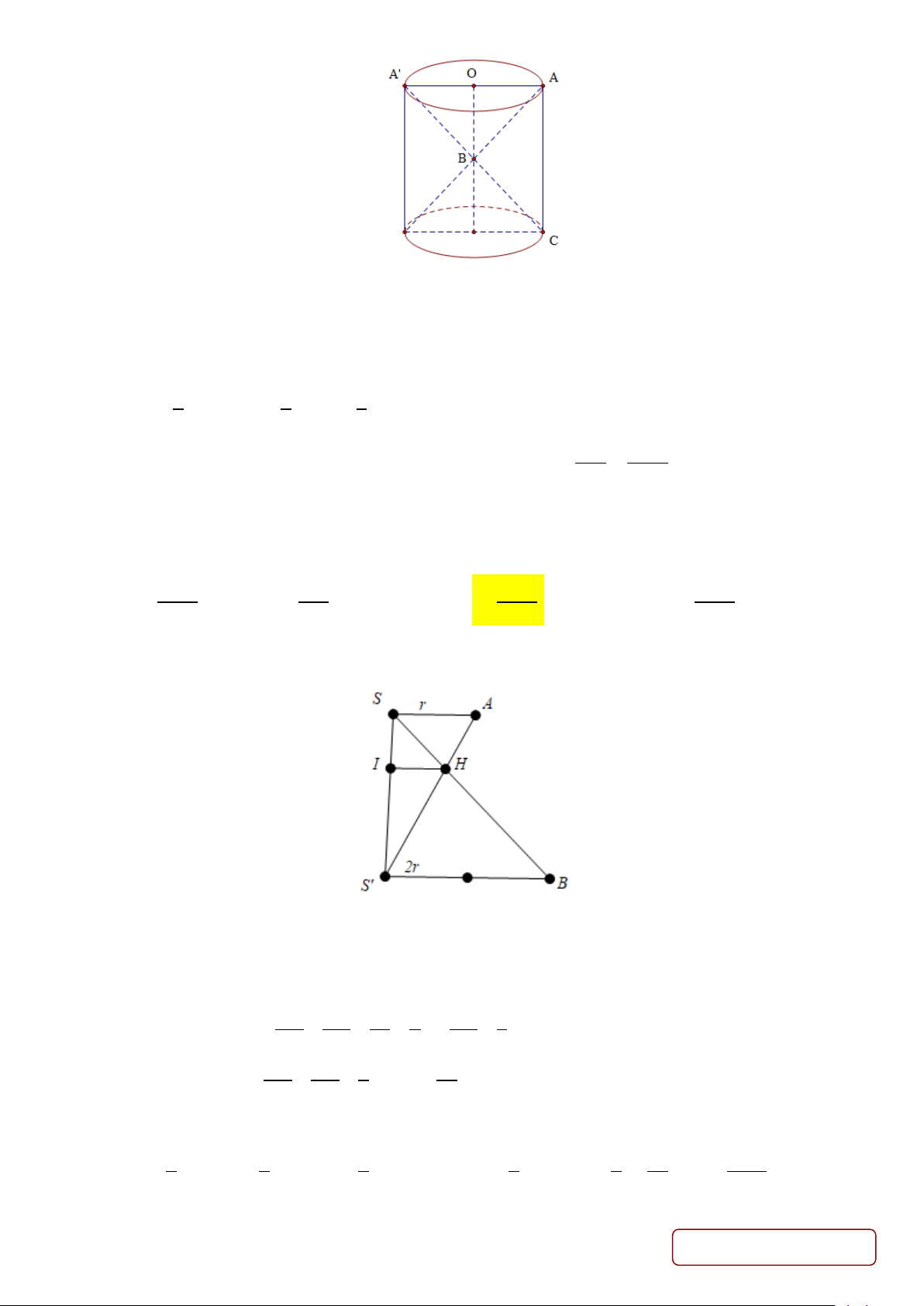
Câu 35. Cho hình chóp S.ABC có đáy là tam giác cân tại 0 , A 120 BAC =
và BC = a 3. Biết
SA = SB = SC = 2 .
a Tính thể tích V của khối chóp S.ABC . Trang 4/29 - Mã đề 235 3 3 3 A. a . B. 3 a . C. a . D. a . 4 2 3
Câu 36. Tính thể tích V của khối lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ biết độ dài cạnh đáy bằng 2a đồng thời
góc tạo bởi A′C và đáy ( ABCD) bằng 30° . 3 3 A. 8 6a V = . B. 8 6a 3 V = 24 6a . C. 3 V = 8 6a . D. V = . 3 9
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a . Góc A bằng 0
60 , O là tâm hình thoi,
SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng 0
45 . Tính theo a thể tích khối chóp S.ABCD . 3 3 A. 3 2a . B. 3 3 2a . C. 3a . D. a . 8 4
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a và SA vuông góc với đáy. Gọi
M là trung điểm của SB , N là điểm thuộc SD sao cho SN = 2ND . Tính thể tích khối tứ diện ACMN . A. 1 3 V = a . B. 1 3 V = a . C. 1 3 V = a . D. 1 3 V = a . 36 6 8 12
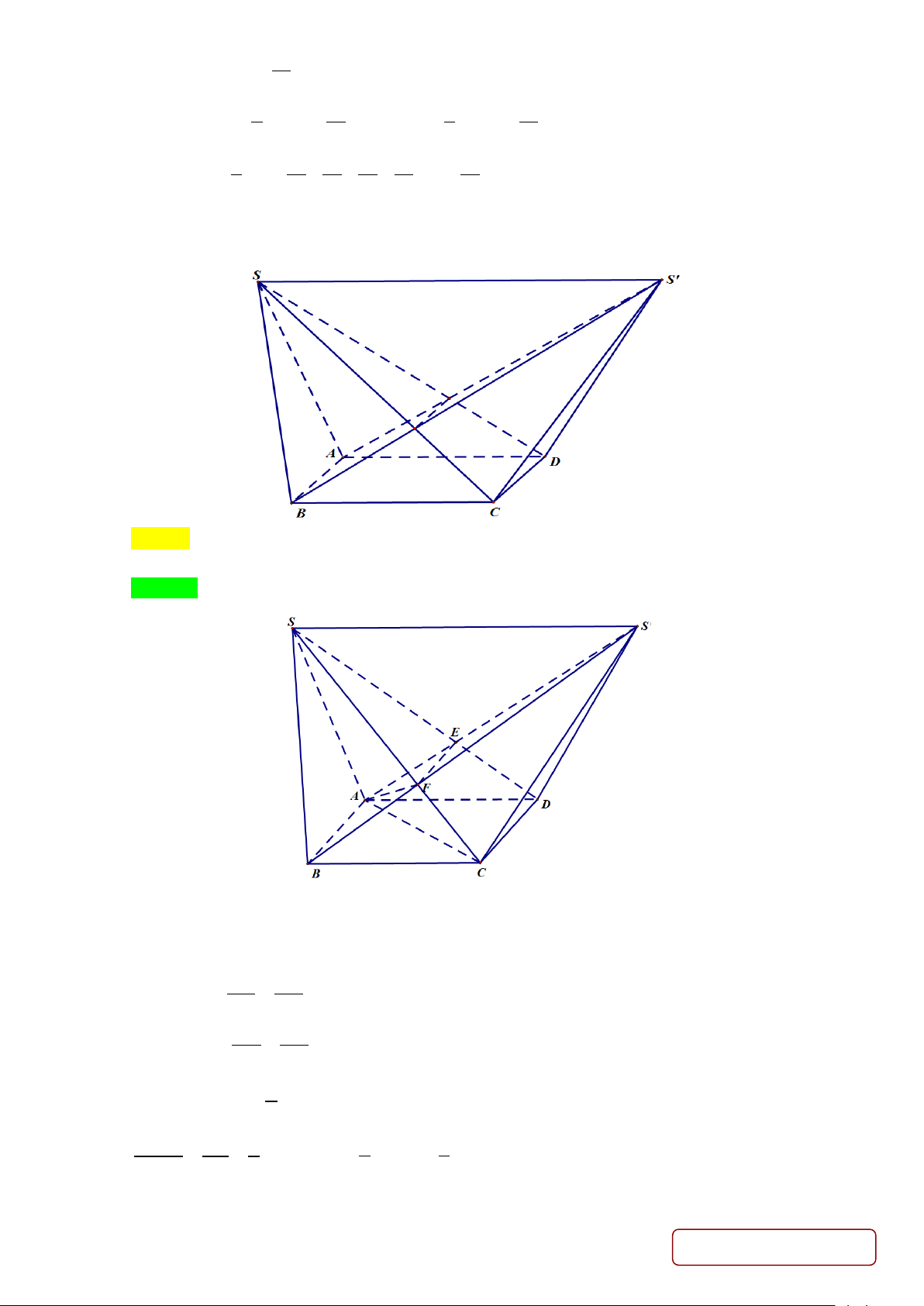
Câu 39. Cho hình chóp S.ABCD có đáy là hình bình hành và thể tích V = 270 . Lấy điểm S′ trong không gian sao cho SS′ = 2
− CB . Tính thể tích phần chung của hai khối chóp S.ABCD và S .′ABCD . A. 120. B.150. C. 180. D. 90.
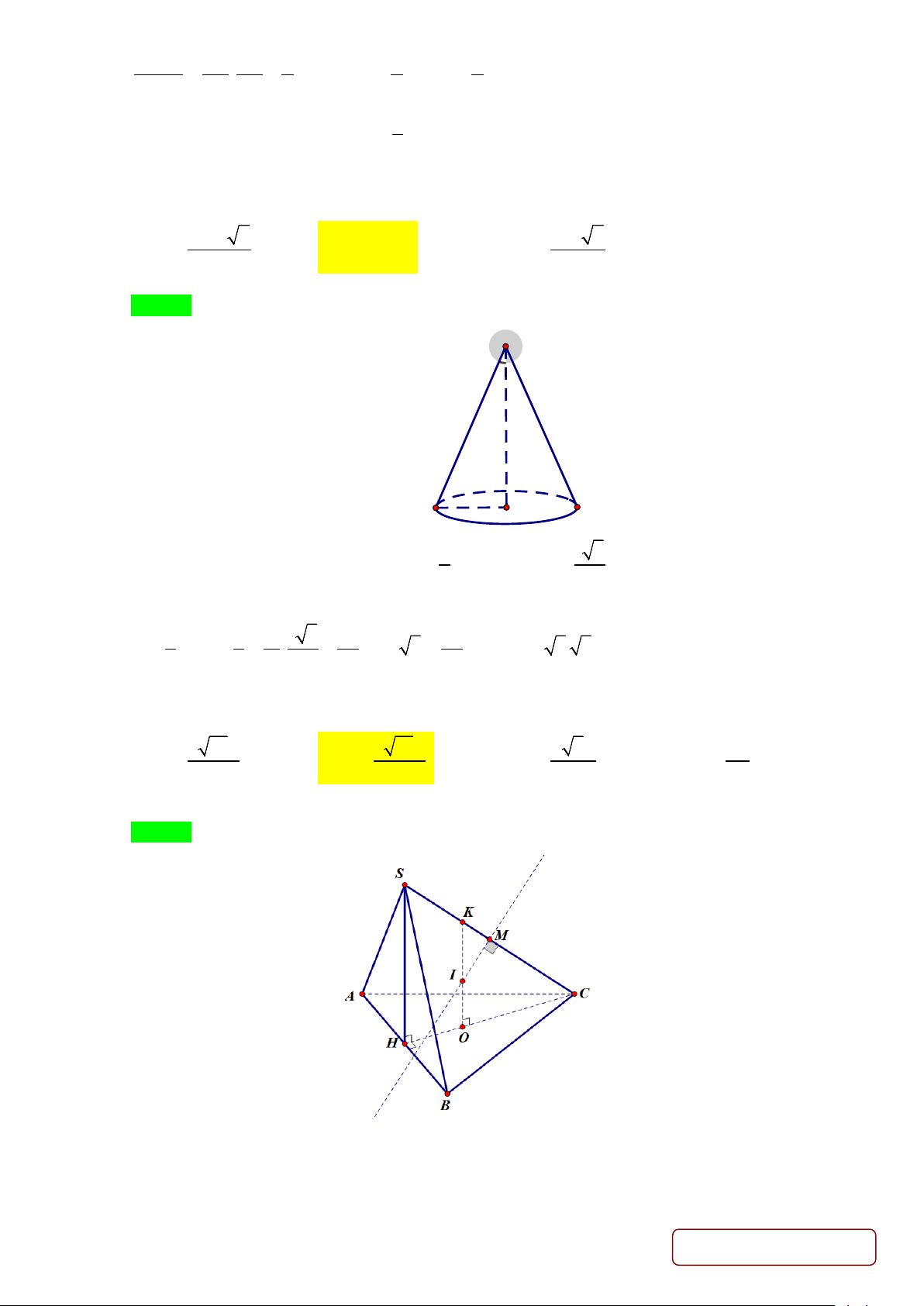
Câu 40. Tính thể tích của hình nón có góc ở đỉnh bằng 60° và diện tích xung quanh bằng 2 6π a 3 3 A. 3π a 2 π V = . B. 3 V a 2 = 3π a . C. V = . D. 3 V = π a . 4 4
Câu 41. Hình chóp S.ABC đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm
trong mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC . A. 5 15π π π π V = . B. 5 15 V = . C. 4 3 V = . D. 5 V = . 18 54 27 3
Câu 42. Cho hình trụ có chiều cao bằng bán kính đáy và bằng 5cm. Mặt phẳng (α) song song với trục, cắt
hình trụ theo một thiết diện có chu vi bằng 26cm. Khoảng cách từ (α) đến trục của hình trụ bằng A. 4 cm. B. 5cm. C. 2 cm. D. 3cm.
Câu 43. Cho tam giác vuông cân ABC có AB = BC = a 2 . Khi quay tam giác ABC quanh đường thẳng đi
qua B và song song với AC ta thu được một khối tròn xoay có thể tích bằng 3 3 A. π π 3 2π a . B. 2 a . C. 4 a . D. 3 π a . 3 3 Trang 5/29 - Mã đề 235
Câu 44. Cho hai khối nón có chung trục SS′ = 3r . Khối nón thứ nhất có đỉnh S , đáy là hình tròn tâm S′ bán
kính 2r . Khối nón thứ hai có đỉnh S′ , đáy là hình tròn tâm S bán kính r . Thể tích phần chung của hai khối nón đã cho bằng 3 3 3 3 A. 4π r π π π . B. r . C. 4 r . D. 4 r . 27 9 9 3 2
Câu 45. Họ các nguyên hàm của hàm số f (x) 3x + 4 = trên khoảng (0;+∞) là x 2 A. 4 3 3 − + C . B. 2 3x x + 4ln x + C C.
+ 4ln x + C . D. 3
x + 4nx + C . 2 x 2 4 f (2 − x ) 4 f (2 − x ) Câu 46. Xét dx ∫
. Nếu đặt u = 2 − x thì dx ∫ bằng 1 x x 1 x x 4 f (u) 2 f (u) 1 f (u) 1 f (u) A. 2 du ∫ . B. 2 du 2 du 2 − du ( ∫ . C. ∫ . D. ∫ . u − 2)2 2 2 2 1 1 (u − 2) 0 (u − 2) 0 (u − 2) 2 Câu 47. Cho
x +1 dx = ln(lna+b) ∫
với a,b là các số nguyên dương. Giá trị biểu thức ab + a + b bằng 2
x + x ln x 1 A. 8 . B. 11. C. 15. D. 7 . ln3 x + Câu 48. Cho e = − + ln c d dx a b ∫
với a,b,c là các số nguyên dương. Giá trị biểu thức 1 x + e +1 9 0
a + b + c + d bằng A. 21. B. 15. C. 23. D. 27 .
Câu 49. Cho hàm số f (x) có f (0) = 4, f ′(0) = 2
− f ′′(x) = x( x + )3 2 2 1 , x ∀ ∈ .
Tích phân 1 f (x)dx ∫ bằng 0 A. 7909 B. 7211 C. 12949 D. 5389 2520 2520 2520 2520 2 1
Câu 50. Cho hàm số f (x) liên tục trên và f (2) =16, f
∫ (x)dx = 4. Tính I = .xf ′ ∫ (2x)dx . 0 0 A. 13. B. 12. C. 20 . D. 7 .
----------------------------Hết----------------------------
Họ và tên thí sinh…………………………………….Số báo danh……………………….
Họ tên, chữ kí của giám thị coi thi………………………………………………………….
(Giám thị không giải thích gì thêm. Thí sinh không được sử dụng tài liệu ) Trang 6/29 - Mã đề 235 ĐÁP ÁN CHI TIẾT
Câu 1: Tập xác định của hàm số 1 y = là sin x − cos x A. π
\{kπ ,k ∈ } . B. \ k2π ,k + ∈ . 4 C. π π \ kπ ,k + ∈ .
D. \ + kπ,k ∈ . 2 4 Lời giải Chọn D.
Hàm số xác định khi π
sin x − cos x ≠ 0 ⇔ tan x ≠ 1 ⇔ x ≠ + kπ ,k ∈ . Suy ra tập xác định 4 π D \ kπ ,k = + ∈ . 4
Câu 2: Tìm tập giá trị của hàm số y = 3sin x − cos x − 2 A. 2; − 3 − − − . B. 3 3; 3 1 . C. [ 4; − 0]. D. [ 2; − 0]. Lời giải Chọn C.
Ta có y = 3 sin x − cos x − 2 ⇔ 3 sin x − cos x = y + 2(*)
Điều kiện để (*) có nghiệm
( )2 +(− )2 ≥(y+ )2 ⇔ (y+ )2 3 1 2 2 ≤ 4 ⇔ 2
− ≤ y + 2 ≤ 2 ⇔ 4 − ≤ y ≤ 0.
Suy ra tập giá trị của hàm số là [ 4; − 0].
Câu 3: Cho khai triển nhị thức Newton của ( − )2 2 3 n
x , biết rằng n là số nguyên dương thỏa mãn 1 3 5 2n 1 C + + + + = . Hệ số của 7 x + C + C + C + n n n ........ n+ 1024 2 1 2 1 2 1 2 1 bằng A. 2099520 − . B. 414720 − . C. 2099520 . D. 414720 . Lời giải Chọn A. 1 3 5 2n 1 + 2 C + + + + = + C + C + C n n n ........ n+ 2 n 2 1 2 1 2 1 2 1 2
⇔ 1024 = 2 n ⇔ n = 5 số hạng tổng quát: k 10 T = − +
C 2 −k 3 k k x k 1 10 ( ) Hệ số của 7 x là 7 3 C 2 3 − = 10 ( )7 - 2099520.
Câu 4: Cho đa giác đều 2018 đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác đều và có một góc lớn hơn 100° A. 2 2018C . B. 3 2018C . C. 3 C . D. 3 2018C 896 896 1009 897 Lời giải Chọn A.
Đa giác đều 2018 đỉnh chia đường tròn ngoại tiếp đa giác đều thành 2018 cung tròn bằng nhau có số đo là 360 độ. 2018
Gọi tam giác cần lập là A
∆ BC thì A có 2018 cách chọn. Sau khi chọn A còn lại 2017 đỉnh, Trang 7/29 - Mã đề 235
Để góc ở đỉnh A có số đo lớn hơn 0
100 thì cung BC không chứa đỉnh A phải có số đo lớn hơn 200° ứng với số cung 360 200 : ≈
1.121,1 cung. (số đo của cung gấp đôi số đo góc nội tiếp cùng chắn 2018 cung đó)
Mà số cung bằng số đỉnh cộng 1.
Do đó giữa B và C (trừ 2 đỉnh B,C ) phải có 1121 đỉnh nên còn lại 2017 −1121 = 896 đỉnh để chọn
cho B và C do đó có 2
C cách chọn B và C . 896 Vậy tất cả có: 2
2018.C tam giác thỏa mãn bài toán. 896
Câu 5: Một tổ có 5 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh để làm trực
nhật.Tính xác suất để 3 học sinh được chọn có cả nam và nữ A. 3 . B. 24 . C. 9 . D. 3 . 8 25 11 4 Lời giải Chọn C
Xác suất cần tính là phần bù của trường hợp các học sinh được chọn là cùng giới tính 3 3 C + C 9 5 6 p =1− = . 3 C 11 11 Câu 6: Biết ( 2 lim + 3 + 2 − + )1 a n n n
= , trong đó a là một phân số tối giản. Tính T =3a −b . b b A. T =−13. B. T =13. C. T =1. D. T = −1 Lời giải Chọn B Ta có:
( n + n+ −n+ ) 2 2 2
n + 3n + 2 − n 3n + 2 3 5 lim 3 2 1 =lim +1=lim +1= +1= . 2 2 n 3n 2 n n 3n 2 n + + + + + + 2 2 u = 1, − u = 3
Câu 7: Cho dãy số (u xác định bởi: 1 2
. Số hạng thứ 7 của dãy là: n ) u = − ∀ ≥ + u u − n n 5 n 6 n , 2 1 1 A. 1023. B. 3261. C. 309. D. 4284 Lời giải Chọn B
Ta có u = 21; u = 87;u = 309;u =1023;u = 3261. 3 4 5 6 7
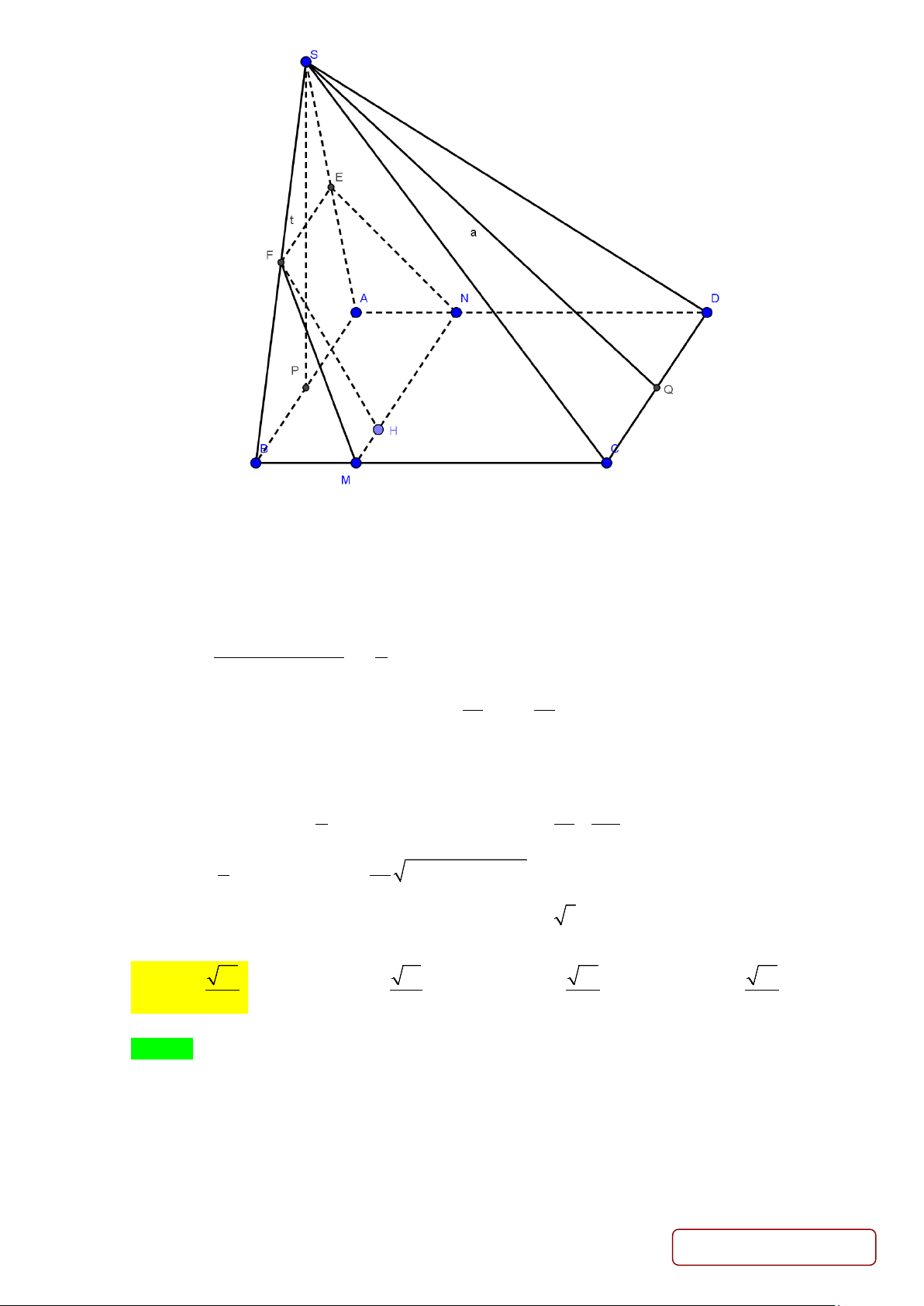
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , SA = SB = a , SC = SD = a 3 . Gọi
E, F lần lượt là trung điểm các cạnh ,
SA SB . Trên cạnh BC lấy M sao cho BM = x ? Tính diện
tích thiết diện của hình chóp với mặt phẳng (MEF ) theo x và a ? A. a 2 2
16x + 8a + a .
B. 3a (4x + a 3). 4 16 C. 3a 2 2
16x + 8a + 3a . D. a 2 2
x −8ax + a . 16 16 Lời giải Chọn C Trang 8/29 - Mã đề 235
Gọi P,Q lần lượt là trung điểm AB , CD .
Tam giác SAB cân tại S ⇒ SP ⊥ AB
Tam giác SCD cân tại S ⇒ SQ ⊥ CD ⇒ SQ ⊥ AB
⇒ AB ⊥ (SPQ) ⇒ AB ⊥ PQ ⇒ AB ⊥ BC ⇒ ABCD là hình vuông. 2 2 2
SB + BC − SC 1 cos SBC = = − 2S . B BC 2 ⇒ = + − 2 2 2 2 a 2 2 . .cos ax MF SB BM SB BM SBC = + x + 4 2 = ⇒ = SAD SBC
EAN FBM & AE = BF; AN = BM
Suy ra EFMN là hình thang cân. 2 Hạ a 2 2 2 2 ax 3a
FH ⊥ MN ⇒ MH = ⇒ FH = MF − MH = x + + 4 2 16 1 a ⇒ S = FM EF + MN =
x + ax + a . EFMN ( ) 3 2 2 16 8 3 2 16
Câu 9: Cho hình chóp tứ giác đều S.ABCD có AB = ,
a SA = a 3 . Gọi G là trọng tâm tam giác SCD . Góc
giữa đường thẳng BG với mặt phẳng ( ABCD) bằng A. 85 arctan . B. 10 arctan . C. 85 arcsin . D. 85 arccos . 17 17 17 17 Lời giải Chọn A
Gọi M là trung điểm CD , kẻ GK song song với SO và cắt OM tại K , suy ra K là hình chiếu
của G trên mp( ABCD) . Trang 9/29 - Mã đề 235 S G A D O K M B C
suy ra BG ( ABCD) ( )= , GBK . 2 a Ta có: a 2 AO = , a 10 SO = , 1 a 10 GK = SO =
, vì OK = OM nên OK = , suy ra 2 2 3 6 3 3 a 34 BK = . Vậy
(BG ABCD )= GK 85 tan ,( ) tan GBK = = . 6 BK 17
Câu 10: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa đường thẳng SA và mặt phẳng
(ABC) bằng 60°. Gọi G là trọng tâm tam giác ABC , tính khoảng cách giữa hai đường thẳng GC và SA . A. a 5 . B. a 5 . C. a 2 . D. a . 10 5 5 5 Lời giải Chọn B
Do S.ABC là hình chóp tam giác đều, G là trọng tâm tam giác ABC nên SG ⊥ ( ABC) . Dựng hình
chữ nhật AEGF , gọi H là hình chiếu vuông góc của G trên SF .
Ta có GE//AF nên GE// (SAF ) , suy ra
d (GC, SA) = d (GC,(SAF )) = d (G,(SAF )) = GH .
Ta có (SA ( ABC)) = , SAG ⇒ SAG = 60° .
Tam giác ABC đều cạnh a nên 1 a 3 a 3 AG = . = . 3 2 3
Trong tam giác SAG có = a 3 SG A . G tan SAG = .tan 60° = a ; a GF = AE = . 3 2
Do GH là đường cao trong tam giác SGF vuông tại G nên: 2 2 SG .GF a 5 GH = = . 2 2 SG + GF 5 Trang 10/29 - Mã đề 235 Câu 11: Cho hàm số 1 3 2
y = − x + 4x − 5x −17 . Phương trình y′ = 0 có hai nghiệm x ; x . Khi đó tổng x + x 3 1 2 1 2 bằng: A. 8 − . B. 5. C. 5 − . D. 8 . Lời giải Chọn D Ta có 2 2
y′ = −x + 8x − 5 ⇒ y′ = 0 ⇔ −x + 8x − 5 = 0. − − Phương trình b 8
y′ = 0 có hai nghiệm x ; x . Khi đó tổng x + x = = = 8 . 1 2 1 2 a 1 − 2
ax + bx +1, x ≥ 0
Câu 12: Cho hàm số f (x) =
. Khi hàm số có đạo hàm tại x = 0 , hãy tính T = a + 2b . 0
ax − b −1. x < 0 A. T = 4 − .
B. T = 0 . C. T = 6 − . D. T = 4 . Lời giải Chọn C Ta có, f (0) =1 − + f x f 0
Đạo hàm bên phải tại x + + − = 0 : f ′( ) ( ) ( ) 2 ax bx 1 1 0 = lim = lim = b 0 x→0+ x→0 x + x − − f x f 0 Đạo hàm bên trái tại − − + x ax b 2 b 2 = 0 : f (0 ) ( ) ( ) lim lim lim a ′ = = = − 0 x→0− x→0− x→0 x x − x
Vì hàm số có đạo hàm tại x +
= 0 nên tồn tại giới hạn b 2 lim a − ⇒ b = 2 − . Khi đó, 0 x 0− → x f ( − ) b + 2 0 lim a ′ = − = a . x→0− x
Vì hàm số có đạo hàm tại x = 0 nên f (0+ ) = f (0− ′ ′
)⇒ b = a ⇒ a = 2 − . 0
Vậy T = a + 2b = 6 − .
Câu 13: Cho hàm số y = f (x) có đạo hàm là f ′(x) = (x − )2 1 +1. Xét hàm số
g (x) f f (x) 1 2 x 2x = − −
. Số các nghiệm nguyên của bất phương trình g′(x) ≤ 0 là: 2 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn D ′ Ta có g (x) = f (x) 1 2
− x − 2x . f f (x) 1 2 − x − 1 2x ′ ′
= ( f ′(x) − x − 2). f ′ f (x) 2 − x − 2x 2 2 2 ( x 3x) 2 2 . f (x) 1 2 x 2x = − − − + 1 ≤ 0 2
⇔ x − 3x ≤ 0 ⇔ 0 ≤ x ≤ 3. 2 − +
Câu 14: Cho đồ thị hàm số (C) 2x 3 : y =
. Viết phương trình tiếp tuyến của đồ thị (C) tại giao điểm của x −1
(C) với đường thẳng y = x −3 . Trang 11/29 - Mã đề 235
A. y = −x + 3 và y = −x −1.
B. y = −x −3 và y = −x +1.
C. y = x − 3 và y = x +1.
D. y = −x + 2 và y = −x +1. Lời giải Chọn B
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng y = x − 3 là: x = 0 2
− x + 3 = x−3⇔ 2
− x + 3 = (x − )
1 (x −3) (x ≠ ) 1 2
⇔ x − 2x = 0 ⇔ . x −1 x = 2
Do đó giao điểm của đồ thị (C) và đường thẳng y = x − 3 là: (2;− ) 1 ,(0; 3 − ) . − Ta có: 1 y′ = . (x − )2 1
Phương trình tiếp tuyến của (C) tại điểm (2; ) 1
− là: y = −(x − 2) −1 = −x +1.
Phương trình tiếp của (C)tại điểm (0; 3
− ) là: y = −x −3 . Câu 15: Cho hàm số 4
y = x − ( m + ) 2 2 3
4 x + m có đồ thị là (C . Tìm m để đồ thị (C cắt trục hoành tại bốn m ) m )
điểm phân biệt có hoành độ lập thành một cấp số cộng. A. 12 m 12;m − = = . B. m =12. C. 12 m − = . D. 12 m = . 9 9 9 Lời giải Chọn A.
Phương trình hoành độ giao điểm: 4 x − ( m + ) 2 2 3 4 x + m = 0 ( ) 1 Đặt 2
t = x (t ≥ 0), phương trình ( )
1 trở thành: 2t − ( m + ) 2 3 4 t + m = 0 (2)
(C cắt trục hoành tại bốn điểm phân biệt ⇔ ( )
1 có bốn nghiệm phân biệt m ) 2
∆ = 5m + 24m +16 > 0
⇔ (2) có hai nghiệm dương phân biệt ⇔ 2 P = m > 0
S = 3m + 4 > 0 4 m < 4 − ∨ m > − 5 4 m > − ⇔ m ≠ 0 ⇔ 5 (*) 4 m ≠ 0 m > − 3
Khi đó phương trình (2) có hai nghiệm 0 < t < t . Suy ra phương trình ( )
1 có bốn nghiệm phân biệt 1 2
là x = − t < x = − t < x = t < x = t . Bốn nghiệm x , x , x , x lập thành cấp số cộng 1 2 2 1 3 1 4 2 1 2 3 4
⇔ x − x = x − x = x − x ⇔ − t + t = 2 t ⇔ t = 3 t ⇔ t = 9t (3) 2 1 3 2 4 3 1 2 1 2 1 2 1 t
+ t = 3m + 4 (4)
Theo định lý Viet ta có 1 2 2 t t = m (5) 1 2 Trang 12/29 - Mã đề 235 3m + 4 t = 1
Từ (3) và (4) ta suy ra được 10 (6). 9 (3m + 4) t = 2 10
Thay (6) vào (5) ta được 9 (3m + 4)2 2 = m 100 ( m + ) m = 12 3 3 4 =10m ⇔ (thỏa (*)) ( ⇔ m + ) 12 3 3 4 = 10 − m m = − 19
Vậy giá trị m cần tìm là 12 m =12; . m = − 19 Câu 16: Cho hàm số x −1 y =
. Tính đạo hàm cấp n của hàm số. 2 x − 5x + 6 n n n n A. (n) ( 1) − .n! ( 1) − .n! y − − = 2. − B. (n) ( 1) .n! ( 1) .n! y = 2. + n 1 + n 1 (x − 3) (x − 2) + n 1 + n 1 (x − 3) (x − 2) + n n n n C. (n) ( 1) − .n! ( 1) − .n! y − − = 2. − D. (n) ( 1) .n! ( 1) .n! y = 2. −
(x − 3)n (x − 2)n n 1 + n 1 (x − 2) (x − 3) + Lời giải Chọn A. Ta có 2 1 y − = − 2 1 ⇒ y′ = + , 2 2 y′′ = 2. − x − 3 x − 2
(x −3)2 (x − 2)2
(x −3)3 (x − 2)3 n n
Bằng quy nạp, ta chứng minh được (n) ( 1) − .n! ( 1) − .n! y = 2. − n 1 + n 1 (x − 3) (x − 2) +
Câu 17: Cho hàm số y = f (x) có đạo hàm trên . Gọi (C , (C , (C lần lượt là đồ thị của các hàm số 3 ) 2 ) 1 )
y = f (x) , y = g (x) = f f (x)
, y = h( x) = f ( 2 x + )
1 . Biết rằng f (2) = 5, f ′(2) = 2, g′(2) = 4 . Hãy tính h′(2) . A. h′(2) = 2. B. h′(2) = 4.
C. h′(2) = 6 . D. h′(2) = 8. Lời giải Chọn D.
Theo giả thiết ta có: g′(x) = f ′(x). f ′ f (x) ⇒ g′(2) = f ′(2). f ′ f (2)
⇒ 4 = 2. f ′(5) ⇒ f ′(5) = 2 .
Mà h′(x) = xf ( 2 2 ' x + )
1 ⇒ h′(2) = 4 f ′(5) = 8 3 Câu 18: Hàm số x 2 y = −
+ x − mx +1 nghịch biến trên khoảng (0;+∞) khi và chỉ khi 3
A. m∈[1;+∞) .
B. m∈(1;+∞) .
C. m∈[0;+∞) .
D. m∈(0;+∞) . Lời giải Chọn A. Tập xác định . Ta có 2
y′ = −x + 2x − m . Để hàm số nghịch biến trên (0;+∞) thì y′ ≤ 0 ∀x∈(0;+∞) hay 2 2
−x + 2x − m ≤ 0 ⇔ m ≥ −x + 2 . x Trang 13/29 - Mã đề 235 Xét hàm số 2
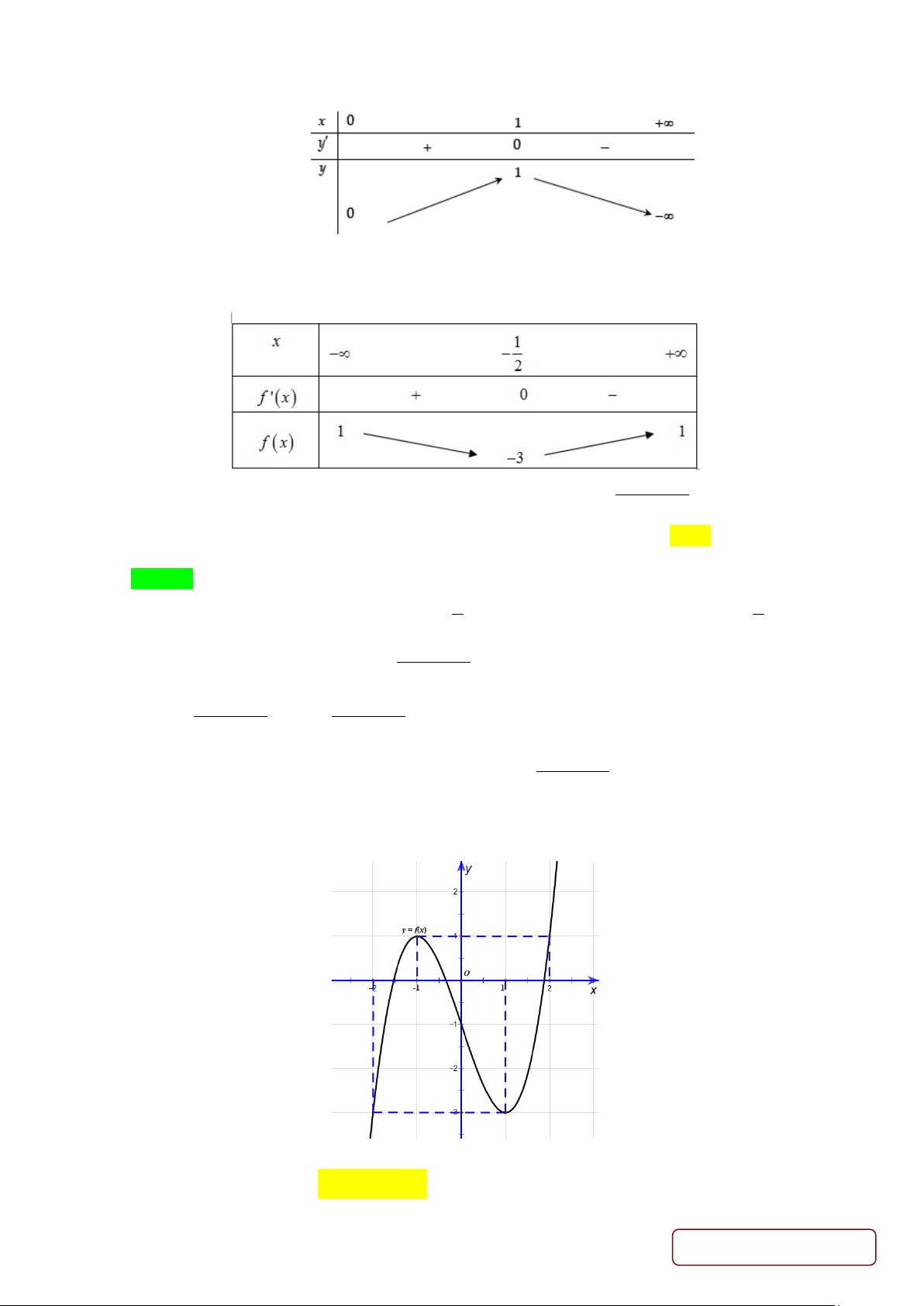
y = −x + 2x trên (0;+∞), ta có y′ = 2
− x + 2, y′ = 0 ⇔ x =1. Bảng biến thiên
Max y =1. Do đó m ≥ Max y =1. (0;+∞) (0;+∞)
Câu 19: Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số 1 y = là 2 f (x) −1 A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn D
Xét phương trình f (x) − = ⇔ f (x) 1 2 1 0
= . Dựa vào BBT, phương trình f (x) 1 = có 2 nghiệm 2 2
phân biệt. Do đó đồ thị hàm số 1 y = có 2 tiệm cận đứng. 2 f (x) −1 Và 1 1 lim = = . x→+∞ ( ) 1; lim x f x →−∞ − f (x) 1 2 1 2 −1 Do đó 1
y =1 là tiệm cận ngang của đồ thị hàm số y = . 2 f (x) −1
Vậy đồ thị có hai đường tiệm cận đừng và 1 đường tiệm cận ngang.
Câu 20: Cho hàm số y = f (x) liên tục trên và có đồ thị như hình bên.
Phương trình f (2sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn [ π
− ;π ] khi và chỉ khi A. m∈{ 3 − ; } 1 . B. m∈( 3 − ; ) 1 . C. m∈[ 3 − ; ) 1 . D. m∈( 3 − ; ] 1 . Lời giải Trang 14/29 - Mã đề 235 Chọn B
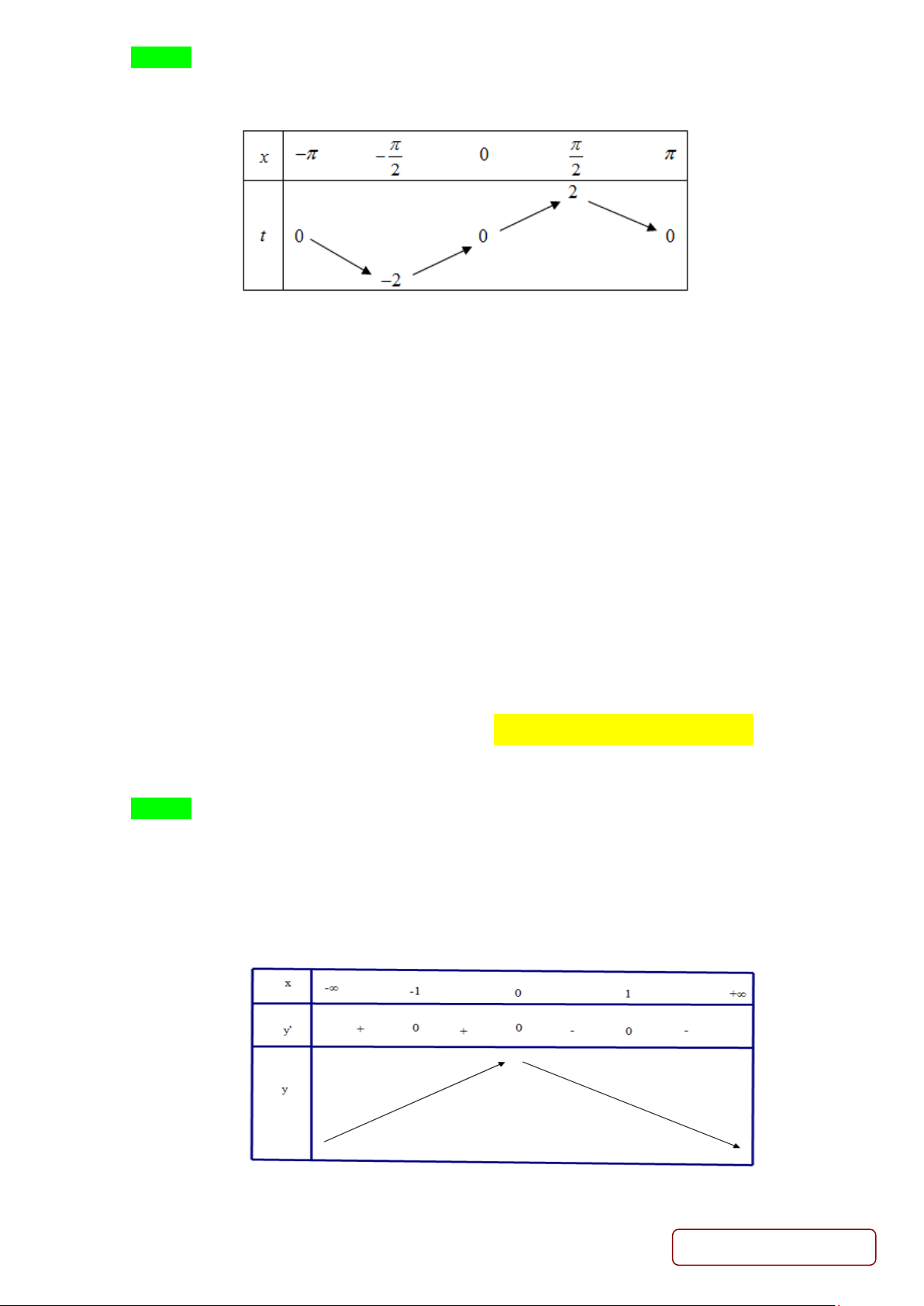
Đặt t = 2sin x
Ta có bảng biến thiên trên [ π − ;π ].
Với t = 0 , cho ta ba nghiệm phân biệt x∈[ ; −π π]. Với mỗi t ∈( 2; − 2) \{ }
0 , cho ta hai nghiệm phân biệt x ∈[ ; −π π]. Với mỗi t ∈{ 2; − }
2 , cho ta một nghiệm duy nhất x ∈[ ; −π π].
Phương trình f (2sin x) = m có đúng ba nghiệm phân biệt thuộc đoạn [ π − ;π ] ⇔ trên đoạn [ 2;
− 2], phương trình f (t) = m có đúng một nghiệm duy nhất t = 0 ; hoặc có một nghiệm t ∈{± }
2 và một nghiệm thuộc t ∈( 2; − 2) \{ } 0 .
+ Nếu t = 0 là nghiệm ⇒ m = f (0) = 1
− . Ta có: f (t) = 1
− có 3 nghiệm phân biệt thuộc [ 2; − 2]. (KTM). t = 2 − + Nếu t = 2
− là nghiệm ⇒ m = f ( 2 − ) = 3
− . Ta có: f (t) = 3 − ⇔ . (KTM). t = 1 t = 1 −
+ Nếu t = 2 là nghiệm ⇒ m = f (2) =1. Ta có: f (t) =1 ⇔ . (KTM). t = 2 Vậy m∈{ 3 − ; } 1 .
Câu 21: Cho hàm số f (x) = ( − x )2019 2 1
. Khẳng định nào sau đây là đúng?.
A. Hàm số đồng biến trên .
B. Hàm số đồng biến trên ( ;0 −∞ ).
C. Hàm số nghịch biến trên ( ;0 −∞ ).
D. Hàm số nghịch biến trên . Lời giải Chọn B
Ta có: f ′(x) = − x ( − x )2018 2 2019.2 . 1 x = 1 − f (x) 0 ′ = ⇔ x = 0 x = 1 Bảng biến thiên:
Dựa vào BBT, ta có: hàm số đồng biến trên ( ;0 −∞ ). Trang 15/29 - Mã đề 235
Câu 22: Cho hàm số = ( ) 4 3 2
y f x = mx + nx + px + qx + r và hàm số y = f ′(x) có đồ thị như hình vẽ bên.
Biết f (a) > 0 , hỏi đồ thị hàm số y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm? A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B
Từ đồ thị ta suy ra phương trình f ′(x) = 0 có ba nghiệm đơn là x = a , x = b , x = c .
Từ đó ta có bảng biến thiên
Do f (a) > 0 nên để đồ thị hàm số y = f (x) cắt trục hoành tại nhiều điểm nhất có thể thì
f (c) < 0 . Khi đó y = f (x) cắt trục hoành tại 2 điểm x = x ∈ ;
b c và x = x > c . 1 ( ) 2
Câu 23: Tìm tập xác định D của hàm số y = (x − x − ) 2 4 2 3 4 ?
A. D = (−∞;− ) 1 ∪(4;+∞) .
B. D = (−∞; 2 − ) ∪(2;+∞) .
C. D = (−∞; 2 − ]∪[2;+∞) .
D. D = (−∞;+∞) . Lời giải Chọn B
Điều kiện xác định của hàm số : 4 2
x − 3x − 4 > 0 ⇔ x < 2 − ∨ 2 < x .
Câu 24: Giả sử phương trình 2
log x − m + 2 log x + 2m = 0 có hai nghiệm thực phân biệt x , x thỏa mãn 2 ( ) 2 1 2
x + x = 6 . Giá trị của biểu thức − là 1 2 x x 1 2 A. 3. B. 8. C. 2. D. 4 Lời giải Chọn C log x = 2 x = 4 2
log x − m + 2 log x + 2m = 0 ⇔ ⇔
4 2m 6 m 1. 2 ( ) 2 2 log x m = x = 2m 2
Khi đó, phương trình có 2 nghiệm thực phân biệt là {4; }
2 suy ra x − x = 2 . 1 2
Câu 25: Một người nhận hợp đồng dài hạn làm việc cho một công ty với mức lương khởi điểm của mỗi tháng
trong 3 năm đầu tiên là 6 triệu đồng /tháng. Tính từ ngày đầu tiên làm việc, cứ sau đúng 3 năm liên
tiếp thì tăng lương 10% so với mức lương một tháng người đó đang hưởng . Nếu tính theo hợp đồng
thì tháng đầu tiên của năm thứ 16 người đó nhận được mức lương là bao nhiêu ? Trang 16/29 - Mã đề 235 A. ( )4
6. 1,1 triệu đồng. B. ( )6
6. 1,1 triệu đồng. C. ( )5
6. 1,1 triệu đồng. D. ( )16 6. 1,1 triệu đồng. Lời giải Chọn C
Gọi A là số tiền lương một tháng trong 3 năm đầu .
Mức lương tháng đầu tiên nhận được trong năm thứ 4 là : T = A + .
A 0,1 = A 1+ 0,1 = . A 1,1 đồng . 1 ( ) ( )
Mức lương tháng đầu tiên nhận được trong năm thứ 7 là :
T = T +T .0,1 = T (1+ 0 ) ,1 = T .(1 ) ,1 = A(1 )2 ,1 đồng . 2 1 1 1 1
Mức lương tháng đầu tiên nhận được trong năm thứ 10 là :
T = T +T .0,1 = T (1+ 0 ) ,1 = T .(1 ) ,1 = A(1 )3 ,1 đồng . 3 2 2 2 2
Mức lương tháng đầu tiên nhận được trong năm thứ 13 là :
T = T +T .0,1 = T (1+ 0 ) ,1 = T .(1 ) ,1 = A(1 )4 ,1 đồng . 4 3 3 3 3
Vậy tháng lương đầu tiên của năm thứ 16 là :
T = T +T .0,1 = T .1,1 = A(1, )5 6 1 = 6.10 . 1,1 đồng. 5 4 4 4 ( )5
Câu 26: Cho ba số a + log 3, a + log 3, a + log 3 theo thứ tự lập thành một cấp số nhân. Công bội của cấp 2 4 8 số nhân đó bằng A. 1. B. 1 . C. 1 . D. 1 . 4 2 3 Lời giải Chọn D.
Theo giả thiết ta có (a + log 3)2 = a + log 3 a + log 3 . 4 ( 2 ) ( 8 ) Suy ra 2
a + 2a log 3+ (log 3)2 2
= a + a log 3+ log 3 + log 3.log 3. 4 4 ( 2 8 ) 2 8 1 ⇔ a + ( )2 4 1 log 3
log 3 = a log 3+ (log 3)2 1 1 1 a ⇔ = − log 3. 2 2 2 2 4 3 3 2 3 4 3 1 ⇔ a = − log 3 . 2 4 Vậy 3 a + log 3 = log 3 ; 1
a + log 3 = log 3 . Suy ra công bội của cấp số nhân bằng 1 . 2 2 4 4 2 4 3
Câu 27: Tích các nghiệm của phương trình log (x + 2) + log (x −5)2 + log 8 = 0 2 4 1 là 2 A. 12 − . B. 18 − . C. 36. D. 2 − . Lời giải Chọn A x + 2 > 0 x > 2 −
Điều kiện xác định ( ⇔ x − 5 )2 > 0 x ≠ 5
Khi đó log (x + 2) + log (x − 5)2 + log 8 = 0 2 4 1 2
⇔ log x + 2 + log x − 5 − 3 = 0 2 ( ) 2
⇔ log x + 2 x − 5 = 3 2 ( ) Trang 17/29 - Mã đề 235
⇔ (x + 2) x −5 = 8 TH1: Với x∈( 2; − 5) 3+ 17 x = (tm) Ta có ( )
1 ⇔ (x + 2)(5− x) = 8 2
⇔ x − 3x − 2 = 0 2 ⇔ 3− 17 x = (tm) 2
TH2: Với x∈(5;+∞) x = 3 − (loai) Ta có ( )
1 ⇔ (x + 2)(x −5) = 8 2
⇔ x − 3x −18 = 0 ⇔ x = 6 (tm) ±
Suy ra tập nghiệm của phương trình là 3 17 S ;6 =
⇒ tích các nghiệm là 12 − . 2
Câu 28: Cho hàm số y = f (x) liên tục và có đạo hàm trên . Hàm số y = f ′(x) có bảng xét dấu như sau Bất phương trình ( ) cos x f x > e
+ m có nghiệm x 0; ∈ khi và chỉ khi 2
A. m f ≤ − 1.
B. m < f − 1.
C. m ≥ f (0) − e .
D. m ≤ f (0) − e . 2 2 Lời giải Chọn B
Xét hàm số ( ) = ( ) cosx g x
f x − e xác định và liên tục trên đoạn 0; . 2 ′( ) = ′( ) cos + sin . x g x f x x e .
Trên khoảng 0;
có f ′(x) > 0 và 0 < sin x <1 nên g′(x) > 0. 2
Suy ra hàm số g (x) đồng biến trên khoảng 0;
⇒ max g (x) = g = f − 1. 2 0; 2 2 2 ( ) cosx > + ⇔ < ( ) cosx f x e m m f x − e
⇔ m < g (x) (*)
Bất phương trình (*) có nghiệm x 0; ∈
khi và chỉ khi m < max g (x) ⇔ m < f − 1. 2 0; 2 2 1
Câu 29: Cho hàm số ( ) = log + 3x −3x f x x
. Tính tổng bình phương các giá trị của tham số m để phương trình 1 f + f ( 2
x − 2x + 2) = 0
có đúng 3nghiệm phân biệt bằng 2 x m 1 − + A. 5 . B. 7 . C. 3. D. 2 . 2 2 Lời giải Trang 18/29 - Mã đề 235 Chọn B 1
Hàm số f (x) có tập xác định là D = (0;+∞) . Ta có ′( ) 1 x 1 = + 3 ln 3+ .3x f x .ln 3 > 0, x ∀ > 0 , 2 x ln10 x
do đó hàm số đồng biến trên khoảng (0;+∞). 1 1
Nhận xét: Nếu v∈(0;+∞) thì 1 1
= log + 3v − 3v = −log − 3v + 3v f v = −
f (v) . Ngược lại nếu v v
f (u) = − f (v) thì 1 u = . v Do đó 1 f + f ( 2 x − x + ) 1 2 2 = 0 ⇔ f = − f ( 2 x − 2x + 2) 2 x m 1 2 x m 1 − + − + 2 1 1
2x − 2m = x − 2x +1 2 ⇔ =
⇔ 2 x − m +1 = x − 2x + 2 ⇔ 2 2
2 x − m +1 x − 2x + 2
2x − 2m = −x + 2x −1 2 2
2x − 2m = x − 2x +1
2m = −x + 4x −1 = f (x) ⇔ ⇔ 2 2
2x − 2m = −x + 2x −1
2m = x +1 = g (x)
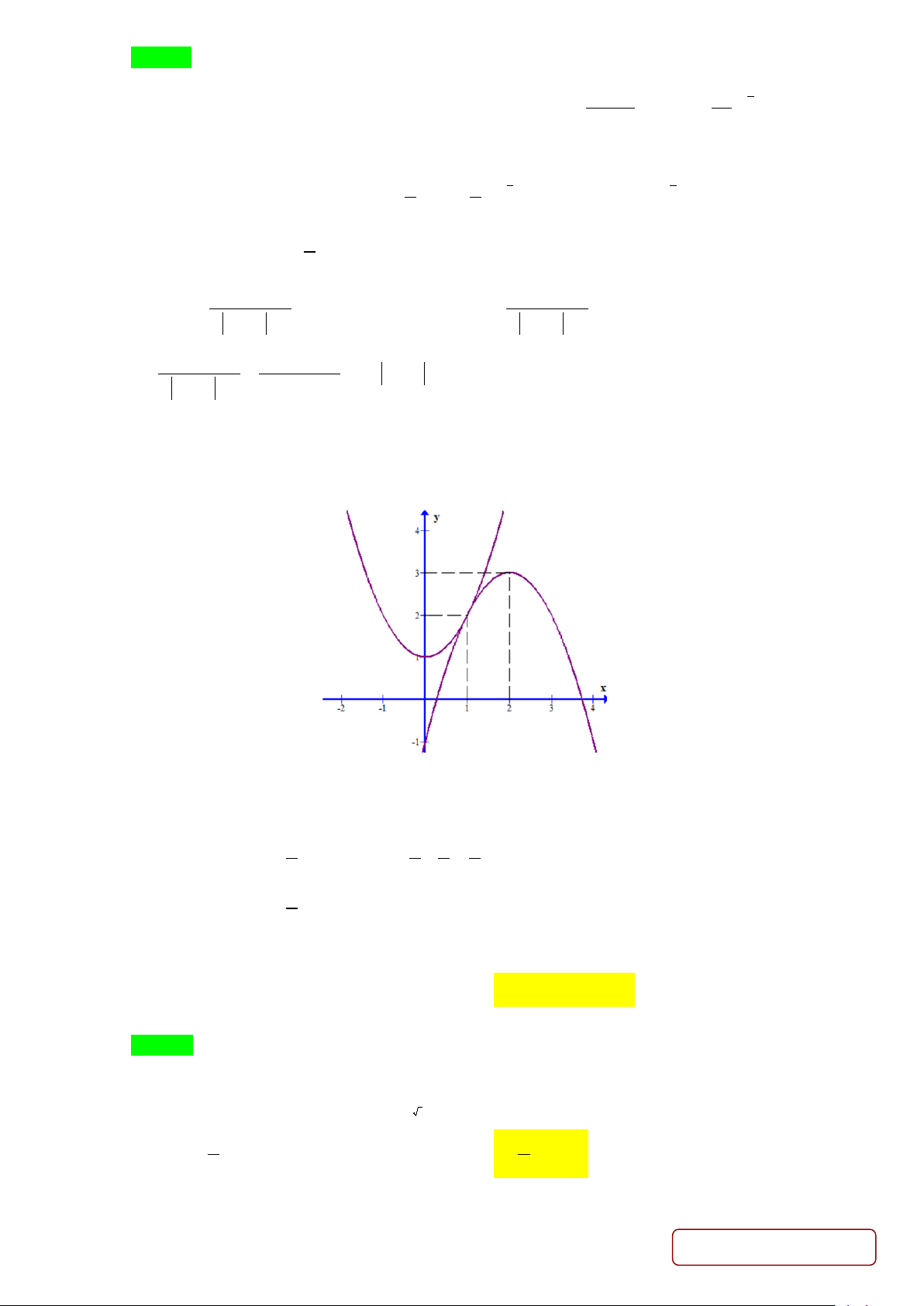
Vẽ đồ thị hàm số f (x) và g (x) trên cùng hệ trục ta được:
Để phương trình đã cho có đúng 3nghiệm thì đường thẳng y = 2m cắt hai đồ thị trên tại đúng 3 điểm m =1 2m = 2 3 2 9 1 7
⇔ 2m = 3 ⇔ m = ⇒ ∑m =1+ + = . 2 4 4 2 2m =1 1 m = 2
Câu 30: Hàm số = ( 2 − + ) 1 x y x x e có đạp hàm A. ′ = (2 − ) 1 x y x e .
B. ′ = ( 2 − ) x y x x e .
C. ′ = ( 2 + ) x y x x e . D. ′ = ( 2 + ) 1 x y x e . Lời giải Chọn C
= ( 2 − + ) x ⇒ ′ = ( − ) x + ( 2 − + ) x = ( 2 1 2 1 1 + ) x y x x e y x e x x e x x e .
Câu 31: Tìm nghiệm của bất phương trình 2 log x 2 2log2 2 x + x − 20 ≤ 0 A. 1 0 < x ≤
B. 1 ≤ x ≤ 2 2 2 Trang 19/29 - Mã đề 235
C. 1 ≤ x ≤ 2 D. 1 1 ≤ x ≤ . 3 3 2 Lời giải Chọn B
Điều kiện: x > 0 2 log x 2 2 2 2log2 2 x + x − 20 ≤ 0 4log2 x 2log2 ⇔ 2 x + x − 20 ≤ 0 log2 x 2log2 ⇔ 16 x + x − 20 ≤ 0 Đặt log = ⇒ = 2t x t x 2 BPT 2
16t (2t )2t 2 2 20 0 16t 4t ⇔ + − ≤ ⇔ + − 20 ≤ 0 Đặt 2
4t = u ,u ≥1 (vì 2 t 0 u = 4 ≥ 4 =1) BPT 2
⇔ u + u − 20 ≤ 0 ⇔ 5 − ≤ u ≤ 4
Kết hợp với u ≥1 ⇒1≤ u ≤ 4 2 t 2 2
⇒1≤ 4 ≤ 4 ⇔ 0 ≤ t ≤1 ⇔ t ≤1 ⇔ 1 − ≤ t ≤1 ⇔ 1 − ≤ log x ≤1 1 − 1
⇔ 2 ≤ x ≤ 2 ⇔ ≤ x ≤ 2 2 2
Câu 32: Xét các số nguyên dương a,b sao cho phương trình 2
a ln x + bln x + 5 = 0 có hai nghiệm phân biệt
x , x và phương trình 2
5log x + blog x + a = 0 có hai nghiệm phân biệt x , x thỏa mãn x x > x x . 1 2 3 4 1 2 3 4
Tìm giá trị nhỏ nhất S của S = 2a + 3b min A. S = 30. B. S = 25. C. S = 33. D. S =17 . min min min min Lời giải Chọn. A.
Điều kiện để phương trình có nghĩa và có nghiệm là x > 0 và 2
b − 20ab > 0 +) Xét phương trình 2
a ln x + bln x + 5 = 0 .
Đặt t = ln x . Khi đó pt 2
⇔ at + bt + 5 = 0
Phương trình có nghiệm t = ln x ,t = ln x là hai nghiệm của phương trình, theo định lí Viét ta có: 1 1 2 2 b t + t = ln b − a
x x = − ⇔ x x = e . 1 2 1 2 1 2 a +) Xét phương trình 2
5log x + blog x + a = 0
Đặt u = log x . Khi đó: Pt 2
⇔ 5u + bu + a = 0 .
Giả sử u = ln x ,u = ln x là hai nghiệm của phương trình, theo định lí Viets, ta có 1 3 2 4 b
u + u = log(x x ) b − 5 = − ⇔ x x =10 . 1 2 3 4 3 4 5 b b b Do đó − − b − a 5 5
x x > x x ⇔ e >10 ⇔ − > ln10 1 2 3 4 a b b 1 ln10 5 ⇔ − > − ln10 ⇔ < ⇔ a > a a a 5 ln10 Theo giả thiết: *
a ∈ N ⇒ a ≥ 3 2 *
b − 20a > 0,b∈ N ⇒ b ≥ 8 Vậy ta có
S = 2a + 3b ≥ 2.3+ 3.8 = 30 ⇒ S = 30 . min
Câu 33: Khối đa diện nào sau đây có các mặt không phải là tam giác đều?
A. Khối bát diện đều.
B. Khối mười hai mặt đều.
C. Khối tứ diện đều.
D. Khối hai mươi mặt đều. Trang 20/29 - Mã đề 235 Lời giải Chọn B
Khối mười hai mặt đều có các mặt là ngũ giác đều.
Câu 34: Mệnh đề nào sao đây đúng?
A. Hình bát diện đều có 8 đỉnh, 12 cạnh và 6 mặt.
B. Hình bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
C. Hình bát diện đều có 6 đỉnh, 8 cạnh và 8 mặt.
D. Hình bát diện đều có 8 đỉnh, 12 cạnh và 8 mặt. Lời giải Chọn B
Hình bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
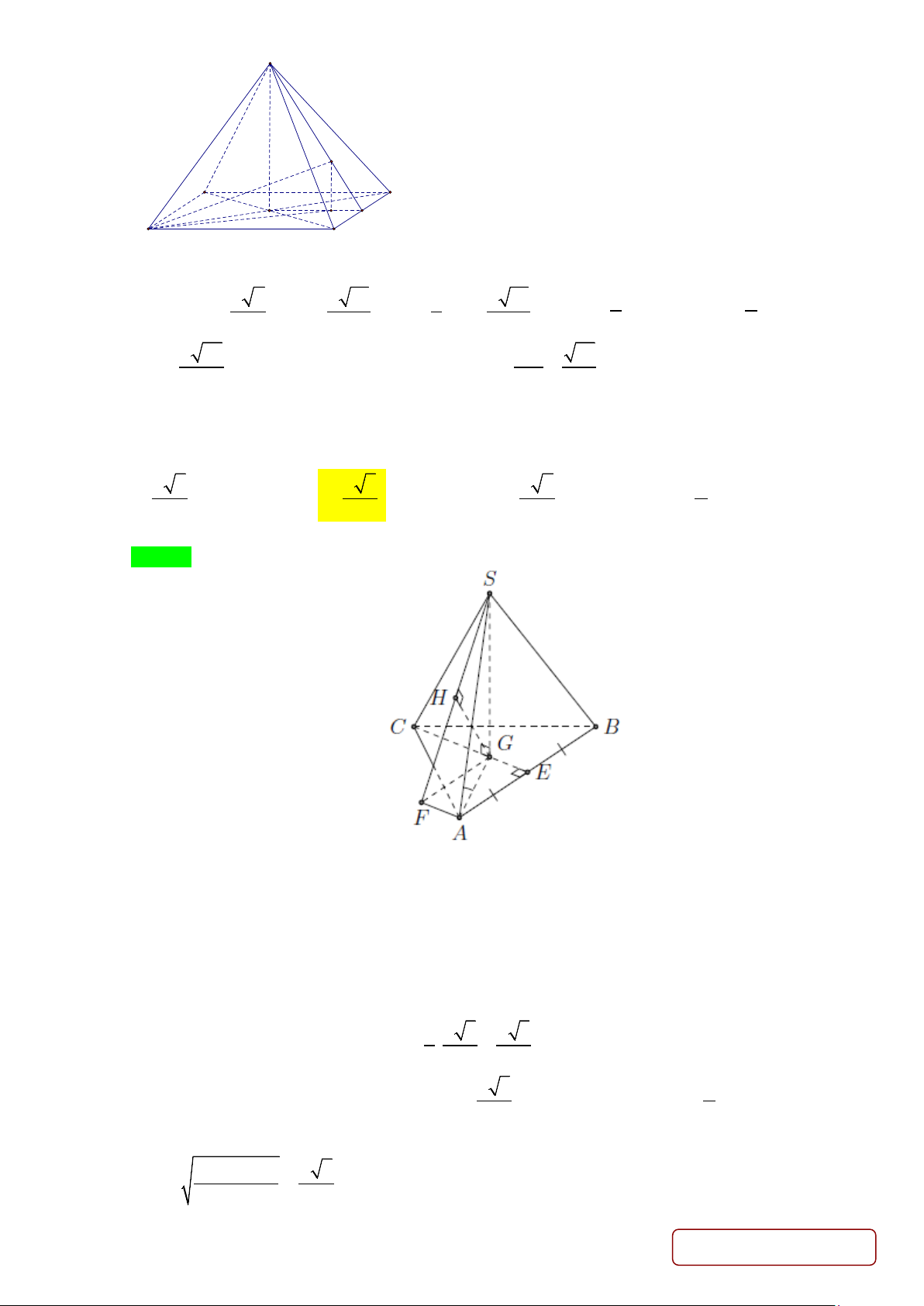
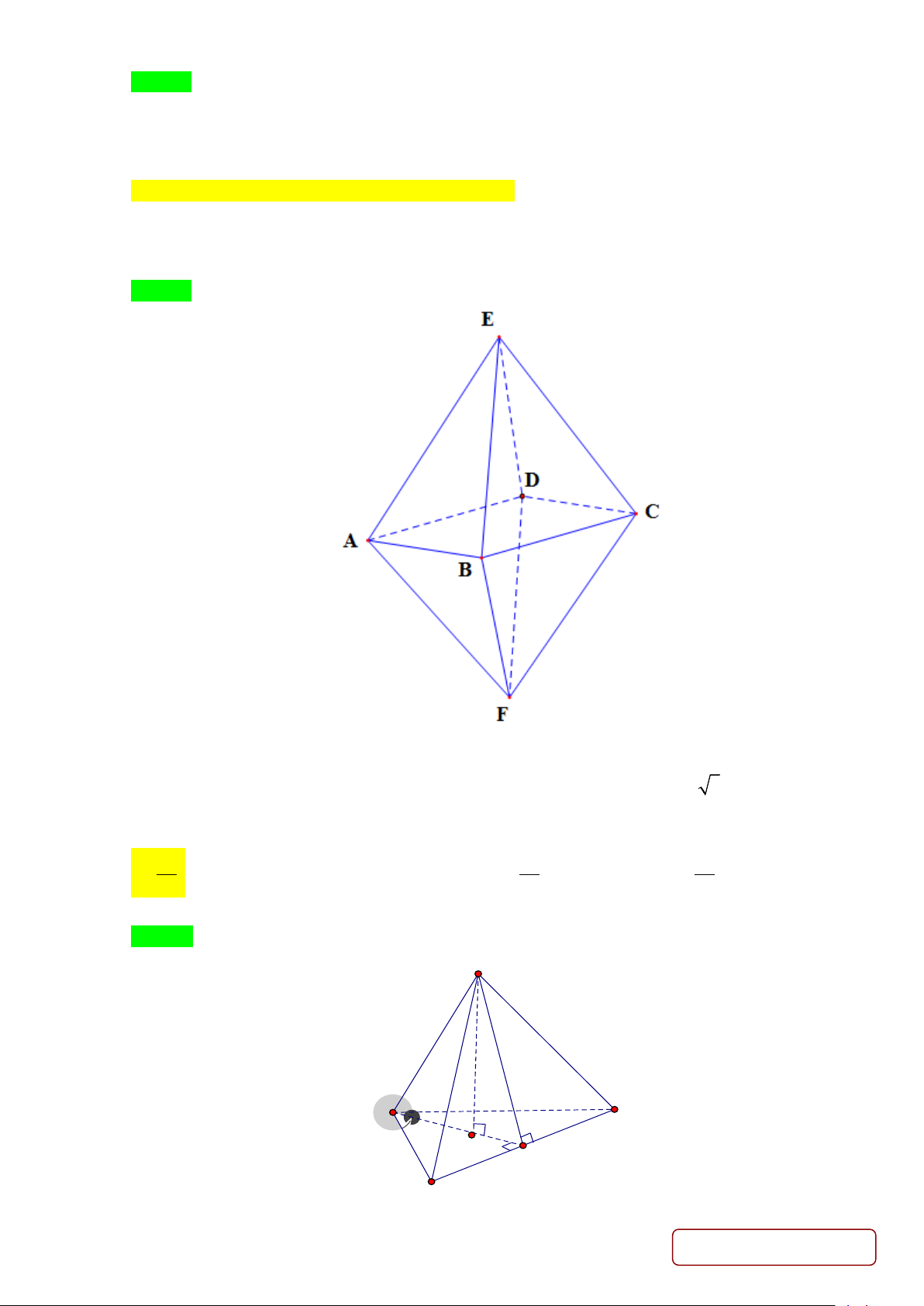
Câu 35: Cho hình chóp S.ABC có đáy là tam giác cân tại 0 , A 120 BAC =
và BC = a 3. Biết
SA = SB = SC = 2 .
a Tính thể tích V của khối chóp S.ABC . 3 3 3 A. a . B. 3 a . C. a . D. a . 4 2 3 Lời giải Chọn A S A C 60° H M B Trang 21/29 - Mã đề 235
Gọi M là trung điểm BC ⇒ AM ⊥ BC.
Gọi H là hình chiếu vuông góc của S xuống đáy. Vì SA = SB = SC nên H là tâm đường tròn ngoại
tiếp tam giác ABC ⇒ H ∈ AM.
Xét tam giác vuông ABM : BM = = = , AB a AB AC a AM = = . 0 sin 60 2 2 2 1 a 3 Diện tích tam giác 0 ABC : S = AB AC = ABC . sin120 . 2 4 a Xét tam giác vuông 2 2 13
SBM : SM = SB − BM = . 2
SA+ AM + SM 5 + 13 p = = . a SAM 2 4 Diện tích tam giác : 2 a 3 1 a S
= p p − SA p − AM p − SM =
= SH ⇒ SH = a SAM ( )( )( ) . 3. 4 2 2 2 3 1 a 3 a
Thể tích của khối chóp S.ABC :V = a = S ABC . . 3 . . . 3 4 4
Câu 36: Tính thể tích V của khối lăng trụ tứ giác đều ABC . D A′B C ′ D
′ ′ biết độ dài cạnh đáy bằng 2a đồng
thời góc tạo bởi A′C và đáy ( ABCD) bằng 30° . 3 3 A. 8 6a V = . B. 8 6a 3 V = 24 6a . C. 3 V = 8 6a . D. V = . 3 9 Lời giải Chọn A A' D' B' C' D A B 2a C
Ta có góc tạo bởi A′C và đáy ( ABCD) là góc A′CA = 30° , và AC = 2 2a , suy ra và ′ = ′ 1 2 6
AA A C tan A′CA = 30° = .2 a 2 = .a . 3 3 3 ⇒ = ( )2 2 6 8 6 2 . . a V a a = . 3 3
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a . Góc A bằng 0
60 , O là tâm hình thoi,
SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng 0
45 . Tính theo a thể tích khối chóp S.ABCD . 3 3 A. 3 2a . B. 3 3 2a . C. 3a . D. a . 8 4 Trang 22/29 - Mã đề 235 Lời giải Chọn D. S A B D O A C D O B C
Ta có: (SO ( ABC )) = (SO AO) = 0 ; D ; SOA = 45 ⇒ S
∆ AO vuông cân tại A. a 3 ⇒ SO = AO = ( ABD ∆ đều ) . 2 2 2 a 3 a 3 S = S = = . ABCD 2 ABD ∆ 2 4 2 2 3 1
1 a 3 a 3 a ⇒ V = SA S = = . S ABCD . ABCD . . . 3 3 2 2 4
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a và SA vuông góc với đáy.
Gọi M là trung điểm của SB , N là điểm thuộc SD sao cho SN = 2ND . Tính thể tích khối tứ diện ACMN . A. 1 3 V = a . B. 1 3 V = a . C. 1 3 V = a . D. 1 3 V = a . 36 6 8 12 Lời giải Chọn D S M N A D B C Ta có V = V − V +V +V +V . ACMN S.ABCD
( S.AMN S.CMN M.ABC N.ACD ) Với 1 1 3 V = SA S = a S ABCD . . 3 ABCD 3 V SM SN 3 1 a 1 S AMN 1 2 1 . = . = . = , mà V = V = suy ra 3 V = a . V SB SD S.ABD S. 2 ABCD 6 S.AMN 18 S ABD 2 3 3 . Trang 23/29 - Mã đề 235 Tương tự 1 3 V = a S.CMN 18 Lại có 1 1 3 V = V = a ; 1 1 3 V = V = a . M .ABC S. 2 ABC 12 N.ACD S. 3 ACD 18 Vậy 1 3 1 1 1 1 3 1 3 V = a − + + + a = a . ACMN 3 18 18 12 18 12
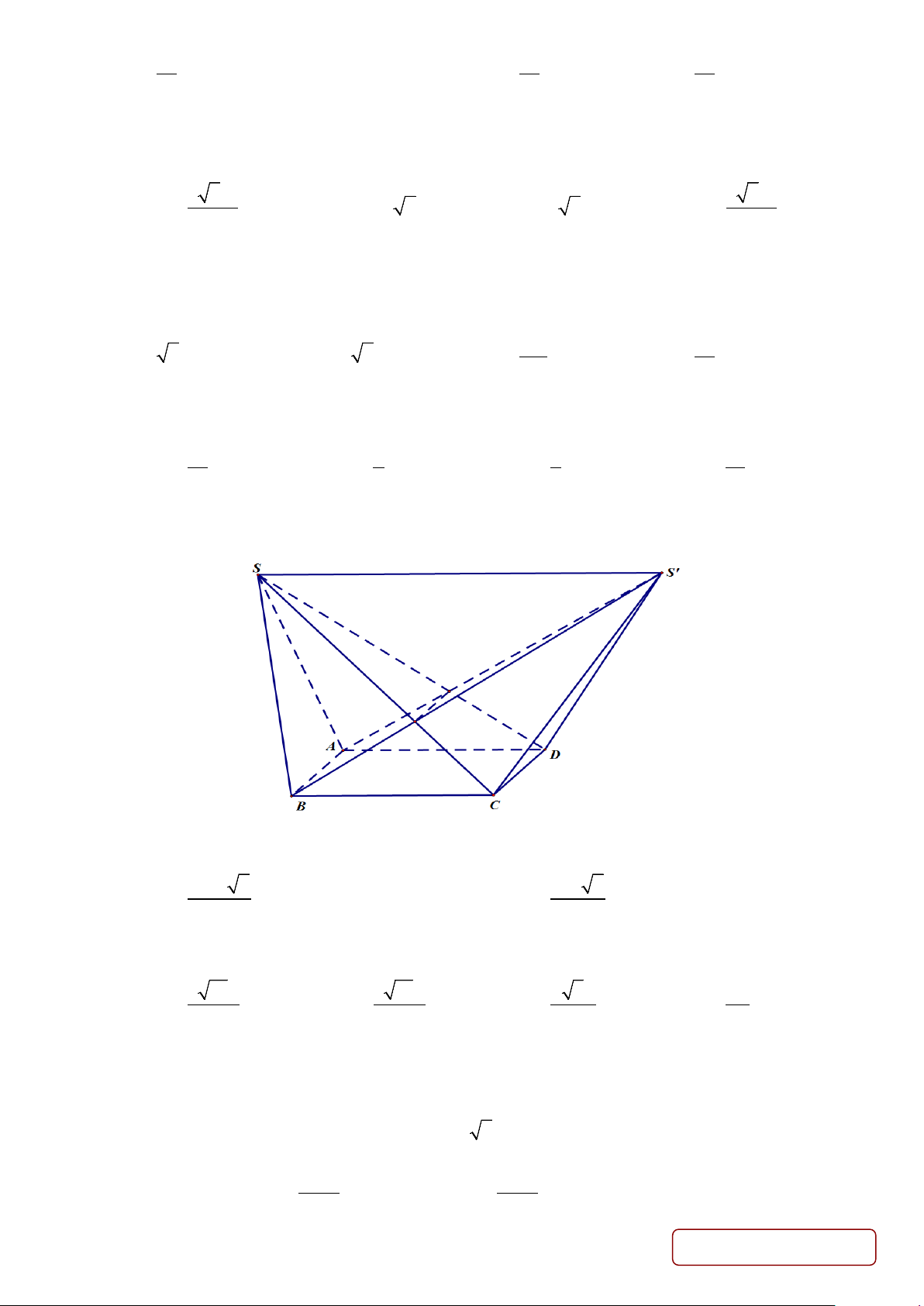
Câu 39: Cho hình chóp S.ABCD có đáy là hình bình hành và thể tích V = 270 . Lấy điểm S′ trong không gian sao cho SS′ = 2
− CB . Tính thể tích phần chung của hai khối chóp S.ABCD và S .′ABCD . A. 120. B.150. C. 180. D. 90. Lời giải Chọn A. Gọi E = S A
′ ∩ SD , F = S B
′ ∩ SC . Phần chung của hai khối chóp S.ABCD và S .′ABCD là đa diện ABCDEF .
Ta có: VABCDEF = S
V .ABCD − S V .ABFE . SF SS′ SS′//BC ⇒ = = 2 . FC BC′ SS′//AD SE SS ⇒ = = 2. ED AD 1 S
V .ABC = S
V .ACD = S V . . 2 ABCD S V .ABF SF 2 2 1 = = ⇒ S
V .ABF = S
V .ABC = S V .ABCD . S V .ABC SC 3 3 3 Trang 24/29 - Mã đề 235 S V .AFE SF SE 4 4 2 = . = ⇒ S
V .AFE = S
V .ACD = S V .ABCD . S V .ACD SC SD 9 9 9 Suy ra: 5 S
V .ABFE = S
V .ABF + S
V .AFE = S V .ABCD =150. 9
Vậy: VABCDEF = S
V .ABCD − S V .ABFE =120.
Câu 40: Tính thể tích của hình nón có góc ở đỉnh bằng 60° và diện tích xung quanh bằng 2 6π a 3 3 A. 3π a 2 π V = . B. 3 V = 3π a . C. a 2 V = . D. 3 V = π a . 4 4 Lời giải Chọn B. A 30° l r B O C
Tam giác ABC đều cạnh l , bán kính l r = , chiều cao l 3 h = thể tích khối nón là 2 2 2
S = π rl = π a 2 2 2
⇒ rl = 6a ⇒ l =12a . xq 6 2 1 2 1 l l 3 1 2
V = π r h = π. . = πl .l. 3 1 2 3 =
π.12a .2a 3. 3 = 3π a . 3 3 4 2 24 24
Câu 41: Hình chóp S.ABC đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong
mặt phẳng vuông góc với đáy. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABC . A. 5 15π π π π V = . B. 5 15 V = . C. 4 3 V = . D. 5 V = . 18 54 27 3 Lời giải Chọn B
Gọi H là trung điểm của AB . Trang 25/29 - Mã đề 235 (
SAB) ⊥ ( ABC) Ta có: (
SAB) ∩ ( ABC) = AB ⇒ SH ⊥ ( ABC) . SH ⊂
(SAB);SH ⊥ AB
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . Qua O dựng đường thẳng song song với SH ,
cắt SC tại K . Khi đó đường thẳng OK là trục đường tròn ngoại tiếp đáy của hình chóp S.ABC .
Gọi M là trung điểm của BC . Dựng mặt phẳng trung trực của BC , mặt phẳng này cắt đường thẳng
OK tại I . Điểm I là tâm mặt cầu ngoại tiếp hình chóp S.ABC .
Do OK //SH nên: OK CO 2 2 2 3 3 =
= ⇒ OK = SH = . = . SH CH 3 3 3 2 3 CK CO 2 2 2 1 2 1 =
= ⇒ CK = SC ⇒ CM + MK = SC ⇒ SC + MK = SC ⇒ MK = SC SC CH 3 3 3 2 3 6 1 2 2 6 ⇒ MK = SH + CH = 6 12 Dễ thấy S
∆ HC vuông cân tại H ⇒ =
OKC HSC = 45 ⇒ IMK ∆ vuông cân tại M 3 ⇒ IK = 2MK = . 6 Ta có: 3 2 2 2 2 15
OI = OK − IK =
⇒ R = IC = OI + OC = OI + OK = . 6 6
Thể tích khối cầu ngoại tiếp hình chóp S.ABC là: 4 3 5 15π V = π R = . 3 54
Câu 42: Cho mặt cầu (S ) tâm O có diện tích bằng 2
400π cm . Mặt phẳng (P) cách tâm O một khoảng bằng
6cm và cắt mặt cầu (S ) theo thiết diện là một đường tròn. Tính bán kính r của đường tròn đó.
A. r = 7cm .
B. r = 10cm .
C. r = 40cm .
D. r = 8cm . Lời giải Chọn D
Gọi R là bán kính mặt cầu , ta có diện tích mặt cầu: 2
S = 4π R = 400π ⇔ R = 10cm
Mặt phẳng (P) cách tâm O một khoảng bằng 6cm và cắt mặt cầu (S ) theo thiết diện là một đường
tròn bán kính r , ta có: 2 2 2
r = R − d (O (P)) 2 2 ,
= 10 − 6 = 64 ⇔ r = 8cm.
Câu 43: Cho tam giác vuông cân ABC có AB = BC = a 2 . Khi quay tam giác ABC quanh đường thẳng đi
qua B và song song với AC ta thu được một khối tròn xoay có thể tích bằng 3 3 A. π π 3 2π a . B. 2 a . C. 4 a . D. 3 π a . 3 3 Lời giải Chọn C Trang 26/29 - Mã đề 235
AC = 2a ; OA = OB = a ; O B ′ = O C ′ = a .
Thể tích khối trụ tròn xoay sinh ra khi cho hình chữ nhật AOO C
′ quay quanh OO′ là 2 2 3
V = π OA AC = π a .2a = 2π a . T . .
Thể tích khối nón đỉnh B , đáy là đường tròn tâm O là 1 2 V = π OA OB 1 2 = π a .a 1 3 = π a . N . . 3 3 3 3 π 3 π
Thể tích khối tròn xoay cần tìm là V = V − V 3 = 2π − 2. a a 4 a = . T 2 N 3 3
Câu 44: Cho hai khối nón có chung trục SS′ = 3r . Khối nón thứ nhất có đỉnh S , đáy là hình tròn tâm S′
bán kính 2r . Khối nón thứ hai có đỉnh S′ , đáy là hình tròn tâm S bán kính r . Thể tích phần
chung của hai khối nón đã cho bằng 3 3 3 3 A. 4π r π π π . B. r . C. 4 r . D. 4 r . 27 9 9 3 Lời giải Chọn C
Ta có phần chung của hai khối nón đã cho gồm hai hình nón (H là hình nón đỉnh S bán kính 1 ) IH
và (H là hình nón đỉnh S′ bán kính 2 ) IH SH SA r 1 S ∆ AH SH 1 B ∆ S H ′ ⇒ = = = ⇒ = . HB S B ′ 2r 2 SB 3 IH SH 1 2r S ∆ IH S ∆ S B ′ ⇒ = = ⇒ IH = . S B ′ SB 3 3
Thể tích phần chung của hai khối nón đã cho bằng 2 3 1 2 1 2 1 2 = + π = π ( + ) 1 2 1 2r 4π π . . . = π . = π ′ ′ ′ .3 r V IH SI IH S I IH SI S I IH SS r = . 3 3 3 3 3 3 9 Trang 27/29 - Mã đề 235 2
Câu 45: Họ các nguyên hàm của hàm số f (x) 3x + 4 = trên khoảng (0;+∞) là x 2 A. 4 3 3 − + C . B. 2 3x x + 4ln x + C C.
+ 4ln x + C . D. 3
x + 4nx + C . 2 x 2 Lời giải Chọn C 2 2 2 Ta có 3x + 4 4 3x 3 d = 3 + d = + 4ln x x x x x + C = + 4ln x + ∫ ∫ C . x x 2 2 4 f (2 − x ) 4 f (2 − x ) Câu 46: Xét dx ∫
. Nếu đặt u = 2 − x thì dx ∫ bằng 1 x x 1 x x 4 f (u) 2 f (u) 1 f (u) 1 f (u) A. 2 du ∫ . B. 2 du 2 du 2 − du ( ∫ . C. ∫ . D. ∫ . u − 2)2 2 2 2 1 1 (u − 2) 0 (u − 2) 0 (u − 2) Lời giải Chọn C
Theo giả thiết: u = 2 − x ⇒ x = 2 − u ⇒ x = ( −u)2 2
Khi đó: dx = 2(u − 2)du .
Đổi cận: x =1 u =1, x = 4 u = 0. 4 f (2 − x )
0 f u .2. u − 2 1 f (u) Ta có: I = dx ∫ ( ) ( ) ⇒ I = du ∫ = 2 du 3 ∫ . 2 1 x x 1 (2−u) 0 (u − 2) 2 Câu 47: Cho
x +1 dx = ln(lna+b) ∫
với a,b là các số nguyên dương. Giá trị biểu thức ab + a + b bằng 2
x + x ln x 1 A. 8 . B. 11. C. 15. D. 7 . Lời giải Chọn A. 1 2 2 1+ 2 Có x +1 x d(x + ln x) 2 dx = dx =
= ln (x + ln x) = ln(ln 2 + 2) ∫ 2 ∫ ∫ 1
x + x ln x x + ln x x + ln x 1 1 1
Vậy a = b = 2 ⇒ ab + a + b = 8 . ln3 x + Câu 48: Cho e = − + ln c d dx a b ∫
với a,b,c là các số nguyên dương. Giá trị biểu thức 1 x + e +1 9 0
a + b + c + d bằng A. 21. B. 15. C. 23. D. 27 . Lời giải Chọn C. Đặt x t = e +1 2 x ⇒ t = e +1 x 2 ⇒ e = t −1 x
⇒ e dx = 2tdt .
Đổi cận x = 0 ⇒ t = 2 ; x = ln 3 ⇒ t = 2 . Khi đó 2 2 (2tdt) 2 2 3+ 8 I = = (2 −
)dt = (2t − 2ln | t +1|) = 4 − 8 + ln( ) ∫ 1 ∫ . + t t +1 2 9 2 2
Vậy a = 4,b = 8,c = 3,d = 8 và a + b + c + d = 23. Trang 28/29 - Mã đề 235
Câu 49: Cho hàm số f (x) có f (0) = 4, f ′(0) = 2
− f ′′(x) = x( x + )3 2 2 1 , x ∀ ∈ .
Tích phân 1 f (x)dx ∫ bằng 0 A. 7909 B. 7211 C. 12949 D. 5389 2520 2520 2520 2520 Lời giải Chọn A
Tích phân từng phần, ta có: 1 f (x) 1
dx = f (x)d (x − ) 1 = (x − ) 1 f (x)1 1 − (x − ∫ ∫ ∫
)1f ′(x)dx 0 0 0 0 2 = f ( ) 1 − x − f ′ ∫
(x)dx = f ( ) 1 − f ′ ∫ (x) x 1 0 ( 1) 0
d − x + 0 0 2 2 1 2 2 = f ( ) x 1
− − x + f ′(x) 1 x 1 0
+ ∫ − x + f ′′(x)dx 0 2 2 2 2 0 2 = f ( ) 1 + f ′( ) 1 x 1 0
0 + ∫ − x + x(2x + )3 2 1 dx 0 2 2 2 2 1 1 x 1
= + × − + ∫ − x + x( x + )3 2 7909 4 ( 2) 2 1 dx = 0 2 2 2 2520 2 1
Câu 50: Cho hàm số f (x) liên tục trên và f (2) =16, f
∫ (x)dx = 4. Tính I = .xf ′ ∫ (2x)dx . 0 0 A. 13. B. 12. C. 20 . D. 7 . Lời giải Chọn D
Đặt t = 2x ⇒ dt = 2dx .
Đổi cận: x = 0 ⇒ t = 0; x =1⇒ t = 2 2 1 I = tf ′ ∫ (t)dt 4 0 u = t du = dt Đặt ⇒ dv = f (t)dt ′
v = f (t) 2 1
I = tf (t) 2 − f ∫ (t) 1
dt = (2 f (2) − 0 f (0) − 4) = 7 4 0 4 0 Trang 29/29 - Mã đề 235