
Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG LỚP 9 QUẬN ĐỐNG ĐA
NĂM HỌC 2023 - 2024 Môn: TOÁN Ngày khảo sát: 17/4/2024
Thời gian làm bài: 120 phút
Bài I (2,0 điểm) 2 x + 6 x + 2 x
Cho hai biểu thức : A = B = −
với x 0; x 1 x − và 1 x + x − 2 x + 2
1) Tính giá trị biểu thức A khi x = 9. 2) Rút gọn B . A 3) Chứng minh 6 . B
Bài II (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một ô tô đi từ A đến B dài 90km. Khi về ô tô đi theo đường khác dài hơn 10km và mỗi giờ ô tô
đi được nhiều hơn lúc đi 10km nên thời gian về ít hơn thời gian đi là 15 phút. Tính vận tốc lúc đi và lúc về?
2) Một lon nước ngọt hình trụ có đường kính đáy là 6cm, độ dài trục là 11cm. Tính thể tích lon
nước ngọt (cho 3,14)
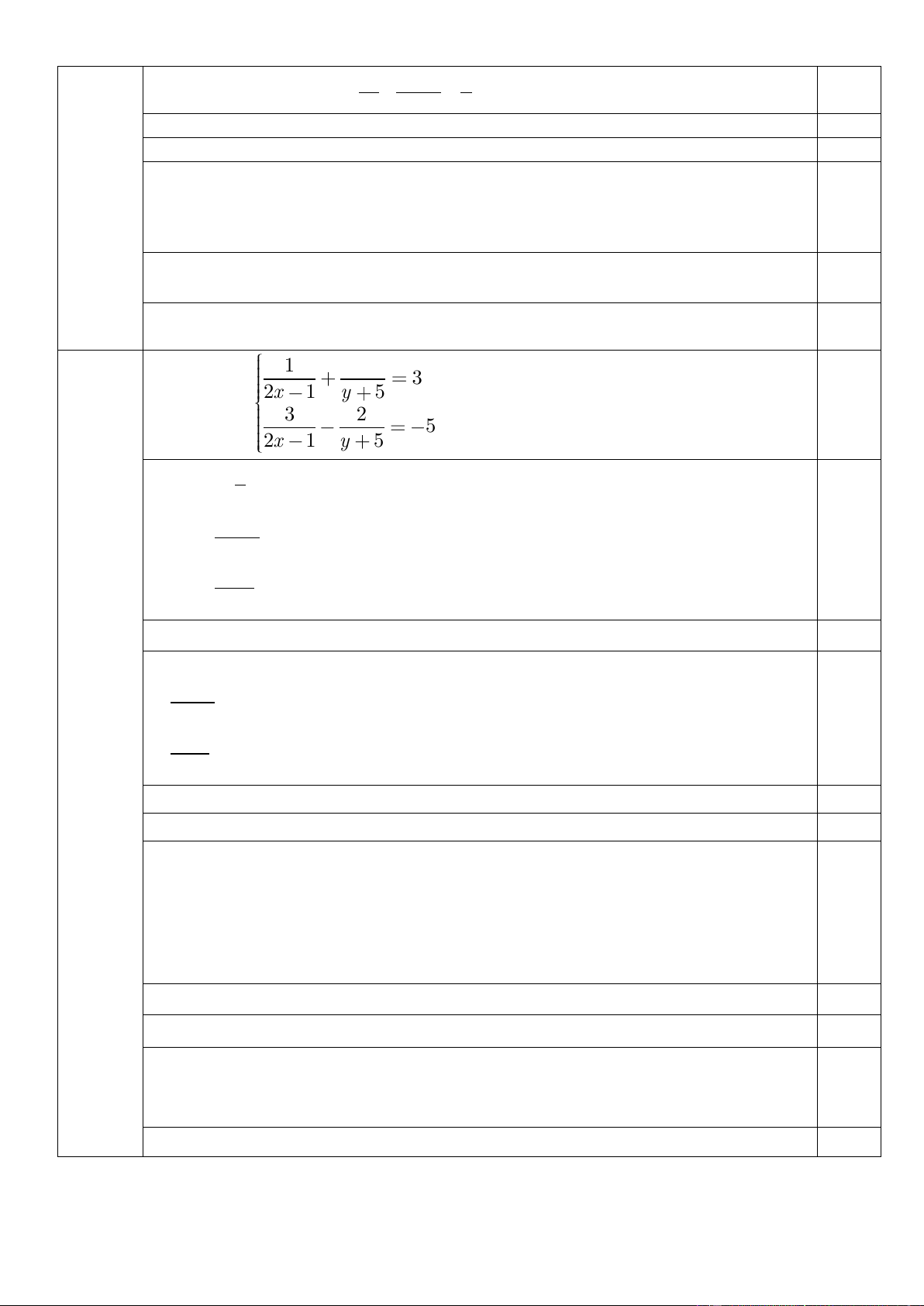
Bài III (2,0 điểm) 1 4 3 2x 1 y 5
1) Giải hệ phương trình: 3 2 5 2x 1 y 5
2) Trong mặt phẳng tọa độ Oxy , cho parabol 2 (P) : y
x và đường thẳng (d) : y mx m 1
( m là tham số).
a) Tìm m để (d) cắt ( P) tại hai điểm phân biệt.
b) Gọi x , x là hoành độ giao điểm của (d) và ( P) . Tìm tất cả các giá trị của m để 2 x x . 1 2 1 2
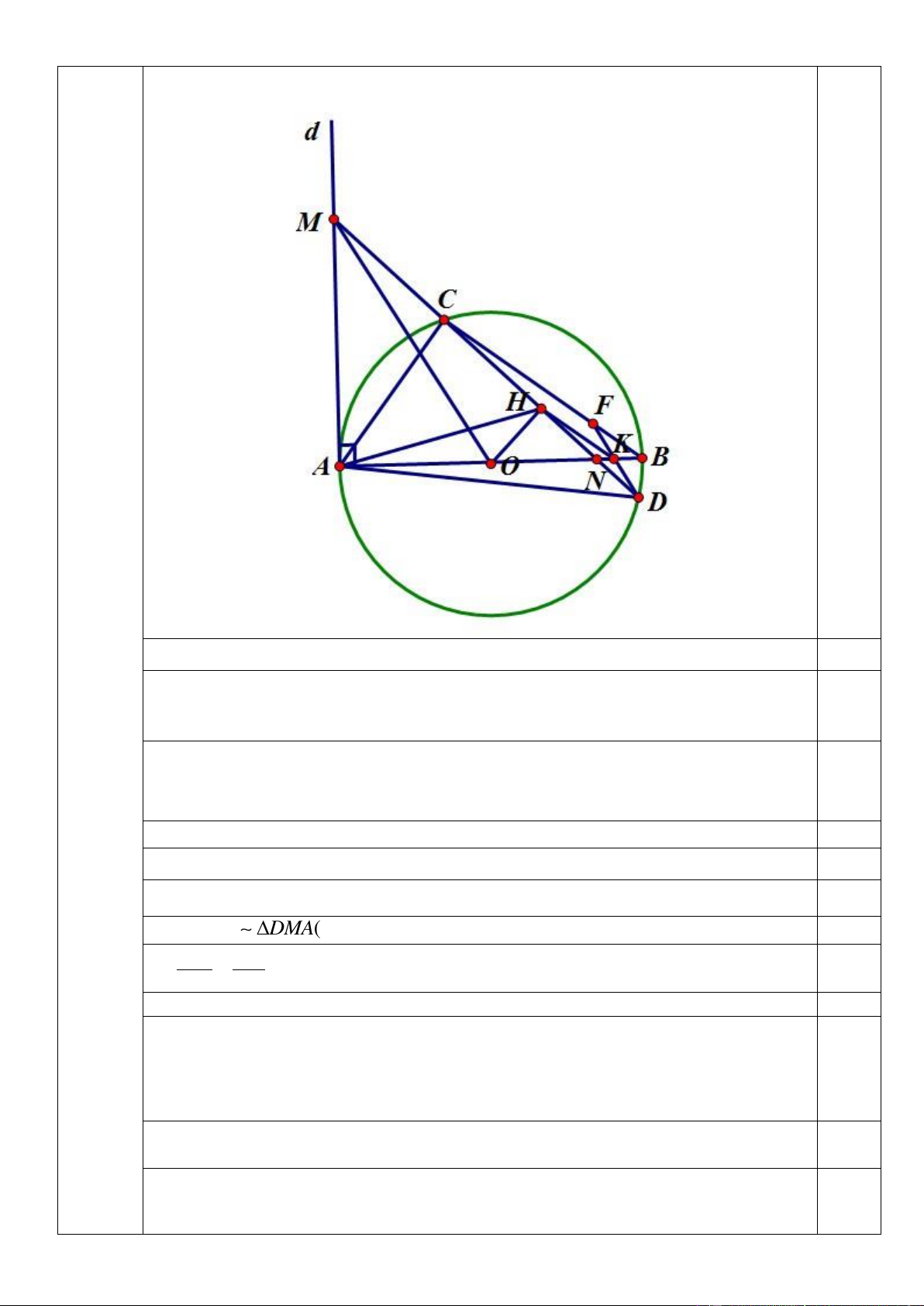
Bài IV (3,0 điểm) Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn
(O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và
B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D (C nằm giữa M và D). Gọi H là trung
điểm của đoạn thẳng CD.
1) Chứng minh 4 điểm A, O, H, M cùng nằm trên một đường tròn. 2) Chứng minh 2
MA = MC.MD .
3) Đường thẳng qua D song song với MO cắt AB và BC lần lượt tại K và F. Chứng minh tứ
giác AHKD nội tiếp và K là trung điểm của đoạn thẳng DF.
Bài V (0,5 điểm) Cho hai số thực a và b thoả mãn (a + b − )2 1
= ab . Tìm giá trị nhỏ nhất của biểu 9
thức P = a + b + a + . b ----------HẾT----------
Cán bộ coi thi không giải thích gì thêm.
HƯỚNG DẪN CHẤM KHẢO SÁT TOÁN 9
NĂM HỌC 2023 – 2024
(Ngày khảo sát 17.4.2024) Bài Nội dung Biểu điểm Bài I 2 x + 6 + 2đ = x 2 x = − 2,0
Cho hai biểu thức : A và B với x 0; x 1 x −1 x + x − 2 x + 2 điểm
1) Tính giá trị biểu thức A khi x = 9. 0.5đ
+ Thay x = 9 (TMĐK) vào biểu thức A ta đc : 0.25đ 2 9 + 6 12 3 A = = = 9 −1 8 2 3
Vậy giá trị của biểu thức A = khi x = 9 0.25đ 2
2) Rút gọn B (đk : x 0; x 1) 1đ x + 2 x x + 2 x B = − = − 0,25 x + x − 2 x + 2
( x +2)( x − )1 x +2 x + 2 − x ( x −1) + − + 0,25 = x 2 x x ( = x + 2)( x − ) 1
( x +2)( x − )1 x + 2 0,25 = ( x + 2)( x − ) 1 1 =
với x 0; x 1 x −1 0,25 A 0.5đ 3) Chứng minh 6 . B A 2 x + 6 4 = = 2 +
với x 0; x 1 B x +1 x +1 0.25đ 4 2 +
2 + 4 = 6 với x 0; x 1 x +1 0.25đ Bài II
1. Một ô tô đi từ A đến B dài 90km. Khi về ô tô đi theo đường khác dài hơn 2.5
10km và mỗi giờ ô tô đi được nhiều hơn lúc đi 10km nên thời gian về ít hơn 2đ điểm
thời gian đi là 15 phút. Tính vận tốc lúc đi và lúc về?
+ Gọi vận tốc ô tô lúc đi từ A đến B là x (km/h; x >0); đổi 15 phút = 0.25đ 1 90 (h)
+ Thời gian ô tô đi từ A đến B là: ( 0.25đ h) 4 x
+ Vận tốc ô tô đi từ B về A là : x + 10 (km/h) 0.25đ 90 +10 100
+ Thời gian ô tô đi từ B về A là: = (h ) x +10 x +10 0.25đ
=> Ta có phương trình : 9 0 100 1 − = 0.25đ x x +10 4
+ Giải phương trình thu được x = 40 (tmđk) và x = - 90 (loại) 0.5đ + Kết luận 0.25đ 0.5đ
2) Một lon nước ngọt hình trụ có đường kính đáy là 6cm, độ dài trục là
11cm. Tính thể tích lon nước ngọt ( cho 3,14)
Ta có R= 3cm, h=11cm nên V= R2h = 3,14.9.11= 310,86 (cm3) 0.25đ
Vậy thể tích của lon nước ngọt là 310,86 cm3. 0.25đ Bài III 1 4 3 2,0 2x 1 y 5 1đ điểm 1) Giải hệ : 3 2 5 2x 1 y 5 + Đk: 1 0.25đ x ; y 5 − 2 1 = a − + Đặ 2x 1 t 1 = b y + 5 + Giải được a = 1 − ;b =1. 0.25đ Thay: 1 + = 1 − 2x −1 = 1 − x = 0 (tmđk) 2x −1 0.25đ 1 +
=1 y + 5 =1 y = 4 − (tmđk) y + 5
+ Kết luận………………. 0.25đ 2) 1đ
a) Xét phương trình hoành độ giao điểm của đường thẳng (d) và parabol ( ) P : 2
x = mx − m +1 2
x − mx + m −1 = 0 (1)
a + b + c = 1− m + m −1 = 0 0.25đ
nên phương trình (1) có nghiệm 1 và m −1 + Vì (d) cắt ( )
P tại hai điểm phân biệt nên 1 m −1 m 2 0.25đ
b) x ,x thỏa mãn 2 x = x . 0,5đ 1 2 1 2 m = 2(TM ) 0.25đ TH1: = (m − )2 1 1 m = 0(TM ) Vậy m = 0 thì…. TH2: 2
1 = m −1 m = 2(TM ) 0.25đ
Bài IV Vẽ hình đúng đến câu 1) 3,0 điểm 0,25đ
1) Chứng minh 4 điểm : A, O, H, M cùng nằm trên một đường tròn. 0.75đ
Vì MA là tiếp tuyến của ( ) O 0 MAO = 90
H là trung điểm của CD OH ⊥ CD tại H 0
OHC = OHM = 90 0.25đ
Xét tứ giác AOHM có: 0 0 0
MAO + OHM = 90 + 90 = 180 mà hai góc này là hai
góc đối nhau nên tứ giác AOHM là tứ giác nội tiếp 0.25đ
4 điểm : A, O, H, M cùng nằm trên một đường tròn (đpcm) 0.25đ
2) Chứng minh rằng: 2
MA = MC.MD 1đ 0.25đ Xét A MC và D
MA ta có: M chung; MDA = MAC 0.25đ (cùng chắn AC) A MC D M ( A g.g) 0.25đ AM MC 2 =
MA = MC.MD(dpcm) DM MA 0.25đ
3) Chứng minh tứ giác AHKD nội tiếp và K là trung điểm của đoạn thẳng DF. 1đ
Ta có: DK // MO (gt) MDK = DMO (hai góc so le trong)
Vì AOHM là tứ giác nội tiếp (cm câu a) HMO = HAO (cùng chắn OH )
BAH = MDK (= DMO) 0.25đ
Tứ giác AHKD là tứ giác nội tiếp (hai đỉnh kề cùng nhìn cạnh đối diện dưới các 0.25đ góc bằng nhau)
Tứ giác AHKD nội tiếp DAK = DHK (góc nội tiếp cùng chắn DK) 0.25đ
DAB = DCB (góc nội tiếp cùng chắn BD) DCB = DHK Mà DC ,
B DHK ở vị trí đồng vị nên HK // CB => HK // CF . Mặt khác H là trung điể 0.25đ
m của CD => K là trung điểm của DF Bài V
Cho hai số thực a và b thoả mãn (a + b − )2 1
= ab . Tìm giá trị nhỏ nhất của biểu 0,5 điểm 9
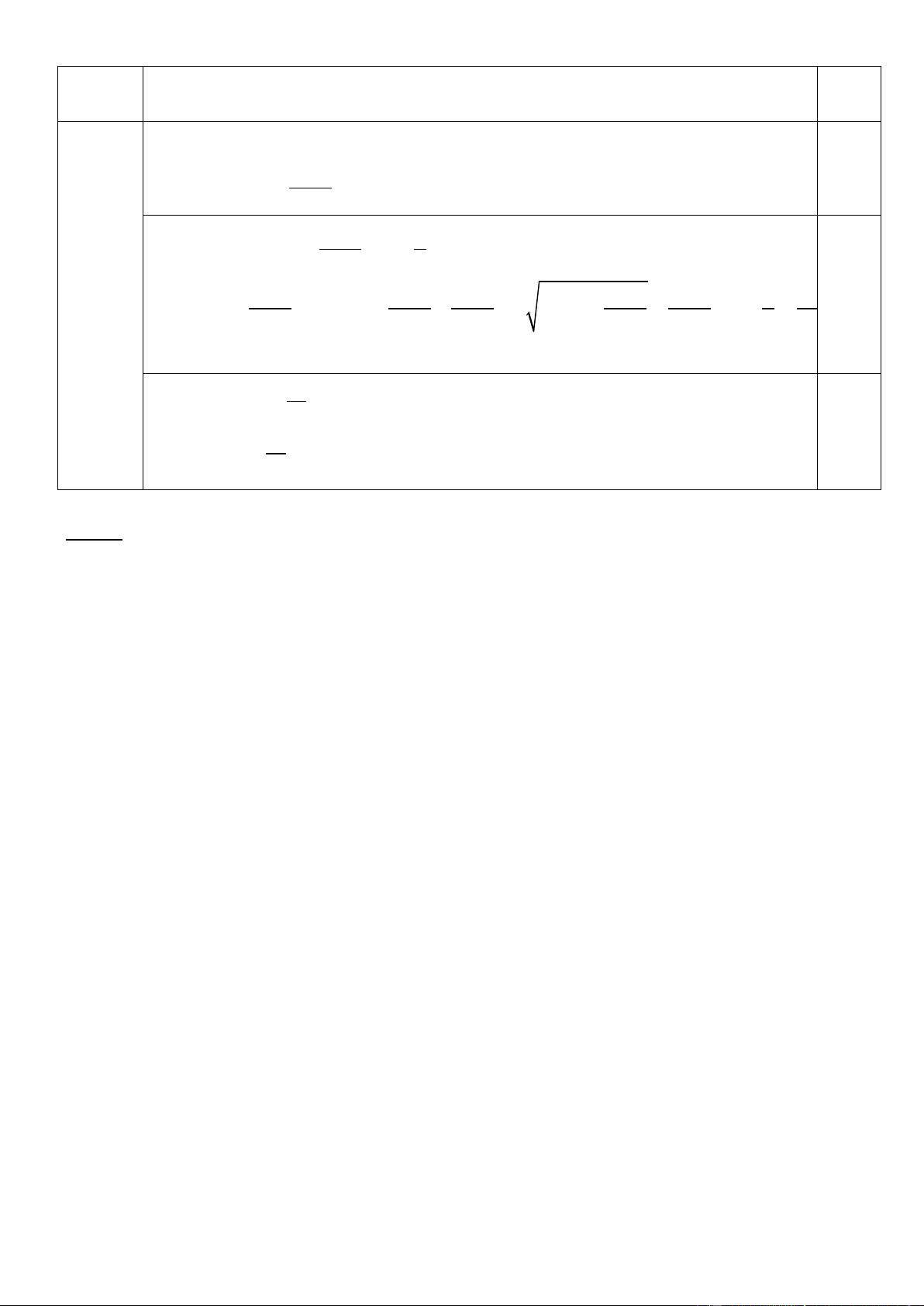
thức P = a + b + . a + b 2 ( + a + b − )2 a b 2 1 = ab
a + b 2 2 3 9
P = a + b + = (a + b) 4 5 + + (a +b) 4 5 5 13 2 . + 4 + = a + b a + b a + b a + b a + b 2 2 0.25đ Dấu “=” có 13 P = . Khi a = b = 1 2 13 0.25đ KL: Min P = , khi a = b = 1 2
Lưu ý: Các cách làm khác nếu đúng vẫn cho điểm tối đa.




