PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT HỌC SINH GIỎI LỚP 8 HUYỆN GIA VIỄN
NĂM HỌC 2023 – 2024 MÔN: TOÁN (ĐỀ CHÍNH THỨC)
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề này gồm 05 câu, 02 trang) Câu 1 (5,5 điểm).
1. Phân tích các đa thức sau thành nhân tử: a) 5 4 3 2
2x − 3x + 6x −8x + 3 b) (x y)3 + ( y z)3 + (z x)3 – – – 2 2 2. Cho biểu thức x + x  x +1 1 2 −  = : x P  + + 2 2 x 2x 1  x x 1 x x  − + − − 
a) Tìm ĐKXĐ và rút gọn P . b) Tìm x để 1 P − = . 2
c) Tìm giá trị nhỏ nhất của P khi x >1
Câu 2 (3,0 điểm).
1. Cho a,b,c đôi một khác nhau thỏa mãn: 2 2 2 2
(a + b + c) = a + b + c Chứng minh rằng: a b c + + = 0 2 2 2
a + 2bc b + 2ca c + 2ab 2. Cho đa thức: 3 2
f (x) = x + ax + bx + c với a, b,c là các số thực . Biết đa thức f(x) chia cho
đa thức x + 1 dư – 4 và chia cho đa thức x – 2 dư 5. Tính giá trị của 2025 2025 2025 2025 2025 2025 A = (a + b )(b − c )(c + a )
Câu 3 (4,0 điểm).
1. Giải phương trình: ( 2x − x + )2 − (x + )2 = ( 3 3 1 2 1 5 x + ) 1
2. Tìm tất cả các cặp số nguyên (x, y) thỏa mãn đẳng thức: 2 2
x + 2y + 2xy + y − 2 = 0
Câu 4 (6,0 điểm).
1. Cho hình chop S.ABC có đáy là tam giác đều ABC cạnh bằng 3a và cạnh bên SA bằng
2a(với a>0). Tính độ dài đường cao của hình chóp và thể của hình chóp.
2. Cho tam giác ABC vuông cân tại A . Trên tia đối của tia AC lấy điểm M sao cho
0 < AM < AC . Gọi K là hình chiếu vuông góc của M trên BC , MK cắt AB tại H . Gọi
E, F lần lượt là trung điểm của CH và BM , O là điểm cách đều ba điểm B,C, M . Chứng minh rằng: a) CH = BM b)  0 EAK = 45 c) A .
B BM = AK.CB
d) Các đường thẳng AK, EF, OH đồng quy.
Câu 5 (1,5 điểm).
1) Hai số phân biệt được chọn ngẫu nhiên từ tập hợp { 2; − 1 − ;0;3;4; } 5
và đem nhân với nhau. Hỏi xác suất để tích bằng 0 là bao nhiêu?
2. Cho a,b,c là các số dương thỏa mãn: 2 2 2
a + b + c ≤ abc . Chứng minh: a b c 1 + + ≤ 2 2 2
a + bc b + ca c + ab 2
---------------Hết--------------- UBND HUYỆN ..........
HƯỚNG DẪN CHẤM KSCL HỌC SINH GIỎI
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Môn: Toán 8 Năm học 2023 - 2024 (HDC gồm 04 trang) Câu Đáp án Điểm 1. (1,5 điểm) a) 5 4 3 2 5 4 4 3 3 2 2
2x − 3x + 6x −8x + 3 = 2x − 2x − x + x + 5x − 5x − 3x + 3 4 = x (x − ) 3 − x (x − ) 2
+ x (x − ) − ( 2 2 1 1 5 1 3 x − ) 1 0,25 (x − )2 3 2
1 (2x + x + 6x + 3) 0,25 (x − )2 ( 2 1 x + 3)(2x + ) 1 0,25
b) (x – y)3 + (y – z)3 + (z – x)3
Đặt x – y = a , y – z = b, z – x = c thì a + b + c = 0. 3 3 3 3 3 3 3 3
⇒ (a + b) = (−c) ⇔ a + b + 3ab(a + b) = −c ⇔ a + b + c = 3abc 0,5
Vậy: (x y)3 + ( y z)3 + (z x)3 – – –
= 3(x − y)(y − z)(z − x) 0,25 2. (4,0 điểm) a) (1,5 điểm)
ĐKXĐ: x ≠ 0; x ≠1; x ≠ 1 − 0,25 2 Ta có: x(x + ) 1 (x + ) 1 (x − ) 1 x 2 −  = : x P  + + (  x − )2 1 x  (x − ) 1 x(x − ) 1 x(x − ) 1  0,5 2 2 x(x + ) 1 x −1+ x + 2 x x +1 + = : − x ( ) x 1 = : (x − )2 1 x(x − ) 1 (x − )2 1 x(x − ) 1 0,25 Câu 1
(5,5điểm) x(x+ )1 x(x− ) 2 1 x = ⋅ = (x − )2 1 x +1 x −1 2 0,5 Vậy, x P =
với x ≠ 0; x ≠1; x ≠ 1 − . x −1 b) (1,0 điểm) 2 Để 1 P − =
với x ≠ 0; x ≠1; x ≠ 1 − suy ra x 1 − =
với x ≠ 0; x ≠1; x ≠ 1 − 0,5 2 x −1 2  1 x = 2 2x x 1 ... (2x ) 1 (x ) 1 0  ⇒ = − + ⇔ ⇔ − + = ⇔ 2  0,25 x = 1 −
Vì x ≠ 0; x ≠1; x ≠ 1 − nên chọn 1 x = 2 0,25 Vậy, 1 − 1 P = ⇔ x = 2 2
c) (1,5 điểm) 2 2 Ta có: x
x −1+1 (x − ) 1 (x + ) 1 +1 1 P = = = = x + + = (x − ) 1 1 1 + + 2 0,5 x −1 x −1 x −1 x −1 x −1
Với x >1 nên x −1> 0 và 1 > 0 . Áp dụng BĐT Cô-si cho 2 số x −1 0,25 dương (x − ) 1 và 1 ta có : 1 1 x −1+ ≥ 2 (x −1). = 2 x −1 x −1 x −1 P ≥ (x − ) 1 2 1 + 2 = 2 + 2 = 4 0,25 x −1 Dấu « = » 1 ⇔ x −1 =
với x >1 ⇔ x = 2( thỏa ĐKXĐ) x −1 0,25
Vậy, GTNN (P) = 4 ⇔ x = 2 0,25 Câu 2 (3 điểm)
2.1.(1,5 điểm) Cho a,b,c đôi một khác nhau thỏa mãn: 2 2 2 2
(a + b + c) = a + b + c Chứng minh rằng: a b c + + = 0 2 2 2
a + 2bc b + 2ca c + 2ab Ta có: 2 2 2 2
(a + b + c) = a + b + c ⇔ ab + bc + ca = 0 ⇒ bc = −ab − ca 0,25 2 2 2
a + 2bc = a + bc + bc = a − ab − ca + bc = (a − b)(a − c) 0,25 Tương tự: 2 2
b + 2ca = (b − c)(b − a);c + 2ab = (c − a)(c − b) 0,25 Do đó: a b c a b c + + = + + 2 2 2
a + 2bc b + 2ca c + 2ab (a − b)(a − c) (b − a)(b − c) (c − a)(c − b) 0,5
−a(b − c) − b(c − a) − c(a − b) = = 0
(a − b)(b − c)c − a) 0,25
2.2. (1,5điểm) Cho đa thức: 3 2
f (x) = x + ax + bx + c với a, b,c là các số
thực . Biết đa thức f(x) chia cho đa thức x + 1 dư – 4 và chia cho đa
thức x – 2 dư 5. Tính giá trị của 2025 2025 2025 2025 2025 2025 A = (a + b )(b − c )(c + a )
Đa thức f(x) chia cho đa thức x + 1 dư – 4 nên ta có: f ( 1) − = 4
− ⇔ a − b + c = 3 − (1) 0,25
Đa thức f(x) chia cho đa thức x - 2 dư 5 nên ta có:
f (2) = 5 ⇔ 4a + 2b + c = 3 − (2) 0,25
Từ (1) và (2) ⇒ a −b + c = 4a + 2b + c ⇔ 3a +3b = 0 ⇔ a = b − 0,25 2025 2025 2025 2025 ⇒ a + b = ( b − ) + b = 0 0,5 Vậy : 2025 2025 2025 2025 2025 2025 A = (a + b )(b − c )(c + a ) = 0 0,25 2 2 2
3.1.(2,0 điểm): Giải phương trình: (x − x + ) − (x + ) = ( 3 3 1 2 1 5 x + ) 1 Vì x = 1
− không là nghiệm của phương trình nên chia cả hai vế cho 3 x +1 ta được: 0,5 2 − + + x x 1 x 1 3 − 2 = 5 2 x +1 x − x +1 Đặt 2 x − x +1 t = x+1 0,5 2 1 2
⇒ 3t − = 5 ⇔ 3t − 5t − 2 = 0 ⇔ t = 2,t = − t 3 Với: 2 3 13 t 2 x 3x 1 0 x ± = ⇔ − − = ⇔ = 0,5 2 Với: 1 2 0,25 Câu 3
t = − ⇔ 3x − 2x + 4 = 0 3 Phương trình vô nghiệm (4,0 điểm)
Vậy phương trình có 2 nghiệm: 3 13 x ± = 0,25 1,2 2 3.2. (2,0 điểm) 2 2
x + 2y + 2xy + y − 2 = 0 ⇔ 2
−(x + y) = (y −1)(y + 2) (*) 0,25 Vì 2
−(x + y) ≤ 0 với mọi x, y nên từ (*) ta có − + ≤ ⇔ − ≤ ≤ (y 1)(y 2) 0 2 y 1 0,25
Vì y ∈ nên y ∈{ 2; − −1;0; } 1 0,25 Với y = 2
− thay vào đẳng thức ta được x = 2 0,25 Với y = 1
− thay vào đẳng thức ta có x∉ (loại) 0,25
Với y = 0 thay vào đẳng thức ta có x∉ (loại) 0,25
Với y =1 thay vào đẳng thức ta được x = 1 − 0,25
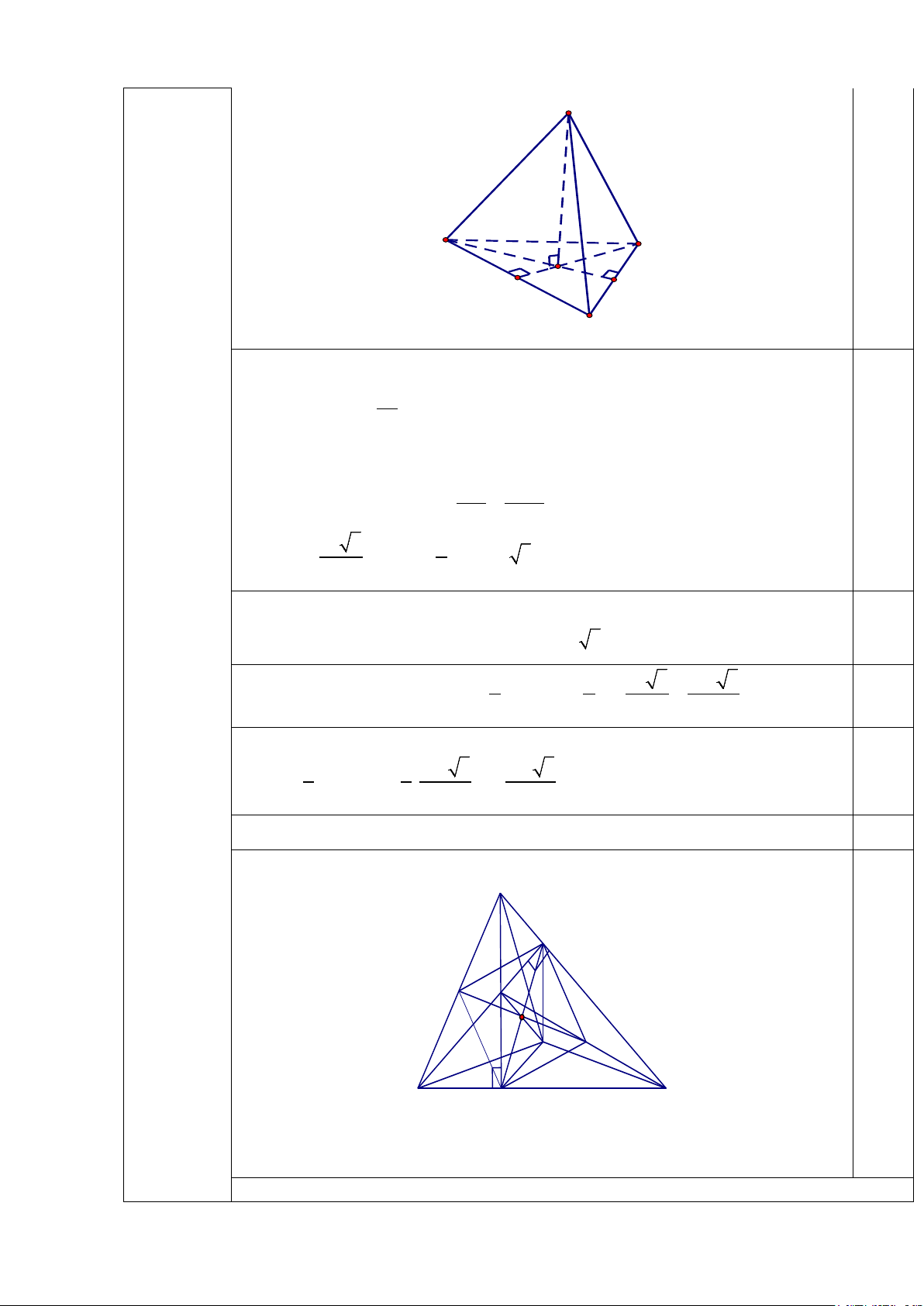
Vậy các cặp số nguyên ( x ; y ) cần tìm là (2;− 2),( 1; − 1) 0,25 4.1.(1,5điểm) S 2a A C H 0,25 M 3a điểm B Do A
∆ BC đều nên H là trọng tâm A
∆ BC , CH cắt AB tại M 0,5 => MA = MB= 3a 2 Xét MA ∆
C vuông tại M, ta có: 2 2 2 2 2 2 9a 27a
CM = AC − AM = 9a − = 4 4 3a 3 2 ⇒ CM =
⇒ CH = CM = a 3 2 3 Xét S
∆ HC vuông tại H, ta có: 0,25 2 2 2 2 2 2
SH = SC − CH = (2a) − (a 3) = a ⇒ SH = a 2 1 1 3a 3 9a 3 Diện tích của A ∆ BClà : S = AB CM = a = 0,25 ABC . . .3 . 2 2 2 4
Thể tích của hình chóp S. ABC là : 0,25 2 3 1 1 9a 3 3a 3 V = S SH = a = S ABC . ABC. . . . 3 3 4 4 4.2(4,5điểm) M A F H 0,25 I E O Câu 4 (6,0 điểm) B C K a) (1,0 điểm). Xét C ∆ HA và B ∆ MA có  = 
ACH ABM (cùng phụ với  BMC ) 0,5
AB = AC ,  =  0 CAH BAM = 90 ⇒ C ∆ HA = B
∆ MA (g-c-g)⇒ CH = BM 0,5 b) (1,25 điểm). 1
Ta có AE = KE = HC (1) (do AE, KE là hai đường trung tuyến ứng 2 0,25
với cạnh huyền của hai tam giác vuông HAC và HKC ) 1
Tương tự có AF = KF = MB (2) 2 0,25
mà CH = BM (theo chứng minh trên) (3)
Từ (1), (2) và (3) ⇒ tứ giác AFKE là hình thoi. 0,25
ΔAEC và ΔAFB có AF = AE, AC = AB,MB = HC ⇒ EC = FB 0,25 ⇒ A ∆ EC = A ∆ FB ⇒  =  CAE BAF Mà  +  0
BAE EAC = 90 ⇒  =  +  0 EAF AF B BAE = 90
Suy ra tứ giác AFKE là hình vuông.
=>AK là tia phân giác của  ⇒  1 =  1 0 0 EAF EAK EAF = .90 = 45 0,25 2 2 C) (1,0 điểm). C ∆ AB và CKM ∆
có C chung,  =  0 CAB CKM = 90 0,25 ⇒ C ∆ AB  CKM ∆ (g-g) CA CB CA CK ⇒ = ⇒ = CK CM CB CM ⇒ C ∆ AK  C ∆ BM (c-g-c) 0,25 CA AK ⇒ = AB AK ⇒ = CB BM CB BM 0,25 ⇒ A .
B BM = AK.CB 0,25
4) (1,0điểm).
Tứ giác AFKE là hình vuông suy ra AK và EF cắt nhau tại trung điểm mỗi đường. 0,25 MK ∆
C vuông tại K ,  0 C = 45 ⇒ MK ∆
C vuông cân tại K
⇒ KM = KC , mà OM = OC ⇒ KO là đường trung trực của MC . 0,25 ⇒ KO⊥ MC Mà HA ⊥ MC ⇒ KO / /HA
OB = OC, AB = AC ⇒ AO là đường trung trực của BC .
⇒ AO⊥ BC, mà KH ⊥ BC ⇒ AO / /KH 0,25
Suy ra tứ giác AOKH là hình bình hành suy ra AK và OH cắt nhau tại
trung điểm mỗi đường.
Vậy AK, EF, OH đồng quy. 0,25 5.1(0,75điểm)
1. Hai số phân biệt được trọn ngẫu nhiên từ tập hợp { 2; − 1 − ;0;3;4; } 5
và đem nhân với nhau. Hỏi xác suất để tích bằng 0 là bao nhiêu
Các trường hợp có thể sảy ra là: +){ 2; − − } 1 ;{ 2; − } 0 ;{ 2; − } 3 ;{ 2; − } 4 ;{ 2; − } 5 +){ 1; − } 0 ;{ 1; − } 3 ;{ 1; − } 4 ;{ 1; − } 5 +){0; } 3 ;{0; } 4 ;{0; } 5 0,25 +){3; } 4 ;{3; } 5 +){4; } 5
Và ngược lại đổi vị trí hai số trong các cặp số trên
Số các kết quả sảy ra khi chọn hai số phân biệt từ tập hợp đã cho là 15.2=30 0,25
Khi tích của hai số đã chọn bằng 0 thì số hạng đầu tiên bằng 0 hoặc số Câu 5
hạng thứ 2 bằng 0, ta có 10 trường hợp như thế. (1,5điểm). 10 1 0,25
Vậy xác xuất cần tìm là = 30 3 5.2(0,75điểm)
2. Cho a,b,c là các số dương thỏa mãn: 2 2 2
a + b + c ≤ abc . Chứng minh: a b c 1 + + ≤ 2 2 2
a + bc b + ca c + ab 2
Áp dụng BĐT : AM – GM ta có : a b c 1 1 1 a + b + c + + ≤ + + = (1) 0,25 2 2 2
a + bc b + ca c + ab 2 bc 2 ca 2 ab 2 abc 2 2 2
(a − b) + (b − c) + (c − a) ≥ 0 với mọi a,b,c 2 2 2
⇔ a + b + c ≥ ab + bc + ca
Chứng minh tương tự : ab + bc + ca ≥ abc( a + b + c) 0,25
⇒ abc ≥ abc( a + b + c) a + b + c ≤ 1(2) abc Từ (1) và (2) a b c 1 ⇒ + + ≤ 2 2 2
a + bc b + ca c + ab 2 0,25
Dấu “=” xảy ra khi và chỉ khi: a = b = c = 3
Lưu ý khi chấm bài:
- Trên đây chỉ là sơ lược các bước giải, lời giải của học sinh cần lập luận chặt chẽ, hợp
logic. Nếu học sinh trình bày cách làm khác mà đúng thì cho điểm các phần theo thang điểm tương ứng.
- Với bài 4, nếu học sinh vẽ hình sai hoặc không vẽ hình thì không chấm.
Document Outline

• PHÒNG GIÁO DỤC VÀ ĐÀO TẠO