Đề khảo sát HSG Toán 9 lần 3 năm 2023 – 2024 phòng GD&ĐT Tam Kỳ – Quảng Nam

UBND TP. TAM KÝ
KÝ KHO ST HÅC SINH GIÄI LÎP 9 LN 3 PHÁNG GIO DÖC V O TO NM HÅC 2023 - 2024 MÆN TON · ch½nh thùc Ng y 06 th¡ng 03 n«m 2024
Thíi gian 150 phót(khæng kº thíi gian ph¡t · ) C¥u 1. (4.0 iºm) 2 a) Cho f(n) = p p
vîi n l sè nguy¶n d÷ìng. T½nh gi¡ trà cõa biºu thùc 2n + 1 + 2n 1
P = f(1) + f(2) + f(3) + ::: + f(60):
b) T¼m t§t c£ c¡c gi¡ trà cõa tham sè m º ph÷ìng tr¼nh x2 2(3m 1)x + m2 m 4 = 0 câ hai nghi»m ph¥n bi»t x p
1; x2 thäa m¢n x1 + x2 + px1x2 = 2024 x1 + x2 x1x2 : C¥u 2. (4.0 iºm) p a) Gi£i ph÷ìng tr¼nh: 4 x x 1 = 32x4 + 80x3 50x2 + 3. b) Gi£i h» ph÷ìng tr¼nh: ( p x 2 y + 1 = 3 p x3 4x2 y + 1 9x 8y = 52 4xy
C¥u 3. (4.0 iºm). Cho tam gi¡c ABC, k´ c¡c ÷íng ph¥n gi¡c trong AD; BE; CF cõa tam gi¡c ABC. Chùng minh r¬ng p a) AD = AB:AC BD:DC 1 1 1 1 1 1 b) + + < + + AB AC BC AD BE CF
C¥u 4. (4.0 iºm). Cho ÷íng trán (O; R) v iºm M cè ành ð b¶n ngo i ÷íng trán. Tø M k´ c¡c
ti¸p tuy¸nMA, MB v c¡t tuy¸n MCD ¸n ÷íng trán (O; R), vîi A, B l c¡c ti¸p iºm. C, D thuëc
÷íng trán (O) sao cho MC < MD, CD < 2R. Gåi E l trung iºm cõa CD.
a) Chùng minh bèn iºm A, E, O, B còng n¬m tr¶n mët ÷íng trán.
b) Gåi F l giao iºm cõa AB v OE. Chùng minh F C l ti¸p tuy¸n cõa ÷íng trán (O; R).
c) Gåi T l iºm thay êi tr¶n cung nhä AB cõa ÷íng trán (O). Ti¸p tuy¸n t¤i T cõa ÷íng trán (O)c­t
MA, MB l¦n l÷ñt t¤i c¡c iºm I, K. Chùng minh r¬ng chu vi tam gi¡c MIK khæng êi. X¡c ành và
tr½ cõa iºm T tr¶n cung nhä AB sao cho tam gi¡c MIK câ di»n t½ch lîn nh§t. C¥u 5. (5.0 iºm)
a) T¼m t§t c£ c¡c bë ba sè nguy¶n tè (p; q; r) sao cho p + q + r = pqr 200.
b) Cho c¡c sè thüc a; b; c; d 1. T¼m t§t c£ c¡c gi¡ trà thüc cõa k sao cho
a3 + b3 + c3 + d3 + 1 k(a + b + c + d) . ===H¸t===
L÷u þ: Th½ sinh khæng ÷ñc ph²p sû döng t i li»u. Gi¡m thà khæng ÷ñc gñi þ g¼ th¶m.
Hå v t¶n th½ sinh. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Sè b¡o danh. . . . . . . . . . . . ........... UBND THÀNH PHỐ TAM KỲ
KHẢO SÁT HỌC SINH GIỎI LỚP 9-LẦN 3
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO Năm học: 2023 – 2024 Ngày 06 tháng 03 năm 2024 Môn: TOÁN HƯỚNG DẪN CHẤM Câu Nội dung Điểm 1 a) (2.0 điểm) (4.0 Ta có điểm) 2 2n 1  2n 1 0.5 f (n)  
(do 2n 1  2n 1  0 )
2n 1  2n 1 2n 1  2n 1 2 2n 1  2n 1   2n 1  2n 1 0.5 (2n 1)  (2n 1) Khi đó
P   3  1   5  3   7  5 ...  121  119 0.5
 121  1 111 10 . 0.5 b) (2.0 điểm) Phương trình 2 x   m   2 2 3
1 x  m  m  4  0  
1 có hai nghiệm phân biệt 0.25 2  
  0  8m  5m  5  0 2  5  135  8 m    0; m       16  32 0.25 x  x  2 3m 1  1 2  
Theo định lí Vi-ét, ta có:  2 x x  m  m  4  1 2 0.25 x x xác định 2
 x x  0  m  m  4  0 (*) 1 2 1 2
Đặt u  x  x  x x ; v  x  x  x x 1 2 1 2 1 2 1 2 2 2  x  3x Ta có . u v   x  x 2 2 2  x x  x    0; x  , x 0.25 1 2 1 2  1  1 2  2  4
Suy ra u và v luôn cùng dấu. Do đó u  v  u  v .
Hướng dẫn chấm môn Toán – Thi khảo sát HSG lớp 9 lần 3 năm học 2023-2024 Ta có
x  x  x x  x  x  x x  2024 1 2 1 2 1 2 1 2 0.5
 x  x  x x  x  x  x x  2024 1 2 1 2 1 2 1 2  x  x 1012 1 2  2 3m 1 1012 m 169 3m 1 506 0.5 3m 1 506       
505 (thỏa điều kiện (*)). 3m 1 506 m    3 2 a) (2.0 điểm) (4.0 Điều kiện: x 1. 0.25 điểm) Ta có    0.5 x  x   2 1 4 1  4 x 1   3  3    2  1 5
Dấu đẳng thức xảy ra khi và chỉ khi x 1   x  . 2 4 0.25 Lại có 2  5  4 3 2 2 3
 2x  80x  50x  3  3  32x x   3    4  0.5 x  0  5 
Dấu đẳng thức xảy ra khi và chỉ khi x x 0       5 . 0.25  4  x   4
Qua hai đánh giá trên ta thấy, phương trình đã cho có nghiệm duy nhất 5 0.25 x  . 4 b) (2.0 điểm) Điều kiện: y  1  . 0.25 Ta có: x  3  x  3
x  2 y 1  3  2 y 1  x  3     0.75 4   y   1   x  32 2 4y  x  6x  5 Thay 2
4y  x  6x  5 vào phương trình thứ hai của hệ phương trình ta được: 3 2 0.5
x  x  x    x   2
x  x      x 2 2 3 9 2 6 5 52 x  6x  5
Hướng dẫn chấm môn Toán – Thi khảo sát HSG lớp 9 lần 3 năm học 2023-2024 x  3 2
 x  4x  21  0  
. So với điều kiện x  3, chọn nghiệm x  7 x  7 0.5 Thay vào phương trình 2
4y  x  6x  5 ta được y  3.
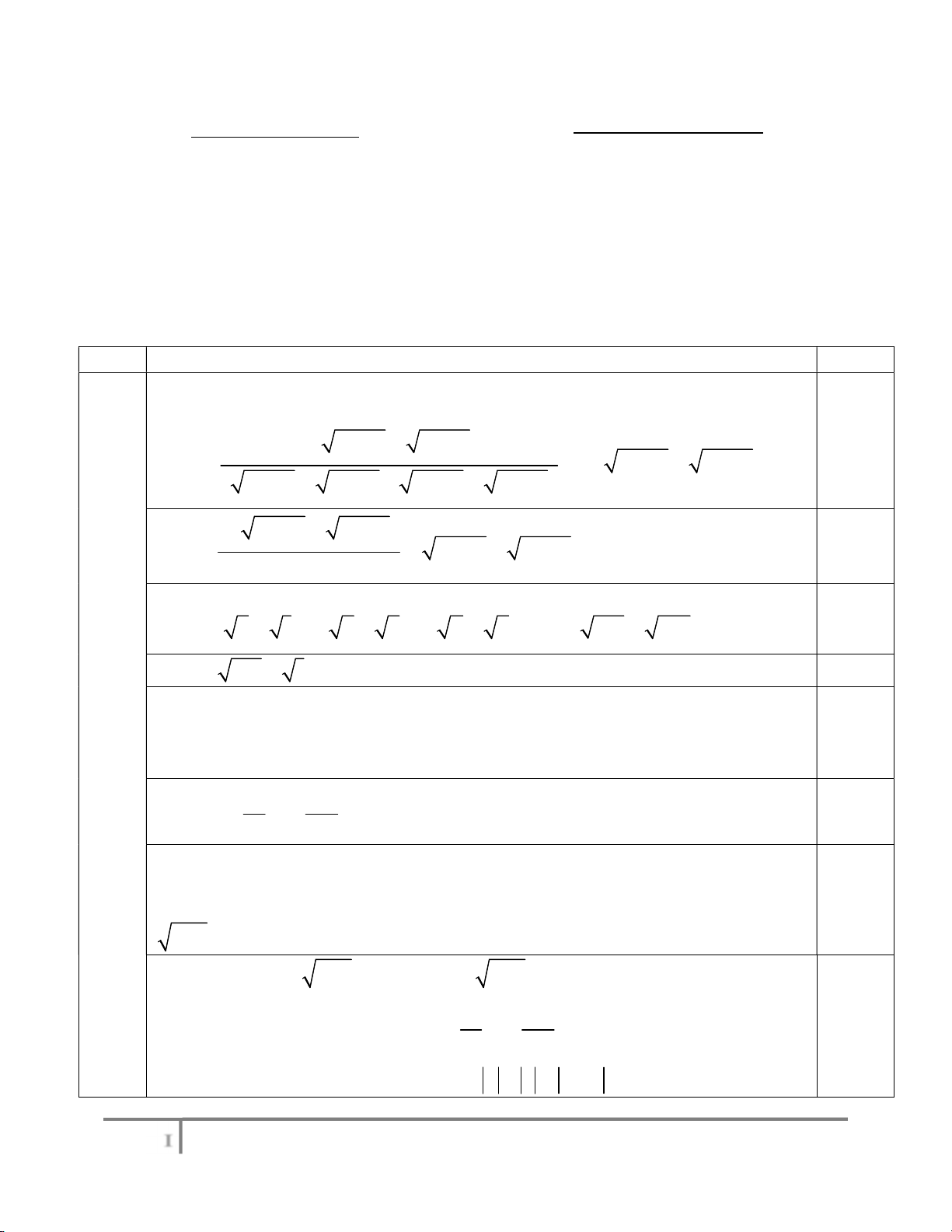
Vậy hệ phương trình đã cho có nghiệm duy nhất là: 7;3 . 3 Hình vẽ (3.0 M điểm) A 2 1 E F J B C D K a) (1.5 điểm)
Lấy K thuộc tia đối của tia DA sao cho  AKB   ACB . AD AC 0.5 Vì ACD  ∽ AKB (g.g)    A . B AC  A . D AK (1) AB AK DC AC AD Vì DAC  ∽ DBK (g.g)     B . D DC  DK.AD (2) DK BK BD 0.5
Trừ (1) và (2) vế theo vế ta được
AB AC  DC BD  AD  AK  KD 2 . . .  A . D AD  AD 0.5 hay AD  A . B AC  B . D DC .
Hướng dẫn chấm môn Toán – Thi khảo sát HSG lớp 9 lần 3 năm học 2023-2024 b) (1.5 điểm)
Qua B kẻ đường thẳng song song với AD , cắt đường thẳng AC tại M 0.25
ABM cân tại A  AM  AB .
Theo bất đẳng thức tam giác: MB  AM  AB  MB  2AB 0.25 AD CA AC AC Do AD//BM nên    BM CM AC  AM AC  AB
(do CM  AC  AM ; AM  AB ) AD AC   0.5 BM AC  AB AC AC.2AB 2A . B AC  AD  .BM   AC  AB AC  AB AC  AB 1 AC  AB 1 1 1  1 1       .    (3) AD 2A . B AC 2AC 2AB 2  AC AB  1 1  1 1  Tương tự,  .    (4) BE 2  AB BC  0.25 1 1  1 1   .    (5) CF 2  AC BC 
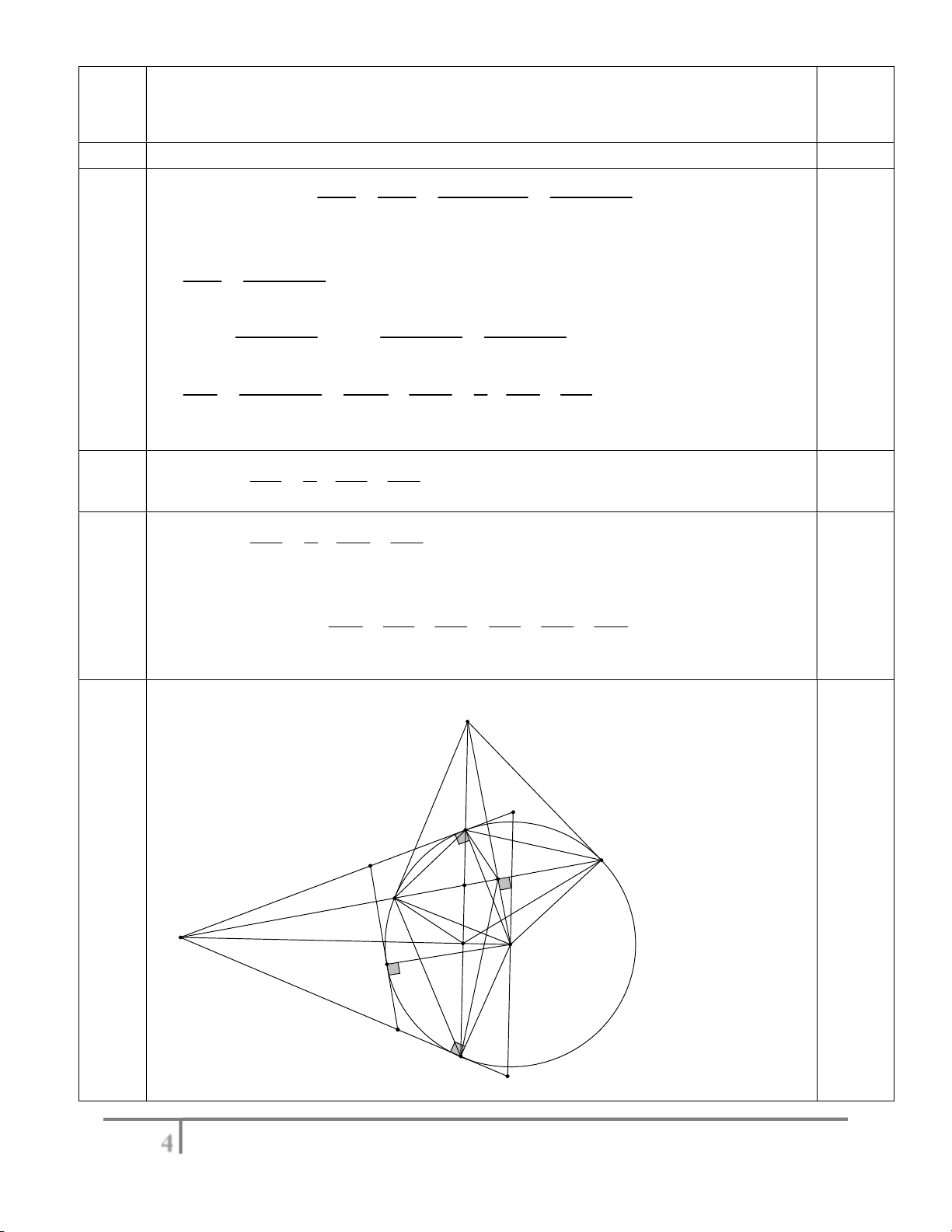
Cộng vế theo vế các bất đẳng thức (3), (4) và (5) ta được: 1 1 1 1 1 1 0.25      . AD BE CF AB BC AC 4 Hình vẽ (4.0 F điểm) A1 A I D E C G H M O T K B B1
Hướng dẫn chấm môn Toán – Thi khảo sát HSG lớp 9 lần 3 năm học 2023-2024 a) (1.0 điểm) Xét tứ giác AOBM có: 
MAO  90 (vì MA là tiếp tuyến của đường tròn (O) ) 0.5 
MBO  90 (vì MB là tiếp tuyến của đường tròn (O) )   MAO  
MBO  90  90 180
Do đó tứ giác AOBM nội tiếp đường tròn đường kính MO (1)
Vì E là trung điểm của đoạn thẳng CD nên OE  CD
Xét MOE vuông tại E nên nội tiếp đường tròn đường kính MO (2)
Từ (1) và (2) suy ra 5 điểm A, E , O , B , M cùng nằm trên đường tròn 0.5 đường kính MO .
Vậy bốn điểm A, E , O , B cùng nằm trên một đường tròn. b) (1.0 điểm) OE OM O  EM ∽ OHF (g.g)   OH OF 0.5 2 2
 OE.OF  OM .OH  OA  OC . OE OC   . OC OF OE OC Xét O  EC và O  CF có  và  EOC   COF . OC OF Do đó O  EC O  ∽ CF (c.g.c) . Suy ra  OEC   OCF  90 0.5 .
Mà D (O) nên FC là tiếp tuyến của đường tròn  ; O R. c) (2.0 điểm)
Do IK là tiếp tuyến của đường tròn (O) tại T nên IT  IA và KT  KB
 IK  IT  KT  IA  KB Kí hiệu C là chu vi MIK 0.5 MIK Ta có: C
 MI  MK  IK  MI  MK  IA  KB  MA  MB  2MA MIK
mà điểm A và M cố định nên MA không đổi. Do đó C không đổi MIK
Qua O kẻ đường thẳng song song AB cắt MA tại A , cắt MB tại B . 1 1 Ta có:  KOI   KOT   1 TOI   1 BOT   1 TOA   AOB   AOM   MA B   MB A 1 1 1 1 2 2 2 Từ đó suy ra IOA  ∽ IOK∽ O  B K (g.g) 1 1 0.5 IA OB 2 A B 1 1   hay 1 1 IA .B K  OA .OB  (không đổi) OA B K 1 1 1 1 4 1 1
Hướng dẫn chấm môn Toán – Thi khảo sát HSG lớp 9 lần 3 năm học 2023-2024 Ta có: 1 S  S  S  S  S
 MO.A B  R IK  IA  KB  MIK MA B KOI IOA KOB    1 1 1 1 1 1 1 1 2
Mà MI  IK  KM  2MA (chứng minh trên) nên
IK  2MA  MI  MK  2MA  MA  IA  MB  KB 1 1   1 1   0.5 2MA  2MA  IA  KB 1 1 1 1  S
 MO.A B  R 2MA  2MA  2IA  2KB  IMK  1 1  1 1 1  2  1
 MO.A B  R.AA  R IA  KB 1 1 1  1 1  2
Áp dụng bất đẳng thức AM – GM, ta có: 2 A B 1 1 IA  KB  2 IA .KB  2  A B 1 1 1 1 1 1 4 0.5 1  S
 MO. A B  R. AA  RA B . IMK 1 1 1 1 1 2
Dấu “=” xảy ra  IA  KB  T   AB sao cho IK // AB . 1 1 n 5 a) (2.5 điểm)
(5.0 Không mất tính tổng quát, giả sử p  q  r . Phương trình đã cho tương điểm) đương với
(qr 1)( p 1)  (r 1)(q 1)  202. 0.5 Nếu p lẻ thì ,
q r cũng lẻ. Khi đó vế trái của phương trình trên chia hết
cho 4 nhưng vế phải thì không (vô lí). Do đó p  2.
Thay p  2 vào phương trình trên ta được 4
2qr  q  r  202  4qr  2q  2r 1  405  (2q 1)(2r 1)  5.3 . 0.5
Do 3  2q 1 2r 1 nên 2
9  (2q 1)  (2q 1)(2r 1)  405 . Suy ra 3  2q 1 0 2 .
Mà 2q 1 lẻ nên 2q 1{3;5;9;15}. 0.25
Nếu 2q 1 3  q  2 thì r  68 (không phải là số nguyên tố nên loại). 0.25
Nếu 2q 1  5  q  3 thì r  41(là số nguyên tố nên thỏa). 0.25
Nếu 2q 1  9  r  5 thì r  23(là số nguyên tố nên thỏa). 0.25
Nếu 2q 1 15  q  8 thì loại vì không phải là số nguyên tố. 0.25
Vậy tất cả các bộ ba số nguyên tố cần tìm là (2,5,23),(2,3,41) cùng các hoán vị của nó. Lưu ý 0.25
Nếu thiếu cụm từ “các hoán vị của nó” thì trừ 0.25 điểm.
Hướng dẫn chấm môn Toán – Thi khảo sát HSG lớp 9 lần 3 năm học 2023-2024 b) (2.5 điểm) 3 0.5
Nếu a  b  c  d  1  thì 3   k.( 4  ) . Do đó k  . 4 1 1 1 3 3
Nếu a  b  c  d  thì 4. 1  k (
. 4. ) . Suy k  . Vì vậy k  . 2 8 2 4 4 0.5 3
Với k  , ta sẽ chứng minh bất đẳng thức 4 3 3 3 3 3
a  b  c  d 1 (a  b  c  d), a  , , b , c d  1. 4 0.5 Đầu tiên, ta chứng minh 3 4x 1 3x, x   1  . Thật vậy 3 2
4x 1  3x  (x 1)(2x 1)  0 luôn đúng với mọi x  1.
Áp dụng bất đẳng thức trên ta có 3 4a 1 3a , 3 4b 1 3b, 0.5 3 4c 1 3c , 3 4d 1 3d .
Cộng vế theo vế bốn bất đẳng thức trên ta được 3 3 3 3 3
a  b  c  d 1 (a  b  c  d), a  , , b , c d  1. 4 0.5 3
Vậy k  là giá trị cần tìm. 4 ===Hết=== Lưu ý :
- Những câu, những ý nào thí sinh làm khác với đáp án nhưng lập luận hợp lý
và đáp số đúng vẫn đạt điểm tối đa ở câu đó, ý đó.
- Những kiến thức mới thí sinh đưa vào bài làm nếu đúng vẫn được chấp nhận
bởi vì đây là đối tượng học sinh giỏi có năng khiếu Toán.
- Khuyến khích những cách giải sáng tạo, độc đáo và có cộng điểm thưởng cho những cách giải này.
Hướng dẫn chấm môn Toán – Thi khảo sát HSG lớp 9 lần 3 năm học 2023-2024
Document Outline

• De KS Toan 9_Tam Ky_2023.2024 (lần 3)
• HDC KS Toan 9_Tam Ky_2023.2024 (lần 3)