Đề khảo sát Toán 9 lần 2 năm 2023 – 2024 phòng GD&ĐT thành phố Hải Dương

UBND THÀNH PHỐ HẢI DƯƠNG
ĐỀ KHẢO SÁT HỌC SINH LỚP 9 – LẦN 2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 - 2024 MÔN TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút
(Đề gồm 06 câu, 01 trang) Câu 1 (2,0 điểm) 2x 1
a) Giải phương trình  5 3 2x   1  y  3
b) Giải hệ phương trình 
x 3y 1 0 Câu 2 (2,0 điểm)  x  2 5 1 
a) Rút gọn biểu thức A      : 
  x  4 với x  0; x  4; x 16 x  3 x  x  6 2  x  
b) Cho hai đường thẳng d  y   2 : m  
1 x  2m  3 và d ' : y 10x  6  m, với m là tham số.
Tìm m để hai đường thẳng đã cho song song với nhau. Câu 3 (2,0 điểm)
a) Công ty HD xây dựng kế hoạch cho 2 phân xưởng sản xuất với tổng sản phẩm làm được là 520 sản
phẩm. Tuy nhiên, các phân xưởng đều rất trách nhiệm và áp dụng tốt kĩ thuật nên đã nâng cao hiệu quả
công việc. Vì thế, phân xưởng thứ nhất vượt mức so với kế hoạch là 10%, phân xưởng thứ hai vượt mức
so với kế hoạch là 20% và tổng số sản phẩm sản xuất được của 2 phân xưởng là 596 sản phẩm. Hỏi theo
kế hoạch ban đầu, mỗi phân xưởng làm bao nhiêu sản phẩm?
b) Cho phương trình 2
x  m   2 2
1 x  m  2  0 , với m là tham số. Tìm m để phương trình có hai
nghiệm phân biệt x ; x thoả mãn 2 2
x  3x  2 2
m  x x 1 . 1 2 1 2  1 2
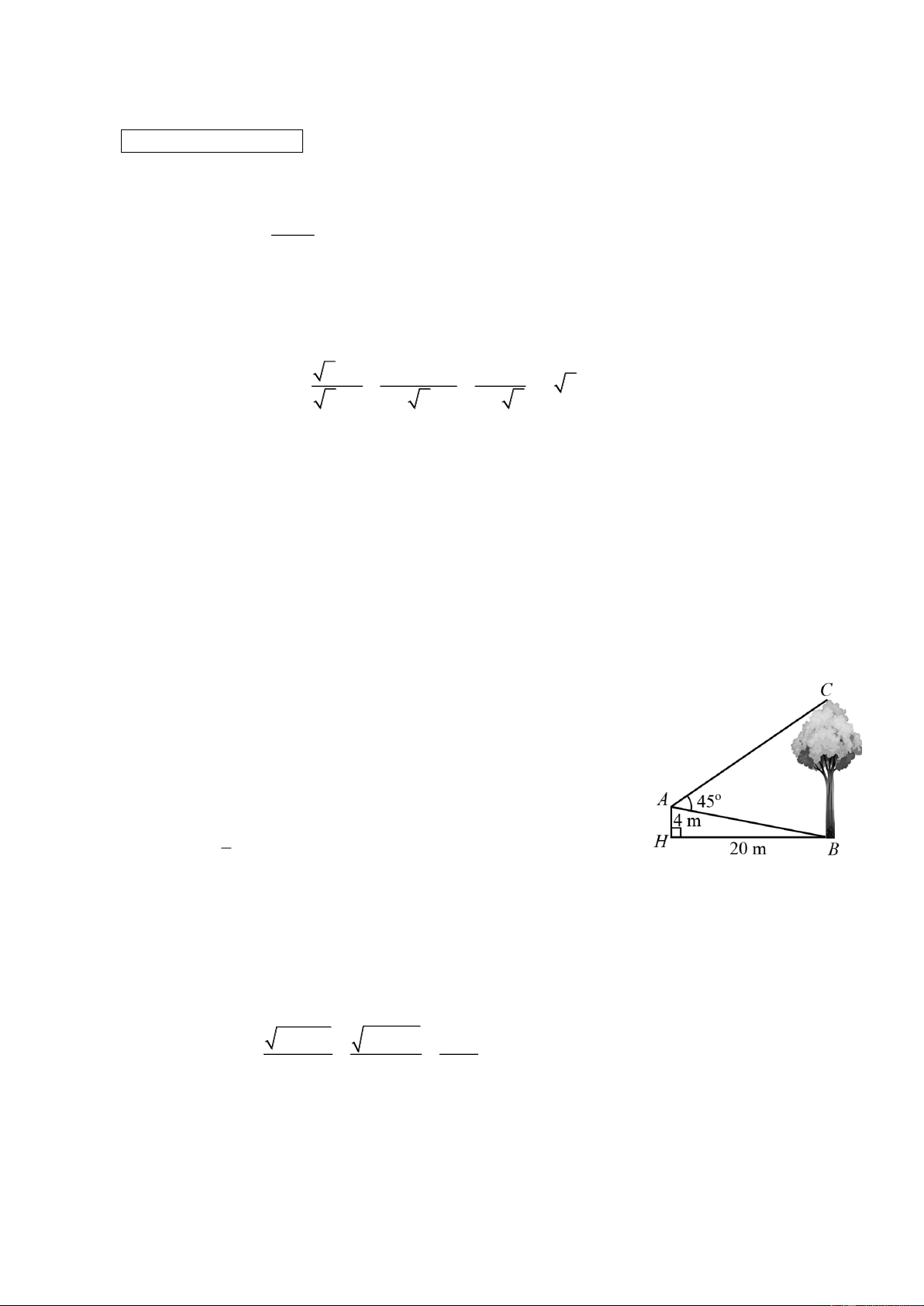
Câu 4 (1,0 điểm). Một người đứng ở vị trí A trên nóc một ngôi nhà cao
4 m đang quan sát một cây cao, cách ngôi nhà 20 m và đo được 0
BAC  45 (tham khảo hình vẽ). Tính chiều cao của cây đó (theo đơn vị
mét, làm tròn kết quả đến hàng phần mười), biết rằng nếu góc  nhọn và 1 thoả mãn tan   thì ta chọn 0  11 . 5
Câu 5 (2,0 điểm). Cho tam giác nhọn ABC có AB  AC , các đường cao BD và CE cắt nhau tại H .
a) Chứng minh rằng tứ giác ADHE nội tiếp đường tròn.
b) Gọi M là trung điểm của BC , đường thẳng DE cắt BC tại N , AH cắt BC tại K . Chứng minh
rằng DEK  DMC và NH  AM .
Câu 6 (1,0 điểm). Cho x, y là các số thực không âm, thoả mãn x  2 và xy  2 y  2 . Tìm giá trị lớn 2 2 x  2x y  2 y 1
nhất của biểu thức B    x 1 y 1 x  y
UBND THÀNH PHỐ HẢI DƯƠNG
ĐỀ KHẢO SÁT HỌC SINH LỚP 9 – LẦN 2
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2023 – 2024 MÔN: TOÁN HƯỚNG DẪN CHẤM
Thời gian làm bài: 120 phút
(Đề gồm 06 câu, 01 trang) Câu Đáp án Điểm 1a 2x 1
a) Giải phương trình  5 . 3 2x 1 + Ta có
 5  2x 1  15 0,5 3
 2x  16  x  8 0,5
+ Vậy phương trình có nghiệm là x  8 . 1b 2x   1  y  3
b) Giải hệ phương trình  .
x 3y 1 0 2x   1  y  3
2x  y  5 + Ta có    0,25
x 3y 1 0
x  3y  1 
6x  3y  15 7x 14    x 2      0,5
x  3y  1 
x  3y  1 
x  3y  1 x  2 x  2     3  y  3 y 1 0,25
+ Vậy hệ phương trình có nghiệm  ; x y  2;  1 . 2a  x  2 5 1 
a) Rút gọn biểu thức A      : 
  x  4 x  3 x  x  6 2  x  
với x  0; x  4; x  16 .  x  2 5 1  + Ta có A      :    x  4 x  3 x  x  6 2  x  
  x 2 x 2  5 x  3 1  0,5       
x  3 x  2  x  3 x  2  x  3 x  2 .  x  4  x  x 12 1  
x  3 x  2 . x  4
 x 4 x 3 1  1   .
x  3 x  2 . x  4 x  2 0,5 1 + Vậy A  . x  2 2b
b) Cho hai đường thẳng d  y   2 : m  
1 x  2m  3 và d ' : y 10x  6  m, với m
là tham số. Tìm m để hai đường thẳng đã cho song song với nhau. 2 m 1 10
+ Điều kiện để hai đường thẳng song song là  0,5
2m  3  6  m 2 m  9    m  3  3  m  9 0,5 + Vậy m  3  . 3a
a) Công ty HD xây dựng kế hoạch cho 2 phân xưởng sản xuất với tổng sản phẩm làm
được là 520 sản phẩm. Tuy nhiên, các phân xưởng đều rất trách nhiệm và áp dụng tốt
kĩ thuật nên đã nâng cao hiệu quả công việc. Vì thế, phân xưởng thứ nhất vượt mức
so với kế hoạch là 10%, phân xưởng thứ hai vượt mức so với kế hoạch là 20% và tổng
số sản phẩm sản xuất được của 2 phân xưởng là 596 sản phẩm. Hỏi theo kế hoạch
ban đầu, mỗi phân xưởng làm bao nhiêu sản phẩm?
+ Gọi số sản phẩm theo kế hoạch mà phân xưởng thứ nhất và thứ hai làm được lần
lượt là x, y (sản phẩm) ( , x y  ) 0,25
Tổng sản phẩm làm được là 520 sản phẩm nên x  y  520
+ Thực tế, số sản phẩm phân xưởng thứ nhất làm được là x 10%x 1,1x , 0,25
số sản phẩm phân xưởng thứ hai làm được là y  20%y  1, 2y
+ Số sản phẩm mà 2 phân xưởng làm được là 596 nên 1,1x 1, 2y  596
x  y  520 0,25
Ta có hệ phương trình  1
 ,1x 1, 2y  596 x  280  
(thoả mãn điều kiện)  y  240 0,25
+ Vậy theo kế hoạch, số sản phẩm 2 phân xưởng làm là 280 và 240 sản phẩm. 3b
b) Cho phương trình 2
x  m   2 2
1 x  m  2  0 , với m là tham số. Tìm m để
phương trình có hai nghiệm phân biệt x ; x thoả mãn 2 2
x  3x  2 2
m  x x 1 . 1 2 1 2  1 2
+ Điều kiện để phương trình có hai nghiệm phân biệt là     0,25 m  2   2 ' 0 1 m  2  0 1
 2m 1  0  m  2 0,25 1 + Vậy m 
thì phương trình có hai nghiệm phân biệt x ; x 2 1 2
x  x  2 m 1 1  1 2     + Theo Viét:  2
x x  m  2 2  1 2   Từ giả thiết 2 2
x  3x  2 2
m  x x   2 2
1  x  2x x  3x  2 2 m 1 1 2 1 2 1 1 2 2  0,25
 x  x x 3x  2 m1 m1  2 m1 x 3x  2 m1 m1 1 2   1 2       1 2     1 Vì m  nên 2m  
1  0, do đó x  3x  m 1 (3) 2 1 2  7m  5 x   1  4 + Từ   1 ,  3 ta được  . m  3 x  2  4    0,25
m  m   m 1 7 5 3  Thay vào 2 : 2 2
 m  2  9m  26m 17  0  17 16 m   9 1
Kết hợp điều kiện m 
, ta có m  1 thoả mãn yêu cầu bài toán. Vậy m  1. 2 4
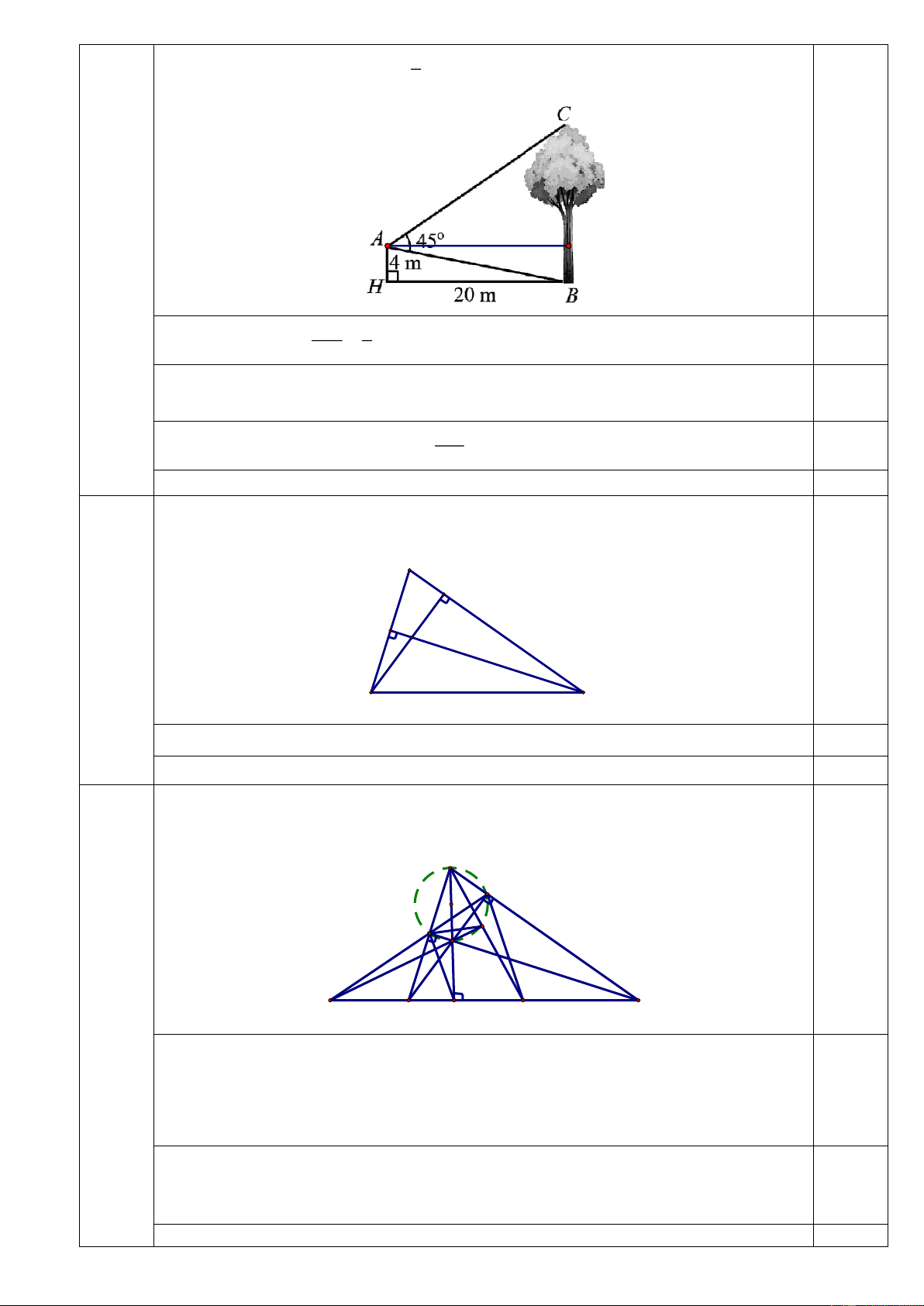
Một người đứng ở vị trí A trên nóc một ngôi nhà cao 4 m đang quan sát một cây
cao, cách ngôi nhà 20 m và đo được 0
BAC  45 (tham khảo hình vẽ). Tính chiều cao
của cây đó (theo đơn vị mét, làm tròn kết quả đến hàng phần mười), biết rằng nếu 1
góc  nhọn và thoả mãn tan   thì ta chọn 0  11 . 5 K AH 1 + Ta có 0 tan ABH    ABH  11 . 0,25 BH 5
+ Kẻ AK vuông góc với BC tại K . Vì AK / / BH nên 0
KAB  ABH  11 0,25 Do đó 0 0 0
CAK  45 11  34 CK
+ Xét tam giác ACK có 0 tan CAK 
 CK  AK.tan 34  13,5 (m) 0,25 AK
+ Chiều cao của cây là Chiều cao cây là BC  BK  KC  4 13,5 17,5 (m) 0,25 5a
Cho tam giác nhọn ABC có AB  AC , các đường cao BD và CE cắt nhau tại H .
a) Chứng minh rằng tứ giác ADHE nội tiếp đường tròn. A D E H C B + Do B ,
D CE là các đường cao cắt nhau tại H nên 0
AEH  ADH  90 0,5 + Tứ giác ADHE có 0
AEH  ADH  180 nên tứ giác ADHE nội tiếp đường tròn. 0,5 5b
b) Gọi M là trung điểm của BC , đường thẳng DE cắt BC tại N , AH cắt BC tại
K . Chứng minh rằng DEK  DMC và NH  AM . A D E I H N C B K M
+ Tứ giác ADHE nội tiếp nên DAH  DEH
Tứ giác BKHE nội tiếp nên HBK  HEK 0,25 Mà 0
DAH  C  HBK  C  90  DAH  HBK
Do đó DEK  DEH  HEK  2.HBK  2.DBM (1)
+ Tam giác DBC vuông tại D và có DM là trung tuyến  DM  BM  MC
Có DMC  DBM  BDM  2.DBM (2) 0,25
+ Từ (1) và (2) ta có DEK  DMC
+ Gọi I là giao điểm của đường thẳng NH và đường tròn ngoại tiếp tứ giác ADHE 0,25 Ta sẽ chứng minh ,
A I , M thẳng hàng.
Ta có tứ giác ADHE nội tiếp đường tròn đường kính AH , do đó 0 AIH  90 (3) NE NI Có N  EI N
 HD g.g   
 NE.ND  NH.NI NH ND
+ Do DEK  DMC nên tứ giác DEKM nội tiếp NE NK Có N
 EK NMD g.g   
 NE.ND  NM .NK NM ND NH NK
Vậy NH .NI  NK.NM  
. Tam giác NHK và NMI có chung góc N NM NI 0,25 Từ đó suy ra N  HK N  MI  .c .
g c . Do đó NHK  NMI  tứ giác HIMK nội tiếp 0  HIM  90 (4) + Từ (3), (4) ta có 0
AIH  HIM  180 , tức là ,
A I , M thẳng hàng. Do vậy NH  AM 6
Cho x, y là các số thực không âm, thoả mãn x  2 và xy  2 y  2 . Tìm giá trị lớn 2 2 x  2x y  2 y 1
nhất của biểu thức B    . x 1 y 1 x  y
+ Từ giả thiết xy  2 y  2   x   1   y  
1  3  x   1  y   1 1 1 3     . x  y 
x   y   1 1 1 1 1 0,25 Ta cũng có 1 1 1 B  1     x   1 2 1  y  2 1 x  y + Đặ 1 1 t a  ;b   , a b  0 x 1 y 1 Khi đó ab ,
a b thoả mãn a  b  3ab  1 và 2 2
B  1 a  1 b  a  b 3 0,25
+ Ta có 1  a  b  3ab  a  b 
.a  b2 . 4
Do đó a  b2  a  b    a  b   a  b   2 3 4 4 0 2 3 3
2  0  a  b  3
(vì a  b  2  0, với mọi , a b  0 )  a  b  4 2
+ Lại có: 1 a  1 b 
22  a  b   2 2 2 2 2  2 2     2  3   ab
1 a  b 1 1 1 3 1 1 0,25       a  b a b a b . 3 3 3 3 2 3 6 1
Dấu "=" xảy ra khi a  b  3 ab 4 2 1 8 2 1 + Vậy 2 2
B  1 a  1 b     a  b 3 6 6 0,25 8 2 1 1 x  4
Giá trị lớn nhất của B là
. Dấu "=" xảy ra khi a  b  , khi đó  6 3  y  2
----------------------------------Hết----------------------------------