Đề khảo sát Toán 9 năm 2022 – 2023 phòng GD&ĐT Hoàn Kiếm – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 năm học 2022 – 2023 phòng GD&ĐT Hoàn Kiếm – Hà Nội giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
trường
Preview text:
UBND QUẬN HOÀN KIẾM
ĐỀ KHẢO SÁT CHẤT LƯỢNG
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
Môn: Toán học, Lớp 9
Năm học 2022 – 2023 ĐỀ CHÍNH THỨC
Ngày khảo sát: 24/5/2023
(Đề thi gồm 01 trang)
Thời gian làm bài: 120 phút (không kể thời gian phát đề) x 2 5 3 x 14
Bài I. (2,0 điểm) Cho hai biểu thức A và B
với x 0; x 4 x 2 x 2 4 x
1) Tính giá trị của biểu thức A khi x 16 .
2) Rút gọn biểu thức B .
3) Xét biểu thức P .
A B . Tìm tất cả giá trị của x sao cho 2P 3 P . Bài II. (2,0 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một mảnh đất hình chữ nhật có chiều dài lớn hơn chiều rộng 12m và diện tích mảnh đất bằng 2 85m .
Tính chiều dài và chiều rộng của mảnh đất theo đơn vị mét?
2) Một quả địa cầu hành chính có đường kính bằng 33cm . Tính diện tích
bề mặt của quả địa cầu, lấy 3,14 .
Bài III. (2,5 điểm) 1 x 1 4 y 1
1) Giải hệ phương trình: 2 3 x 1 7 y 1
2) Trong mặt phẳng tọa độ Oxy , cho parabol P 2
: y x và đường thẳng d 2
: y mx m 4
a) Với m 2 , tìm tọa độ giao điểm của đường thẳng d và parabol P .
b) Tìm tất cả giá trị của m để đường thẳng d cắt parabol P tại điểm A x ; y nằm bên trái 1 1
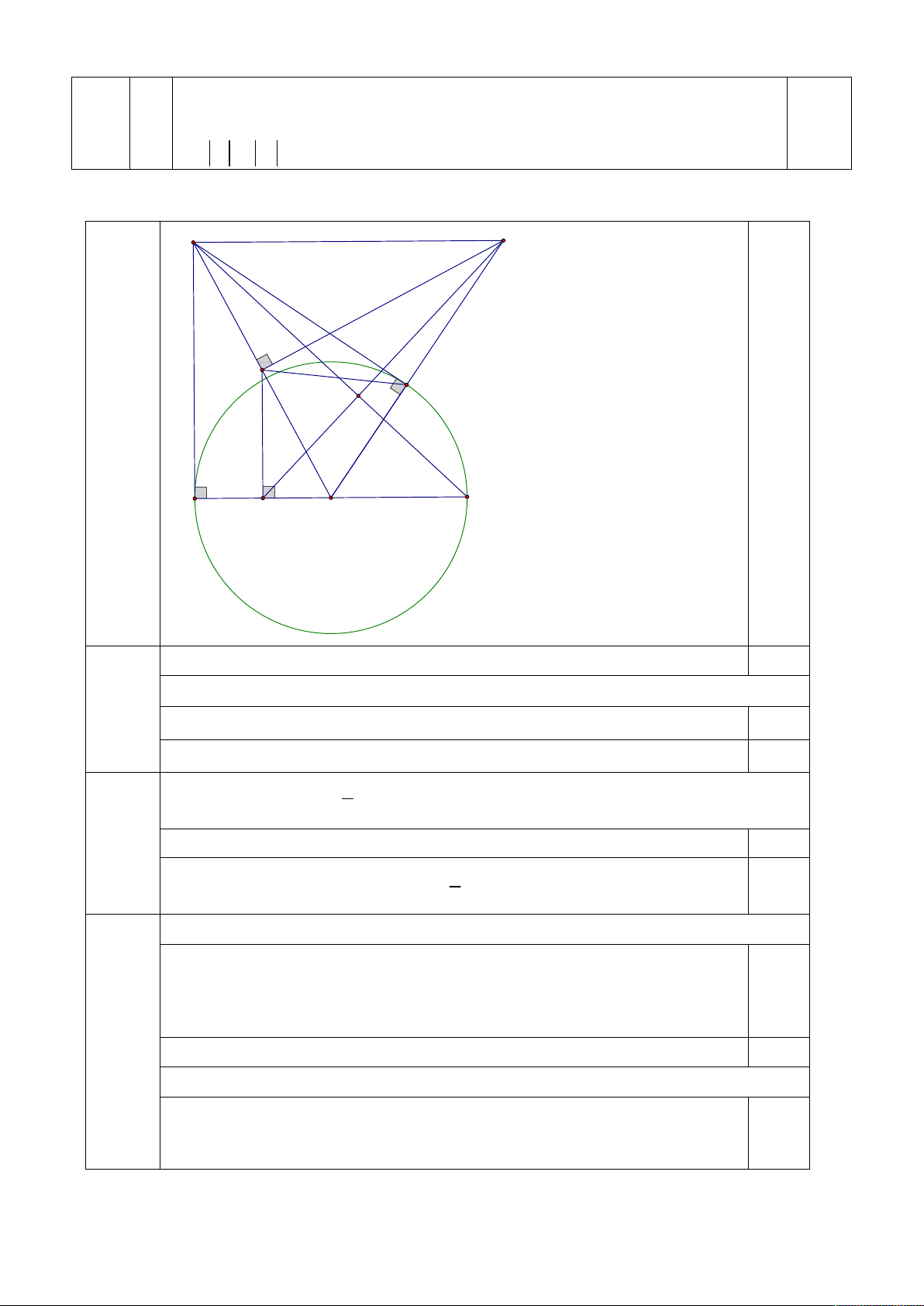
trục tung và điểm B x ; y nằm bên phải trục tung sao cho x x 3 . 2 2 1 2 Bài IV. (3,0 điểm) Cho đường tròn ;
O R và một điểm M nằm ngoài đường tròn. Kẻ tiếp tuyến , MA MB với đường tròn ; O R ( ,
A B là các tiếp điểm). Vẽ đường kính AD , lấy I là trung điểm của đoạn thẳng
MO , gọi C là hình chiếu vuông góc của I lên AO .
1) Chứng minh bốn điểm M , ,
A O, B thuộc một đường tròn;
2) Đường thẳng vuông góc với MO tại điểm I cắt đường thẳng OB tại điểm E . Chứng minh 1 2 O . B OE OM 2 3) Chứng minh I
ME đồng dạng với COI và CE MD .
Bài V. (0,5 điểm) Với các số thực không âm x, y, z thỏa mãn x y z 1 . x y z
Tìm giá trị lớn nhất của biểu thức P 2 x 2 y 2 z
…………..……. Hết ………………… UBND QUẬN HOÀN KIẾM
HƯỚNG DẪN CHẤM KHẢO SÁT
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
MÔN TOÁN LỚP 9 NĂM HỌC 2022 - 2023
Ngày khảo sát: 24/5/2023 Bài Ý
Đáp án – Hướng dẫn chấm Điểm Bài I 1)
Tính giá trị của biểu thức A khi x 16 0,5 đ (2,0 điểm) 0,25
Thay x 16 (TMĐK) vào biểu thức A 16 2 A 3 16 2 0.25 2) 5 3 x 14 Rút gọn B 1,0 đ x 2 4 x 5 3 x 14 B 0,25 x 2
x 2 x 2
5. x 2 3 x 14 B 0,25
x 2 x 2 2 x 4 B 0,25
x 2 x 2 2 B 0,25 x 2 3)
Xét biểu thức P .
A B . Tìm tất cả giá trị của x sao cho 2P 3 P . 0,5đ x 2 2 2 Ta có P . A B . x 2 x 2 x 2 0,25 P 0
2P 3 P P 3 2
P 2P 3 0 64
Giải P 3 ta được x TM. KL… 0,25 9 Bài 1)
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình: 1,5 đ II
Gọi chiều rộng mảnh đất là x ( x 0 , m) 0,25 (2,0 điểm)
Chiều dài của mảnh đất là x 12 (m) 0,25
Diện tích mảnh đất hình chữ nhật là x x 2 . 12 m 0,25
Vì diện tích mảnh đất bằng 2
85m nên ta có phương trình x x 2 .
12 85 x 12x 85 0
x 5tm
Giải phương trình ta được (t/m) x 1 7l 0,5
Vậy chiều rộng mảnh đất là 5m, chiều dài là 17m
Lưu ý: Học sinh giải phương trình bậc hai bằng máy tính ra kết quả luôn thì 0,25
cho nửa số điểm phần giải phương trình
Tính diện tích bề mặt của quả địa cầu 0,5 đ 2)
Bán kính của quả địa cầu là 33:2 = 16,5 (cm) 0,25
Tính được diện tích bề mặt của quả địa cầu: 2 2 S R 2 4 4.3,14.16,5 3419, 46 cm 0,25 Bài 1) 1 III x 1 4 y 1 2,5
Giải hệ phương trình: 1,0đ 2 điểm 3 x 1 7 y 1 1 x 1 4 y 1
(điều kiện: x 1; y 1 ) 0,25 2 3 x 1 7 y 1 x 1 3 Giải được 1 0,5 1 y 1 x 8
Giải được nghiệm của hệ là 0,25 y 2
a) Với m 2 , tìm tọa độ giao điểm của đường thẳng d và parabol P . 0,75đ
Với m 2 , phương trình hoành độ giao điểm của đường thẳng d và parabol 0,25 P là: 2
x 2x 8 0
2a) Giải được x 2;x 4 0,25
Tìm được tọa độ giao điểm của đường thẳng d và parabol P là: 0,25 2 ;4;4;16
b) Tìm tất cả giá trị của m để đường thẳng d cắt parabol P tại điểm
A x ; y nằm bên trái trục tung và điểm B x ; y nằm bên phải trục tung sao 2 2 1 1 0,75đ
cho x x 3 . 1 2
phương trình hoành độ giao điểm của d và P : 2b) 2 2
x mx m 4 0 . Học sinh chỉ ra được phương trình này có hai nghiệm trái 0,25
dấu với mọi giá trị của tham số m x 0 x x 1 1 1 Lập luận chỉ ra 0,25 x 0 x x 2 2 2
x x m Theo định lí vi –ét 1 2 2
x .x m 4 1 2 0,25
x x
x x 3 m 3 m 3 .KL…. 1 2 1 2 Bài IV. M E 3,0 điểm I B F D A C O
Vẽ hình đúng đến ý a 0,25
Chứng minh bốn điểm M , ,
A O, B thuộc một đường tròn 1)
c/m: góc MAO = góc MBO = 90 ; 0,5
Chứng minh được M , ,
A O, B nằm trên một đường tròn. 0,25 1 2 Chứng minh O .
B OE OM 2 2)
Chứng minh được OIE đồng dạng OBM (g.g) 0,5 1 Chứng minh được 2 O .
B OE OI.OM OM 0,5 2 Chứng minh I
ME đồng dạng với COI
IE là đường trung trực của MO nên EM = EO, suy ra tam giác EMO cân tại E, do đó góc EMO = góc EOM 0,25
Sử dụng tính chất của tiếp tuyến cắt nhau ta chứng minh được góc MOA =
góc MOB, do đó góc IOC = góc EMI 3) Chứng minh được I
ME đồng dạng với CO I (g.g) 0,25
Chứng minh CE MD
Gọi giao điểm của CE và MD là F
Có tam giác CIO và tam giác IEM đồng dạng (cmt) và chỉ ra C là trung điểm 0,25 của OA nên 1 OD IC CO 2 OD IC IE IE IM 1 OM OD OM OM 2
Lại có góc CIE = 90 + góc CIO = 90 + góc AMO
Mà góc MOD = 90 + góc AMO (góc ngoài tam giác AMO)
Do đó tam giác ICE và ODM đồng dạng (c.g.c) suy ra góc OMD = góc IEC hay góc IMF = góc IEF
góc IMF = góc IEF nên tứ giác IMEF nội tiếp, suy ra góc MFE = góc MIE = 0,25
90 , suy ra CE MD Bài V
Với các số thực không âm ,
x y, z thỏa mãn x y z 1. 0,5điểm x y z
Tìm giá trị lớn nhất của biểu thức P 0,5 2 x 2 y 2 z Với ,
x y, z không âm thỏa mãn x y z 1 nên suy ra 1 x Ta có 1 x 2 x 2 x y z
Chứng minh tương tự ta được y; z 2 y 2 z 0,5 x y z Ta có P
x y z 1 2 x 2 y 2 z
Vậy GTLN của P bằng 1. Dấu = xảy ra khi x; ; y z 0;0;
1 và các hoán vị
Lưu ý: Học sinh có cách giải khác đúng, vẫn cho điểm tối đa