Đề khảo sát Toán 9 năm 2023 – 2024 phòng GD&ĐT Đông Anh – Hà Nội
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra khảo sát chất lượng môn Toán 9 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Đông Anh, thành phố Hà Nội; kỳ thi được diễn ra vào thứ Sáu ngày 12 tháng 04 năm 2024; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Preview text:
HƯỚNG DẪN CHẤM
KIỂM TRA KHẢO SÁT LỚP 9 NĂM HỌC 2023 - 2024 Môn: Toán A. Hướng dẫn chung
- Học sinh giải theo cách khác mà đúng, đủ các bước thì giám khảo chấm điểm tối đa.
- Trong mỗi bài, nếu ở một bước nào đó bị sai thì các bước sau có liên quan không được điểm.
- Bài hình học bắt buộc phải vẽ đúng hình thì mới chấm điểm, nếu không có hình vẽ đúng ở phần
nào thì giám khảo không ghi điểm phần lời giải liên quan đến hình của phần đó.
- Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn. B. Nội dung, biểu điểm Bài Ý Nội dung Điểm
1) Thay x = 25 (TMĐK) vào biểu thức A ta được: I √25 − 3 (2đ) 1 𝐴 = (0,5đ) 0,25 √25 + 5 1 𝐴 = 0,25 5 4 2𝑥 − √𝑥 − 13 √𝑥 𝐵 = + − 0,25 √𝑥 + 3 𝑥 − 9 √𝑥 − 3 4 2𝑥−√𝑥−13 + − √𝑥 2 𝐵 = 0,25 √𝑥+3 (√𝑥+3)(√𝑥−3) √𝑥−3 (1đ)
4√𝑥−12+2𝑥−√𝑥−13−𝑥−3√𝑥 𝐵 = (√𝑥+3)(√𝑥−3) 0,25 𝑥−25 𝐵 = (√𝑥+3)(√𝑥−3) 0,25 3) √𝑥−5 P = A.B = √𝑥+3
𝑥 − 1 = 2(√𝑥 + 3). 𝑃 + 3√𝑥 + 5 (x ≥ 0; x ≠ 9) 3
⇔ 𝑥 − 1 = 2√𝑥 − 10 + 3√𝑥 + 5 (0,5đ)
⇔ 𝑥 + 9 − 2√𝑥 − 3√𝑥 + 5 = 0
⇔ 2𝑥 + 18 − 4√𝑥 − 6√𝑥 + 5 = 0
⇔ (𝑥 + 5 − 6√𝑥 + 5 + 9) + (𝑥 − 4√𝑥 + 4) = 0 2 2
⇔ (√𝑥 + 5 − 3) + (√𝑥 − 2) = 0 0,25
Giải ra tìm được x=4 (thỏa mãn ĐKXĐ), Vậy x= 4 0,25 II
1.Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x km/h (2,5đ) ĐK x>0 1 0,25 (2đ) 24
Thời gian của người đi xe đạp khi đi từ A đến B là h. 𝑥 0,25
Vận tốc của người đi xe đạp khi đi từ B đến A là x + 4 km/h 0,25 24
Thì thời gian của người đi xe đạp khi đi từ B đến A là h. 𝑥+4 0,25 1
Vì thời gian về ít hơn thời gian đi là 30 phút bằng h nên ta có 2 24 24 1 0,25 pt: − = 𝑥 𝑥+4 2 x2 +4x – 192 = 0 0,25 x = 12 (TM) x = -16 (KTM) 0,25
Vậy vận tốc của người đi xe đạp khi đi từ A đến B là 12 km/h 0,25 𝑆 2
𝑥𝑞 = 2𝜋𝑅ℎ ≈ 2.3,14.3,5.8 = 175,84(𝑐𝑚2) 0,25 (0,5đ)
Vậy diện tích phần giấy cần dùng khoảng 175,84 cm2 0,25 III √𝑥 − 5 + 3𝑦 = 16 (2đ) { 2√𝑥 − 5 − 𝑦 = 4 2√𝑥 − 5 + 6𝑦 = 32 ⇔ { ĐK: 𝑥 ≥ 5 2√𝑥 − 5 − 𝑦 = 4 0,25 1 (1đ) 7𝑦 = 28 𝑦 = 4 ⇔ { ⇔ { 0,25 √𝑥 − 5 + 3𝑦 = 16 √𝑥 − 5 = 16 − 12 = 4 𝑦 = 4 ⇔ { 𝑥 − 5 = 16 0,25 𝑦 = 4 ⇔ { 𝑥 = 21(𝑇𝑀) 0,25
Vậy hệ pt có nghiệm duy nhất là (21;4) a) Tính 𝛥 = 𝑚2 + 8 ∆ 0,25 > 0 với mọi m
Suy ra phương trình có 2 nghiệm phân biệt 𝑥1, 𝑥2 với mọi m 0,25 2 𝑥1 + 𝑥2 = 𝑚 (1đ)
b) Áp dụng định lý Vi-ét, ta có: { 𝑥1𝑥2 = −2 Để 𝑥2 2
1 + 𝑥2 = 8 ⇔ (𝑥1 + 𝑥2)2 − 2𝑥1𝑥2 = 8 0,25 Suy ra 𝑚2 + 4 = 8 ⇔ 𝑚2 = 4 ⇔ 𝑚 = ±2 0,25
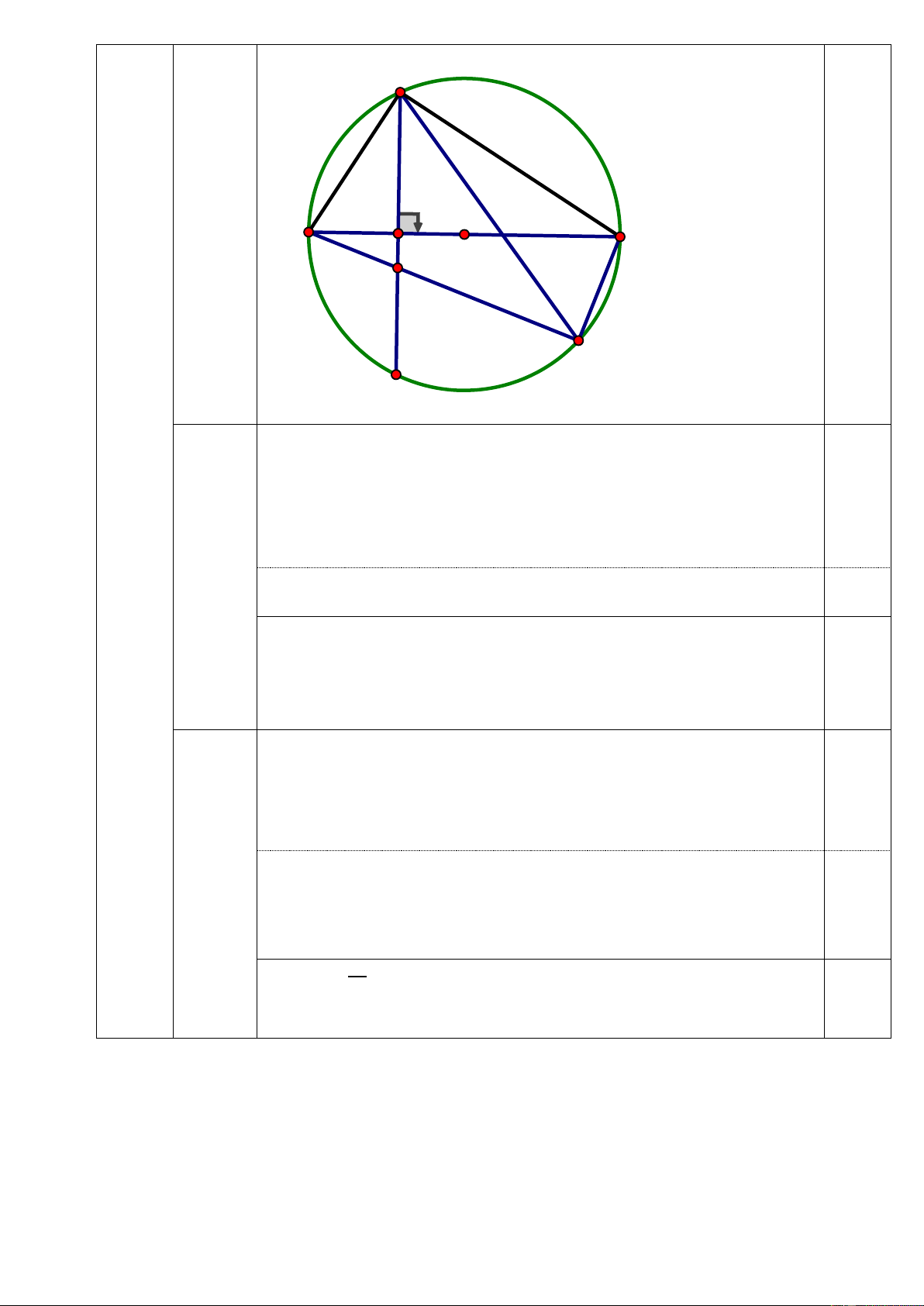
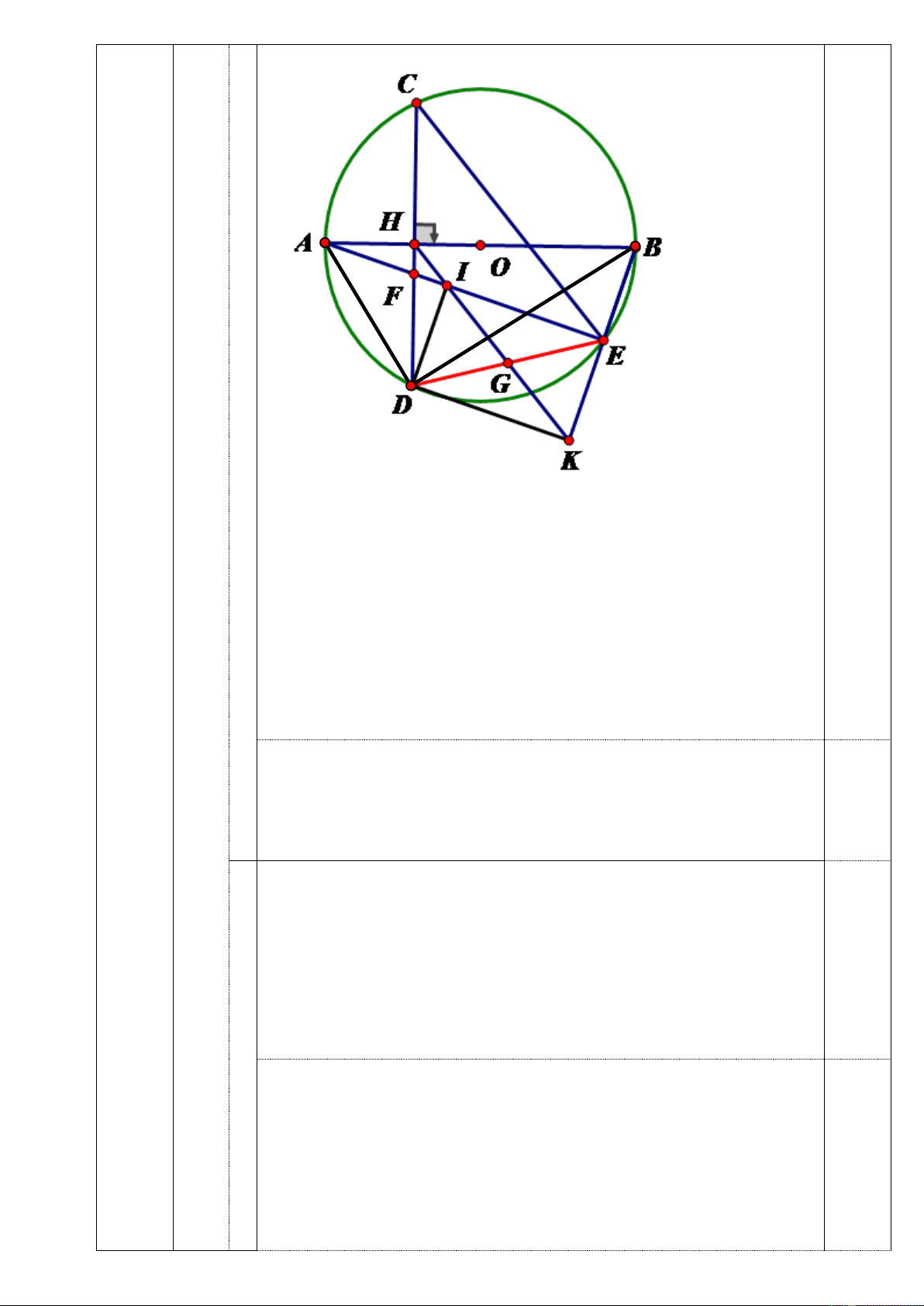
Vậy 𝑚 = ±2 là giá trị cần tìm. IV (3đ) C Vẽ hình đúng H A đến ý a 0,25 B O F E D
Xét (O) đường kính AB có 𝐴𝐸𝐵
̂ = 90𝑜 (góc nội tiếp chắn nửa
đường tròn đường kính AB) ⇒ 𝐵𝐸𝐹 ̂ = 90𝑜 0,25
𝐶𝐷 ⊥ 𝐴𝐵 tại H ⇒ 𝐵𝐻𝐹 ̂ = 90𝑜 1 (0,75đ) 0,25
Xét tứ giác BEFH có: 𝐵𝐻𝐹 ̂ + 𝐵𝐸𝐹 ̂ = 180𝑜
Mà chúng ở vị trí đối diện 0,25
⇒Tứ giác BHFE nội tiếp đường tròn.
Xét (O) có: AB là đường kính, 𝐴𝐵 ⊥ 𝐶𝐷 tại H (gt).
⇒ 𝐶𝐻 = 𝐻𝐷 (quan hệ đường kính, dây cung). 0,25
=>H là trung điểm của đoạn thẳng CD 0,25 2 Xét (O) có: 𝐴𝐶𝐵
̂ = 90𝑜 (góc nội tiếp chắn nửa đường tròn) (1đ)
Xét △ 𝐴𝐵𝐶 vuông tại C, có CH là đường cao 0,25
⇒ 𝐶𝐻2 = 𝐴𝐻. 𝐻𝐵 𝐶𝐷 Mà 𝐶𝐻 =
(H là trung điểm của đoạn thẳng CD) 2 0,25
Nên 𝐶𝐷2 = 4. 𝐴𝐻. 𝐻𝐵
𝐻𝐼//𝐶𝐸 ⇒ 𝐷𝐻 ̂𝐼 = 𝐷𝐶𝐸 ̂ (2 góc so le trong) Xét (O) có: 𝐷𝐴𝐸 ̂ = 𝐷𝐶𝐸
̂ (2 góc nội tiếp cùng chắn cung DE) ⇒ 𝐷𝐻 ̂𝐼 = 𝐷𝐴𝐸 ̂ ⇒ 𝐷𝐻 ̂𝐼 = 𝐷𝐴𝐼 ̂ 0,25 3
Xét tứ giác DAHI có: 𝐷𝐻 ̂𝐼 = 𝐷𝐴𝐼 ̂ (1đ)
Mà H, A là 2 đỉnh kề nhau cùng nhìn cạnh DI
⇒Tứ giác AHID nội tiếp đường tròn.
Xét đường tròn ngoại tiếp tứ giác AHID, có: 𝐴𝐻𝐷 ̂ = 𝐴𝐼𝐷
̂ ( 2 góc nội tiếp cùng chắn cung AD) Mà 𝐴𝐻𝐷 ̂ = 90𝑜 ⇒ 𝐴𝐼𝐷 ̂ = 90𝑜 0,25 Xét (O) có 𝐷𝐵𝐸 ̂ = 𝐷𝐴𝐸
̂ (2 góc nội tiếp cùng chắn cung DE) 𝐷𝐴𝐸 ̂ = 𝐷𝐴𝐼 ̂ = 𝐷𝐻 ̂𝐼 (cmt) ⇒ 𝐷𝐻 ̂𝐼 = 𝐷𝐵𝐸 ̂ Hay 𝐷𝐻𝐾 ̂ = 𝐷𝐵𝐾 ̂
⇒Tứ giác DHBK nội tiếp đường tròn. ⇒ 𝐷𝐻𝐵 ̂ = 𝐷𝐾𝐵 ̂ = 180𝑜 Mà: 𝐷𝐻𝐵 ̂ = 90𝑜 0,25 ⇒ 𝐷𝐾𝐵 ̂ = 90𝑜 ⇒ 𝐷𝐾𝐸 ̂ = 90𝑜
Xét tứ giác DIEK có: 𝐷𝐼𝐸 ̂ = 𝐼𝐸𝐾 ̂ = 𝐷𝐾𝐸 ̂ = 90𝑂
⇒Tứ giác DIEK là hình chữ nhật
⇒IK = DE và IK, DE cắt nhau tại trung điểm G của mỗi đường.
Mà GD = GK => ∆ DGK cân tại G. 0,25 V
Áp dụng BĐT Cauchy cho hai số dương: (0,5đ) 𝑥2 1 + 𝑦 𝑥2 1 + 𝑦 + ≥ 2√ . = 𝑥 1+y 4 1+y 4 𝑦2 1 + 𝑧 𝑦2 1 + 𝑧 + ≥ 2√ . = 𝑦 1+z 4 1+z 4 𝑧2 1 + 𝑥 𝑧2 1 + 𝑥 + ≥ 2√ . = 𝑧 {1+x 4 1+x 4
Cộng vế với vế ba BĐT trên ta được: 𝑥2 1 + 𝑦 𝑦2 1 + 𝑧 𝑧2 1 + 𝑥 ( + ) + ( + ) + ( + ) 1 + 𝑦 4 1 + 𝑧 4 1 + 𝑥 4 ≥ (𝑥 + 𝑦 + 𝑧) 𝑥2 𝑦2 𝑧2 3 𝑥 + 𝑦 + 𝑧 ⇔ + + ≥ − − + (𝑥 + 𝑦 + 𝑧) 1+y 1+z 1+x 4 4 𝑥2 𝑦2 𝑧2 3(𝑥 + 𝑦 + 𝑧) 3 3 3 3 ⇔ + + ≥ − ≥ . 3. 3 − = 0,25 1+y 1+z 1+x √𝑥𝑦𝑧 4 4 4 4 2 3 ⇔ 𝐴 ≥ 2
Dấu “=” xảy ra ⇔ 𝑥 = 𝑦 = 𝑧 = 1 (TM). 0,25 3
Vậy giá trị nhỏ nhất của A là khi x= y = z = 1. 2
Document Outline
- Doc1
- Hướng Dẫn Chấm Toán khảo sát Lớp9 T4.2024.