Đề khảo sát Toán 9 năm 2023 – 2024 phòng GD&ĐT Quỳnh Lưu – Nghệ An
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi thử và khảo sát chất lượng học sinh môn Toán 9 giai đoạn học kỳ 2 năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Quỳnh Lưu, tỉnh Nghệ An; kỳ thi được diễn ra vào ngày 28 tháng 03 năm 2024; đề thi có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!
Preview text:
PHÒNG GD&ĐT QUỲNH LƯU ĐỀ THI THỬ - KHẢO SÁT CHẤT LƯỢNG HS LỚP 9
HỌC KỲ 2, NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Đề thi môn: TOÁN
(Đề thi gồm có 02 trang)
Thời gian thi: 120 phút (Không kể thời gian giao đề)
Ngày thi: 28 tháng 03 năm 2024
Câu 1. (2,5 điểm) a) Tính b) Rút gọn biểu thức
với x ≥ 0 và x ≠1
c) Tìm giá trị của a để đường thẳng y = ax – 7 đi qua điểm có toạ độ M (-1; 2).
Câu 2. (2.0 điểm) a) Giải phương trình b) Cho biết phương trình
có hai nghiệm dương phân biệt x1, x2
sao cho x1 < x2 . Không giải phương trình, tính giá trị biểu thức
Câu 3. (2,0 điểm)
a) Một quyển sách Toán có giá bìa 30000 đồng, đang được giảm giá 5%. Một
quyển sách Văn có giá bìa 40000 đồng, đang được giảm giá 10%. Trong thời gian
giảm giá, nhà sách đó bán được tất cả 120 quyển sách Văn và Toán, thu được về số
tiền là 3795000 đồng. Hỏi nhà sách đó đã bán được bao nhiêu quyển sách Văn, bao
nhiêu quyển sách Toán?
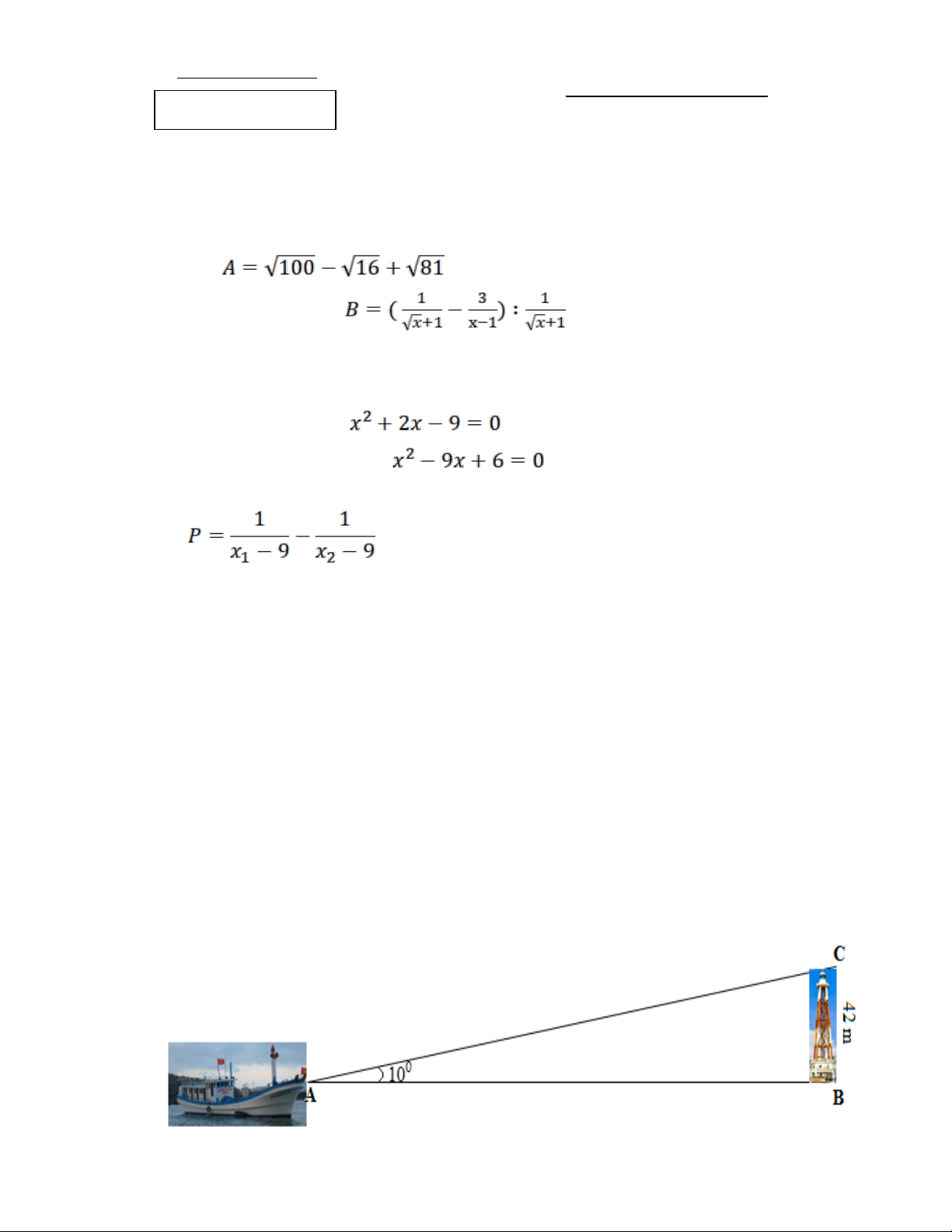
b) Hải đăng Đá Lát là một trong 7 ngọn hải đăng cao nhất Việt Nam, được đặt trên
đảo Đá Lát ở vị trí cực Tây Quần đảo, thuộc xã đảo Trường Sa, huyện Trường Sa,
tỉnh Khánh Hòa. Ngọn hải đăng được xây dựng năm 1994, cao 42 mét, có tác dụng
chỉ vị trí đảo, giúp tàu thuyền hoạt động trong vùng biển Trường Sa định hướng và
xác định được vị trí mình. Một người đi trên tàu đánh cá muốn đến ngọn hải đăng Đá
Lát, người đó đứng trên mũi tàu cá và dùng giác kế đo được góc giữa mũi tàu và tia
nắng chiếu từ đỉnh ngọn hải đăng đến tàu là 10°(hình vẽ dưới đây). Tính khoảng cách
AB từ tàu đến ngọn hải đăng (làm tròn đến chữ số thập phân thứ nhất).
Câu 4. (3,0 điểm)
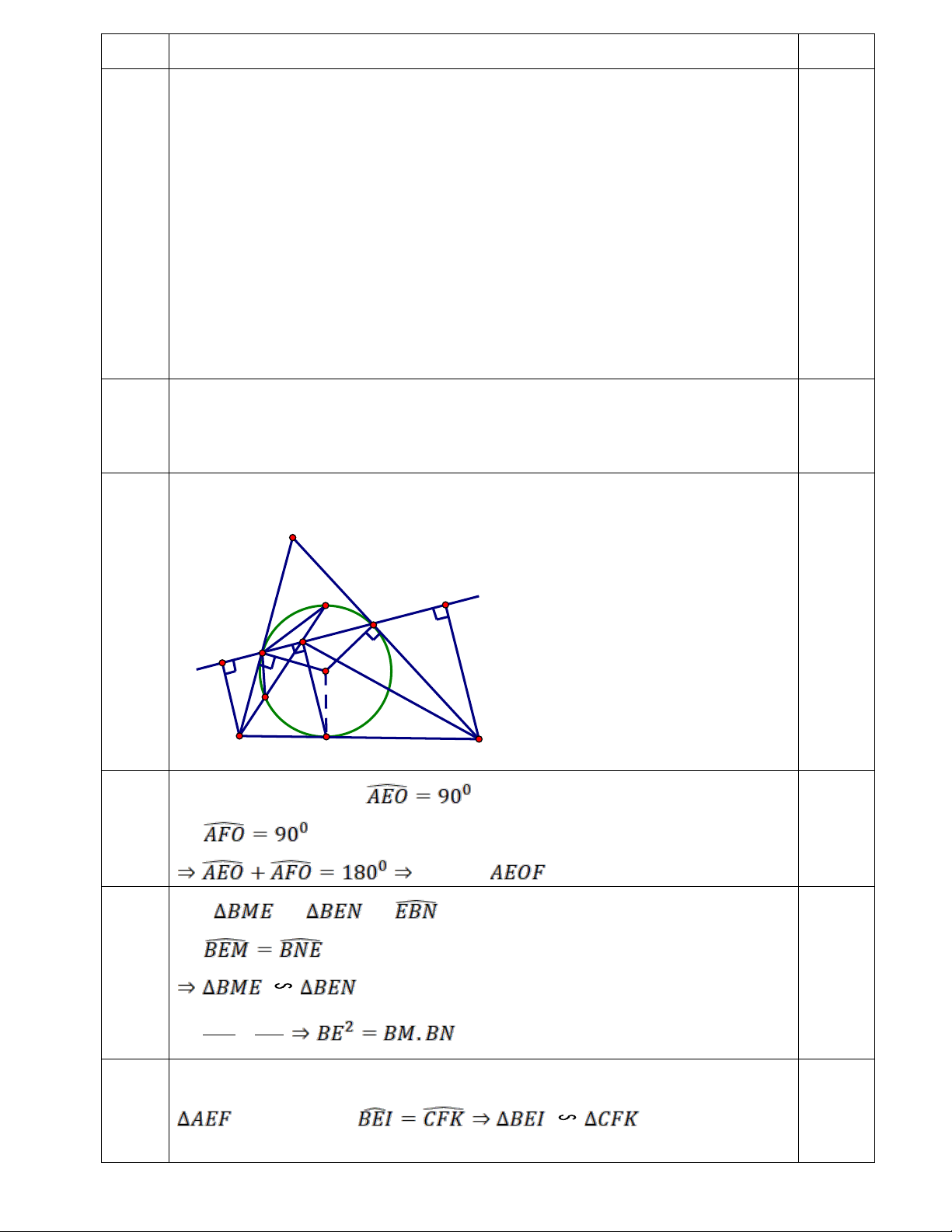
Cho tam giác ABC ngoại tiếp đường tròn (O). Gọi D, E, F lần lượt là tiếp điểm
giữa các cạnh BC, AB, AC với đường tròn (O). Kẻ DH vuông góc EF tại H.
a) Chứng minh rằng: tứ giác AEOF nội tiếp đường tròn.
b) Tia BH cắt đường tròn tại M và N sao cho M nằm giữa B và H, H nằm giữa M và N. Chứng minh: BE2 = BM.BN. c) Chứng minh rằng:
Câu 5. (0,5 điểm) Giải hệ phương trình:
----------------HẾT---------------
Họ tên thí sinh: ………………………………………… Số báo danh: ……………
Thí sinh không được sử dụng tài liệu, giám thị coi thi không giải thích gì thêm.
HƯỚNG DẪN CHẤM ĐỀ THI THỬ - KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9
Học kỳ 2, Năm học: 2023 – 2024 Đề thi môn: Toán CÂU NỘI DUNG ĐIỂM Câu 1 1a =10 1,0
(1,0 (tính đúng mỗi ý = 9 được 0,25đ) điểm) 1b (1,0 điểm) 1 3 1 x −1− 3 1 = − = : x + ( x + )1( x −
( x + )1( x − )1 x +1 ) : 1 1 x +1 0,5 x − 4 = x −1 0,5 1c
Đường thẳng y = ax – 7 đi qua điểm có toạ độ M(-1; 2) 0,25 (0,5 nên 2 = a(-1) – 7 0,25 điểm) a = - 9 Câu 2 2a Phương trình 0,5
(1,0 Có ∆ = 4+36 = 40 > 0
điểm) Nên phương trình có hai nghiệm phân biệt 0,25 x = 1 − + 10 0,25 1 và x = 1 − − 10 2 2b phương trình
có hai nghiệm dương phân biệt x1, x2 0,25 (1,0 sao cho x1 < x2
điểm) nên x1 + x2 = 9 và x1 . x2 = 6 (theo hệ thức vi-ét) 0,25 2 Vì x x − x x + x − 4x .x 57 0,25 1 < x2 nên 2 ( 2 1 1 2 )2 1 2 P = = = 6 36 36 57 ⇒ P = 0,25 6 Câu 3 3a
Gọi số quyển sách Văn là x (quyển) (x là số nguyên dương, 0
(1,5 số quyển sách Toán là y (quyển) (y là số nguyên dương, 0,25 điểm) 0 Theo đề ta có hệ pt: 0,5 x + y =120
40000(100% −10%)x + 30000(100% − 5%)y = 3795000
Suy ra: x = 50(nhận) và y = 70(nhận) 0,5
Vậy Số quyển sách Văn là 50 (quyển)
Số quyển sách Toán là 70 (quyển) 0,25 3b Xét A
∆ BC vuông tại B có AB = BC.cot A = 42.cot10° = 42.tan80° ≈ 238,2 0,25 (0,5
Vậy khoảng cách từ tàu đến ngọn hải đăng là 238,2 m. 0,25 điểm) Câu 4 Vẽ hình đúng A 0,5 N K F I E H O M B C D 4a Xét tứ giác AEOF có 0,25 (1,0 và 0,25 điểm) Tứ giác nội tiếp đường tròn 0,5 4b Xét và có chung 0,25 (1,0 và (cùng chắn cung EM) 0,25 điểm) (g-g) 0,25 BM BE ⇒ = BE BN 0,25 4c
Kẻ BI và CK vuông góc với EF (I và K thuộc EF) (0,5 cân tại A nên (g-g) 0,25 điểm) Ta có Chứng minh (2) 0,25 Từ (1) và (2) suy ra (c-g-c) Câu 5 ĐK y+1 ≥ 0 ;
(0,5 + Nhận thấy x = 0 vô nghiệm
điểm) + xét x ≠ 0 ta có: 0,25 ; ;
Thử lại ta thấy hệ phương trình đã cho có nghiệm là: 0,25 ; ;
Lưu ý: Học sinh có thể giải theo cách khác, nếu đúng vẫn được điểm tối đa.
----------------HẾT---------------