Đề khảo sát Toán 9 năm 2023 – 2024 trường THCS Minh Khai – Hà Nội

TRƯỜNG THCS MINH KHAI
KHẢO SÁT NĂNG LỰC HỌC SINH LỚP 9 NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn thi: TOÁN ĐỀ A
Thời gian làm bài: 120 phút (không kể thời gian phát đề) Ngày thi: 22/3/2024
(Đề thi có 05 câu, gồm 01 trang)
Câu I (2,0 điểm). Cho biểu thức: x x − 3 2 x − 6 x + 3 P = − −
với x ≥ 0; x ≠ 9 x − 2 x − 3 x +1 x − 3
1. Rút gọn biểu thức P.
2. Tính giá trị của biểu thức P khi x = 3− 2 2 .
Câu II (2,0 điểm).
1. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) : y = ax + .
b Tìm a,b
để đường thẳng (d) có hệ số góc bằng 3 và đi qua điểm M ( 1; − 2) .
2. Giải hệ phương trình: x − y = 2 3x   + 2y =11
Câu III (2,0 điểm). 1. Giải phương trình: 2
x − 3x + 2 = 0 . 2. Cho phương trình 2 2
x − 2mx − m − 2 = 0 (m là tham số). Tìm các giá trị của m
để phương trình có hai nghiệm x , x (với x < x ) thỏa mãn hệ thức 1 2 1 2 2
x − 2 x − 3x x = 3m + 3m + 4 . 2 1 1 2
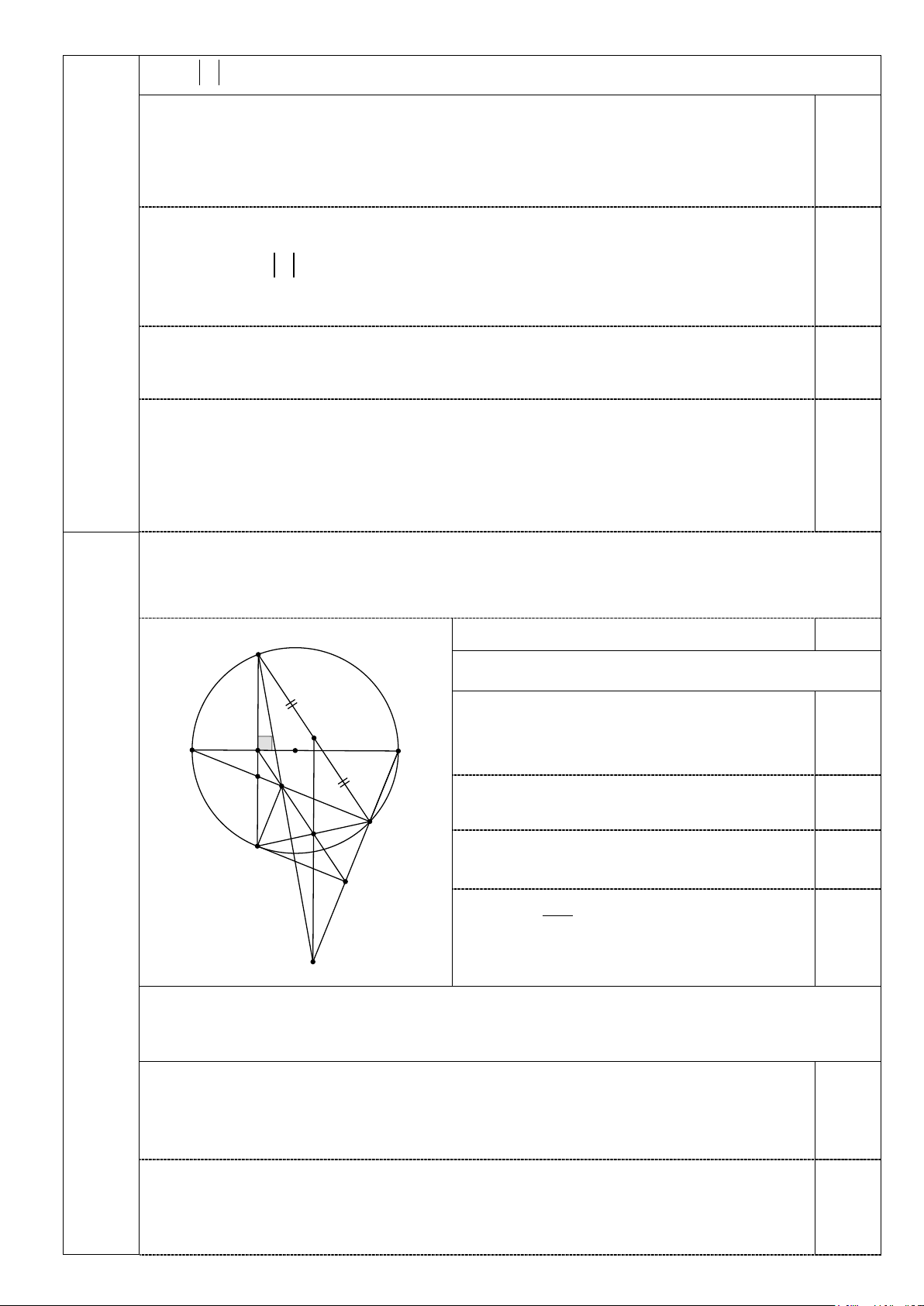
Câu IV (3,0 điểm). Cho đường tròn tâm (O) đường kính AB , lấy điểm H thuộc
đường kính AB , qua điểm H kẻ dây CD vuông góc với đường kính AB, lấy điểm
E thuộc cung nhỏ BD ( E khác B và D); AE cắt CD tại điểm F .
1. Chứng minh: Tứ giác BEFH nội tiếp. 2. Chứng minh: 2
CD = 4.AH.HB
3. Đường thẳng đi qua H song song với CE , cắt đường thẳng AE và BE lần
lượt tại I và K . Gọi G là giao điểm của DE và IK, M là trung điểm của đoạn
thẳng CE. Chứng minh: DI ⊥ AE và ba đường thẳng CI, MG, BE đồng quy.
Câu V (1,0 điểm). Cho các số thực không âm x, y, z thỏa mãn xy + yz + zx = 3xyz.
Tìm giá trị nhỏ nhất của biểu thức x y z 3 Q = + + + xyz . 2 2 2 1+ y 1+ z 1+ x 2
-------------------------------------- HẾT ----------------------------------------------
Họ và tên thí sinh: ..............................................................................
SBD: ................................................................
Chữ ký của CBCT1: ........................................................................
Chữ ký của CBCT2: ................................ TRƯỜNG THCS HƯỚNG DẪN CHẤM MINH KHAI Môn thi: TOÁN Hướng dẫn chung:
1) Nếu học sinh giải cách khác với cách nêu trong hướng dẫn chấm này, mà đúng, thì
vẫn được điểm tối đa của phần (câu) tương ứng.
2) Trong câu hình, nếu học sinh không vẽ hình hoặc vẽ sai cơ bản thì không cho điểm câu đó. Câu Nội dung Điểm 1. ĐK : x ≥ 0;;x ≠ 9 ( − ) − − ( − )2 2 x 3 x x 3 2 x 3 − ( x +3)( x + − + )1 x x 3 x 3 P = ( − − = 0,50 x + )1( x −3) x +1 x − 3 ( x + )1( x −3)
= x x −3− 2x +12 x −18− x − 4 x −3 x x −3x +8 x − 24 ( = x + ) 1 ( x −3)
( x + )1( x −3) I 0,50
x( x −3)+8( x −3) (x +8)( x −3) x + (2,0đ) = ( = = 8 x + ) 1 ( x −3)
( x + )1( x −3) x +1 Vậy với + x x ≥ 0;;x ≠ 9 thì P = 8 0,25 x +1 2. Với x = − = ( − )2 3 2 2 2 1 ⇒ x = 2 −1 0,25 Thay P vào ta có : 11 2 2 11 2 4 P − − = = 2 2 0,50
1. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) có phương trình y = ax +b.
Tìm a,b để đường thẳng (d) có hệ số góc bằng 3 và đi qua điểm M ( 1; − 2) .
Đường thẳng (d) có hệ số góc bằng 3 nên suy ra a = 3. 0,50 II
Mặt khác (d) đi qua M ( 1;
− 2) ta có −a + b = 2 ⇔ 3
− + b = 2 ⇔ b = 5. Vậy giá (2,0đ) 0,50
trị cần tìm là a = 3;b = 5.
2. Ta có hệ PT 2x − 2y = 4 5  x =15 x = 3 x = 3 ⇔  ⇔ ⇔  ⇔ 0,75 3   x 2y 11  + = x − y = 2 y = x − 2 y =1
Vậy hệ PT có nghiệm duy nhất ( x; y) = (3; 1) 0,25
1. Giải phương trình 2
x − 3x + 2 = 0.
Ta có a + b + c =1+ ( 3 − ) + 2 = 0 . 0,50 c III
Suy ra phương trình có hai nghiệm phân biệt x =1; x = = 2. 1 2 (2,0đ) a 0,50
Vậy phương trình có tập nghiệm là S = {1; } 2 .
2. Cho phương trình 2 2
x − 2mx − m − 2 = 0 ( m là tham số). Tìm các giá trị của m để
phương trình có hai nghiệm x , x x < x thỏa mãn hệ thức 1 2 ( 1 2 ) 2
x − 2 x − 3x x = 3m + 3m + 4. 2 1 1 2 Ta có ∆ = (−m)2 2 2 '
− (−m − 2) = 2m + 2 > 0, m
∀ ∈ R nên phương trình luôn có
x + x = 2m (1) 0,25
hai nghiệm x , x x < x . Khi đó theo Viet, ta có 1 2 1 2 ( 1 2 )  . 2
x .x = −m −  2 (2) 1 2 Do 2
x .x = −m − 2 < 0 ⇒ x < 0; x > 0. 1 2 1 2 Giả thiết 2
x − 2 x − 3x x = 3m + 3m + 4 2 1 1 2 0,25 2 2
⇔ 2x + x − 3(−m − 2) = 3m + 3m + 4 ⇔ 2x + x = 3m − 2 (3) 1 2 1 2
x + x = 2m x = m − 2 Từ (1),(3) ta có 1 2 1  ⇔ 2x x 3m 2  0,25 + = − x = m +   2 1 2 2
Thay x = m − 2; x = m + 2 1 2 vào (2) , ta được ( m = − m − 2)(m + 2) 1 2 2
= −m − 2 ⇔ 2m = 2 ⇔  (thỏa mãn). 0,25 m = 1
Vậy giá trị cần tìm là m = 1 − và m =1.
Qua điểm H kẻ dây CD vuông góc với đường kính AB , lấy điểm E thuộc cung nhỏ BD
( E khác B và D ); AE cắt CD tại điểm F .
1. Chứng minh: Tứ giác BEFH nội tiếp.
1. HS chứng minh tứ giác BEFH nội tiếp. 1,0 C 2. Chứng minh: 2
CD = 4.AH.HB Xét ( ;
O R) có dây CD ⊥ AB tại H M ⇒ H
H là trung điểm của CD (quan hệ giữa 0,25 A B đường kính và dây). O F Xét (O) có:  90o ACB = (góc nội tiếp chắn I 0,25 G nửa đường tròn) E Xét A
∆ BC vuông tại C , có CH là đường D IV cao 2
⇒ CH = AH.HB 0,25 K (2,0đ) Mà CD CH = . Nên 2
CD = 4.AH.HB 2 0,25 N
3. Đường thẳng đi qua H song song với CE , cắt đường thẳng AE và BE lần lượt tại I và
K . Gọi G là giao điểm của DE và IK, M là trung điểm của đoạn thẳng CE. Chứng minh:
DI ⊥ AE và ba đường thẳng CI, MG, BE đồng quy. ⇒  =  HI //CE
DHI DCE (2 góc đồng vị) Xét (O; R) có:  = 
DAE DCE (2 góc nội tiếp cùng chắn cung DE ) 0,25 ⇒ = DHI DAE ⇒  =  DHI DAI
Xét tứ giác DAHI có:  = 
DHI DAI , Mà H, A là 2 đỉnh kề nhau
⇒ Tứ giác AHID nội tiếp. ⇒  = 
AHD AID (2 góc nội tiếp cùng chắn cung AD) 0,25 Mà  = ° ⇒  AHD 90
AID = 90° ⇒ DI ⊥ AE Xét (O;R) có  = 
DBE DAE (2 góc nội tiếp cùng chắn cung DE) Mà  = 
DAE DHI (cmt) ⇒  =  DHI DBE
Xét tứ giác DIEK có:  =  =  DIE IEK DKE = 90° 0,25
⇒ Tứ giác DIEK là hình chữ nhật
⇒ IK và DE cắt nhau tại trung điểm mỗi đường ⇒ G là trung điểm của IK .
Giả sử CI cắt BK tại N ; NG cắt CE tại M’ Ta có: // ' IG NG IG CM ⇒ =
(Hệ quả định lí Ta let) CM ' NM ' // ' GK NG GK M E ⇒ = IG GK ⇒ = M 'E NM ' CM ' M 'E 0,25
Mà IG = GK (G là trung điểm IK )
⇒ CM ' = M 'E ⇒ M’ là trung điểm của CE
⇒ M trùng M’ ⇒ M , G, N thẳng hàng Vậy CI, MG, BE đồng quy
Cho các số thực không âm x, y, z thỏa mãn xy + yz + zx = 3xyz.
Tìm giá trị nhỏ nhất của biểu thức x y z 3 Q = + + + xyz . 2 2 2 1+ y 1+ z 1+ x 2
Vì xy + yz + zx = 3xyz.nên 1 1 1 + + = 3 x y z 0,25 Mà (  
x + y + z) 1 1 1 + +
≥ 9 ⇒ x + y + z ≥   3 (1)  x y z  2 2 Ta có: x xy xy xy = x − ≥ x − = x − ( Vì 2
1+ y ≥ 2y > 0 ) 0,25 2 2 1+ y 1+ y 2y 2 V
(1,0đ) Tương tự y yz ≥ − ; z zx y ≥ z − 2 2 1+ z 2 1+ x 2 Suy ra x y z + + ≥ xy yz zx x − + y − + z − 2 2 2 1+ y 1+ z 1+ x 2 2y 2 x y z 1 ⇔ + + +
xy + yz + zx ≥ x + y + z 2 2 2 ( ) 1+ y 1+ z 1+ x 2 0,25 x y z 3 ⇔ + +
+ xyz ≥ x + y + z (2) 2 2 2 1+ y 1+ z 1+ x 2
Từ (1) và (2), ta được Q ≥ 3. 0,25
Khi x = y = z =1 thì Q = 3 .Vậy giá trị nhỏ nhất của biểu thức Q bằng 3.
------------------ Hết -----------------
TRƯỜNG THCS MINH KHAI
KHẢO SÁT NĂNG LỰC HỌC SINH LỚP 9 NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn thi: TOÁN ĐỀ B
Thời gian làm bài: 120 phút (không kể thời gian phát đề) Ngày thi: 22/3/2024
(Đề thi có 05 câu, gồm 01 trang)
Câu I (2,0 điểm). Cho biểu thức: y y − 3 2 y − 6 y + 3 Q = − −
với y ≥ 0; y ≠ 9 y − 2 y − 3 y +1 y − 3
1. Rút gọn biểu thức Q.
2. Tính giá trị của biểu thức Q khi y = 3− 2 2 .
Câu II (2,0 điểm).
1. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) : y = ax + .
b Tìm a,b
để đường thẳng (d) có hệ số góc bằng 2 và đi qua điểm M ( 1; − 2) .
2. Giải hệ phương trình: x − y = 2 3x   + 2y = 6
Câu III (2,0 điểm). 1. Giải phương trình: 2
x − 4x + 3 = 0 . 2. Cho phương trình 2 2
x − 2mx − m − 2 = 0 (m là tham số). Tìm các giá trị của m
để phương trình có hai nghiệm x , x (với x > x ) thỏa mãn hệ thức 1 2 1 2 2
x + 2 x − 3x x = 3m + 3m + 4 . 2 1 1 2
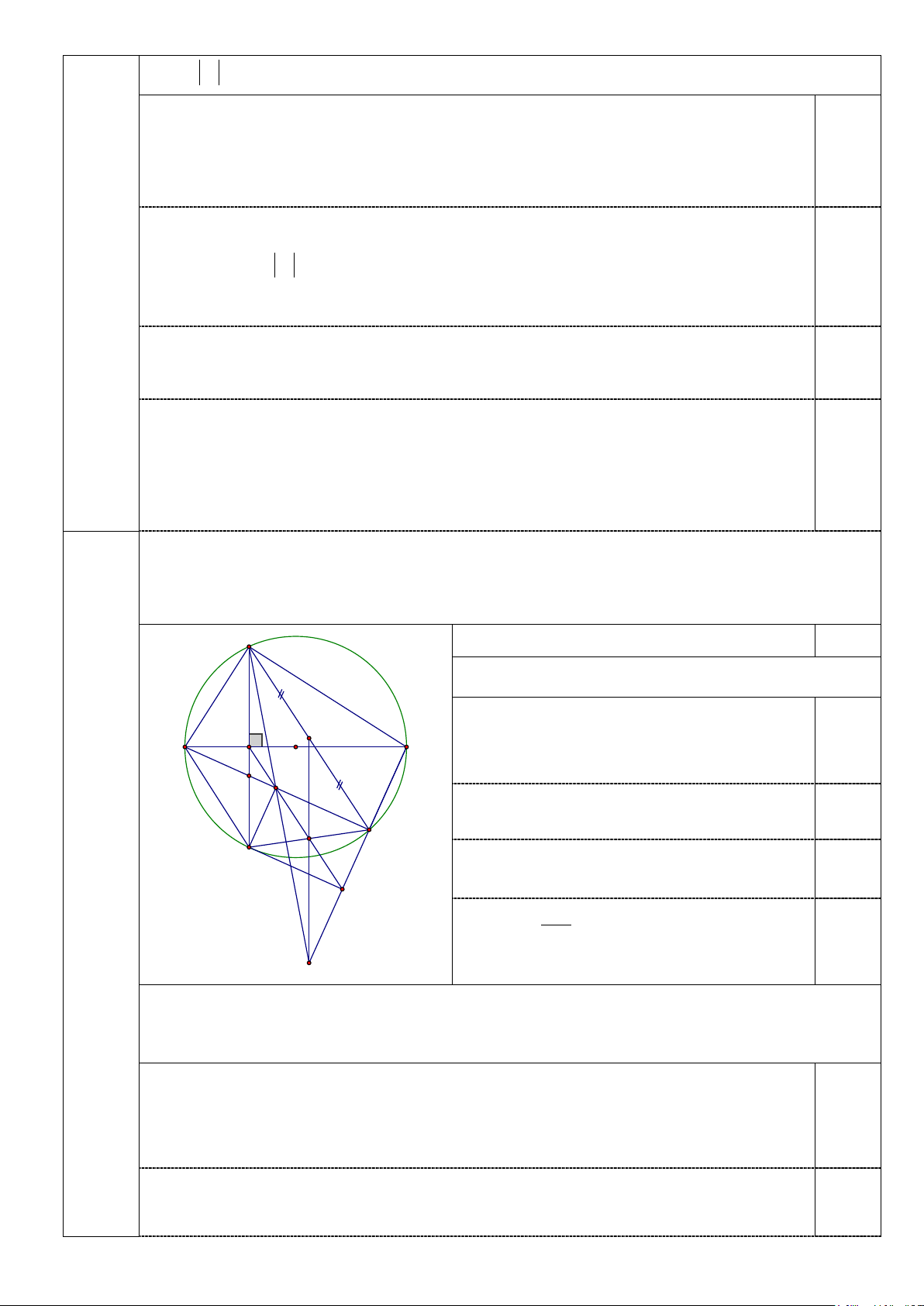
Câu IV (3,0 điểm). Cho đường tròn tâm (O) đường kính AB , lấy điểm Q thuộc
đường kính AB , qua điểm Q kẻ dây CD vuông góc với đường kính AB, lấy điểm
E thuộc cung nhỏ BD ( E khác B và D); AE cắt CD tại điểm F .
1. Chứng minh: Tứ giác BEFQ nội tiếp. 2. Chứng minh: 2 CD = 4.A . Q QB
3. Đường thẳng đi qua Q song song với CE , cắt đường thẳng AE và BE lần
lượt tại I và K . Gọi G là giao điểm của DE và IK, M là trung điểm của đoạn
thẳng CE. Chứng minh: DI ⊥ AE và ba đường thẳng CI, MG, BE đồng quy.
Câu V (1,0 điểm). Cho các số thực không âm a,b,c thỏa mãn ab + bc + ca = 3 . abc
Tìm giá trị nhỏ nhất của biểu thức a b c 3 A = + + + abc . 2 2 2 1+ b 1+ c 1+ a 2
-------------------------------------- HẾT ----------------------------------------------
Họ và tên thí sinh: ..............................................................................
SBD: ................................................................
Chữ ký của CBCT1: ........................................................................
Chữ ký của CBCT2: ................................ TRƯỜNG THCS HƯỚNG DẪN CHẤM MINH KHAI Môn thi: TOÁN Hướng dẫn chung:
1) Nếu học sinh giải cách khác với cách nêu trong hướng dẫn chấm này, mà đúng, thì
vẫn được điểm tối đa của phần (câu) tương ứng.
2) Trong câu hình, nếu học sinh không vẽ hình hoặc vẽ sai cơ bản thì không cho điểm câu đó. Câu Nội dung Điểm 1. ĐK : y ≥ 0;;y ≠ 9 y y 3 ( − ) y 3 − − ( − )2 2 y 3 y y 3 2 y 3 − ( y +3)( y + − + )1 Q = ( − − = 0,50 y + )1( y −3) y +1 y − 3 ( y + )1( y −3)
= y y −3− 2y +12 y −18− y − 4 y −3 y y −3y +8 y − 24 ( y ) = +1 ( y −3)
( y + )1( y −3) I 0,50
y ( y −3)+8( y −3) ( y +8)( y −3) y + (2,0đ) = ( = 8 y ) = +1 ( y −3)
( y + )1( y −3) y +1 Vậy với y + y ≥ 0; y ≠ 9 thì Q = 8 y +1 0,25 2. Với y = − = ( − )2 3 2 2 2 1 ⇒ y = 2 −1 0,25 Thay P vào ta có : 11 2 2 11 2 4 P − − = = 2 2 0,50
1. Trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) có phương trình y = ax +b.
Tìm a,b để đường thẳng (d) có hệ số góc bằng 2 và đi qua điểm M ( 1; − 2) .
Đường thẳng (d) có hệ số góc bằng 2 nên suy ra a = 2 . 0,50 II
Mặt khác (d) đi qua M ( 1;
− 2) ta có −a + b = 2 ⇔ 3
− + b = 2 ⇔ b = 5. Vậy giá (2,0đ) 0,50
trị cần tìm là a = 2;b = 5.
2. Ta có hệ PT x − y = 2 2x − 2y = 4 5  x =10 x = 2 x = 2 ⇔  ⇔ ⇔  ⇔ 0,75 3x     + 2y = 6 3  x + 2y = 6 x − y = 2 y = x − 2 y = 0
Vậy hệ PT có nghiệm duy nhất ( x; y) = (2; 0) 0,25
1. Giải phương trình 2
x − 4x + 3 = 0.
Ta có a + b + c =1+ ( 4 − ) + 3 = 0 . 0,50 c III
Suy ra phương trình có hai nghiệm phân biệt x =1; x = = 3. 1 2 (2,0đ) a 0,50
Vậy phương trình có tập nghiệm là S = {1; } 3 .
2. Cho phương trình 2 2
x − 2mx − m − 2 = 0 ( m là tham số). Tìm các giá trị của m để
phương trình có hai nghiệm x , x x > x thỏa mãn hệ thức 1 2 ( 1 2 ) 2
x + 2 x − 3x x = 3m + 3m + 4. 2 1 1 2 Ta có ∆ = (−m)2 2 2 '
− (−m − 2) = 2m + 2 > 0, m
∀ ∈ R nên phương trình luôn có
x + x = 2m (1) 0,25
hai nghiệm x , x x > x . Khi đó theo Viet, ta có 1 2 1 2 ( 1 2 )  . 2
x .x = −m −  2 (2) 1 2 Do 2
x .x = −m − 2 < 0 ⇒ x > 0; x < 0. 1 2 1 2 Giả thiết 2
x + 2 x − 3x x = 3m + 3m + 4 2 1 1 2 0,25 2 2
⇔ 2x + x − 3(−m − 2) = 3m + 3m + 4 ⇔ 2x + x = 3m − 2 (3) 1 2 1 2
x + x = 2m x = m − 2 Từ (1),(3) ta có 1 2 1  ⇔ 2x x 3m 2  0,25 + = − x = m +   2 1 2 2
Thay x = m − 2; x = m + 2 1 2 vào (2) , ta được ( m = − m − 2)(m + 2) 1 2 2
= −m − 2 ⇔ 2m = 2 ⇔ 
(không tmđk x > 0; x < 0. ). 0,25 m = 1 1 2
Vậy không có giá trị của m.
Qua điểm Q kẻ dây CD vuông góc với đường kính AB , lấy điểm E thuộc cung nhỏ BD
( E khác B và D ); AE cắt CD tại điểm F .
1. Chứng minh: Tứ giác BEFQ nội tiếp. C
1. HS chứng minh tứ giác BEFQ nội tiếp. 1,0 2. Chứng minh: 2 CD = 4.A . Q QB Xét ( ;
O R) có dây CD ⊥ AB tại Q M Q
⇒ Q là trung điểm của CD (quan hệ giữa 0,25 A O B
đường kính và dây). F I Xét (O) có:  90o ACB = (góc nội tiếp chắn 0,25 G nửa đường tròn) E D Xét A
∆ BC vuông tại C , có CQ là đường IV 0,25 K cao 2 ⇒ CQ = A . Q QB (2,0đ) Mà = CD CQ . Nên 2 CD = 4.A . Q QB 2 0,25 N
3. Đường thẳng đi qua Q song song với CE , cắt đường thẳng AE và BE lần lượt tại I và
K . Gọi G là giao điểm của DE và IK, M là trung điểm của đoạn thẳng CE. Chứng minh:
DI ⊥ AE và ba đường thẳng CI, MG, BE đồng quy.  
QI //CE ⇒ DQI = DCE (2 góc đồng vị) Xét (O; R) có:  = 
DAE DCE (2 góc nội tiếp cùng chắn cung DE ) 0,25 ⇒  DQI = DAE ⇒  DQI =  DAI
Xét tứ giác DAQI có:  DQI = 
DAI , Mà Q, A là 2 đỉnh kề nhau 0,25
⇒ Tứ giác AQID nội tiếp. ⇒  AQD = 
AID (2 góc nội tiếp cùng chắn cung AD) Mà  AQD = ° ⇒  90
AID = 90° ⇒ DI ⊥ AE Xét (O;R) có  = 
DBE DAE (2 góc nội tiếp cùng chắn cung DE) Mà  DAE =  DQI (cmt) ⇒  DQI =  DBE
Xét tứ giác DIEK có:  =  =  DIE IEK DKE = 90° 0,25
⇒ Tứ giác DIEK là hình chữ nhật
⇒ IK và DE cắt nhau tại trung điểm mỗi đường ⇒ G là trung điểm của IK .
Giả sử CI cắt BK tại N ; NG cắt CE tại M’ Ta có: // ' IG NG IG CM ⇒ =
(Hệ quả định lí Ta let) CM ' NM ' // ' GK NG GK M E ⇒ = IG GK ⇒ = M 'E NM ' CM ' M 'E 0,25
Mà IG = GK (G là trung điểm IK )
⇒ CM ' = M 'E ⇒ M’ là trung điểm của CE
⇒ M trùng M’ ⇒ M , G, N thẳng hàng Vậy CI, MG, BE đồng quy
Cho các số thực không âm a,b,c thỏa mãn ab + bc + ca = 3 . abc
Tìm giá trị nhỏ nhất của biểu thức a b c 3 A = + + + abc . 2 2 2 1+ b 1+ c 1+ a 2
Vì ab + bc + ca = 3 . abc nên 1 1 1 + + = 3 0,25 a b c
Mà (a b c) 1 1 1  + + + +
≥ 9 ⇒ a + b + c ≥   3 (1)  a b c  2 2
Ta có: a = − ab ≥ − ab = − ab a a a ( Vì 2
1+ b ≥ 2b > 0 ) 0,25 V 2 2 1+ b 1+ b 2b 2
(1,0đ) Tương tự b ≥ − bc; c ≥ − ca b c 2 2 1+ c 2 1+ a 2
Suy ra a + b + c ≥ − ab + − bc + − ca a b c 2 2 2 1+ b 1+ c 1+ a 2 2c 2 a b c 1 ⇔ + + +
ab + bc + ca ≥ a + b + c 0,25 2 2 2 ( ) 1+ b 1+ c 1+ a 2 a b c 3 ⇔ + +
+ abc ≥ a + b + c (2) 2 2 2 1+ b 1+ c 1+ a 2
Từ (1) và (2), ta được A ≥ 3. 0,25
Khi a = b = c =1 thì A = 3.Vậy giá trị nhỏ nhất của biểu thức A bằng 3.
------------------ Hết -----------------