Đề kiểm tra cuối học kì 2 Toán 11 năm 2023 – 2024 sở GD&ĐT Bắc Ninh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KÌ II BẮC NINH
NĂM HỌC: 2023 - 2024 Môn: Toán 11 (Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Nghiệm của phương trình x 1 2   8 là 5 A. x  3 . B. x  2 . C. x  1  . D. x   . 2
Câu 2. Đạo hàm của hàm số   3x f x  là A.   1 .3x f x x    .
B.    3x f x . 3x
C.    3x f x ln 3 .
D. f  x  . ln 3
Câu 3. Cho hình chóp S.ABCD có đáy là hình chữ nhật, SA vuông góc với mặt phẳng đáy. Góc
giữa đường thẳng SB và mặt phẳng  ABCD là A.  BSA . B.  SAB . C.  SBA . D.  SBC .
Câu 4. Cho khối lăng trụ có diện tích đáy bằng 2 a
3 và chiều cao bằng 2a . Thể tích của khối lăng trụ đã cho bằng 3 2a 3 3 a 3 3 a 3 A. 3 2a 3 . B. . C. . D. . 3 2 6
Câu 5. Phương trình log  2
x  2  log x có tất cả bao nhiêu nghiệm? 2  2 A. 0 . B. 1. C. 2 . D. 3 .
Câu 6. Tập nghiệm của bất phương trình ln 5x   1  0 là  2   1   1 2   1  A. ;    . B. ;    . C. ;   . D. 0;   .  5   5   5 5   5 
Câu 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , cạnh bên SA vuông góc
với mặt phẳng đáy. Mệnh đề nào dưới đây là mệnh đề sai?
A. SAB   ABC  .
B. SAC    ABC  .
C. SAB  SBC  .
D. SAB  SAC  . 1 Câu 8. Cho hàm số 3 2 y 
x  3x  5x 1. Gọi x , x là các nghiệm của phương trình 3 1 2
y  0  x  x . Giá trị của biểu thức S  2x  x bằng 1 2  2 1 A. 9  . B. 4 . C. 4  . D. 9 .
Câu 9. Một vật chuyển động thẳng theo phương trình: S t  2
 t  2t  5 m , trong đó t là thời
gian chuyển động được tính bằng giây s , S t  là quãng đường chuyển động của vật theo thời
gian t . Tại thời điểm t  2 giây, vận tốc của vật là A. 13 m/s . B. 4 m/s . C. 8 m/s . D. 6 m/s . 2x 1
Câu 10. Cho hàm số y 
có đồ thị là C  . Phương trình tiếp tuyến của C  tại điểm x 1 A0  ;1 là
A. y  x 1.
B. y  x 1.
C. y  x 1.
D. y  x 1.
Câu 11. Cho số thực a  0 . Nếu x  3 là một nghiệm của bất phương trình x 2024 a  a   1 thì
số nghiệm nguyên dương của bất phương trình   1 là A. 2024 . B. 2025 . C. 2023. D. Vô số.
Câu 12. Cho hình chóp tứ giác đều S.ABCD có AB  a , AC cắt BD tại O , SO  a . Khoảng
cách từ điểm O đến mặt phẳng  SCD bằng a 2 a 5 a 5 a A. . B. . C. . D. . 2 5 2 2
II. TỰ LUẬN (7,0 điểm)
Câu 1 (2,0 điểm) 2
a) Giải phương trình: x x 1 2   2x .
b) Giải bất phương trình: log  x  2  log 2x  3 .
Câu 2 (2,0 điểm)   
a) Cho hàm số f  x  cot 2x  
 . Tính f 0 .  6  1 b) Cho hàm số 3 2 y 
x  x  x có đồ thị là C  . Viết phương trình tiếp tuyến của C  3
biết rằng tiếp tuyến đó tạo với hai trục tọa độ một tam giác vuông cân.
Câu 3 (2,5 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a ,  o
ABC  60 . Mặt bên SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Gọi H , M , N lần lượt là
trung điểm của AB , SA và CD .
a) Chứng minh rằng SH   ABCD và tính theo a thể tích khối chóp S.ABCD .
b) Gọi  là số đo góc nhị diện  ,
A SC, B. Tính cos .
c) Tính theo a khoảng cách giữa hai đường thẳng BM và SN .
Câu 4 (0,5 điểm)    
Một vật dao động điều hòa có phương trình dao động là x t   4 cos t    , trong đó  4 6 
t  0 là thời gian dao động và được tính bằng giây s ; x t  là li độ của dao động và được tính 
bằng centimet cm . Tại thời điểm lần đầu tiên vật đạt vận tốc bằng
cm/s thì gia tốc của vật 2 bằng bao nhiêu? ===== Hết ===== 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
ĐỀ KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC 2023 - 2024
(Hướng dẫn chấm có 03 trang) Môn: Toán 11
I. TRẮC NGHIỆM (3,0 điểm)
Với mỗi câu: Trả lời đúng được 0,25 điểm, trả lời sai 0 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B C C A B A D D D A C B
II. TỰ LUẬN (7,0 điểm) Câu
Lời giải sơ lược Điểm 1. (2,0 điểm) 2 a) x x 1  x 2 2
 2  x  x 1  x 0,5 2
 x  2x 1  0  x  1 . 0,5 2x  3  0
b) log  x  2  log 2x  3   0,25
x  2  2x  3   3 x  3   2   x  5 0,5 2 x  5   3 
Vậy tập nghiệm của bất phương trình là ;5   . 0,25  2  2. (2,5 điểm) 2
a) Ta có: f  x     2  sin 2x    0,5  6   f 0  8  . 0,5 b) Ta có: 2
y  x  2x 1  1  Gọi 3 2 M ; m
m  m  m   là tiếp điểm.  3  0,25
Vì tiếp tuyến tại M của C  tạo với hai trục tọa độ một tam giác vuông cân nên hệ số
 ym  1
góc của tiếp tuyến bằng 1 hoặc 1, tức là: 
 ym  1   2
m  2m 1  1 m  0    0,25 2 
m  2m 1  1  m  2  
+) Với m  0  M 0;0  phương trình tiếp tuyến là: y  x (loại vì tiếp tuyến đi qua 0,25 O ) 3 4 +) Với m  3   M  3  ; 1
 6  phương trình tiếp tuyến là: y  x  (t/m) 3 0,25 4
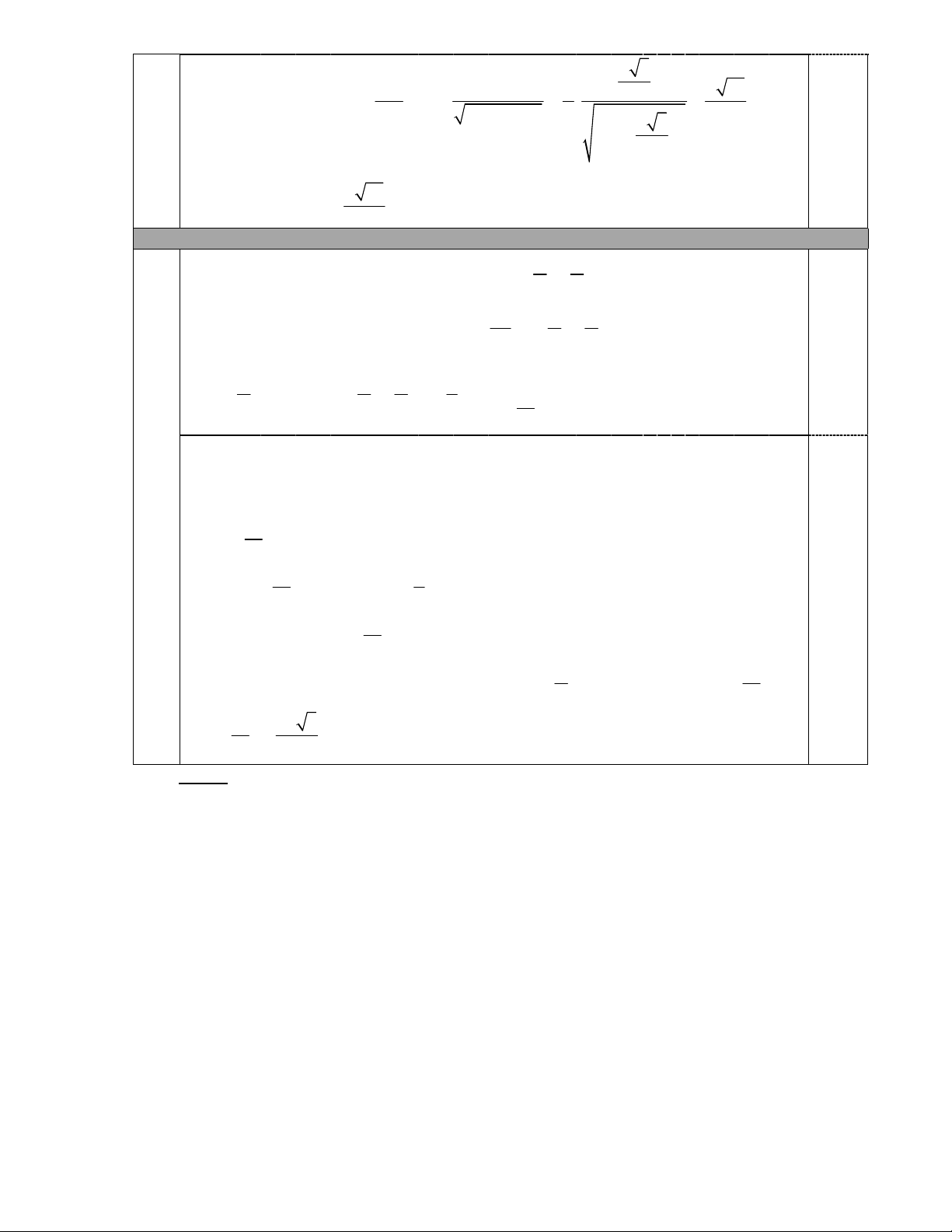
Vậy pt tiếp tuyến cần tìm là y  x  . 3 3. (2,5 điểm) a) Vì SA 
B đều  SH  AB S
Mà  SAB   ABCD 0,25 K
 SH   ABCD M 1
Vì SH   ABCD  V  SH .S I S . ABCD 3 ABCD SA  B là tam giác đều cạnh D a 3 A a  SH  2 H N 0,5  2 a 3 S  .
AB BC.sin ABC  B C ABCD 2
(Vẽ đúng hình ý a được 0,25 điểm) 2 3 1 a 3 a 3 a  V  . .  . S .ABCD 3 2 2 4 b) Dễ thấy A
 BC đều  AC  BC  a  các tam giác SAC và SBC lần lượt cân tại A và B . 0,5  AI  SC
Gọi I là trung điểm của  SC  
 AIB là góc phẳng nhị diện  , A SC, B . BI  SC  2 2 3a 3a Ta có: 2 2 2 2 2
SC  SH  CH 
 SI  IC  2 8 2 5a 2 2 2
IA  SA  SI  8 0,5 2 5a Tương tự: 2 IB  8  2 2 2
IA  IB  AB 1
 cos  cos AIB   . 2I . A IB 5 c) Ta có: A
 CD đều  AN  CD  AN  AB
 AN  SAB  SAN   SAB SA 
B đều  BM  SA 0,25
 BM   SAN 
Dựng MK  SN tại K  MK là đoạn vuông góc chung của BM và SN
 d  BM , SN   MK 4 a 3  AN AN a a 21
MK  MS.sin MSK  MS.  MS. 2  .  . SN 2 2 SA  AN 2 2 14  a 3  2 a    2 0,25   a 21
Vậy: d  BM , SN   . 14 4. (0,5 điểm)    
Vận tốc tức thời của vật là v t   xt     sin t    cm/s  4 6  2     
Gia tốc tức thời của vật là a t   x t    t     2 cos cm/s  4  4 6  0,25 t  8k      1 v t   cm/s  sin t        16 k  2  4 6  2 t   8k  3 Với t  8k
Do t  0  8k  0  k  0
Mà k    k  1  t  8   1 16 Với t   8k 3 16 2 Do t  0 
 8k  0  k   3 3 0,25 16
Mà k    k  0  t  2 3  16 Từ  
1 và 2 suy ra lần đầu tiên vật đạt vận tốc là cm/s tại thời điểm t  s 2 3 2  16   3  a     2 cm/s  .  3  8
Lưu ý: Các cách giải khác đáp án, nếu đúng vẫn cho điểm theo các bước tương ứng. 5