Đề kiểm tra giữa học kì 1 Toán 9 năm 2021 – 2022 trường THCS Nguyễn Du – Hà Nội
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề kiểm tra giữa học kì 1 Toán 9 năm học 2021 – 2022 trường THCS Nguyễn Du, phường Trung Văn, quận Nam Từ Liêm, thành phố Hà Nội; đề thi có hướng dẫn giải chi tiết. Mời bạn đọc đón xem.
Preview text:
TRƯỜNG THCS NGUYỄN DU
ĐỀ KIỂM TRA GIỮA HỌC KÌ I Năm học: 2021 -2022 MÔN: TOÁN HỌC 9
Thời gian làm bài: 90 phút ĐỀ 1
Bài I. (2,5 điểm) 1. Thực hiện phép tính: 3 2 a) 75 4 3 2 27 b) 6 - - 4 - 2 3 4 3 - 2
2. Giải phương trình: √ √ x + 7 1 3 x + 8
Bài II. (2 điểm) Cho hai biểu thức: : A = và B = + + x -1 x + 2 1- x x + x - 2 với x 0 , x 1
a) Tính giá trị của A biết x = 9 b) Rút gọn B
c) Tìm các giá trị nguyên của x để biểu thức P = A.B có giá trị nguyên
Bài III. (2,5 điểm)
1) Bác An đi xe máy từ nhà đến công ty với vận tốc 36km/h. Bác An ở lại làm việc trong
1 giờ 30 phút rồi đi xe máy quay về nhà với vận tốc 45km/h, tổng cộng hết 6 giờ kể cả
thời gian làm việc. Tính quãng đường từ nhà đến công ty của bác An.
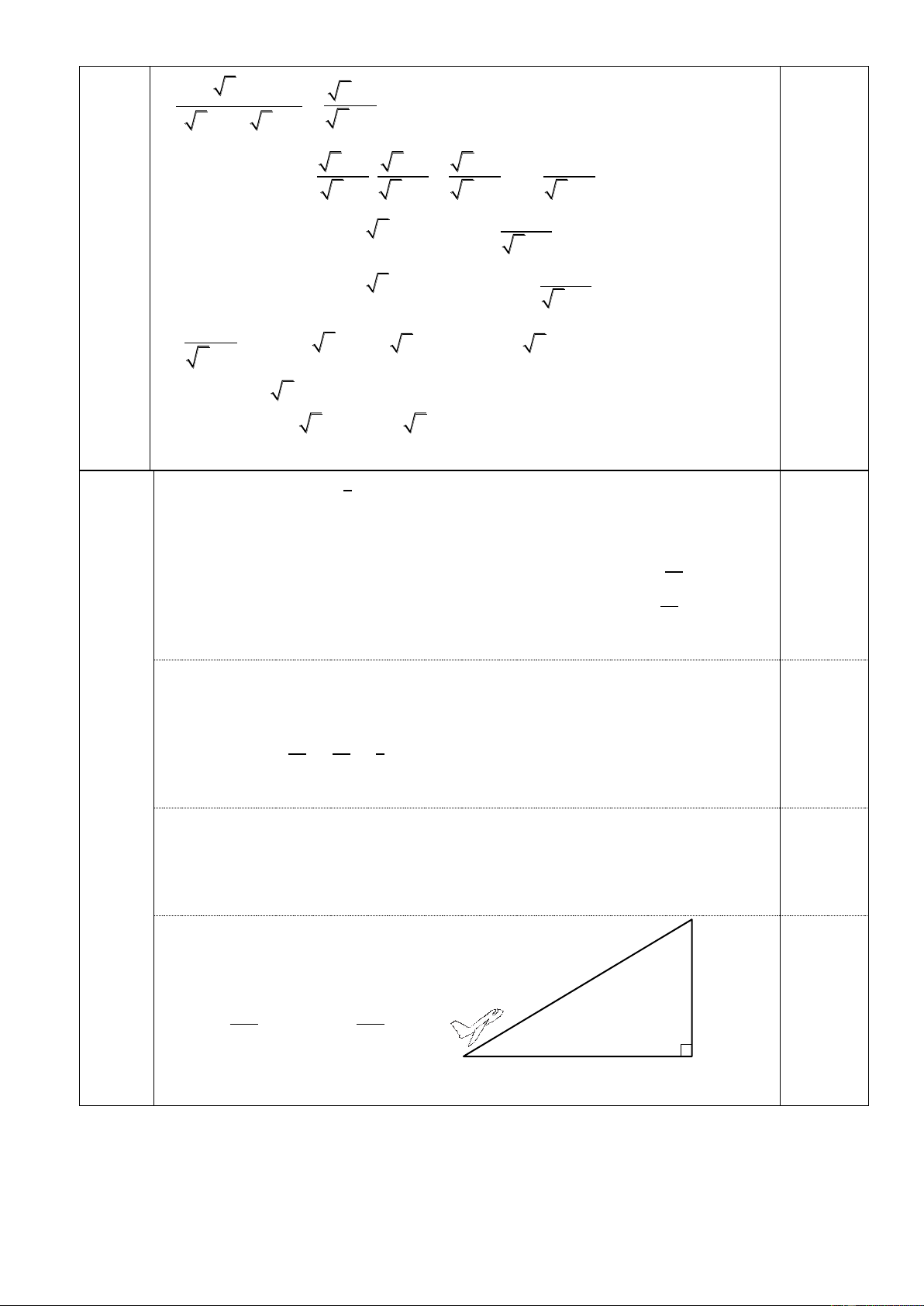
2) Một chiếc máy bay cất cánh. Đường bay lên tạo với phương nằm ngang một góc 300. Hỏi
sau khi bay được quãng đường 9km thì máy bay đã bay lên được độ cao là bao nhiêu km theo
phương thẳng đứng?
Bài IV. (2,5 điểm)
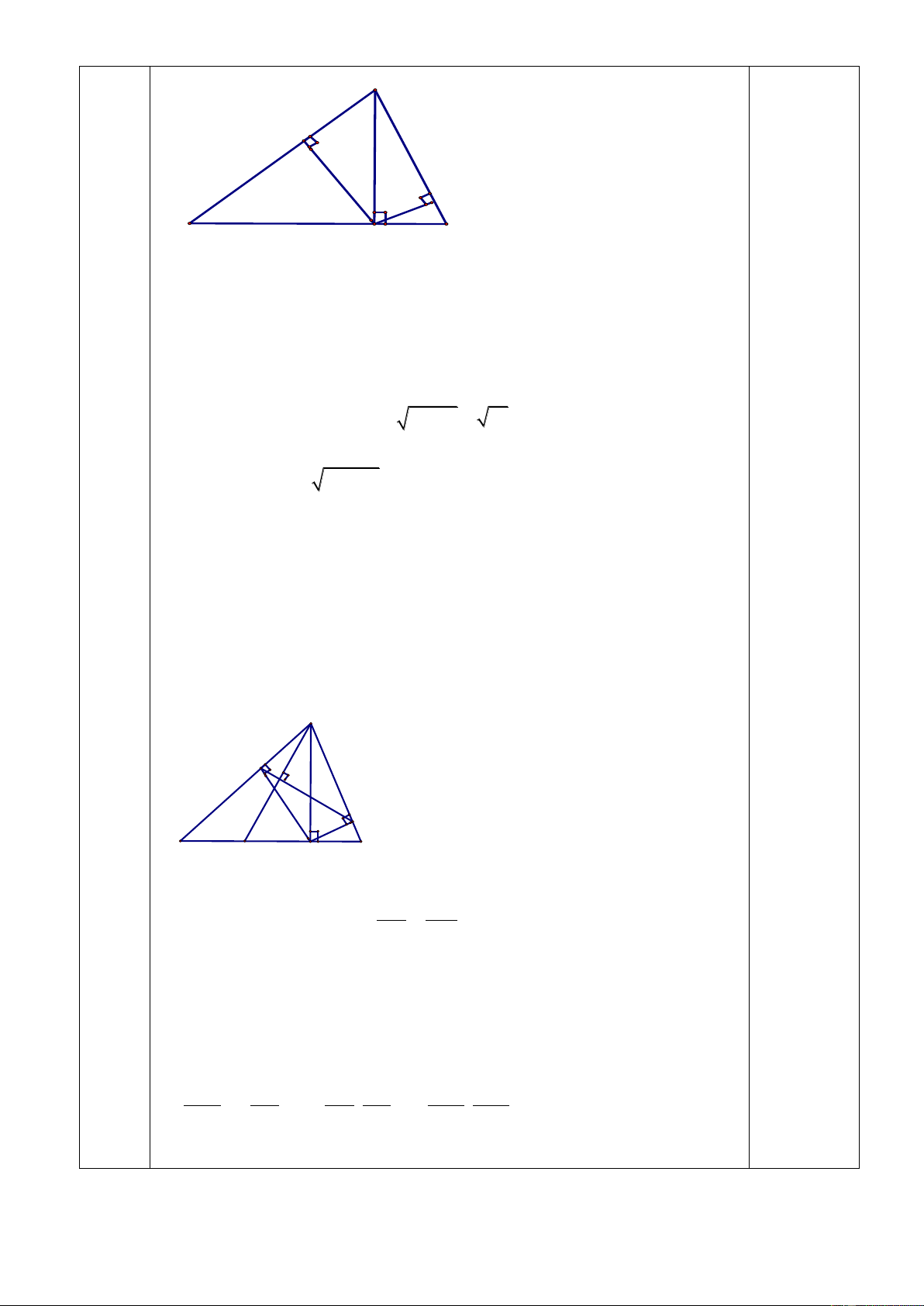
Cho tam giác ABC nhọn có đường cao AI. Gọi N là hình chiếu của I trên AB.
a) Biết AN = 3,6 cm; BN = 6,4 cm. Tính AI, NI
b) Kẻ IM vuông góc với AC tại M. Chứng minh AB.AN =AC.AM
c) Đường thẳng qua A và vuông góc với MN cắt BC tại D; MN cắt AI tại O SAON 2 2 Chứng minh rằng = sin B.sin C SADC
Bài V. (0,5 điểm)
Tìm giá trị lớn nhất của biểu thức: P
x 6 12 x
--------Chúc các em làm bài tốt--------
TRƯỜNG THCS NGUYỄN DU
ĐỀ KIỂM TRA GIỮA HỌC KÌ I Năm học: 2021 -2022 MÔN: TOÁN HỌC 9
Thời gian làm bài: 90 phút
A. MA TRẬN ĐỀ KIỂM TRA: Vận dụng Vận dụng Tổng Nội dung Nhận biết Hiểu ( Thấp) ( Cao) điểm(%) 1. Rút gọn biểu Tính đúng Tính đúng thức số các biểu biểu thức căn thức căn bậc hai phức
bậc hai đơn tạp hơn liên giản quan đến trục căn thức, khử mẫu, hằng đẳng thức Bài 1.1.a Bài 1.1.b 1,5 0,75 0,75 15%
2. Phương trình vô Giải được tỷ phương trình chứa căn thức bậc hai Bài 1.2 1 1 10% 3. Rút gọn biểu Tính được Rút gọn được Đề xuất và thức chứa căn giá trị của biểu thức giải được các thức bậc hai biểu thức chứa căn thức bài toán liên khi biết giá bậc hai quan đến trị của biến biểu thức chứa CTBH Bài 2.a Bài 2. b Bài 2.c 2 0,5 1 0,5 20% 4. Giải bài toán Lập luận và bằng cách lập giải được bài phương trình toán bằng cách lập phương trình dạng chuyển động Bài 3.1 2 2,0 20%
5. Hệ thức về cạnh Vẽ hình
Tính được độ Vận dụng Đề xuất và và góc trong tam đúng dài các cạnh được các hệ đưa ra được
giác vuông, tỉ số và các góc thức lượng phương pháp lượng giác vào giải bài giải bài toán tập 0,25 Bài 3.2 Bài 4. b Bài 4.c 0,5 1 0,5 Bài 4.a 3 0,75 30% 6.Bài toán nâng Làm được cao bài với nội dung yêu cầu Bài 5 0,5 0,5 5% Tổng điểm (%) 1,5 3,0 4,0 1,5 10 100% 15% 30% 40% 15%
TRƯỜNG THCS NGUYỄN DU
ĐỀ KIỂM TRA GIỮA HỌC KÌ I Năm học: 2021 -2021 MÔN: TOÁN HỌC 9
Thời gian làm bài: 90 phút
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM BÀI NỘI DUNG ĐIỂM 1) 0,75
a) 75 4 3 2 27 5 3 4 3 6 3 7 3 3 2 6 4 2 3 4 3 2 0,75 6 2( 3 2) 2 b) 3 ( 3 1) Bài 1 2 ( 3 2)( 3 2)
3 3 2 3 4 3 1
3 3 2 3 4 3 1 4 3 5 0,25 2) Đk √ √ ( ) 0,75 x2 - 3x – 4 = 0 (x +1) (x-4) = 0
x= -1 (thỏa mãn). x = 4 (thỏa mãn)
Vậy nghiệm của phương trình là x = -1; x = 4 2,5điểm 0,5đ
a) Ta có: x 9 (thoả mãn điều kiện) vào A; √ √
b) Với x 0 , x 1 ta có: 1 3 x 8 1 3 x 8 B x 2
x 1 x 2 x Bài 2 x 2 1 x x x 2 1 0,5 3 x 1 x 2 x 8
x 2 x 1
x 2 x 1 x 2 x 1
x 1 3 x 2 x 8 0,5
x 1 3 x 6 x 8 x 2 x 1
x 2 x 1
x 2 x 1
x 2 x 1 x 2 1 x 1
x 2 x 1 x 2 x 7 x 1 x 7 5 c) Ta có: P . A B . 1 x 1 x 2 x 2 x 2 5
TH1: x 0 , x 1, x ¢ , x Z P 1 I( o L ai) x 2 5
TH2: x 0 , x 1, x ¢ , x Z P Z 1 Z 0,25 x 2 0,25 5
¢ 5M x 2 x 2Ö5 x 2 1 ; 5 x 2
Mà x 2 2 với x 0 , x 1
Do đó: x 2 5 x 3 x 9 (thoả mãn)
Vậy x 9 thì P .
A B có giá trị nguyên
1) Đổi 1giờ 30 phút = giờ 0,75
Gọi quãng đường từ nhà bác An đến công ty dài là: x (km; x > 0) Bài 3
Thời gian bác An đi từ nhà đến công ty với vận tốc 36km/h là (giờ)
Thời gian bác An đi từ công ty về nhà với vận tốc 45km/h là (giờ)
Vì thời gian bác An đi và về tổng cộng hết 6 giờ kể cả thời gian làm việc, 0,5 ta có phương trình:
Giải phương trình tìm được: x = 90 (t/m) 0,75
Vậy quãng đường từ nhà đến công ty của người đó dài 90km
2) Gọi BC là quãng đường máy bay bay được
CA là độ cao của máy bay theo phương thẳng đứng 0,25 Xét ABC vuông tại A: AC AC 0 sin B sin 30 BC 9 300 B 0
AC 9.sin 30 4,5(k ) m A
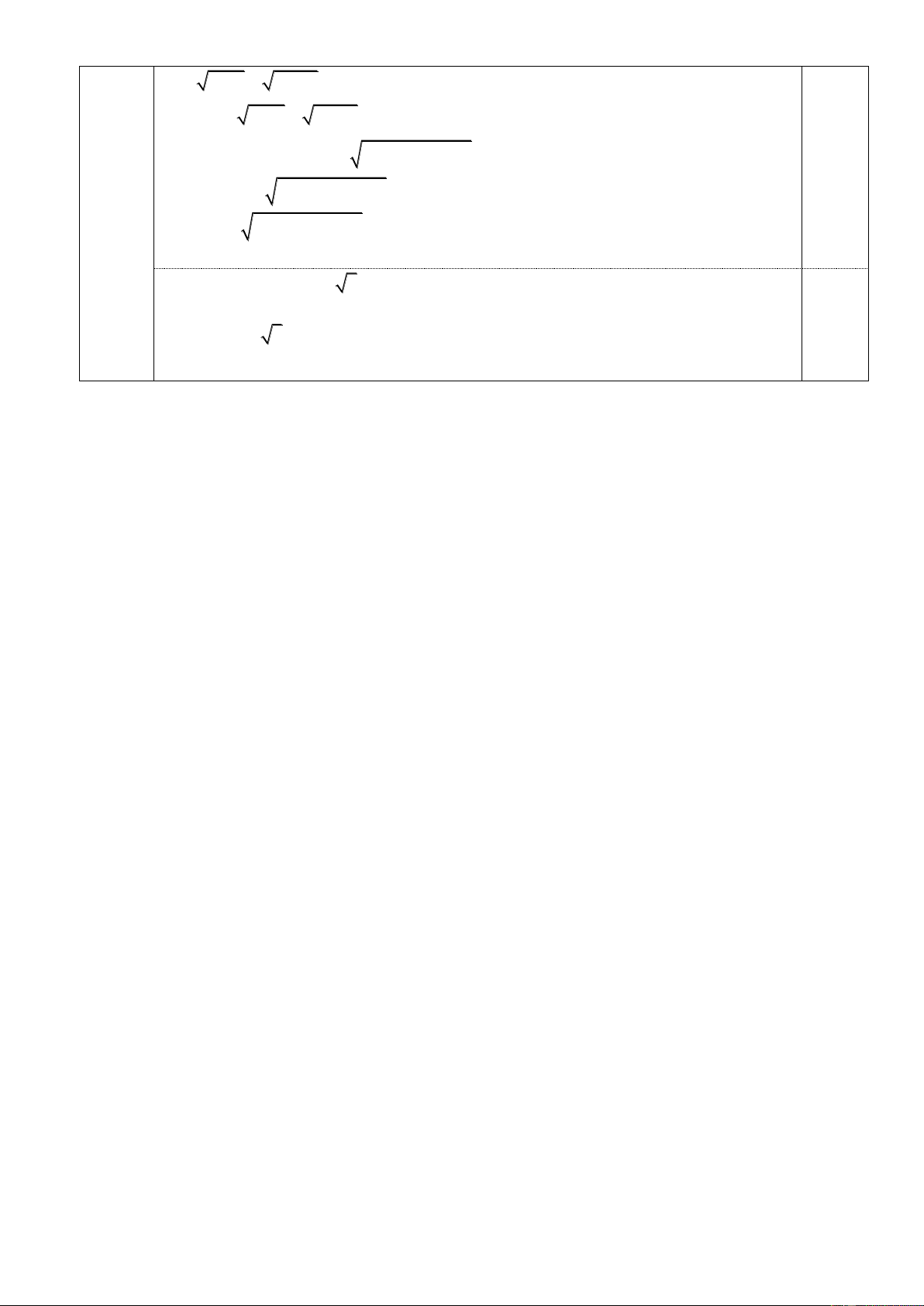
Vậy S máy bay đã bay lên được 4,5 km so với phương thẳng đứng. A 3,6 N 6,4 M C B I 0,25. Vẽ hình đúng
Biết AN 3,6cm ; BN 6, 4cm . Tính AI, NI 0,5
Ta có: AB AN NB 3,6 6, 4 10cm 0,25
Áp dụng hệ thức lượng trong tam giác vuông AIB có 0,75 AIB 90 ; IN AB Bài 4 Ta có: 2
AI AN.AB AI 3, 6.10 36 6cm Và: 2
IN AN.NB
NI 3, 6.6, 4 4,8cm 0,75 b. Chứng minh A . B AN A . C AM Xét ABI có : AIB 90 ; IN AB
Áp dụng hệ thức lượng trong tam giác vuông ta có: 2 A .
B AN AI (1)
Áp dụng hệ thức lượng trong tam giác vuông AIC có: AIC 90 ; IM AC 2
AM.AC AI (2)
Từ (1) và (2) A . B AN A . C AM (đpcm A 3,6 N J O 6,4 M C B D I
Gọi J là giao điểm của AD và MN AN AM
Ta có: AN.AB AM.AC AC AB
Dễ dàng chứng minh được A
NM ∽ A CB ( . c g.c)
AMJ ABI; ACD ANO (1) Mà 0 CAD AMJ 90 0
NAO ABI 90 NAO CAD (2) Từ (1);(2) A
DC ∽ A
ON (g.g) 2 2 2 2 S AN AN AI AN AI AON . . 2 2 S AC AI AC AI AC ADC = 2 2 o c s NA . O sin C = 2 2 sin . B sin C . P
x 6 12 x
Điều kiện: 6 x 12 0,25
A x 6 12 x2 2 2
A x 6 12 x 2 x 612 x Bài 2 5
A 6 2 x 612 x 2
A 6 2 x 612 x 6 x 6 12 x 12 2 A 12 hay A 2 3 0,25
Dấu “=” xảy ra khi x 6 12 x x 9 (TMĐK) Amax 2 3 ……