Đề kiểm tra giữa học kỳ 1 Toán 11 Cánh diều - Đề 3 (có đáp án)

Đề kiểm tra giữa học kỳ 1 Toán 11 Cánh diều - Đề 3 có đáp án được soạn dưới dạng file PDF gồm 5 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

41 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

5 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ I-ĐỀ 3
MÔN TOÁN 11-CÁNH DIỀU
PHẦN I. TRẮC NGHIỆM:
Câu 1: Nếu một góc lượng giác có số đo là thì số đo radian của nó là
A. . B. . C. . D. .
Câu 2: Điểm cuối của góc lượng giác ở góc phần tư thứ mấy nếu , tan trái dấu?
A. Thứ I. B. Thứ II hoặc IV. C. Thứ II hoặc III. D. Thứ I hoặc IV.
Câu 3: Giả sử các biểu thức đều có nghĩa. Công thức nào sau đây là đúng?
A. B. C. . D. .
Câu 4: Trong mặt phẳng tọa độ , trên đường tròn lượng giác gọi điểm là điểm biểu diễn của góc
. Lấy điểm đối xứng với qua gốc tọa độ. Khi đó là điểm biểu diễn của góc có số đo bằng
bao nhiêu?
A. . B. C. D. .
Câu 5: Cho góc thỏa mãn . Giá trị của là
A. B. . C. D. .
Câu 6: Cho góc thỏa mãn và . Giá trị của biểu thức là
A. B. . C. D. .
Câu 7: Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số đối xứng qua gốc tọa độ .
B. Đồ thị hàm số đối xứng qua trục .
C. Đồ thị hàm số đối xứng qua trục .
D. Đồ thị hàm số đối xứng qua gốc tọa độ .
Câu 8: Hàm số có tập xác định là hàm số tuần hoàn nếu tồn tại một số khác 0 sao cho
ta có và
A. . B. . C. . D.
.
Câu 9: Trong các hàm số , có bao nhiêu hàm số đồng biến trên khoảng
?
45
a
=-
!
2
p
-
4
p
-
4
p
2
p
a
sin
a
a
2
2
1
1cot
cos
+=x
x
2
2
1
1 tan
sin
+=-x
x
tan cot 1×=-xx
Oxy
M
3
p
a
=
N
M
N
3
p
-
2
3
p
6
p
4
3
p
a
5
sin cos
4
aa
+=
sin cos
aa
=×P
9
16
=P
9
32
=P
9
8
=P
1
8
=P
a
2
p
ap
<<
4
sin
5
a
=
24
25
=-P
24
25
=P
12
25
=-
P
12
25
=P
( )
sin==yfx x
O
Oy
( )
tan==yfx x
Oy
O
( )
=yfx
D
T
"ÎxD
,+Î -ÎxT DxT D
( ) ( )
+=fxT fx
( ) ( )
+=-fxT fx
( ) ( )
2
p
+=fxT fx
( ) ( )
2
p
+=-fxT fx
sin , cos , tan , cot== = =yxy xyxyx
0;
2
p
æö
ç÷
èø
Trang 2
A. 0 . B. 1. C. 2. D. 3 .
Câu 10: Tập xác định của hàm số là
A. . B.
C. . D. .
Câu 11: Tập giá trị của hàm số là
A. . B. . C. . D. .
Câu 12: Nghiệm đặc biệt nào sau đây là sai?
A. B. .
C. D. .
Câu 13: Cho đồ thị hàm số trên như hình vẽ.
Có bao nhiêu giá trị của thỏa mãn ?
A. 0 . B. 1. C. 2 . D. 3 .
Câu 14: Phương trình có nghiệm là
A. . B. .
C. và . . D. và .
Câu 15: Phương trình có nghiệm là
A. B. C. D.
D
1
1 sin
=
-
y
x
{ }
,Z
p
=Î!DkkÇ
,Z;
2
p
p
ìü
=+Î
íý
îþ
!DkkÇ
2, Z
2
p
p
ìü
=+Î
íý
îþ
!DkkÇ
=ÆD
T
2; 10
éù
=
ëû
T
2; 7
éù
=
ëû
T
7; 10
éù
=
ëû
T
[ ]
0;1=T
( )
cos 0 2
2
p
p
=Û= + Î!xxkk
( )
sin 0
p
=Û= Î!xxkk
( )
sin 1 2
2
p
p
=Û = + Î!xxkk
( )
sin 1 2
2
p
p
=- Û =- + Î!xxkk
tan=yx
33
;
22
pp
æö
-
ç÷
èø
;
22
pp
æö
Î-
ç÷
èø
x
tan 0=x
sin2 sin3=xx
2
,
55
pp
=+ Î!xkk
2,
p
=Î!xk k
2
p
=xk
2,
5
p
p
=+ Î!xkk
2
p
=xk
2
,
55
pp
=+ Î!xkk
3
cot3
3
=-x
,
3
p
p
=- + Î!xkk
,
9
p
p
=- + Î!xkk
2,
9
p
p
=- + Î!xkk
,
93
pp
=- + Î!xkk
Trang 3
Câu 16: Với , cho dãy số các số tự nhiên chia hết cho Số hạng đầu tiên của dãy
số là
A. . B. . C. . D. .
Câu 17: Với , trong các dãy số cho bởi số hạng tổng quát sau, dãy số nào là dãy số giảm ?
A. B. C. . D. .
Câu 18: Với , cho dãy số gồm tất cả các số nguyên dương chia 3 dư 2 theo thứ tự tăng dần. Số
hạng tổng quát của dãy số này là
A. B. C. . D. .
Câu 19: Cho cấp số cộng với và . Công sai của cấp số cộng đã cho bằng
A. -6 . B. 4 . C. 6 . D. 10 .
Câu 20: Cho cấp số cộng có và . Khẳng định nào sau đây là đúng?
A. B. . C. . D. .
Câu 21: Bà chủ quán trà sữa muốn trang trí cho đẹp nên quyết định thuê nhân công xây một bức tường
bằng gạch với xi măng (như hình vẽ bên dưới), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có
ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là
bao nhiêu viên? (hình ảnh dưới đây là hình ảnh minh họa hàng gạch dưới cùng có 5 viên)
A. 25250 . B. 250500 . C. 12550 . D. 125250 .
Câu 22: Trong các khẳng định sau, khẳng định nào đúng?
A. Nếu 3 điểm là 3 điểm chung của 2 mặt phẳng và thì thẳng hàng.
B. Nếu thẳng hàng và có điểm chung là , thì cũng là 2 điểm chung của
và .
C. Nếu 3 điểm là 3 điểm chung của 2 mặt phẳng và phân biệt thì không thẳng
hàng.
D. Nếu thẳng hàng và là 2 điểm chung của và thì cũng là điểm chung của
.
Câu 23: Cho bốn điểm không đồng phẳng. Giao tuyến của hai mặt phẳng và là
A. . B. . C. . D. .
*
Î •n
( )
n
u
3:0,3,6,9,…
( )
n
u
1
6=u
1
0=u
1
3=u
1
9=u
*
În Q
( )
n
u
n
u
1
=
n
u
n
2
=
n
un
(3)=-
n
n
u
2
63=-+
n
un n
*
În Q
( )
n
u
3
2
=
n
n
u
2
1=+
n
u
n
32=-
n
un
32=+
n
un
( )
n
u
1
2=u
2
8=u
1
3=-u
1
2
=d
( )
1
31
2
=- + +
n
un
( )
1
31
4
=- + +
n
un
( )
1
31
2
=- + -
n
un
( )
1
31
4
=- + -
n
un
X
,,ABC
( )
P
( )
Q
,,ABC
,,ABC
( ) ( )
,PQ
A
,BC
( )
P
( )
Q
,,ABC
( )
P
( )
Q
,,ABC
,,ABC
,AB
( )
P
( )
Q
C
( )
và
()PQ
,,,ABCD
( )
ABC
( )
ACD
AB
AC
BC
AD
Trang 4
Câu 24: Một hình chóp có đáy là ngũ giác thì số cạnh của hình chóp là
A. 5 cạnh. B. 6 cạnh. C. 9 cạnh. D. 10 cạnh.
Câu 25: Khẳng định nào sau đây là đúng về hình tứ diện đều?
A. Mặt đáy là hình thoi. B. Mặt đáy là hình vuông.
C. Mặt bên là tam giác cân. D. Mặt bên luôn là tam giác đều.
Câu 26: Cho tứ diện . Gọi và lần lượt là trung điểm của và là trọng tâm tam giác
. Giao điểm của đường thẳng và mặt phẳng là
A. Điểm . B. Giao điểm của đường thẳng và .
C. Giao điểm của đường thẳng và . D. Giao điểm của đường thẳng và .
Câu 27: Cho tứ diện . Gọi lần lượt là trung điểm của và . Mặt phẳng qua
cắt lần lượt tại và . Biết cắt tại . Ba điểm nào sau đây thẳng hàng?
A. . B. . C. . D. .
Câu 28: Cho đường thẳng chứa trong mặt phẳng . Có bao nhiêu đường thẳng chứa trong và
song song với đường thẳng ?
A. 0 . B. 1 . C. 2. D. Vô số.
Câu 29: Trong không gian cho các mệnh đề sau:
(I) Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì song song với nhau.
(II) Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai
đường thẳng đó.
(III) Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy song song với
nhau.
(IV) Qua điểm không thuộc đường thẳng , kẻ được đúng một đường thẳng song song với .
Số mệnh đề đúng là
A. 0 . B. 1. C. 2. D. 3 .
Câu 30: Trong không gian, cho ba đường thẳng . Trong các mệnh đề sau mệnh đề nào đúng?
. Nếu và cắt nhau, và cắt nhau thì và cắt nhau.
A. Nếu và không cắt nhau thì và song song.
B. Nếu và chéo nhau thì và không cùng thuộc một mặt phẳng.
C. Nếu và cùng chéo nhau với thì song song với .
Câu 31: Cho hình chóp . Gọi lần lượt là trung điểm của và . Giao tuyến của hai
mặt phẳng và là một đường thẳng song song với
A. đường thẳng . B. đường thẳng . C. đường thẳng . D. đường thẳng .
Câu 32: Cho đường thẳng song song với mặt phẳng . Nếu mặt phẳng chứa và cắt theo
giao tuyến thì và là hai đường thẳng
A. cắt nhau. B. trùng nhau. C. chéo nhau. D. song song với nhau.
Câu 33: Cho mặt phẳng và hai đường thẳng song song và . Khẳng định nào sau đây là đúng?
ABCD
E
F
AB
;CD G
BCD
EG
( )
ACD
F
EG
AF
EG
AC
EG
CD
ABCD
,MN
AB
CD
( )
a
MN
,AD BC
P
Q
MP
NQ
I
,,IAC
,,IBD
, ,IAB
, ,ICD
a
( )
P
( )
P
a
A
d
d
,,abc
D
a
b
b
c
a
c
a
b
a
b
b
c
b
c
a
b
c
a
b
×S ABCD
,IJ
AB
BC
( )
SAC
( )
SIJ
AD
AB
AC
BD
a
( )
a
( )
b
a
( )
a
b
b
a
( )
P
a
b
Trang 5
A. Nếu song song với thì cũng song song với .
B. Nếu cắt thì cũng cắt .
C. Nếu chứa thì cũng chứa .
D. Nếu chứa thì song song với .
Câu 34: Cho hình chóp có đáy là hình bình hành. Các điểm lần lượt là trọng tâm các tam
giác và và . Gọi là trung điểm . Chọn mệnh đề đúng trong các mệnh đề sau
A. . B. . C. . D. .
Câu 35: Cho hình chóp có đáy là hình bình hành. Gọi là trọng tâm tam giác và
là trung điểm của . Lấy điểm trên đoạn sao cho . Đường thẳng qua và song
song với cắt tại . Đường thẳng không song song với mặt phẳng dưới đây?
A. . B. . C. . D. .
PHẦN II. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm) Giải các phương trình lượng giác:
a) . b) .
Bài 2. (1,0 điểm) Cho hình chóp có đáy là hình bình hành. Gọi là mặt phẳng
đi qua trung điểm của cạnh , song song với cạnh và cắt các cạnh , lần lượt
tại các điểm . Chứng minh tứ giác là hình thang.
Bài 3. (1,0 điểm) Số giờ có ánh sáng mặt trời của một thành phố trong ngày thứ của năm 2023
(có 365 ngày) được cho bởi một hàm số , với và . Vào
ngày nào trong năm thì thành phố có nhiều giờ có ánh sáng mặt trời nhất?
ĐÁP ÁN
1
2
3
4
5
6
7
B
C
D
D
B
A
A
8
9
10
11
12
13
14
A
C
C
B
A
B
D
15
16
17
18
19
20
21
D
B
A
D
C
C
D
22
23
24
25
26
27
28
D
B
D
D
B
B
D
29
30
31
32
33
34
35
B
B
C
D
B
C
D
( )
P
a
( )
P
b
( )
P
a
( )
P
b
( )
P
a
( )
P
b
( )
P
a
( )
P
b
×S ABCD
,IJ
SAB
SAD
M
CD
( )
//IJ SCD
( )
//IJ SBM
( )
//IJ SBD
( )
//IJ SBC
.S ABCD
ABCD
G
SAB
I
AB
M
AD
3=AD AM
M
AB
CI
J
GJ
( )
SCD
( )
SBC
( )
SAC
( )
SAD
sin 3c os 2+=xx
2
2
1
3cot 5
cos
+=x
x
.S ABCD
ABCD
( )
a
M
SB
AB
,SA SD
SC
,,QPN
MNPQ
A
t
( )
4sin 60 10
178
p
éù
=-+
êú
ëû
yt
Ît Q
0 365<£t
A
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

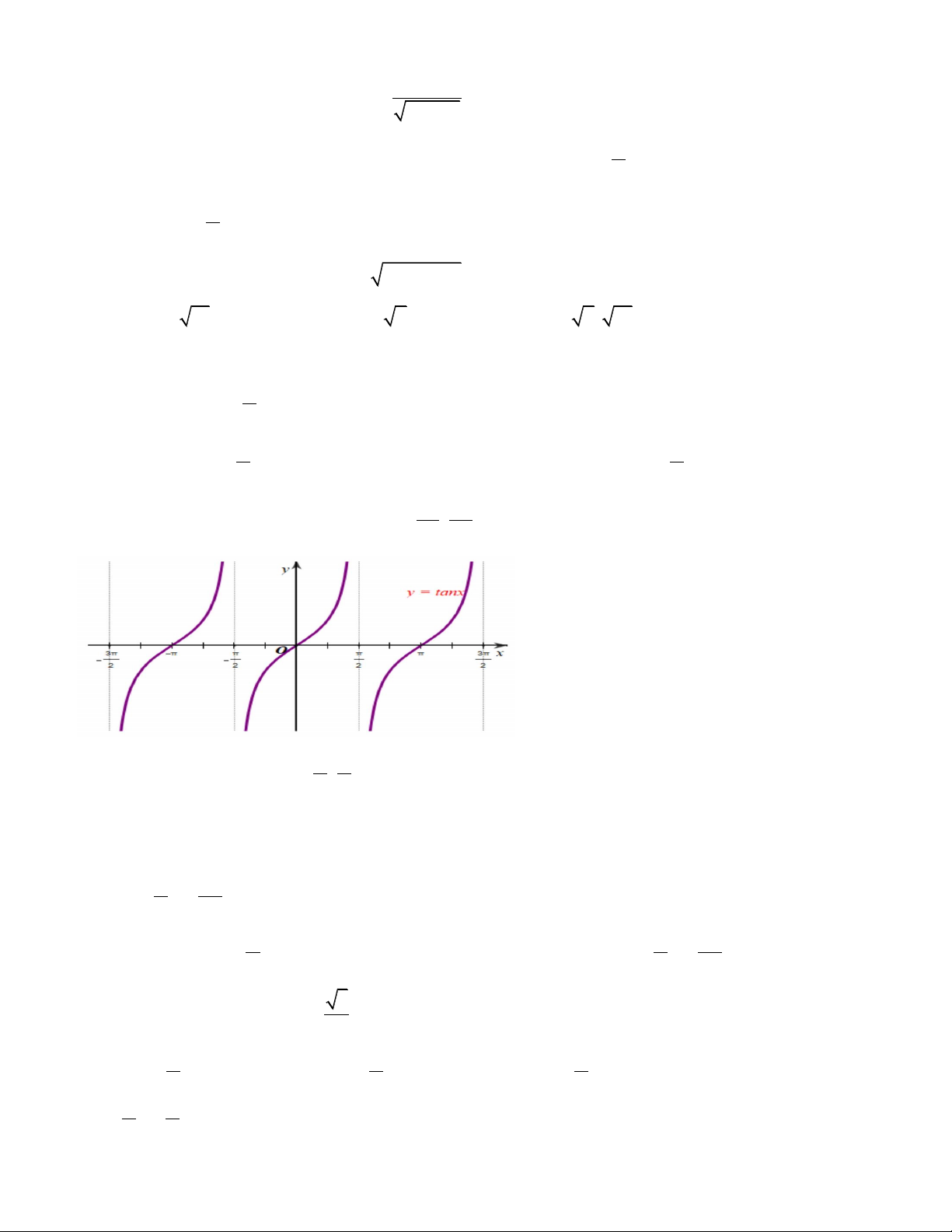
Preview text:

ĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ I-ĐỀ 3
MÔN TOÁN 11-CÁNH DIỀU PHẦN I. TRẮC NGHIỆM:
Câu 1: Nếu một góc lượng giác có số đo là a = 45
- ! thì số đo radian của nó là p p p p A. - . B. - . C. . D. . 2 4 4 2
Câu 2: Điểm cuối của góc lượng giác a ở góc phần tư thứ mấy nếu sina , tan a trái dấu? A. Thứ I.
B. Thứ II hoặc IV.
C. Thứ II hoặc III. D. Thứ I hoặc IV.
Câu 3: Giả sử các biểu thức đều có nghĩa. Công thức nào sau đây là đúng? 1 1 A. 2 1+ cot x = B. 2 1+ tan x = -
C. tanx ×cotx = 1 - . D. 2 2
sin x + cos x = 1. 2 cos x 2 sin x
Câu 4: Trong mặt phẳng tọa độ Oxy , trên đường tròn lượng giác gọi điểm M là điểm biểu diễn của góc p
a = . Lấy điểm N đối xứng với M qua gốc tọa độ. Khi đó N là điểm biểu diễn của góc có số đo bằng 3 bao nhiêu? p p p 4p A. - 2 . B. C. D. . 3 3 6 3 Câu 5: Cho góc a 5
thỏa mãn sina + cosa = . Giá trị của P = sina ×cosa là 4 9 9 9 1 A. P = B. P = . C. P = D. P = . 16 32 8 8 p 4
Câu 6: Cho góc a thỏa mãn
< a < p và sina = . Giá trị của biểu thức P = sin2(a +p ) là 2 5 24 24 12 P 12 A. P = - B. P = . C. = - D. P = . 25 25 25 25
Câu 7: Mệnh đề nào sau đây là sai?
A. Đồ thị hàm số y = f (x) = sinx đối xứng qua gốc tọa độ O .
B. Đồ thị hàm số y = f (x) = cosx đối xứng qua trục Oy .
C. Đồ thị hàm số y = f (x) = tanx đối xứng qua trục Oy .
D. Đồ thị hàm số y = f (x) = tanx đối xứng qua gốc tọa độ O .
Câu 8: Hàm số y = f (x) có tập xác định D là hàm số tuần hoàn nếu tồn tại một số T khác 0 sao cho
"x Î D ta có x +T Î ,
D x -T Î D và
A. f (x +T ) = f (x).
B. f (x +T ) = - f (x).
C. f (x +T ) = 2p f (x). D.
f (x +T ) = 2 - p f (x).
Câu 9: Trong các hàm số y = sinx, y = cosx, y = tanx, y = cotx , có bao nhiêu hàm số đồng biến trên khoảng æ p ö 0; ? ç ÷ è 2 ø Trang 1 A. 0 . B. 1. C. 2. D. 3 . 1
Câu 10: Tập xác định D của hàm số y = là 1- sinx ìp ü A. D = ! Ç { p k ,k Î } Z .
B. D = ! Ç í + kp ,k Î Zý; î 2 þ ìp ü
C. D = ! Ç í + k2p ,k Î Zý . D. D = Æ . î 2 þ
Câu 11: Tập giá trị T của hàm số 2
y = 7 - 3cos x là
A. T = é2; 10 ù .
B. T = é2; 7 ù.
C. T = é 7; 10 ù . D. T = [0; ] 1 . ë û ë û ë û
Câu 12: Nghiệm đặc biệt nào sau đây là sai? p
A. cosx = 0 Û x =
+ k2p (k Î!)
B. sinx = 0 Û x = p k (k Î!). 2 p p
C. sinx =1 Û x =
+ k2p (k Î!) D. sinx = 1
- Û x = - + k2p (k Î!). 2 2 æ 3p 3p ö
Câu 13: Cho đồ thị hàm số y = tanx trên - ; như hình vẽ. ç ÷ è 2 2 ø æ p p ö
Có bao nhiêu giá trị của x Î - ;
thỏa mãn tanx = 0 ? ç ÷ è 2 2 ø A. 0 . B. 1. C. 2 . D. 3 .
Câu 14: Phương trình sin2x = sin3x có nghiệm là p 2p A. x = + k , k Î! .
B. x = k2p , k Î! . 5 5 p p 2p
C. x = k2p và x =
+ k2p ,k Î!. .
D. x = k2p và x = + k , k Î! . 5 5 5 3
Câu 15: Phương trình cot3x = - có nghiệm là 3 p p p
A. x = - + kp ,k Î!
B. x = - + kp ,k Î!
C. x = - + k2p ,k Î! D. 3 9 9 p p x = - + k , k Î! 9 3 Trang 2 Câu 16: Với *
n Î • , cho dãy số (u 3: 0,3,6,9,…
n ) các số tự nhiên chia hết cho
Số hạng đầu tiên của dãy số (un ) là
A. u = 6.
B. u = 0.
C. u = 3. D. u = 9 . 1 1 1 1 Câu 17: Với *
nÎQ , trong các dãy số (u u
n ) cho bởi số hạng tổng quát
sau, dãy số nào là dãy số giảm ? n 1 A. u = B. 2 u = n
C. u = (-3)n . D. 2
u = n - 6n + 3. n n n n n Câu 18: Với *
nÎQ , cho dãy số (un ) gồm tất cả các số nguyên dương chia 3 dư 2 theo thứ tự tăng dần. Số
hạng tổng quát của dãy số này là 3n 2 A. u =
B. u = 1+
C. u = 3n - 2 .
D. u = 3n + 2 . n 2 n n n n
Câu 19: Cho cấp số cộng (u u = 2 u = 8 n ) với và
. Công sai của cấp số cộng đã cho bằng 1 2 A. -6 . B. 4 . C. 6 . D. 10 . 1
Câu 20: Cho cấp số cộng có u = 3
- và d = . Khẳng định nào sau đây là đúng? 1 2 1 1 1 1 A. u = 3 - + (n + u = 3 - + (n + u = 3 - + (n - u = 3 - + (n - n )1 n )1 n ) 1 n ) 1 B. . C. . D. . 2 4 2 4
Câu 21: Bà chủ quán trà sữa X muốn trang trí cho đẹp nên quyết định thuê nhân công xây một bức tường
bằng gạch với xi măng (như hình vẽ bên dưới), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có
ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là
bao nhiêu viên? (hình ảnh dưới đây là hình ảnh minh họa hàng gạch dưới cùng có 5 viên) A. 25250 . B. 250500 . C. 12550 . D. 125250 .
Câu 22: Trong các khẳng định sau, khẳng định nào đúng? A. Nếu 3 điểm ,
A B,C là 3 điểm chung của 2 mặt phẳng (P) và (Q) thì ,
A B,C thẳng hàng. B. Nếu ,
A B,C thẳng hàng và (P),(Q) có điểm chung là A , thì B,C cũng là 2 điểm chung của (P) và (Q). C. Nếu 3 điểm ,
A B,C là 3 điểm chung của 2 mặt phẳng (P) và (Q) phân biệt thì ,
A B,C không thẳng hàng. D. Nếu ,
A B,C thẳng hàng và ,
A B là 2 điểm chung của (P) và (Q) thì C cũng là điểm chung của (P) Q và ( ).
Câu 23: Cho bốn điểm ,
A B,C, D không đồng phẳng. Giao tuyến của hai mặt phẳng ( ABC) và ( ACD) là A. AB . B. AC . C. BC . D. AD . Trang 3
Câu 24: Một hình chóp có đáy là ngũ giác thì số cạnh của hình chóp là A. 5 cạnh. B. 6 cạnh. C. 9 cạnh. D. 10 cạnh.
Câu 25: Khẳng định nào sau đây là đúng về hình tứ diện đều?
A. Mặt đáy là hình thoi.
B. Mặt đáy là hình vuông.
C. Mặt bên là tam giác cân.
D. Mặt bên luôn là tam giác đều.
Câu 26: Cho tứ diện ABCD . Gọi E và F lần lượt là trung điểm của AB và ;
CD G là trọng tâm tam giác
BCD . Giao điểm của đường thẳng EG và mặt phẳng ( ACD) là A. Điểm F .
B. Giao điểm của đường thẳng EG và AF .
C. Giao điểm của đường thẳng EG và AC .
D. Giao điểm của đường thẳng EG và CD .
Câu 27: Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và CD . Mặt phẳng (a ) qua MN cắt ,
AD BC lần lượt tại P và Q . Biết MP cắt NQ tại I . Ba điểm nào sau đây thẳng hàng? A. I, , A C .
B. I, B, D . C. I, , A B.
D. I,C, D .
Câu 28: Cho đường thẳng a chứa trong mặt phẳng (P). Có bao nhiêu đường thẳng chứa trong (P) và
song song với đường thẳng a ? A. 0 . B. 1 . C. 2. D. Vô số.
Câu 29: Trong không gian cho các mệnh đề sau:
(I) Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng thì song song với nhau.
(II) Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
(III) Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy song song với nhau.
(IV) Qua điểm A không thuộc đường thẳng d , kẻ được đúng một đường thẳng song song với d . Số mệnh đề đúng là A. 0 . B. 1. C. 2. D. 3 .
Câu 30: Trong không gian, cho ba đường thẳng a,b, c. Trong các mệnh đề sau mệnh đề nào đúng?
D . Nếu a và b cắt nhau, b và c cắt nhau thì a và c cắt nhau.
A. Nếu a và b không cắt nhau thì a và b song song.
B. Nếu b và c chéo nhau thì b và c không cùng thuộc một mặt phẳng.
C. Nếu a và b cùng chéo nhau với c thì a song song với b .
Câu 31: Cho hình chóp S × ABCD . Gọi I, J lần lượt là trung điểm của AB và BC . Giao tuyến của hai
mặt phẳng (SAC) và (SIJ ) là một đường thẳng song song với
A. đường thẳng AD .
B. đường thẳng AB .
C. đường thẳng AC .
D. đường thẳng BD .
Câu 32: Cho đường thẳng a song song với mặt phẳng (a ). Nếu mặt phẳng (b ) chứa a và cắt (a ) theo
giao tuyến b thì b và a là hai đường thẳng
A. cắt nhau. B. trùng nhau. C. chéo nhau.
D. song song với nhau.
Câu 33: Cho mặt phẳng (P) và hai đường thẳng song song a và b . Khẳng định nào sau đây là đúng? Trang 4
A. Nếu (P) song song với a thì (P) cũng song song với b .
B. Nếu (P) cắt a thì (P) cũng cắt b .
C. Nếu (P) chứa a thì (P) cũng chứa b .
D. Nếu (P) chứa a thì (P) song song với b .
Câu 34: Cho hình chóp S × ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm các tam
giác và SAB và SAD . Gọi M là trung điểm CD . Chọn mệnh đề đúng trong các mệnh đề sau
A. IJ / / (SCD).
B. IJ / / (SBM ).
C. IJ / / (SBD).
D. IJ / / (SBC) .
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB và
I là trung điểm của AB . Lấy điểm M trên đoạn AD sao cho AD = 3AM . Đường thẳng qua M và song
song với AB cắt CI tại J . Đường thẳng GJ không song song với mặt phẳng dưới đây?
A. (SCD).
B. (SBC).
C. (SAC). D. (SAD).
PHẦN II. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm) Giải các phương trình lượng giác: a) 1
sinx + 3cosx = 2 . b) 2 + 3cot x = 5. 2 cos x
Bài 2. (1,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi (a ) là mặt phẳng
đi qua trung điểm M của cạnh SB , song song với cạnh AB và cắt các cạnh ,
SA SD , SC lần lượt
tại các điểm Q, P, N . Chứng minh tứ giác MNPQ là hình thang.
Bài 3. (1,0 điểm) Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2023 é p
(có 365 ngày) được cho bởi một hàm số ù y = 4sin
(t -60) +10, với t ÎQ và 0 < t £ 365. Vào ê178 ú ë û
ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất? ĐÁP ÁN 1 2 3 4 5 6 7 B C D D B A A 8 9 10 11 12 13 14 A C C B A B D 15 16 17 18 19 20 21 D B A D C C D 22 23 24 25 26 27 28 D B D D B B D 29 30 31 32 33 34 35 B B C D B C D Trang 5