Đề kiểm tra giữa học kỳ 1 Toán 11 Kết nối tri thức - Đề 5 (có đáp án)

Đề kiểm tra giữa học kỳ 1 Toán 11 Kết nối tri thức - Đề 5 có đáp án được soạn dưới dạng file PDF gồm 8 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

48 24 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Sách: Kết nối tri thức

Thông tin:

7 trang 6 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
ĐỀ 5-1
ĐỀ ÔN TẬP HỌC KỲ I
MÔN: TOÁN 11
I. TRẮC NGHIỆM( 5 điểm).
Câu 1: Trong các công thức dưới đây, công thức nào đúng?
A. B.
C. D.
Câu 2: Phương trình có tập nghiệm là
A. B.
C. D.
Câu 3: Trong các công thức dưới đây, công thức nào đúng?
A. B.
C. D.
Câu 4: Cho cấp số nhân có công bội Gọi là tổng của số hạng đầu của cấp số nhân. Khẳng
định nào sau đây đúng?
A. . B. . C. . D. .
Câu 5: Cho cấp số cộng với và Công sai của cấp số cộng đã cho bằng
A. . B. . C. . D. .
Câu 6: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số được liệt kê ở bốn
phương án A, B, C, D?
A. . B. . C. . D. .
Câu 7: Cho dãy số , biết với . Ba số hạng đầu tiên của dãy số đó là lần lượt là những
số nào dưới đây?
A. B. C. D.
Câu 8: Cho cấp số nhân với và
Tính tổng 5 số hạng đầu của cấp số nhân đó
A. . B. . C. . D. .
Câu 9: Tập xác định hàm số là
A. B.
C. D.
Câu 10: Cho . Giá trị bằng
A. . B. . C. . D. .
cos cos 2sin sin .
22
ab ab
ab
+-
-=-
cos cos 2 cos cos .
22
ab ab
ab
+-
-=
cos cos 2sin sin .
22
ab ab
ab
+-
-=
cos cos 2 cos cos .
22
ab ab
ab
+-
-=-
sin sinx
a
=
{ }
|.Skk
pa
=+ Î!
{ }
2; 2 | .Sk kk
apapp
=+ +- Î!
{ }
2| .Skk
pa
=+ Î!
( )
sin cos sin sin cos .ab a b a b-= +
( )
sin sin cos sin cos .ab a b b a-= -
( )
sin sin cos cos sin .ab a a b b-= -
( )
sin cos cos sin sin .ab a b a b-= -
( )
n
u
1.q ¹
n
S
n
( )
1
1
1
n
n
uq
S
q
-
=
-
( )
1
1
n
n
q
S
q
-
=
-
( )
1
1
1
n
n
uq
S
q
-
=
-
( )
1
1
1
n
n
uq
S
q
-
=
-
( )
n
u
1
3u =
2
5.u =
4
8
2
6
sinyx=
tanyx=
cotyx=
cosyx=
( )
n
u
1
1
1
3
nn
u
uu
+
=-
ì
í
=+
î
1n ³
4;7; 10.
1;2;5.-
1; 4; 7 .
1;3;7.-
( )
n
u
2q =
1
3u =-
5
96S =-
5
486S =-
5
93S =-
5
122S =
tanyx=
\,.
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
{ }
\, .Dkk
p
=Î!"
\2,.
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
{ }
\2, .Dkk
p
=Î!"
1
cos =
3
a
cos2
a
7
cos2
9
a
=-
7
cos2
9
a
=
1
cos2
3
a
=
2
cos2
3
a
=
Trang 2
Câu 11: Cho cấp số cộng có và Tính số hạng thứ 15 của cấp số cộng trên.
A. B. C. D.
Câu 12: Cho góc hình học có số đo bằng (hình 1.4). Số đo của các góc lượng giác là
A. sđ . B. sđ .
C. sđ . D. sđ .
Câu 13: Tìm tất các các giá trị thực của tham số để phương trình có nghiệm.
A. B. C. D.
Câu 14: Một đường tròn có bán kính bằng . Tính độ dài của cung trên đường tròn có số đo (làm
tròn lấy chữ số thập phân).
A. . B. . C. . D. .
Câu 15: Trong các dãy số hữu hạn được cho dưới đây, dãy số nào là dãy số tăng?
A. B. C. D.
II. TỰ LUẬN( 5 điểm).
Câu 1: (1 điểm) Cho dãy số với . Viết 4 số hạng đầu của dãy số trên.
Câu 2: (2 điểm) Giải phương trình:
a) b)
Câu 3: (1 điểm) Cho và . Tính giá trị của biểu thức
Câu 4: (1 điểm) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân
theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số
51 đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc
thứ tăng so với giá của mỗi số ở bậc thứ n là 5%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1243 số trong tháng 1, hỏi tháng 1 trường THPT X phải
đóng bao nhiêu tiền điện?
------ HẾT ------
ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A
C
B
D
C
A
B
C
A
A
B
B
C
A
B
II. PHẦN TỰ LUẬN
Câu 1: (1đ) Cho dãy số với . Viết 4 số hạng đầu của dãy số trên.
4 số hạng của dãy số là: 2, 7, 12, 17.
Viết đúng mỗi số hạng được 0,25điểm
( )
n
u
1
5u =-
3.d =
15
45.u =
15
37.u =
15
35.u =
15
47.u =
uOv
0
60
( )
,Ou Ov
( )
00
,60.180,Ou Ov k k=+ ŒZ
( )
00
,60.360,Ou Ov k k=+ ŒZ
( )
00
,60.180,Ou Ov k k=- ŒZ
( )
00
,60.360,Ou Ov k k=- + ŒZ
m
cos 2xm=-
1 1.m-£ £
1.m £
1 3.m££
1.m ³-
10 cm
0
35
2
6,11cm
6, 31cm
6, 01cm
6, 21cm
2, 4,1, 3,1.
2, 4, 6,8,10.
5, 4, 3, 2,1.
1,1,1,1,1.
( )
n
u
53
n
un=-
1
cos
2
x =
sin 2 cos 0
3
xx
p
æö
-+=
ç÷
èø
3
sin
5
a
=-
3
2
p
pa
<<
cot 2 tan
tan 3cot
P
aa
aa
-
=
+
1n +
( )
n
u
53
n
un=-
Trang 3
Câu 2: Giải phương trình:
b)
Giải:
b)
Giải:
Câu 3: Cho và . Tính giá trị của biểu thức
Giải:
nên
Câu 4: (1đ) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số 51
đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc thứ
tăng so với giá của mỗi số ở bậc thứ n là 5%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1243 số trong tháng 1, hỏi tháng 1 trường THPT X phải
đóng bao nhiêu tiền điện?
1
cos
2
x =
1
cos cos cos
23
xx
p
=Û =
2
3
()
2
3
xk
k
xk
p
p
p
p
é
=+
ê
ÛÎ
ê
ê
=- +
ê
ë
!
sin 2 cos 0
3
xx
p
æö
-+=
ç÷
èø
sin 2 cos 0
3
xx
p
æö
-+=
ç÷
èø
sin 2 cos
3
xx
p
æö
Û=+
ç÷
èø
os( 2 ) cos
23
cxx
pp
æö
Û-=+
ç÷
èø
22
23
22
23
xx k
xx k
pp
p
pp
p
é
-=++
ê
Û
ê
ê
-=--+
ê
ë
2
18 3
()
5
2
6
k
x
k
xk
pp
p
p
é
=+
ê
ÛÎ
ê
ê
=+
ê
ë
!
3
sin
5
a
=-
3
2
p
pa
<<
cot 2 tan
tan 3cot
P
aa
aa
-
=
+
3
2
p
pa
<<
cos 0
a
<
22
sin cos 1
aa
+=
2
cos 1 sin
aa
Þ=--
2
34
1
55
æö
=- - - =-
ç÷
èø
3
tan
4
a
=
4
cot
3
a
=
cot 2 tan 2
tan 3cot 57
P
aa
aa
-
==-
+
1n +
Trang 4
Giải:
a) Gọi U
1
là số tiền phải trả cho các số điện từ 1 đến 50.
U
2
là số tiền phải trả cho các số điện từ 51 đến 100.
U
1
, U
2, ,
… U
n
lập thành cấp số nhân với q=1,05.
Ta có :
b) U
24
là số tiền phải trả cho các số điện từ 1151 đến 1200.
Số tiền phải trả cho 1200 số đầu tiên là
Số tiền phải trả cho số từ 1201 đến 1243 là
Vậy số tiền tháng 1 trường THPT X phải đóng là
ĐỀ 5-2
ĐỀ ÔN TẬP HỌC KỲ I
MÔN: TOÁN 11
I. TRẮC NGHIỆM( 5 điểm).
Câu 1: Cho . Giá trị bằng
A. . B. . C. . D. .
Câu 2: Tìm tất các các giá trị thực của tham số để phương trình có nghiệm.
A. B. C. D.
Câu 3: Cho cấp số cộng có và Tính số hạng thứ 15 của cấp số cộng trên.
A. B. C. D.
Câu 4: Trong các dãy số hữu hạn được cho dưới đây, dãy số nào là dãy số giảm?
A. B. C. D.
Câu 5: Cho cấp số nhân có công bội Gọi là tổng của số hạng đầu của cấp số nhân. Khẳng
định nào sau đây đúng?
A. . B. . C. . D. .
Câu 6: Cho góc hình học có số đo bằng (hình dưới). Số đo của các góc lượng giác là
A. sđ . B. sđ .
C. sđ . D. sđ .
1
50 1700 85000( ); 1, 05Ux dq== =
21
.89250()UUq d==
24
11
1
. 3782670(d)
1
q
SU
q
-
=»
-
24
2
43.1700.1, 05 235755( )Sd=»
11
4018425(d)SS+»
2
sin =
3
a
cos2
a
1
cos2
3
a
=
2
cos2
3
a
=
1
cos2
9
a
=
7
cos2
9
a
=-
m
2 sin xm=
2.m £
1 1.m-£ £
2 2.m-£ £
1.m ³-
( )
n
u
1
3u =
5.d =-
15
47.u =-
15
45.u =
15
67.u =-
15
37.u =
1, 5, 4, 3, 2 .
5, 4, 3, 2,1.
2, 4, 6, 8,10.
1,1,1,1,1.
( )
n
u
1.q ¹
6
S
6
( )
6
1
6
1
1
uq
S
q
-
=
-
( )
6
1
6
1
1
uq
S
q
-
=
-
( )
6
1
6
1
1
uq
S
q
-
=
-
( )
5
1
6
1
1
uq
S
q
-
=
-
uOv
0
45
( )
,Ou Ov
( )
00
,45.360,Ou Ov k k=- + ŒZ
( )
00
,45.180,Ou Ov k k=+ ŒZ
( )
00
,45.360,Ou Ov k k=+ ŒZ
( )
00
,45.180,Ou Ov k k=- ŒZ
45
0
Trang 5
Câu 7: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D
A. . B. . C.. D. .
Câu 8: Một đường tròn có bán kính bằng . Tính độ dài của cung trên đường tròn có số đo (làm
tròn lấy chữ số thập phân).
A. . B. . C. . D. .
Câu 9: Cho cấp số cộng với và công sai Số hạng thứ 2 của cấp số cộng đã cho bằng
A. . B. . C. . D. .
Câu 10: Cho dãy số , biết với . Ba số hạng đầu tiên của dãy số đó là lần lượt là
những số nào dưới đây?
A. B. C. D.
Câu 11: Cho cấp số nhân với và
Tính tổng 5 số hạng đầu của cấp số nhân đó
A. . B. . C. . D. .
Câu 12: Trong các công thức sau, công thức nào sai?
A. B. C. D.
Câu 13: Tập xác định hàm số là
A. B.
C. D.
Câu 14: Trong các công thức dưới đây, công thức nào đúng?
A. B.
C. D.
Câu 15: Phương trình có tập nghiệm là
A. B.
C. D.
II. TỰ LUẬN( 5 điểm).
Câu 1: (1 điểm) Cho dãy số với . Viết 4 số hạng đầu của dãy số trên.
Câu 2: (2 điểm) Giải phương trình:
c) b)
Câu 3: (1 điểm) Cho và . Tính giá trị của biểu thức
Câu 4: (1 điểm) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân
theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số
tanyx=
cotyx=
sinyx=
cosyx=
20 cm
0
25
2
6,12cm
8, 37cm
6, 01cm
8, 73cm
( )
n
u
1
3u =
5.d =
6
2
4
8
( )
n
u
1
1
1
3
nn
u
uu
+
=
ì
í
=-
î
1n ³
1; .3;9-
1; 4; 7 .
1; 3; 9 .- -
1;3;7.-
( )
n
u
2q =-
1
3u =
5
93S =
5
96S =-
5
33S =-
5
33S =
22
cos 2 cos sin .aaa=+
2
cos 2 1 – 2sin .aa=
2
cos 2 2 cos – 1.aa=
22
cos 2 cos – sin .aaa=
cotyx=
{ }
\, .Dkk
p
=Î!"
\2,.
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
\,.
2
Dkk
p
p
ìü
=+Î
íý
îþ
!"
{ }
\2, .Dkk
p
=Î!"
( )
cos sin cos cos sin .ab a b a b-= -
( )
cos os cos sin sin .ab ca b a b-= -
( )
cos sin cos cos sin .ab a b a b-= +
( )
cos os cos sin sin .ab ca b a b-= +
cos cosx
a
=
{ }
2| .Skk
pa
=+ Î!
{ }
|.Skk
pa
=+ Î!
{ }
;|.Sk kk
aapp p
+-=+ Î!
( )
n
u
45
n
un=-
3
cos
2
x =
cos2 sin 0
3
xx
p
æö
-+=
ç÷
èø
3
cos
5
a
=-
2
p
ap
<<
2 cot tan
tan 3cot
P
aa
aa
-
=
+
Trang 6
51 đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc
thứ tăng so với giá của mỗi số ở bậc thứ n là 4%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1324 số trong tháng 2, hỏi tháng 2 trường THPT X phải
đóng bao nhiêu tiền điện?
------ HẾT ------
ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
C
C
C
B
B
C
D
D
D
A
D
A
A
D
C
II. PHẦN TỰ LUẬN
Câu 1: (1đ) Cho dãy số với . Viết 4 số hạng đầu của dãy số trên.
4 số hạng của dãy số là: -1, 3, 7, 11.
Câu 2: (2đ) Giải phương trình:
a)
Giải:
b)
Giải:
Câu 3: (1đ) Cho và . Tính giá trị của biểu thức
Giải:
Do nên
Suy ra,
1n +
( )
n
u
45
n
un=-
3
cos
2
x =
3
cos cos cos
26
xx
p
=Û =
2
6
()
2
6
xk
k
xk
p
p
p
p
é
=+
ê
ÛÎ
ê
ê
=- +
ê
ë
!
cos2 sin 0
3
xx
p
æö
-+=
ç÷
èø
cos2 sin 0
3
xx
p
æö
-+=
ç÷
èø
cos2 sin
3
xx
p
æö
Û=+
ç÷
èø
sin ( 2 ) sin
23
xx
pp
æö
Û-=+
ç÷
èø
22
23
22
23
xx k
xxk
pp
p
pp
pp
é
-=++
ê
Û
ê
ê
-=--+
ê
ë
2
18 3
()
2
6
k
x
k
xk
pp
p
p
é
=+
ê
ÛÎ
ê
-
ê
=+
ê
ë
!
3
cos
5
a
=-
2
p
ap
<<
2 cot tan
tan 3cot
P
aa
aa
-
=
+
2
p
ap
<<
sin 0
a
>
22
sin cos 1
aa
+=
2
sin 1 osc
aa
Þ=-
2
34
1
55
æö
=-- =
ç÷
èø
4
tan
3
a
=-
3
cot
4
a
=-
Trang 7
Câu 4: (1đ) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số 51
đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc thứ
tăng so với giá của mỗi số ở bậc thứ n là 4%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1324 số trong tháng 2, hỏi tháng 2 trường THPT X
phải đóng bao nhiêu tiền điện?
Giải:
a) Gọi U
1
là số tiền phải trả cho các số điện từ 1 đến 50.
U
2
là số tiền phải trả cho các số điện từ 51 đến 100.
U
1
, U
2, ,
… U
n
lập thành cấp số nhân với q=1,04.
Ta có :
b) U
26
là số tiền phải trả cho các số điện từ 1251 đến 1300.
Số tiền phải trả cho 1300 số đầu tiên là
Số tiền phải trả cho số từ 1301 đến 1324 là
Vậy số tiền tháng 2 trường THPT X phải đóng là
2 cot tan 2
tan 3cot 43
P
aa
aa
-
==
+
1n +
1
50.1700 85000( ); 1, 04Udq== =
21
.88400()UUq d==
26
11
1
. 3766498(d)
1
q
SU
q
-
=»
-
26
2
24.1700.1, 04 113117( )Sd=»
11
3879615(d)SS+»
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ĐỀ 5-1
ĐỀ ÔN TẬP HỌC KỲ I MÔN: TOÁN 11
I. TRẮC NGHIỆM( 5 điểm).
Câu 1: Trong các công thức dưới đây, công thức nào đúng? a + b a - b a + b a - b
A. cos a - cosb = 2 - sin sin .
B. cos a - cosb = 2cos cos . 2 2 2 2 a + b a - b a + b a - b
C. cos a - cosb = 2sin sin .
D. cos a - cosb = 2 - cos cos . 2 2 2 2
Câu 2: Phương trình sin x = sina có tập nghiệm là
A. S = {a + k2p; a - + k2p | k Î } ! .
B. S = {a + kp | k Î } ! .
C. S = {a + k2p;p -a + k2p | k Î } ! .
D. S = {a + k2p | k Î } ! .
Câu 3: Trong các công thức dưới đây, công thức nào đúng?
A. sin (a -b) = cosasinb +sin acos . b
B. sin (a -b) = sin acosb -sinbcosa .
C. sin (a -b) = sin acosa -cosbsinb .
D. sin (a -b) = cosacosb -sin asinb .
Câu 4: Cho cấp số nhân (u q ¹ 1. S n n ) có công bội Gọi
là tổng của số hạng đầu của cấp số nhân. Khẳng n
định nào sau đây đúng? u 1 n - q (1 n - q ) u 1 n - q u 1 n - q 1 ( ) 1 ( ) 1 ( ) A. S = . B. S = . C. S = . D. S = . n 1- q n 1- q n q -1 n 1- q
Câu 5: Cho cấp số cộng (u u = 3 u = 5. n ) với và
Công sai của cấp số cộng đã cho bằng 1 2 A. 4 . B. 8 . C. 2 . D. 6 .
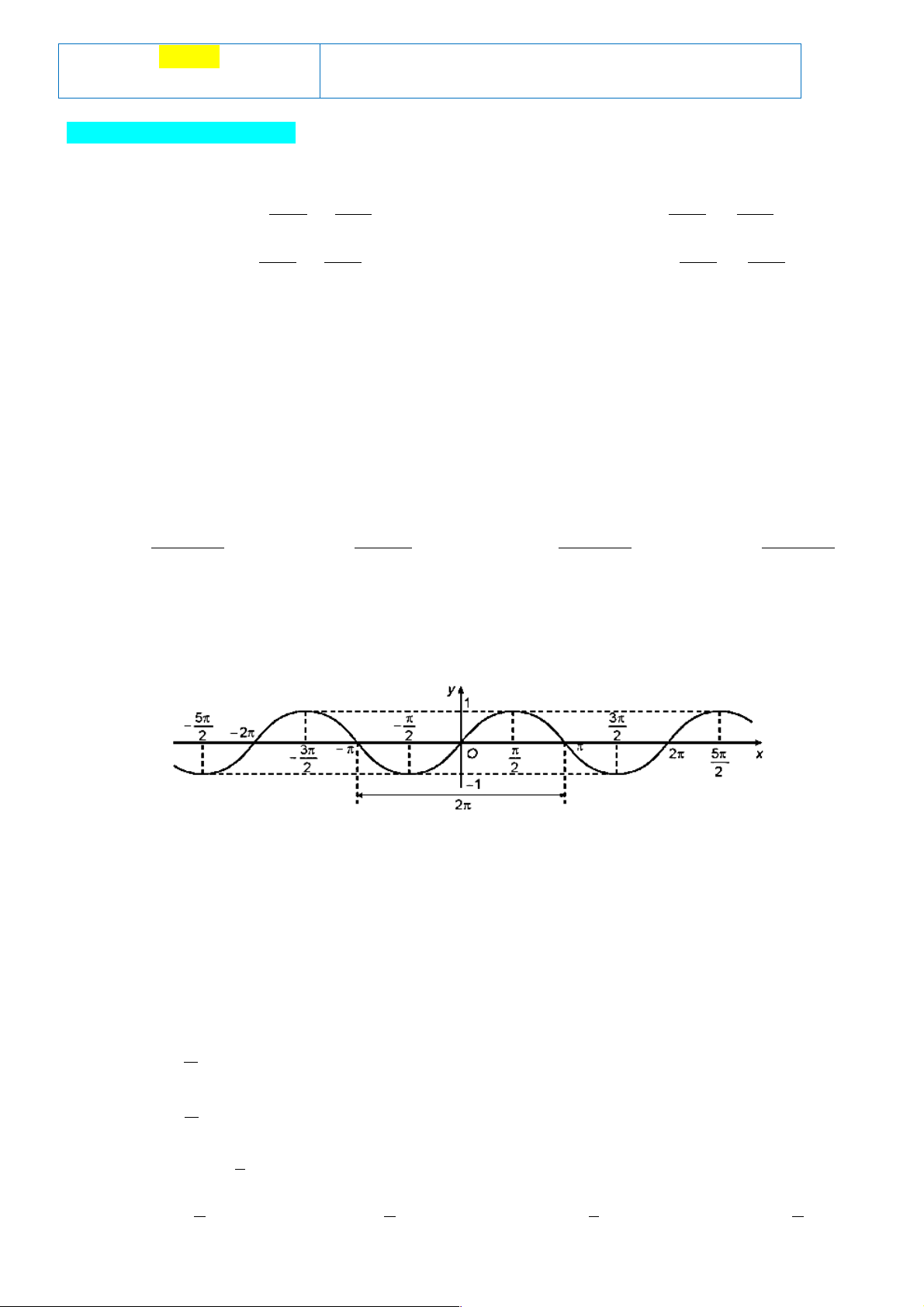
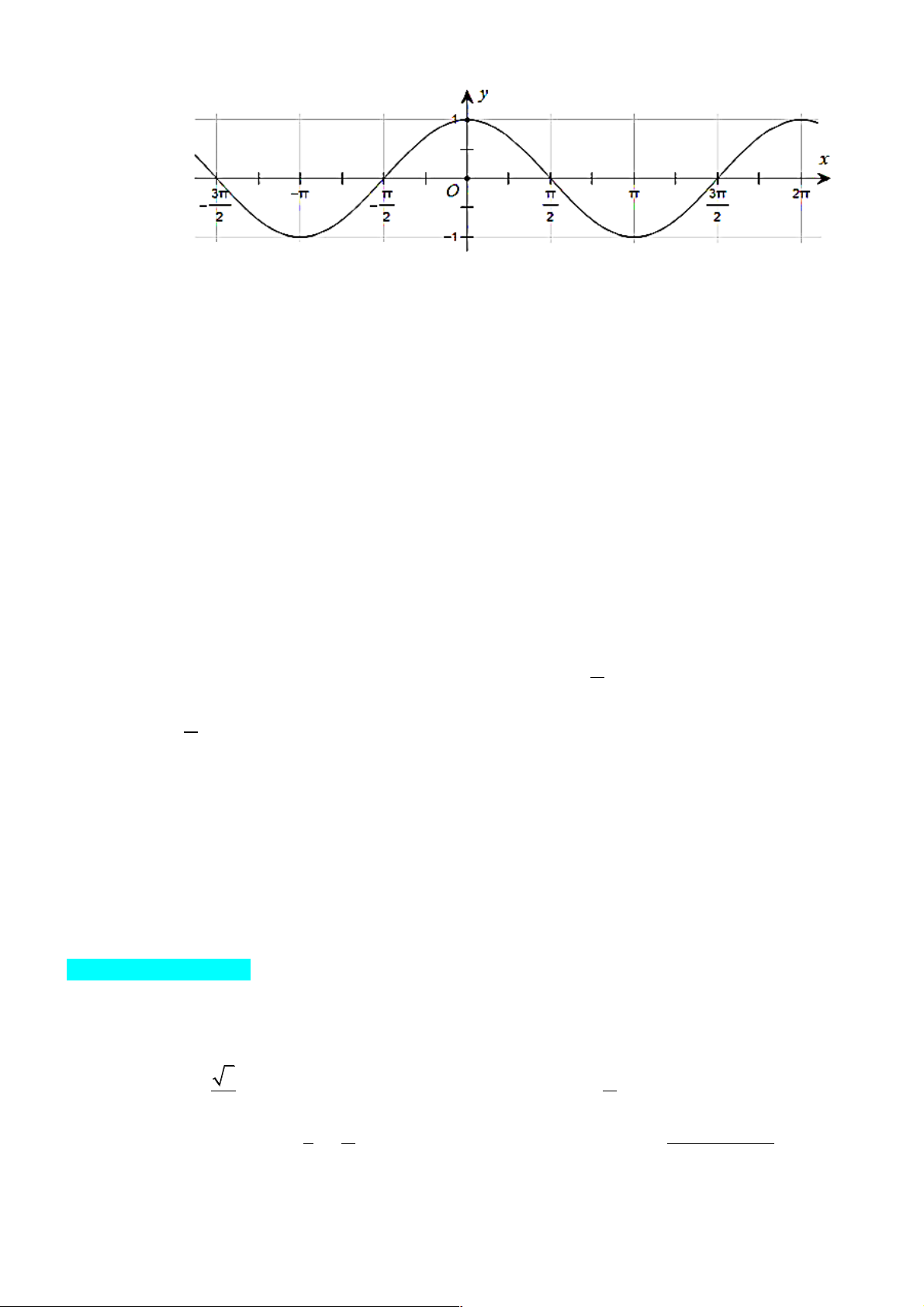
Câu 6: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong các hàm số được liệt kê ở bốn
phương án A, B, C, D?
A. y = sin x .
B. y = tan x.
C. y = cot x.
D. y = cos x . u ì = 1 -
Câu 7: Cho dãy số (u 1 n ³ 1 n ) , biết í với
. Ba số hạng đầu tiên của dãy số đó là lần lượt là những u = u + 3 î n 1+ n số nào dưới đây? A. 4;7;10. B. 1 - ;2;5. C. 1;4;7. D. 1 - ;3;7.
Câu 8: Cho cấp số nhân (u q = 2 u = 3 - n ) với và
Tính tổng 5 số hạng đầu của cấp số nhân đó 1 A. S = 96 - . B. S = 486 - . C. S = 93 - . D. S = 122. 5 5 5 5
Câu 9: Tập xác định hàm số y = tan x là ìp ü
A. D = ! \ í + kp ,k Î"ý.
B. D = ! \{kp,k Î } " . î 2 þ ìp ü
C. D = ! \ í + k2p ,k Î"ý.
D. D = ! \{k2p,k Î } " . î 2 þ 1
Câu 10: Cho cosa = . Giá trị cos2a bằng 3 7 A. cos2a = - 7 . B. cos2a = 1 . C. cos2a = 2 . D. cos2a = . 9 9 3 3 Trang 1
Câu 11: Cho cấp số cộng (u u = 5 - d = 3. n ) có và
Tính số hạng thứ 15 của cấp số cộng trên. 1
A. u = 45.
B. u = 37.
C. u = 35. D. u = 47. 15 15 15 15
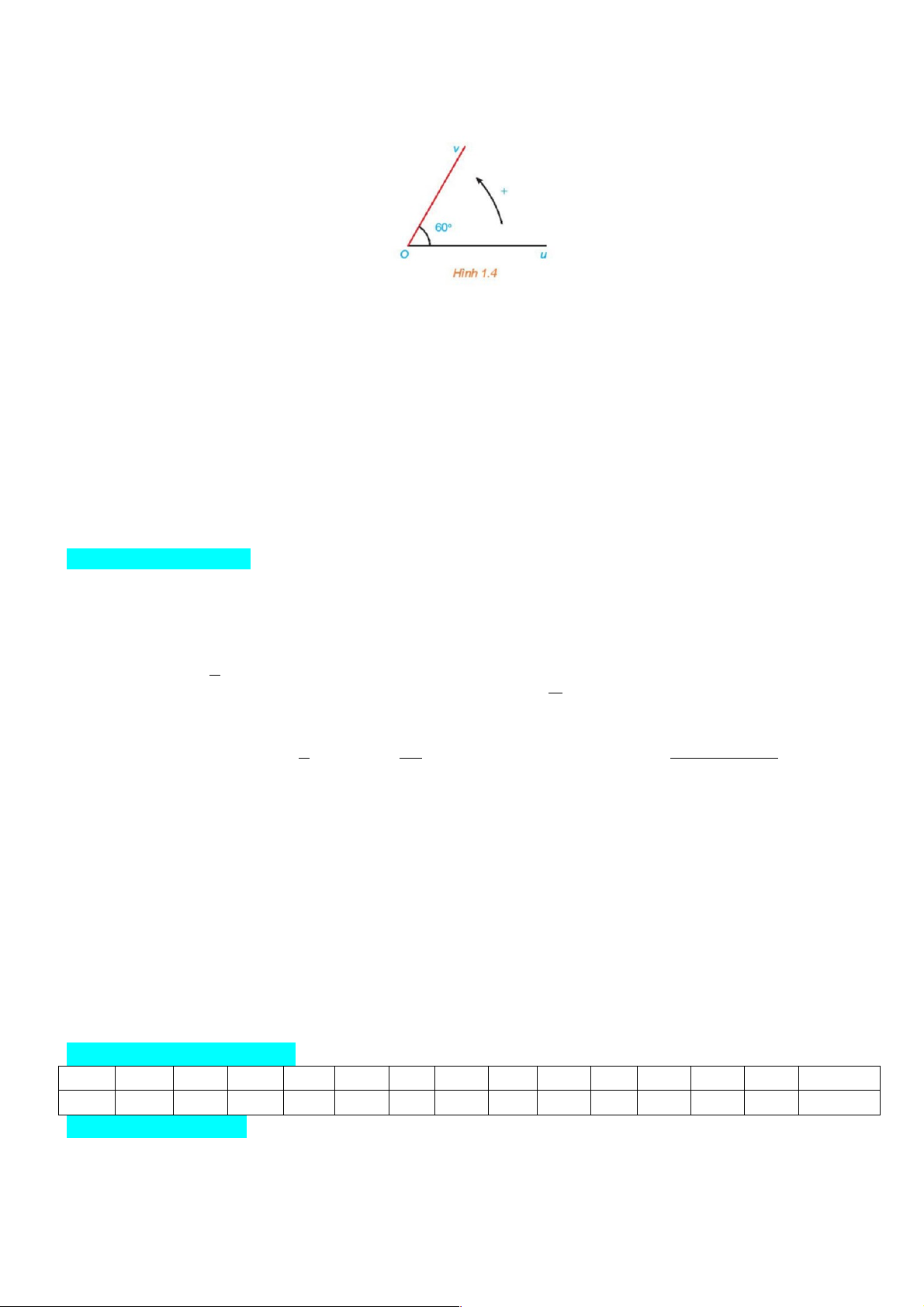
Câu 12: Cho góc hình học uOv có số đo bằng 0
60 (hình 1.4). Số đo của các góc lượng giác (Ou,Ov) là
A. sđ(Ou Ov) 0 0 ,
= 60 + k.180 ,k ŒZ .
B. sđ(Ou Ov) 0 0 ,
= 60 + k.360 ,k ŒZ .
C. sđ(Ou Ov) 0 0 ,
= 60 - k.180 ,k ŒZ .
D. sđ(Ou Ov) 0 0 ,
= - 60 + k.360 ,k ŒZ .
Câu 13: Tìm tất các các giá trị thực của tham số m để phương trình cos x = m - 2 có nghiệm. A. 1 - £ m £1.
B. m £ 1.
C. 1 £ m £ 3. D. m ³ 1. -
Câu 14: Một đường tròn có bán kính bằng 10 cm . Tính độ dài của cung trên đường tròn có số đo 0 35 (làm
tròn lấy 2 chữ số thập phân).
A. 6,11cm.
B. 6,31cm .
C. 6,01cm . D. 6, 21cm.
Câu 15: Trong các dãy số hữu hạn được cho dưới đây, dãy số nào là dãy số tăng? A. 2, 4,1,3,1. B. 2, 4,6,8,10. C. 5, 4,3, 2,1. D. 1,1,1,1,1. II. TỰ LUẬN( 5 điểm).
Câu 1: (1 điểm) Cho dãy số (u u = 5n - 3 n ) với
. Viết 4 số hạng đầu của dãy số trên. n
Câu 2: (2 điểm) Giải phương trình: 1 cos x = æ p ö a) 2
b) sin 2x - cos x + = 0 ç ÷ è 3 ø 3 p a - a
Câu 3: (1 điểm) Cho sina = - 3 và p < a < cot 2 tan
. Tính giá trị của biểu thức P = 5 2 tana + 3cota
Câu 4: (1 điểm) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân
theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số
51 đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc
thứ n +1 tăng so với giá của mỗi số ở bậc thứ n là 5%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1243 số trong tháng 1, hỏi tháng 1 trường THPT X phải
đóng bao nhiêu tiền điện?
------ HẾT ------ ĐÁP ÁN I. PHẦN TRẮC NGHIỆM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 A C B D C A B C A A B B C A B II. PHẦN TỰ LUẬN
Câu 1: (1đ) Cho dãy số (u u = 5n - 3 n ) với
. Viết 4 số hạng đầu của dãy số trên. n
4 số hạng của dãy số là: 2, 7, 12, 17.
Viết đúng mỗi số hạng được 0,25điểm Trang 2
Câu 2: Giải phương trình: 1 b) cos x = 2 Giải: é p x = + k2p 1 p ê cos x 3 = Û cos x = co s Û ê (k Î!) 2 3 p ê x = - + k2p êë 3 æ p ö
b) sin 2x - cos x + = 0 ç ÷ è 3 ø Giải: æ p ö æ p ö sin 2x - cos x + = 0 ç ÷
Û sin 2x = cos x + ç ÷ è 3 ø è 3 ø p æ p ö Û o
c s( - 2x) = cos x + ç ÷ 2 è 3 ø ép p
- 2x = x + + k2p ê 2 3 Û êp p ê
- 2x = -x - + k2p êë 2 3 é p k2p x = + ê 18 3 Û ê (k Î!) 5p êx = + k2p êë 6 3 p a - a Câu 3: Cho sina = - 3 và p < a < cot 2 tan
. Tính giá trị của biểu thức P = 5 2 tana + 3cota Giải: 3p p < a < nên cosa < 0 2 2 2 sin a + cos a =1 2 æ 3 ö 4 2 Þ 3 cosa = - 1-sin a = - 1- - = - tana = 4 cota = ç ÷ è 5 ø 5 4 3 cota - 2 tana 2 P = = - tana + 3cota 57
Câu 4: (1đ) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số 51
đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc thứ
n +1 tăng so với giá của mỗi số ở bậc thứ n là 5%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1243 số trong tháng 1, hỏi tháng 1 trường THPT X phải
đóng bao nhiêu tiền điện? Trang 3 Giải:
a) Gọi U1 là số tiền phải trả cho các số điện từ 1 đến 50.
U2 là số tiền phải trả cho các số điện từ 51 đến 100.
U1 , U2, , … Un lập thành cấp số nhân với q=1,05. Ta có : U = 50 1700 x
= 85000(d); q =1,05 1
U = U .q = 89250(d) 2 1
b) U24 là số tiền phải trả cho các số điện từ 1151 đến 1200.
Số tiền phải trả cho 1200 số đầu tiên là 24 1- q S = U . » 3782670(d) 1 1 1- q
Số tiền phải trả cho số từ 1201 đến 1243 là 24
S = 43.1700.1,05 » 235755(d) 2
Vậy số tiền tháng 1 trường THPT X phải đóng là
S + S » 4018425(d) 1 1 ĐỀ 5-2
ĐỀ ÔN TẬP HỌC KỲ I MÔN: TOÁN 11
I. TRẮC NGHIỆM( 5 điểm). 2
Câu 1: Cho sina = . Giá trị cos2a bằng 3 1 A. cos2a = 2 . B. cos2a = 1 . C. cos2a = 7 . D. cos2a = - . 3 3 9 9
Câu 2: Tìm tất các các giá trị thực của tham số m để phương trình 2sin x = m có nghiệm.
A. m £ 2. B. 1 - £ m £ 1. C. 2 - £ m £ 2. D. m ³ 1. -
Câu 3: Cho cấp số cộng (u u = 3 d = 5. - n ) có và
Tính số hạng thứ 15 của cấp số cộng trên. 1 A. u = 47. -
B. u = 45. C. u = 67. - D. u = 37. 15 15 15 15
Câu 4: Trong các dãy số hữu hạn được cho dưới đây, dãy số nào là dãy số giảm?
A. 1,5, 4,3, 2. B. 5, 4,3, 2,1. C. 2, 4,6,8,10. D. 1,1,1,1,1.
Câu 5: Cho cấp số nhân (u q ¹ 1. S 6 n ) có công bội Gọi
là tổng của số hạng đầu của cấp số nhân. Khẳng 6
định nào sau đây đúng? u 1- q u ( 6 1- q u ( 6 1- q u ( 5 1- q 1 ) 1 ) 1 ) 1 ( )6 A. S = . B. S = . C. S = . D. S = . 6 1- q 6 1- q 6 q -1 6 1- q
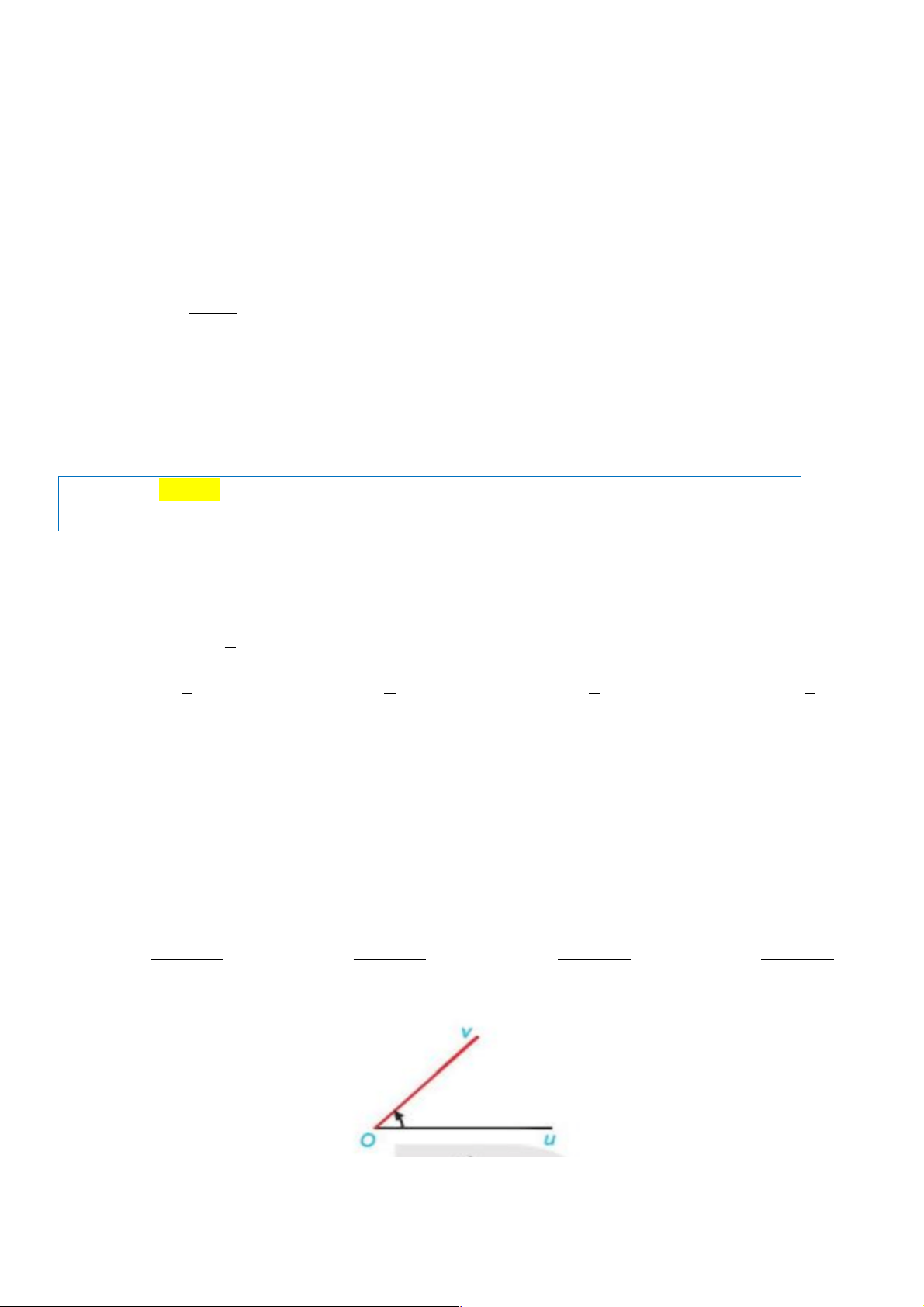
Câu 6: Cho góc hình học uOv có số đo bằng 0
45 (hình dưới). Số đo của các góc lượng giác (Ou,Ov) là 450
A. sđ(Ou Ov) 0 0 ,
= - 45 + k.360 ,k ŒZ .
B. sđ(Ou Ov) 0 0 ,
= 45 + k.180 ,k ŒZ .
C. sđ(Ou Ov) 0 0 ,
= 45 + k.360 ,k ŒZ .
D. sđ(Ou Ov) 0 0 ,
= 45 - k.180 , k ŒZ . Trang 4
Câu 7: Đường cong trong hình dưới đây là đồ thị của hàm số nào trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D
A. y = tan x.
B. y = cot x.
C.. y = sin x
D. y = cos x .
Câu 8: Một đường tròn có bán kính bằng 20cm . Tính độ dài của cung trên đường tròn có số đo 0 25 (làm
tròn lấy 2 chữ số thập phân).
A. 6,12cm .
B. 8,37cm.
C. 6,01cm . D. 8,73cm .
Câu 9: Cho cấp số cộng (u u = 3 d = 5. n ) với và công sai
Số hạng thứ 2 của cấp số cộng đã cho bằng 1 A. 6 . B. 2 . C. 4 . D. 8 . u ì =1
Câu 10: Cho dãy số (u 1 n ³ 1 n ) , biết í với
. Ba số hạng đầu tiên của dãy số đó là lần lượt là u = 3 - u î n 1+ n
những số nào dưới đây? A. 1;- 3; . 9 B. 1;4;7. C. 1;- 3;- 9. D. 1 - ;3;7.
Câu 11: Cho cấp số nhân (u q = -2 u = 3 n ) với và
Tính tổng 5 số hạng đầu của cấp số nhân đó 1
A. S = 93. B. S = 96 - . C. S = 33 - . D. S = 33. 5 5 5 5
Câu 12: Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a = cos a + sin . a B. 2 cos 2a = 1– 2sin . a C. 2
cos 2a = 2cos a –1. D. 2 2
cos 2a = cos a – sin . a
Câu 13: Tập xác định hàm số y = cot x là ìp ü
A. D = ! \{kp,k Î } " .
B. D = ! \ í + k2p ,k Î"ý. î 2 þ ìp ü
C. D = ! \ í + kp ,k Î"ý.
D. D = ! \{k2p,k Î } " . î 2 þ
Câu 14: Trong các công thức dưới đây, công thức nào đúng?
A. cos(a -b) = sin acosb -cosasin . b
B. cos(a -b) = o
c sa cosb -sin asin b .
C. cos(a -b) = sin acosb + cosasin . b
D. cos(a -b) = o
c sacosb + sin asin . b
Câu 15: Phương trình cosx = cosa có tập nghiệm là
A. S = {a + k2p | k Î } ! .
B. S = {a + kp | k Î } ! .
C. S = {a + k2p; a - + k2p | k Î } ! .
D. S = {a + kp;p -a + kp | k Î } ! . II. TỰ LUẬN( 5 điểm).
Câu 1: (1 điểm) Cho dãy số (u u = 4n - 5 n ) với
. Viết 4 số hạng đầu của dãy số trên. n
Câu 2: (2 điểm) Giải phương trình: 3 æ p ö c) cos x =
b) cos2x - sin x + = 0 ç ÷ 2 è 3 ø 3 p 2cota - tana
Câu 3: (1 điểm) Cho cosa = - và < a < p . Tính giá trị của biểu thức P = 5 2 tana + 3cota
Câu 4: (1 điểm) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân
theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số Trang 5
51 đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc
thứ n +1 tăng so với giá của mỗi số ở bậc thứ n là 4%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1324 số trong tháng 2, hỏi tháng 2 trường THPT X phải
đóng bao nhiêu tiền điện?
------ HẾT ------ ĐÁP ÁN I. PHẦN TRẮC NGHIỆM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 C C C B B C D D D A D A A D C II. PHẦN TỰ LUẬN
Câu 1: (1đ) Cho dãy số (u u = 4n - 5 n ) với
. Viết 4 số hạng đầu của dãy số trên. n
4 số hạng của dãy số là: -1, 3, 7, 11.
Câu 2: (2đ) Giải phương trình: 3 a) cos x = 2 Giải: é p x = + k2p 3 p ê cos x = Û cos x = cos 6 Û ê (k Î!) 2 6 p ê x = - + k2p êë 6 æ p ö
b) cos2x - sin x + = 0 ç ÷ è 3 ø Giải: æ p ö æ p ö p æ p ö cos2x - sin x +
= 0 Û cos2x = sin x +
Û sin ( - 2x) = sin x + ç ÷ ç ÷ ç ÷ è 3 ø è 3 ø 2 è 3 ø ép p é p p - k2 2x = x + + k2p ê x = + 2 3 ê Û ê 18 3 Û ê (k Î!) p p ê p -
- 2x = p - x - + k2p ê ê x = + k2p ê ë 2 3 ë 6 3 p 2cota - tana
Câu 3: (1đ) Cho cosa = - và < a < p . Tính giá trị của biểu thức P = 5 2 tana + 3cota Giải: p Do
< a < p nên sina > 0 2 2 2 2 æ 3 ö 4 sin a + cos a =1 2 Þ sina = 1- o c s a = 1- - = ç ÷ è 5 ø 5 4 Suy ra, tana = - 3 cota = - 3 4 Trang 6 2cota - tana 2 P = = tana + 3cota 43
Câu 4: (1đ) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho người dân theo
hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 50 số: bậc 1 từ số thứ 1 đến số thứ 50, bậc 2 từ số 51
đến số 100, bậc 3 từ số thứ 101 đến số thứ 150,…Bậc 1 có giá là 1700 đồng/1 số, giá của mỗi số ở bậc thứ
n +1 tăng so với giá của mỗi số ở bậc thứ n là 4%.
a) Tính số tiền phải trả cho các số điện từ 51 đến 100.
b) Biết rằng trường THPT X sử dụng hết 1324 số trong tháng 2, hỏi tháng 2 trường THPT X
phải đóng bao nhiêu tiền điện? Giải:
a) Gọi U1 là số tiền phải trả cho các số điện từ 1 đến 50.
U2 là số tiền phải trả cho các số điện từ 51 đến 100.
U1 , U2, , … Un lập thành cấp số nhân với q=1,04. Ta có :
U = 50.1700 = 85000(d); q =1,04 1
U = U .q = 88400(d) 2 1
b) U26 là số tiền phải trả cho các số điện từ 1251 đến 1300.
Số tiền phải trả cho 1300 số đầu tiên là 26 1- q S = U . » 3766498(d) 1 1 1- q
Số tiền phải trả cho số từ 1301 đến 1324 là 26
S = 24.1700.1,04 » 113117(d ) 2
Vậy số tiền tháng 2 trường THPT X phải đóng là
S + S » 3879615(d) 1 1 Trang 7