SỞ GD&ĐT QUẢNG TRỊ
ĐỀ KIỂM TR GIỮA HỌC KỲ I
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
NĂM HỌC:2020 – 2021 ĐỀ CHÍNH THỨC
Môn: Toán 11 - Mã đề: 01 (Đề có 01 trang)
(Thời gian làm bài: 90 phút) ĐỀ 01
Câu 1: (2,0 điểm). Tìm tập xác định của các hàm số: 1 1 a) y  . b) y  . cos x 1 2sin x 1
Câu 2: (4,0 điểm). Giải các phương trình lượng giác sau: a) 2sin x  3  0 b)  0
tan x  30   3  0 c) 2
cos x  sin x 1  0
d) sin x  3 cos x  1.
Câu 3: (2,0 điểm). Trong mặt phẳng Oxy cho vectơ u  2; 
1 ; A3; 4 và đường thẳng
d : x  y 1  0 .
a) Tìm tọa độ điểm A' là ảnh của điểm A qua phép T . u
b) Tìm phương trình đường thẳng d ' là ảnh của đường thẳng d qua T . u
Câu 4: (1,0 điểm).
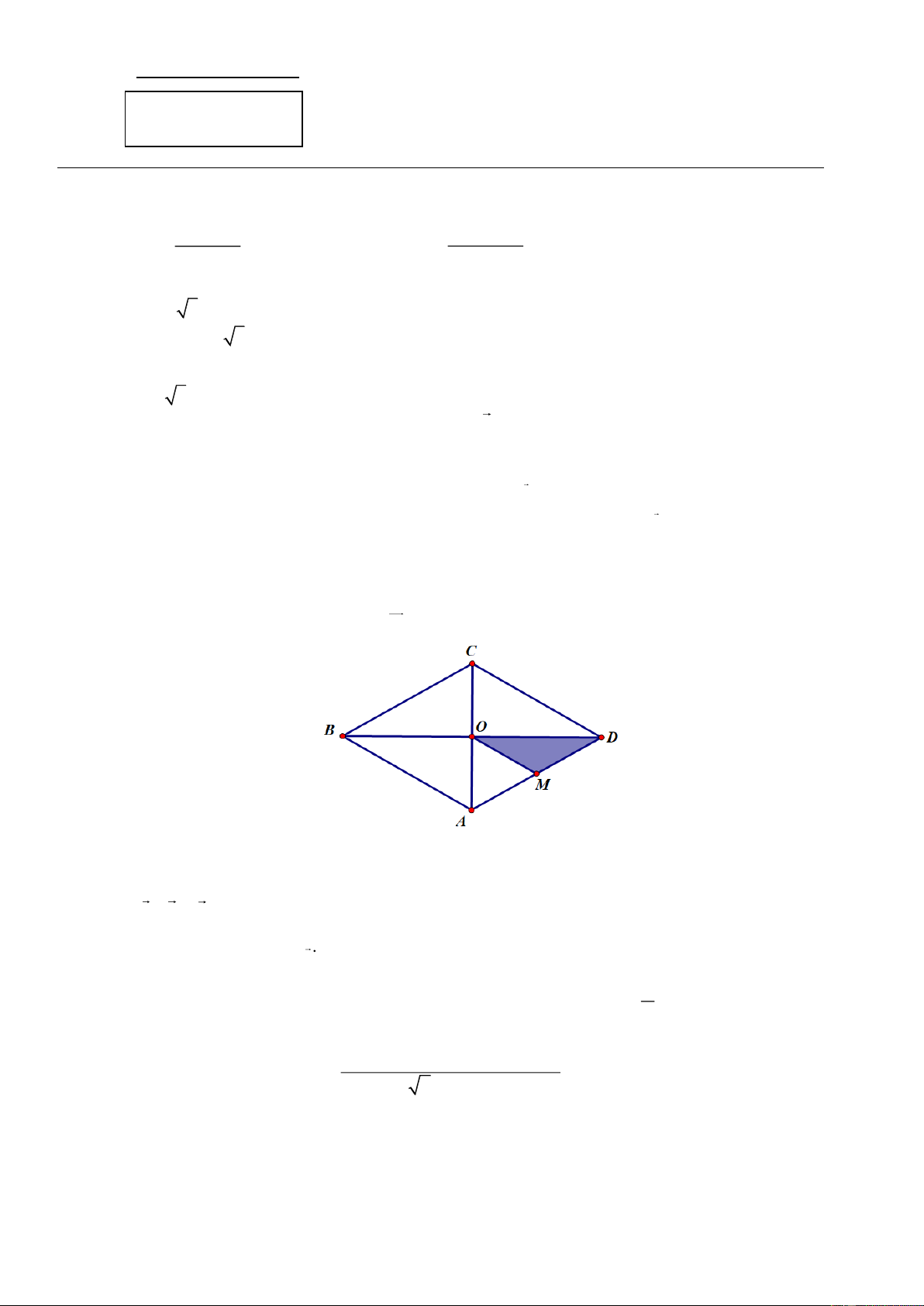
a) Cho hình thoi ABCD có tâm là O . Gọi M là trung điểm AD (như hình vẽ bên dưới).
Tìm ảnh của tam giác OMD qua T . OB
b) Trong mặt phẳng Oxy cho A3;0; B 0;6 và có G là trọng tâm O
 AB (với O là gốc tọa độ). Phép tịnh
tiến theo u ( u  0 ) biến điểm A thành điểm G . Viết phương trình đường tròn C ' là ảnh của đường tròn
ngoại tiếp tam giác OAB qua T . u   
Câu 5: ( 1,0 điểm). Tìm tất cả các nghiệm của phương trình sau trên khoảng ;3    2   6 6
2 sin x  cos x  sin x cos x  0. 2  2sin x
-------------------------------- Hết ------------------------------ SỞ GD&ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
NĂM HỌC:2020 – 2021 ĐỀ CHÍNH THỨC
Môn: Toán 11 - Mã đề: 02 (Đề có 01 trang)
(Thời gian làm bài: 90 phút) ĐỀ 02
Câu 1: (2,0 điểm). Tìm tập xác định của các hàm số: 1 1 a) y  . b) y  . sin x 1 2cos x 1
Câu 2: (4,0 điểm). Giải các phương trình lượng giác sau: a) 2cos x 1  0 b)  0
cot x  60   3  0 c) 2
sin x  cos x 1  0
d) 3 sin x  cos x  1 .
Câu 3: (2,0 điểm). Trong mặt phẳng Oxy cho vectơ u   2  ; 
1 ; A4;3 và đường thẳng
d : x  y 1  0 .
a) Tìm tọa độ điểm A' là ảnh của điểm A qua phép T . u
b) Tìm phương trình đường thẳng d ' là ảnh của đường thẳng d qua T . u
Câu 4: (1,0 điểm).
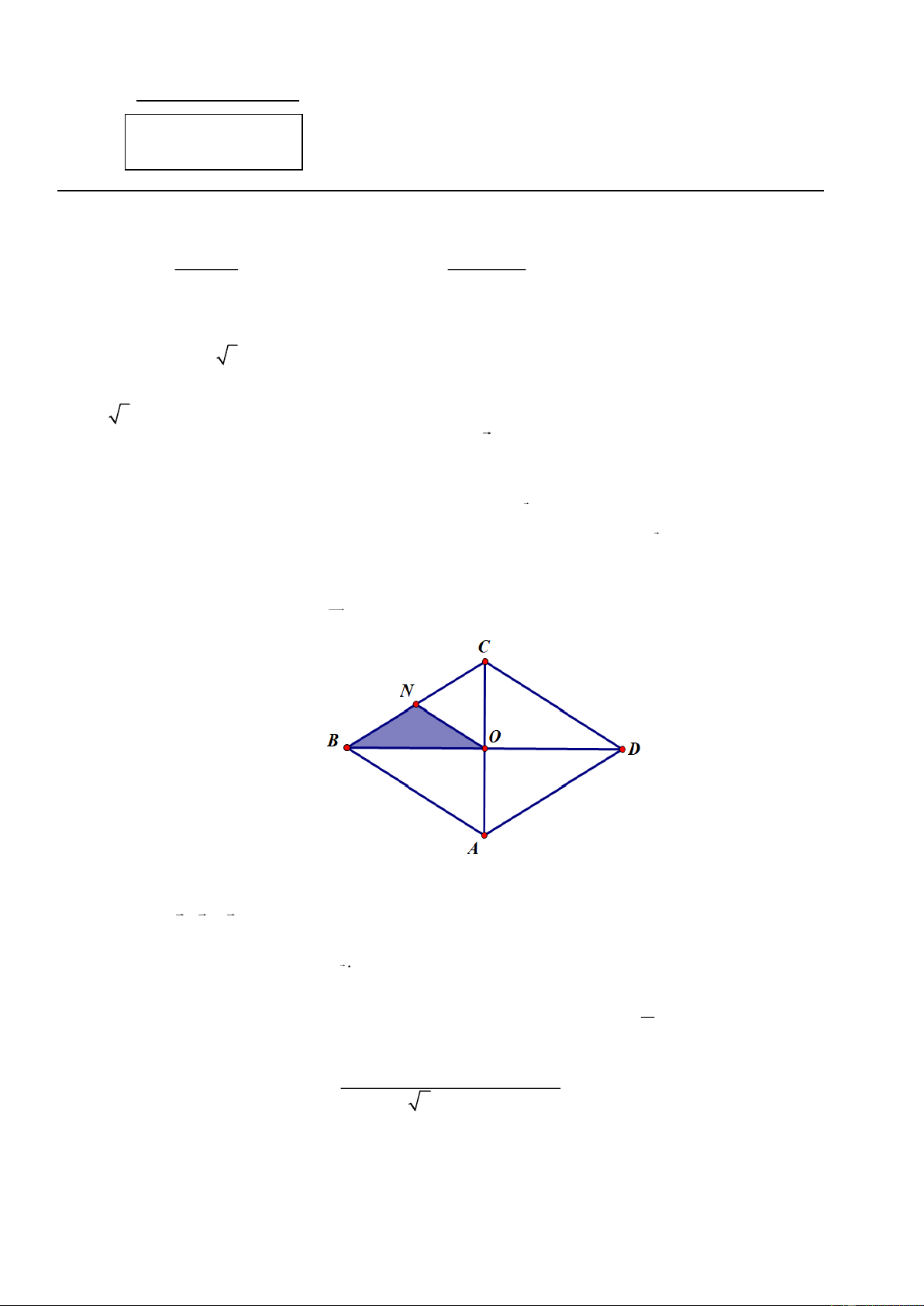
a) Cho hình thoi ABCD có tâm là O . Gọi N là trung điểm BC (như hình vẽ bên dưới).
Tìm ảnh của tam giác ONB qua T . OD
b) Trong mặt phẳng Oxy cho A 3  ;0; B0; 6
  và có G là trọng tâm O
 AB (với O là gốc tọa độ). Phép
tịnh tiến theo u u  0 biến điểm A thành điểm G . Viết phương trình đường tròn C ' là ảnh của đường
tròn ngoại tiếp tam giác OAB qua T . u   
Câu 5: ( 1,0 điểm). Tìm tất cả các nghiệm của phương trình sau trên khoảng ;3    2   6 6
2 sin x  cos x  sin x cos x  0. 2  2sin x
-------------------------------- Hết ------------------------------
SỞ GD&ĐT QUẢNG TRỊ
HDC KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC 2020 - 2021 TRƯỜNG THPT TXQT MÔN TOÁN KHỐI 11 Mã đề: 01 Câu Lời giải Điểm C1 1 a) Hàm số: y 
xác định khi cos x 1  0  cos x  1  x  k2 k  . 2,0 cos x 1 0,5
điểm Vậy txđ D  \k2, k  . 0,5 1 b) Hàm số: y  xác định khi 2sin x 1   x   k2 1  6
2sin x 1  0  sin x    k  . 2 5  0,5 x   k2  6   Vậy txđ 5  D  \   k2 ,
 k2,k  .  0,5 6 6  C2.
Giải các phương trình lượng giác sau 4,0đ   0,5+0, x   k2 3   3 5
a) 2sin x  3  0  sin x   sin   k  . 2 3 2  x   k2  3 b)  0
tan x  30   3  0   1 0,5+0, Đk:  0 x   0 0 cos 30
 0  x  120  1
k 80 k   5     0 x       0   0 0 0 0 0 1 tan 30 3 tan 60  x  30  6  0  1
k 80  x  30  1
k 80 k  
sin x  2 (vn)  0,5+0, c) 2 2
cos x  sin x 1  0   sin x  sin x  2  0 
 x    k2 k   . sin x  1  2 5 1 3 1   1    1 
sin x  3 cos x  1  sin x  cos x 
 sin .xcos  cos .xsin   sin x    sin   2 2 2 3 3 2  3  2 6 0,5      d) x    k2 x   k2   3 6 2     k  .  5 7   x    k2 x   k2  3 6  6 0,5 C3.
Trong mặt phẳng Oxy cho vectơ u  2; 
1 ; A3; 4 và đường thẳng d : x  y 1  0 2,0đ  x '  5
a) Ta có: T : A3;4  A' x '; y '    A'5;3. 1,0 u y '  3
b) Ta có T : d  d ' nên d / /d ' hoặc d  d ' suy ra pt d ' có dạng d ' : x  y  c  0 u Lấy M 0  ;1  d . 0,5  x '  2
Ta có T : M 0 
;1  M ' x '; y '  
 M '2;0d '  c  2  . u y '  0 0,5
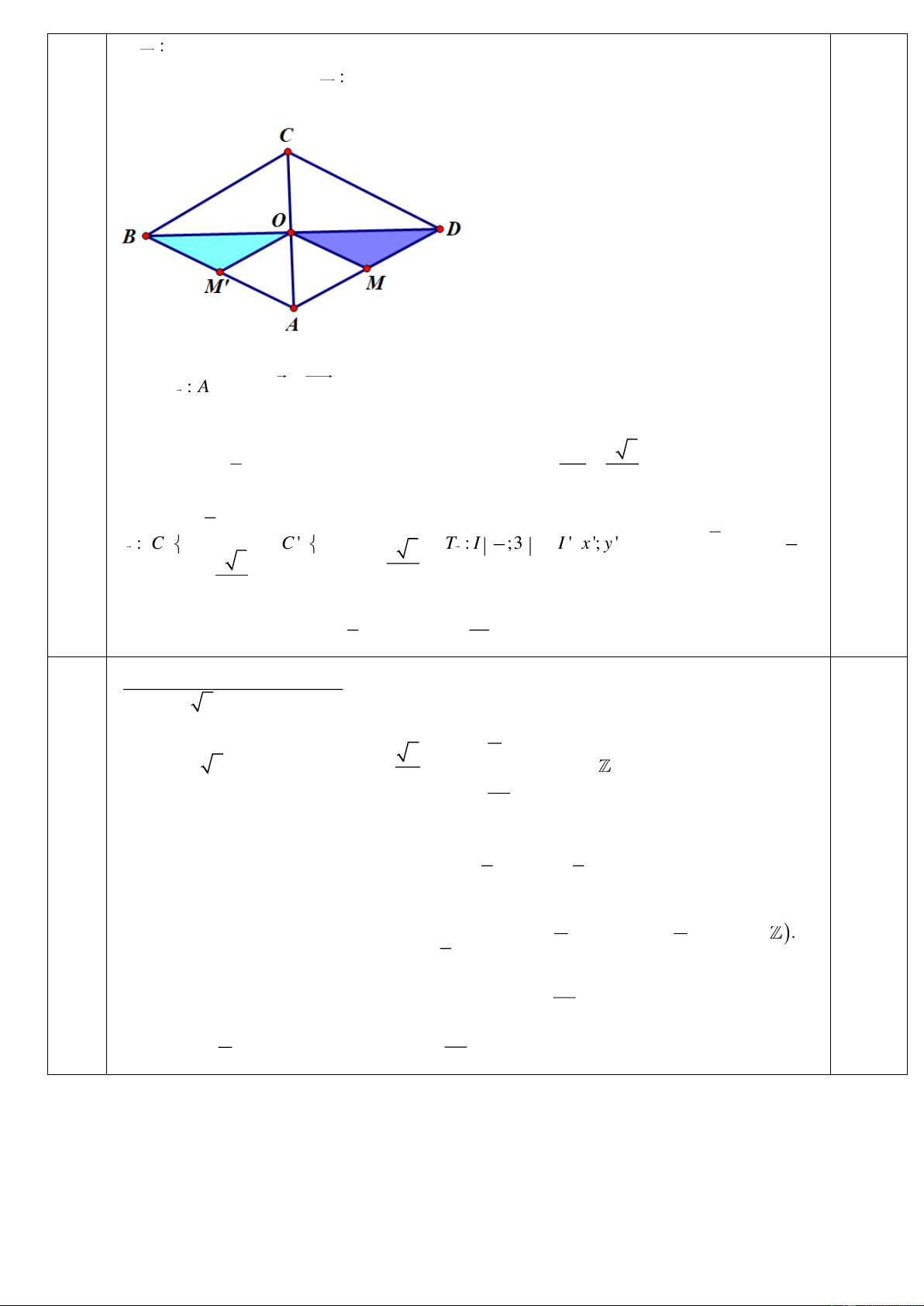
Vậy pt d’ là d ': x  y  2  0. C4. T : O  B OB 1,0đ a) D  O . Suy ra T : O  MD  B
 M 'O (với M ' là trung điểm của AB ) OB 0,25 M  M ' 0,25
b)Ta có tọa độ trọng tâm G của tam giác O
 AB là G1;2 .
Ta có T : A  G  u  AG   2  ;2. u
Gọi C  là đường tròn ngoại tiếp tam giác O
 AB . Do tam giác O
 AB vuông tại O nên 0,25   3  AB 3 5 C  có tâm I ;3 
 là trung điểm AB và bán kính R    2  2 2   3  I ;3 I '    x'; y'  1            T C  2   C  3   T I  I   x y  x ' 1 : ' : ;3 ' '; '   2  I '  ;5 .   u 3 5 u      2    2 3 5 R ' R  0,25   y '  5 R 2  2 2 Vậy phương trình    C  1 x      y  2 45 ' : 5  .  2  4 C5.  6 6
2 sin x  cos x  sin x cos x 1,0đ  0 (1) 2  2sin x   x   k2   Điều kiện: 2 4
2  2sin x  0  sin x    , k  0,25 2 3 x   k2  4 Khi đó,   (1)  2  3 1 6 6
sin x  cos x 2
 sin x cos x  0  2 1 sin 2x  sin 2x  0    4  2 0,25 sin 2x 1   2   3
 sin 2x  sin 2x  4  0  4
 2x   k2  x   k k  .
sin 2x   (vn) 2 4  3 
Đối chiếu điều kiện ta có nghiệm của phương trình là 5 x   k2 0,25 4     Suy ra trên ;3   có một nghiệm là 5 x  .  2  4 0,25
SỞ GD&ĐT QUẢNG TRỊ
HDC KIỂM TRA GIỮA KỲ I NĂM HỌC 2020 - 2021 TRƯỜNG THPT TXQT MÔN TOÁN KHỐI 11 Mã đề: 02 Câu Lời giải Điểm C1. 1  a) Hàm số: y 
xác định khi sin x 1  0  sin x  1  x 
 k2 , k   . sin x 1 2 0,5 2,0đ  
Vậy txđ D  \   k2, k  .  0,5 2  a)1đ 1 b) Hàm số: y  xác định khi b)1 2cos x 1 đ   0,5 x   k2 1  3
2 cos x 1  0  cos x    k  . 2   x    k2  3   Vậy txđ  D  \   k2 , 
 k2 ,k  .  0,5 3 3 
C2. Giải các phương trình lượng giác sau 4,0đ  2 0,5+0, x   k2 1 2    3 5
a) 2 cos x 1  0  cos x    cos     k  . 2  3  2  x    k2  3 b)  0
cot x  60   3  0   1 0,5+0, Đk:  0 x   0 0 sin 60
 0  x  60  1
k 80 k   5     0 x      0 0 0 0 0 0 1 cot 60 3 cot 30
 x  60  30  1
k 80  x  90  1
k 80 k  
cos x  2 (vn) c) 2 2
sin x  cos x 1  0   cos x  cos x  2  0 
 x    k2 k   . cos x  1  0,5+0, 3 1 1   1    1 
3 sin x  cos x  1 
sin x  cos x 
 sin .xcos  cos .xsin   sin x    sin   5 2 2 2 6 6 2  6  2 6    d) x    k2 x  k2  6 6     0,5 2 k  .  5   x   k2 x    k2  3  6 6 0,5 C3.
Trong mặt phẳng Oxy cho vectơ u   2  ; 
1 ; A4;3 và đường thẳng d : x  y 1  0 2,0đ  x '  2
a) Ta có: T : A4;3  A' x '; y '    A'2;4. 1,0 u a)1đ   y ' 4 b)1
b) Ta có T : d  d ' nên d / /d ' hoặc d  d ' suy ra pt d ' có dạng d ' : x  y  c  0 u đ Lấy M 0;  1  d . 0,5  x '  2 
Ta có T : M 0;  
1  M ' x '; y '    M '0; 2
 d '  c  2. u y '  0 0,5
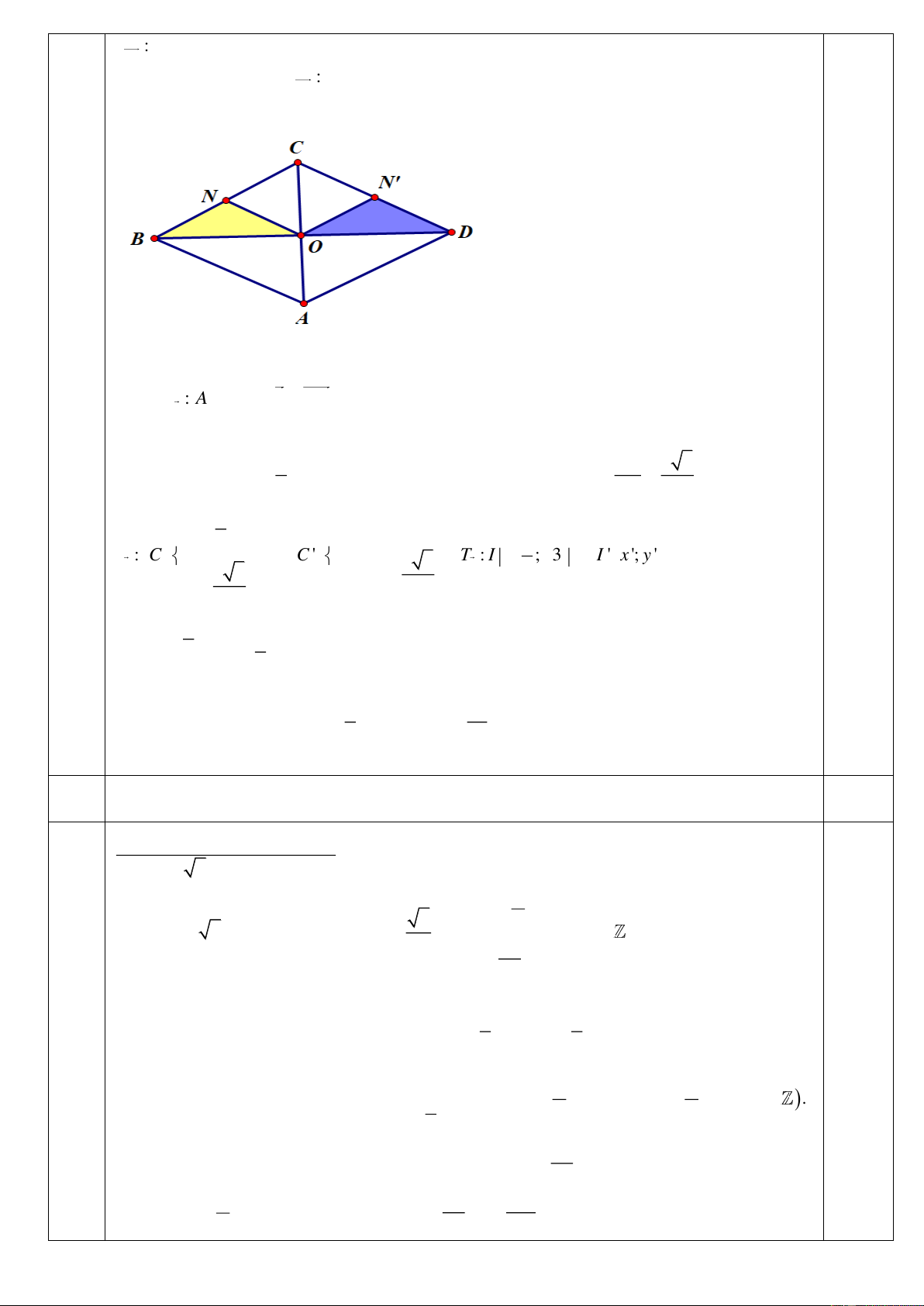
Vậy pt d’ là d ': x  y  2  0. C4. T : O  D OD 1,0đ
N  N '. Suy ra T : O  NB  D
 N 'O (với N ' là trung điểm của CD ) OD B  O 0.25đ a)0, 5đ b)0, 5đ 0.25đ
b)Ta có tọa độ trọng tâm G của tam giác O
 AB là G  1  ; 2   .
Ta có T : A  G  u  AG  2; 2  . u Gọi 
C  là đường tròn ngoại tiếp tam giác O
 AB . Do tam giác O
 AB vuông tại O  3  AB 3 5
nên C  có tâm I  ; 3  
 là trung điểm AB và bán kính R    2  2 2   3  I  ; 3  I '    x'; y'       0,25 T C  2   C  3 : ' 
 T : I  ; 3   I '   x'; y' u 3 5 u      2 3 5 R ' R  R   2   2  1  x '   1    2  I ' ; 5  .     2  y '  5  2 0,25 Vậy phương trình    C  1 x      y  2 45 ' : 5  .  2  4 C5. 1,0đ  6 6
2 sin x  cos x  sin x cos x  0 (1) 2  2sin x   x    k2   Điều kiện: 2 4
2  2sin x  0  sin x     , k  0,25 2 5 x   k2  4 Khi đó,   (1)  2  3 1 6 6
sin x  cos x 2
 sin x cos x  0  2 1 sin 2x  sin 2x  0    4  2 sin 2x  1  0,25   2   3
 sin 2x  sin 2x  4  0  4
 2x    k2  x    k k  .
sin 2x  (vn) 2 4  3  0,25
Đối chiếu điều kiện ta có nghiệm của phương trình là 3 x   k2 4      Suy ra trên ;3   có một nghiệm là 3 11 x  , x  . 0,25  2  4 4