Đề kiểm tra giữa học kỳ 1 Toán 11 năm 2023 – 2024 sở GD&ĐT Bắc Ninh
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kỳ 1 môn Toán 11 năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Bắc Ninh; đề thi hình thức 30% trắc nghiệm (12 câu) + 70% tự luận (04 câu), thời gian làm bài 90 phút (không kể thời gian giao đề); đề thi có đáp án và hướng dẫn chấm điểm.
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 BẮC NINH
NĂM HỌC 2023 – 2024
Môn: TOÁN – Lớp 11
(Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1. Đổi số đo của góc 120 sang đơn vị radian ta được A. 2 .
B. . y 3 6 B 4 M C. . D. . 3 4 5
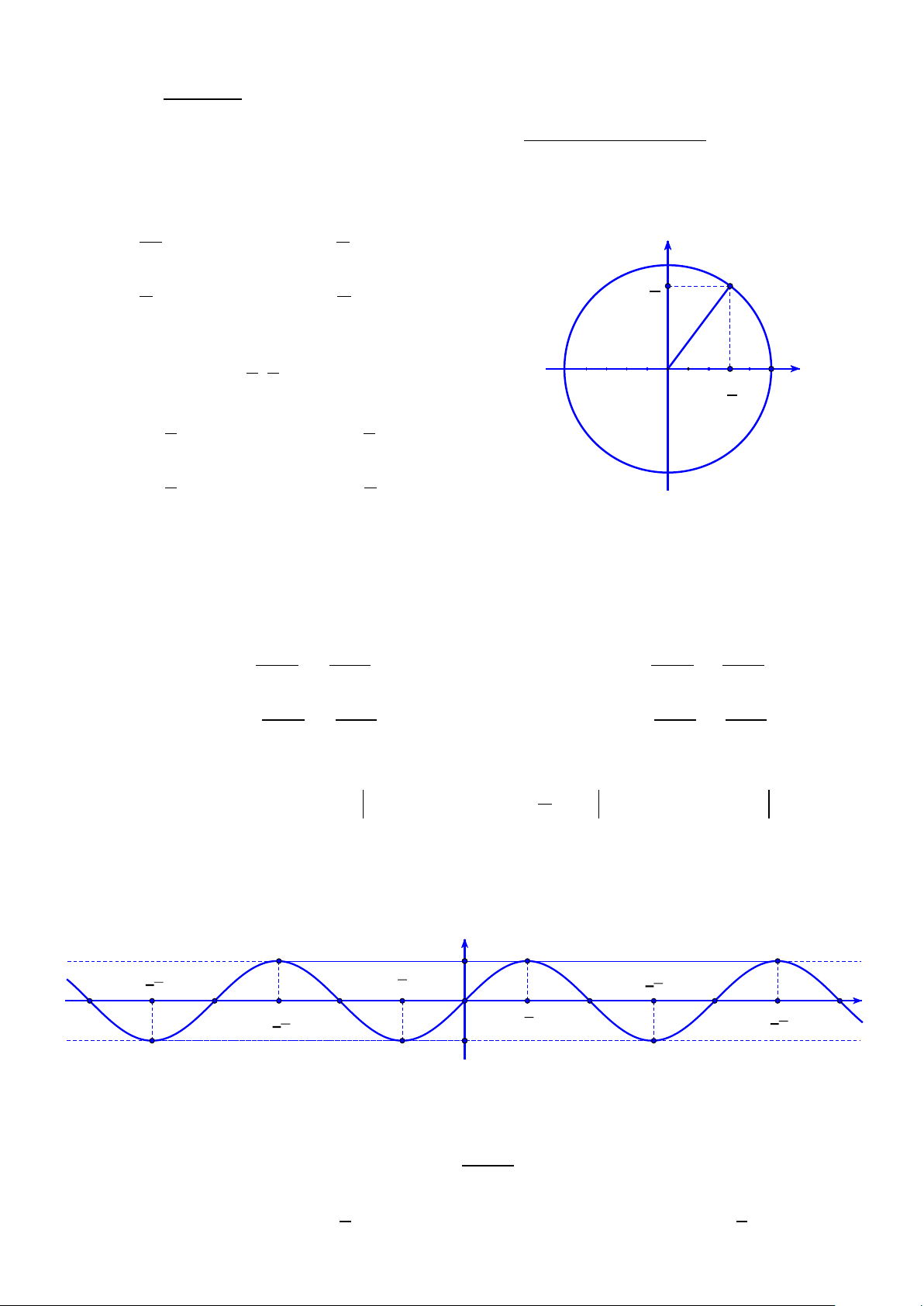
Câu 2. Gọi M là điểm trên đường tròn lượng giác sao cho ,
OA OM . Biết 3 4 M ;
, khẳng định nào sau đây đúng? 5 5 A' O 3 A x 5 A. 3 sin . B. 3 cos . 5 5 B' C. 3 sin . D. 4 cos . 4 5
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A. cosa b cosa cosb sina sinb .
B. cosa b cosa cosb sina sinb .
C. cosa b sina cosb cosa sinb .
D. cosa b sina cosb cosa sinb .
Câu 4. Trong các khẳng định sau, khẳng định nào sai? A. a b a b a b a b
sina sinb 2 sin cos .
B. sina sinb 2 cos sin . 2 2 2 2 C. a b a b a b a b
cosa cosb 2 cos cos .
D. cosa cosb 2 sin sin . 2 2 2 2
Câu 5. Tập xác định của hàm số y cotx là A. . B.
\ k k . C. \ k k
. D. \ k2 k . 2
Câu 6. Hàm số nào sau đây là hàm số chẵn trên ?
A. y cosx .
B. y sinx .
C. y tanx .
D. y x cosx .
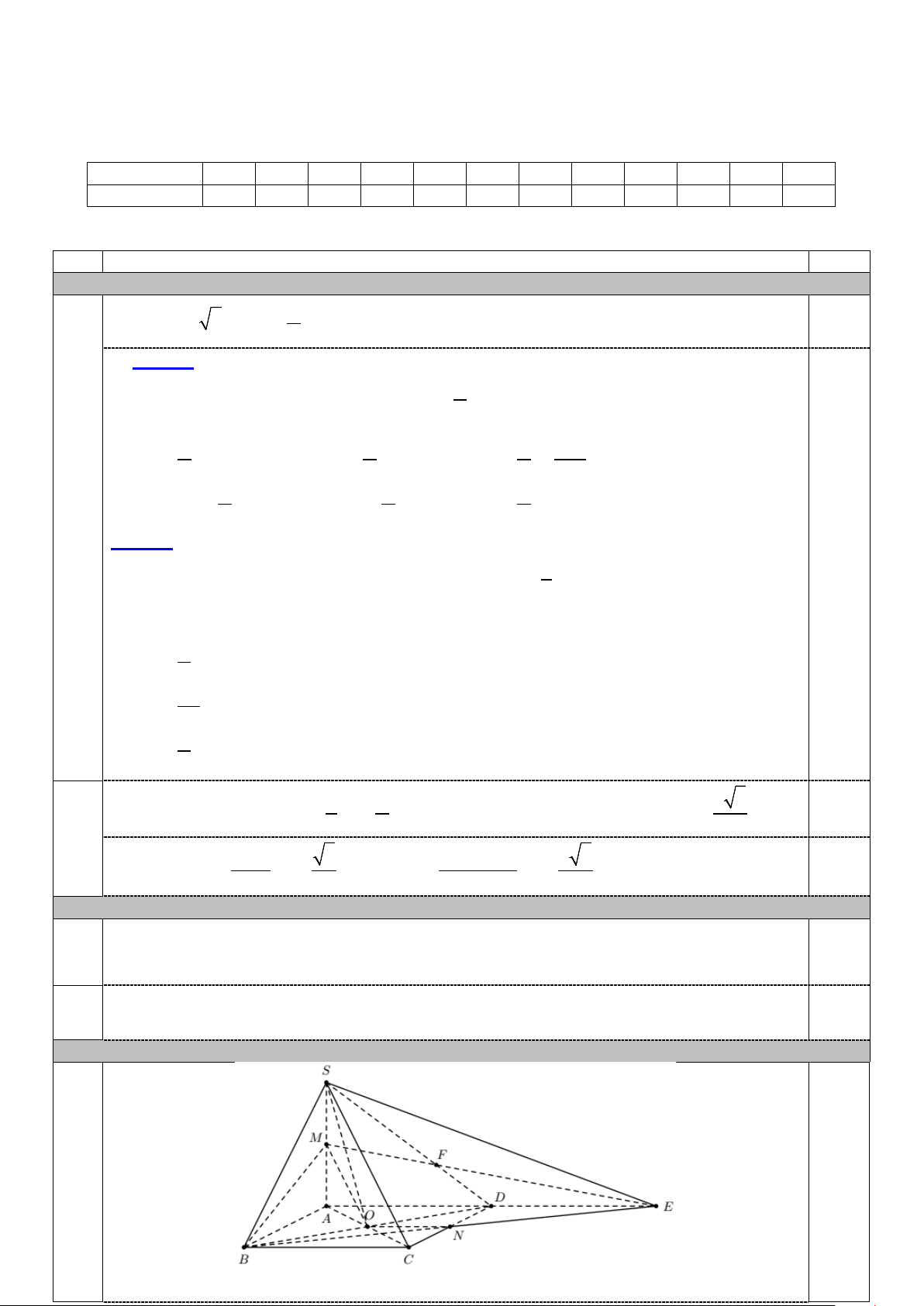
Câu 7. Cho hàm số y sinx có đồ thị như hình vẽ dưới đây. y -5π -π 1 3π 2 2 2 x -3π -2π -3π -π O π π 2π 5π 3π 2 2 2 -1
Dựa vào đồ thị, hãy cho biết có bao nhiêu giá trị của x trên đoạn 3 ;3
để sinx 0 ? A. 5. B. 7 . C. 11. D. 13 .
Câu 8. Cho dãy số 2n 1
u có số hạng tổng quát là * u
, n . Số hạng đầu của dãy số là n n n 1 A. 3 1 u 1 .
B. u .
C. u 3 . D. u . 1 1 2 1 1 2 Trang 1
Câu 9. Trong các mệnh đề sau, mệnh đề nào sai?
A. Có hai đường thẳng phân biệt cùng đi qua hai điểm phân biệt cho trước.
B. Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
C. Có một và chỉ một mặt phẳng đi qua ba điểm phân biệt không thẳng hàng.
D. Nếu một đường thẳng đi qua hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều
thuộc mặt phẳng đó.
Câu 10. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng phân biệt không song song thì chéo nhau.
B. Hai đường thẳng không có điểm chung thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
Câu 11. Nếu một hình chóp có đáy là ngũ giác thì số cạnh của hình chóp đó là A. 5. B. 6. C. 9. D. 10 .
Câu 12. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm AD và AC . Gọi G là trọng tâm tam giác
BCD . Giao tuyến của hai mặt phẳng GMN và BCD là
A. Đường thẳng đi qua M và song song với AB . B. Đường thẳng đi qua N và song song với BD .
C. Đường thẳng đi qua G và song song với CD . D. Đường thẳng đi qua G và song song với BC .
II. PHẦN TỰ LUẬN (7,0 điểm) Câu 13. (2,5 điểm)
1) Giải các phương trình sau:
a) tanx 3 ; b) sin2x cosx 0 . 2) Cho góc a thỏa mãn 1
sina và a . Tính cosa và tan 2a . 3 2
Câu 14. (1,0 điểm) Anh Hùng vừa được tuyển dụng vào một công ty, được cam kết lương năm đầu sẽ là 150
triệu đồng và lương mỗi năm tiếp theo sẽ được tăng thêm 18 triệu đồng. Gọi T (triệu đồng) là lương năm thứ n
n mà anh Hùng làm việc cho công ty đó. Khi đó ta có *
T 150,T T
18, n ,n 2 . 1 n n 1
1) Tính lương của anh Hùng vào năm thứ 3 làm việc cho công ty.
2) Chứng minh T là dãy số tăng. n
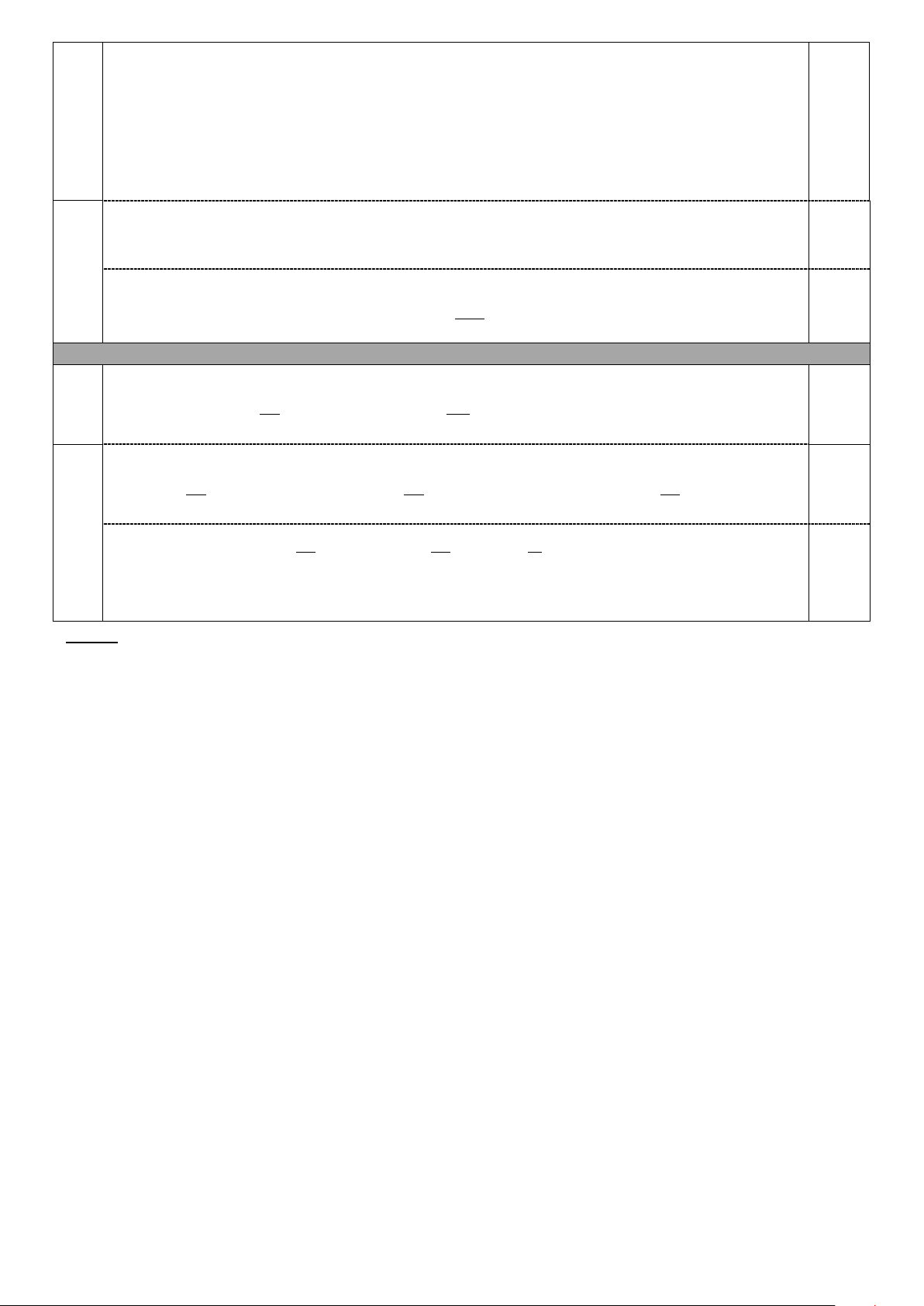
Câu 15. (2,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O . Gọi M,N lần lượt là
trung điểm của SA và CD .
1) Tìm giao tuyến của hai mặt phẳng SAC và SBD.
2) Chứng minh OM song song với mặt phẳng SCD.
3) Gọi F là giao điểm của SD và mặt phẳng BMN . Tính tỉ số SF . FD
Câu 16. (1,0 điểm) Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được
mô phỏng bởi công thức
h t 31 3 sin t 9, với h tính bằng độ C và t là thời gian trong ngày tính 12
bằng giờ ( 0 t 24 ).
1) Tính nhiệt độ ngoài trời ở thành phố đó vào lúc 7 giờ tối.
2) Vào lúc mấy giờ trong ngày thì nhiệt độ ngoài trời ở thành phố đó là cao nhất?
-------- Hết -------- Trang 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
KIỂM TRA GIỮA HỌC KỲ 1 NĂM HỌC 2023 – 2024 ¯¯¯¯¯¯¯¯¯¯
Môn: Toán – Lớp 11
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
I. PHẦN TRẮC NGHIỆM (3,0 điểm): Mỗi câu trả lời đúng 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A B A D B A B B A C D C
II. PHẦN TỰ LUẬN (7,0 điểm) Câu
Lời giải sơ lược Điểm 13. (2,5 điểm) a)
tan x 3 x k , k . 0,5 3 b) Cách 1:
sin 2x cos x 0 sin 2x cos x cos 2x cosx . 2 0,5 k2 x
2x k2
3x k2 x 2 2 6 3 ,k . 0,5 x 2x k2 x k2 x k2 2 2 2 1) Cách 2: 1 x x x sin x sin 2 cos 0 2 sin 1 cos x 0 2 cosx 0 x
k2 6 5 x
k2,k . 6 x k 2 Ta có 2 2 8
cos a 1 sin a . Vì a nên cosa 0 . Do đó 2 2 cosa . 0,5 2) 9 2 3 Suy ra sina 2 2 tana 4 2 tana tan 2a . 0,5 2 cosa 4 1 tan a 7 14. (1,0 điểm)
Lương của anh Hùng ở năm thứ 2 là T T 18 150 18 168 (triệu đồng). 1) 2 1 0,5
Lương của anh Hùng ở năm thứ 3 là T T 18 168 18 186 (triệu đồng). 3 2 2) Vì * T
T 18 0, n nên T là dãy số tăng. 0,5 n n 1 n 15. (2,5 điểm) 1) 1,0
Gọi O AC BD . Ta được SAC SBD SO .
Xét tam giác SAC có O , M lần lượt là trung điểm của AC và SA nên OM là đường
trung bình của tam giác SAC , suy ra OM SC . 0,5 2) OM SC Ta có S
C SCD OM SCD. 0,5 OM SCD
Trong mặt phẳng ABCD có BN AD E . 3) 0,25
Trong mặt phẳng SAD có EM SD F F SD BMN .
Tam giác SAE có D là trung điểm của AE ; M là trung điểm của SA. Suy ra SF
F là trọng tâm tam giác SAE , do đó 2 . 0,25 FD 16. (1,0 điểm)
Nhiệt độ ngoài trời lúc 7 giờ tối là 1) h 5 19 31 3 sin 19 9 31 3 sin 32.5 . 0,5 12 6 Ta luôn có 1 sin
t 9 1 3 3sin t 9 3 28 31 3sin t 9 34 . 0,25 12 12 12 2) Do đó
h t 34 sin t 9 1
t 9 k2 t 15 24k,k . 12 12 2 0,25
Vì 0 t 24 nên t 15 .
Vậy vào thời điểm 15 giờ thì nhiệt độ ở thành phố đó lớn nhất.
Lưu ý: Các cách giải khác đáp án, nếu đúng vẫn cho điểm theo các bước tương ứng.
Document Outline
- Toan 11.KTGK1.23.24.De
- Toan-11.KTGK1.23.24.DA