Đề kiểm tra giữa học kỳ 2 Toán 8 năm 2022 – 2023 sở GD&ĐT Bắc Ninh
Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề kiểm tra đánh giá chất lượng giữa học kỳ 2 môn Toán 8 năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Bắc Ninh; đề thi được biên soạn theo hình thức 30% trắc nghiệm kết hợp 70% tự luận (theo điểm số), trong đó phần trắc nghiệm gồm 06 câu, phần tự luận gồm 04 câu, thời gian học sinh làm bài thi là 90 phút (không kể thời gian phát đề); đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm; kỳ thi được diễn ra vào thứ Năm ngày 16 tháng 03 năm 2023.
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KÌ II BẮC NINH NĂM HỌC 2022-2023 Môn: Toán - Lớp 8 (Đề có 01 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Câu 1. Phương trình nào sau đây là phương trình bậc nhất một ẩn? A. 2 x − 1 = 0 .
B. 2x − 6 = 0 .
C. 0x + 8 = 0 . D. (x − )( 5 x − ) 3 = 0.
Câu 2. Nếux = 2
− là nghiệm của phương trình 2x + k = x − 1 thì A. k = 2 − . B. k = 1 − .
C. k = 1. D. k = 2.
Câu 3. Tổng tất cả các nghiệm của phương trình (3x − 7)(x − 1) = 0 là A. 10 − . B. 10 . C. 8 . D. 8 − . 3 3
Câu 4. Cho a thỏa mãn (a + )2 2
1 = a − 2a + 5 . Hỏi a là nghiệm phương trình nào? A. 2 − x + 4 = 0 . B. 2
x + 4x = 4 .
C. 5x − 5 = 0. D. 4x + 4 = 0.
Câu 5. Cho hình chữ nhật ABCD có AB = 8 cm, AD = 10 cm . Hình vuông cạnh AC có diện tích là A. 2 36 cm . B. 2 164 cm . C. 2 324 cm . D. 2 80 cm .
Câu 6. Đường phân giác AD của tam giác ABC chia cạnh BC thành hai phần CD = 2,5;BD = 3 , khi đó
tỉ số AB bằng AC A. 6 . B. 5 . C. 5 . D. 6 . 11 11 6 5
II. TỰ LUẬN (7,0 điểm)
Câu 7. (2,5 điểm) Giải các phương trình sau
a) 2x – 3 = 5 .
b) (x + 2)(3x – 15) = 0 . c) 2x − 1 x + 4 + x x = . d) 3 2 4 14 . 3 2 x 1 x 2
(x 1)(x 2)
Câu 8. (1,0 điểm) Một người đi từ A đến B với vận tốc 36 km/h. Khi đến B , người đó nghỉ lại 30 phút rồi
quay trở về A với vận tốc lớn hơn vận tốc lúc đi là 9 km/h. Thời gian kể từ lúc đi từ A đến lúc trở về đến
A là 5 giờ. Tính độ dài quãng đường AB .
Câu 9. (3,0 điểm) Cho tam giác ABC vuông tạiA , đường caoAH .
1. Chứng minh rằng tam giác ABC đồng dạng với tam giác HBA.
2. Qua B kẻ đường thẳng d vuông góc vớiBC . Gọi M là trung điểm của AB . Đường thẳng qua M
vuông góc với AB cắt đường thẳng d tại K và cắt BC tại I . Chứng minh rằng: 2
a) Tam giácBKI đồng dạng với tam giác BC
ABC ; KI.AC = . 2
b) KC đi qua trung điểm của AH . 2 2 + − 7 x x ( 2x − 9 3 3 )
Câu 10. (0,5 điểm) Giải phương trình: + 6 − = 0 . 2 x − 2 x + 2 x − 4 -----Hết-----
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022-2023 ¯¯¯¯¯¯¯¯¯¯ Môn: Toán - Lớp 8
(Hướng dẫn chấm có 4 trang)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
PHẦN 1: TRẮC NGHIỆM (3,0 điểm) Mỗi câu đúng được 0,5 điểm Câu 1 2 3 4 5 6 Đáp án B C B C B D
PHẦN 2: TỰ LUẬN (7,0 điểm) Câu
Lời giải sơ lược Điểm
Giải các phương trình sau a) 2x – 3 = 5
b) (x + 2)(3x – 15) = 0 7 2,0 c) 2x − 1 x + 4 − + x x = d) 3 2 4 2 − = 3 2 x + 1 x − 2
(x + 1).(x − 2) 2x – 3 = 5 a) ⇔ 2x = 8 0,25 ⇔ x = 4 0,25
Tập nghiệm của phương trình là S = { } 4
(x + 2)(3x – 15) = 0 b) x + 2 = 0 x = 2 − 0,25 ⇔ ⇔ 3x − 15 = 0 x = 5 0,25
Tập nghiệm của phương trình là S = { 2 − ; } 5 − + 2x 1 x 4 c) + x = 3 2
⇔ 2 (2x − 1) + 6x = 3(x + 4) 0,25
⇔ 4x − 2 + 6x = 3x + 12 ⇔ 7x = 14 ⇔ x = 2 0,25
Tập nghiệm của phương trình là S = { } 2 − 3 2 4x 14 − = ÐKXÐ: x ≠ 1; − x ≠ 2 + − + −
d) x 1 x 2 (x 1).(x 2) 3(x − 2) 2(x + 1) 4x − 14 ⇔ − =
(x + 1).(x − 2) (x + 1).(x − 2)
(x + 1).(x − 2) 0,25
⇒ 3(x − 2) − 2(x + 1) = 4x − 14
⇔ 3x − 6 − 2x − 2 = 4x − 14 ⇔ 3 − x = 6 −
⇔ x = 2 (không thỏa mãn ĐKXĐ) 0,25
Vậy phương trình vô nghiệm
Một người đi từ A đến B với vận tốc 36 km/h. Khi đến B , người đó nghỉ lại 30 phút 8
rồi quay trở về A với vận tốc lớn hơn vận tốc lúc đi là 9 km/h. Thời gian kể từ lúc đi 1,5
từ A đến lúc trở về đến A là 5 giờ. Tính độ dài quãng đường AB ?
Gọi độ dài quãng đường AB dài là x (km) (x > 0) 0,25 Thời gian đi từ x
A đến B là (giờ) 36 x 1
Thời gian đi từ B về A là
(giờ). Đổi 30 phút = (giờ). 0,25 45 2
Theo bài ra ta có phương trình: x 1 x + + = 5 0,25 36 2 45
Giải phương trình ta được x = 90 (thỏa mãn điều kiện của ẩn) 0,5
Vậy độ dài quãng đường AB là 90km. 0,25
Cho tam giác ABC vuông tạiA , đường caoAH .
1. Chứng minh rằng tam giác ABC đồng dạng với tam giác HBA.
2. Qua B kẻ đường thẳng d vuông góc vớiBC . Gọi M là trung điểm của AB .
Đường thẳng qua M vuông góc với AB cắt đường thẳng d tại K và cắt BC tại I . 9 Chứng minh rằng: 3,0 2 a) Tam giác BC
BKI đồng dạng với tam giác ABC ; KI.AC = . 2
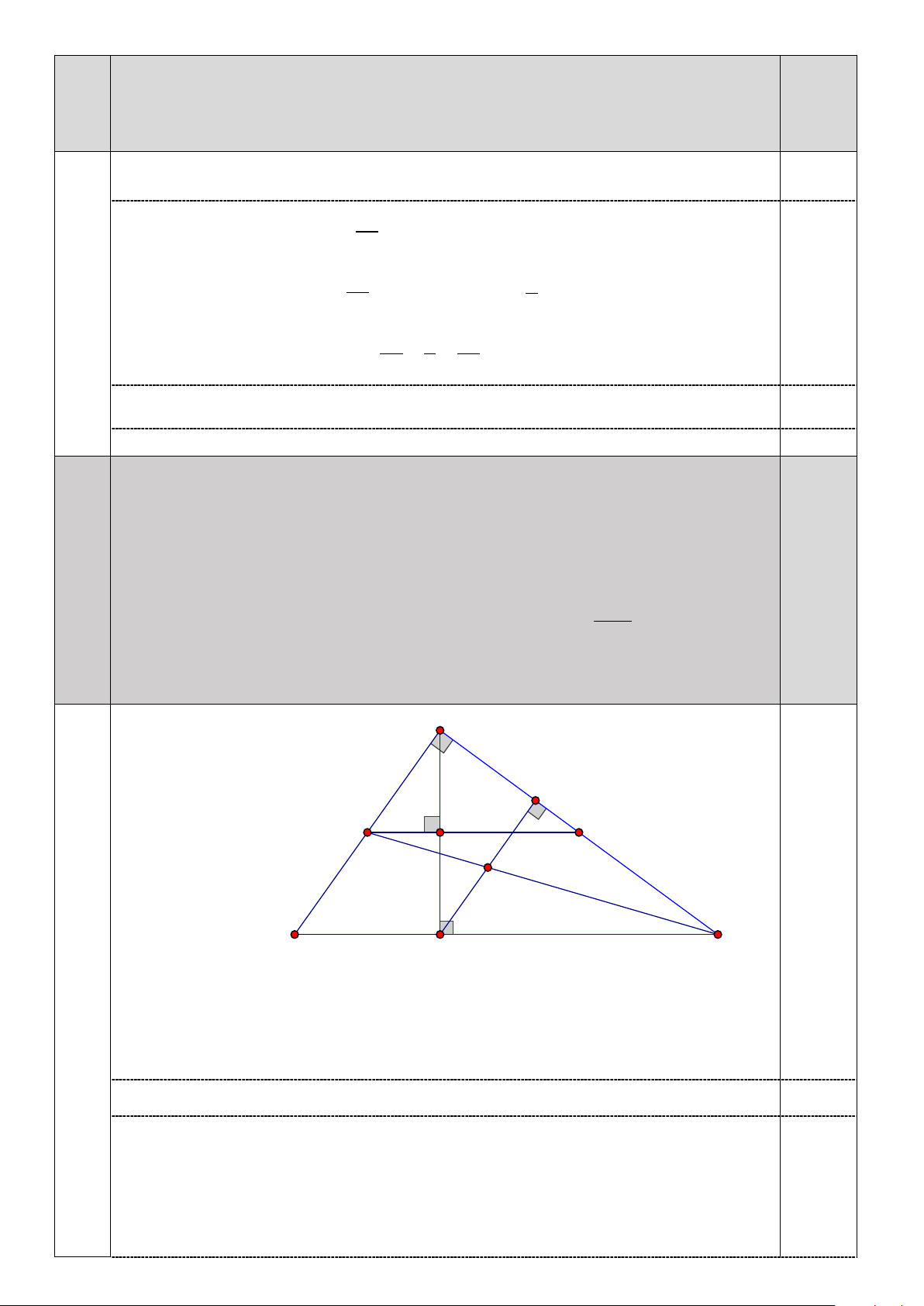
b) KC đi qua trung điểm của AH . B H M I K F E A C - Vẽ hình đúng 0,25 phần 1 - Viết GT- KL 0,25 đúng
1) Chứng minh được A ∆ BC ∽ H ∆ BA 1,0 2.a) Xét B ∆ KM có
BKM + KBM = 90° Mà
ABC + KBM = 90° Do đó
BKM = ABC hay BKI = ABC 0,25
Xét ∆BKI và ∆ABC có:
BKI = ABC (chứng minh trên); KBI = BAC = 0 90 Khi đó BK ∆ I ∽ A
∆ BC (g.g) 0,25 KI BI ⇒ =
⇒ KI.AC = BI.BC (1) BC AC
Ta có MI ⊥ AB;AB ⊥ AC ⇒ MI AC Xét A
∆ BC có M là trung điểm của AB ; MI AC nên I là trung điểm của BC 2 Do đó BC BI.BC = (2) 2 2 Từ (1) và (2) suy ra BC 0,5 KI.AC = 2
2.b) Gọi E là giao điểm của BK và AC ; F là giao điểm của CK và AH Xét EB ∆
C có I là trung điểm củaBC ;KI EC nên K là trung điểm của BE . Ta có AF CF AF EK ⇒ = KE CK 0,25 Ta có FH CF FH BK ⇒ = BK CK Do đó FH AF = BK KE
Mà KB = KE nên FH = AF hay F là trung điểm của AH . 0,25 2 2 + − 7 x x ( 2x − 9 3 3 )
10 Giải phương trình: + 6 − = 0 . 0,5 2 x − 2 x + 2 x − 4 2 2 + − 7 x x ( 2x − 9 3 3 ) + 6 − = 0 ĐKXĐ: x ≠ 2 ± 2 x − 2 x + 2 x − 4 Đặt x + 3 x − 3 = a;
= b khi đó ta được phương trình: x − 2 x + 2 2 2
a − 7ab + 6b = 0
⇔ (a − b)(a − 6b) = 0 a = b ⇔ 0,25 a = 6b
Với a = b ta được: x + 3 x − 3 = x (−2 + )x + ⇒ x ( 2
3 x + 2) = (x − 3)(x − 2) 2 2
⇔ x + 5x + 6 = x − 5x + 6 ⇔ 10x = 0 ⇔ x = 0 (TMĐK)
Với a = 6b ta được: 0,25 x + 3 x − = 3 6. x (−2 x x 3)( + 2 ⇒ +
x + 2) = 6(x − 3)(x − 2) ⇔ 2 x + 5x + 6 = 2 6x − 30x + 36 ⇔ 2
5x − 35x + 30 = 0 ⇔ 2 x − 7x + 6 = 0
⇔ (x − 1)(x − 6) = 0 x = 1 ⇔ (TMÐK) x = 6
Tập nghiệm của phương trình là S = {0;1; } 6
Lưu ý: Học sinh làm cách khác đúng cho điểm tối đa
======Hết ======
Document Outline
- Toan 8.KTGK2.22.23.de
- Toan 8.KTGK2.22.23.da