Đề kiểm tra giữa kì 1 Toán 10 năm 2021 – 2022 trường Lương Thế Vinh – Hà Nội

Đề kiểm tra giữa kì 1 Toán 10 năm 2021 – 2022 trường THCS & THPT Lương Thế Vinh – Hà Nội được biên soạn theo hình thức đề 100% trắc nghiệm, thời gian làm bài 90 phút, đề thi có đáp án, mời bạn đọc đón xem

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 10

Môn: Toán 10

Thông tin:

14 trang 9 tháng trước

Tác giả:

Profile Thanh Tâm
Câu 1. Tìm tập xác định của hàm số
1
1
x
y
x
.
A.
1;3 .
D.
2; .
Câu 3. Trong các hàm số sau, hàm số nào không phải là hàm số chẵn?
A.
3
y x x
. B.
2
3
y
x
. C.
3
y x x
. D.
4
3
y x x
.
Câu 4. Hàm số nào trong các hàm số sau đây là hàm số bậc nhất ?
A.
1
.
y
x
B.
1 3
y x
. C.
2
2
y x x
. D.
3
y
.
Câu 5. Hàm số nào dưới đây có đồ thị như hình bên ?
A.
D
0;1
. B.
D
0;1
. C.
D
0;1
. D.
D
0;1
.
Câu 2. Cho hàm số
y f
x
có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào ?
;0
.
B. (0; 2) . C.
TRƯỜNG THCS&THPT
LƯƠNG THẾ VINH
KIỂM TRA GIỮA KÌ I NĂM HỌC 2021 - 2022
MÔN TOÁN - LỚP 10
A.
1
1
3
y x
. B.
2
1
3
y x
. C.
2
1
3
y x
. D.
1
1
3
y x
.
Câu 6. Với những giá trị nào của m để hàm số
2
( 4) 1 2
y m x m
là hàm số bậc nhất ?
A.
m
. B.
2
2
m
m
.
C.
2
m
. D.
2
2
m
m
.
Câu 7. Cho parabol
2
: 6 5
P y x x
. Tìm tọa độ đỉnh của
P
.
A.
3; 4
. B.
3;4
. C.
3;4
. D.
3; 4
.
Câu 8. Hàm số bậc hai
2
3 4 1
y x x
có trục đối xứng là đường nào dưới đây ?
A.
2
3
x
. B.
2
3
x
. C.
2
3
y
. D.
4
3
x
.
Câu 9. Bảng biến thiên của hàm số
2
3 6 5
y x x
là bảng nào sau đây ?
A. B.
C. D.
Câu 10. Khẳng định nào sau đây sai ?
A. Đồ thị hàm số
2
2 2 3
y x x
luôn cắt trục tung.
B. Hàm số
2
2 2 3
y x x
nghịch biến trên khoảng
1
;
4
.
C. Đồ thị hàm số
2
2 2 3
y x x
luôn cắt trục hoành tại hai điểm phân biệt.
D. Hàm số
2
2 2 3
y x x
đồng biến trên khoảng
1
;
4

.
Câu 11. Với giá trị nào của m để đồ thị hàm số
2 2
2
y x x m
có đỉnh nằm trên đường thẳng
1
y x
?
A.
1
m
. B.
1
m
. C.
1
m
. D.
2
m
.
Câu 12. Cho hàm số có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
0
m
2
y ax bx c
A.
0
a
,
0
b
,
0
c
.
B.
0
a
,
0
b
,
0
c
.
C. .
D.
0
a
,
0
b
,
0
c
.
Câu 13. Cho hàm số
2
2 8 5
y x x
. Với mọi
,
x
khẳng định nào sau đây là đúng ?
A. Giá trị nhỏ nhất của hàm số là
3
.
B. Giá trị lớn nhất của hàm số là
3
.
C. Giá trị lớn nhất của hàm số là
5
.
D. Hàm số không có giá trị lớn nhất và nhỏ nhất.
Câu 14. Đường thẳng nào sau đây cắt trục đối xứng của parabol
2
2 4 3
y x x
tại điểm có tung độ
gấp đôi hoành độ?
A.
2 1
y x
. B.
2 1
y x
. C.
1
y x
. D.
2
y x
.
Câu 15. Giá trị nào của
m
dưới đây để đường thẳng
2 1
y mx
không có điểm chung với Parabol
2
3
y x
?
A.
1
m
. B.
2
m
. C.
3
m
. D.
4
m
.
Câu 16. Cho hàm số bậc hai
2
( )
y f x ax bx c
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của tham số m để đường thẳng
1
y m
cắt đồ thị hàm số
2
( )
y f x ax b x c
tại bốn
điểm phân biệt ?
0, 0, 0
a b c
A. 2. B. 3. C. 4. D. 5.
Câu 17. Điều kiện của phương trình
2
2 1
5 2
1
x
x
x
là
A.
1 5
x
. B.
1 5
x
. C.
1 5
x
. D.
1 5
x
.
Câu 18. Tập nghiệm của phương trinh
4
0
( 2) 2
x
x x x
là
A.
2
S
. B.
2
S
. C.
S
. D.
2
S
.
Câu 19. Phương trình
2
4 2 0
x x x
có bao nhiêu nghiệm ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 20. Phương trình nào sau đây là phương trình bậc nhất:
A.
2 1 0
x
. B.
1
1 0
x
. C.
2
3 4 0
x
. D.
3 1 0
x
.
Câu 21. Cho phương trình
0
ax b
. Chọn khẳng định sai.
A. Phương trình có nghiệm duy nhất khi
0
a
.
B. Phương trình vô nghiệm khi
0
a
và
0
b
.
C. Phương trình vô nghiệm khi
0
a
và
0
b
.
D. Phương trình có nghiệm
x
khi
0
a
và
0
b
.
Câu 22. Tìm tất cả các giá trị của tham số
m
sao cho phương trình
2 1 0
m x m
có nghiệm
duy nhất.
A.
2
m
. B.
1
m
. C.
1
m
. D.
2
m
.
Câu 23. Với giá trị nào của tham số
m
thì phương trình
22
4 2 0
m x m m
vô nghiệm ?
A.
2
m
. B.
2
m
. C.
2
m
. D.
4
m
.
Câu 24. Phương trình
2
( 1)
2
m x m m
có nghiệm khi:
A.
1
m
. B. m
. C.
0
m
.
D. Không có
m
nào.
Câu 25. Số
2
là nghiệm của phương trình bậc hai nào trong các phương trình sau ?
A.
2
4 3 0.
x x
B.
2
2 3 2 0.
x x
C.
2
2 3 2 0.
x x
D.
3
8 0.
x
Câu 26. Nghiệm của phương trình
2
2 5 7 0
x x
có thể xem là hoành độ giao điểm của hai đồ thị hàm
số nào sau đây ?
A.
2
2
y x
và
5 7
y x
. B.
2
2
y x
và
5 7
y x
.
C.
2
2
y x
và
5 7
y x
. D.
2
2
y x
và
5 7
y x
.
Câu 27. Phương trình
2 2
( 1) 1 0
m x mx
có số nghiệm là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 28. Phương trình bậc hai nào dưới đây nhận hai số
2 1
và
2 1
làm nghiệm.
A.
2
8 1 0
x x
. B.
2
8 1 0
x x
. C.
2
8 1 0
x x
. D.
2
8 1 0
x x
.
Câu 29. Phương trình
2
0 0
ax bx c a
có hai nghiệm phân biệt trái dấu khi và chỉ khi:
A.
0
.
0
S
B .
0
.
0
S
C.
0.
P
D.
0.
P
Câu 30. Phương trình
2
(1 ) 3 1 0
m x x
có hai nghiệm âm phân biệt khi giá trị của m là
A.
5
1
4
m
. B.
5
1
4
m
. C.
5
1
4
m
. D.
5
1
4
m
.
Câu 31. Cho phương trình
2
2 3 0,
x mx
giá trị của để phương trình có hai nghiệm
1 2
,
x x
sao
cho biểu thức
2 2
1 2 1 2
4( )
x x x x
đạt giá trị lớn nhất là:
A.
2
m
. B.
1
m
. C.
1
m
. D. .
Câu 32. Tìm tất cả các giá trị thực của m để phương trình
2
2 4 5
x x m
có đúng hai nghiệm phân
biệt thuộc đoạn
1;2
.
A.
5 7
m
. B.
5 7
m
. C.
1 5
m
. D.
1 7
m
.
Câu 33. Cho hàm số
2
( 1) 3
y x m x
có đồ thị , đường thẳng có phương trình
y x m
. Tìm
m
để
( )
d
cắt
( )
P
tại hai điểm phân biệt
A
,
B
sao cho độ dài đoạn thẳng
AB
có giá trị
nhỏ nhất.
A.
3
m
. B.
1
2
m
. C.
2
m
D.
1
m
.
Câu 34. Cho hai điểm
3;2 , 1;4
A B
. Tính
AB
.
Câu 35. Cho tam giác
ABC
có
1;2 , 3; 1 , 2;3
A B C
. Tọa độ
2
u AB BC
 
là
A.
9;10
. B.
7;5
. C.
3;9
. D.
6;8
.
Câu 36. Trong hệ trục tọa độ
,
Oxy
cho
3 2
u i j
và
2
v i xj
. Tìm
x
sao cho
u
và
v
cùng
phương.
m
2
m
P
d
A.
5 2
. B.
2 5
. C.
3 5
. D.
3 2
.
A.
1
3
x
. B.
4
3
x
. C.
1
2
x
. D.
3
x
.
Câu 37. Trong hệ trục tọa độ
Oxy
, cho
1;2
A
,
2;3
B
. Tọa độ điểm
C
nằm trên trục tung sao cho
, ,
A B C
thẳng hàng là
A.
3;0
C
. B.
1
0;
3
C
. C.
7
0;
3
C
. D.
4
0;
3
C
Câu 38. Trong hệ trục tọa độ
,
Oxy
cho
2; 1 , 0; 2 , (2; 3)
A B C
. Gọi
M
là trung điểm của
AC
.
Tọa độ điểm
D
sao cho
2
BD BM CA
  
là
A.
2; 6
D
. B.
0; 3
D
. C.
3;1
D
. D.
4; 3
E
.
Câu 39. Trong hệ trục tọa độ
Oxy
, cho tam giác
ABC
có
2; 1
A
,
1; 5
B
và
C
thuộc trục
Ox
.
Trọng tâm
G
của tam giác ABC nằm trên đường phân giác góc phần tư thứ hai của hệ trục tọa
độ Oxy. Tọa độ của điểm
C
là
A.
1;0
C
. B.
3;0
C
. C.
0;2
C
. D.
2;0
.
Câu 40. Trong hệ trục tọa độ
Oxy
, cho
1;1
A
,
1; 3
B
. Tìm tọa độ điểm
M
thuộc trục Oy sao cho
2 2
10
AM BM
(đơn vị độ dài).
A.
2;0
M
. B.
0;1
M
. C.
0; 2
M
. D.
0; 1
M
.
Câu 41. Trong hệ trục tọa độ
Oxy
, cho
2;1 , 1;0 , 0; 2
A B C
. Tìm tọa độ điểm
M
thuộc trục
Ox
sao cho
2 3
MA MB MC
nhỏ nhất.
A.
2;1
M
. B.
3;0
M
. C.
2;0
M
. D.
4;0
M
.
Câu 42. Trong hệ tọa độ Oxy, cho điểm
3 1
( , )
2 2
P
nằm trên nửa đường tròn đơn vị. Giá trị
3
2
bằng
giá trị lượng giác nào sau đây của góc
POx
?
Câu 43. Cho góc tù
, khẳng định nào sau đây là sai ?
A.
cos 0
. B.
tan 0
. C.
sin 0
. D.
cot 0
.
Câu 44. Cho
2
sin
3
và
0 0
90 180 .
Hãy tính
cos
.
A.
3
3
. B.
1
3
. C.
1
3
. D.
3
2
.
Câu 45. Cho
là góc tù và
2
sin
5
. Giá trị của biểu thức
3cos 4sin
A
bằng
A.
sin
. B.
cos
. C.
tan
. D.
cot
.
1
5
. D.
1
2 5
.
Câu 46. Cho
4
tan
3
và
0 0
0 90 .
Hãy tính
cos .
A.
3
2
. B.
3
5
3
5
. D.
7
3
.
Câu 47. Cho hai vectơ
a
và
b
khác
0
. Xác định góc
giữa hai vectơ
a
và
b
khi
2 . . .
a b a b
A.
0
180 .
B.
0
120 .
C.
0
90 .
D.
0
60 .
Câu 48. Cho tam giác ABC vuông cân tại A, cạnh
AC a
. Tính
.
AB AC
 
.
A.
. 0
AB AC
 
. B.
2
.
AB AC a
 
. C.
. 0
AB BC
 
. D.
2
. 2
AB AC a
 
.
Câu 49. Cho tam giác ABC đều có độ dài các cạnh là
6.
Điểm M thỏa mãn điều kiện
1
2
BM BC
 
.
Tính
.
BM BA
 
.
A.
. 9 3
BM BA

. B.
. 9 3
BM BA

. C.
. 9
BM BA
 
 
.
Câu 50. Cho hình vuông
ABCD
có cạnh là
a
. Điểm
E
là trung điểm của cạnh
AB
. Tính
.
EB CA
 
.
A.
2
2
a
. B.
2
2
a
. C.
2
2
a
. D.
2
2
a
.
----------------HẾT----------------
TỔNG: 50 câu
A.
5
. B.
2 5
. C.
. C.
. D.
BM .BA 9
Câu 1. Tìm tập xác định của hàm số
1
1
x
y
x
.
A.
0;1
D
. B.
0;1
D
. C.
0;1
D
. D.
0;1
D
.
Câu 2. Cho hàm số
y f x
có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào ?
A.
;0 .
B.
(0; 2)
. C.
1;3 .
D.
2; .
Câu 3. Trong các hàm số sau, hàm số nào không phải là hàm số chẵn?
A.
3
y x x
. B.
2
3
y
x
. C.
3
y x x
. D.
4
3
y x x
.
Câu 4. Hàm số nào trong các hàm số sau đây là hàm số bậc nhất ?
A.
1
.
y
x
B.
1 3
y x
. C.
2
2
y x x
. D.
3
y
.
Câu 5. Hàm số nào dưới đây có đồ thị như hình bên ?
TRƯỜNG THCS&THPT
LƯƠNG THẾ VINH
KIỂM TRA GIỮA KÌ I NĂM HỌC 2021 - 2022
MÔN TOÁN - LỚP 10
A.
1
1
3
y x
. B.
2
1
3
y x
. C.
2
1
3
y x
. D.
1
1
3
y x
.
Câu 6. Với những giá trị nào của m để hàm số
2
( 4) 1 2
y m x m
là hàm số bậc nhất ?
A.
m
. B.
2
2
m
m
.
C.
2
m
. D.
2
2
m
m
.
Câu 7. Cho parabol
2
: 6 5
P y x x
. Tìm tọa độ đỉnh của
P
.
A.
3; 4
. B.
3;4
. C.
3;4
. D.
3; 4
.
Câu 8. Hàm số bậc hai
2
3 4 1
y x x
có trục đối xứng là đường nào dưới đây ?
A.
2
3
x
. B.
2
3
x
. C.
2
3
y
. D.
4
3
x
.
Câu 9. Bảng biến thiên của hàm số
2
3 6 5
y x x
là bảng nào sau đây ?
A. B.
C. D.
Câu 10. Khẳng định nào sau đây sai ?
A. Đồ thị hàm số
2
2 2 3
y x x
luôn cắt trục tung.
B. Hàm số
2
2 2 3
y x x
nghịch biến trên khoảng
1
;
4
.
C. Đồ thị hàm số
2
2 2 3
y x x
luôn cắt trục hoành tại hai điểm phân biệt.
D. Hàm số
2
2 2 3
y x x
đồng biến trên khoảng
1
;
4

.
Câu 11. Với giá trị nào của m để đồ thị hàm số
2 2
2
y x x m
có đỉnh nằm trên đường thẳng
1
y x
?
A.
1
m
. B.
1
m
. C.
1
m
. D.
2
m
.
Câu 12. Cho hàm số có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
0
m
2
y ax bx c
A.
0
a
,
0
b
,
0
c
.
B.
0
a
,
0
b
,
0
c
.
C. .
D.
0
a
,
0
b
,
0
c
.
Câu 13. Cho hàm số
2
2 8 5
y x x
. Với mọi
,
x
khẳng định nào sau đây là đúng ?
A. Giá trị nhỏ nhất của hàm số là
3
.
B. Giá trị lớn nhất của hàm số là
3
.
C. Giá trị lớn nhất của hàm số là
5
.
D. Hàm số không có giá trị lớn nhất và nhỏ nhất.
Câu 14. Đường thẳng nào sau đây cắt trục đối xứng của parabol
2
2 4 3
y x x
tại điểm có tung độ
gấp đôi hoành độ?
A.
2 1
y x
. B.
2 1
y x
. C.
1
y x
. D.
2
y x
.
Câu 15. Giá trị nào của
m
dưới đây để đường thẳng
2 1
y mx
không có điểm chung với Parabol
2
3
y x
?
A.
1
m
. B.
2
m
. C.
3
m
. D.
4
m
.
Câu 16. Cho hàm số bậc hai
2
( )
y f x ax bx c
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của tham số m để đường thẳng
1
y m
cắt đồ thị hàm số
2
( )
y f x ax b x c
tại bốn
điểm phân biệt ?
0, 0, 0
a b c
A. 2. B. 3. C. 4. D. 5.
Câu 17. Điều kiện của phương trình
2
2 1
5 2
1
x
x
x
là
A.
1 5
x
. B.
1 5
x
. C.
1 5
x
. D.
1 5
x
.
Câu 18. Tập nghiệm của phương trinh
4
0
( 2) 2
x
x x x
là
A.
2
S
. B.
2
S
. C.
S
. D.
2
S
.
Câu 19. Phương trình
2
4 2 0
x x x
có bao nhiêu nghiệm ?
A.
0.
B.
1.
C.
2.
D.
3.
Câu 20. Phương trình nào sau đây là phương trình bậc nhất:
A.
2 1 0
x
. B.
1
1 0
x
. C.
2
3 4 0
x
. D.
3 1 0
x
.
Câu 21. Cho phương trình
0
ax b
. Chọn khẳng định sai.
A. Phương trình có nghiệm duy nhất khi
0
a
.
B. Phương trình vô nghiệm khi
0
a
và
0
b
.
C. Phương trình vô nghiệm khi
0
a
và
0
b
.
D. Phương trình có nghiệm
x
khi
0
a
và
0
b
.
Câu 22. Tìm tất cả các giá trị của tham số
m
sao cho phương trình
2 1 0
m x m
có nghiệm
duy nhất.
A.
2
m
. B.
1
m
. C.
1
m
. D.
2
m
.
Câu 23. Với giá trị nào của tham số
m
thì phương trình
22
4 2 0
m x m m
vô nghiệm ?
A.
2
m
. B.
2
m
. C.
2
m
. D.
4
m
.
Câu 24. Phương trình
2
( 1)
2
m x m m
có nghiệm khi:
A.
1
m
. B. m
. C.
0
m
.
D. Không có
m
nào.
Câu 25. Số
2
là nghiệm của phương trình bậc hai nào trong các phương trình sau ?
A.
2
4 3 0.
x x
B.
2
2 3 2 0.
x x
C.
2
2 3 2 0.
x x
D.
3
8 0.
x
Câu 26. Nghiệm của phương trình
2
2 5 7 0
x x
có thể xem là hoành độ giao điểm của hai đồ thị hàm
số nào sau đây ?
A.
2
2
y x
và
5 7
y x
. B.
2
2
y x
và
5 7
y x
.
C.
2
2
y x
và
5 7
y x
. D.
2
2
y x
và
5 7
y x
.
Câu 27. Phương trình
2 2
( 1) 1 0
m x mx
có số nghiệm là
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 28. Phương trình bậc hai nào dưới đây nhận hai số
2 1
và
2 1
làm nghiệm.
A.
2
8 1 0
x x
. B.
2
8 1 0
x x
. C.
2
8 1 0
x x
. D.
2
8 1 0
x x
.
Câu 29. Phương trình
2
0 0
ax bx c a
có hai nghiệm phân biệt trái dấu khi và chỉ khi:
A.
0
.
0
S
B .
0
.
0
S
C.
0.
P
D.
0.
P
Câu 30. Phương trình
2
(1 ) 3 1 0
m x x
có hai nghiệm âm phân biệt khi giá trị của m là
A.
5
1
4
m
. B.
5
1
4
m
. C.
5
1
4
m
. D.
5
1
4
m
.
Câu 31. Cho phương trình
2
2 3 0,
x mx
giá trị của để phương trình có hai nghiệm
1 2
,
x x
sao
cho biểu thức
2 2
1 2 1 2
4( )
x x x x
đạt giá trị lớn nhất là:
A.
2
m
. B.
1
m
. C.
1
m
. D. .
Câu 32. Tìm tất cả các giá trị thực của m để phương trình
2
2 4 5
x x m
có đúng hai nghiệm phân
biệt thuộc đoạn
1;2
.
A.
5 7
m
. B.
5 7
m
. C.
1 5
m
. D.
1 7
m
.
Câu 33. Cho hàm số
2
( 1) 3
y x m x
có đồ thị , đường thẳng có phương trình
y x m
. Tìm
m
để
( )
d
cắt
( )
P
tại hai điểm phân biệt
A
,
B
sao cho độ dài đoạn thẳng
AB
có giá trị
nhỏ nhất.
A.
3
m
. B.
1
2
m
. C.
2
m
D.
1
m
.
Câu 34. Cho hai điểm
3;2 , 1;4
A B
. Tính
AB
.
A.
5 2
. B.
2 5
. C.
3 5
. D.
3 2
.
Câu 35. Cho tam giác
ABC
có
1;2 , 3; 1 , 2;3
A B C
. Tọa độ
2
u AB BC
 
là
A.
9;10
. B.
7;5
. C.
3;9
. D.
6;8
.
Câu 36. Trong hệ trục tọa độ
,
Oxy
cho
3 2
u i j
và
2
v i xj
. Tìm
x
sao cho
u
và
v
cùng
phương.
m
2
m
P
d
A.
1
3
x
. B.
4
3
x
. C.
1
2
x
. D.
3
x
.
Câu 37. Trong hệ trục tọa độ
Oxy
, cho
1;2
A
,
2;3
B
. Tọa độ điểm
C
nằm trên trục tung sao cho
, ,
A B C
thẳng hàng là
A.
3;0
C
. B.
1
0;
3
C
. C.
7
0;
3
C
. D.
4
0;
3
C
Câu 38. Trong hệ trục tọa độ
,
Oxy
cho
2; 1 , 0; 2 , (2; 3)
A B C
. Gọi
M
là trung điểm của
AC
.
Tọa độ điểm
D
sao cho
2
BD BM CA
  
là
A.
2; 6
D
. B.
0; 3
D
. C.
3;1
D
. D.
4; 3
E
.
Câu 39. Trong hệ trục tọa độ
Oxy
, cho tam giác
ABC
có
2; 1
A
,
1; 5
B
và
C
thuộc trục
Ox
.
Trọng tâm
G
của tam giác ABC nằm trên đường phân giác góc phần tư thứ hai của hệ trục tọa
độ Oxy. Tọa độ của điểm
C
là
A.
1;0
C
. B.
3;0
C
. C.
0;2
C
. D.
2;0
.
Câu 40. Trong hệ trục tọa độ
Oxy
, cho
1;1
A
,
1; 3
B
. Tìm tọa độ điểm
M
thuộc trục Oy sao cho
2 2
10
AM BM
(đơn vị độ dài).
A.
2;0
M
. B.
0;1
M
. C.
0; 2
M
. D.
0; 1
M
.
Câu 41. Trong hệ trục tọa độ
Oxy
, cho
2;1 , 1;0 , 0; 2
A B C
. Tìm tọa độ điểm
M
thuộc trục
Ox
sao cho
2 3
MA MB MC
nhỏ nhất.
A.
2;1
M
. B.
3;0
M
. C.
2;0
M
. D.
4;0
M
.
Câu 42. Trong hệ tọa độ Oxy, cho điểm
3 1
( , )
2 2
P
nằm trên nửa đường tròn đơn vị. Giá trị
3
2
bằng
giá trị lượng giác nào sau đây của góc
POx
?
A.
sin
. B.
cos
. C.
tan
. D.
cot
.
Câu 43. Cho góc tù
, khẳng định nào sau đây là sai ?
A.
cos 0
. B.
tan 0
. C.
sin 0
. D.
cot 0
.
Câu 44. Cho
2
sin
3
và
0 0
90 180 .
Hãy tính
cos
.
A.
3
3
. B.
1
3
. C.
1
3
. D.
3
2
.
Câu 45. Cho
là góc tù và
2
sin
5
. Giá trị của biểu thức
3cos 4sin
A
bằng
A.
5
. B.
2 5
. C.
1
5
. D.
1
2 5
.
Câu 46. Cho
4
tan
3
và
0 0
0 90 .
Hãy tính
cos .
A.
3
2
. B.
3
5
. C.
3
5
. D.
7
3
.
Câu 47. Cho hai vectơ
a
và
b
khác
0
. Xác định góc
giữa hai vectơ
a
và
b
khi
2 . . .
a b a b
A.
0
180 .
B.
0
120 .
C.
0
90 .
D.
0
60 .
Câu 48. Cho tam giác ABC vuông cân tại A, cạnh
AC a
. Tính
.
AB AC
 
.
A.
. 0
AB AC
 
. B.
2
.
AB AC a
 
. C.
. 0
AB BC
 
. D.
2
. 2
AB AC a
 
.
Câu 49. Cho tam giác ABC đều có độ dài các cạnh là
6.
Điểm M thỏa mãn điều kiện
1
2
BM BC
 
.
Tính
.
BM BA
 
.
A.
. 9 3
BM BA

. B.
. 9 3
BM BA

. C.
. 9
BM BA
 
. D.
. 9
BM BA
 
.
Câu 50. Cho hình vuông
ABCD
có cạnh là
a
. Điểm
E
là trung điểm của cạnh
AB
. Tính
.
EB CA
 
.
A.
2
2
a
. B.
2
2
a
. C.
2
2
a
. D.
2
2
a
.
----------------HẾT----------------
TỔNG: 50 câu
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THCS&THPT
KIỂM TRA GIỮA KÌ I NĂM HỌC 2021 - 2022 LƯƠNG THẾ VINH MÔN TOÁN - LỚP 10 1 x
Câu 1. Tìm tập xác định của hàm số y  . 1 x A. D  0;1 . B. D  0;1 . C. D  0;1 . D. D  0;1.
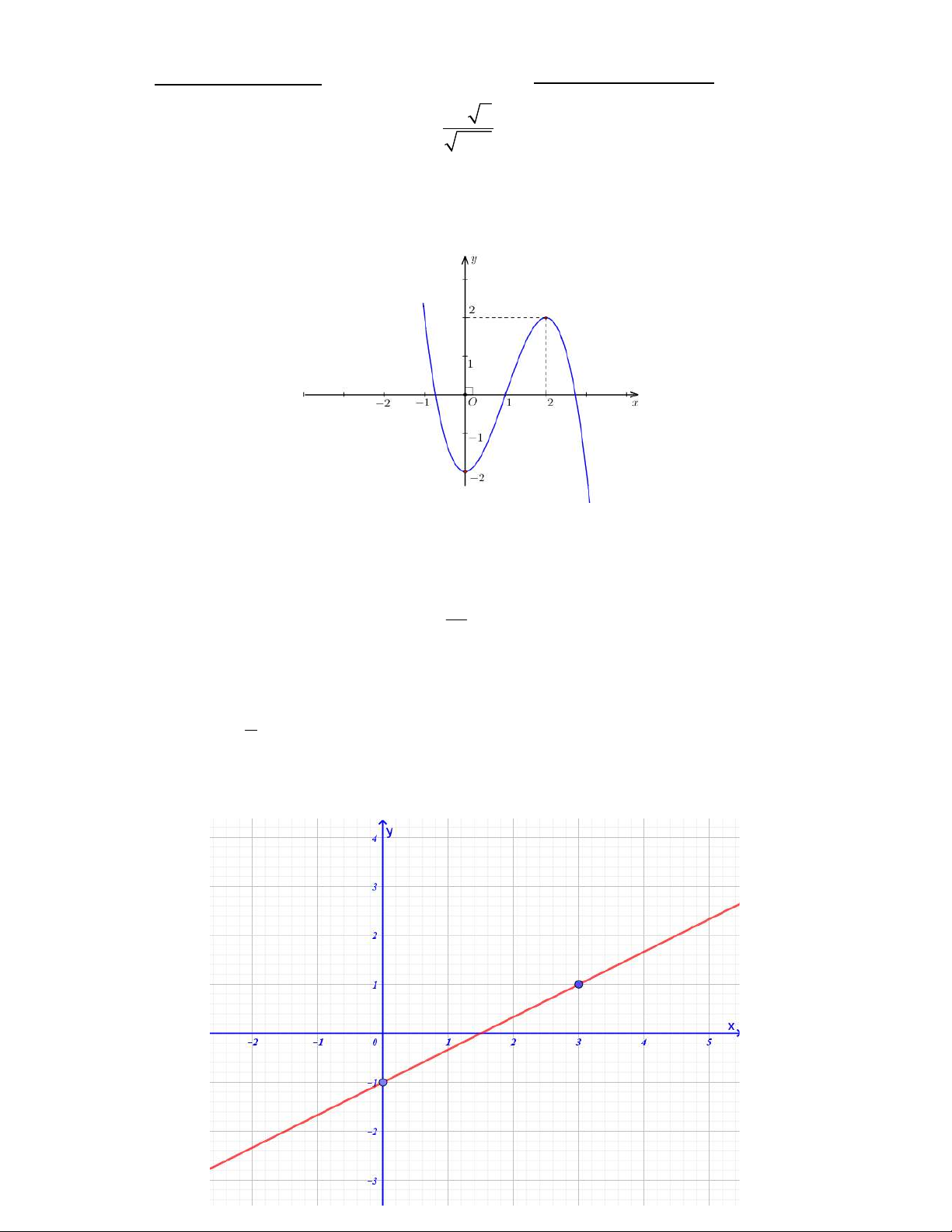
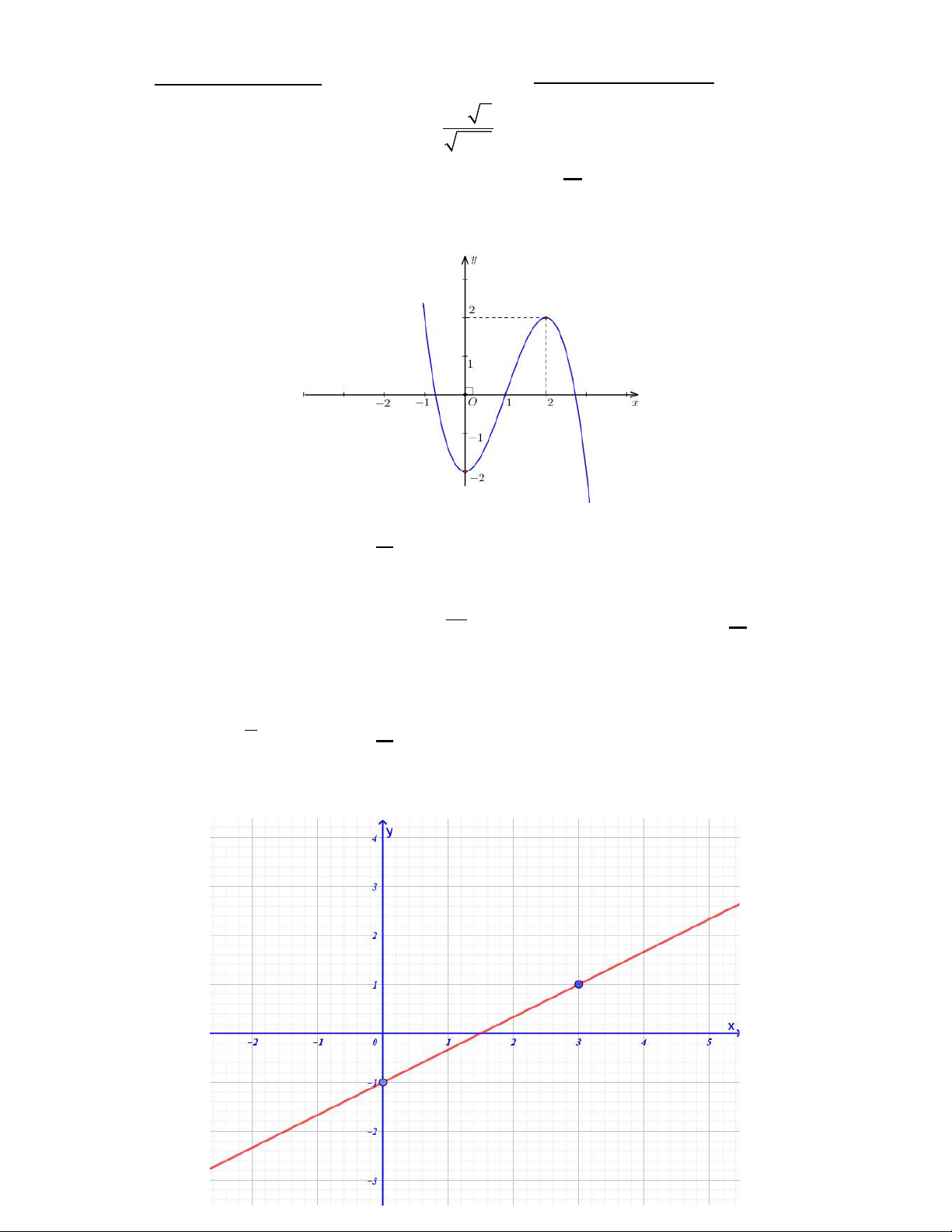
Câu 2. Cho hàm số y  f  x có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào ? A. ;0. B. (0; 2) . C. 1;3. D. 2;.
Câu 3. Trong các hàm số sau, hàm số nào không phải là hàm số chẵn? 3 A. 4 2 y  x 3x . B. y   . C. 4 2 y  x 3x . D. 4 y  x 3x. 2 x
Câu 4. Hàm số nào trong các hàm số sau đây là hàm số bậc nhất ? 1 A. y  . B. y 13x . C. 2 y  x 2x . D. y  3. x
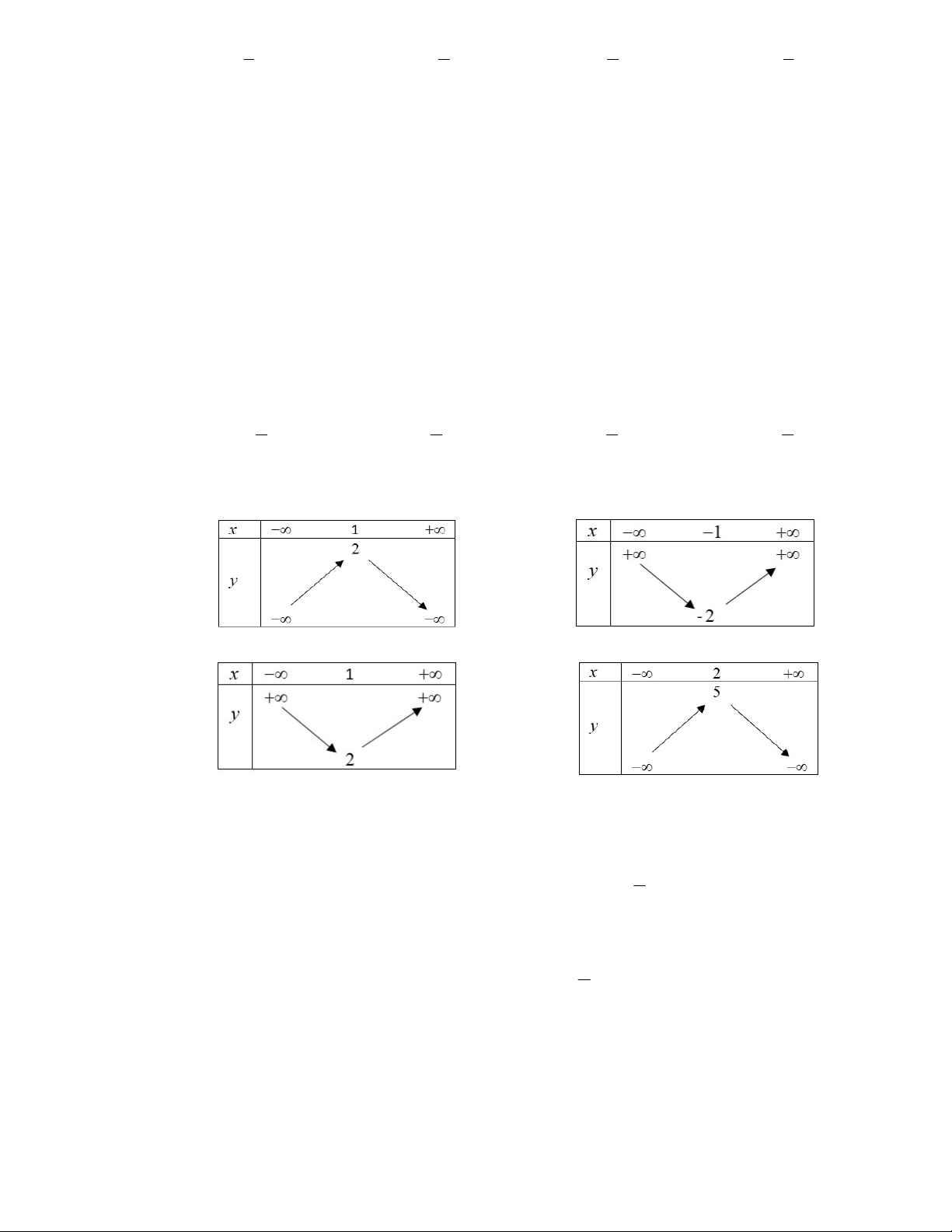
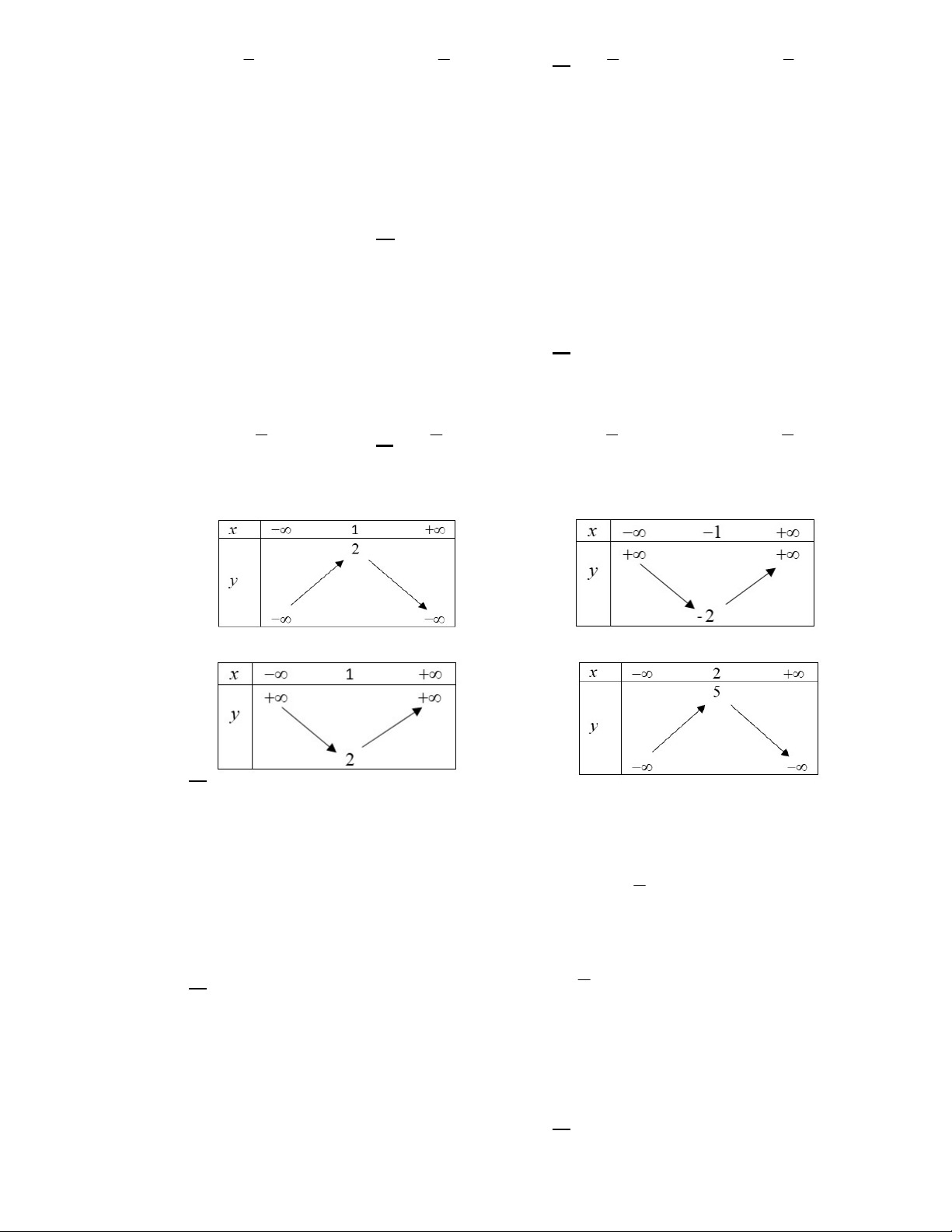
Câu 5. Hàm số nào dưới đây có đồ thị như hình bên ? 1 2 2 1 A. y  x 1 . B. y   x 1 . C. y  x 1 . D. y  x 1. 3 3 3 3
Câu 6. Với những giá trị nào của m để hàm số 2
y  (m 4)x 12m là hàm số bậc nhất ?  m  2 A. m   . B.  . m  2  m  2 C. m  2 . D.  . m  2 Câu 7. Cho parabol P 2
: y  x  6x  5 . Tìm tọa độ đỉnh của P . A. 3;4 . B.  3  ;4. C.3;  4 . D.  3  ; 4   . Câu 8. Hàm số bậc hai 2
y  3x  4x 1 có trục đối xứng là đường nào dưới đây ? 2 2 2 4 A. x   . B. x  . C. y  . D. x  . 3 3 3 3
Câu 9. Bảng biến thiên của hàm số 2
y 3x 6x5 là bảng nào sau đây ? A. B. C. D.
Câu 10. Khẳng định nào sau đây sai ? A. Đồ thị hàm số 2
y  2x 2x3 luôn cắt trục tung.  1  B. Hàm số 2
y  2x 2x3 nghịch biến trên khoảng  ;     .  4  C. Đồ thị hàm số 2
y  2x 2x3 luôn cắt trục hoành tại hai điểm phân biệt.  1  D. Hàm số 2
y  2x 2x3 đồng biến trên khoảng ;    .  4 
Câu 11. Với giá trị nào của m để đồ thị hàm số 2 2
y  x 2xm m  0 có đỉnh nằm trên đường thẳng y  x 1? A. m  1 . B. m  1  . C. m  1 . D. m  2 . Câu 12. Cho hàm số 2
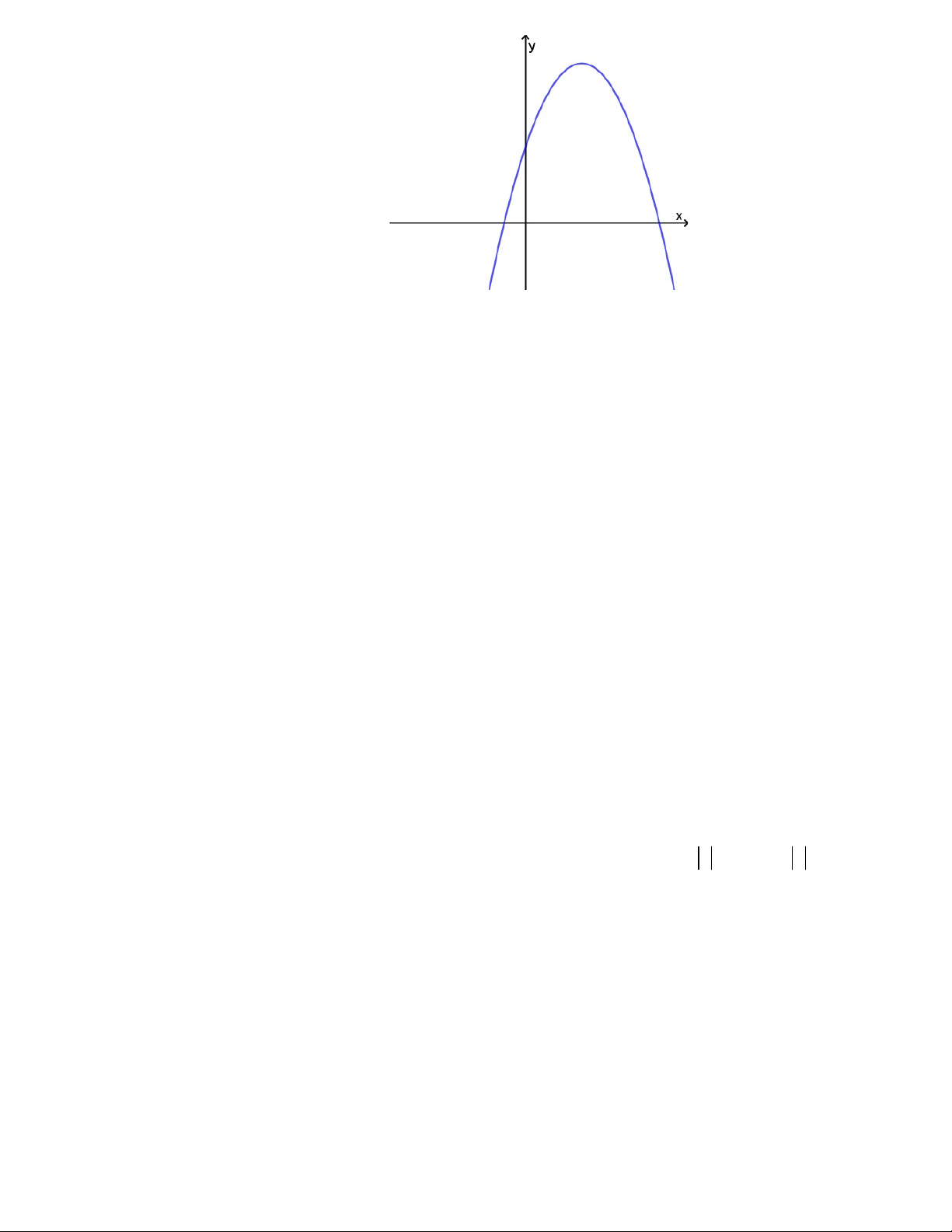
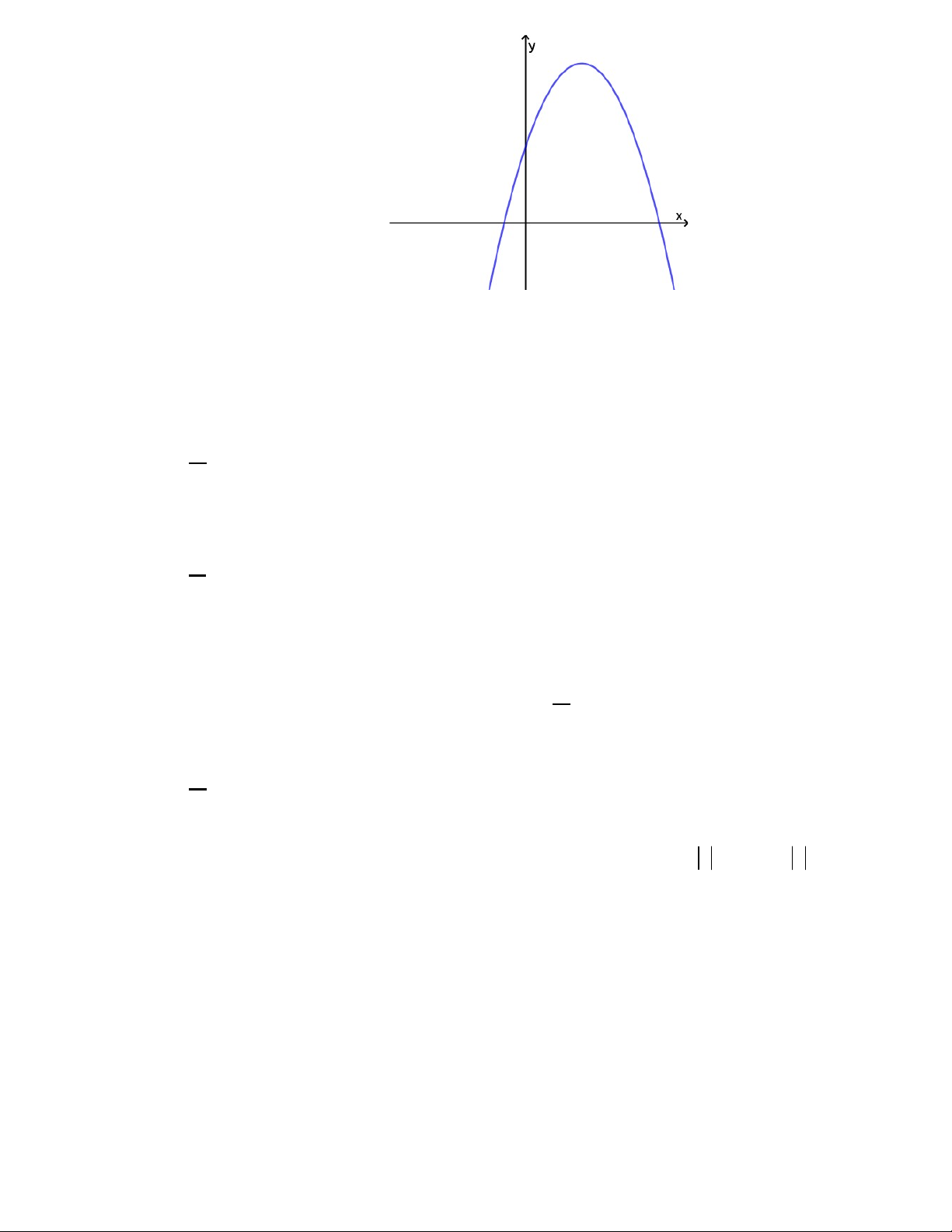
y  ax  bx  c có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
A. a  0 , b  0, c  0.
B. a  0 , b  0, c  0 .
C. a  0, b  0, c  0 .
D. a  0 , b  0, c  0. Câu 13. Cho hàm số 2
y  2x  8x  5 . Với mọi x  , khẳng định nào sau đây là đúng ?
A. Giá trị nhỏ nhất của hàm số là 3 .
B. Giá trị lớn nhất của hàm số là 3 .
C. Giá trị lớn nhất của hàm số là 5 .
D. Hàm số không có giá trị lớn nhất và nhỏ nhất.
Câu 14. Đường thẳng nào sau đây cắt trục đối xứng của parabol 2
y  2x 4x 3 tại điểm có tung độ gấp đôi hoành độ? A. y  2x 1. B. y  2x  1. C. y  x 1. D. y  x  2 .
Câu 15. Giá trị nào của m dưới đây để đường thẳng y  2mx 1 không có điểm chung với Parabol 2 y  x 3? A. m  1. B. m  2 . C. m  3. D. m  4 .
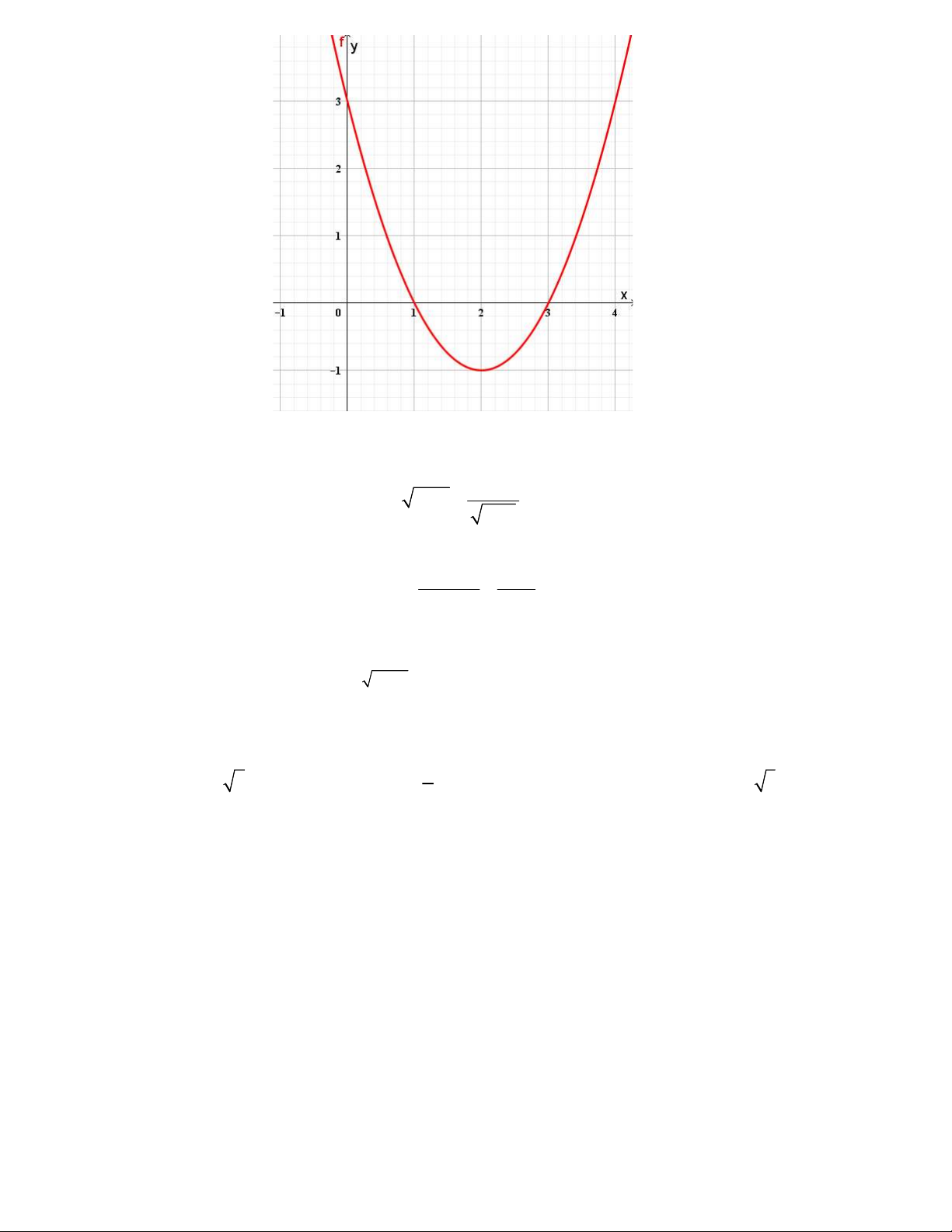
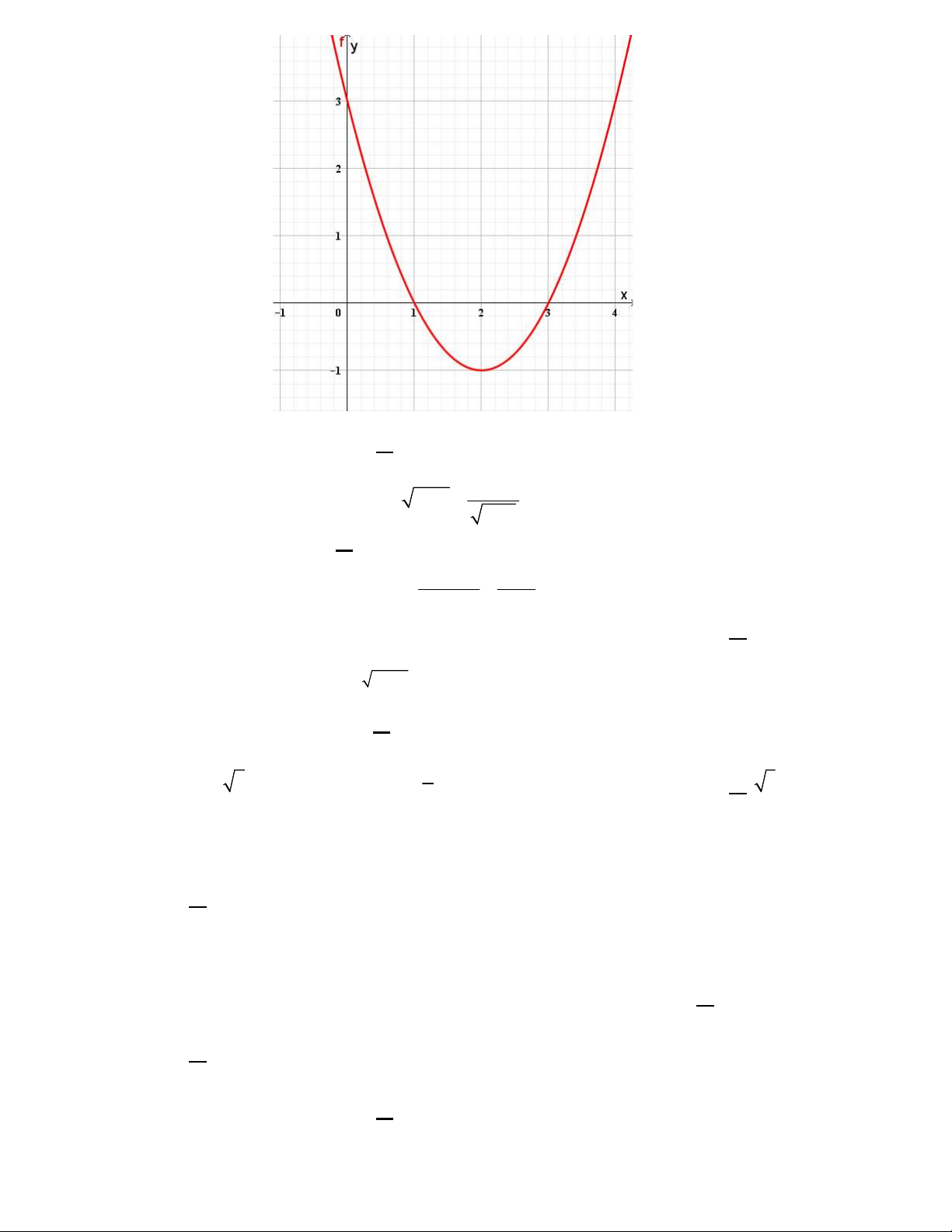
Câu 16. Cho hàm số bậc hai 2
y  f (x)  ax  bx  c có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của tham số m để đường thẳng y  m 1
 cắt đồ thị hàm số 2
y  f ( x )  ax  b x  c tại bốn điểm phân biệt ? A. 2. B. 3. C. 4. D. 5. 2 2x 1
Câu 17. Điều kiện của phương trình 5  x   2 là x 1 A. 1 x 5.
B. 1 x 5. C. 1 x 5. D. 1 x 5.
Câu 18. Tập nghiệm của phương trinh 4 x   0 là x(x  2) 2  x A. S    2 . B. S    2 . C. S   . D. S    2 .
Câu 19. Phương trình x  2
x 4 x 2  0 có bao nhiêu nghiệm ? A. 0. B. 1. C. 2. D. 3.
Câu 20. Phương trình nào sau đây là phương trình bậc nhất: 1 A. 2 x 1 0 . B. 1  0 . C. 2 3x  4  0 . D. 3x 1  0. x
Câu 21. Cho phương trình ax  b  0. Chọn khẳng định sai.
A. Phương trình có nghiệm duy nhất khi a  0 .
B. Phương trình vô nghiệm khi a  0 và b  0.
C. Phương trình vô nghiệm khi a  0 và b  0.
D. Phương trình có nghiệm x   khi a  0 và b 0.
Câu 22. Tìm tất cả các giá trị của tham số m sao cho phương trình m  2x 1 m  0 có nghiệm duy nhất. A. m  2  .
B. m  1. C. m 1. D. m  2  .
Câu 23. Với giá trị nào của tham số m thì phương trình  2 4  m  2
x  m  m  2  0 vô nghiệm ? A. m  2  . B. m  2 . C. m  2  . D. m  4 . Câu 24. Phương trình 2
(m1)x  m m2 có nghiệm khi: A. m  1. B. m   . C. m  0 . D. Không có m nào.
Câu 25. Số 2 là nghiệm của phương trình bậc hai nào trong các phương trình sau ? A. 2 x 4x 3  0. B. 2 2x 3x 2  0. C. 2 2x 3x 2  0. D. 3 x 8  0.
Câu 26. Nghiệm của phương trình 2
2x 5x 7  0 có thể xem là hoành độ giao điểm của hai đồ thị hàm số nào sau đây ? A. 2 y  2x và y  5  x 7 . B. 2 y  2x và y  5x 7 . C. 2 y  2x và y  5x 7 . D. 2 y  2x và y  5  x 7 . Câu 27. Phương trình 2 2 (m 1
 )x mx1 0 có số nghiệm là A. 0 . B. 1. C. 2. D. 3 .
Câu 28. Phương trình bậc hai nào dưới đây nhận hai số 2 1 và 2 1 làm nghiệm. A. 2 x  8x 1  0 . B. 2 x  8x 1  0 . C. 2 x  8x 1 0. D. 2 x  8x1 0. Câu 29. Phương trình 2
ax bx c  0 a 0 có hai nghiệm phân biệt trái dấu khi và chỉ khi: 0 0 A.  .  . P  D. P  0. S   B . 0  S   C. 0. 0  Câu 30. Phương trình 2 (1 )
m x 3x 1 0 có hai nghiệm âm phân biệt khi giá trị của m là 5 5 5 5 A.   m  1. B.   m  1. C.   m  1. D.   m  1. 4 4 4 4 Câu 31. Cho phương trình 2
x  2mx  3  0, giá trị của m để phương trình có hai nghiệm x , x sao 1 2 cho biểu thức 2 2
4(x  x )  x  x đạt giá trị lớn nhất là: 1 2 1 2 A. m  2  . B. m1 . C. m  1  . D. m  2 .
Câu 32. Tìm tất cả các giá trị thực của m để phương trình 2 2
 x  4x  m 5 có đúng hai nghiệm phân
biệt thuộc đoạn 1;2 . A. 5  m  7 . B. 5  m  7 . C. 1   m  5 . D. 1   m  7. Câu 33. Cho hàm số 2
y  x (m1)x 3 có đồ thị P , đường thẳng d  có phương trình y  xm . Tìm m để (d) cắt ( )
P tại hai điểm phân biệt A, B sao cho độ dài đoạn thẳng AB có giá trị nhỏ nhất. 1 A. m  3  . B. m  . C. m  2 D. m  1. 2 
Câu 34. Cho hai điểm A 3
 ;2, B1;4. Tính AB . A. 5 2 . B. 2 5 . C. 3 5 . D. 3 2 .   
Câu 35. Cho tam giác ABC có A 1  ;2, B3; 
1 ,C 2;3 . Tọa độ u  2 AB  BC là A.  9  ;10. B. 7;5 . C.  3  ;9 . D. 6;8 .        
Câu 36. Trong hệ trục tọa độ Oxy, cho u  3
 i 2 j và v  2i  xj . Tìm x sao cho u và v cùng phương. 1 4 1 A. x  . B. x   . C. x  . D. x 3. 3 3 2
Câu 37. Trong hệ trục tọa độ Oxy , cho A1; 2 , B2; 
3 . Tọa độ điểm C nằm trên trục tung sao cho , A B,C thẳng hàng là  1   7   4  A. C 3;0 . B. C 0;    . C. C 0;  . D. C 0;    3   3   3 
Câu 38. Trong hệ trục tọa độ Oxy, cho A2;  1 , B0; 2  ,C(2; 3
 ). Gọi M là trung điểm của AC .   
Tọa độ điểm D sao cho BD  BM  2CA là A. D2; 6   . B. D 0;3 . C. D 3  ;  1 . D. E 4;3 .
Câu 39. Trong hệ trục tọa độ Oxy , cho tam giác ABC có A2;   1 , B1;  5 và C thuộc trục Ox .
Trọng tâm G của tam giác ABC nằm trên đường phân giác góc phần tư thứ hai của hệ trục tọa
độ Oxy. Tọa độ của điểm C là A. C 1;0 . B. C3;0 . C. C 0; 2 . D.  2  ;0 .
Câu 40. Trong hệ trục tọa độ Oxy , cho A1;  1 , B1; 
3 . Tìm tọa độ điểm M thuộc trục Oy sao cho 2 2
AM  BM  10 (đơn vị độ dài). A. M  2  ;0. B. M 0;  1 . C. M 0; 2 . D. M 0;  1 .
Câu 41. Trong hệ trục tọa độ Oxy , cho A2;  1 , B 1  ;0, C0; 2
 . Tìm tọa độ điểm M thuộc trục
  
Ox sao cho MA2MB 3MC nhỏ nhất. A. M 2;  1 . B. M 3;0 . C. M 2;0 . D. M 4;0 . 3 1 3
Câu 42. Trong hệ tọa độ Oxy, cho điểm P(
, ) nằm trên nửa đường tròn đơn vị. Giá trị bằng 2 2 2
giá trị lượng giác nào sau đây của góc    POx ? A. sin  . B. cos . C. tan . D. cot .
Câu 43. Cho góc tù  , khẳng định nào sau đây là sai ? A. cos  0 . B. tan  0 . C. sin   0 . D. cot   0 . 2 0 0 Câu 44. Cho sin 
và 90    180 . Hãy tính cos . 3 3 1 1 3 A.  . B.  . C. . D. . 3 3 3 2 2
Câu 45. Cho  là góc tù và sin 
. Giá trị của biểu thức A  3cos  4sin bằng 5 1 1 A. 5 . B. 2 5 . C. . D. . 5 2 5 4 0 0
Câu 46. Cho tan  và 0    90 . Hãy tính cos  . 3 3 3 3 A. . B.  . C. . D. 7 . 2 5 5 3        
Câu 47. Cho hai vectơ a và b khác 0 . Xác định góc  giữa hai vectơ a và b khi 2 . a b  a . b . A.   0 180 . B.   0 120 . C.   0 90 . D.   0 60 .  
Câu 48. Cho tam giác ABC vuông cân tại A, cạnh AC  a . Tính AB.AC .          A. AB.AC  0 . B. 2 AB.AC  a . C. AB.BC  0 . D. 2 AB.AC  2a .  
Câu 49. Cho tam giác ABC đều có độ dài các cạnh là 6. Điểm M thỏa mãn điều kiện 1 BM   BC . 2   Tính BM .BA .         A. BM .BA  9 3 . B. BM .BA  9 3 . C. BM .BA  9 . D. BM .BA  9 . 
Câu 50. Cho hình vuông ABCD có cạnh là a . Điểm E là trung điểm của cạnh AB . Tính EB.CA . 2 A. 2 a 2a . B.  . C. 2 2a . D. 2 2a . 2
----------------HẾT---------------- TỔNG: 50 câu TRƯỜNG THCS&THPT
KIỂM TRA GIỮA KÌ I NĂM HỌC 2021 - 2022 LƯƠNG THẾ VINH MÔN TOÁN - LỚP 10 1 x
Câu 1. Tìm tập xác định của hàm số y  . 1 x A. D  0;  1 . B. D  0;  1 . C. D  0;  1 . D. D  0;  1 .
Câu 2. Cho hàm số y  f  x có đồ thị như hình vẽ. Hàm số đồng biến trên khoảng nào ? A.  ;  0. B. (0; 2) . C. 1;3. D. 2;.
Câu 3. Trong các hàm số sau, hàm số nào không phải là hàm số chẵn? 3 A. 4 2 y  x 3x . B. y   . C. 4 2 y  x 3x . D. 4 y  x 3x. 2 x
Câu 4. Hàm số nào trong các hàm số sau đây là hàm số bậc nhất ? 1 A. y  . B. y 13x . C. 2 y  x 2x . D. y  3. x
Câu 5. Hàm số nào dưới đây có đồ thị như hình bên ? 1 2 2 1 A. y  x 1 . B. y   x 1 . C. y  x 1 . D. y  x 1. 3 3 3 3
Câu 6. Với những giá trị nào của m để hàm số 2
y  (m 4)x 12m là hàm số bậc nhất ?  m  2 A. m   . B.  . m  2  m  2 C. m  2 . D.  . m  2 Câu 7. Cho parabol P 2
: y  x  6x  5 . Tìm tọa độ đỉnh của P . A. 3;4 . B.  3  ;4. C.3;  4 . D.  3  ; 4   . Câu 8. Hàm số bậc hai 2
y  3x  4x 1 có trục đối xứng là đường nào dưới đây ? 2 2 2 4 A. x   . B. x  . C. y  . D. x  . 3 3 3 3
Câu 9. Bảng biến thiên của hàm số 2
y 3x 6x5 là bảng nào sau đây ? A. B. C. D.
Câu 10. Khẳng định nào sau đây sai ? A. Đồ thị hàm số 2
y  2x 2x3 luôn cắt trục tung.  1  B. Hàm số 2
y  2x 2x3 nghịch biến trên khoảng  ;     .  4  C. Đồ thị hàm số 2
y  2x 2x3 luôn cắt trục hoành tại hai điểm phân biệt.  1  D. Hàm số 2
y  2x 2x3 đồng biến trên khoảng ;    .  4 
Câu 11. Với giá trị nào của m để đồ thị hàm số 2 2
y  x 2xm m  0 có đỉnh nằm trên đường thẳng y  x 1? A. m  1 . B. m  1  . C. m  1 . D. m  2 . Câu 12. Cho hàm số 2
y  ax  bx  c có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?
A. a  0 , b  0, c  0.
B. a  0 , b  0, c  0 .
C. a  0, b  0, c  0 .
D. a  0 , b  0, c  0. Câu 13. Cho hàm số 2
y  2x  8x  5 . Với mọi x  , khẳng định nào sau đây là đúng ?
A. Giá trị nhỏ nhất của hàm số là 3 .
B. Giá trị lớn nhất của hàm số là 3 .
C. Giá trị lớn nhất của hàm số là 5 .
D. Hàm số không có giá trị lớn nhất và nhỏ nhất.
Câu 14. Đường thẳng nào sau đây cắt trục đối xứng của parabol 2
y  2x 4x 3 tại điểm có tung độ gấp đôi hoành độ? A. y  2x 1. B. y  2x  1. C. y  x 1. D. y  x  2 .
Câu 15. Giá trị nào của m dưới đây để đường thẳng y  2mx 1 không có điểm chung với Parabol 2 y  x 3? A. m  1. B. m  2 . C. m  3. D. m  4 .
Câu 16. Cho hàm số bậc hai 2
y  f (x)  ax  bx  c có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của tham số m để đường thẳng y  m 1
 cắt đồ thị hàm số 2
y  f ( x )  ax  b x  c tại bốn điểm phân biệt ? A. 2. B. 3. C. 4. D. 5. 2 2x 1
Câu 17. Điều kiện của phương trình 5  x   2 là x 1 A. 1 x 5.
B. 1 x 5. C. 1 x 5. D. 1 x 5.
Câu 18. Tập nghiệm của phương trinh 4 x   0 là x(x  2) 2  x A. S    2 . B. S    2 . C. S   . D. S    2 .
Câu 19. Phương trình x  2
x 4 x 2  0 có bao nhiêu nghiệm ? A. 0. B. 1. C. 2. D. 3.
Câu 20. Phương trình nào sau đây là phương trình bậc nhất: 1 A. 2 x 1 0 . B. 1  0 . C. 2 3x  4  0 . D. 3x 1  0. x
Câu 21. Cho phương trình ax  b  0. Chọn khẳng định sai.
A. Phương trình có nghiệm duy nhất khi a  0 .
B. Phương trình vô nghiệm khi a  0 và b  0.
C. Phương trình vô nghiệm khi a  0 và b  0.
D. Phương trình có nghiệm x   khi a  0 và b 0.
Câu 22. Tìm tất cả các giá trị của tham số m sao cho phương trình m  2x 1 m  0 có nghiệm duy nhất. A. m  2  .
B. m  1. C. m 1. D. m  2  .
Câu 23. Với giá trị nào của tham số m thì phương trình  2 4  m  2
x  m  m  2  0 vô nghiệm ? A. m  2  . B. m  2 . C. m  2  . D. m  4 . Câu 24. Phương trình 2
(m1)x  m m2 có nghiệm khi: A. m  1. B. m   . C. m  0 . D. Không có m nào.
Câu 25. Số 2 là nghiệm của phương trình bậc hai nào trong các phương trình sau ? A. 2 x 4x 3  0. B. 2 2x 3x 2  0. C. 2 2x 3x 2  0. D. 3 x 8  0.
Câu 26. Nghiệm của phương trình 2
2x 5x 7  0 có thể xem là hoành độ giao điểm của hai đồ thị hàm số nào sau đây ? A. 2 y  2x và y  5  x 7 . B. 2 y  2x và y  5x 7 . C. 2 y  2x và y  5x 7 . D. 2 y  2x và y  5  x 7 . Câu 27. Phương trình 2 2 (m 1
 )x mx1 0 có số nghiệm là A. 0 . B. 1. C. 2. D. 3 .
Câu 28. Phương trình bậc hai nào dưới đây nhận hai số 2 1 và 2 1 làm nghiệm. A. 2 x  8x 1  0 . B. 2 x  8x 1  0 . C. 2 x  8x 1 0. D. 2 x  8x1 0. Câu 29. Phương trình 2
ax bx c  0 a 0 có hai nghiệm phân biệt trái dấu khi và chỉ khi: 0 0 A.  .  . P  D. P  0. S   B . 0  S   C. 0. 0  Câu 30. Phương trình 2 (1 )
m x 3x 1 0 có hai nghiệm âm phân biệt khi giá trị của m là 5 5 5 5 A.   m  1. B.   m  1. C.   m  1. D.   m  1. 4 4 4 4 Câu 31. Cho phương trình 2
x  2mx  3  0, giá trị của m để phương trình có hai nghiệm x , x sao 1 2 cho biểu thức 2 2
4(x  x )  x  x đạt giá trị lớn nhất là: 1 2 1 2 A. m  2  . B. m1 . C. m  1  . D. m  2 .
Câu 32. Tìm tất cả các giá trị thực của m để phương trình 2 2
 x  4x  m 5 có đúng hai nghiệm phân
biệt thuộc đoạn 1;2 . A. 5  m  7 . B. 5  m  7 . C. 1   m  5 . D. 1   m  7. Câu 33. Cho hàm số 2
y  x (m1)x 3 có đồ thị P , đường thẳng d  có phương trình y  xm . Tìm m để (d) cắt ( )
P tại hai điểm phân biệt A, B sao cho độ dài đoạn thẳng AB có giá trị nhỏ nhất. 1 A. m  3  . B. m  . C. m  2 D. m  1. 2 
Câu 34. Cho hai điểm A 3
 ;2, B1;4. Tính AB . A. 5 2 . B. 2 5 . C. 3 5 . D. 3 2 .   
Câu 35. Cho tam giác ABC có A 1  ;2, B3; 
1 ,C 2;3 . Tọa độ u  2 AB  BC là A.  9  ;10. B. 7;5 . C.  3  ;9 . D. 6;8 .        
Câu 36. Trong hệ trục tọa độ Oxy, cho u  3
 i 2 j và v  2i  xj . Tìm x sao cho u và v cùng phương. 1 4 1 A. x  . B. x   . C. x  . D. x 3. 3 3 2
Câu 37. Trong hệ trục tọa độ Oxy , cho A1; 2 , B2; 
3 . Tọa độ điểm C nằm trên trục tung sao cho , A B,C thẳng hàng là  1   7   4  A. C 3;0 . B. C 0;    . C. C 0;  . D. C 0;    3   3   3 
Câu 38. Trong hệ trục tọa độ Oxy, cho A2;  1 , B0; 2  ,C(2; 3
 ). Gọi M là trung điểm của AC .   
Tọa độ điểm D sao cho BD  BM  2CA là A. D2; 6   . B. D 0;3 . C. D 3  ;  1 . D. E 4;3 .
Câu 39. Trong hệ trục tọa độ Oxy , cho tam giác ABC có A2;   1 , B1;  5 và C thuộc trục Ox .
Trọng tâm G của tam giác ABC nằm trên đường phân giác góc phần tư thứ hai của hệ trục tọa
độ Oxy. Tọa độ của điểm C là A. C 1;0 . B. C3;0 . C. C 0; 2 . D.  2  ;0 .
Câu 40. Trong hệ trục tọa độ Oxy , cho A1;  1 , B1; 
3 . Tìm tọa độ điểm M thuộc trục Oy sao cho 2 2
AM  BM  10 (đơn vị độ dài). A. M  2  ;0. B. M 0;  1 . C. M 0; 2 . D. M 0;  1 .
Câu 41. Trong hệ trục tọa độ Oxy , cho A2;  1 , B 1  ;0, C0; 2
 . Tìm tọa độ điểm M thuộc trục
  
Ox sao cho MA2MB 3MC nhỏ nhất. A. M 2;  1 . B. M 3;0 . C. M 2;0 . D. M 4;0 . 3 1 3
Câu 42. Trong hệ tọa độ Oxy, cho điểm P(
, ) nằm trên nửa đường tròn đơn vị. Giá trị bằng 2 2 2
giá trị lượng giác nào sau đây của góc    POx ? A. sin  . B. cos . C. tan . D. cot .
Câu 43. Cho góc tù  , khẳng định nào sau đây là sai ? A. cos  0 . B. tan  0 . C. sin   0 . D. cot   0 . 2 0 0 Câu 44. Cho sin 
và 90    180 . Hãy tính cos . 3 3 1 1 3 A.  . B.  . C. . D. . 3 3 3 2 2
Câu 45. Cho  là góc tù và sin 
. Giá trị của biểu thức A  3cos  4sin bằng 5 1 1 A. 5 . B. 2 5 . C. . D. . 5 2 5 4 0 0
Câu 46. Cho tan  và 0    90 . Hãy tính cos  . 3 3 3 3 A. . B.  . C. . D. 7 . 2 5 5 3        
Câu 47. Cho hai vectơ a và b khác 0 . Xác định góc  giữa hai vectơ a và b khi 2 . a b  a . b . A.   0 180 . B.   0 120 . C.   0 90 . D.   0 60 .  
Câu 48. Cho tam giác ABC vuông cân tại A, cạnh AC  a . Tính AB.AC .          A. AB.AC  0 . B. 2 AB.AC  a . C. AB.BC  0 . D. 2 AB.AC  2a .  
Câu 49. Cho tam giác ABC đều có độ dài các cạnh là 6. Điểm M thỏa mãn điều kiện 1 BM   BC . 2   Tính BM .BA .         A. BM .BA  9 3 . B. BM .BA  9 3 . C. BM .BA  9 . D. BM .BA  9 . 
Câu 50. Cho hình vuông ABCD có cạnh là a . Điểm E là trung điểm của cạnh AB . Tính EB.CA . 2 A. 2 a 2a . B.  . C. 2 2a . D. 2 2a . 2
----------------HẾT---------------- TỔNG: 50 câu
Document Outline

  • ĐỀ THI GHK1-LTV-2021-2022-CHI CO DE BAI
  • ĐỀ THI GHK1-LTV-2021-2022