


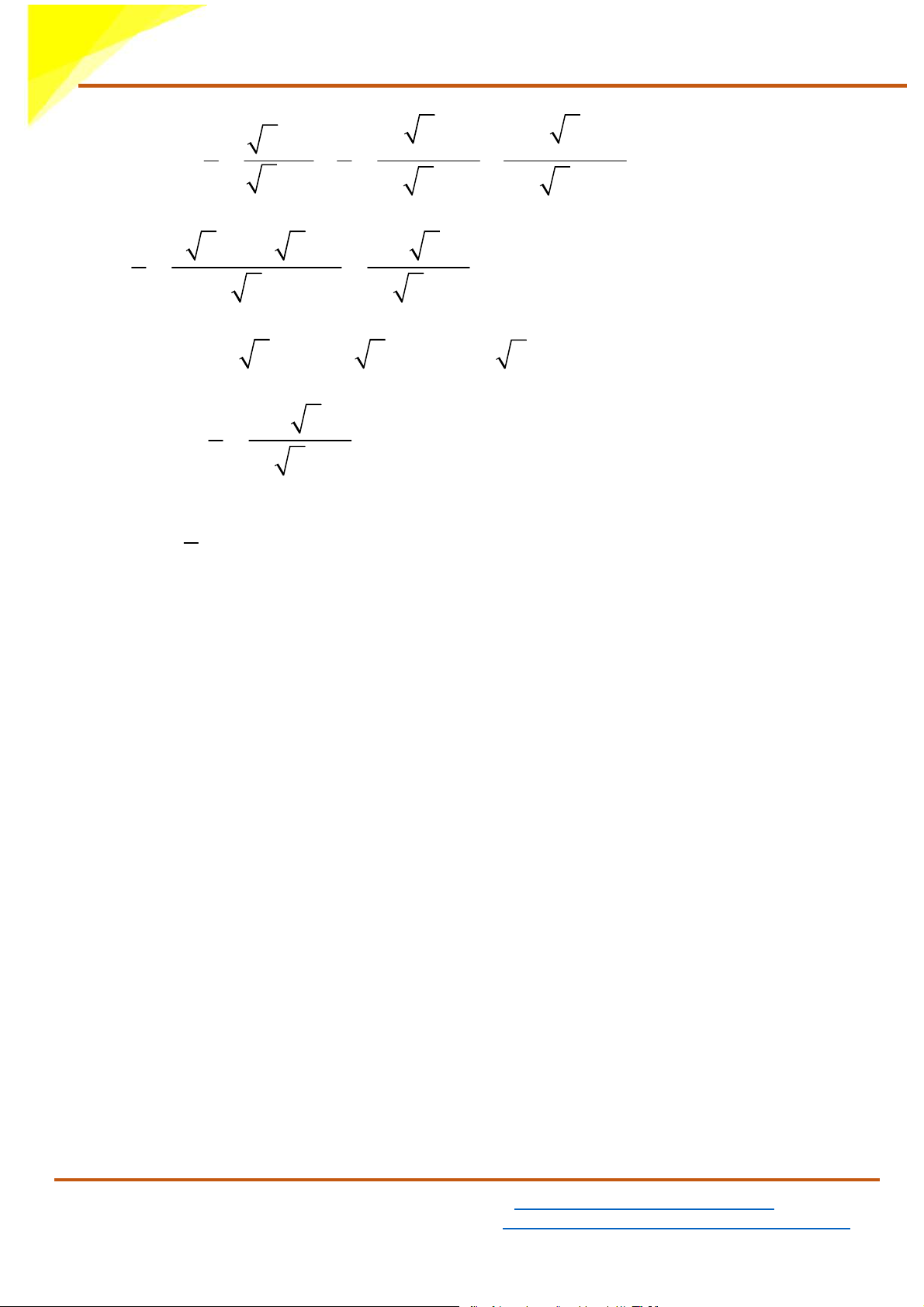







Preview text:
1/1 4
Thầy Phúc Toán – GV dạy Toán Online
ĐỀ KIỂM TRA HỌC KÌ I
UBND HUYỆN PHÚC THỌ
NĂM HỌC 2018 − 2019
PHÒNG GIÁO DỤC & ĐÀO TẠO MÔN: TOÁN 9
Thời gian làm bài: 90 phút. Câu 1. (2,0 điểm) + Cho biểu thức x 3 1 x M = + và N =
với x > 0,x ≠ 9 x − 9 x + 3 x − 3
a) Tính giá trị của biểu thức N khi x = 4
b) Rút gọn biểu thức B = M : N c) Chứng minh 1 B > 3 Câu 2. (2,0 điểm) Giải phương trình a) 2 4x + 4x + 1 = 6 b) 1
4x + 20 + x + 5 − 9x + 45 = 4 3 Câu 3. (2,0 điểm)
Cho đường thẳng y = (k + 1)x + k (d)
a) Tìm giá trị của k để đường thẳng (d) đi qua điểm ( A 1;2)
b) Tìm giá trị của k để đường thẳng (d) song song với đường thẳng y = 2x + 3
c) Tìm điểm cố định mà (d) luôn đi qua với mọi k
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 2/1 4
Thầy Phúc Toán – GV dạy Toán Online Câu 4. (3,5 điểm)
Cho AC là đường kính của đường tròn tâm (O;R). Trên tiếp tuyến tại
A của (O;R), lấy điểm I sao cho IA lớn hơn R . Từ I vẽ tiếp tuyến thứ
hai với (O;R) với tiếp điểm là B . Qua O kẻ đường thẳng vuông góc với
AC cắt đường thẳng BC tại H .
a) Chứng minh BC //OI
b) Chứng minh rằng tứ giác AOHI là hình chữ nhật
c) Tia OB cắt IH tại K . Chứng minh tam giác IOK cân.
d) Khi AI = 2R, tính diện tích tam giác ABC Câu 5. (0,5 điểm) Cho , a ,
b c là ba số dương thỏa mãn điều kiện a + b + c = 1 + + +
Tìm giá trị nhỏ nhất của biểu thức
(1 a)(1 b)1 c) A =
(1 −a)(1 −b)1 −c)
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 3/1 4
Thầy Phúc Toán – GV dạy Toán Online HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm). + Cho biểu thức x 3 1 x M = + và N =
với x > 0,x ≠ 9 x − 9 x + 3 x − 3
a) Tính giá trị của biểu thức N khi x = 4
b) Rút gọn biểu thức B = M : N c) Chứng minh 1 B > 3 Lời giải
a) Thay x = 4 (thỏa mãn điều kiện) vào biểu thức N , ta được: 4 2 2 N = = = = 2 − 4 − 3 2 − 3 1 − + b) x 3 1 x
B = M : N = + : x − 9 x + 3 x − 3 x + 3 x − 3 x B = ( +
x + 3)( x − 3) ( x + 3)( x − 3) : x − 3 x + 3 + x − 3 x x + x x − 3 B = ( = ⋅
x + 3)( x − 3) : x − 3 ( x + 3)( x − 3) x
x ( x +1)( x − 3) B = (
x + 3)( x − 3) x x + 1 B = x + 3
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 4/1 4
Thầy Phúc Toán – GV dạy Toán Online 3 + − + x + ( x 1) 1.( x 3 1 1 1 ) c) Xét B − = − = + 3 x + 3 3 3( x + 3) 3( x + 3) 1
3 x + 3 − x − 3 2 x B − = = 3 3( x + 3) 3( x + 3)
Mà x > 0 nên x > 0 ⇒ 2 x > 0 và 3( x + 3) > 0 Do đó: 1 2 x B − = ( > x + ) 0 3 3 3 Vậy 1 B > 3
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 5/1 4
Thầy Phúc Toán – GV dạy Toán Online Câu 2. (2,0 điểm) Giải phương trình a) 2 4x + 4x + 1 = 6 b) 1
4x + 20 + x + 5 − 9x + 45 = 4 3 Lời giải
a) Điều kiện xác định: x ∈ ℝ 2 2
4x + 4x + 1 = 6 ⇔ (2x + 1) = 6 ⇔ 2x + 1 = 6 5 x = 2x +1 = 6 2x = 5 2 ⇔ ⇔ ⇔
(thỏa điều kiện xác định) 2x + 1 = 6 − 2x = 7 − 7 − x = 2 −
Vậy tập nghiệm của phương trình là: 7 5 S = ; 2 2
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 6/1 4
Thầy Phúc Toán – GV dạy Toán Online
b) Điều kiện xác định 4x + 20 ≥ 0 x + 5 ≥ 0 ⇔ x ≥ 5 − 9x 45 0 + ≥ 1
4x + 20 + x + 5 − 9x + 45 = 4 3 1
⇔ 4(x + 5) + x + 5 − 9(x + 5) = 4 3 1
⇔ 2 x + 5 + x + 5 − ⋅3 x + 5 = 4 3
⇔ 2 x + 5 + x + 5 − x + 5 = 4
⇔ 2 x + 5 = 4 ⇔ x + 5 = 2 ⇔ x + 5 = 4 x = 1
− (thỏa điều kiện x ≥ 5 − )
Vậy tập nghiệm của phương trình là S = {− } 1
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 7/1 4
Thầy Phúc Toán – GV dạy Toán Online Câu 3. (2,0 điểm)
Cho đường thẳng y = (k + 1)x + k (d)
a) Tìm giá trị của k để đường thẳng (d) đi qua điểm ( A 1;2)
b) Tìm giá trị của k để đường thẳng (d) song song với đường thẳng y = 2x + 3
c) Tìm điểm cố định mà (d) luôn đi qua với mọi k Lời giải
a) Vì đường thẳng (d) đi qua điểm (
A 1;2) nên thay x = 1;y = 2 vào
phương trình: y = (k + 1)x + k , ta được: 2 = (k + 1).1 + k
⇔ 2 = k + 1 + k ⇔ 2k = 1 1 ⇔ k = 2
b) Đường thẳng (d) song song với đường thẳng y = 2x + 3 khi k + 1 = 2 ⇔ k = 1 k ≠ 3
Vậy k = 1 thì đường thẳng (d) song song với đường thẳng y = 2x + 3
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 8/1 4
Thầy Phúc Toán – GV dạy Toán Online
c) Gọi M(x ;y ) là điểm cố định mà (d) luôn đi qua 0 0
Thay x = x ;y = y vào phương trình y = (k + 1)x + k , ta được: 0 0
y = (k + 1)x + k ⇔ kx + x + k = y 0 0 0 0 0
⇔ kx + x + k −y = 0 0 0 0
⇔ k(x +1)+ x − y = 0 (1) 0 0 0 x +1 = 0 x = 1 − x = 1 −
Để (1) luôn đúng với mọi k 0 0 0 ⇔ ⇔ ⇔ x − y = 0 x = y y = 1 − 0 0 0 0 0
Vậy (d) luôn đi qua điểm cố định M( 1 − ; 1 − ) với mọi k
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 9/1 4
Thầy Phúc Toán – GV dạy Toán Online Câu 4. (3,5 điểm)
Cho AC là đường kính của đường tròn tâm (O;R). Trên tiếp tuyến tại
A của (O;R), lấy điểm I sao cho IA lớn hơn R . Từ I vẽ tiếp tuyến thứ
hai với (O;R) với tiếp điểm là B . Qua O kẻ đường thẳng vuông góc với
AC cắt đường thẳng BC tại H
a) Chứng minh BC //OI
b) Chứng minh rằng tứ giác AOHI là hình chữ nhật
c) Tia OB cắt IH tại K . Chứng minh tam giác IOK cân.
d) Khi AI = 2R, tính diện tích tam giác ABC Lời giải
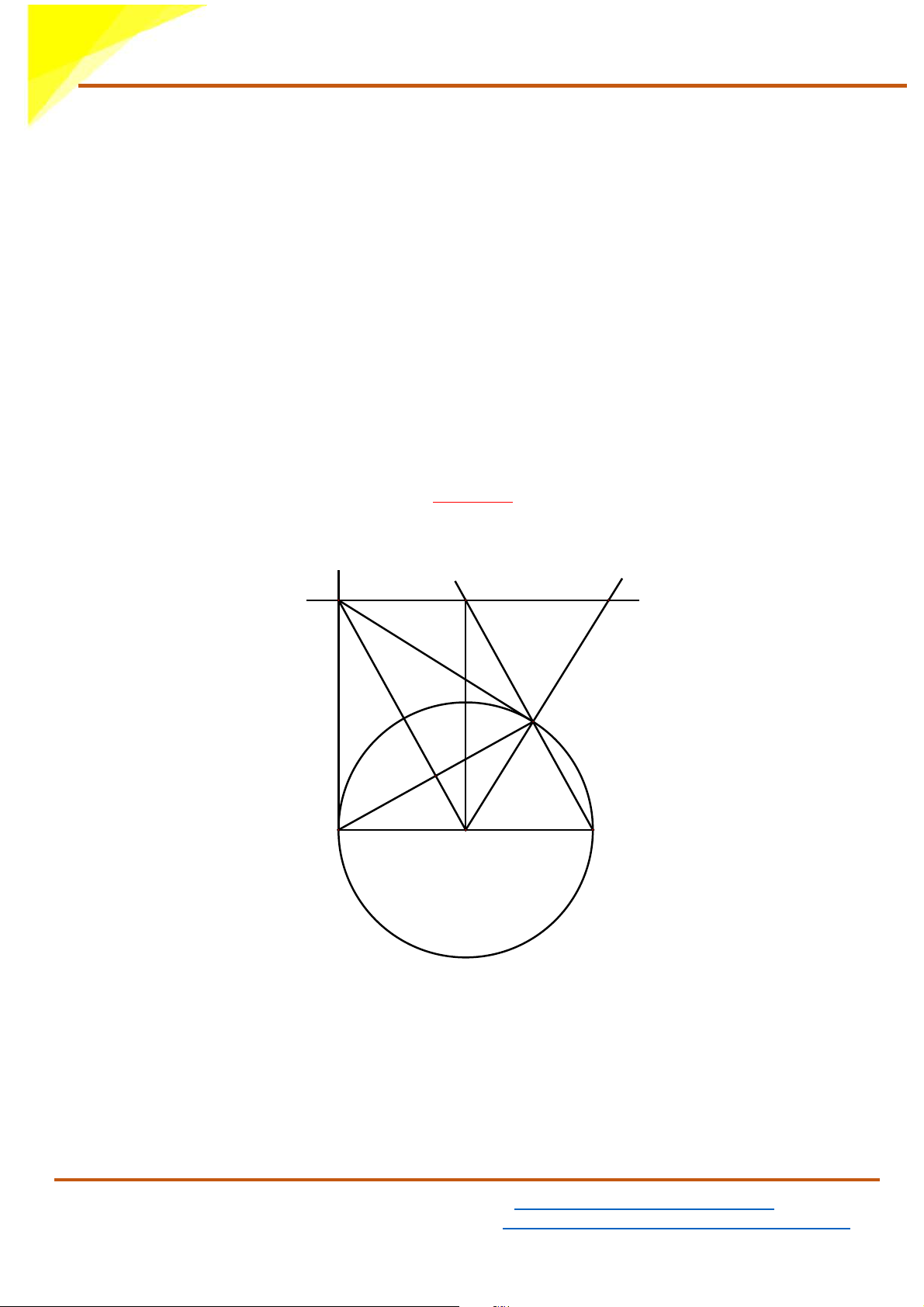
a) Chứng minh BC //OI I K H B E C A O
Xét (O;R) có AI và BI là các tiếp tuyến cắt nhau tại I nên IA = IB
Ta lại có: OA =OB = R
Do đó: OI là đường trung trực của đoạn thẳng AB ⇒OI ⊥ AB
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 10/ 14
Thầy Phúc Toán – GV dạy Toán Online Vì A
∆ BC nội tiếp đường tròn đường kính AC nên 0 ABC = 90
⇒ AB ⊥ BC OI ⊥ AB
⇒ BC //OI BC ⊥ AB
b) Chứng minh rằng tứ giác AOHI là hình chữ nhật
Xét tứ giác AOHI có: 0
IAO = 90 (vì AI là tiếp tuyến của (O;R) tại A) (1) 0
AOH = 90 (vì OH ⊥ AC ) (2) Xét A ∆ IO và O ∆ HC có: 0 IAO = HOC = 90
OA =OC = R
IOA = HCO (Hai góc đồng vị, BD / /OI ) Do đó: A ∆ IO = O
∆ HC(g.c.g)
⇒ IO = HC (Hai cạnh tương ứng) Mà IO //HC
⇒ Tứ giác IOCH là hình bình hành.
⇒ IH //OC hay IH //AC (vì O là trung điểm của AC ) IH / /AC 0
⇒ IH ⊥OH ⇒OHI = 90 (3) OH ⊥ AC
Từ (1), (2) và (3) suy ra tứ giác AOHI là hình chữ nhật.
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 11/ 14
Thầy Phúc Toán – GV dạy Toán Online
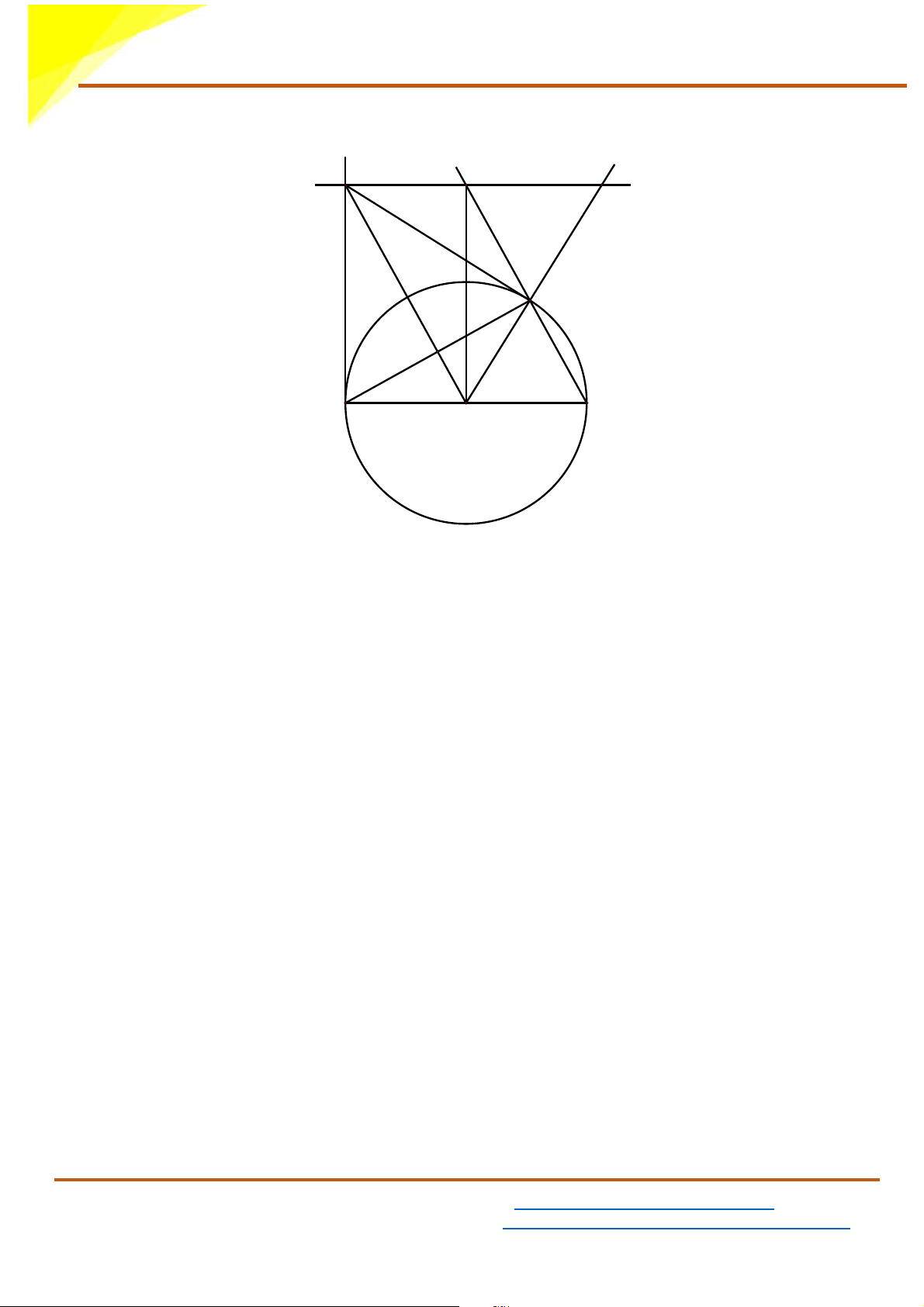
c) Tia OB cắt IH tại K . Chứng minh tam giác IOK cân. I K H B E C A O
Vì tứ giác AOHI là hình chữ nhật nên 0 AIH = 90 Ta có: 0
OIK = 90 − AIO Ta lại có: 0
AOI = 90 − AIO (vì O
∆ AI vuông tại A) ⇒ AOI =OIK
Mà IOK = AOI (tính chất 2 tiếp tuyến cắt nhau)
Suy ra: OIK =OIK Vậy I
∆ OK cân tại K
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 12/ 14
Thầy Phúc Toán – GV dạy Toán Online
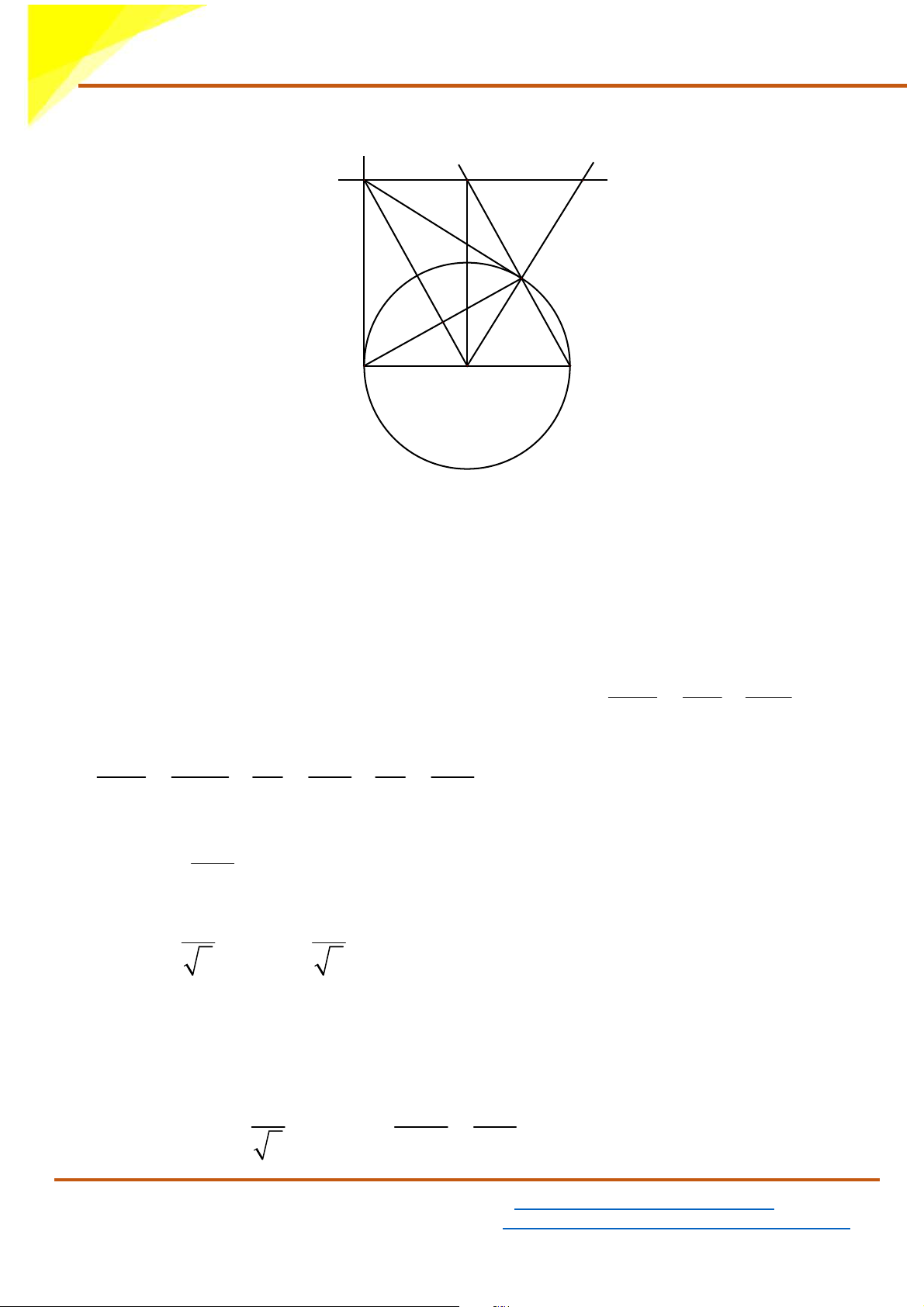
d) Khi AI = 2R, tính diện tích tam giác ABC I K H B E C A O
Gọi E là giao điểm của OI và AB
Theo câu a) ta có: OI là đường trung trực của đoạn thẳng AB
⇒ AB ⊥OI tại E và AE = EB Xét I
∆ AO vuông tại A, có AE ⊥OI .
Theo hệ thức lượng trong tam giác vuông, ta có: 1 1 1 = + 2 2 2 AE IA OA 1 1 1 1 1 5 = + = + = 2 2 2 2 2 2 AE (2R) R 4R R 4R 2 4R 2 ⇒ AE = 5 2R 4R ⇒ AE = ⇒ AB =
(Vì E là trung điểm của đoạn thẳng AB ) 5 5
Áp dụng định lí Pitago vào A
∆ BC vuông tại B 2 2 2 2 2 2
AC = AB + BC ⇒ BC = AC − AB 2 2 2 4R 16R 4R 2 2 2
BC = (2R) − = 4R − = 5 5 5
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 13/ 14
Thầy Phúc Toán – GV dạy Toán Online 2R ⇒ BC = 5 2 Diện tích tam giác 1 1 4R 2R 4R ABC là: S
= ⋅AB ⋅BC = ⋅ ⋅ = ABC 2 2 5 5 5
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017 14/ 14
Thầy Phúc Toán – GV dạy Toán Online Câu 5. (0,5 điểm) Cho , a ,
b c là ba số dương thỏa mãn điều kiện a + b + c = 1 + + +
Tìm giá trị nhỏ nhất của biểu thức
(1 a)(1 b)1 c) A =
(1 −a)(1 −b)1 −c) Lời giải Vì a, ,
b c > 0 và a + b + c = 1 nên ta có:
1 −a = b + c > 0 ;
1 −b = a +c > 0 ;
1 −c = a + b > 0 Ta có:
1 + a = 1 + (1 −b −c) = (1 −b) + (1 −c) ≥ 2 (1 −b)(1 −c) (BĐT Cauchy)
Tương tự: 1 +b ≥ 2 (1 −a)(1 −c) (BĐT Cauchy)
1 + c ≥ 2 (1 −a)(1 −b) (BĐT Cauchy) 2 2 2
(1 + a)(1 + b)(1 + c) ≥ 8 (1 −a) (1 −b) (1 −c) = 8(1 −a)(1 −b)(1 −c)
(1 + a)(1 + b)1 + c) ⇒ ≥ 8
(1 −a)(1 −b)1 −c)
Dấu “=” xảy ra khi 1 −a = 1 −b = 1 −c ⇔ a = b = c 1
Mà a +b +c = 1 ⇒ a = b = c = 3
Vậy giá trị nhỏ nhất của A là 8 khi 1
a = b = c = 3
GV: Nguyễn Hữu Phúc 0888014879 Facebook: https://facebook.com/nhphuclk
Youtube:https://youtube.com/nguyenhuuphuc2017




