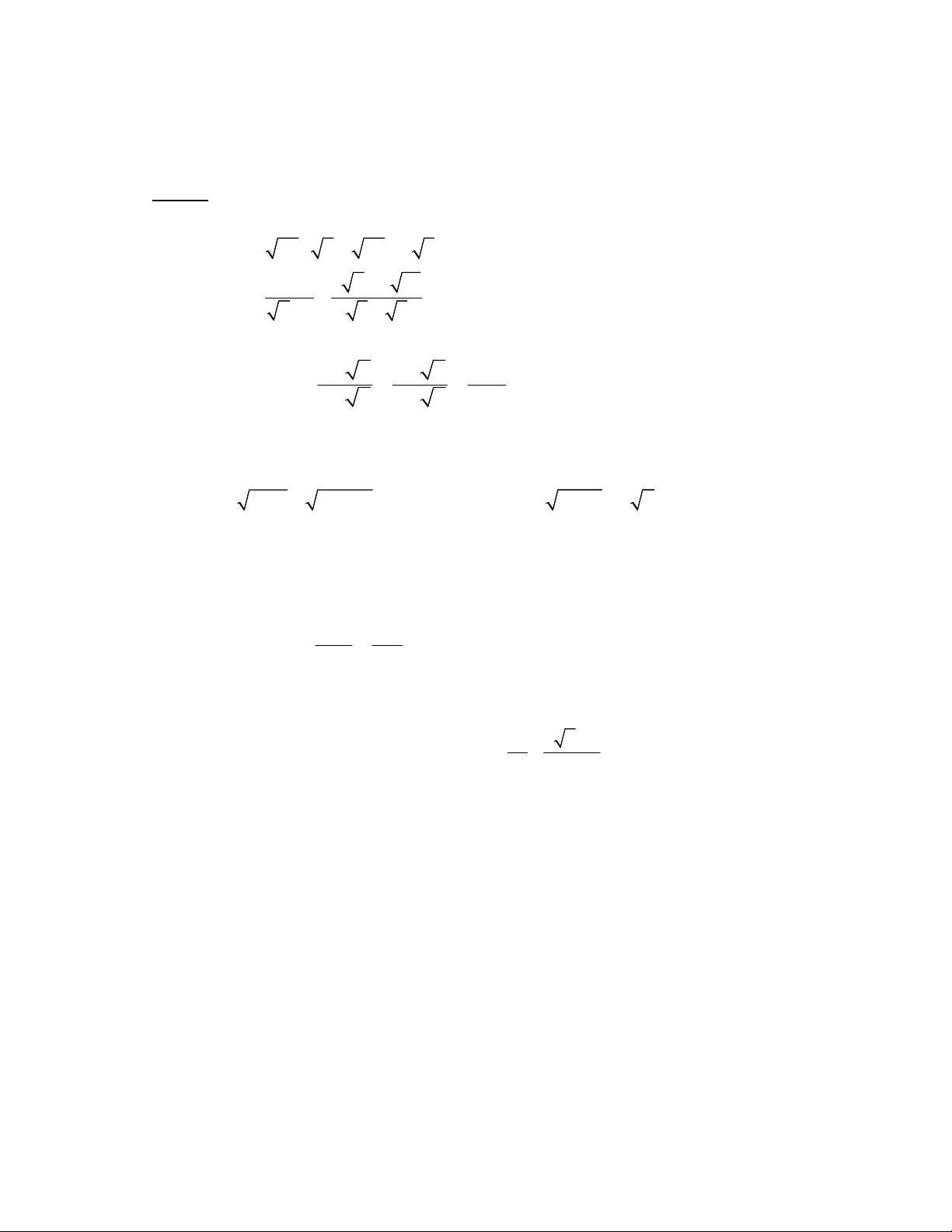
Preview text:
TRƯỜNG THCS TRẦN MAI NINH
KHẢO SÁT CHẤT LƯỢNG GIỮA KỲ I THÀNH PHỐ THANH HÓA NĂM HỌC 2020 - 2021 MÔN: TOÁN - LỚP: 9
Thời gian làm bài: 90 phút (không kể phát đề) ĐỀ LẺ
Câu 1 (2,0 điểm): Rút gọn các biểu thức sau: a) A = 45 : 5 72 3 8 3 3 6 3 10 b) B = 2 1 3 5 Câu 2 (2,0 điểm): Cho biểu thức: 1 b 1 b 4 b B . 1 b 1 b 1 b
a) Tìm điều kiện của b để B xác định và rút gọn B.
b) Tìm giá trị của b để B > - 1.
Câu 3 (2,0 điểm): Giải các phương trình sau:
a) x 2 9x 18 4 0 . b) 5x 1 2 x 0 . Câu 4 (3,0 điểm):
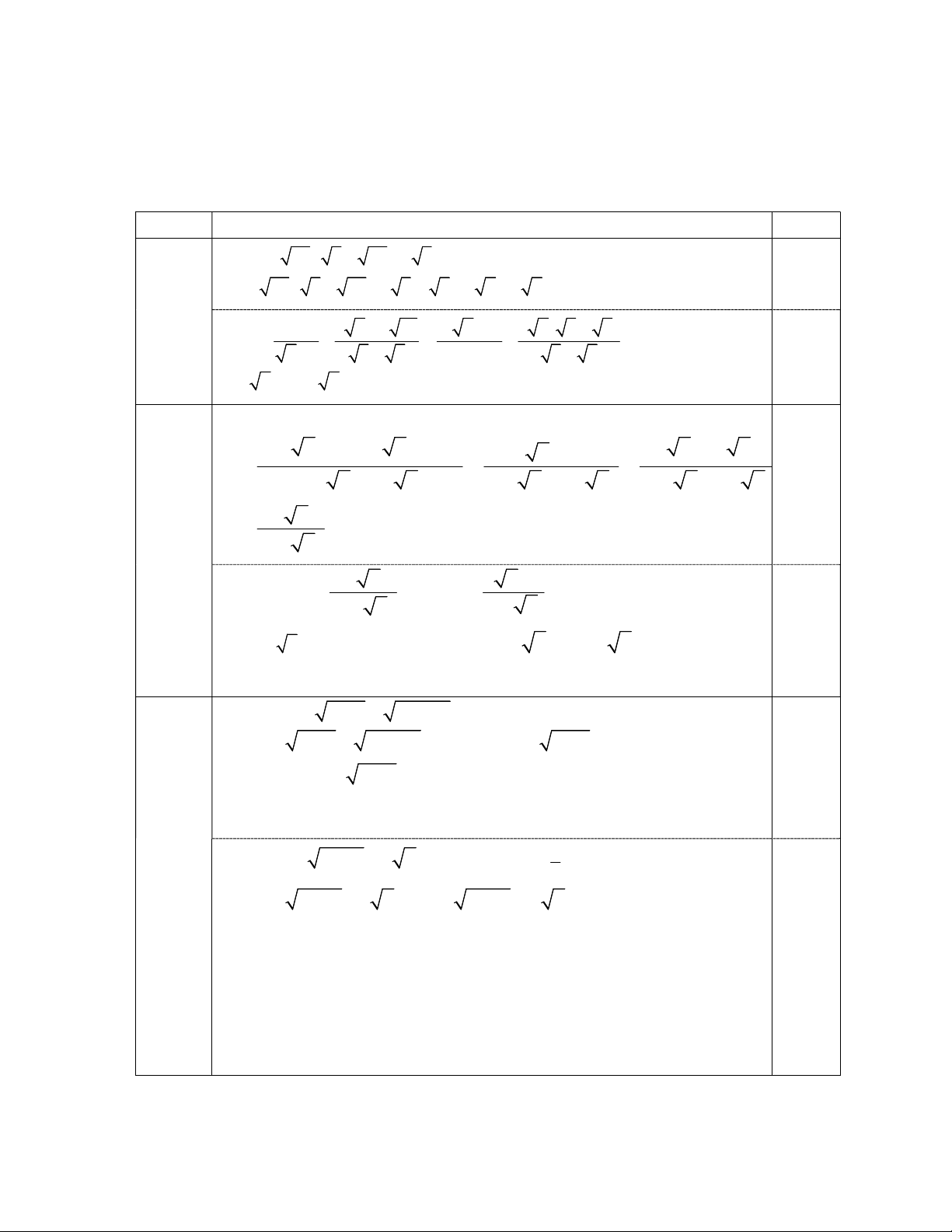
Cho ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC.
a) Cho AB = 6cm, AC = 8cm. Tính AH. 2 AB HB b) Chứng minh . 2 AC CH
c) Chứng minh BC . BE . CF = AH3. Câu 5 (1,0 điểm):
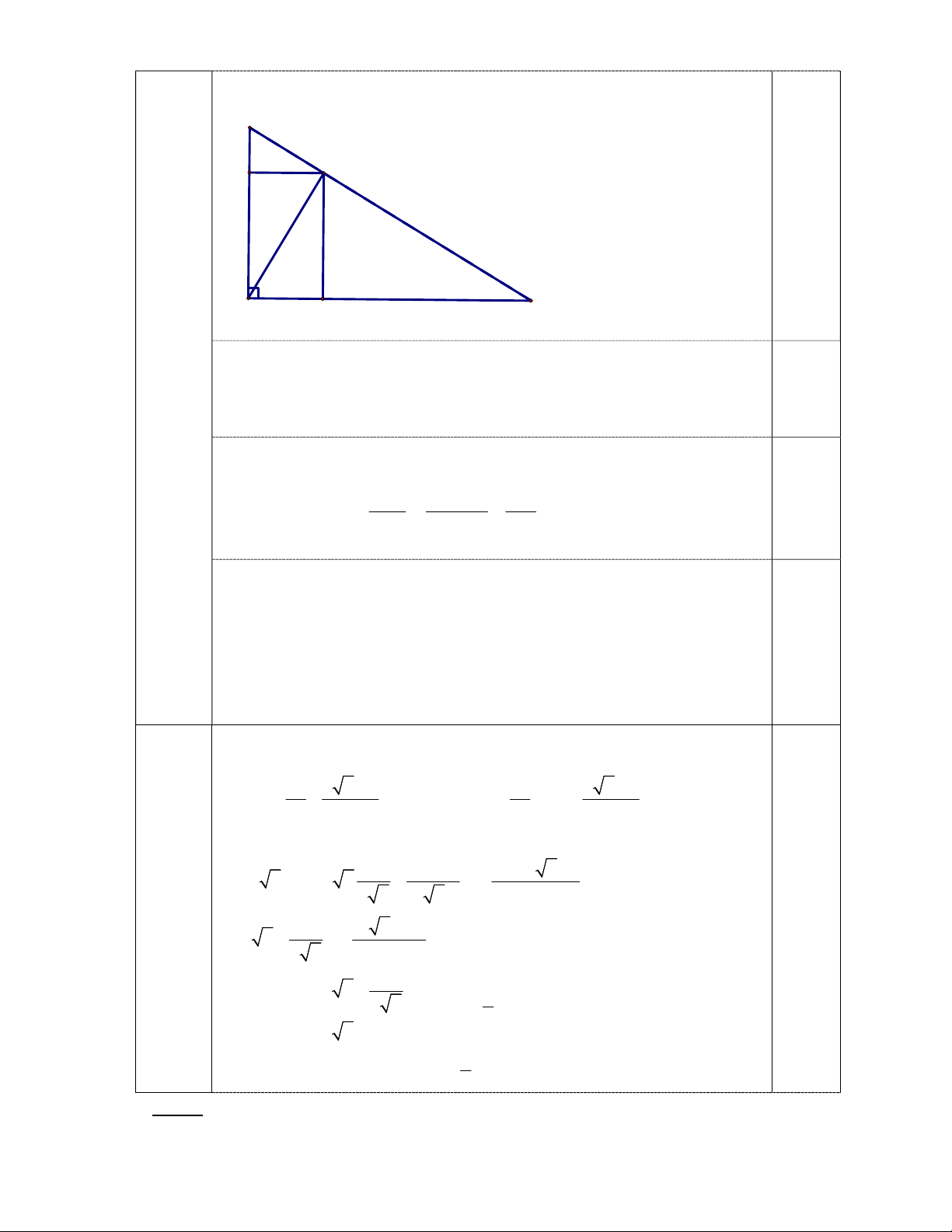
Tìm giá trị nhỏ nhất của biểu thức: 1 4 x 3 A 4x 2021 với x > 0. 4x x 1 ======== HẾT ========
ĐÁP ÁN ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA KỲ I MÔN: TOÁN - LỚP: 9 NĂM HỌC: 2020 - 2021 ĐỀ LẺ Câu Nội dung Điểm a) A = 45 : 5 72 3 8 1,0
A= 45 : 5 72 3 8 9 6 2 6 2 3 Câu 1 0,5đ 3 3 6 3 10 3( 2 1) 3 2( 3 5) b) B 2 1 3 5 2 1 3 5 0,5đ 3 2 3 3 2 3 a) ĐKXĐ 0 b 1 ( * ) 0,5
b 2 b 2 1 1 4b 4 b 1 4 4 b b b B 0,5 1 b 1 b
1 b 1 b 1 b 1 b 4 b B 0,25 1 b Câu 2 0,25 b) 4 b 3 b 1 B 1 1 0 0 (1) 1 b 1 b
Do 3 b 1 0 với mọi 0 nên 1 b 0 b 1 0,25
0 b 1 ( thỏa mãn (*) ). Kết luận : 0 b 1 0,25
a) x 2 9x 18 4 0 . ĐKXĐ: x 2
x 2 9x 18 4 0 4 2 x 2 0 0,5
4 2 x 2 2 x 2 x 6 Câu 3 x= 6 (thỏa mãn đkxđ) 0,5
Vậy phương trình đã cho có nghiệm là: x = 6 b) 5x 1 2 x 0 . 1 0,25 ĐKXĐ: x 5
5x 1 2 x 0 5x 1 2 x 5x 1 4x x 1 0,5 x =1 thỏa mãn ĐKXĐ
Vậy phương trình đã cho có nghiệm là: x =1 0,25
- Vẽ hình và viết GT, KL 0,5 B H E A F C
Câu 4 a) Áp dụng định lí PiTaGo vào ABC ta có BC2 = AB2 + AC2 0,5 tính được BC = 10cm,
+) Áp dụng hệ thức lượng vào tam giác vuông ABC, đường cao
AH có: AB . AC = AH . BC. Khi đó tính được AH = 4,8 cm 0.5
b) Áp dụng hệ thức lượng vào tam giác vuông ABC, đường cao
AH có AB2 = BH . BC (1) AC2 = CH . BC (2 ) 0,5 2 AB BH.BC BH Từ (1) và (2) có : . 2 AC CH.BC CH 0,5
c) Áp dụng hệ thức lượng vào tam giác vuông ABC, đường cao
AH có AH2 = BH . HC => AH4 = BH2. CH2 BH2 = BE . AB; CH2 = AC . CF => AH4 = BE. AB. AC. CF 0,25
Mà AB . AC = AH . BC => AH4 = BE. CF. BC.AH => BC . BE . CF = AH3. 0,25 Với x > 0, ta có: 1 4 x 3 1 4 x 3 A 4x 2021 (4x 2 ) (4 ) 2019 4x x 1 4x x 1 1 1 4x 4 x 1 2 (2 x) 2.2 x 2019 0,5 2 2 x (2 x) x 1 2 1 (2 x 1) 2 Câu 5 (2 x ) 2019 2019 2 x x 1 1 2 x 0 1 A 2019 0,5 2 x x 4 2 x 1 0 1
Vậy GTNN của A là 2019 tại x 4
Lưu ý: Học sinh không vẽ hình hoặc vẽ sai hình không chấm bài hình.
Học sinh có cách giải khác thì chấm điểm tương ứng.