
















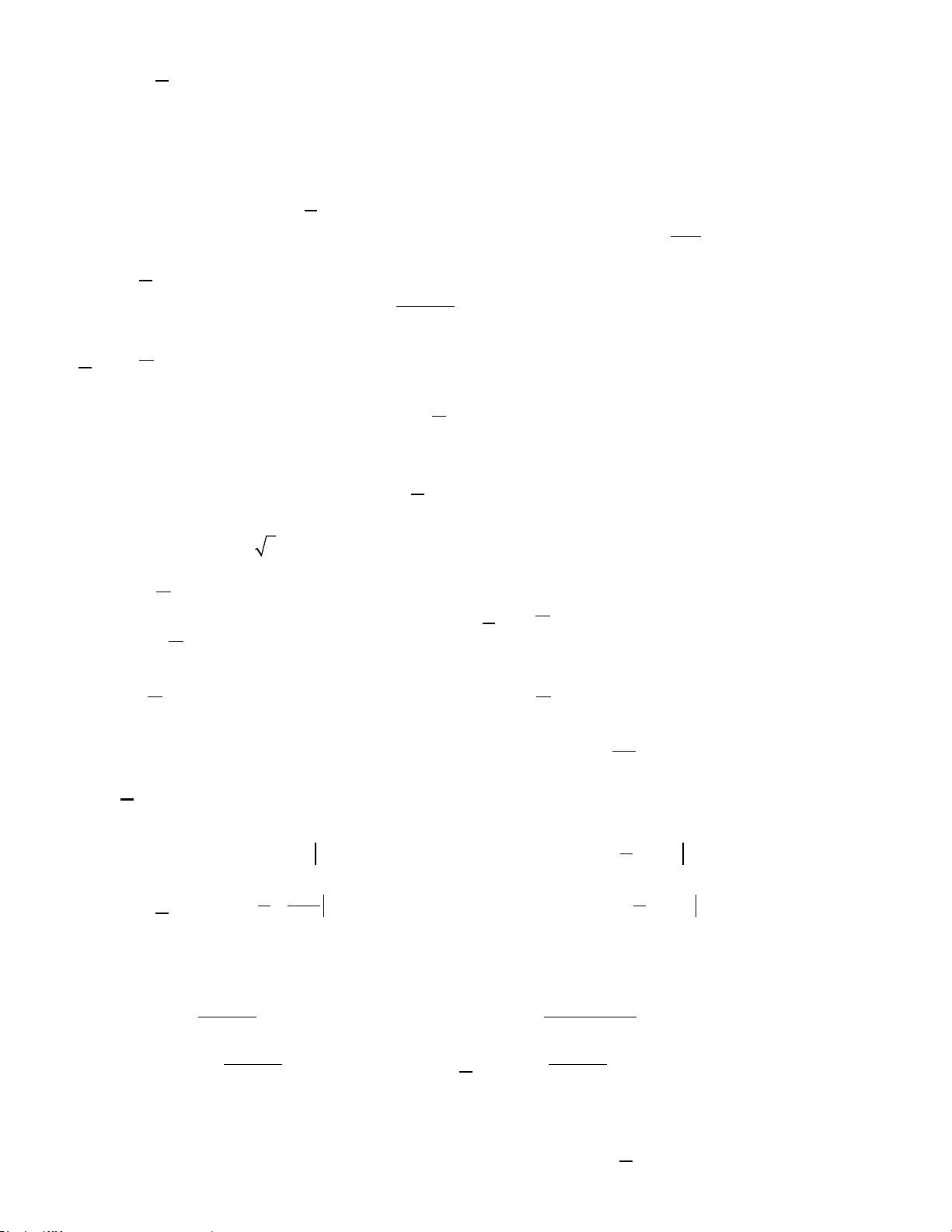





Preview text:
SỞ GIÁO DỤC & ĐÀO TẠO THANH HÓA ĐỀ KHẢO SÁT CHẤT LƯỢNG CÁC MÔN THI
TRƯỜNG THPT BA ĐÌNH
TN THPT LẦN 1, NĂM HỌC 2023 - 2024 Môn: Toán, Lớp 11. Mã đề thi: 555
Thời gian làm bài: 90 phút;
(50 câu trắc nghiệm)
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
Câu 1: Cho các giới hạn: lim f (x) = 2; lim g (x) = 3 , hỏi lim 3 f (x) + 4g (x) bằng x→ 0 x x→ 0 x x→ 0 x A. 17 . B. 2 . C. 18. D. 6 − .
Câu 2: Công thức nào sau đây là đúng với cấp số cộng có số hạng đầu u1, công sai d ,
n∈, n ≥ 2 ?
A. u = u + d .
B. u = u + n − d . n 1 1 ( ) n 1
C. u = u + n + d .
D. u = u − n − d . n 1 1 ( ) n 1 1 ( )
Câu 3: Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AB . Gọi M và N lần lượt là
trung điểm của các cạnh AD và SA . Tìm khẳng định đúng
A. MN // (SAC) .
B. MN //(ABCD) .
C. MN // (SBC) .
D. MN // (SBD).
Câu 4: Hàm số nào sau đây không liên tục tại x = 2 A. 2023 y + = . B. 3x 1 y = . x − 2 x − 22 C. x − 2 y + = . D. 2x 5 y = . x + 2 2 x − 2
Câu 5: Cho hình tứ diện ABCD . Khẳng định nào sau đây đúng?
A. AB và CD song song.
B. AB và CD chéo nhau.
C. Tồn tại một mặt phẳng chứa AB và CD .
D. AB và CD cắt nhau.
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm của AC và BD
. Gọi M , N lần lượt là trung điểm các cạnh SB,SD . Đường thẳng MN song song với đường
thẳng nào trong các đường thẳng sau? A. AC . B. BD . C. SO . D. BC .
Trang 1/6 - Mã đề thi 555
Câu 7: Cho hình hộp ABC . D A′B C ′ D
′ ′ . Mệnh đề nào sau đây sai? A. (BDD B ′ ′) // ( ACC A ′ ′). B. ( ABB A ′ ′) // (CDD C ′ ′).
C. ( ABCD) // ( A′B C ′ D ′ ′) .
D. ( AA′D D ′ ) // (BCC B ′ ′) .
Câu 8: Đổi số đo của góc α =120° sang rađian ta được A. π π π π . B. . C. 2 . D. 3 . 2 3 3 4
Câu 9: Trong các mệnh đề sau, mệnh đề nào sai? A.
sin x 1 x k2 , k .
B. tanx 0 x k , k . 2 C.
cotx 1 x k , k .
D. cosx 0 x k2 , k . 4 2
Câu 10: Cho cấp số nhân u với số hạng đầu u = 2
− và công bội q = 5
− . Viết bốn số hạng n 1
đầu tiên của cấp số nhân. A. 2 − ; 10; 50; − 250 B. 2 − ; 10; 50; 250 C. 2 − ; −10; − 50; − 250 D. 2 − ; 10; −50; 250 2 Câu 11: Tính n −1 L = lim . 3
n→+∞ n + n + 3 A. L =1. B. L = 0. C. L = 3. D. L = 2.
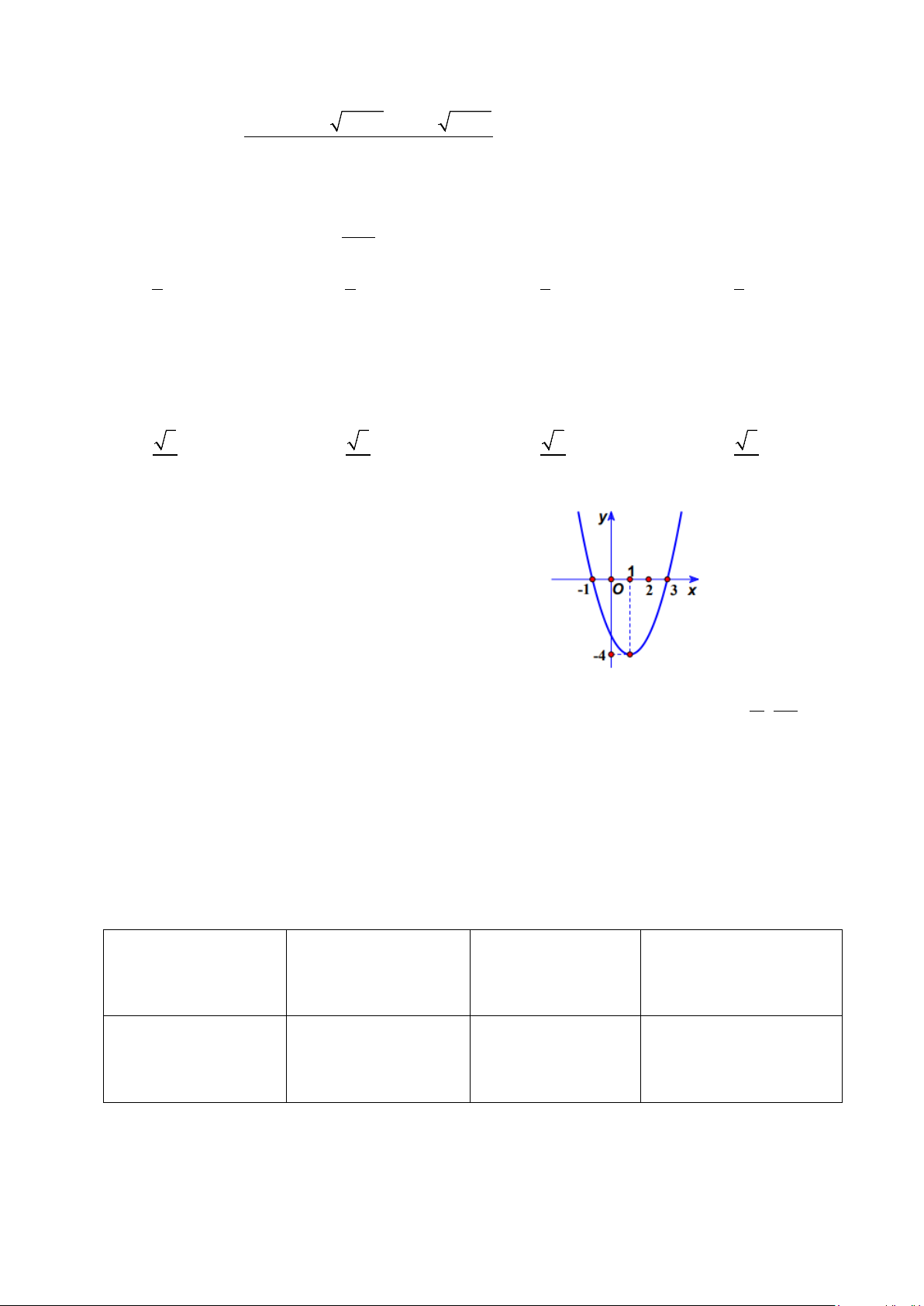
Câu 12: Đường cong dưới đây là đồ thị hàm số nào?
A. y = sin x .
B. y =1+ cos x .
C. y = cos x .
D. y = sin 2x .
Câu 13: Phương trình π sin x = s 2 in có nghiệm là 3 2π x = + k2π A. 3 π
với k . B. 2 x = −
+ k2π với k . π x = + k2π 3 3 C. 2π π x =
+ kπ với k D. 2 x = ±
+ k2π với k . 3 3
Câu 14: Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào giảm? n ) n n
A. u = n + B. 4 u = n . n 4. 3 C. u = 3 − .n D. u = (− ) 1 n (5n − n ) n 1 .
Trang 2/6 - Mã đề thi 555 u = 1 1
Câu 15: Cho dãy số (u biết: với * . Hãy tìm u n ) n ∈ N u = u 2 n 1 2 + n 1 + A. u = u = u = u = 2 4 B. 2 1 C. 2 2 D. 2 3
Câu 16: Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Ba điểm không thẳng hàng. B. Một đường thẳng và một điểm thuộc nó.
C. Hai đường thẳng chéo nhau. D. Ba điểm mà nó đi qua.
Câu 17: Phát biểu nào sau đây là sai? A. 1 lim = 0 ( * k ∈ N ) .
B. lim c = c ( c là hằng số). k n→+∞ n n→+∞ C. 1 lim = 0. D. lim n q = 0 ( q > ) 1 . n→+∞ n n→+∞
Câu 18: Cho cấp số cộng (u biết u = và u = . Hãy tìm 2 7 1 4 u n ) 3 A. u = B. u = C. u = D. u = 3 11 3 3 3 28 3 10 Câu 19: Tính −x + 2 N = lim . x→+∞ x +1 A. 1 − . B. 6 . C. 1. D. 2 .
Câu 20: Cho cấp số nhân có (u có u = 2 và u = 6 . Tìm công bội n ) 1 2 q . A. 1 q = . B. 1 q = . C. q =12 . D. q = 3. 3 12 u = 5
Câu 21: Cho dãy số (u 1 u n ) với
. Số hạng tổng quát của dãy số là số hạng nào u = n n 1 u + n n + dưới đây? A. (n − ) 1 n u − = . B. (n ) 1 u = + . n 5 n n 2 2 C. (n + ) 1 u = + . D. (n 1)(n 1) u − + = + . n 5 n 5 n 2 2
Câu 22: Phương trình 3 cot x −1 = 0 có nghiệm là π π
A. x = + kπ (k ∈) .
B. x = + k2π (k ∈) 6 3 π = + π π x k2
C. x = + kπ (k ∈) . D. 6 (k ∈). 3 π
x = − + k2π 6
Câu 23: Cho cấp số nhân (u 2
n ) có u = 3; q = . Chọn kết quả đúng. 1 3 n 1 −
A. (u là một dãy số tăng. B. 2 u = . n 3. n ) 3 n
C. Bốn số hạng tiếp theo của cấp số nhân là : 4 6 8 2; ; ; . D. 2 u = n 3. 3 3 3 3
Câu 24: Cho cấp số cộng (un )có 1
u = 3,công sai d = 2. Tổng 20 số hạng đầu tiên của cấp số cộng đã cho bằng
Trang 3/6 - Mã đề thi 555 A. 610. B. 440. C. 420. D. 480.
Câu 25: Số nghiệm thực của phương trình 2sin π x +1 = 0 trên đoạn 3 − ;10π là: 2 A. 12 B. 11 C. 20 D. 21 π
Câu 26: Trên đường tròn lượng giác, điểm biểu diễn góc lượng giác có số đo 11 − thuộc góc 3 phần tư thứ A. IV B. III C. I D. II
Câu 27: Tìm tập xác định của hàm số cos x y = . sin x −1 π A.
\{kπ ,k ∈ } .
B. \ + kπ,k ∈ . 2 π C.
\{k2π ,k ∈ } .
D. \ + k2π,k ∈ . 2
Câu 28: Cho hình lăng trụ ABC.A’B’C’. Gọi I và I ' lần lượt là trung điểm của AB, A’B’. Qua
phép chiếu song song lên mặt phẳng chiếu (A’B’C’) theo phương chiếu AI ' biến I thành điểm nào sau đây ? A. A’ B. I ' C. B’ D. C’
Câu 29: Cho bốn điểm không đồng phẳng A, B, C, D. Gọi I, K lần lượt là trung điểm của AD và
BC. Giao tuyến của hai mặt phẳng (IBC) và (KAD) là A. AK B. DK C. IK D. BC
Câu 30: Tìm tập giá trị T của hàm số y 3cos 2x 5.
A. T 2;8.
B. T 1; 1.
C. T 1;1 1.
D. T 5;8. 2 4x −3x +1
Câu 31: Cho hai số thực a và b thỏa mãn lim
− ax − b = 0. Khi đó a + b bằng x→+∞ x + 2 A. 4 . B. 4 − . C. 7 − . D. 7 . Câu 32: Giới hạn + + =
+ , với a,b∈ . Tính S =5a +b →−∞ ( 2 lim
5x 2x x 5) a 5 b x A. S = −1. B. S = 5 − . C. S =5 D. S = 2 2
ax − (a − 2)x − 2 khi x ≠ 1
Câu 33: Cho hàm số f (x)= x + 3 − 2 2 8 + a khi x =1
Gọi S là tập hợp các giá trị của tham số a để hàm số liên tục tại x =1. Tính tổng các phần tử của S. A. 4 B. 5 C. 6 D. 7
Câu 34: Giới hạn + + − =
, (với a là phân số tối giản), khi đó a + b →+∞ ( 2 lim 4 3. 2 2 a n n n n ) b b bằng A. 3 B. 5 C. 1 D. 7
Câu 35: Tập nghiệm của phương trình sin(2x +π ) + sin x =0 là A. π S k2π; k2π k = − + ∈ . B. π
S = k2π; + k2π k ∈ . 3 3
Trang 4/6 - Mã đề thi 555
C. S = {k2π;π + k2π k ∈ } k . D. π 2π S k2π; k = + ∈ . 3 3
Câu 36: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu (α ) (β ) và a ⊂ (α ), b ⊂ (β ) thì a .b
B. Nếu a b và a ⊂ (α ), b ⊂ (β ) thì (α ) (β ).
C. Nếu (α ) (β ) và a ⊂ (α ), b ⊂ (β ) thì a và b chéo nhau.
D. Nếu (γ ) ∩(α ) = a, (γ ) ∩(β ) = b và (α ) (β ) thì a .b
Câu 37: Có bao nhiêu giá trị nguyên của m∈[0;10] để phương trình sau 2
msin 2x + cos 4x = m π π
có bốn nghiệm phân biệt trong đoạn 5 ; − ? 8 8 A. 3 B. 2 C. 1 D. 0
Câu 38: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Gọi H, I, K lần lượt là trung điểm của , SA AB, .
CD Khẳng định nào sau đây đúng ?
A. HK // (SBD) .
B. HK // (SAD) .
C. HK // (SBC) .
D. HK // (SAC) . Câu 39: Giới hạn
an − bn + − n = (a,b (. Khi đó 2 2 a + b bằng n→+∞ ( 2 ) 1 lim 1 2 A. 9 B. 2 C. 13 D. 5
Câu 40: Cho hình chóp tứ giác S.ABCD . Gọi I , J, K lần lượt là trọng tâm của các tam
giác ABC , SBC và SAC . Trong các khẳng định sau, khẳng định nào đúng?
A. (IJK ) // (SBC) .
B. (IJK ) // (SAC) .
C. (IJK ) // (SAB) .
D. (IJK ) // (SDC) .
Câu 41: Tổng các nghiệm của phương trình sin xcos x + 2sin x − cos x − 2 = 0trên khoảng (0;100) là π π A. 1023 . B. 248π . C. 495 . D. 512π . 2 2
u + u + u = 3
Câu 42: Tìm công sai d của cấp số cộng (u thỏa mãn 1 2 3
, biết (u là dãy số n ) n ) 2 2 2
u + u + u = 131 1 2 3 tăng. A. d = 8. B. d = 3. C. d = 6 . D. d = 4 .
Câu 43: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung
điểm của các cạnh SB và SD . Khẳng định nào sau đây đúng
A. MN //(ABCD)
B. MN //(SBC)
C. MN //(SBD)
D. MN //(SAB) f (x) − 2
Câu 44: Cho hàm số y = f (x) xác định trên và thỏa mãn lim = 3 . Tính giới hạn x→ − 1 x +1 f ( x) 2 + 4 3− f (x) −8 L = lim 2 x→ −1 x −1 A. L = 12 − . B. L = 0 . C. L = 9 . D. L = 3 − .
Trang 5/6 - Mã đề thi 555
Câu 45: Cho tứ diện ABCD có M, N lần lượt là trung điểm của BC và CD. Gọi K là điểm tùy ý
thuộc miền trong tam giác ABD. Giao tuyến của (KMN) và (ABD) có tính chất là:
A. nằm trong mặt phẳng (ACD)
B. Song song với BD C. Cắt cạnh BD
D. Cắt cạnh AC. Câu 46: Cho hàm số 2
y = f (x) = ax + bx + c ( a ≠ 0)
có đồ thị như hình vẽ bên. Hỏi phương trình 2 . a f (cosx) + .
b f (cosx) + c = 0 π π
có bao nhiêu nghiệm trong khoảng 7 ; ? 2 2 A. 5 B. 4 C. 2 D. 3
Câu 47: Cho hình hộp ABCD.A’B’C’D’. Gọi I, J lần lượt là hai điểm nằm trên đường chéo B’D
và AC sao cho IJ // BC’. Tỉ số IJ bằng: BC ' A. 1 B. 3 C. 1 D. 1 2 4 3 4
Câu 48: Cho hình chóp S.ABCD có BC // AD, BC = 2, AD =1, AB = .
b Tam giác SAD đều. Mặt
phẳng (P) đi qua điểm M trên cạnh AB và song song với các đường thẳng SA và BC, đồng thời
cắt CD, SC, SB theo thứ tự tại N, P, Q. Đặt AM = x, (0 < x < b). Gọi S(x) là diện tích của tứ
giác MNPQ. Khi đó S(x) lớn nhất bằng: A. 3 B. 3 C. 3 D. 3 12 2 6 3 2 3 Câu 49: Cho
(x + 2024) 1+ ax − 2024 1 lim
+ bx = 4048. Khi đó 2a−3b bằng x→0 x A. 12288 B. 12 C. 1012 D. 6 3 u = 1
Câu 50: Cho dãy số (u xác định bởi 2
. Biết số hạng tổng quát của dãy n ) 1 u = ∀ ∈ + n n ; * 1 4 − 4un số (u là 1 1 u = +
với a,b,c∈ = + + n ) n
. Tính S a b c a b + cn
A. S =3.
B. S = − 5 .
C. S = 7 .
D. S = −1 ----------- HẾT ---------- Người ra đề Người thẩm định đề Điện thoại học sinh (ký và ghi rõ họ tên) (ký và ghi rõ họ tên) phản ánh sau buổi khảo sát (nếu cần) 0986723021 Thầy Lê Hoàng Tuấn Mai Huy Sáu
Nguyễn Văn Tiến
Trang 6/6 - Mã đề thi 555
SỞ GIÁO DỤC & ĐÀO TẠO THANH HÓA ĐỀ KHẢO SÁT CHẤT LƯỢNG CÁC MÔN THI
TRƯỜNG THPT BA ĐÌNH
TN THPT LẦN 1, NĂM HỌC 2023 - 2024 Môn: Toán, Lớp 11. Mã đề thi: 666
Thời gian làm bài: 90 phút;
(50 câu trắc nghiệm)
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm của AC và BD
. Gọi M , N lần lượt là trung điểm các cạnh SB,SD . Đường thẳng MN song song với đường
thẳng nào trong các đường thẳng sau? A. AC . B. BC . C. BD . D. SO . u = 1 1
Câu 2: Cho dãy số (u biết: với * . Hãy tìm u n ) n ∈ N u = u 2 n 1 2 + n 1 + A. u = u = u = u = 2 2 B. 2 4 C. 2 3 D. 2 1
Câu 3: Hàm số nào sau đây không liên tục tại x = 2 A. 2023 y + − + = . B. 2x 5 y = . C. x 2 y = . D. 3x 1 y = . x − 2 2 x − 2 x + 2 x − 22
Câu 4: Công thức nào sau đây là đúng với cấp số cộng có số hạng đầu u1, công sai d ,
n∈, n ≥ 2 ?
A. u = u + n + d .
B. u = u + n − d . n 1 1 ( ) n 1 1 ( )
C. u = u + d .
D. u = u − n − d . n 1 1 ( ) n 1
Câu 5: Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AB . Gọi M và N lần lượt là
trung điểm của các cạnh AD và SA . Tìm khẳng định đúng.
A. MN // (ABCD) .
B. MN //(SAC) .
C. MN // (SBC) .
D. MN // (SBD).
Câu 6: Cho hình hộp ABC . D A′B C ′ D
′ ′ . Mệnh đề nào sau đây sai? A. ( ABB A ′ ′) // (CDD C ′ ′). B. (BDD B ′ ′) // ( ACC A ′ ′).
C. ( ABCD) // ( A′B C ′ D ′ ′) .
D. ( AA′D D ′ ) // (BCC B ′ ′) .
Câu 7: Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào giảm? n ) n n
A. u = n + B. 4 u = n . n 4. 3 C. u = (− ) 1 n (5n − D. u = − n 3 .n n )1.
Trang 1/6 - Mã đề thi 666
Câu 8: Trong các mệnh đề sau, mệnh đề nào sai? A.
cos x 0 x k2 , k .
B. cotx 1 x k , k . 2 4 C.
tan x 0 x k , k .
D. sinx 1 x k2 , k . 2
Câu 9: Cho cấp số nhân u với số hạng đầu u = 2
− và công bội q = 5
− . Viết bốn số hạng đầu n 1 tiên của cấp số nhân. A. 2 − ; 10; 50; − 250 B. 2 − ; 10; 50; 250 C. 2 − ; −10; − 50; − 250 D. 2 − ; 10; −50; 250 Câu 10: Tính −x + 2 N = lim . x→+∞ x +1 A. 1 − . B. 6 . C. 1. D. 2 .
Câu 11: Phương trình π sin x = s 2 in có nghiệm là 3 A. 2π π x =
+ kπ với k B. 2 x = ±
+ k2π với k . 3 3 2π x = + k2π C. 3 π
với k . D. 2 x = −
+ k2π với k . π x = + k2π 3 3
Câu 12: Cho hình tứ diện ABCD . Khẳng định nào sau đây đúng?
A. AB và CD chéo nhau.
B. AB và CD cắt nhau.
C. Tồn tại một mặt phẳng chứa AB và CD .
D. AB và CD song song.
Câu 13: Đổi số đo của góc α =120° sang rađian ta được A. 3π π π π . B. . C. 2 . D. . 4 3 3 2
Câu 14: Cho các giới hạn: lim f (x) = 2; lim g (x) = 3 , hỏi lim 3 f (x) + 4g (x) bằng x→ 0 x x→ 0 x x→ 0 x A. 6 − . B. 2 . C. 17 . D. 18.
Câu 15: Phát biểu nào sau đây là sai?
A. lim c = c ( c là hằng số). B. 1 lim = 0 ( * k ∈ N ) . n→+∞ k n→+∞ n C. 1 lim = 0. D. lim n q = 0 ( q > ) 1 . n→+∞ n n→+∞
Câu 16: Cho cấp số cộng (u biết u = u = 1
4 và 2 7 . Hãy tìm u n ) 3 A. u = B. u = C. u = D. u = 3 11 3 3 3 10 3 28
Câu 17: Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Một đường thẳng và một điểm thuộc nó.
B. Ba điểm mà nó đi qua.
C. Ba điểm không thẳng hàng.
D. Hai đường thẳng chéo nhau.
Câu 18: Cho cấp số nhân có (u có u = 2 và u = 6 . Tìm công bội n ) 1 2 q . A. 1 q = . B. 1 q = . C. q =12 . D. q = 3. 3 12
Trang 2/6 - Mã đề thi 666 2 Câu 19: Tính n −1 L = lim . 3
n→+∞ n + n + 3 A. L =1. B. L = 0. C. L = 3. D. L = 2.
Câu 20: Đường cong dưới đây là đồ thị hàm số nào?
A. y = sin 2x .
B. y = sin x .
C. y = cos x .
D. y =1+ cos x . Câu 21: Giới hạn + + =
+ , với a,b∈ . Tính S =5a +b →−∞ ( 2 lim
5x 2x x 5) a 5 b x A. S = −1. B. S = 5 − . C. S =5 D. S = 2
Câu 22: Tìm tập giá trị T của hàm số y 3cos 2x 5.
A. T 2;8.
B. T 1; 1.
C. T 1;1 1.
D. T 5;8. 2 4x −3x +1
Câu 23: Cho hai số thực a và b thỏa mãn lim
− ax − b = 0. Khi đó a + b bằng x→+∞ x + 2 A. 7 . B. 7 − . C. 4 − . D. 4 .
Câu 24: Số nghiệm thực của phương trình 2sin π x +1 = 0 trên đoạn 3 − ;10π là: 2 A. 12 B. 21 C. 11 D. 20 π
Câu 25: Trên đường tròn lượng giác, điểm biểu diễn góc lượng giác có số đo 11 − thuộc góc 3 phần tư thứ A. IV B. III C. I D. II
Câu 26: Cho hình lăng trụ ABC.A’B’C’. Gọi I và I ' lần lượt là trung điểm của AB, A’B’. Qua
phép chiếu song song lên mặt phẳng chiếu (A’B’C’) theo phương chiếu AI ' biến I thành điểm nào sau đây ? A. A’ B. I ' C. B’ D. C’
Câu 27: Cho bốn điểm không đồng phẳng A, B, C, D . Gọi I, K lần lượt là trung điểm của AD và
BC . Giao tuyến của hai mặt phẳng (IBC) và (KAD) là A. AK B. DK C. IK D. BC
Câu 28: Cho cấp số nhân (u 2
n ) có u = 3; q = . Chọn kết quả đúng. 1 3 n 1 − A. 2 u =
. B. (u là một dãy số tăng. n ) n 3. 3 n C. 2 u =
D. Bốn số hạng tiếp theo của cấp số nhân là : 4 6 8 2; ; ; . n 3. 3 3 3 3 2
ax − (a − 2)x − 2 khi x ≠ 1
Câu 29: Cho hàm số f (x)= x + 3 − 2 2 8 + a khi x =1
Trang 3/6 - Mã đề thi 666
Gọi S là tập hợp các giá trị của tham số a để hàm số liên tục tại x =1. Tính tổng các phần tử của S. A. 5 B. 4 C. 6 D. 7
Câu 30: Cho cấp số cộng (un )có 1
u = 3,công sai d = 2. Tổng 20 số hạng đầu tiên của cấp số cộng đã cho bằng A. 420. B. 480. C. 610. D. 440. u = 5
Câu 31: Cho dãy số (u 1 u n ) với
. Số hạng tổng quát của dãy số là số hạng nào u = n n 1 u + n n + dưới đây? A. (n − ) 1 n u = . B. (n 1)(n 1) u − + = + . n 5 n 2 2 C. (n + ) 1 u − = + . D. (n ) 1 u = + . n 5 n n 5 n 2 2
Câu 32: Giới hạn + + − =
, (với a là phân số tối giản), khi đó a + b →+∞ ( 2 lim 4 3. 2 2 a n n n n ) b b bằng A. 3 B. 1 C. 7 D. 5
Câu 33: Phương trình 3 cot x −1 = 0 có nghiệm là π x = + k2π π A. 6 (k ∈).
B. x = + kπ (k ∈) . π
x = − + k2π 3 6 π π
C. x = + k2π (k ∈)
D. x = + kπ (k ∈) . 3 6
Câu 34: Tìm tập xác định của hàm số cos x y = . sin x −1
A. \{k2π,k ∈ } .
B. \{kπ,k ∈ } . π π C. \ k2π ,k + ∈ .
D. \ + kπ,k ∈ . 2 2
Câu 35: Tập nghiệm của phương trình sin(2x +π ) + sin x =0 là A. π S k2π; k2π k = − + ∈ . B. π
S = k2π; + k2π k ∈ . 3 3
C. S = {k2π;π + k2π k ∈ } k . D. π 2π S k2π; k = + ∈ . 3 3
Câu 36: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu a b và a ⊂ (α ), b ⊂ (β ) thì (α ) (β ).
B. Nếu (γ ) ∩(α ) = a, (γ ) ∩(β ) = b và (α ) (β ) thì a .b
C. Nếu (α ) (β ) và a ⊂ (α ), b ⊂ (β ) thì a .b
D. Nếu (α ) (β ) và a ⊂ (α ), b ⊂ (β ) thì a và b chéo nhau.
Trang 4/6 - Mã đề thi 666
Câu 37: Tổng các nghiệm của phương trình sin xcos x + 2sin x − cos x − 2 = 0trên khoảng (0;100) là π π A. 495 . B. 248π . C. 512π . D. 1023 . 2 2
Câu 38: Cho hình chóp tứ giác S.ABCD . Gọi I , J, K lần lượt là trọng tâm của các tam
giác ABC , SBC và SAC . Trong các khẳng định sau, khẳng định nào đúng?
A. (IJK ) // (SAC) .
B. (IJK ) // (SBC) .
C. (IJK ) // (SAB) .
D. (IJK ) // (SDC) .
Câu 39: Cho tứ diện ABCD có M, N lần lượt là trung điểm của BC và CD. Gọi K là điểm tùy ý
thuộc miền trong tam giác ABD. Giao tuyến của (KMN) và (ABD) có tính chất là:
A. Song song với BD
B. Cắt cạnh AC.
C. nằm trong mặt phẳng (ACD) D. Cắt cạnh BD
Câu 40: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung
điểm của các cạnh SB và SD . Khẳng định nào sau đây đúng
A. MN //(ABCD)
B. MN //(SBC)
C. MN //(SBD)
D. MN //(SAB)
u + u + u = 3
Câu 41: Tìm công sai d của cấp số cộng (u thỏa mãn 1 2 3
, biết (u là dãy số n ) n ) 2 2 2
u + u + u = 131 1 2 3 tăng A. d = 8. B. d = 3. C. d = 6 . D. d = 4 .
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Gọi H, I, K lần lượt là trung điểm của , SA AB, .
CD Khẳng định nào sau đây đúng ?
A. HK // (SBD) .
B. HK // (SBC) .
C. HK // (SAD) .
D. HK // (SAC) . f (x) − 2
Câu 43: Cho hàm số y = f (x) xác định trên và thỏa mãn lim = 3 . Tính giới hạn x→ − 1 x +1 f ( x) 2 + 4 3− f (x) −8 L = lim 2 x→ −1 x −1 A. L = 12 − . B. L = 0 . C. L = 9 . D. L = 3 − .
Câu 44: Có bao nhiêu giá trị nguyên của m∈[0;10] để phương trình sau 2
msin 2x + cos 4x = m π π
có bốn nghiệm phân biệt trong đoạn 5 ; − ? 8 8 A. 2 B. 3 C. 0 D. 1 Câu 45: Giới hạn
an − bn + − n = (a,b (. Khi đó 2 2 a + b bằng n→+∞ ( 2 ) 1 lim 1 2 A. 9 B. 2 C. 13 D. 5 3 u = 1
Câu 46: Cho dãy số (u xác định bởi 2
. Biết số hạng tổng quát của dãy n ) 1 u = ∀ ∈ + n n ; * 1 4 − 4un số (u là 1 1 u = +
với a,b,c∈ = + + n ) n
. Tính S a b c a b + cn
Trang 5/6 - Mã đề thi 666
A. S =3.
B. S = − 5 .
C. S = 7 . D. S = −1 2 3 Câu 47: Cho
(x + 2024) 1+ ax − 2024 1 lim
+ bx = 4048. Khi đó 2a−3b bằng x→0 x A. 12288 B. 12 C. 1012 D. 6
Câu 48: Cho hình hộp ABCD.A’B’C’D’. Gọi I, J lần lượt là hai điểm nằm trên đường chéo B’D
và AC sao cho IJ // BC’. Tỉ số IJ bằng: BC ' A. 1 B. 1 C. 3 D. 1 2 4 4 3
Câu 49: Cho hình chóp S.ABCD có BC // AD, BC = 2, AD =1, AB = .
b Tam giác SAD đều. Mặt
phẳng (P) đi qua điểm M trên cạnh AB và song song với các đường thẳng SA và BC, đồng thời
cắt CD, SC, SB theo thứ tự tại N, P, Q. Đặt AM = x, (0 < x < b). Gọi S(x) là diện tích của tứ
giác MNPQ. Khi đó S(x) lớn nhất bằng: A. 3 B. 3 C. 3 D. 3 2 6 3 12 Câu 50: Cho hàm số 2
y = f (x) = ax + bx + c ( a ≠ 0)
có đồ thị như hình vẽ bên. π π Hỏi phương trình 2 . a f (cosx) + .
b f (cosx) + c = 0 có bao nhiêu nghiệm trong khoảng 7 ; ? 2 2 A. 5 B. 2 C. 4 D. 3
----------------------------------------------- ----------- HẾT ---------- Người ra đề Người thẩm định đề Điện thoại học sinh (ký và ghi rõ họ tên) (ký và ghi rõ họ tên) phản ánh sau buổi khảo sát (nếu cần) 0986723021 Thầy Lê Hoàng Tuấn Mai Huy Sáu
Nguyễn Văn Tiến
Trang 6/6 - Mã đề thi 666 mamon made cautron dapan MÔN TOÁN 555 1 C MÔN TOÁN 555 2 B MÔN TOÁN 555 3 D MÔN TOÁN 555 4 A MÔN TOÁN 555 5 B MÔN TOÁN 555 6 B MÔN TOÁN 555 7 A MÔN TOÁN 555 8 C MÔN TOÁN 555 9 D MÔN TOÁN 555 10 D MÔN TOÁN 555 11 B MÔN TOÁN 555 12 C MÔN TOÁN 555 13 A MÔN TOÁN 555 14 C MÔN TOÁN 555 15 D MÔN TOÁN 555 16 A MÔN TOÁN 555 17 D MÔN TOÁN 555 18 A MÔN TOÁN 555 19 A MÔN TOÁN 555 20 D MÔN TOÁN 555 21 B MÔN TOÁN 555 22 C MÔN TOÁN 555 23 B MÔN TOÁN 555 24 B MÔN TOÁN 555 25 A MÔN TOÁN 555 26 C MÔN TOÁN 555 27 D MÔN TOÁN 555 28 C MÔN TOÁN 555 29 C MÔN TOÁN 555 30 A MÔN TOÁN 555 31 C MÔN TOÁN 555 32 A MÔN TOÁN 555 33 A MÔN TOÁN 555 34 D MÔN TOÁN 555 35 D MÔN TOÁN 555 36 D MÔN TOÁN 555 37 C MÔN TOÁN 555 38 C MÔN TOÁN 555 39 B MÔN TOÁN 555 40 C MÔN TOÁN 555 41 B MÔN TOÁN 555 42 A MÔN TOÁN 555 43 A MÔN TOÁN 555 44 D MÔN TOÁN 555 45 B MÔN TOÁN 555 46 B MÔN TOÁN 555 47 C MÔN TOÁN 555 48 D MÔN TOÁN 555 49 B MÔN TOÁN 555 50 A MÔN TOÁN 666 1 C MÔN TOÁN 666 2 C MÔN TOÁN 666 3 A MÔN TOÁN 666 4 B MÔN TOÁN 666 5 D MÔN TOÁN 666 6 B MÔN TOÁN 666 7 D MÔN TOÁN 666 8 A MÔN TOÁN 666 9 D MÔN TOÁN 666 10 A MÔN TOÁN 666 11 C MÔN TOÁN 666 12 A MÔN TOÁN 666 13 C MÔN TOÁN 666 14 D MÔN TOÁN 666 15 D MÔN TOÁN 666 16 B MÔN TOÁN 666 17 C MÔN TOÁN 666 18 D MÔN TOÁN 666 19 B MÔN TOÁN 666 20 C MÔN TOÁN 666 21 A MÔN TOÁN 666 22 A MÔN TOÁN 666 23 B MÔN TOÁN 666 24 A MÔN TOÁN 666 25 C MÔN TOÁN 666 26 C MÔN TOÁN 666 27 C MÔN TOÁN 666 28 A MÔN TOÁN 666 29 B MÔN TOÁN 666 30 D MÔN TOÁN 666 31 D MÔN TOÁN 666 32 C MÔN TOÁN 666 33 B MÔN TOÁN 666 34 C MÔN TOÁN 666 35 D MÔN TOÁN 666 36 B MÔN TOÁN 666 37 B MÔN TOÁN 666 38 C MÔN TOÁN 666 39 A MÔN TOÁN 666 40 A MÔN TOÁN 666 41 A MÔN TOÁN 666 42 B MÔN TOÁN 666 43 D MÔN TOÁN 666 44 D MÔN TOÁN 666 45 B MÔN TOÁN 666 46 A MÔN TOÁN 666 47 B MÔN TOÁN 666 48 D MÔN TOÁN 666 49 C MÔN TOÁN 666 50 C MÔN TOÁN 777 1 D MÔN TOÁN 777 2 C MÔN TOÁN 777 3 B MÔN TOÁN 777 4 D MÔN TOÁN 777 5 A MÔN TOÁN 777 6 A MÔN TOÁN 777 7 A MÔN TOÁN 777 8 C MÔN TOÁN 777 9 D MÔN TOÁN 777 10 C MÔN TOÁN 777 11 A MÔN TOÁN 777 12 B MÔN TOÁN 777 13 B MÔN TOÁN 777 14 C MÔN TOÁN 777 15 B MÔN TOÁN 777 16 B MÔN TOÁN 777 17 D MÔN TOÁN 777 18 D MÔN TOÁN 777 19 C MÔN TOÁN 777 20 B MÔN TOÁN 777 21 D MÔN TOÁN 777 22 A MÔN TOÁN 777 23 A MÔN TOÁN 777 24 D MÔN TOÁN 777 25 B MÔN TOÁN 777 26 D MÔN TOÁN 777 27 A MÔN TOÁN 777 28 B MÔN TOÁN 777 29 C MÔN TOÁN 777 30 D MÔN TOÁN 777 31 B MÔN TOÁN 777 32 A MÔN TOÁN 777 33 C MÔN TOÁN 777 34 B MÔN TOÁN 777 35 C MÔN TOÁN 777 36 C MÔN TOÁN 777 37 A MÔN TOÁN 777 38 A MÔN TOÁN 777 39 D MÔN TOÁN 777 40 A MÔN TOÁN 777 41 C MÔN TOÁN 777 42 D MÔN TOÁN 777 43 D MÔN TOÁN 777 44 A MÔN TOÁN 777 45 B MÔN TOÁN 777 46 D MÔN TOÁN 777 47 C MÔN TOÁN 777 48 C MÔN TOÁN 777 49 B MÔN TOÁN 777 50 C MÔN TOÁN 888 1 A MÔN TOÁN 888 2 C MÔN TOÁN 888 3 B MÔN TOÁN 888 4 C MÔN TOÁN 888 5 A MÔN TOÁN 888 6 B MÔN TOÁN 888 7 C MÔN TOÁN 888 8 B MÔN TOÁN 888 9 D MÔN TOÁN 888 10 A MÔN TOÁN 888 11 C MÔN TOÁN 888 12 C MÔN TOÁN 888 13 D MÔN TOÁN 888 14 B MÔN TOÁN 888 15 B MÔN TOÁN 888 16 A MÔN TOÁN 888 17 D MÔN TOÁN 888 18 B MÔN TOÁN 888 19 B MÔN TOÁN 888 20 D MÔN TOÁN 888 21 A MÔN TOÁN 888 22 D MÔN TOÁN 888 23 C MÔN TOÁN 888 24 A MÔN TOÁN 888 25 B MÔN TOÁN 888 26 C MÔN TOÁN 888 27 B MÔN TOÁN 888 28 C MÔN TOÁN 888 29 C MÔN TOÁN 888 30 A MÔN TOÁN 888 31 A MÔN TOÁN 888 32 B MÔN TOÁN 888 33 B MÔN TOÁN 888 34 C MÔN TOÁN 888 35 D MÔN TOÁN 888 36 D MÔN TOÁN 888 37 C MÔN TOÁN 888 38 B MÔN TOÁN 888 39 D MÔN TOÁN 888 40 D MÔN TOÁN 888 41 D MÔN TOÁN 888 42 D MÔN TOÁN 888 43 A MÔN TOÁN 888 44 A MÔN TOÁN 888 45 A MÔN TOÁN 888 46 A MÔN TOÁN 888 47 C MÔN TOÁN 888 48 B MÔN TOÁN 888 49 D MÔN TOÁN 888 50 B
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 11
https://toanmath.com/khao-sat-chat-luong-toan-11
TRƯỜNG THPT BA ĐÌNH ĐÁP ÁN ĐỀ KHẢO SÁT CHẤT LƯỢNG CÁC MÔN THI TN
TỔ TOÁN- TIN Năm học: 2023- 2024 Môn toán, khối 11
Đề gốc: S00 (Thời gian: 90 phút)
Câu 1. Đổi số đo của góc α =120° sang rađian ta được A. π π π π . B. 3 . C. 2 . D. . 2 4 3 3
Câu 2. Đường cong dưới đây là đồ thị hàm số nào?
A. y =1+ cos x .
B. y = sin 2x .
C. y = sin x .
D. y = cos x .
Câu 3. Phương trình π sin x = s 2 in có nghiệm là 3 2π x = + k2π A. 2π x =
+ kπ với k B. 3
với k . 3 π x = + k2π 3 C. 2π π x = −
+ k2π với k . D. 2 x = ±
+ k2π với k . 3 3
Câu 4. Trong các mệnh đề sau, mệnh đề nào sai? A.
tan x 0 x k , k .
B. cotx 1 x k , k . 4 C.
sin x 1 x k2 , k .
D. cosx 0 x k2 , k . 2 2 u = 1 1
Câu 5. Cho dãy số (u biết: với * . Hãy tìm u n ) n ∈ N u = u 2 n 1 2 + n 1 + A. u = u = u = u = 2 1 B. 2 2 C. 2 4 D. 2 3
Câu 6. Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào giảm? n ) n n
A. u = n + B. u = (− )
1 n (5n − C. 4 u = D. u = − n 3 .n n . n )1. n 4. 3
Câu 7. Cho cấp số cộng (u biết u = và u = . Hãy tìm 2 7 1 4 u n ) 3 A. u = B. u = C. u = D. u = 3 28 3 3 3 11 3 10
Câu 8. Công thức nào sau đây là đúng với cấp số cộng có số hạng đầu u , công sai d , n∈, n ≥ 2 ? 1
A. u = u + n + d .
B. u = u + n − d . n 1 1 ( ) n 1 1 ( )
C. u = u − n − d .
D. u = u + d . n 1 1 ( ) n 1
Câu 9. Cho cấp số nhân có (u có u = 2 và u = 6 . Tìm công bội n ) 1 2 q . A. 1 q = .
B. q =12 .
C. q = 3. D. 1 q = . 12 3
Câu 10. Cho cấp số nhân u với số hạng đầu u = 2
− và công bội q = 5
− . Viết bốn số hạng đầu tiên của n 1 cấp số nhân. A. 2 − ; 10; 50; − 250 B. 2 − ; 10; −50; 250 C. 2 − ; 10; 50; 250 D. 2 − ; −10; − 50; − 250
Câu 11. Phát biểu nào sau đây là sai?
A. limc = c ( c là hằng số). B. lim n q = 0 ( *
q >1;n∈ N ) . C. 1 lim = 0( * n∈ N ) . D. 1 lim = 0 ( *
k,n∈ N ). n k n 2 n −1
Câu 12. Tính L = lim . 3 n + n + 3
A. L =1. B. L = 0. C. L = 3. D. L = 2. Câu 13. Tính −x + 2 N = lim . x→+∞ x +1 A. 6 . B. 1 − . C. 1. D. 2 .
Câu 14. Cho các giới hạn: lim f (x) = 2; lim g (x) = 3 , hỏi lim 3 f (x) + 4g (x) bằng x→ 0 x x→ 0 x x→ 0 x A. 17 . B. 2 . C. 18. D. 6 − .
Câu 15. Hàm số nào sau đây không liên tục tại x = 2 A. 2023 y + − + = . B. 3x 1 y = . C. x 2 y = . D. 2x 5 y = . x − 2 x − 22 x + 2 2 x − 2
Câu 16. Cho hình tứ diện ABCD . Khẳng định nào sau đây đúng?
A. AB và CD song song. B. AB và CD chéo nhau.
C. Tồn tại một mặt phẳng chứa AB và CD . D. AB và CD cắt nhau.
Câu 17. Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?
A. Ba điểm không thẳng hàng. B. Một đường thẳng và một điểm thuộc nó.
C. Hai đường thẳng chéo nhau. D. Ba điểm mà nó đi qua.
Câu 18. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm của AC và BD . Gọi
M , N lần lượt là trung điểm các cạnh SB,SD . Đường thẳng MN song song với đường thẳng nào trong các đường thẳng sau? A. AC . B. BD . C. SO . D. BC .
Câu 19. Cho hình chóp S.ABCD có đáy là hình thang đáy lớn AB . Gọi M và N lần lượt là trung điểm
của các cạnh AD và SA . Tìm khẳng định đúng.
A. MN // (SAC) .
B. MN //(ABCD) .
C. MN // (SBD).
D. MN // (SBC).
Câu 20. Cho hình hộp ABC . D A′B C ′ D
′ ′ . Mệnh đề nào sau đây sai? A. (BDD B ′ ′) // ( ACC A ′ ′). B. ( ABB A ′ ′) // (CDD C ′ ′).
C. ( ABCD) // ( A′B C ′ D ′ ′) .
D. ( AA′D D ′ ) // (BCC B ′ ′) .
Câu 21. Cho hình lăng trụ ABC.A’B’C’, gọi I và I ' lần lượt là trung điểm của AB, A’B’. Qua phép chiếu
song song lên mặt phẳng chiếu (A’B’C’) theo phương chiếu AI ' biến I thành điểm nào sau đây ?
A. A’ B. B’ C. C’ D. I ' π
Câu 22. Trên đường tròn lượng giác, điểm biểu diễn góc lượng giác có số đo 11 −
thuộc góc phần tư thứ 3
A. I B. II C. III D. IV
Câu 23. Tìm tập xác định của hàm số cos x y = . sin x −1 A. π \ k2π ,k +
∈ . B. \{k2π,k ∈ } . 2 C. π
\{kπ ,k ∈ } .
D. \ + kπ,k ∈ . 2
Câu 24. Tìm tập giá trị T của hàm số y 3cos 2x 5.
A. T 5;8.
B. T 2;8.
C. T 1;1 1.
D. T 1; 1.
Câu 25. Phương trình 3 cot x −1 = 0 có nghiệm là π x = + k2π π A. 6 (k ∈).
B. x = + kπ (k ∈) . π
x = − + k2π 3 6 π π
C. x = + k2π (k ∈)
D. x = + kπ (k ∈) . 3 6
Câu 26. Số nghiệm thực của phương trình π 2sin x +1 = 0 3 trên đoạn − ;10π là: 2
A. 12 B. 11 C. 20 D. 21
Câu 27. Tập nghiệm của phương trình sin(2x +π ) + sin x =0 là
A. S = {k2π;π + k2π k ∈ } . B. π S k2π; k2π k = + ∈ . 3 C. π k2π S k2π; k = + ∈ . D. π
S = k2π;− + k2π k ∈ . 3 3 3 u = 5
Câu 28. Cho dãy số (u 1 u n ) với
. Số hạng tổng quát của dãy số là số hạng nào dưới đây? u = n n 1 u + n n + A. (n − ) 1 n u = . B. (n 1)(n 1) u − + = + . n 5 n 2 2 C. (n + ) 1 u − = + . D. (n ) 1 u = + . n 5 n n 5 n 2 2
Câu 29. Cho cấp số cộng (un )có 1
u = 3,công sai d = 2. Tổng 20 số hạng đầu tiên của cấp số cộng đã cho bằng A. 480. B. 420. C. 610. D. 440.
Câu 30. Cho cấp số nhân (u 2
n ) có u = 3; q = . Chọn kết quả đúng. 1 3 n 1 − A. 2 u = .
B. (u là một dãy số tăng. n ) n 3. 3 n C. 2 u =
D. Bốn số hạng tiếp theo của cấp số nhân là : 4 6 8 2; ; ; . n 3. 3 3 3 3
Câu 31. Giới hạn + + − =
, (với a là phân số tối giản), khi đó a + b bằng →+∞ ( 2 lim 4 3. 2 2 a n n n n ) b b A. 7 B. 3 C. 5 D. 1 2 4x −3x +1
Câu 32. Cho hai số thực a và b thỏa mãn lim
− ax − b = 0. Khi đó a + b bằng x→+∞ x + 2 A. 4 . B. 4 − . C. 7 − . D. 7 . Câu 33. Giới hạn + + =
+ , với a,b∈ . Tính S =5a +b →−∞ ( 2 lim
5x 2x x 5) a 5 b x A. S = −1. B. S = 5 − . C. S =5
D. S = 2 2
ax − (a − 2)x − 2 khi x ≠ 1
Câu 34. Cho hàm số f (x)= x + 3 − 2 2 8 + a khi x =1
Gọi S là tập hợp các giá trị của tham số a để hàm số liên tục tại x =1. Tính tổng các phần tử của S.
A. 4 B. 5 C. 6 D. 7
Câu 35. Cho bốn điểm không đồng phẳng A, B, C, D. Gọi I và K lần lượt là trung điểm của AD và BC. Giao
tuyến của hai mặt phẳng (IBC) và (KAD) là:
A. IK B. BC C. AK D. DK
Câu 36. Cho tứ diện ABCD có M, N lần lượt là trung điểm của BC và CD. Gọi K là điểm tùy ý thuộc miền
trong tam giác ABD. Giao tuyến của (KMN) và (ABD) có tính chất là:
A. Cắt cạnh AC. B. Song song với BD
C. Cắt cạnh BD D. nằm trong mặt phẳng (ACD)
Câu 37. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung điểm của
các cạnh SB và SD (hình vẽ kèm theo). Khẳng định nào sau đây đúng
A. MN //(SBD)
B. MN //(SAB)
C. MN //(ABCD)
D. MN //(SBC)
Câu 38. Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Gọi H, I, K lần lượt là trung điểm của , SA AB, .
CD Khẳng định nào sau đây đúng ?
A. HK // (SAC) .
B. HK // (SBD) .
C. HK // (SBC) .
D. HK // (SAD) .
Câu 39. Cho hình chóp tứ giác S.ABCD . Gọi I , J, K lần lượt là trọng tâm của các tam giác ABC , SBC
và SAC . Trong các khẳng định sau, khẳng định nào đúng?
A. (IJK ) // (SBC) .
B. (IJK ) // (SAC) .
C. (IJK ) // (SAB) .
D. (IJK ) // (SDC) .
Câu 40. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Nếu (α ) (β ) và a ⊂ (α ), b ⊂ (β ) thì a .b
B. Nếu (α ) (β ) và a ⊂ (α ), b ⊂ (β ) thì a và b chéo nhau.
C. Nếu a b và a ⊂ (α ), b ⊂ (β ) thì (α ) (β ).
D. Nếu (γ ) ∩(α ) = a, (γ ) ∩(β ) = b và (α ) (β ) thì a .b
Câu 41. Có bao nhiêu giá trị nguyên của m∈[0;10] để phương trình sau 2
msin 2x + cos 4x = m có bốn π π
nghiệm phân biệt trong đoạn 5 ; − ? 8 8
A. 3 B. 1 C. 0 D. 2 Giải : Chọn B 2
msin 2x + cos 4x = m ⇔ m(1− cos 4x) + 2cos 4x = 2m ⇔ (2 − m)cos 4x = m (1)
+) m = 2 thì ph (1) vô nghiệm +) m m
≠ 2 thì (1) ⇔ cos 4x = . 2 − m π π π π Vì 5 x ; ∈ − m nên 5 − ≤ 4x ≤
. Từ yêu cầu bài toán, suy ra : 0 ≤
< 1. Mà m∈[0;10]nên 8 8 2 2 2 − m
m = 0. Vậy có một giá trị là m = 0
Câu 42. Tổng các nghiệm của phương trình sin xcos x + 2sin x − cos x − 2 = 0 trên khoảng (0;100) là π π A. 1023 . B. 248π . C. 495 . D. 512π . 2 2 Giải: Chọn B. π
sin x cos x + 2sin x − cos x − 2 = 0 ⇔ (sin x −1)(cosx + 2) = 0 ⇔ sin x −1 = 0 ⇔ x = + k2π 2
Vì x∈(0;100) nên k = 0; 1; 2 …; 15. Suy ra tổng các nghiệm S =248π
u + u + u = 3
Câu 43. Tìm công sai d của cấp số cộng (u thỏa mãn 1 2 3
, biết (u là dãy số tăng n ) n ) 2 2 2
u + u + u = 131 1 2 3
A. d = 8.
B. d = 3.
C. d = 6 . D. d = 4 . Giải: Chọn A u + u + u = 3 3 u = 3 u =1
Vì (u là CSC nên u +u =2u . Vậy 1 2 3 2 2 ⇔ ⇔ n ) 1 3 2 2 2 2 2 2 2 2 2 u + u + u =131 u + u + u =131 u + u =130 1 2 3 1 2 3 1 3 u + u = 2 u + u = 2 1 3 1 3 u + u = 2 1 3 ⇔ ⇔ ⇔ u = 7;
− u = 9 ( vì (u là dãy số tăng) n ) 2 2 u + 1 3 u =130 u + u − 2u u =130 u u = 63 − 1 3 ( 1 3)2 1 3 1 3 Vậy d = 8 Câu 44. Giới hạn
an − bn + − n = (a,b (. Khi đó 2 2 a + b bằng n→+∞ ( 2 ) 1 lim 1 2 A. 9 B. 2 C. 13 D. 5 Giải: Chọn B.
a − n − bn an bn n + − + − = ⇔
= . Để giới hạn đã cho là số thực thì a -1= 0 hay a n→+∞ ( ) 2 2 1 ( 1) 1 1 lim 1 lim n→+∞ 2 2
an − bn +1+ n 2 1 − + b − + = 1. Khi đó bn
an − bn + − n = ⇔ = n 1 ⇔ lim = n→+∞ ( 2 ) 1 1 1 lim 1 lim n→+∞ 2 2 n − bn +1+1 2 n→+∞ b 1 2 1− + +1 n n b − 1 ⇔ = hay b = -1. Vậy 2 2 a + b = 2 2 2 f (x) − 2
Câu 45. Cho hàm số y = f (x) xác định trên và thỏa mãn lim = 3 . Tính giới hạn x→ − 1 x +1 f ( x) 2 + 4 3− f (x) −8 L = lim 2 x→ −1 x −1 A. L = 3 − . B. L = 0 . C. L = 9 . D. L = 12 − . Giải: Chọn A. f ( x) 2 + 4 3− f (x) −8 f ( x) 2 − 4 + 4( 3− f (x) −1) Với x ≠ 1
− , ta có g(x) = = 2 2 x −1 x −1 f ( x) 2 − 4 4( 3− f
(x) −1) f (x)− 2 f (x)+ 2 2 − f (x) g(x) = + = . + 4 2 2 x −1 x −1 x +1 x −1 ( 3− f (x) 2 +1)(x −1)
f (x) − 2 f (x) + 2 f (x) − 2 1 f (x) − 2 g(x) = . − 4 . . Vì lim = 3 nên . Khi đó x +1 x −1
(x +1) (x −1)( 3− f (x) +1) x→ − 1 x +1 2 + 2 1 L = 3. − 4.3. = 3 − 2 − 2 − ( 3− 2 +1)
Câu 46. Cho hình chóp S.ABCD có BC // AD, BC = 2, AD =1, AB = .
b tam giác SAD đều. Mặt phẳng (P)
đi qua điểm M trên cạnh AB và song song với các đường thẳng SA và BC, đồng thời cắt CD, SC, SB theo
thứ tự tại N, P, Q. Đặt AM = x, (0 < x < b). AM = x, (0 < x < b). Gọi S(x) là diện tích của tứ giác
MNPQ. Khi đó S(x) lớn nhất bằng: A. 3 B. 3 C. 3 D. 3 2 12 3 6 Giải: Chon C
Do (P) // SA và BC nên (P) // (SAD) . Suy ra MQ // SA, NP // SD. Ta có MN // PQ // AD // BC.
Theo Talet trong hình thang có BM CN = (1) BA CD
Theo Talet trong tam giác SAB có: BM BQ MQ = = (2) BA BS SA
Theo Talets trong tam giác SCD có: CN CP PN = = (3) CD CS SD Từ (1), (2) và (3) suy ra: b − x 2 = = ; x = ; b + x MQ NP PQ MN = . b b b 2
Thiết diện là hình thang cân và khi đó 1
S = (MN + PQ) 2
MN − PQ
(3x + b)(b − x) 3 MQ − = 2 2 2 4b 2 Ta có
(3x + b)(b − x) 3 (3x + b)(3b − 3x) 3
3 3x + b + 3b − 3x S = = ≤ ( Theo Cô-Si) 2 2 2 4b 12b 12b 2 Vậy 3 S ≤
, đẳng thức xảy ra khi 3x + b = 3b – 3x hay b x = . 3 3
Câu 47. Cho hình hộp ABCD.A’B’C’D’. Gọi I, J lần lượt là hai điểm nằm trên đường chéo B’D và AC sao
cho IJ // BC’. Tỉ số IJ bằng: BC ' A. 1 B. 3 C. 1 D. 1 2 4 3 4 Giải: Chọn C
Gọi E là điểm đối xứng với C qua B. Qua phép chiếu song song theo phương C’B trên mặt phẳng (ABCD) thì:
+) Điểm B’ biến thành E
+) Điểm D biến thành chính nó
Nên B’D biến thành ED. Mà I thuộc B’D nên J thuộc ED. Vậy J là giao điểm của AC và ED. Trong
(B’DE) từ J ta dựng JI // EB’ (với I thuộc B’D). Khi đó I, J là 2 điểm cần dựng. Ta có IJ IJ DJ 1 = = =
BC ' B 'E DE 3 Câu 48. Cho hàm số 2
y = f (x) = ax + bx + c ( a ≠ 0) có đồ thị như hình vẽ bên. Hỏi phương trình π π 2 . a f (cosx) + .
b f (cosx) + c = 0 có bao nhiêu nghiệm trong khoảng 7 ; ? 2 2
A. 5 B. 2 C. 4 D. 3 Giải: Chọn C
Đặt t = cos x , t ∈[ 1; − ]
1 ; u = f (t) . Khi đó phương trình 2 . a f (cosx) + .
b f (cosx) + c = 0 (1), trở thành 2
au + bu + c =0 (2). t = t ∈ 1; − 0 1 ( ) f (t) = −1 t = t ∈ 2;3 2 ( )
Từ đồ thị suy ra phương trình (2) có 2 nghiệm là -1 và 3. Nên (2) ⇔ ⇔ f (t) =3 t = t ∈ ; −∞ −1 3 ( )
t = t ∈ 3;+ ∞ 4 ( ) π π Vì 7 x ; ∈
nên cos x = t có 4 nghiệm phân biệt. Vậy phương trình đã cho có 4 nghiệm trong 2 2 1 π π khoảng 7 ; . 2 2 3 u = 1
Câu 49. Cho dãy số (u xác định bởi 2
. Biết số hạng tổng quát của dãy số (u là n ) n ) 1 u = ∀ ∈ + n n ; * 1 4 − 4un 1 1 u = +
với a,b,c∈ = + + n
. Tính S a b c a b + cn
A. S =3.
B. S = − 5 .
C. S = 7 .
D. S = −1 Giải: chọn A 1 1 1 1 2u − − u n 1 1 2 2 u = ⇔ − = − ⇔ − = ⇔ = + u + u n 2 n+ 1 n n 1 1 1 4 − 4u − u − u u − − + u n 2 4 4 n 2 2 2 n 2 n 1 2 n 1 1 1 1 ⇔ = 1 − + . (1) 2u − − + u n 1 2 n 1 1 Đặt 1 1 v = ⇒ v = . Vậy (1) 1
⇔ v = + − hay (v là CSC với d = -1 và v = . Vậy n ) + v n n ( 1) n n 1 2u + − u − 1 1 2 n 1 2 n+ 1 1
số hạng tổng quát của (v là: 1 3
v = + n − − = − n . Từ đó suy ra: 1 1 u = + . n ( 1)( 1) n ) 2 2 n 2 3− 2n
Vậy a = 2, b = 3 và c = -2. Khi đó S =3. 2 3 Câu 50. Cho
(x + 2024) 1+ ax − 2024 1 lim
+ bx = 4048. Khi đó 2a−3b bằng x→0 x
A. 12 B. 6 C. 1012 D. 12288 Giải: chon A 2 3 3 Với
(x + 2024) 1+ ax − 2024 1+ bx 1+ ax −1+1− 1+ x bx ≠ 0 ta có: 3 f (x) = = x 1+ ax + 2024 x x 3 ( ) = 1+ + 2024 a b f x x ax ( − ax ) 2024 2 3 3 1+ bx + + + + + 1 1 1 ax 1
Vậy lim ( ) 2024 a b f x = − =
4048 ⇒ 2a − 3b = 12 3 2 x→0
Document Outline
- ĐỀ THI KSCL CÁC MÔN THI TN_MÔN TOÁN_555
- ĐỀ THI KSCL CÁC MÔN THI TN_MÔN TOÁN_666
- ĐÁP ÁN ĐỀ THI KSCL CÁC MÔN THI TN_MÔN TOÁN_dapancacmade - Copy (2)
- Table1
- Đáp án chi tiết-ĐỀ KHẢO SÁT TOÁN 11 - SÁU




