30 trang 24 lượt tải

Đề KSCL Toán 12 ôn thi THPT Quốc gia năm 2018 – 2019 trường chuyên Vĩnh Phúc lần 2

48

Đề KSCL Toán 12 ôn thi THPT Quốc gia năm 2018 – 2019 trường chuyên Vĩnh Phúc lần 2 mã đề 234 gồm 06 trang với 50 câu hỏi và bài toán trắc nghiệm khách quan

Chủ đề: Đề thi THPTQG môn Toán năm 2019 79 tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Profile

Thanh Hoa

1 năm trước
Danh sách Quiz
/30
Trang 1/6 - Mã đề thi 234
SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
TRƯỜNG THPT CHUYÊN VĨNH PHÚC
(Đề thi có 6 trang)
ĐỀ KSCL CÁC MÔN THI THPT QUỐC GIA - LẦN 2
NĂM HỌC 2018-2019
MÔN TOÁN 12
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề)
Mã đề thi 234
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
Câu 1: Tìm giá trị cực tiểu
CT
y
của hàm số
3
3 4y x x
.
A.
6.
CT
y
. B.
1
CT
y
. C.
2
CT
y
. D.
1.
CT
y
Câu 2: Phương trình:
3
log 3 2 3
x
có nghiệm là
A.
25
3
x
. B.
. C.
29
3
x
. D.
11
3
x
.
Câu 3: Đồ thị hàm số
2
1
4
x
y
x
có bao nhiêu đường tiệm cận?
A.
4
. B.
0
. C.
1
. D.
2
.
Câu 4: Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức lãi kép với
lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng, người đó có số tiền là
10
triệu đồng. Hỏi số tiền
T
gần
với số tiền nào nhất trong các số sau.
A.
613.000
đồng. B.
645.000
đồng. C.
635.000
đồng. D.
535.000
đồng.
Câu 5: Cho hàm số
2016
2
khi 1
2018 1 2018
khi 1
x x
x
f x
x x
k x
. Tìm k để hàm số
f x
liên tục
tại
1x
.
A.
2 2019.
k B.
2017. 2018
.
2
k
C.
1.
k
D.
20016
2019.
2017
k
Câu 6: Cho biểu thức
3
3
4
.
P x x x
, với
0.
x
Mệnh đề nào dưới đây đúng ?
A.
1
2
.P x
B.
7
12
.P x
C.
5
8
.P x
D.
7
24
.P x
Câu 7: Có bao nhiêu giá trị nguyên của
x
để hàm số
1 3
y x x
đạt giá trị nhỏ nhất.
A.
4.
B.
5.
C.
2.
D.
3.
Câu 8: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
.a
A.
3
.
2
a
B.
3
3
.
4
a
C.
3
3
.
2
a
D.
3
2
.
3
a
Câu 9: Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Trang 2/6 - Mã đề thi 234
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
A.
3
3 1.
y x x
B.
3 2
3 1.
y x x
C.
3 2
3 1.
y x x
D.
3 2
3 1.
y x x
Câu 10: Đường thẳng
2
y
là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây?
A.
2 1
.
1
x
y
x
B.
3 4
.
2
x
y
x
C.
1
.
2
x
y
x
D.
1
.
2 1
x
y
x
Câu 11: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12
y x x x m
có
5
điểm cực trị.
A.
16
. B.
. C.
. D.
.
Câu 12: Biết rằng tập các giá trị của tham số
m
để phương trình
3 9 2 1 3 1 0
x x
m m m
có
hai nghiệm phân biệt là một khoảng
;a b
. Tính tích
.a b
.
A.
4
. B.
. C.
2.
. D.
3
.
Câu 13: Cho hình chóp
.
S ABC
có
,SA a
2 ,SB a
4SC a
và
0
60 .
ASB BSC CSA
Tính
thể tích khối chóp
.
S ABC
theo
a
.
A.
3
2
3
a
. B.
3
8 2
3
a
. C.
3
4 2
3
a
. D.
3
2 2
3
a
.
Câu 14: Giá trị của biểu thức
2 2 2 2
log 2 log 4 log 8 ... log 256
M bằng
A.
. B.
. C.
. D.
2
8log 256
.
Câu 15: Kí hiệu
max ;a b
là số lớn nhất trong hai số
, .a b
Tìm tập nghiệm S của bất phương trình
2 1
3
max log ; log 1.
x x
A.
1
;2 .
3
S
B.
0;2 .
S
C.
1
0; .
3
S
D.
2; .
S

Câu 16: Với
a
là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A.
1
log 3 log
3
a a
. B.
3
1
log log
3
a a
. C.
3
log 3loga a
. D.
log 3 3loga a
.
Câu 17: Gọi
M ,N
là hai điểm di động trên đồ thị
C
của hàm số
3 2
3 4y x x x
sao cho tiếp
tuyến của
C
tại
và
N
luôn song song với nhau. Hỏi khi
M ,N
thay đổi, đường thẳng
MN
luôn đi qua nào trong các điểm dưới đây ?
A. Điểm
1; 5 .
N
B. Điểm
1; 5 .
M
C. Điểm
1;5 .
Q
D. Điểm
1;5 .
P
Câu 18: Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
( 3;1)
M
và đường tròn
2 2
: 2 6 6 0
C x y x y
. Gọi
1 2
,T T
là các tiếp điểm của các tiếp tuyến kẻ từ
đến (C). Tính
khoảng cách từ
O
đến đường thẳng
1 2
.TT
A.
5.
B.
5.
C.
3
.
5
D.
2 2.
Trang 3/6 - Mã đề thi 234
Câu 19: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ?
A.
4
. B.
9.
C.
3
. D.
6.
Câu 20: Đường thẳng
có phương trình
2 1y x
cắt đồ thị của hàm số
3
3y x x
tại hai điểm
A
và
B
với tọa độ được kí hiệu lần lượt là
;
A A
A x y
và
;
B B
B x y
trong đó
B A
x x
. Tìm
B B
x y
?
A.
5
B B
x y
B.
2
B B
x y
C.
4
B B
x y
D.
7
B B
x y
Câu 21: Hàm số
4 2
2 1
y x x
nghịch biến trên các khoảng nào sau đây?
A.
- ;-1
và
0;+
B.
;0

và
1;+ .
C.
1;0
và
1;+
D.
; 1
và
0;1 .
Câu 22: Giá trị lớn nhất của hàm số
3 2
2 3 12 2y x x x
trên đoạn
1;2
thuộc khoảng nào dưới
đây?
A.
3;8
. B.
7;8
. C.
2;14
. D.
12;20
.
Câu 23: Cho hàm số
y f x
. Hàm số
y f x
có đồ thị trên một khoảng
K
như hình vẽ bên.
Trong các khẳng định sau, có tất cả bao nhiêu khẳng định đúng ?
I
: Trên
K
, hàm số
y f x
có hai điểm cực trị.
II
: Hàm số
y f x
đạt cực đại tại
3
x
.
III
: Hàm số
y f x
đạt cực tiểu tại
1
x
.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 24: Với
n
là số tự nhiên lớn hơn
2
, đặt
3 3 4 3
3 4 5
1 1 1 1
...
n
n
S
C C C C
. Tính
lim
n
S
A.
1
. B.
3
2
. C.
3
. D.
1
3
.
Câu 25: Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
là
A.
;2
S 
. B.
;1
S

. C.
1;S

D.
2;S

.
Câu 26: Khối cầu bán kính
2R a
có thể tích là
A.
3
32
3
a
. B.
3
6
a
. C.
2
16
a
. D.
3
8
3
a
.
Câu 27: Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và mặt đáy bằng
60
.
Tính diện tích xung quanh của hình nón đỉnh
S
, đáy là hình tròn ngoại tiếp tam giác
.ABC
A.
2
3
3
a
. B.
2
7
6
a
. C.
2
7
4
a
. D.
2
10
8
a
.
Câu 28: Trong mặt phẳng với hệ tọa độ
Oxy
, cho elip
2 2
: 1
25 9
x y
E
. Điểm
M E
sao cho
0
1 2
90 .
F MF Tìm bán kính đường tròn nội tiếp tam giác
1 2
.MF F
Trang 4/6 - Mã đề thi 234
A.
2.
B.
4.
C.
1.
D.
Câu 29: Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
2018; 2018
để phương trình
2
1 sin sin 2 cos2 0
m x x x
có nghiệm ?
A.
4036
. B.
2020
. C.
4037
. D.
2019
.
Câu 30: Cho hàm số
y f x
có đồ thị
f x
như hình vẽ
Hàm số
2
1
2
x
y f x x
nghịch biến trên khoảng nào trong các khoảng dưới đây?
A.
2; 0
. B.
3; 1
. C.
3;

. D.
1; 3
.
Câu 31: Tìm tất cả các giá trị tham số
m
để bất phương trình
2
6 2 8 1
x x x x m
nghiệm đúng với mọi
2;8 .
x
A.
16.
m
B.
15.
m
C.
8.
m
D.
2 16.
m
Câu 32: Tìm tập xác định
D
của hàm số
1
2
3
3 1
y x
.
A.
1 1
; ;
3 3
D
 
. B.
D
.
C.
1
\
3
D
. D.
1 1
; ;
3 3
D
 
.
Câu 33: Số cạnh của hình mười hai mặt đều là
A. Mười sáu B. Ba mươi C. Hai mươi D. Mười hai
Câu 34: Cho hình chóp tứ giác đều có góc giữa mặt bên và mặt đáy bằng
60
. Biết rằng mặt cầu
ngoại tiếp hình chóp đó có bán kính
3.
R a Tính độ dài cạnh đáy của hình chóp tứ giác đều nói
trên.
A.
12
5
a
. B.
. C.
3
2
a
. D.
9
4
a
.
Câu 35: Biết rằng phương trình
e e 2cos
x x
ax
(
a
là tham số) có
3
nghiệm thực phân biệt. Hỏi
phương trình
e e 2cos 4
x x
ax
có bao nhiêu nghiệm thực phân biệt ?
A.
5
. B.
10
. C.
6
. D.
11
.
Câu 36: Cho khối nón có bán kính đáy
3
r và chiều cao
4
h
. Tính thể tích
V
của khối nón đã
cho.
Trang 5/6 - Mã đề thi 234
A.
16 3
V
. B.
16 3
3
V
. C.
12
V
. D.
4
V
.
Câu 37: Giá trị nhỏ nhất của hàm số
2sin 3
sin 1
x
y
x
trên
0;
2
là
A.
5.
B.
2.
C.
3.
D.
Câu 38: Cho hình lăng trụ tam giác đều
.
ABC A B C
có
,AB a
2 .AA a
Tính khoảng cách giữa
hai đường thẳng
AB
và
.A C
A.
3
.
2
a
B.
2 5
.
5
a
C.
5.
a D.
2 17
.
17
a
Câu 39: Trong mặt phẳng với hệ tọa độ
Oxy,
giả sử điểm
( ; )A a b
thuộc đường thẳng
: 3 0
d x y
và cách
: 2 1 0
x y
một khoảng bằng
5.
Tính
P ab
biết
0.
a
A.
4.
B.
C.
2.
D.
4.
Câu 40: Một hình trụ có bán kính đáy bằng
r
và có thiết diện qua trục là một hình vuông. Tính
diện
tích toàn phần của hình trụ đó.
A.
2
4 .r
B.
2
6 .r
C.
2
8 .r
D.
2
2 .r
Câu 41: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1
x mx m
y
x
trên
1;2
bằng 2. Số phần tử của tập
S
là
A.
3.
B.
1.
C.
4.
D.
2.
Câu 42: Cho
a
,
b
là các số thực dương thỏa mãn
1b
và
a b a
. Tìm giá trị nhỏ nhất của
biểu thức
log 2log .
a
b
b
a
P a
b
A.
6
. B.
7
. C.
5
. D.
4
.
Câu 43: Một hình trụ có độ dài đường cao bằng
3
, các đường tròn đáy lần lượt là
;1
O
và
';1
O
.
Giả sử
AB
là đường kính cố định của
;1
O
và
MN
là đường kính thay đổi trên
';1
O
. Tìm giá trị
lớn nhất
max
V
của thể tích khối tứ diện
.ABCD
A.
max
2.
V
B.
max
6.
V
C.
max
1
.
2
V
D.
max
1.
V
Câu 44: Trong mặt phẳng tọa độ
Oxy
, cho hình chữ nhật
OMNP
với
0;10
M
,
100;10
N
,
100;0
P
Gọi S là tập hợp tất cả các điểm
;A x y
với
,x y
nằm bên trong (kể cả trên cạnh) của
hình chữ nhật
OMNP
. Lấy ngẫu nhiên một điểm
;
A x y S
. Tính xác suất để
90
x y
.
A.
169
200
. B.
473
500
. C.
845
1111
. D.
86
101
.
Câu 45: Tập xác định của
2
ln 5 6
y x x
là
A.
2; 3
. B.
2; 3
. C.
; 2 3;

. D.
; 2 3;

.
Câu 46: Cho
3
.e
x
f x x
. Tập nghiệm của bất phương trình
0
f x
là
A.
1
;
3

. B.
1
0;
3
. C.
1
;
3
. D.
0;1
.
Câu 47: Cho khối chóp
.
S ABCD
có thể tích bằng
3
2a
và đáy ABCD là hình bình hành. Biết diện tích
tam giác SAB bằng
2
.a
Tính khoảng cách giữa hai đường thẳng
SB
và
.CD
Trang 6/6 - Mã đề thi 234
A.
.a
B.
3
.
2
a
C.
3 .a
D.
2
.
2
a
Câu 48: Đạo hàm của hàm số
1 2
e
x
y
là
A.
1 2
2e
x
y
. B.
1 2
2e
x
y
. C.
1 2
e
.
2
x
y
D.
1 2
e
x
y
.
Câu 49: Tập nghiệm của bất phương trình
2 2
2log 1 log 5 1
x x
là
A.
3;5
. B.
1;3
. C.
1;3
. D.
1;5
.
Câu 50: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
3 2
1
4 2
3
y x mx x
đồng biến
trên tập xác định của nó ?
A.
4.
B.
2.
C.
5.
D.
3
-----------------------------------------------
----------- HẾT ----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 1/24 – BTN 044
SỞ GD VÀ ĐT VĨNH PHÚC
TRƯỜNG CHUYÊN VĨNH PHÚC
KHẢO SÁT CHẤT LƯỢNG LẦN 2 - MÔN TOÁN
Năm học 2018 – 2019
Thời gian: 90 phút
Họ và tên học sinh…………………….. Lớp…… Số báo danh ….…………
MÃ ĐỀ 234
Câu 1. [2D1.2-2] Tìm giá trị cực tiểu
CT
y
của hàm số
3
3 4
y x x
.
A.
6
CT
y
. B.
1
CT
y
. C.
2
CT
y
. D.
1
CT
y
.
Câu 2. [2D2.5-2] Phương trình:
3
log 3 2 3
x
có nghiệm là
A.
25
3
x . B.
87
. C.
29
3
x . D.
11
3
x
.
Câu 3. [2D1.4-2] Đồ thị hàm số
2
1
4
x
y
x
có bao nhiêu đường tiệm cận?
A.
4
B.
0
. C.
1
. D.
2
.
Câu 4. [2D2.1-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức
lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng, người đó có số tiền là
10
triệu đồng.
Hỏi số tiền
T
gần với số tiền nào nhất trong các số sau.
A.
613.000
đồng. B.
645.000
đồng. C.
635.000
đồng. C.
535.000
đồng
Câu 5. [1D4.3-3] Cho hàm số
2016
2
khi 1
2018 1 2018
khi 1
x x
x
f x
x x
k x
. Tìm
k
để hàm số
f x
liên tục tại
1
x
.
A.
2 2019.
k B.
2017. 2018
.
2
k C.
1.
k
D.
20016
2019.
2017
k
Câu 6. [2D2.1-2] Cho biểu thức
3
3
4
.
P x x x
, với
0.
x
Mệnh đề nào dưới đây đúng?
A.
1
2
P x
. B.
7
12
P x
. C.
5
8
P x
. D.
7
24
P x
.
Câu 7. [2D1.3-2] Có bao nhiêu giá trị nguyên của
x
để hàm số
1 3
y x x
đạt giá trị nhỏ nhất.
A.
4
. B.
5
. C.
2
. D.
3
.
Câu 8.
[
2H1.3-1] Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
.
a
A.
3
2
a
. B.
3
3
4
a
. C.
3
3
2
a
. D.
3
2
3
a
.
Câu 9. [2D1.5-2] Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
3 1
y x x
.
B.
3 2
3 1
y x x
.
C.
3 2
3 1
y x x
.
D.
3 2
3 1
y x x
.
Câu 10. [2D2.4-1] Đường thẳng
2
y
là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây?
A.
2 1
1
x
y
x
. B.
3 4
2
x
y
x
. C.
1
2
x
y
x
. D.
1
2 1
x
y
x
.
x
y
1
1
2
3
O
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 2/24 – BTN 044
Câu 11. [2D1.2-4] Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12
y x x x m
có
5
điểm cực trị?
A.
16
. B.
44
. C.
26
. D.
27
.
Câu 12. [2D2.5-3] Biết rằng tập các giá trị của tham số
m
để phương trình
3 9 2 1 3 1 0
x x
m m m
có hai nghiệm phân biệt là một khoảng
;
a b
. Tính tích
.
ab
.
A.
4
. B.
3
. C.
2
. D.
3
.
Câu 13. [2H1.2-3] Cho hình chóp
.
S ABC
có
SA a
,
2
SB a
,
4
SC a
và
60
ASB BSC CSA
.
Tính thể tích khối chóp
.
S ABC
theo
a
.
A.
3
2
3
a
. B.
3
8 2
3
a
. C.
3
4 2
3
a
. D.
3
2 2
3
a
.
Câu 14. [2D2.2-2] Giá trị của biểu thức
2 2 2 2
log 2 log 4 log 8 ... log 256
M bằng
A.
48
. B.
56
. C.
36
. D.
2
8log 256
.
Câu 15. [2D2.7-2] Kí hiệu
max ;
a b
là số lớn nhất trong hai số
a
,
b
. Tìm tập nghiệm
S
của bất
phương trình
2 1
3
max log ; log 1
x x
.
A.
1
;2
3
S
. B.
0;2
S . C.
1
0;
3
S
. D.
2;S
.
Câu 16. [2D2.3-1] Với
a
là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A.
1
log 3 log
3
a a
. B.
3
1
log log
3
a a
. C.
3
log 3log
a a
. D.
log 3 3log
a a
.
Câu 17. [2D1.5-4] Gọi
M
,
N
là hai điểm di động trên đồ thị
C
của hàm số
3 2
3 4
y x x x
sao
cho tiếp tuyến của
C
tại
M
và
N
luôn song song với nhau. Hỏi khi
,
M N
thay đổi, đường
thẳng
MN
luôn đi qua nào trong các điểm dưới đây?
A. Điểm
1; 5
N
. B. Điểm
1; 5
M
. C. Điểm
1;5
Q . D. Điểm
1;5
P .
Câu 18. [2D1.5-4] Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
3;1
M và đường tròn
2 2
: 2 6 6 0
C x y x y
. Gọi
1
T
,
2
T
là các tiếp điểm của các tiếp tuyến kẻ từ
M
đến
C
.
Tính khoảng cách từ
O
đến đường thẳng
1 2
TT
.
A.
5
. B.
5
. C.
3
5
. D.
2 2
.
Câu 19. [2H1.2-2] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
A.
4
. B.
9.
C.
3
. D.
6.
Câu 20. [2D1.5-2] Đường thẳng
có phương trình
2 1
y x
cắt đồ thị của hàm số
3
3
y x x
tại
hai điểm
A
và
B
với tọa độ được kí hiệu lần lượt là
;
A A
A x y
và
;
B B
B x y
trong đó
B A
x x
. Tìm
B B
x y
?
A.
5
B B
x y
. B.
2
B B
x y
. C.
4
B B
x y
. D.
7
B B
x y
.
Câu 21. [2D1.1-1] Hàm số
4 2
2 1
y x x
nghịch biến trên các khoảng nào sau đây?
A.
; 1

và
0;+
. B.
;0
 và
1;+
.
C.
1;0
và
1;+
. D.
; 1

và
0;1
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 3/24 – BTN 044
Câu 22. [2D1.3-1] Giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
thuộc khoảng
nào dưới đây?
A.
3;8
. B.
7;8
. C.
2;14
. D.
12;20
.
Câu 23. [2D1.2-2] Cho hàm số
y f x
. Hàm số
y f x
có đồ thị trên một khoảng
K
như hình vẽ bên.
Trong các khẳng định sau, có tất cả bao nhiêu khẳng định đúng?
I
: Trên
K
, hàm số
y f x
có hai điểm cực trị.
II
: Hàm số
y f x
đạt cực đại tại
3
x
.
III
: Hàm số
y f x
đạt cực tiểu tại
1
x
.
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 24. [1D4.1-3] Với
n
là số tự nhiên lớn hơn
2
, đặt
3 3 3 3
3 4 5
1 1 1 1
...
n
n
S
C C C C
. Tính
lim
n
S
A.
1
. B.
3
2
. C.
3
. D.
1
3
.
Câu 25. [1D2.2-3] Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
là
A.
;2
S . B.
;1
S

. C.
1;S

D.
2;S
.
Câu 26. [2H2.1-1] Khối cầu bán kính
2
R a
có thể tích là
A.
3
32
3
a
. B.
3
6
a
. C.
2
16
a
. D.
3
8
3
a
.
Câu 27. [2H2.1-2] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và mặt
đáy bằng
60
. Tính diện tích xung quanh của hình nón đỉnh
S
, đáy là hình tròn ngoại tiếp tam
giác
ABC
.
A.
2
3
3
a
. B.
2
7
6
a
. C.
2
7
4
a
. D.
2
10
8
a
.
Câu 28. [0H3.5-3] Trong mặt phẳng với hệ tọa độ
Oxy
, cho elip
2 2
: 1
25 9
x y
E
. Điểm
M E
sao
cho
1 2
90
F MF
. Tìm bán kính đường tròn nội tiếp tam giác
1 2
MF F
.
A.
2
. B.
4
. C.
1
. D.
1
2
.
Câu 29. [1D1.4-3] Có bao nhiêu giá trị nguyên của
m
thuộc đoạn
2018;2018
để phương trình
2
1 sin sin 2 cos2 0
m x x x
có nghiệm?
A.
4036
. B.
2020
. C.
4037
. D.
2019
.
Câu 30. [2D1.1-4] Cho hàm số
y f x
có đồ thị
f x
như hình vẽ bên. Hàm số
2
1
2
x
y f x x
nghịch biến trên khoảng nào trong các khoảng
dưới đây?
A.
2; 0
. B.
3; 1
.
C.
3;

. D.
1; 3
.
O
x
y
1
x
2
x
3
x
x
y
O
3
3
3
3
5
1
1
3
2
1
2
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 4/24 – BTN 044
Câu 31. [0D3.2-3] Tìm tất cả các giá trị tham số
m
để bất phương trình
2
6 2 8 1
x x x x m
nghiệm đúng với mọi
2;8
x .
A.
16
m
. B.
15
m
. C.
8
m
. D.
2 16
m
.
Câu 32. [2D2.2-1] Tìm tập xác định
D
của hàm số
1
2
3
3 1
y x
.
A.
1 1
; ;
3 3
D
 
. B.
D
.
C.
1
\
3
D
. D.
1 1
; ;
3 3
D
 
.
Câu 33. [2H1.2-1] Số cạnh của hình mười hai mặt đều là
A. Mười sáu. B. Ba mươi. C. Hai mươi. D. Mười hai.
Câu 34. [2H1.3-3] Cho hình chóp tứ giác đều có góc giữa mặt bên và mặt đáy bằng
60
. Biết rằng mặt
cầu ngoại tiếp hình chóp đó có bán kính
3.
R a Tính độ dài cạnh đáy của hình chóp tứ giác
đều nói trên.
A.
12
5
a
. B.
2
a
. C.
3
2
a
. D.
9
4
a
.
Câu 35. [2D2.5-3] Biết rằng phương trình
e e 2cos
x x
ax
(
a
là tham số) có
3
nghiệm thực phân
biệt. Hỏi phương trình
e e 2cos 4
x x
ax
có bao nhiêu nghiệm thực phân biệt?
A.
5
. B.
10
. C.
6
. D.
11
.
Câu 36. [2H2.1-1] Cho khối nón có bán kính đáy
3
r và chiều cao
4
h
. Tính thể tích
V
của khối
nón đã cho.
A.
16 3
V
. B.
16 3
3
V
. C.
12
V
. D.
4
V
.
Câu 37. [2D1.3-3] Giá trị nhỏ nhất của hàm số
2sin 3
sin 1
x
y
x
trên
0;
2
là
A.
5.
B.
2.
C.
3.
D.
5
.
2
Câu 38. [1H3.5-3] Cho hình lăng trụ tam giác đều
.
ABC A B C
có
AB a
,
2 .
AA a
Tính khoảng
cách giữa hai đường thẳng
AB
và
A C
.
A.
3
.
2
a
B.
2 5
.
5
a
C.
5.
a D.
2 17
.
17
a
Câu 39. [0H3.1-2] Trong mặt phẳng với hệ tọa độ
Ox ,
y
giả sử điểm
( ; )
A a b
thuộc đường thẳng
: 3 0
d x y
và cách
: 2 1 0
x y
một khoảng bằng
5.
Tính
P ab
biết
0.
a
A.
4
. B.
2
. C.
2
. D.
4
.
Câu 40. [2H2.1-1]
Một
hình
trụ có bán kính đáy bằng
r
và có thiết diện qua trục là một hình vuông.
Tính
diện tích toàn phần của hình trụ đó.
A.
2
4
r
. B.
2
6
r
. C.
2
8
r
. D.
2
2
r
.
Câu 41. [2D1.3-3] Gọi
S
là
tập
hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của
hàm số
2
1
x mx m
y
x
trên
1;2
bằng
2
. Số phần tử của tập
S
là
A.
3
. B.
1
. C.
4
. D.
2
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 5/24 – BTN 044
Câu 42. [2D2.4-3] Cho
a
,
b
là
các
số thực dương thỏa mãn
1
b
và
a b a
. Tìm giá trị nhỏ nhất
của biểu thức log 2log
a
b
b
a
P a
b
.
A.
6
. B.
7
. C.
5
. D.
4
.
Câu 43. [2H2.2-3] Một hình trụ có độ dài đường cao bằng
3
, các đường tròn đáy lần lượt là
;1
O và
;1
O
. Giả sử
AB
là đường kính cố định của
;1
O và
CD
là đường kính thay đổi trên
;1
O
. Tìm giá trị lớn nhất
max
V
của thể tích khối tứ diện
ABCD
.
A.
max
2
V
. B.
max
6
V
. C.
max
1
2
V
. D.
max
1
V
.
Câu 44. [1D2.5-4] Trong mặt phẳng tọa độ
Oxy
, cho hình chữ nhật
OMNP
với
0;10
M ,
100;10
N ,
100;0
P Gọi
S
là tập hợp tất cả các điểm
;
A x y
với ,x y
nằm bên trong (kể cả trên
cạnh) của hình chữ nhật
OMNP
. Lấy ngẫu nhiên một điểm
;
A x y S
. Tính xác suất để
90
x y
.
A.
169
200
. B.
473
500
. C.
845
1111
. D.
86
101
.
Câu 45. [2D2.3-2] Tập xác định của
2
ln 5 6
y x x
là
A.
2; 3
. B.
2; 3
. C.
; 2 3;

. D.
; 2 3;

.
Câu 46. [2D2.4-2] Cho
3
.e
x
f x x
. Tập nghiệm của bất phương trình
0
f x
là
A.
1
;
3

. B.
1
0;
3
. C.
1
;
3
. D.
0;1
.
Câu 47. [2H1.3-2] Cho khối chóp
.
S ABCD
có thể tích bằng
3
2
a
và đáy
ABCD
là hình bình hành. Biết
diện tích tam giác
SAB
bằng
2
.
a
Tính khoảng cách giữa hai đường thẳng
SB
và
CD
.
A.
a
. B.
3
2
a
. C.
3
a
. D.
2
2
a
.
Câu 48. [2D2.4-1] Đạo
hàm
của hàm số
1 2
e
x
y
là
A.
1 2
2e
x
y
. B.
1 2
2e
x
y
. C.
1 2
e
.
2
x
y
D.
1 2
e
x
y
.
Câu 49. [2D2.5-2] Tập
nghiệm
của bất phương trình
2 2
2log 1 log 5 1
x x
là
A.
3;5
. B.
1;3
. C.
1;3
. D.
1;5
.
Câu 50. [2D1.1-2] Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
3 2
1
4 2
3
y x mx x
đồng
biến trên tập xác định của nó?
A.
4
. B.
2
. C.
5
. D.
3
.
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 6/24 – BTN 044
ĐÁP ÁN THAM KHẢO
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
C
D
C
A
C
B B B
A
D
B D
C
A
C
C
C
C
A
D
D
A
B D
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
B C
B A
B A
B A
C
D
D
D
B B D
C
A
D
A
C
C
B B C
HƯỚNG DẪN GIẢI
Câu 1. [2D1.2-2] Tìm giá trị cực tiểu
CT
y
của hàm số
3
3 4
y x x
.
A.
6
CT
y
. B.
1
CT
y
. C.
2
CT
y
. D.
1
CT
y
.
Lời giải
Chọn A.
Ta có:
2
3 3, 0 1
y x y x
.
Bảng biến thiên
Vậy
6
CT
y
.
Câu 2. [2D2.5-2] Phương trình:
3
log 3 2 3
x
có nghiệm là
A.
25
3
x . B.
87
. C.
29
3
x . D.
11
3
x
.
Lời giải
Chọn C.
Ta có:
3
29
log 3 2 3 3 2 27
3
x x x .
Câu 3. [2D1.4-2] Đồ thị hàm số
2
1
4
x
y
x
có bao nhiêu đường tiệm cận?
A.
4
B.
0
. C.
1
. D.
2
.
Lời giải
Chọn D.
Tập xác định của hàm số là
2;2
.
Ta có
2 2
lim , lim
x x
y y

 
.
Đồ thị hàm số có 2 bao nhiêu đường tiệm cận.
Câu 4. [2D2.1-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền
T
theo hình thức
lãi kép với lãi suất
0,6%
mỗi tháng. Biết sau
15
tháng, người đó có số tiền là
10
triệu đồng.
Hỏi số tiền
T
gần với số tiền nào nhất trong các số sau.
A.
613.000
đồng. B.
645.000
đồng. C.
635.000
đồng. C.
535.000
đồng
Lời giải
Chọn C.
Đặt
0.6%
a
.
Số tiền cả lãi lẫn gốc sau n kì là
x

1
1

y
0
0
y

2
6

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 7/24 – BTN 044
1 1 1
n
n
T
T a a
a
Suy ra
.
635301
1 1 1
n
n
T a
T
a a
Câu 5. [1D4.3-3] Cho hàm số
2016
2
khi 1
2018 1 2018
khi 1
x x
x
f x
x x
k x
. Tìm
k
để hàm số
f x
liên tục tại
1
x
.
A.
2 2019.
k B.
2017. 2018
.
2
k C.
1.
k
D.
20016
2019.
2017
k
Lời giải
Chọn A.
Ta có:
2016 2016
1 1 1
2 2015
1
2 2015
1
1
2 1 1
lim lim lim
2018 1 2018 2018 1 2018
1 1 ... 1 2018 1 2018
lim
2018 1 2018 2018 1 2018
1 1 ... 1 2018 1 2018
lim
2017 2017
1
lim
x x x
x
x
x
x x x x
f x
x x x x
x x x x x x
x x x x
x x x x x x
x
2 2015
1 ... 2018 1 2018
2 2019
2017
x x x x x
Để hàm số liên tục tại
1
x
thì
1
lim (1) 2 2019
x
f x f k
Câu 6.
[2D2.1-2] Cho biểu thức
3
3
4
.
P x x x
, với
0.
x
Mệnh đề nào dưới đây đúng?
A.
1
2
P x
. B.
7
12
P x
. C.
5
8
P x
. D.
7
24
P x
.
Lời giải
Chọn C.
Ta có
7 5
7 15
3
3
4
3
3
4
8 8
2 24
. . .
P x x x x x x x x x
.
Câu 7. [2D1.3-2] Có bao nhiêu giá trị nguyên của
x
để hàm số
1 3
y x x
đạt giá trị nhỏ nhất.
A.
4
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn B.
Ta có
1 3
y x x
2 2, 1
4, 3 1
2 2, 3
x x
x
x x
.
Trên
1;
, ta có
4
y
và dấu bằng xảy ra khi
1
x
.
Trên
3;1
, ta có
4
y
và có bốn giá trị nguyên của
x
thuộc khoảng này.
Trên
; 3

, ta có
2 2 4
y x
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 8/24 – BTN 044
Vậy
min
4
y
và có
5
giá trị nguyên của
x
để
min
4
y
.
Câu 8.
[2H1.3-1] Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng
.
a
A.
3
2
a
. B.
3
3
4
a
. C.
3
3
2
a
. D.
3
2
3
a
.
Lời giải
Chọn B.
Ta có
2
3
4
day
a
S và chiều cao
h a
nên suy ra
3
3
4
a
V .
Câu 9. [2D1.5-2] Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
3
3 1
y x x
. B.
3 2
3 1
y x x
. C.
3 2
3 1
y x x
. D.
3 2
3 1
y x x
.
Lời giải
Chọn B.
Nhánh đầu tiên của đồ thị đi lên nên hệ số
0
a
. Vậy loại phương án A và D.
Hàm số có hai điểm cực trị là
0
x
và
2
x
nên chọn phương án B.
Câu 10. [2D2.4-1] Đường thẳng
2
y
là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây?
A.
2 1
1
x
y
x
. B.
3 4
2
x
y
x
. C.
1
2
x
y
x
. D.
1
2 1
x
y
x
.
Lời giải
Chọn A.
Ta có
2 1
lim 2
1
x
x
x

nên
2
y
là đường tiệm cận ngang của đồ thị hàm số.
Câu 11. [2D1.2-4] Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 3 2
3 4 12
y x x x m
có
5
điểm cực trị?
A.
16
. B.
44
. C.
26
. D.
27
.
Lời giải
Chọn D.
Xét hàm số
4 3 2
3 4 12
f x x x x m
trên
D
.
3 2
12 12 24
f x x x x
;
0
f x
1
0
2
x
x
x
.
Bảng biến thiên
x
y
1
1
2
3
O
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 9/24 – BTN 044
Vì
m
nguyên dương nên để hàm số có
5
điểm cực trị
5 0
5 32
32 0
m
m
m
.
Vậy có
27
giá trị nguyên dương
m
.
Câu 12. [2D2.5-3] Biết rằng tập các giá trị của tham số
m
để phương trình
3 9 2 1 3 1 0
x x
m m m
có hai nghiệm phân biệt là một khoảng
;
a b
. Tính tích
.
ab
.
A.
4
. B.
3
. C.
2
. D.
3
.
Lời giải
Chọn B.
Đặt
3
x
t
;
0
t
.
Phương trình trở thành:
2
3 2 1 1 0
m t m t m
2
2
3 2 1
2 1
t t
m
t t
với
0
t
và
1 2
t
.
Phương trình có hai nghiệm phân biệt
Đường thẳng
d
:
y m
có hai điểm chung với đồ thị
hàm số
2
2
3 2 1
2 1
t t
f t
t t
với
0
t
và
1 2
t
.
2
2
2
8 4
0
2 1
t t
f t
t t
.
Bảng biến thiên
Dựa vào bảng biến thiên phương trình có hai nghiệm phân biệt
1 3
m
1
a
và
3
b
. Do đó
3
ab
.
Câu 13. [2H1.2-3] Cho hình chóp
.
S ABC
có
SA a
,
2
SB a
,
4
SC a
và
60
ASB BSC CSA
.
Tính thể tích khối chóp
.
S ABC
theo
a
.
A.
3
2
3
a
. B.
3
8 2
3
a
. C.
3
4 2
3
a
. D.
3
2 2
3
a
.
Lời giải
Chọn D.
2 1
0

t
f t
f t
1


3
x

1
0
2

f x
0
0
0
f x

5
m
m
32
m

TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 10/24 – BTN 044
S
B
A
C
Áp dụng công thức giải nhanh đối với khối chóp
.
S ABC
Ta có
2 2 2
1 2
1 2.cos .cos .cos cos cos cos
6 12
abc
V abc x y z x y z .
a
,
b
,
c
lần lượt là độ dài các cạnh
SA
,
SB
,
SC
.
x
,
y
,
z
lần lượt là số đo các góc
ASB
,
BSC
,
CSA
.
Vậy:
3 3
8 2 2 2
12 3
a a
V .
Câu 14. [2D2.2-2] Giá trị của biểu thức
2 2 2 2
log 2 log 4 log 8 ... log 256
M bằng
A.
48
. B.
56
. C.
36
. D.
2
8log 256
.
Lời giải
Chọn C.
2 2 2 2
log 2 log 4 log 8 ... log 256 1 2 3 .... 8 36
M
.
Câu 15. [2D2.7-2] Kí hiệu
max ;
a b
là số lớn nhất trong hai số
a
,
b
. Tìm tập nghiệm
S
của bất
phương trình
2 1
3
max log ; log 1
x x
.
A.
1
;2
3
S
. B.
0;2
S . C.
1
0;
3
S
. D.
2;S
.
Lời giải
Chọn A.
Nếu
1
x
:
2 1
3
max log ; log 1
x x
2
log 1 1 2
x x
.
Nếu
0 1
x
:
2 1
3
max log ; log 1
x x
1
3
1
log 1 1
3
x x
.
Vậy
1
;2
3
S
.
Câu 16. [2D2.3-1] Với
a
là số thực dương bất kì, mệnh đề nào dưới đây đúng?
A.
1
log 3 log
3
a a
. B.
3
1
log log
3
a a
. C.
3
log 3log
a a
. D.
log 3 3log
a a
.
Lời giải
Chọn C.
Câu 17. [2D1.5-4] Gọi
M
,
N
là hai điểm di động trên đồ thị
C
của hàm số
3 2
3 4
y x x x
sao
cho tiếp tuyến của
C
tại
M
và
N
luôn song song với nhau. Hỏi khi
,
M N
thay đổi, đường
thẳng
MN
luôn đi qua nào trong các điểm dưới đây?
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 11/24 – BTN 044
A. Điểm
1; 5
N
. B. Điểm
1; 5
M
. C. Điểm
1;5
Q . D. Điểm
1;5
P .
Lời giải
Chọn C.
Gọi
;
M M
M x y
,
;
N N
N x y
.
Do
,
M N C
nên
3 2
; 3 4
M M M M
M x x x x
,
3 2
; 3 4
N N N N
N x x x x
.
Theo giả thiết tiếp tuyến của
C
tại
M
và
N
luôn song song với nhau nên ta có:
M N
y x y x
2 2
3 6 1 3 6 1
M M N N
x x x x
2 2
3 6 3 6 0
M M N N
x x x x
2 0
N M N M
x x x x
0
2
N M
N M
x x
x x
.
Do
M
và
N
phân biệt nên
N M
x x
, suy ra
2
N M
x x
.
Ta có:
3 3 2 2
3 8
M N M N N M M N
y y x x x x x x
3 2
3 3 2 8
M N M N M N M N M N M N
x x x x x x x x x x x x
3 2
2 6 3 2 2 2 8
M N M N
x x x x
10
.
Từ đây suy ra đường thẳng
MN
luôn đi qua điểm cố định là trung điểm
1;5
Q của
MN
.
Câu 18. [2D1.5-4] Trong mặt phẳng với hệ tọa độ
Oxy
, cho điểm
3;1
M và đường tròn
2 2
: 2 6 6 0
C x y x y
. Gọi
1
T
,
2
T
là các tiếp điểm của các tiếp tuyến kẻ từ
M
đến
C
.
Tính khoảng cách từ
O
đến đường thẳng
1 2
TT
.
A.
5
. B.
5
. C.
3
5
. D.
2 2
.
Lời giải
Chọn C.
Ta xét đường tròn
C
có tâm
1;3
I và bán kính
2
R
.
Theo tính chất tiếp tuyến ta có
1 2
MI TT
tại trung điểm của
1 2
TT
.
Suy ra đường thẳng
1 2
TT
nhận vectơ
4;2
MI
là vtpt.
Giả sử
1 1 1
;
T x y
. Khi đó, phương trình
1 2
TT
có dạng:
1 1
4 2 0
x x y y
.
Suy ra
1 1
1 2
2 2
4 2
,
4 2
x y
d O TT
1 1
4 2
2 5
x y
.
Ta có:
1 1 1
3; 1
MT x y
.
Theo giả thiết ta có:
1 1
. 0
MT IT
1 1 1 1
1 3 3 1 0
x x y y
2 2
1 1 1 1
2 3 4 3 0
x x y y
(1)
Đồng thời ta có:
1
IT R
2 2
1 1
3 1 4
x y
2 2
1 1 1 1
6 9 2 1 4
x x y y
(2)
Lấy (1) – (2) ta được:
1 1
4 2 6
x y
.
Từ đây ta có:
1 1
1 2
4 2
,
2 5
x y
d O TT
6
2 5
3
5
.
Câu 19. [2H1.2-2] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
A.
4
. B.
9.
C.
3
. D.
6.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 12/24 – BTN 044
Lời giải
Chọn C.
Hình hộp chữ nhật có ba kích thước đôi một khác nhau có 3 mặt phẳng đối xứng.
Câu 20. [2D1.5-2] Đường thẳng
có phương trình
2 1
y x
cắt đồ thị của hàm số
3
3
y x x
tại
hai điểm
A
và
B
với tọa độ được kí hiệu lần lượt là
;
A A
A x y
và
;
B B
B x y
trong đó
B A
x x
. Tìm
B B
x y
?
A.
5
B B
x y
. B.
2
B B
x y
. C.
4
B B
x y
. D.
7
B B
x y
.
Lời giải
Chọn A.
Phương trình hoành độ giao điểm
3
2 1 3
x x x
3
3 2 0
x x
1 3
2 3
A A
B B
x y
x y
5
B B
x y
.
Câu 21. [2D1.1-1] Hàm số
4 2
2 1
y x x
nghịch biến trên các khoảng nào sau đây?
A.
; 1

và
0;+
. B.
;0
 và
1;+
. C.
1;0
và
1;+
. D.
; 1

và
0;1
.
Lời giải
Chọn D.
Ta có
3
4 4
y x x
1
0 1
0
x
y x
x
Bảng biến thiên
Hàm số đồng biến trên các khoảng
; 1

và
0;1
.
Câu 22. [2D1.3-1] Giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
thuộc khoảng
nào dưới đây?
A.
3;8
. B.
7;8
. C.
2;14
. D.
12;20
.
Lời giải
Chọn D.
2
6 6 12
y x x
x

1
0
1

y
0
0
0
y


1
0
0
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 13/24 – BTN 044
1 1;2
0
2 1;2
x
y
x
1 15
y
;
1 5
y
;
2 6
y
.
1;2
15 12;20
Max y
.
Câu 23. [2D1.2-2] Cho hàm số
y f x
. Hàm số
y f x
có đồ thị trên một khoảng
K
như hình vẽ bên.
Trong các khẳng định sau, có tất cả bao nhiêu khẳng định đúng?
I
: Trên
K
, hàm số
y f x
có hai điểm cực trị.
II
: Hàm số
y f x
đạt cực đại tại
3
x
.
III
: Hàm số
y f x
đạt cực tiểu tại
1
x
.
A.
2
. B.
3
. C.
1
. D.
0
.
Lời giải
Chọn A.
Dựa vào đồ thị hàm số suy ra bảng biến thiên cho hàm số
f x
như sau:
x
3
00
x
2
x
y'
y
x
1
+
+
0
∞
∞
∞
+
∞
Dựa vào BBT suy ra: hàm số có 2 điểm cực trị, điểm cực tiểu là
1
x x
và điểm cực đại là
2
x x
. Vậy có 2 khẳng định đúng là
I
và
III
.
Câu 24. [1D4.1-3] Với
n
là số tự nhiên lớn hơn
2
, đặt
3 3 3 3
3 4 5
1 1 1 1
...
n
n
S
C C C C
. Tính
lim
n
S
A.
1
. B.
3
2
. C.
3
. D.
1
3
.
Lời giải
Chọn B.
Ta có:
3
3
1 2
! 1 6
3! 3 ! 6 1 2
n
n
n n n
n
C
n C n n n
.
O
x
y
1
x
2
x
3
x
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 14/24 – BTN 044
Khi đó:
6 6 6 6 1 1 1 1
6
1.2.3 2.3.4 3.4.5 2 1 1.2.3 2.3.4 3.4.5 2 1
n
S
n n n n n n
Xét dãy
k
u
:
1 1 1 1 1 1 1 1 1 1
. . .
2 1 2 1 2 2 1 2 1
k
u
k k k k k k k k k k
.
Suy ra:
1 1 1 1 1 1 1
1.2.3 2 1.2 2.3 2 2 6
.
1 1 1 1 1 1 1
2.3.4 2 2.3 3.4 2 6 12
.
1 1 1 1 1 1 1
3.4.5 2 3.4 4.5 2 12 20
.
…
1 1 1 1
2 1 2 2 1 1
n n n n n n n
.
1 1 1 1 1
6. 3
2 2 1 2 1
n
S
n n n n
.
Vậy
1 1 3
lim lim 3
2 1 2
n
S
n n
.
Câu 25. [1D2.2-3] Tập nghiệm
S
của bất phương trình
2
1
5
25
x
x
là
A.
;2
S . B.
;1
S

. C.
1;S

D.
2;S
.
Lời giải
Chọn D.
2 2 2
1
5 5 5 2 2 2
25
x
x x x
x x x
. Vậy
2;S
.
Câu 26. [2H2.1-1] Khối cầu bán kính
2
R a
có thể tích là
A.
3
32
3
a
. B.
3
6
a
. C.
2
16
a
. D.
3
8
3
a
.
Lời giải
Chọn A.
3
3
4 32
3 3
a
V R
.
Câu 27. [2H2.1-2] Cho hình chóp tam giác đều
.
S ABC
có cạnh đáy bằng
a
, góc giữa mặt bên và mặt
đáy bằng
60
. Tính diện tích xung quanh của hình nón đỉnh
S
, đáy là hình tròn ngoại tiếp tam
giác
ABC
.
A.
2
3
3
a
. B.
2
7
6
a
. C.
2
7
4
a
. D.
2
10
8
a
.
Lời giải
Chọn B.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 15/24 – BTN 044
M
O
S
B
A
C
Gọi
M
là trung điểm của
AB
.
1 1 3 3
3 3 2 6
a a
OM CM .
Xét tam giác vuông
1
SOM O v
có
o
3
cos60
3
OM a
SM
SM
.
Xét tam giác vuông
1
SMB M v
có
2 2
2 2
3 21
9 4 6
a a a
SB SM MB .
Ta có bán kính đường tròn ngoại tiếp tam giác
ABC
bằng
2 3
3 3
a
OC CM .
Vậy
2
3 21 7
.
3 6 6
xq
a a a
S rl
.
Câu 28. [0H3.5-3] Trong mặt phẳng với hệ tọa độ
Oxy
, cho elip
2 2
: 1
25 9
x y
E
. Điểm
M E
sao
cho
1 2
90
F MF
. Tìm bán kính đường tròn nội tiếp tam giác
1 2
MF F
.
A.
2
. B.
4
. C.
1
. D.
1
2
.
Lời giải
Chọn C.
F
2
OF
1
M
Ta có
2 2 2
1 2
16 2 8
c a b c F F
, và
1 2
4;0 , 4;0
F F .
Giả sử
2 2
; 1 1
25 9
x y
M x y E
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 16/24 – BTN 044
Tam giác
1 2
MF F
là tam giác vuông đỉnh
M
suy ra
1 2
. 0 4 ; 4 ; 0
MF MF x y x y
2 2
16 0
x y
2 2
16 2
x y .
Thay (2) vào (1) ta có:
2 2
2 2
16
1 144 9 25 225 0
25 9
y y
y y
2
16 81
y
9 5 7
4 4
y x .
Vậy có bốn điểm
1 2 3 4
5 7 9 5 7 9 5 7 9 5 7 9
; , ; , ; , ;
4 4 4 4 4 4 4 4
M M M M
thỏa mãn yêu cầu của bài toán.
Ta có
1 2
1 1
512 160 7, 512 160 7
4 4
MF MF
,
1 2 1 2
2
MF MF F F
p
.
1 2
1 2
1
, . 9
2
MF F
S d M Ox F F
.
Vậy bán kính đường tròn nội tiế tam giác
1 2
1
MF F
S
r
p
.
Câu 29. [1D1.4-3] Có bao nhiêu giá trị nguyên của
m
thuộc đoạn
2018;2018
để phương trình
2
1 sin sin 2 cos2 0
m x x x
có nghiệm?
A.
4036
. B.
2020
. C.
4037
. D.
2019
.
Lời giải
Chọn B.
Ta có
2
1 sin sin 2 cos2 0
m x x x
2 2 2
1 sin sin 2 cos sin 0
m x x x x
2 2
cos 2sin .cos sin 0
x x x m x
1
Thay
sin 0
x
vào phương trình
1
ta được
2
cos 0
x
(vô lí vì
2 2
sin cos 1
x x
)
sin 0
x
, chia hai vế phương trình
1
cho
2
sin
x
ta được phương trình:
2
cot 2cot 0
x x m
2
Phương trình
1
có nghiệm khi phương trình
2
có nghiệm
0
1 0 1
m m
Mà
2018;2018
2018; 2017;...;0;1
m
m
m
có
2020
số nguyên
m
thỏa yêu cầu.
Câu 30. [2D1.1-4] Cho hàm số
y f x
có đồ thị
f x
như hình vẽ
Hàm số
2
1
2
x
y f x x
nghịch biến trên khoảng nào trong các khoảng dưới đây?
x
y
O
3
3
3
3
5
1
1
3
2
1
2
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 17/24 – BTN 044
A.
2; 0
. B.
3; 1
. C.
3;

. D.
1; 3
.
Lời giải
Chọn A.
Ta có
2
1
2
x
y f x x
1 1
y f x x
Hàm số
2
1
2
x
y f x x
nghịch biến
0 1 1
y f x x
1
Đặt
1 1
t x x t
, bất phương trình
1
trở thành
f t t
Đồ thị hàm số
f t
có dạng đồ thị hàm số
f x
Trong hệ trục tọa độ
Oty
, vẽ đường thẳng :
d y t
và đồ thị hàm số
y f t
Đường thẳng
d
cắt đồ thị hàm số
y f t
tại các điểm
3;3 ; 1; 1 ; 3; 3
A B C
Từ đồ thị suy ra
f t t
3
1 3
t
t
1 3
1 1 3
x
x
4
2 0
x
x
Câu 31. [0D3.2-3] Tìm tất cả các giá trị tham số
m
để bất phương trình
2
6 2 8 1
x x x x m
nghiệm đúng với mọi
2;8
x .
A.
16
m
. B.
15
m
. C.
8
m
. D.
2 16
m
.
Lời giải
Chọn B.
Bất phương trình tương đương
2
6 16 2 8 15
x x x x m
Đặt
2 8 ;
x x t
2; 8 0; 5
x t
Bất phương trình trờ thành
2
15
t t m
với
0; 5
t
Xét hàm số
2
15
f t t t
trên
0; 5
.
2 1
f t t
1
0
2
f t t
Bảng biến thiên
t
1
0 5
2

f t
0
f t
15
15
x
y
3
3
3
3
5
1
1
3
2
1
2
1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 18/24 – BTN 044
Nhìn vào bảng biến thiên ta thấy để bất phương trình có nghiệm
15
m
Câu 32. [2D2.2-1] Tìm tập xác định
D
của hàm số
1
2
3
3 1
y x
.
A.
1 1
; ;
3 3
D
 
. B.
D
.
C.
1
\
3
D
. D.
1 1
; ;
3 3
D

.
Lời giải
Chọn A.
Điều kiện xác định
2
1
3
3 1 0
1
3
x
x
x
Câu 33. [2H1.2-1] Số cạnh của hình mười hai mặt đều là
A. Mười sáu. B. Ba mươi. C. Hai mươi. D. Mười hai.
Lời giải
Chọn B.
Câu 34. [2H1.3-3] Cho hình chóp tứ giác đều có góc giữa mặt bên và mặt đáy bằng
60
. Biết rằng mặt
cầu ngoại tiếp hình chóp đó có bán kính
3.
R a Tính độ dài cạnh đáy của hình chóp tứ giác
đều nói trên.
A.
12
5
a
. B.
2
a
. C.
3
2
a
. D.
9
4
a
.
Lời giải
Chọn A.
M
K
C
D
A
B
S
O
I
Gọi
K
là trung điểm của
AB
,
AC BD O
. Góc giữa mặt bên và đáy là góc
60
SKO
.
Gọi
M
là trung điểm của
SA
.
Trong
SOA
dựng đường thẳng trung trực
IM
của
SA
,
I SO
.
Suy ra
I
là tâm mặt cầu ngoại tiếp hình chóp tứ giác.
Giả sử
AB b
, suy ra
2
b
OK
,
2
2
b
OA .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 19/24 – BTN 044
Xét
SOK
có
tan60
SO
OK
3
.tan 60
2
b
SO OK
2 2
2 2
3 2 5
2 2 2
b b b
SA SO OA
Ta có
SMI SOA
(g.g) nên:
SI SM
SA SO
2
2
1 5
. 1 5 3
2 4
2 12
3
2
b
SA
SM SA
SI b
SO SO
b
.
Theo giả thiết
5 3 12
3
12 5
b a b a
.
Câu 35. [2D2.5-3] Biết rằng phương trình
e e 2cos
x x
ax
(
a
là tham số) có
3
nghiệm thực phân
biệt. Hỏi phương trình
e e 2cos 4
x x
ax
có bao nhiêu nghiệm thực phân biệt?
A.
5
. B.
10
. C.
6
. D.
11
.
Lời giải
Chọn C.
Ta có
2
2 2
2 2cos 4
x x
x x
e e e e ax
2
2
2 2
2cos 2 4cos .
2
x x
x
e e ax a
2 2
2 2
2cos . 1
2
2cos . 2
2
x x
x x
x
e e a
x
e e a
Phương trình
1
có ba nghiệm phân biệt, suy ra phương trình
2
cũng có 3 nghiệm phân biệt
và không có nghiệm nào trùng với nghiệm của phương trình
1
.
Vậy phương trình đã cho có
6
nghiệm thực phân biệt.
Câu 36. [2H2.1-1] Cho khối nón có bán kính đáy
3
r và chiều cao
4
h
. Tính thể tích
V
của khối
nón đã cho.
A.
16 3
V
. B.
16 3
3
V
. C.
12
V
. D.
4
V
.
Lời giải
Chọn D.
Tính thể tích
V
của khối nón đã cho là
2
1 1
. .3.4 4
3 3
V r h
.
Câu 37. [2D1.3-3] Giá trị nhỏ nhất của hàm số
2sin 3
sin 1
x
y
x
trên
0;
2
là
A.
5.
B.
2.
C.
3.
D.
5
.
2
Lời giải
Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 20/24 – BTN 044
Đặt
0; 0;1
2
x t
Hàm số đã cho trở thành
2
2 3 1
0, t 0;1
1
1
t
f t f t
t
t
Vậy
0;1
5
min 1
2
f t f
.
Câu 38. [1H3.5-3] Cho hình lăng trụ tam giác đều
.
ABC A B C
có
AB a
,
2 .
AA a
Tính khoảng
cách giữa hai đường thẳng
AB
và
A C
.
A.
3
.
2
a
B.
2 5
.
5
a
C.
5.
a D.
2 17
.
17
a
Lời giải
Chọn D.
M
a
I
2a
C'
B'
A'
C
B
A
Gọi
I AB A B
,
M
là trung điểm của
BC
.
Ta có
//
MI A C
3
// , , ,
BAB M
AB M
V
A C AB M d A C AB d A AB M d B AB M
S
.
Mà
3
1 1 3
.
3 2 12
BAB M ABC
a
V BB S
.
Tam giác
AB M
có
2 2
17 3
5, ,
2 2
a a
AB a B M B B BM AM
.
Áp dụng định lý Hêrong ta có
2
51
8
AB M
a
S
.
Vậy
2 17
, ,
17
a
d A C B A d B B AM
.
Câu 39. [0H3.1-2] Trong mặt phẳng với hệ tọa độ
Ox ,
y
giả sử điểm
( ; )
A a b
thuộc đường thẳng
: 3 0
d x y
và cách
: 2 1 0
x y
một khoảng bằng
5.
Tính
P ab
biết
0.
a
A.
4
. B.
2
. C.
2
. D.
4
.
Lời giải
Chọn B.
Do
;
A a b d
nên
3 0 3
a b a b
. Vậy
3 ;
A b b
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 21/24 – BTN 044
Theo bài:
, 5
d A
2
2
2 3 1
5
2 1
b b
7 5
b
7 5
7 5
b
b
2 1
12 9
b a
b a
. Vì
0
a
nên
1, 2
a b
. Do đó
2
P ab
Câu 40. [2H2.1-1]
Một
hình
trụ có bán kính đáy bằng
r
và có thiết diện qua trục là một hình vuông.
Tính
diện tích toàn phần của hình trụ đó.
A.
2
4
r
. B.
2
6
r
. C.
2
8
r
. D.
2
2
r
.
Lời giải
Chọn B.
Do thiết diện qua trục là một hình vuông nên cạnh của hình vuông bằng
2
r
. Suy ra chiều cao
của hình trụ cũng bằng
2
r
.
Vậy diện tích toàn phần của hình trụ đã cho là:
2
2 2
tp
S rh r
2 2 2
4 6
r r r
.
Câu 41. [2D1.3-3] Gọi
S
là
tập
hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của
hàm số
2
1
x mx m
y
x
trên
1;2
bằng
2
. Số phần tử của tập
S
là
A.
3
. B.
1
. C.
4
. D.
2
.
Lời giải
Chọn D.
Đặt
2
1
x mx m
f x
x
, ta có hàm số
f x
xác định và liên tục trên đoạn
1;2
.
Có:
2
2
2
0
1
x x
f x
x
,
1;2
x .
Suy ra:
1;2
4 3
max 2
3
m
f x f
;
1;2
1 2
min 1
2
m
f x f
.
Do đó
1;2
max max 2 ; 1
f x f f . Theo bài ta có:
2 2
1 2
f
f
1 2
2 2
f
f
Trường hợp 1:
Ta có:
2 2
1 2
f
f
4 3
2
3
1 2
2
2
m
m
2 10
3 3
5 3
2 2
m m
m
2
3
m
.
Trường hợp 2:
Ta có:
1 2
2 2
f
f
1 2
2
2
4 3
2
3
m
m
3 5
2 2
10 2
3 3
m m
m
5
3
m
.
Vậy có giá trị của tham số
m
thỏa yêu cầu bài toán. Do đó tập
S
có hai phần từ.
Câu 42. [2D2.4-3] Cho
a
,
b
là
các
số thực dương thỏa mãn
1
b
và
a b a
. Tìm giá trị nhỏ nhất
của biểu thức log 2log
a
b
b
a
P a
b
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 22/24 – BTN 044
A.
6
. B.
7
. C.
5
. D.
4
.
Lời giải
Chọn C.
Vì
1
b
và 0
a b a
nên
log 1 log
b b
a a
hay
1 log 2
b
a
.
Khi đó log 2log
a
b
b
a
P a
b
log
4 log 1
log 1
b
b
b
a
a
a
1
1 4 log 1
log 1
b
b
a
a
Áp dụng bất đẳng thức Cô si cho hai số dương
1
log 1
b
a
và
4 log 1
b
a
ta có:
1
4 log 1 4
log 1
b
b
a
a
. Suy ra
5
P
. Vậy
min 5
P
khi
a b b
.
Câu 43. [2H2.2-3] Một hình trụ có độ dài đường cao bằng
3
, các đường tròn đáy lần lượt là
;1
O và
;1
O
. Giả sử
AB
là đường kính cố định của
;1
O và
CD
là đường kính thay đổi trên
;1
O
. Tìm giá trị lớn nhất
max
V
của thể tích khối tứ diện
ABCD
.
A.
max
2
V
. B.
max
6
V
. C.
max
1
2
V
. D.
max
1
V
.
Lời giải
Chọn A.
Cách 1: Dựng hình hộp chữ nhật
.
AEBF HCGD
có thể tích
V
như hình vẽ.
H
G
F
E
r
= 1
h
= 3
B
A
D
C
O'
O
Khi đó, đặt
AF x
, với
0 2
x
ta có
2 2 2
4
AE AB AF x
.
Suy ra
. .
V AE AF AH
2
3 . 4
x x
.
Do đó, thể tích khối tứ diện
ABCD
là
1
3
ABCD
V V
2
. 4
x x
2 2
4
x x
2
.
Vậy
max
2
ABCD
V
khi
AEBF
là hình vuông, tức là
AB CD
.
Cách 2:
Ta có
1
. . ; .sin ;
6
ABCD
V AB CD d AB CD AB CD
2sin ;
AB CD
2
.
Vậy
max
2
ABCD
V
khi
sin ; 1
AB CD
hay
AB CD
.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 23/24 – BTN 044
Câu 44. [1D2.5-4] Trong mặt phẳng tọa độ
Oxy
, cho hình chữ nhật
OMNP
với
0;10
M ,
100;10
N ,
100;0
P Gọi
S
là tập hợp tất cả các điểm
;
A x y
với ,x y
nằm bên trong (kể cả trên
cạnh) của hình chữ nhật
OMNP
. Lấy ngẫu nhiên một điểm
;
A x y S
. Tính xác suất để
90
x y
.
A.
169
200
. B.
473
500
. C.
845
1111
. D.
86
101
.
Lời giải
Chọn D.
Ta có
101.11
n S
Số điểm
;
A x y S
thảo mãn
90
x y
là
101.11 10.11 1 2 3 ... 10 946
n A .
Xác suất cần tìm là
86
101
n A
P
n S
.
Câu 45. [2D2.3-2] Tập xác định của
2
ln 5 6
y x x
là
A.
2; 3
. B.
2; 3
. C.
; 2 3;

. D.
; 2 3;

.
Lời giải
Chọn A.
Biểu thức
2
ln 5 6
y x x
xác định
2
5 6 0 2 3
x x x
.
Tập xác định của
2
ln 5 6
y x x
là
2;3
D
Câu 46. [2D2.4-2] Cho
3
.e
x
f x x
. Tập nghiệm của bất phương trình
0
f x
là
A.
1
;
3

. B.
1
0;
3
. C.
1
;
3
. D.
0;1
.
Lời giải
Chọn C.
Ta có
3 3 3 3
.e e 3 .e 1 3 e
x x x x
f x x f x x x
1
0
3
f x x
. Vậy tập nghiệm của bất phương trình
0
f x
là
1
;
3
.
Câu 47. [2H1.3-2] Cho khối chóp
.
S ABCD
có thể tích bằng
3
2
a
và đáy
ABCD
là hình bình hành. Biết
diện tích tam giác
SAB
bằng
2
.
a
Tính khoảng cách giữa hai đường thẳng
SB
và
CD
.
A.
a
. B.
3
2
a
. C.
3
a
. D.
2
2
a
.
Lời giải
Chọn C.
0;10
M
100;10
N
100;0
P
0;0
O
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập Mã đề 234 - Trang 24/24 – BTN 044
; ; ;
d CD SB d CD SAB d C SAB
3 3
2
SABC SABCD
SAB SAB
V V
S S
3
2
3.2.
3
2.
a
a
a
.
Câu 48. [2D2.4-1] Đạo
hàm
của hàm số
1 2
e
x
y
là
A.
1 2
2e
x
y
. B.
1 2
2e
x
y
. C.
1 2
e
.
2
x
y
D.
1 2
e
x
y
.
Lời giải
Chọn B.
Câu 49. [2D2.5-2] Tập
nghiệm
của bất phương trình
2 2
2log 1 log 5 1
x x
là
A.
3;5
. B.
1;3
. C.
1;3
. D.
1;5
.
Lời giải
Chọn B.
Điều kiện:
1 5
x
.
2 2
2log 1 log 5 1
x x
2
2 2
log 1 log 10 2
x x
2
1 10 2 3 3
x x x
. Vậy
1;3
S
Câu 50. [2D1.1-2] Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
3 2
1
4 2
3
y x mx x
đồng
biến trên tập xác định của nó?
A.
4
. B.
2
. C.
5
. D.
3
.
Lời giải
Chọn C.
Ta có:
2
2 4
y x mx
;
2
0 4 0 2 2
y m m
.
Mà
m
, suy ra
2; 1;0;1;2
m . Vậy có
5
giá trị của tham số
m
.
----------HẾT----------

Tài liệu khác của Toán

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC
ĐỀ KSCL CÁC MÔN THI THPT QUỐC GIA - LẦN 2
TRƯỜNG THPT CHUYÊN VĨNH PHÚC NĂM HỌC 2018-2019
(Đề thi có 6 trang) MÔN TOÁN 12
Thời gian làm bài: 90 phút;
(Không kể thời gian giao đề) Mã đề thi 234
Họ, tên thí sinh:..........................................................................
Số báo danh:...............................................................................
Câu 1: Tìm giá trị cực tiểu y của hàm số 3
y  x  3x  4 . CT A. y  6  . . B. y  1. C. y  2 . D. y  1. CT CT CT CT Câu 2: Phương trình: log
3x  2  3 có nghiệm là 3   25 29 11 A. x  . B. 87 . C. x  . D. x  . 3 3 3 x 1
Câu 3: Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 4  x A. 4 . B. 0 . C. 1. D. 2 .
Câu 4: Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức lãi kép với
lãi suất 0, 6% mỗi tháng. Biết sau 15 tháng, người đó có số tiền là 10 triệu đồng. Hỏi số tiền T gần
với số tiền nào nhất trong các số sau. A. 613.000 đồng. B. 645.000 đồng. C. 635.000 đồng. D. 535.000 đồng. 2016  xx  2  khi x  1
Câu 5: Cho hàm số f x   2018x 1  x  2018
. Tìm k để hàm số f x liên tục k khi x  1  tại x  1 . 2017. 2018 20016 A. k  2 2019. B. k  . C. k  1. D. k  2019. 2 2017 Câu 6: Cho biểu thức 3 4 3 P  . x x
x , với x  0. Mệnh đề nào dưới đây đúng ? 1 7 5 7 A. 2 P x . B. 12 P x . C. 8 P x . D. 24 P x .
Câu 7: Có bao nhiêu giá trị nguyên của x để hàm số y x 1  x  3 đạt giá trị nhỏ nhất. A. 4. B. 5. C. 2. D. 3.
Câu 8: Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng . a 3 a 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 2 4 2 3
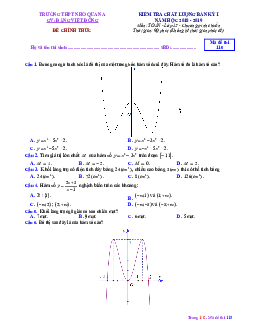
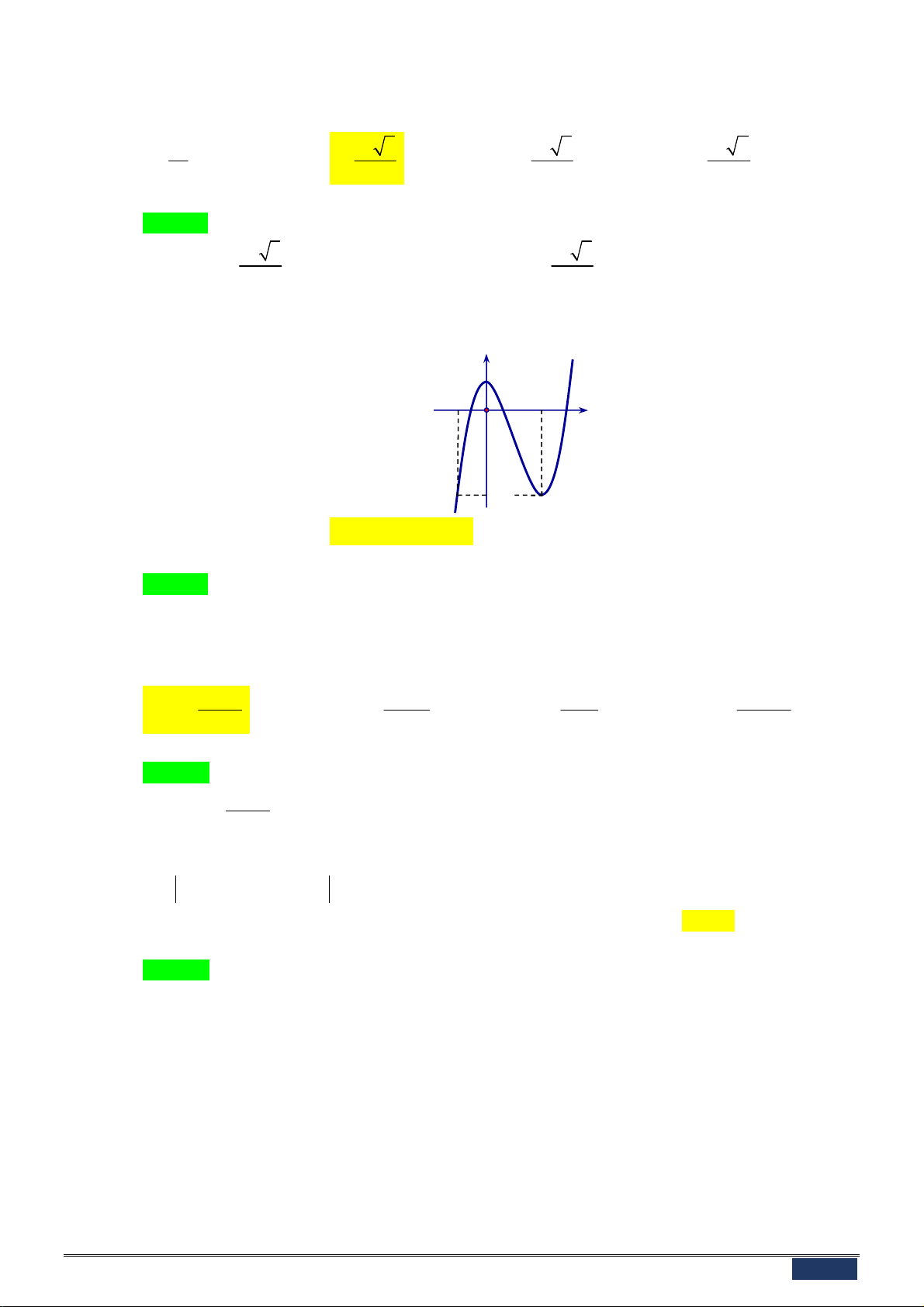
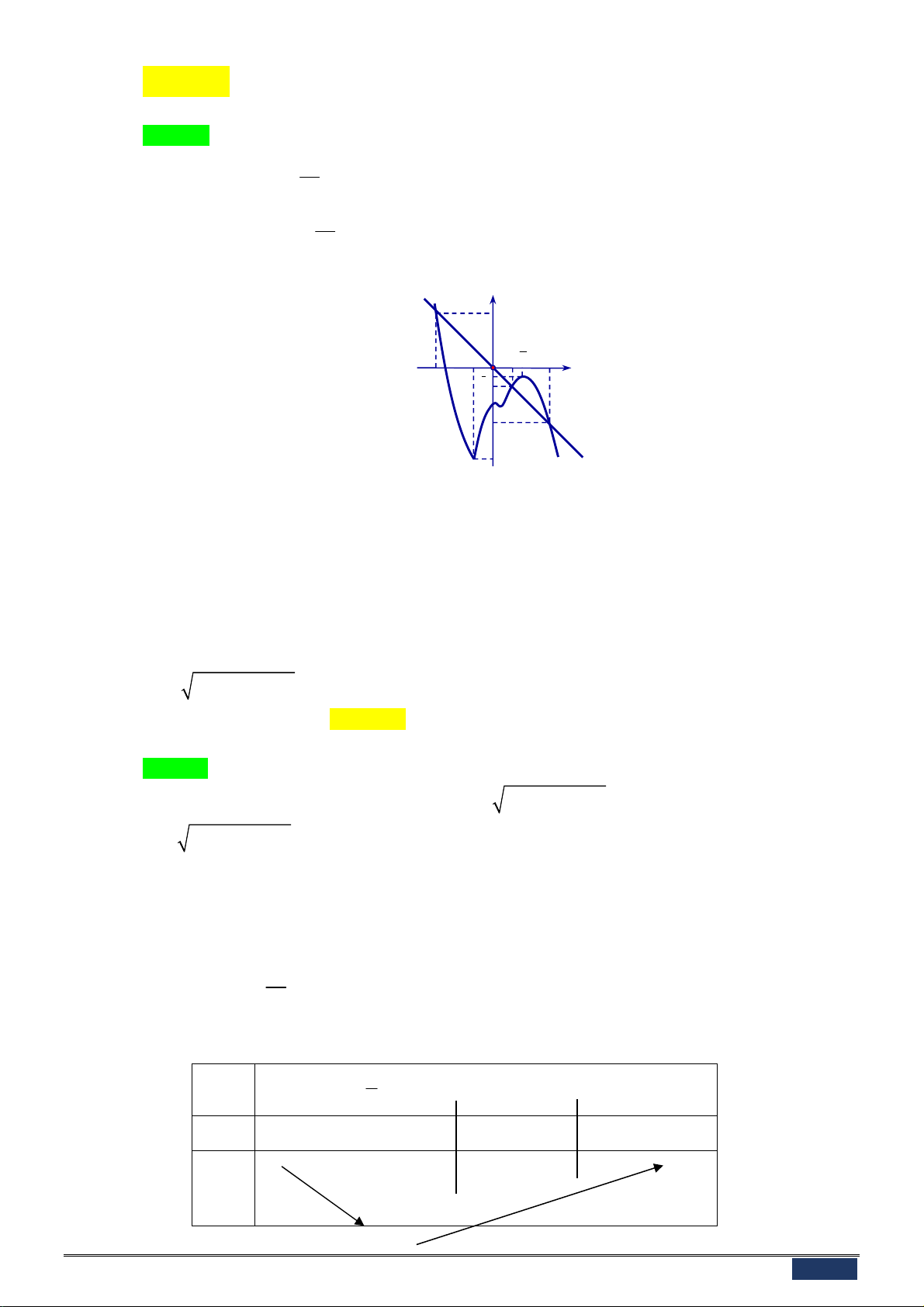
Câu 9: Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Trang 1/6 - Mã đề thi 234 y 3 2 1 x -3 -2 -1 1 2 3 -1 -2 -3 A. 3
y   x  3x 1. B. 3 2
y x  3x 1. C. 3 2
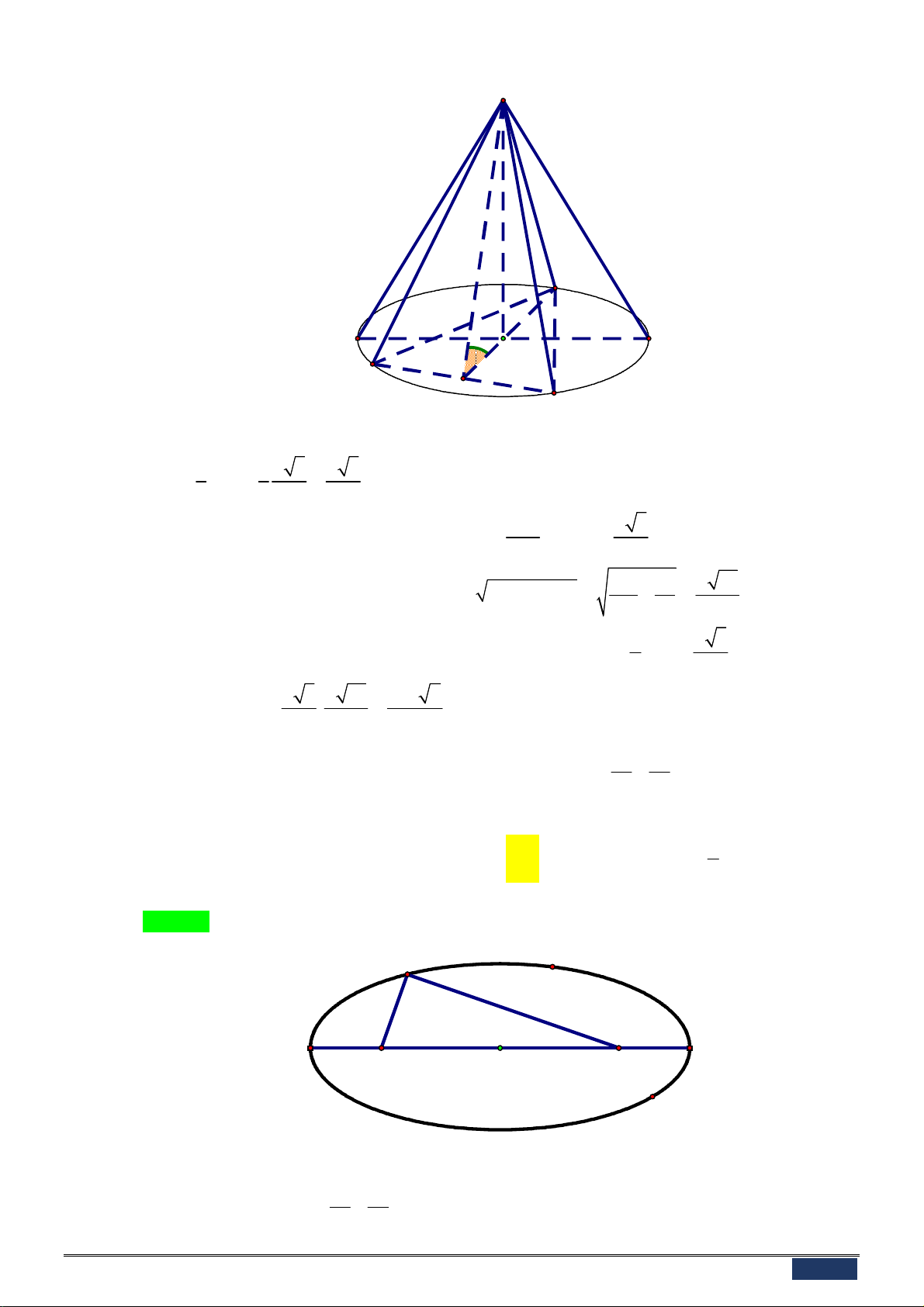
y x  3x 1. D. 3 2
y  x  3x 1.
Câu 10: Đường thẳng y  2 là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây? 2x 1 3x  4 x 1 x 1 A. y  . B. y  . C. y  . D. y  . x 1 x  2 x  2 2  x 1
Câu 11: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 4 3 2
y  3x  4x 12x m có 5 điểm cực trị. A. 16 . B. 44 . C. 26 . D. 27 .
Câu 12: Biết rằng tập các giá trị của tham số m để phương trình   39x  2   1 3x m mm 1  0 có
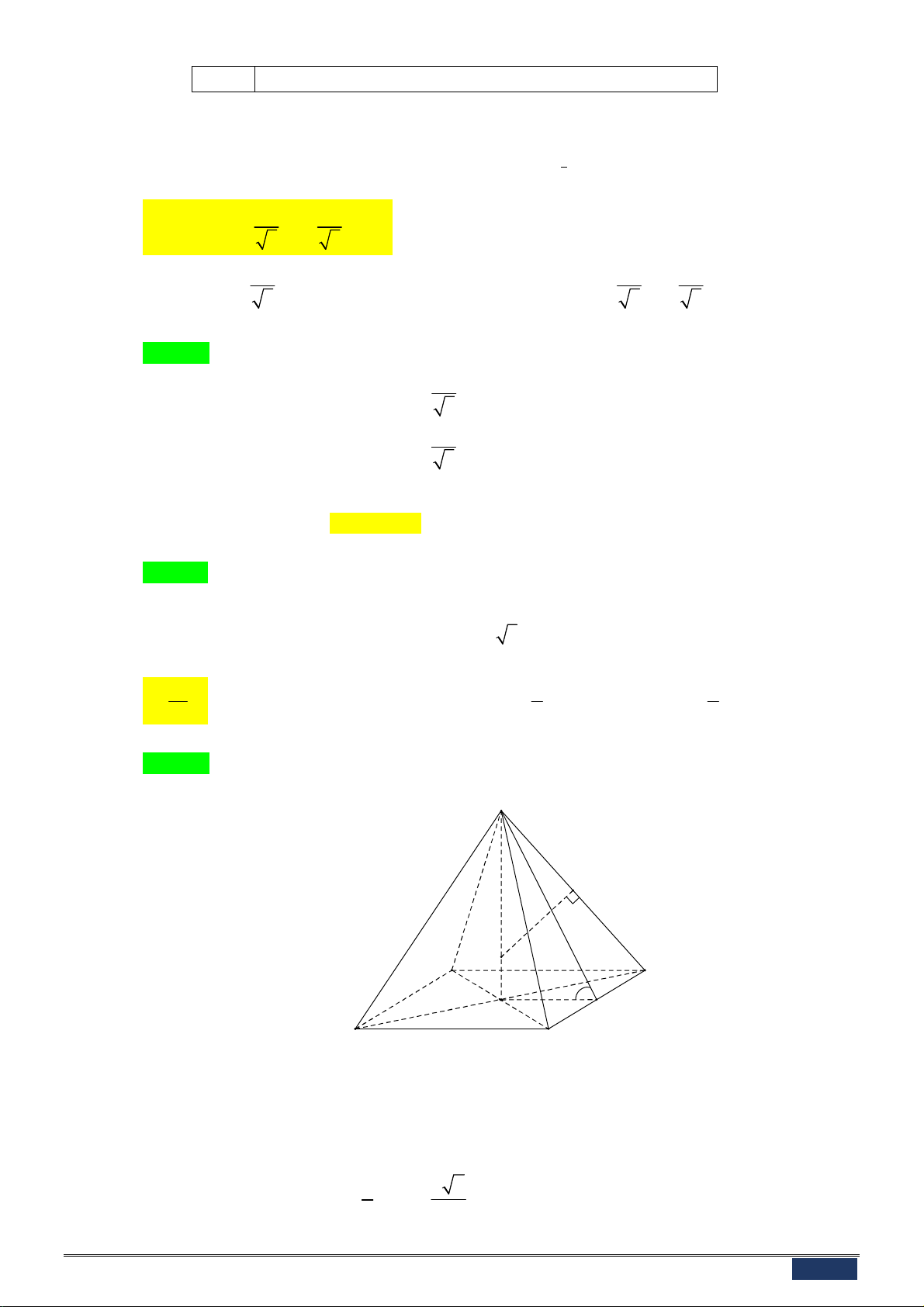
hai nghiệm phân biệt là một khoảng  ; a b . Tính tích . a b . A. 4 . B. 3  . C. 2.. D. 3 .
Câu 13: Cho hình chóp S.ABC có SA a, SB  2a, SC  4a và    0
ASB BSC CSA  60 . Tính
thể tích khối chóp S.ABC theo a . 3 a 2 3 8a 2 3 4a 2 3 2a 2 A. . B. . C. . D. . 3 3 3 3
Câu 14: Giá trị của biểu thức M  log 2  log 4  log 8  ...  log 256 bằng 2 2 2 2 A. 48 . B. 56 . C. 36 . D. 8 log 256 . 2 Câu 15: Kí hiệu max ; a
b là số lớn nhất trong hai số a, .
b Tìm tập nghiệm S của bất phương trình   max log ;
x log x  1. 2 1  3   1   1  A. S  ; 2 .   B. S  0; 2. C. S  0; .  
D. S  2; .  3   3 
Câu 16: Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng? 1 1
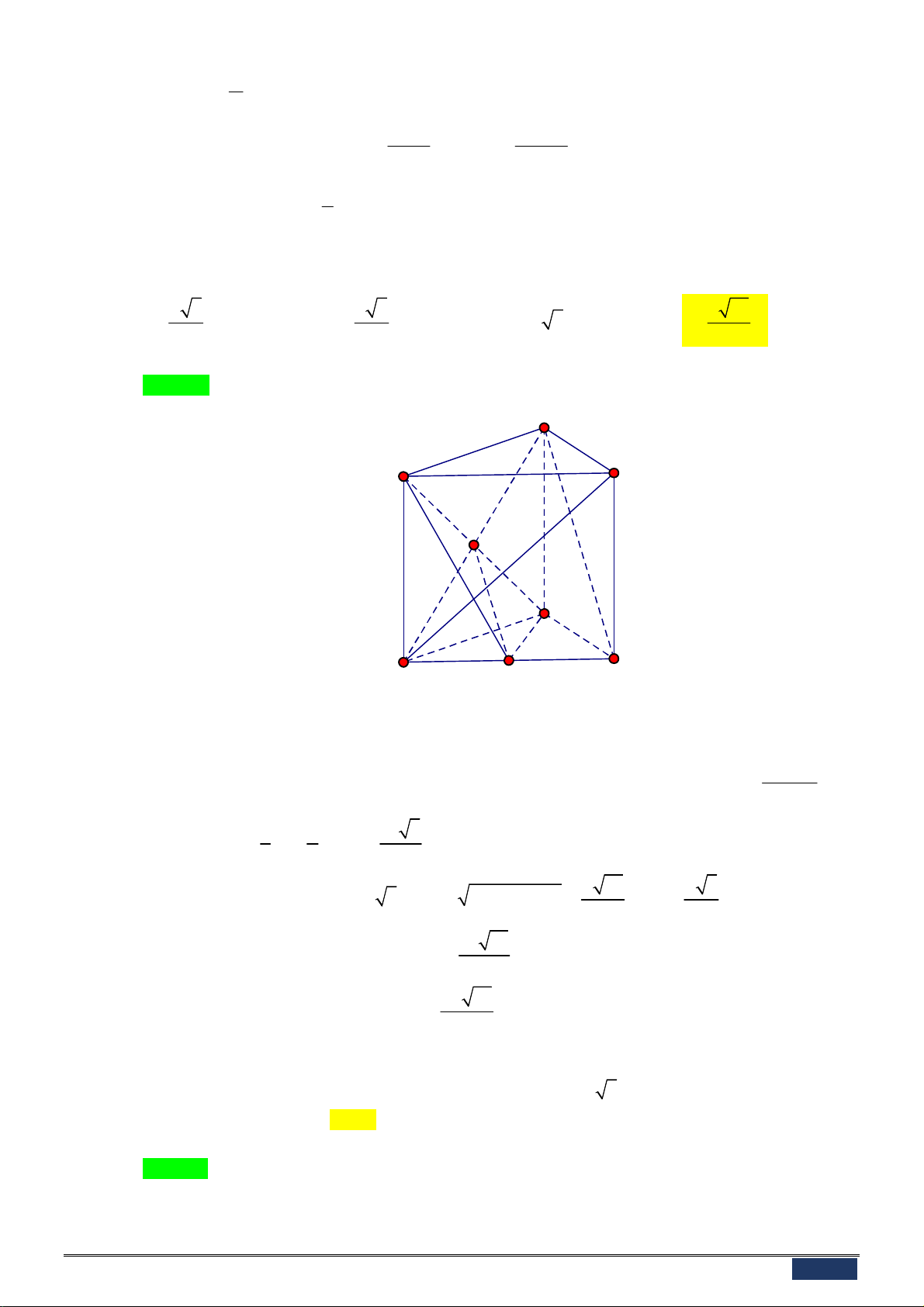
A. log 3a  log a . B. 3 log a  log a . C. 3
log a  3log a .
D. log 3a  3log a . 3 3
Câu 17: Gọi M , N là hai điểm di động trên đồ thị C  của hàm số 3 2
y  x  3x x  4 sao cho tiếp
tuyến của C  tại M và N luôn song song với nhau. Hỏi khi M ,N thay đổi, đường thẳng MN
luôn đi qua nào trong các điểm dưới đây ? A. Điểm N  1  ; 5  . B. Điểm M 1; 5  .
C. Điểm Q 1;5. D. Điểm P  1  ;5.
Câu 18: Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M (3;1) và đường tròn C 2 2
: x y  2x  6 y  6  0 . Gọi T ,T là các tiếp điểm của các tiếp tuyến kẻ từ M đến (C). Tính 1 2
khoảng cách từ O đến đường thẳng T T . 1 2 3 A. 5. B. 5. C. . D. 2 2. 5
Trang 2/6 - Mã đề thi 234
Câu 19: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng ? A. 4 . B. 9. C. 3 . D. 6.
Câu 20: Đường thẳng  có phương trình y  2x 1 cắt đồ thị của hàm số 3
y x x  3 tại hai điểm
A và B với tọa độ được kí hiệu lần lượt là Ax ; y
và B x ; y
trong đó x x . Tìm x y ? B B A A B A B B
A. x y  5
B. x y  2
C. x y  4
D. x y  7 B B B B B B B B Câu 21: Hàm số 4 2
y x  2x 1 nghịch biến trên các khoảng nào sau đây? A. - ;-   1 và 0;+ B.  ;
 0 và 1;+. C.  1  ;0 và 1;+ D.  ;    1 và 0  ;1 .
Câu 22: Giá trị lớn nhất của hàm số 3 2
y  2x  3x 12x  2 trên đoạn  1
 ; 2thuộc khoảng nào dưới đây? A. 3;8 . B.  7  ;8 . C. 2;14 . D. 12; 20 .
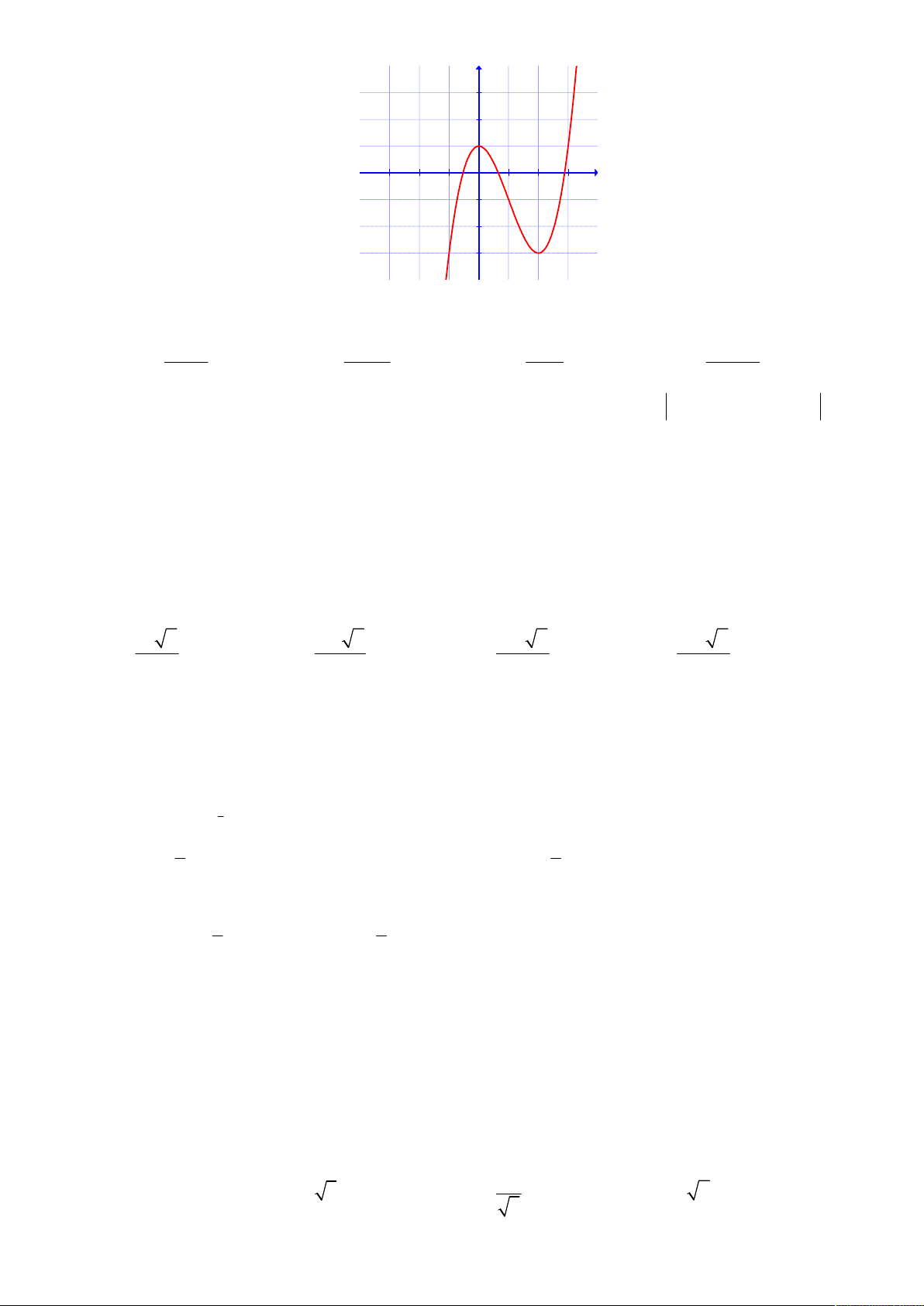
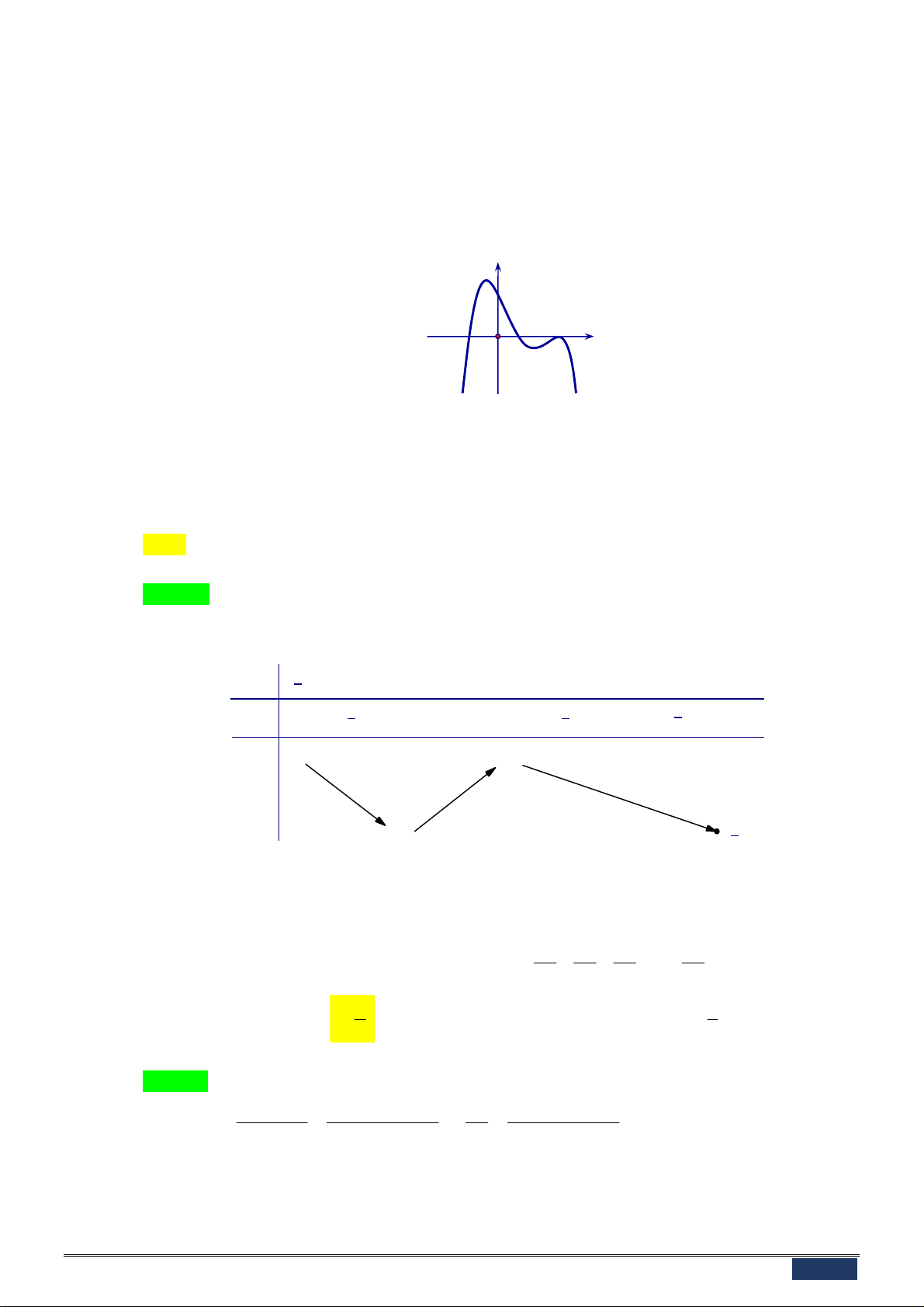
Câu 23: Cho hàm số y f x . Hàm số y f  x có đồ thị trên một khoảng K như hình vẽ bên.
Trong các khẳng định sau, có tất cả bao nhiêu khẳng định đúng ?
I  : Trên K , hàm số y f x có hai điểm cực trị.
II  : Hàm số y f x đạt cực đại tại x . 3
III  : Hàm số y f x đạt cực tiểu tại x . 1 A. 2 . B. 3 . C. 1. D. 0 . 1 1 1 1
Câu 24: Với n là số tự nhiên lớn hơn 2 , đặt S     ...  . Tính lim S n 3 3 4 3 C C C C n 3 4 5 n 3 1 A. 1. B. . C. 3 . D. . 2 3  x x  1 
Câu 25: Tập nghiệm S của bất phương trình 2 5    là  25  A. S   ;  2 . B. S    ;1 .
C. S  1; 
D. S  2;  .
Câu 26: Khối cầu bán kính R  2a có thể tích là 3 32 a 3 8 a A. . B. 3 6 a . C. 2 16 a . D. . 3 3
Câu 27: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , góc giữa mặt bên và mặt đáy bằng 60 .
Tính diện tích xung quanh của hình nón đỉnh S , đáy là hình tròn ngoại tiếp tam giác ABC. 2  a 3 2  a 7 2  a 7 2  a 10 A. . B. . C. . D. . 3 6 4 8 2 2 x y
Câu 28: Trong mặt phẳng với hệ tọa độ Oxy , cho elip  E : 
 1. Điểm M   E  sao cho 25 9  0
F MF  90 . Tìm bán kính đường tròn nội tiếp tam giác MF F . 1 2 1 2
Trang 3/6 - Mã đề thi 234 1 A. 2. B. 4. C. 1. D. . 2
Câu 29: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  2
 018; 2018 để phương trình m   2
1 sin x  sin 2x  cos 2x  0 có nghiệm ? A. 4036 . B. 2020 . C. 4037 . D. 2019 .
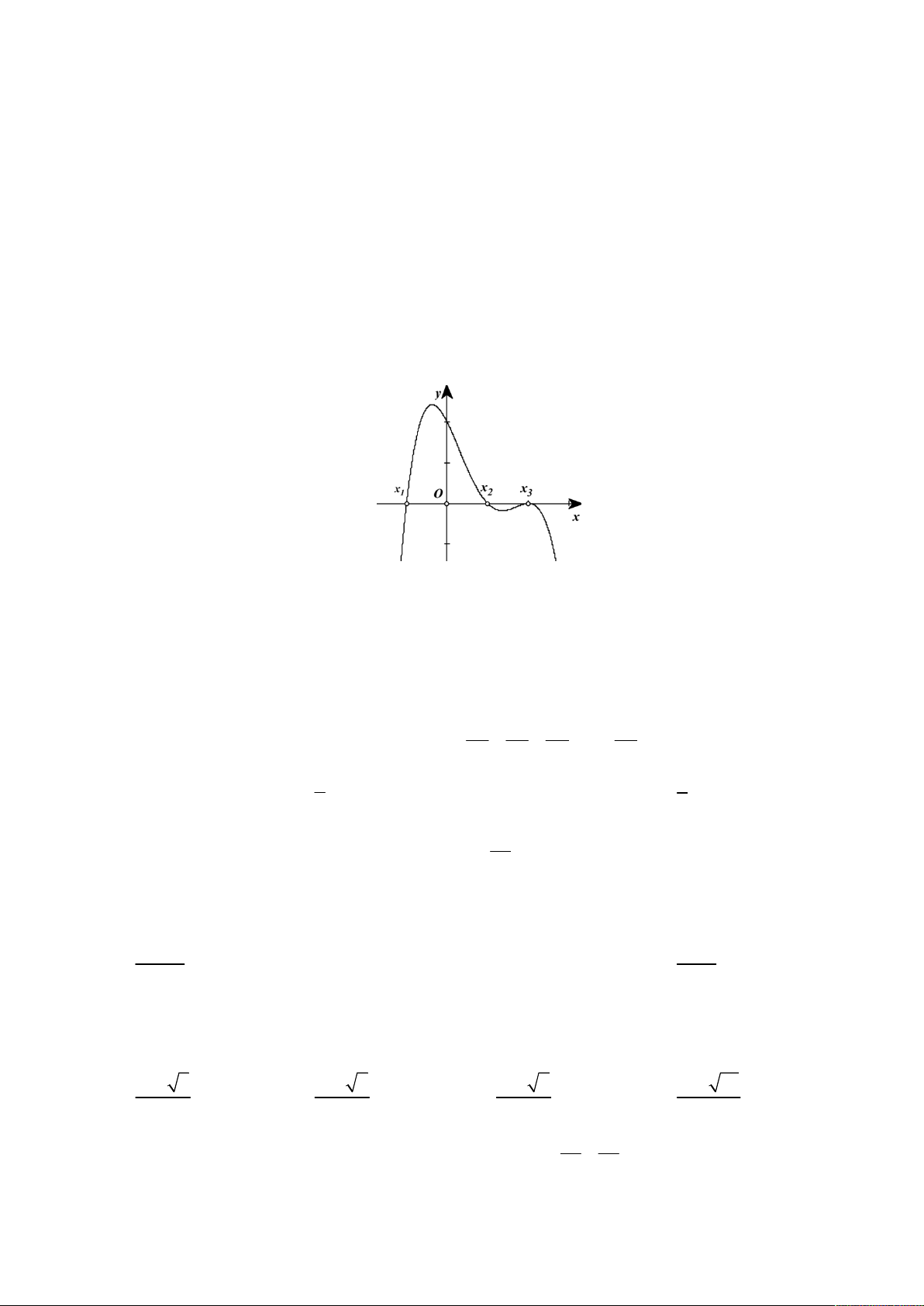
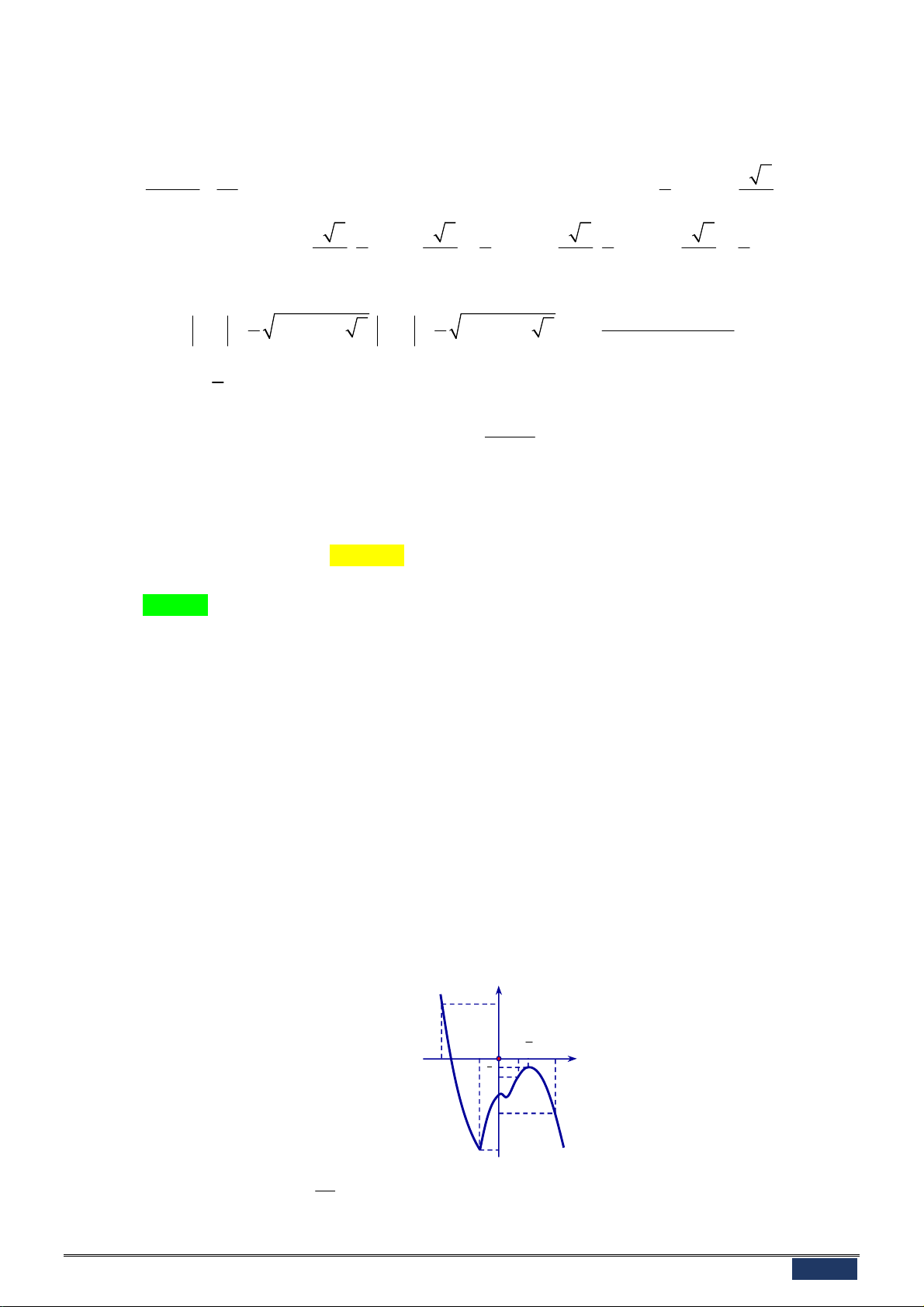
Câu 30: Cho hàm số y f x có đồ thị f  x như hình vẽ 2 x
Hàm số y f 1 x 
x nghịch biến trên khoảng nào trong các khoảng dưới đây? 2 A.  2  ; 0 . B.  3  ;  1 . C. 3;  . D. 1; 3 .
Câu 31: Tìm tất cả các giá trị tham số m để bất phương trình
x    x  x 2 6 2 8
x m 1
nghiệm đúng với mọi x  2  ;8. A. m  16. B. m  15. C. m  8. D. 2   m  16. 1
Câu 32: Tìm tập xác định D của hàm số y   2 x  3 3 1 .  1   1  A. D   ;    ;      . B. D  .  3   3   1   1   1  C. D  \    . D. D   ;    ;      .  3   3   3 
Câu 33: Số cạnh của hình mười hai mặt đều là A. Mười sáu B. Ba mươi C. Hai mươi D. Mười hai
Câu 34: Cho hình chóp tứ giác đều có góc giữa mặt bên và mặt đáy bằng 60 . Biết rằng mặt cầu
ngoại tiếp hình chóp đó có bán kính R a 3. Tính độ dài cạnh đáy của hình chóp tứ giác đều nói trên. 12 3 9 A. a . B. 2a . C. a . D. a . 5 2 4
Câu 35: Biết rằng phương trình ex  ex  2 cos ax ( a là tham số) có 3 nghiệm thực phân biệt. Hỏi
phương trình ex  ex  2 cos ax  4 có bao nhiêu nghiệm thực phân biệt ? A. 5 . B. 10 . C. 6 . D. 11.
Câu 36: Cho khối nón có bán kính đáy r  3 và chiều cao h  4 . Tính thể tích V của khối nón đã cho.
Trang 4/6 - Mã đề thi 234 16 3 A. V  16 3 . B. V  . C. V  12 . D. V  4 . 3 2 sin x  3   
Câu 37: Giá trị nhỏ nhất của hàm số y  trên 0; là sin x 1  2    5 A. 5. B. 2. C. 3. D. . 2
Câu 38: Cho hình lăng trụ tam giác đều ABC.AB C
  có AB a, AA  2 .
a Tính khoảng cách giữa
hai đường thẳng AB và A . Ca 3 2 5 2 17 A. . B. . a C. a 5. D. . a 2 5 17
Câu 39: Trong mặt phẳng với hệ tọa độ Oxy,giả sử điểm (
A a;b) thuộc đường thẳng d : x y  3  0
và cách  : 2x y 1  0 một khoảng bằng 5. Tính P ab biết a  0. A. 4. B. 2 C. 2. D. 4  .
Câu 40: Một hình trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông. Tính diện
tích toàn phần của hình trụ đó. A. 2 4 r . B. 2 6r . C. 2 8 r . D. 2 2 r .
Câu 41: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m y
trên 1; 2 bằng 2. Số phần tử của tập S là x 1 A. 3. B. 1. C. 4. D. 2.
Câu 42: Cho a , b là các số thực dương thỏa mãn b  1 và a b a . Tìm giá trị nhỏ nhất của  a
biểu thức P  log a  2 log . a b    b b A. 6 . B. 7 . C. 5 . D. 4 .
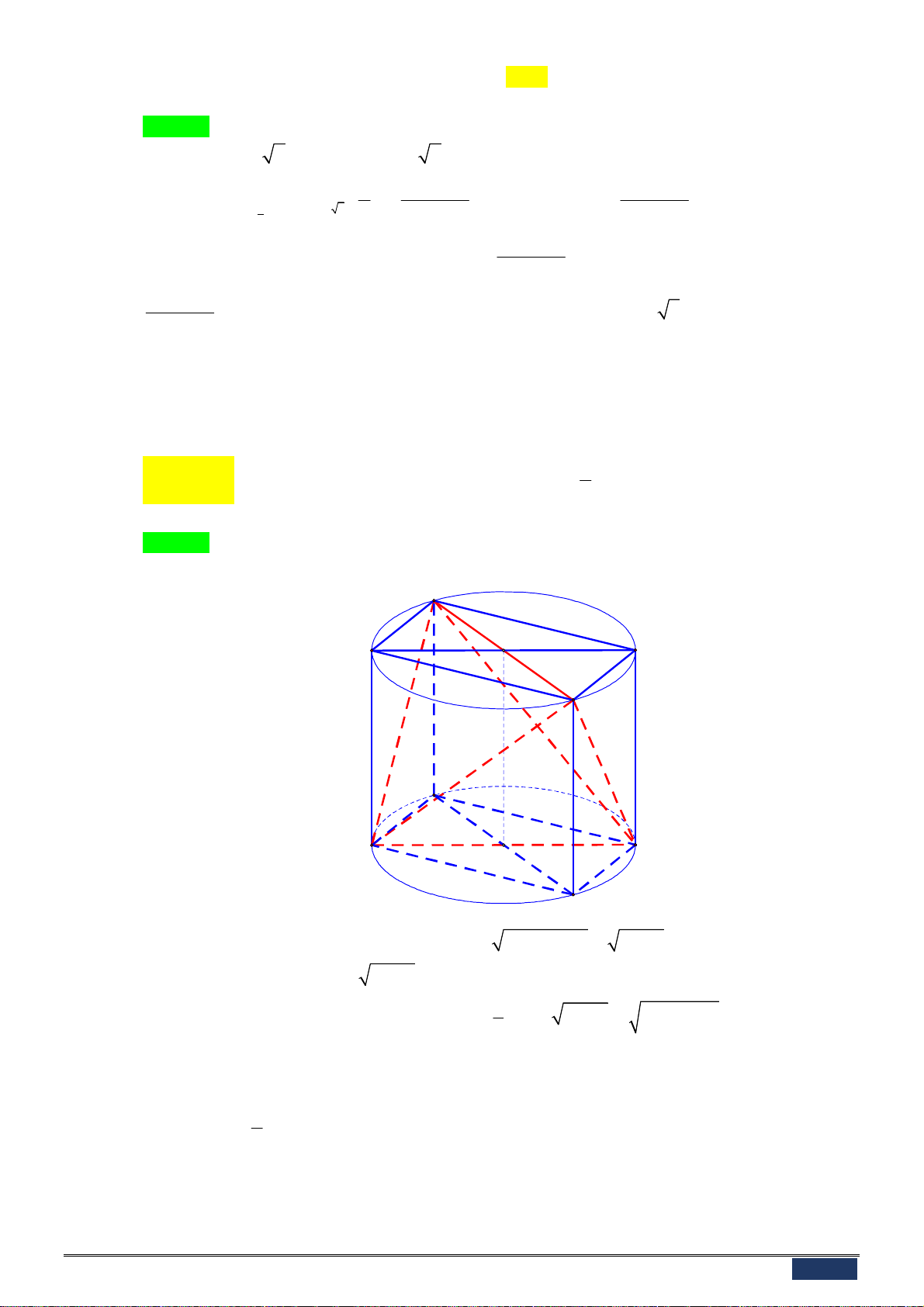
Câu 43: Một hình trụ có độ dài đường cao bằng 3 , các đường tròn đáy lần lượt là   ;1 O và O '  ;1 .
Giả sử AB là đường kính cố định của   ;1 O
và MN là đường kính thay đổi trên O '  ;1 . Tìm giá trị lớn nhất V
của thể tích khối tứ diện A . BCD max 1 A. V  2. B. V  6. C. V  . D. V  1. max max max 2 max
Câu 44: Trong mặt phẳng tọa độ Oxy , cho hình chữ nhật OMNP với M 0;10 , N 100;10 ,
P 100;0 Gọi S là tập hợp tất cả các điểm A ;
x y với x, y   nằm bên trong (kể cả trên cạnh) của
hình chữ nhật OMNP . Lấy ngẫu nhiên một điểm A ;
x y  S . Tính xác suất để x y  90 . 169 473 845 86 A. . B. . C. . D. . 200 500 1111 101
Câu 45: Tập xác định của y   2
ln x  5x  6 là A. 2;  3 . B. 2; 3 . C.  ;
 2 3;   . D.  ;
 2  3;   . Câu 46: Cho   3 .e x f x x  
. Tập nghiệm của bất phương trình f  x  0 là  1   1   1  A.  ;    . B. 0;   . C. ;     . D. 0;  1 .  3   3   3 
Câu 47: Cho khối chóp S.ABCD có thể tích bằng 3
2a và đáy ABCD là hình bình hành. Biết diện tích tam giác SAB bằng 2
a . Tính khoảng cách giữa hai đường thẳng SB và C . D
Trang 5/6 - Mã đề thi 234 3a a 2 A. . a B. . C. 3 . a D. . 2 2
Câu 48: Đạo hàm của hàm số 1 2 e x y   là 12 e x A. 1 2 2e x y    . B. 1 2 2e x y     . C. y   . D. 1 2 e x y    . 2
Câu 49: Tập nghiệm của bất phương trình 2 log x 1  log 5  x 1 là 2   2   A. 3;  5 . B. 1;  3 . C. 1;  3 . D. 1;5 . 1
Câu 50: Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 y
x mx  4x  2 đồng biến 3
trên tập xác định của nó ? A. 4. B. 2. C. 5. D. 3
----------------------------------------------- ----------- HẾT ----------
Trang 6/6 - Mã đề thi 234 SỞ GD VÀ ĐT VĨNH PHÚC
KHẢO SÁT CHẤT LƯỢNG LẦN 2 - MÔN TOÁN
TRƯỜNG CHUYÊN VĨNH PHÚC
Năm học 2018 – 2019 Thời gian: 90 phút
Họ và tên học sinh…………………….. Lớp…… Số báo danh ….………… MÃ ĐỀ 234 Câu 1.
[2D1.2-2] Tìm giá trị cực tiểu y của hàm số 3
y   x  3x  4 . CT A. y  6 . B. y  1  . C. y  2 . D. y  1 . CT CT CT CT Câu 2.
[2D2.5-2] Phương trình: log
3x  2  3 có nghiệm là 3   25 29 11 A. x  . B. 87 . C. x  . D. x  . 3 3 3 x 1 Câu 3.
[2D1.4-2] Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 4  x A. 4 B. 0 . C. 1. D. 2 . Câu 4.
[2D2.1-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức
lãi kép với lãi suất 0, 6% mỗi tháng. Biết sau 15 tháng, người đó có số tiền là 10 triệu đồng.
Hỏi số tiền T gần với số tiền nào nhất trong các số sau. A. 613.000 đồng. B. 645.000 đồng. C. 635.000 đồng. C. 535.000 đồng 2016  xx  2  khi x  1 Câu 5.
[1D4.3-3] Cho hàm số f x   2018x 1  x  2018
. Tìm k để hàm số f x k khi x  1 
liên tục tại x  1 . 2017. 2018 20016
A. k  2 2019. B. k  . C. k  1. D. k  2019. 2 2017 Câu 6.
[2D2.1-2] Cho biểu thức 3 4 3 P  . x x
x , với x  0. Mệnh đề nào dưới đây đúng? 1 7 5 7 A. 2 P x . B. 12 P x . C. 8 P x . D. 24 P x . Câu 7.
[2D1.3-2] Có bao nhiêu giá trị nguyên của x để hàm số y x 1  x  3 đạt giá trị nhỏ nhất. A. 4 . B. 5 . C. 2 . D. 3 . Câu 8.
[2H1.3-1] Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng . a 3 a 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 2 4 2 3 Câu 9.
[2D1.5-2] Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê y
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? 1 A. 3
y  x  3x 1. 1  2 B. 3 2
y x  3x  1. O x C. 3 2
y x  3x 1. D. 3 2
y  x  3x 1. 3 
Câu 10. [2D2.4-1] Đường thẳng y  2 là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây? 2x 1 3x  4 x  1 x  1 A. y  . B. y  . C. y  . D. y  . x 1 x  2 x  2 2  x  1
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 1/24 – BTN 044
Câu 11. [2D1.2-4] Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 4 3 2
y  3x  4x 12x m có 5 điểm cực trị? A. 16 . B. 44 . C. 26 . D. 27 . Câu 12. [2D2.5-3] Biết rằng tập các giá trị của tham số m để phương trình
  39x  2   1 3x m m
m 1  0 có hai nghiệm phân biệt là một khoảng  ; a b . Tính tích . a b . A. 4 . B. 3  . C. 2 . D. 3 .   
Câu 13. [2H1.2-3] Cho hình chóp S.ABC có SA a , SB  2a , SC  4a và ASB BSC CSA  60 .
Tính thể tích khối chóp S.ABC theo a . 3 a 2 3 8a 2 3 4a 2 3 2a 2 A. . B. . C. . D. . 3 3 3 3
Câu 14. [2D2.2-2] Giá trị của biểu thức M  log 2  log 4  log 8  ...  log 256 bằng 2 2 2 2 A. 48 . B. 56 . C. 36 . D. 8 log 256 . 2
Câu 15. [2D2.7-2] Kí hiệu max a; 
b là số lớn nhất trong hai số a , b . Tìm tập nghiệm S của bất   phương trình max log ;
x log x  1. 2 1  3   1   1  A. S  ; 2   .
B. S  0;2 . C. S  0;   .
D. S  2; .  3   3 
Câu 16. [2D2.3-1] Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng? 1 1
A. log 3a  log a . B. 3 log a  log a . C. 3
log a  3log a .
D. log 3a  3log a . 3 3
Câu 17. [2D1.5-4] Gọi M , N là hai điểm di động trên đồ thị C  của hàm số 3 2
y  x  3x x  4 sao
cho tiếp tuyến của C  tại M và N luôn song song với nhau. Hỏi khi M , N thay đổi, đường
thẳng MN luôn đi qua nào trong các điểm dưới đây?
A. Điểm N 1; 5   .
B. Điểm M 1;5 .
C. Điểm Q 1;5 .
D. Điểm P 1;5 .
Câu 18. [2D1.5-4] Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M  3  ;  1 và đường tròn C  2 2
: x y  2x  6 y  6  0 . Gọi T , T là các tiếp điểm của các tiếp tuyến kẻ từ M đến C  . 1 2
Tính khoảng cách từ O đến đường thẳng T T . 1 2 3 A. 5 . B. 5 . C. . D. 2 2 . 5
Câu 19. [2H1.2-2] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? A. 4 . B. 9. C. 3 . D. 6.
Câu 20. [2D1.5-2] Đường thẳng  có phương trình y  2x 1 cắt đồ thị của hàm số 3
y x x  3 tại
hai điểm A và B với tọa độ được kí hiệu lần lượt là Ax ; y và B x ; y trong đó B B A A
x x . Tìm x y ? B A B B
A. x y  5  .
B. x y  2  .
C. x y  4 .
D. x y  7 . B B B B B B B B
Câu 21. [2D1.1-1] Hàm số 4 2
y x  2x 1 nghịch biến trên các khoảng nào sau đây? A.  ;    1 và 0;+ . B.  ;  0 và 1;+ . C.  1  ;0 và 1;+ . D.  ;    1 và 0;  1 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 2/24 – BTN 044
Câu 22. [2D1.3-1] Giá trị lớn nhất của hàm số 3 2
y  2x  3x 12x  2 trên đoạn  1  ; 2 thuộc khoảng nào dưới đây? A. 3;8 . B.  7  ;8 . C. 2;14 . D. 12;20 .
Câu 23. [2D1.2-2] Cho hàm số y f x . Hàm số y f  x có đồ thị trên một khoảng K như hình vẽ bên. y
Trong các khẳng định sau, có tất cả bao nhiêu khẳng định đúng?
I  : Trên K , hàm số y f x có hai điểm cực trị. x x x x
II  : Hàm số y f x đạt cực đại tại x . 1 2 3 3 O
III  : Hàm số y f x đạt cực tiểu tại x . 1 A. 2 . B. 3 . C. 1. D. 0 . 1 1 1 1
Câu 24. [1D4.1-3] Với n là số tự nhiên lớn hơn 2 , đặt S     ...  . Tính lim S n 3 3 3 3 C C C C n 3 4 5 n 3 1 A. 1. B. . C. 3 . D. . 2 3  x x  1 
Câu 25. [1D2.2-3] Tập nghiệm S của bất phương trình 2 5    là  25 
A. S   ;  2 .
B. S   ;   1 .
C. S  1; 
D. S  2; .
Câu 26. [2H2.1-1] Khối cầu bán kính R  2a có thể tích là 3 32 a 3 8 a A. . B. 3 6 a . C. 2 16 a . D. . 3 3
Câu 27. [2H2.1-2] Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , góc giữa mặt bên và mặt
đáy bằng 60 . Tính diện tích xung quanh của hình nón đỉnh S , đáy là hình tròn ngoại tiếp tam giác ABC . 2  a 3 2  a 7 2  a 7 2  a 10 A. . B. . C. . D. . 3 6 4 8 2 2 x y
Câu 28. [0H3.5-3] Trong mặt phẳng với hệ tọa độ Oxy , cho elip  E  : 
 1. Điểm M   E  sao 25 9 
cho F MF  90 . Tìm bán kính đường tròn nội tiếp tam giác MF F . 1 2 1 2 1 A. 2 . B. 4 . C. 1. D. . 2
Câu 29. [1D1.4-3] Có bao nhiêu giá trị nguyên của m thuộc đoạn  2
 018; 2018 để phương trình m   2
1 sin x  sin 2x  cos 2x  0 có nghiệm? A. 4036 . B. 2020 . C. 4037 . D. 2019 .
Câu 30. [2D1.1-4] Cho hàm số y f x có đồ thị f  xy 2 3 x
như hình vẽ bên. Hàm số y f 1 x   x 3 2 1  O 1 2 3
nghịch biến trên khoảng nào trong các khoảng 1  2 x 3  dưới đây? 1  A.  2  ; 0 . B.  3  ;  1 . 3  C. 3; . D. 1; 3 . 5 
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 3/24 – BTN 044 Câu 31. [0D3.2-3] Tìm tất cả các giá trị tham số m để bất phương trình
x    x  x 2 6 2 8
x m 1 nghiệm đúng với mọi x 2;8 . A. m  16 . B. m  15 . C. m  8 . D. 2   m  16 . 1
Câu 32. [2D2.2-1] Tìm tập xác định D của hàm số y   2 x  3 3 1 .  1   1  A. D   ;    ;      . B. D   .  3   3   1   1   1 
C. D   \   . D. D   ;    ;      .  3   3   3 
Câu 33. [2H1.2-1] Số cạnh của hình mười hai mặt đều là A. Mười sáu. B. Ba mươi. C. Hai mươi. D. Mười hai.
Câu 34. [2H1.3-3] Cho hình chóp tứ giác đều có góc giữa mặt bên và mặt đáy bằng 60 . Biết rằng mặt
cầu ngoại tiếp hình chóp đó có bán kính R a 3. Tính độ dài cạnh đáy của hình chóp tứ giác đều nói trên. 12 3 9 A. a . B. 2a . C. a . D. a . 5 2 4
Câu 35. [2D2.5-3] Biết rằng phương trình ex  ex  2 cos ax ( a là tham số) có 3 nghiệm thực phân
biệt. Hỏi phương trình ex  ex  2 cos ax  4 có bao nhiêu nghiệm thực phân biệt? A. 5 . B. 10 . C. 6 . D. 11.
Câu 36. [2H2.1-1] Cho khối nón có bán kính đáy r  3 và chiều cao h  4 . Tính thể tích V của khối nón đã cho. 163
A. V  163 . B. V  .
C. V  12.
D. V  4. 3 2 sin x  3 
Câu 37. [2D1.3-3] Giá trị nhỏ nhất của hàm số y  trên 0; là sin x 1  2    5 A. 5. B. 2. C. 3. D. . 2
Câu 38. [1H3.5-3] Cho hình lăng trụ tam giác đều ABC.AB C
  có AB a , AA  2a. Tính khoảng
cách giữa hai đường thẳng AB và AC . a 3 2 5 2 17 A. . B. . a C. a 5. D. . a 2 5 17
Câu 39. [0H3.1-2] Trong mặt phẳng với hệ tọa độ Oxy, giả sử điểm ( A ;
a b) thuộc đường thẳng
d : x y  3  0 và cách  : 2x y 1  0 một khoảng bằng 5. Tính P ab biết a  0. A. 4 . B. 2  . C. 2 . D. 4  .
Câu 40. [2H2.1-1] Một hình trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông.
Tính diện tích toàn phần của hình trụ đó. A. 2 4 r . B. 2 6 r . C. 2 8 r . D. 2 2 r .
Câu 41. [2D1.3-3] Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của 2
x mx m hàm số y
trên 1;2 bằng 2 . Số phần tử của tập S là x 1 A. 3 . B. 1. C. 4 . D. 2 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 4/24 – BTN 044
Câu 42. [2D2.4-3] Cho a , b là các số thực dương thỏa mãn b  1 và a b a . Tìm giá trị nhỏ nhất  a
của biểu thức P  log a  2 log . a b    b b A. 6 . B. 7 . C. 5 . D. 4 .
Câu 43. [2H2.2-3] Một hình trụ có độ dài đường cao bằng 3 , các đường tròn đáy lần lượt là O;  1 và O ; 
1 . Giả sử AB là đường kính cố định của O; 
1 và CD là đường kính thay đổi trên O ; 
1 . Tìm giá trị lớn nhất V
của thể tích khối tứ diện ABCD . max 1 A. V  2 . B. V  6 . C. V  . D. V  1 . max max max 2 max
Câu 44. [1D2.5-4] Trong mặt phẳng tọa độ Oxy , cho hình chữ nhật OMNP với M 0;10 , N 100;10 ,
P 100;0 Gọi S là tập hợp tất cả các điểm A ;
x y  với x, y  nằm bên trong (kể cả trên
cạnh) của hình chữ nhật OMNP . Lấy ngẫu nhiên một điểm A ;
x y   S . Tính xác suất để
x y  90 . 169 473 845 86 A. . B. . C. . D. . 200 500 1111 101
Câu 45. [2D2.3-2] Tập xác định của y   2
ln x  5x  6 là A. 2;  3 . B. 2; 3 . C.  ;
 2 3;   . D.  ;
 2  3;   . Câu 46. [2D2.4-2] Cho   3 .e x f x x  
. Tập nghiệm của bất phương trình f  x  0 là  1   1   1  A. ;   . B. 0;   . C. ;     . D. 0;  1 .  3   3   3 
Câu 47. [2H1.3-2] Cho khối chóp S.ABCD có thể tích bằng 3
2a và đáy ABCD là hình bình hành. Biết
diện tích tam giác SAB bằng 2
a . Tính khoảng cách giữa hai đường thẳng SB và CD . 3a a 2 A. a . B. . C. 3a . D. . 2 2
Câu 48. [2D2.4-1] Đạo hàm của hàm số 1 2 e x y   là 12 e x A. 1 2 2e x y    . B. 1 2 2e x y     . C. y   . D. 1 2 e x y    . 2
Câu 49. [2D2.5-2] Tập nghiệm của bất phương trình 2 log x 1  log 5  x 1 là 2   2   A. 3;5 . B. 1;  3 . C. 1;  3 . D. 1;5 . 1
Câu 50. [2D1.1-2] Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 y
x mx  4x  2 đồng 3
biến trên tập xác định của nó? A. 4 . B. 2 . C. 5 . D. 3 .
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 5/24 – BTN 044 ĐÁP ÁN THAM KHẢO 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A C D C A C B B B A D B D C A C C C C A D D A B D
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A B C B A B A B A C D D D B B D C A D A C C B B C HƯỚNG DẪN GIẢI Câu 1.
[2D1.2-2] Tìm giá trị cực tiểu y của hàm số 3
y   x  3x  4 . CT A. y  6 . B. y  1  . C. y  2 . D. y  1 . CT CT CT CT Lời giải Chọn A. Ta có: 2
y  3x  3, y  0  x  1  . Bảng biến thiên x  1  1  y  0  0   y 2  6   Vậy y  6 . CT Câu 2.
[2D2.5-2] Phương trình: log
3x  2  3 có nghiệm là 3   25 29 11 A. x  . B. 87 . C. x  . D. x  . 3 3 3 Lời giải Chọn C. 29 Ta có: log
3x  2  3  3x  2  27  x  . 3   3 x 1 Câu 3.
[2D1.4-2] Đồ thị hàm số y
có bao nhiêu đường tiệm cận? 2 4  x A. 4 B. 0 . C. 1. D. 2 . Lời giải Chọn D.
Tập xác định của hàm số là  2  ; 2 .
Ta có lim y  , lim y   . x 2 x 2  
Đồ thị hàm số có 2 bao nhiêu đường tiệm cận. Câu 4.
[2D2.1-3] Một người mỗi tháng đều đặn gửi vào ngân hàng một khoản tiền T theo hình thức
lãi kép với lãi suất 0, 6% mỗi tháng. Biết sau 15 tháng, người đó có số tiền là 10 triệu đồng.
Hỏi số tiền T gần với số tiền nào nhất trong các số sau. A. 613.000 đồng. B. 645.000 đồng. C. 635.000 đồng. C. 535.000 đồng Lời giải Chọn C.
Đặt a  0.6% .
Số tiền cả lãi lẫn gốc sau n kì là
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 6/24 – BTN 044 T T a a      nn 1  1  1 a   T .a Suy ra n T   635301  n 1 a   1 a 1      2016  xx  2  khi x  1 Câu 5.
[1D4.3-3] Cho hàm số f x   2018x 1  x  2018
. Tìm k để hàm số f x k khi x  1 
liên tục tại x  1 . 2017. 2018 20016
A. k  2 2019. B. k  . C. k  1. D. k  2019. 2 2017 Lời giải Chọn A. Ta có: 2016 2016 xx  2 x 1 x 1
lim f x  lim  lim x 1  x 1  x 1
2018x 1  x  2018 
2018x 1  x  2018  2 2015
11 x x  ...  x x  
1  2018x 1  x  2018  lim x 1 
 2018x 1 x  2018 2018x 1 x  2018  2 2015
11 x x  ...  x x  
1  2018x 1  x  2018  lim x 1  2017x  2017 1  2 2015
1 x x  ...  x
 2018x 1  x  2018  lim  2 2019 x 1  2017
Để hàm số liên tục tại x  1 thì lim f x  f (1)  k  2 2019 x 1  4 Câu 6.
[2D2.1-2] Cho biểu thức 3 3 P  . x x
x , với x  0. Mệnh đề nào dưới đây đúng? 1 7 5 7 A. 2 P x . B. 12 P x . C. 8 P x . D. 24 P x . Lời giải Chọn C. 7 7 15 5 3 4 3 Ta có 3 4 3 2 8 24 8 P  . x x x  . x x  . x x xx . Câu 7.
[2D1.3-2] Có bao nhiêu giá trị nguyên của x để hàm số y x 1  x  3 đạt giá trị nhỏ nhất. A. 4 . B. 5 . C. 2 . D. 3 . Lời giải Chọn B. 2x  2, x  1 
Ta có y x 1  x  3  4,  3  x  1.  2
x  2, x  3  
Trên 1;  , ta có y  4 và dấu bằng xảy ra khi x  1. Trên  3  ; 
1 , ta có y  4 và có bốn giá trị nguyên của x thuộc khoảng này. Trên  ;
  3 , ta có y  2  x  2  4 .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 7/24 – BTN 044 Vậy y
 4 và có 5 giá trị nguyên của x để y  4 . min min Câu 8.
[2H1.3-1] Tính thể tích của khối lăng trụ tam giác đều có tất cả các cạnh bằng . a 3 a 3 a 3 3 a 3 3 a 2 A. . B. . C. . D. . 2 4 2 3 Lời giải Chọn B. 2 a 3 3 a 3 Ta có S
và chiều cao h a nên suy ra V  . day 4 4 Câu 9.
[2D1.5-2] Đường cong trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê
ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? y 1 1  2 O x 3  A. 3
y  x  3x 1. B. 3 2
y x  3x  1. C. 3 2
y x  3x 1. D. 3 2
y  x  3x 1. Lời giải Chọn B.
Nhánh đầu tiên của đồ thị đi lên nên hệ số a  0 . Vậy loại phương án A và D.
Hàm số có hai điểm cực trị là x  0 và x  2 nên chọn phương án B.
Câu 10. [2D2.4-1] Đường thẳng y  2 là tiệm cận ngang của đồ thị hàm số nào trong các hàm số sau đây? 2x 1 3x  4 x  1 x  1 A. y  . B. y  . C. y  . D. y  . x 1 x  2 x  2 2  x  1 Lời giải Chọn A. 2x 1 Ta có lim
 2 nên y  2 là đường tiệm cận ngang của đồ thị hàm số. x x 1
Câu 11. [2D1.2-4] Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 4 3 2
y  3x  4x 12x m có 5 điểm cực trị? A. 16 . B. 44 . C. 26 . D. 27 . Lời giải Chọn D.
Xét hàm số f x 4 3 2
 3x  4x 12x m trên D   .  x  1  f  x 3 2
 12x 12x  24x ; f  x  0  x  0 .   x  2  Bảng biến thiên
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 8/24 – BTN 044 x  1  0 2 
f  x  0  0  0   m 
f x 5   m 3  2  m 5  m  0
Vì m nguyên dương nên để hàm số có 5 điểm cực trị    5  m  32 . 32  m  0 
Vậy có 27 giá trị nguyên dương m . Câu 12. [2D2.5-3] Biết rằng tập các giá trị của tham số m để phương trình
  39x  2   1 3x m m
m 1  0 có hai nghiệm phân biệt là một khoảng  ; a b . Tính tích . a b . A. 4 . B. 3  . C. 2 . D. 3 . Lời giải Chọn B. Đặt 3x t  ; t  0 . 2 3t  2t 1
Phương trình trở thành: m   2
3 t  2 m  
1 t m 1  0  m  với t  0 và 2 t  2t 1 t  1 2 .
Phương trình có hai nghiệm phân biệt  Đường thẳng d : y m có hai điểm chung với đồ thị 2 3t  2t 1
hàm số f t 
với t  0 và t  1 2 . 2 t  2t 1 2 8t  4t f t   0 .
t  2t  2 2 1 Bảng biến thiên t 0 2 1  f t    f t   3 1  
Dựa vào bảng biến thiên phương trình có hai nghiệm phân biệt  1
  m  3  a  1  và
b  3 . Do đó ab  3  .   
Câu 13. [2H1.2-3] Cho hình chóp S.ABC có SA a , SB  2a , SC  4a và ASB BSC CSA  60 .
Tính thể tích khối chóp S.ABC theo a . 3 a 2 3 8a 2 3 4a 2 3 2a 2 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 9/24 – BTN 044 S B C A
Áp dụng công thức giải nhanh đối với khối chóp S.ABC 1 abc 2 Ta có 2 2 2 V abc 1 2.cos . x cos .
y cos z  cos x  cos y  cos z  . 6 12
a , b , c lần lượt là độ dài các cạnh SA , SB , SC . x , y , z lần lượt là số đo các góc  ASB ,   BSC , CSA . 3 3 8a 2 2a 2 Vậy: V   . 12 3
Câu 14. [2D2.2-2] Giá trị của biểu thức M  log 2  log 4  log 8  ...  log 256 bằng 2 2 2 2 A. 48 . B. 56 . C. 36 . D. 8 log 256 . 2 Lời giải Chọn C.
M  log 2  log 4  log 8  ...  log 256  1 2  3  ....  8  36 . 2 2 2 2
Câu 15. [2D2.7-2] Kí hiệu max a; 
b là số lớn nhất trong hai số a , b . Tìm tập nghiệm S của bất   phương trình max log ;
x log x  1. 2 1  3   1   1  A. S  ; 2   .
B. S  0;2 . C. S  0;   .
D. S  2; .  3   3  Lời giải Chọn A.  
Nếu x  1 : max log ;
x log x  1  log x  1  1  x  2 . 2 1 2  3    1
Nếu 0  x  1: max log ;
x log x  1  log x  1   x  1. 2 1 1  3 3  3  1  Vậy S  ; 2   .  3 
Câu 16. [2D2.3-1] Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng? 1 1
A. log 3a  log a . B. 3 log a  log a . C. 3
log a  3log a .
D. log 3a  3log a . 3 3 Lời giải Chọn C.
Câu 17. [2D1.5-4] Gọi M , N là hai điểm di động trên đồ thị C  của hàm số 3 2
y  x  3x x  4 sao
cho tiếp tuyến của C  tại M và N luôn song song với nhau. Hỏi khi M , N thay đổi, đường
thẳng MN luôn đi qua nào trong các điểm dưới đây?
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 10/24 – BTN 044
A. Điểm N 1; 5   .
B. Điểm M 1;5 .
C. Điểm Q 1;5 .
D. Điểm P 1;5 . Lời giải Chọn C.
Gọi M x ; y
, N x ; y . N N M M
Do M , N  C  nên M  3 2
x ; x  3x x  4 , N  3 2
x ; x  3x x  4 . N N N NM M M M
Theo giả thiết tiếp tuyến của C  tại M và N luôn song song với nhau nên ta có: y xyx 2 2
 3x  6x 1  3
x  6x 1 2 2
 3x  6x  3x  6x  0 M   N M M N N M M N N
x x  0
  x x   x x  2  0 N M  . N M N M
x x  2  N M
Do M và N phân biệt nên x x , suy ra x x  2 . N M N M
Ta có: y y    3 3
x x    2 2
3 x x    x x   8 M N M N N M M N
   x x 3   x x x x    x x 2 3 3
 2x x    x x   8 M N M N M N M N M N M N     3 2
  2  6x x   3 2  2x x   2  8  . M N M N     10
Từ đây suy ra đường thẳng MN luôn đi qua điểm cố định là trung điểm Q 1;5 của MN .
Câu 18. [2D1.5-4] Trong mặt phẳng với hệ tọa độ Oxy , cho điểm M  3  ;  1 và đường tròn C  2 2
: x y  2x  6 y  6  0 . Gọi T , T là các tiếp điểm của các tiếp tuyến kẻ từ M đến C  . 1 2
Tính khoảng cách từ O đến đường thẳng T T . 1 2 3 A. 5 . B. 5 . C. . D. 2 2 . 5 Lời giải Chọn C.
Ta xét đường tròn C  có tâm I 1;3 và bán kính R  2 .
Theo tính chất tiếp tuyến ta có MI T T tại trung điểm của T T . 1 2 1 2 
Suy ra đường thẳng T T nhận vectơ MI 4; 2 là vtpt. 1 2
Giả sử T x ; y . Khi đó, phương trình T T có dạng: 4 x x  2 y y  0 . 1   1  1  1 1  1 2 4  x  2 y 4x  2 y
Suy ra d O,T T  1 1  1 1  . 1 2 2 2 4  2 2 5 
Ta có: MT x  3; y 1 . 1  1 1  Theo giả thiết ta có:  
MT .IT  0   x 1 x  3  y  3 y 1  0 2 2
x  2x  3  y  4 y  3  0 (1) 1  1   1  1  1 1 1 1 1 1 2 2
Đồng thời ta có: IT R   x  3  y 1  4 2 2
x  6x  9  y  2 y 1  4 (2) 1   1  1 1 1 1 1
Lấy (1) – (2) ta được: 4x  2 y  6  . 1 1 4x  2 y 6 3
Từ đây ta có: d O,T T  1 1    . 1 2 2 5 2 5 5
Câu 19. [2H1.2-2] Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? A. 4 . B. 9. C. 3 . D. 6.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 11/24 – BTN 044 Lời giải Chọn C.
Hình hộp chữ nhật có ba kích thước đôi một khác nhau có 3 mặt phẳng đối xứng.
Câu 20. [2D1.5-2] Đường thẳng  có phương trình y  2x 1 cắt đồ thị của hàm số 3
y x x  3 tại
hai điểm A và B với tọa độ được kí hiệu lần lượt là Ax ; y và B x ; y trong đó B B A A
x x . Tìm x y ? B A B B
A. x y  5  .
B. x y  2  .
C. x y  4 .
D. x y  7 . B B B B B B B B Lời giải Chọn A.
Phương trình hoành độ giao điểm  x  1  y  3 3
2x 1  x x  3 3
x  3x  2  0 A A    
x y  5  . x  2  y  3 B BBB
Câu 21. [2D1.1-1] Hàm số 4 2
y x  2x 1 nghịch biến trên các khoảng nào sau đây? A.  ;   
1 và 0;+ . B.  ;
 0 và 1;+ . C.  1
 ;0 và 1;+ . D.  ;    1 và 0;  1 . Lời giải Chọn D. Ta có 3
y  4x  4x x  1 
y  0  x  1   x  0  Bảng biến thiên x  1  0 1  y  0  0  0    y 1 0 0
Hàm số đồng biến trên các khoảng  ;    1 và 0;  1 .
Câu 22. [2D1.3-1] Giá trị lớn nhất của hàm số 3 2
y  2x  3x 12x  2 trên đoạn  1  ; 2 thuộc khoảng nào dưới đây? A. 3;8 . B.  7  ;8 . C. 2;14 . D. 12;20 . Lời giải Chọn D. 2
y  6x  6x 12
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 12/24 – BTN 044x  1 1  ; 2 y  0  
x  2 1; 2  y   1  15 ; y  
1  5 ; y 2  6 .
Max y  15 12;20 . 1;2
Câu 23. [2D1.2-2] Cho hàm số y f x . Hàm số y f  x có đồ thị trên một khoảng K như hình vẽ bên. y x x x x 1 2 3 O
Trong các khẳng định sau, có tất cả bao nhiêu khẳng định đúng?
I  : Trên K , hàm số y f x có hai điểm cực trị.
II  : Hàm số y f x đạt cực đại tại x . 3
III  : Hàm số y f x đạt cực tiểu tại x . 1 A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn A.
Dựa vào đồ thị hàm số suy ra bảng biến thiên cho hàm số f x như sau: x ∞ x1 x2 x3 + ∞ y' 0 + 0 0 + ∞ y ∞
Dựa vào BBT suy ra: hàm số có 2 điểm cực trị, điểm cực tiểu là x x và điểm cực đại là 1
x x . Vậy có 2 khẳng định đúng là  I  và  III  . 2 1 1 1 1
Câu 24. [1D4.1-3] Với n là số tự nhiên lớn hơn 2 , đặt S     ...  . Tính lim S n 3 3 3 3 C C C C n 3 4 5 n 3 1 A. 1. B. . C. 3 . D. . 2 3 Lời giải Chọn B. n! n n 1 n  2 1 6 3    Ta có: C     . n 3!n  3 3 ! 6 C n n n n   1  2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 13/24 – BTN 044 Khi đó: 6 6 6 6  1 1 1 1  S       6      n  1.2.3 2.3.4 3.4.5 n 2n  1 n  1.2.3 2.3.4 3.4.5 n 2n  1 n        1 1 1  1 1  1  1 1 1 1 
Xét dãy u : u   .   .  . . k k     
k  2k   1 k
2 k 1 k  2 k
2  k 1 k  2 k 1 k  Suy ra: 1 1  1 1  1  1 1          . 1.2.3 2 1.2 2.3  2  2 6  1 1  1 1  1  1 1          . 2.3.4 2  2.3 3.4  2  6 12  1 1  1 1  1  1 1          . 3.4.5 2  3.4 4.5  2  12 20  … 1 1  1 1      . n 2n  1 n
2  n 2 n  1 n  1 n         1  1 1   1 1   S  6.     3  . n  2  2 n n  1   2 n n  1          1 1  3 Vậy lim S  lim 3      . n  2 n  n  1   2     x x  1 
Câu 25. [1D2.2-3] Tập nghiệm S của bất phương trình 2 5    là  25 
A. S   ;  2 .
B. S   ;   1 .
C. S  1; 
D. S  2; . Lời giải Chọn D. x x  1 2  x2 2 5   5
 5 x x  2  2x x  2  
. Vậy S  2; .  25 
Câu 26. [2H2.1-1] Khối cầu bán kính R  2a có thể tích là 3 32 a 3 8 a A. . B. 3 6 a . C. 2 16 a . D. . 3 3 Lời giải Chọn A. 3 4 32 a 3 V  R  . 3 3
Câu 27. [2H2.1-2] Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a , góc giữa mặt bên và mặt
đáy bằng 60 . Tính diện tích xung quanh của hình nón đỉnh S , đáy là hình tròn ngoại tiếp tam giác ABC . 2  a 3 2  a 7 2  a 7 2  a 10 A. . B. . C. . D. . 3 6 4 8 Lời giải Chọn B.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 14/24 – BTN 044 S C O M A B
Gọi M là trung điểm của AB . 1 1 a 3 a 3 OM CM   . 3 3 2 6  OM a 3
Xét tam giác vuông SOM O 1v có o cos 60   SM  . SM 3  2 2 3a a a 21
Xét tam giác vuông SMB M 1v có 2 2 SB SM MB    . 9 4 6 2 a 3
Ta có bán kính đường tròn ngoại tiếp tam giác ABC bằng OC CM  . 3 3 2 a 3 a 21  a 7 Vậy S
 rl .  . xq 3 6 6 2 2 x y
Câu 28. [0H3.5-3] Trong mặt phẳng với hệ tọa độ Oxy , cho elip  E  : 
 1. Điểm M   E  sao 25 9 
cho F MF  90 . Tìm bán kính đường tròn nội tiếp tam giác MF F . 1 2 1 2 1 A. 2 . B. 4 . C. 1. D. . 2 Lời giải Chọn C. M F O F 1 2 Ta có 2 2 2
c a b  16  2c F F  8 , và F 4  ;0 , F 4; 0 . 1   2   1 2 2 2 x y Giả sử M  ;
x y   E      1  1 25 9
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 15/24 – BTN 044
 
Tam giác MF F là tam giác vuông đỉnh M suy ra MF .MF  0  4   ; x y 4  ; x y  0 1 2    1 2 2 2
x 16  y  0 2 2
x  16  y 2 . Thay (2) vào (1) ta có: 2 2 16  y y 9 5 7 2 2 
 1  144  9 y  25y  225  0 2
 16 y  81  y    x   . 25 9 4 4  5 7 9   5 7 9   5 7 9   5 7 9 
Vậy có bốn điểm M  ; , M  ;  , M   ; , M   ;  1 2 3 4   4 4   4 4   4 4   4 4         
thỏa mãn yêu cầu của bài toán.  1  1
MF MF F F Ta có MF  512  160 7 , MF  512 160 7 , 1 2 1 2 p  . 1 2 4 4 2 1 Sd M Ox F F  . MF F  , . 9 1 2 1 2 2 S
Vậy bán kính đường tròn nội tiế tam giác MF F 1 2 r   1 . p
Câu 29. [1D1.4-3] Có bao nhiêu giá trị nguyên của m thuộc đoạn  2
 018; 2018 để phương trình m   2
1 sin x  sin 2x  cos 2x  0 có nghiệm? A. 4036 . B. 2020 . C. 4037 . D. 2019 . Lời giải Chọn B. Ta có m   2
1 sin x  sin 2x  cos 2x  0  m   2 2 2
1 sin x  sin 2x  cos x  sin x  0 2 2  cos x  2sin .
x cos x m sin x  0   1
Thay sin x  0 vào phương trình   1 ta được 2
cos x  0 (vô lí vì 2 2
sin x  cos x  1 )
 sin x  0 , chia hai vế phương trình   1 cho 2
sin x ta được phương trình: 2
cot x  2 cot x m  0 2 Phương trình  
1 có nghiệm khi phương trình 2 có nghiệm
   0  1 m  0  m  1  m  2018  ;  2018 Mà 
m 2018; 2017  ;...; 0;  1 m   
 có 2020 số nguyên m thỏa yêu cầu.
Câu 30. [2D1.1-4] Cho hàm số y f x có đồ thị f  x như hình vẽ y 3 3 1  O 1 2 3 1  2 x 3  1  3  5  2 x
Hàm số y f 1 x 
x nghịch biến trên khoảng nào trong các khoảng dưới đây? 2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 16/24 – BTN 044 A.  2  ; 0 . B.  3  ;  1 . C. 3; . D. 1; 3 . Lời giải Chọn A. 2 x
Ta có y f 1 x 
x y   f 1 x  x 1 2 2 x
Hàm số y f 1 x 
x nghịch biến  y  0  f  1 x  x 1   1 2
Đặt t  1 x x 1  t
 , bất phương trình  
1 trở thành f t  t y 3 3 1  1 2 3 1  2 x 3  1  3  5 
Đồ thị hàm số f t có dạng đồ thị hàm số f  x
Trong hệ trục tọa độ Oty , vẽ đường thẳng d : y t
 và đồ thị hàm số y f t
Đường thẳng d cắt đồ thị hàm số y f t  tại các điểm A 3
 ;3; B 1;  1 ; C 3; 3 t  3 1   x  3   x  4
Từ đồ thị suy ra f t  t       1  t  3  1  1 x  3  2   x  0  Câu 31. [0D3.2-3] Tìm tất cả các giá trị tham số m để bất phương trình
x    x  x 2 6 2 8
x m 1 nghiệm đúng với mọi x 2;8 . A. m  16 . B. m  15 . C. m  8 . D. 2   m  16 . Lời giải Chọn B.
Bất phương trình tương đương 2
x  6x 16  2  x 8  x 15  m
Đặt 2  x 8  x  t; x 2; 8  t 0; 5
Bất phương trình trờ thành 2
t t 15  m với t 0; 5
Xét hàm số f t 2
t t 15 trên 0; 5 .
f t  2t 1 1 
f t  0  t  2 Bảng biến thiên t 1   0 5  2 f t  0  f t  15 1  5
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 17/24 – BTN 044
Nhìn vào bảng biến thiên ta thấy để bất phương trình có nghiệm m  15 1
Câu 32. [2D2.2-1] Tìm tập xác định D của hàm số y   2 x  3 3 1 .  1   1  A. D   ;    ;      . B. D   .  3   3   1   1   1 
C. D   \   . D. D   ;    ;      .  3   3   3  Lời giải Chọn A.  1 x   3 Điều kiện xác định 2 3x 1  0    1  x    3
Câu 33. [2H1.2-1] Số cạnh của hình mười hai mặt đều là A. Mười sáu. B. Ba mươi. C. Hai mươi. D. Mười hai. Lời giải Chọn B.
Câu 34. [2H1.3-3] Cho hình chóp tứ giác đều có góc giữa mặt bên và mặt đáy bằng 60 . Biết rằng mặt
cầu ngoại tiếp hình chóp đó có bán kính R a 3. Tính độ dài cạnh đáy của hình chóp tứ giác đều nói trên. 12 3 9 A. a . B. 2a . C. a . D. a . 5 2 4 Lời giải Chọn A. S M D I A O K C B
Gọi K là trung điểm của AB , AC BD O . Góc giữa mặt bên và đáy là góc  SKO  60 .
Gọi M là trung điểm của SA . Trong S
OA dựng đường thẳng trung trực IM của SA , I SO .
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp tứ giác. b b 2
Giả sử AB b , suy ra OK  , OA  . 2 2
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 18/24 – BTN 044 Xét SOK có SO b 3 tan 60 
SO OK.tan 60  OK 2 2 2  b 3   b 2  b 5 2 2 SA
SO OA         2   2  2     SI SM Ta có SMI SOA (g.g) nên:  SA SO 2 1 2 5b SA SM .SA 1 5 3 2 4  SI     b . SO SO 2 b 3 12 2 5 3 12 Theo giả thiết
b a 3  b a . 12 5
Câu 35. [2D2.5-3] Biết rằng phương trình ex  ex  2 cos ax ( a là tham số) có 3 nghiệm thực phân
biệt. Hỏi phương trình ex  ex  2 cos ax  4 có bao nhiêu nghiệm thực phân biệt? A. 5 . B. 10 . C. 6 . D. 11. Lời giải Chọn C. 2 x x 2  x x       x  Ta có xx 2 2 e ee e  2  2 cos 2   ax  4 2 2  e e  2 cos   ax  2  4cos . a        2  x x    x  2 2 e e  2 cos . a      1  2    x x    x  2 2 e e  2  cos . a   2   2  Phương trình  
1 có ba nghiệm phân biệt, suy ra phương trình 2 cũng có 3 nghiệm phân biệt
và không có nghiệm nào trùng với nghiệm của phương trình   1 .
Vậy phương trình đã cho có 6 nghiệm thực phân biệt.
Câu 36. [2H2.1-1] Cho khối nón có bán kính đáy r  3 và chiều cao h  4 . Tính thể tích V của khối nón đã cho. 163
A. V  163 . B. V  .
C. V  12.
D. V  4. 3 Lời giải Chọn D. 1 1
Tính thể tích V của khối nón đã cho là 2
V  . r h .3.4  4. 3 3 2 sin x  3 
Câu 37. [2D1.3-3] Giá trị nhỏ nhất của hàm số y  trên 0; là sin x 1  2    5 A. 5. B. 2. C. 3. D. . 2 Lời giải Chọn D.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 19/24 – BTN 044 Đặt x  0;  t 0;  1  2    2t  3 1 
Hàm số đã cho trở thành f t 
f t   0, t  0;1 2   t 1 t   1 5
Vậy min f t  f   1  . 0;  1 2
Câu 38. [1H3.5-3] Cho hình lăng trụ tam giác đều ABC.AB C
  có AB a , AA  2a. Tính khoảng
cách giữa hai đường thẳng AB và AC . a 3 2 5 2 17 A. . B. . a C. a 5. D. . a 2 5 17 Lời giải Chọn D. A' B' C' I 2a A a M C B
Gọi I AB  AB , M là trung điểm của BC . Ta có V
MI //AC A C   AB M
  d AC AB  d A  AB M
  d B AB M   3 // , , , BAB M   . SAB M  3 1 1 a 3 Mà VBB . S  . BAB M  3 2 ABC 12 a 17 a 3 Tam giác AB M  có 2 2
AB  a 5, B M   B B   BM  , AM  . 2 2 2 a 51
Áp dụng định lý Hêrong ta có S  . AB M  8 a
Vậy d AC B A
   d B B AM  2 17 , ,  . 17
Câu 39. [0H3.1-2] Trong mặt phẳng với hệ tọa độ Oxy, giả sử điểm ( A ;
a b) thuộc đường thẳng
d : x y  3  0 và cách  : 2x y 1  0 một khoảng bằng 5. Tính P ab biết a  0. A. 4 . B. 2  . C. 2 . D. 4  . Lời giải Chọn B.
Do Aa;b  d nên a b  3  0  a  3  b . Vậy A3  b;b .
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 20/24 – BTN 044
2 3  b  b 1 b  7  5 Theo bài: d  , A   5 
 5  b  7  5   2   2 2 1 b  7  5  b  2   a  1  
. Vì a  0 nên a  1,b  2
 . Do đó P ab  2  b  12   a  9  
Câu 40. [2H2.1-1] Một hình trụ có bán kính đáy bằng r và có thiết diện qua trục là một hình vuông.
Tính diện tích toàn phần của hình trụ đó. A. 2 4 r . B. 2 6 r . C. 2 8 r . D. 2 2 r . Lời giải Chọn B.
Do thiết diện qua trục là một hình vuông nên cạnh của hình vuông bằng 2r . Suy ra chiều cao
của hình trụ cũng bằng 2r .
Vậy diện tích toàn phần của hình trụ đã cho là: 2
S  2 rh  2 r 2 2 2
 4 r  r  6 r . tp
Câu 41. [2D1.3-3] Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của 2
x mx m hàm số y
trên 1;2 bằng 2 . Số phần tử của tập S là x 1 A. 3 . B. 1. C. 4 . D. 2 . Lời giải Chọn D. 2
x mx m
Đặt f x 
, ta có hàm số f x xác định và liên tục trên đoạn 1;2. x 1 2 x  2x
Có: f  x   0 , x  1;2 .  x  2 1 4  3m 1 2m
Suy ra: max f x  f 2 
; min f x  f   1  . 1;2 3 1;2 2  f 2  2   f   1  2 
Do đó max f x  max f 2 ; f   1  . Theo bài ta có:    1;2 f    1  2  f  2  2  Trường hợp 1:  4  3m   2 10 2  f 2  2  m   m     3   3 3 2 Ta có:       m  . f    1  2 1 2m 5 3 3    2   m   2    2 2 Trường hợp 2:  1 2m   3 5 2  f   1  2  m   m     2   2 2 5 Ta có:       m   . f  2  2 4  3m 10 2 3    2   m   3    3 3
Vậy có giá trị của tham số m thỏa yêu cầu bài toán. Do đó tập S có hai phần từ.
Câu 42. [2D2.4-3] Cho a , b là các số thực dương thỏa mãn b  1 và a b a . Tìm giá trị nhỏ nhất  a
của biểu thức P  log a  2 log . a b    b b
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 21/24 – BTN 044 A. 6 . B. 7 . C. 5 . D. 4 . Lời giải Chọn C.
Vì b  1 và 0  a b a nên log
a  1  log a hay 1  log a  2 . b b ba  log a 1
Khi đó P  log a  2 log b   4 log a   1  4 log a   1 b  1 a b    b  log a 1 log a 1 b b b b 1
Áp dụng bất đẳng thức Cô si cho hai số dương
và 4log a  ta có: b  1 log a 1 b 1  4 log a  
1  4 . Suy ra P  5 . Vậy min P  5 khi a b b . log a 1 b b
Câu 43. [2H2.2-3] Một hình trụ có độ dài đường cao bằng 3 , các đường tròn đáy lần lượt là O;  1 và O ; 
1 . Giả sử AB là đường kính cố định của O; 
1 và CD là đường kính thay đổi trên O ; 
1 . Tìm giá trị lớn nhất V
của thể tích khối tứ diện ABCD . max 1 A. V  2 . B. V  6 . C. V  . D. V  1 . max max max 2 max Lời giải Chọn A.
Cách 1: Dựng hình hộp chữ nhật AEBF.HCGD có thể tích V như hình vẽ. D O' H G C h = 3 F A r = 1 B O E
Khi đó, đặt AF x , với 0  x  2 ta có 2 2 2 AE AB AF  4  x .
Suy ra V AE.AF.AH 2  3 . x 4  x . 1
Do đó, thể tích khối tứ diện ABCD là VV 2  . x 4  x 2  x  2 4  x   2 . ABCD 3 Vậy V
 2 khi AEBF là hình vuông, tức là AB CD . ABCD max Cách 2: 1 Ta có VA . B C . D d AB CD
AB CD  2sin  AB;CD  2 . ABCD  ; .sin  ;  6 Vậy V   2 khi sin  A ;
B CD  1 hay AB CD . ABCD max
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 22/24 – BTN 044
Câu 44. [1D2.5-4] Trong mặt phẳng tọa độ Oxy , cho hình chữ nhật OMNP với M 0;10 , N 100;10 ,
P 100;0 Gọi S là tập hợp tất cả các điểm A ;
x y  với x, y  nằm bên trong (kể cả trên
cạnh) của hình chữ nhật OMNP . Lấy ngẫu nhiên một điểm A ;
x y   S . Tính xác suất để
x y  90 . 169 473 845 86 A. . B. . C. . D. . 200 500 1111 101 Lời giải Chọn D. M 0;10 N 100;10 O 0;0 P 100;0
Ta có n S   101.11 Số điểm A  ;
x y   S thảo mãn x y  90 là nA  101.1110.11 1 2  3  ... 10  946 . n A 86
Xác suất cần tìm là P   . n S  101
Câu 45. [2D2.3-2] Tập xác định của y   2
ln x  5x  6 là A. 2;  3 . B. 2; 3 . C.  ;
 2 3;   . D.  ;
 2  3;   . Lời giải Chọn A. Biểu thức y   2
ln x  5x  6 xác định 2
 x  5x  6  0  2  x  3 .
Tập xác định của y   2
ln x  5x  6 là D  2;3 Câu 46. [2D2.4-2] Cho   3 .e x f x x  
. Tập nghiệm của bất phương trình f  x  0 là  1   1   1  A. ;   . B. 0;   . C. ;     . D. 0;  1 .  3   3   3  Lời giải Chọn C. Ta có   3  x     3x 3x       3 .e e 3 .e 1 3 e x f x x f x x x 1  1 
f  x  0  x  . Vậy tập nghiệm của bất phương trình f  x  0 là ;     . 3  3 
Câu 47. [2H1.3-2] Cho khối chóp S.ABCD có thể tích bằng 3
2a và đáy ABCD là hình bình hành. Biết
diện tích tam giác SAB bằng 2
a . Tính khoảng cách giữa hai đường thẳng SB và CD . 3a a 2 A. a . B. . C. 3a . D. . 2 2 Lời giải Chọn C.
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 23/24 – BTN 044 3V 3V 3 3.2.a
d CD; SB  d CD;SAB  d C;SAB SABC SABCD     3a . S 2S 2 2.a SAB SAB
Câu 48. [2D2.4-1] Đạo hàm của hàm số 1 2 e x y   là 12 e x A. 1 2 2e x y    . B. 1 2 2e x y     . C. y   . D. 1 2 e x y    . 2 Lời giải Chọn B.
Câu 49. [2D2.5-2] Tập nghiệm của bất phương trình 2 log x 1  log 5  x 1 là 2   2   A. 3;5 . B. 1;  3 . C. 1;  3 . D. 1;5 . Lời giải Chọn B.
Điều kiện: 1  x  5 . 2 2 log x 1  log 5  x 1  log x 1  log 10  2x 2   2   2   2     x  2 1
 10  2x  3  x  3 . Vậy S  1;  3 1
Câu 50. [2D1.1-2] Có bao nhiêu giá trị nguyên của tham số m để hàm số 3 2 y
x mx  4x  2 đồng 3
biến trên tập xác định của nó? A. 4 . B. 2 . C. 5 . D. 3 . Lời giải Chọn C. Ta có: 2
y  x  2mx  4 ; 2
y  0    m  4  0  2   m  2 .
Mà m   , suy ra m  2  ; 1  ; 0;1; 
2 . Vậy có 5 giá trị của tham số m .
----------HẾT----------
TOÁN HỌC BẮC–TRUNG–NAM sưu tầm và biên tập
Mã đề 234 - Trang 24/24 – BTN 044
Document Outline

  • [toanmath.com] - Đề KSCL Toán 12 ôn thi THPT Quốc gia năm 2018 – 2019 trường chuyên Vĩnh Phúc lần 2
  • 044-THPT CHUYEN VINH PHUC-L2-1819 (1)

Tài liệu liên quan: