Đề ôn tập Toán 9 tháng 02/2020 trường THPT chuyên Hà Nội – Amsterdam
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp đề khảo sát chất lượng học sinh môn Toán 9 THPT chuyên Hà Nội – Amsterdam giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
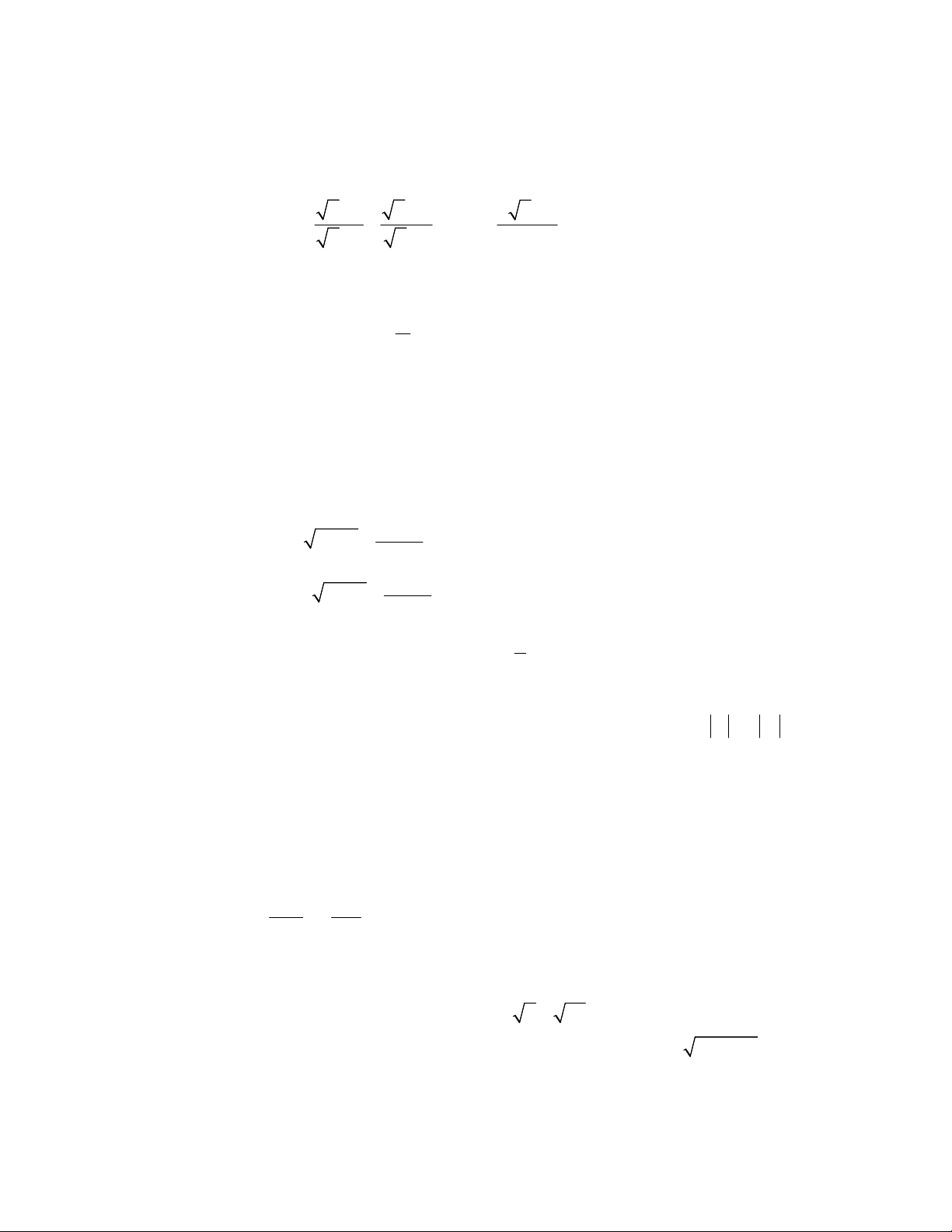
Preview text:
TRƯỜNG THPT CHUYÊN
ĐỀ ÔN TẬP TỔNG HỢP PHÒNG DỊCH n-CoV HÀ NỘI – AMSTERDAM Năm học: 2019 – 2020 TỔ TOÁN – TIN MÔN TOÁN LỚP 9
Thời gian làm bài: 120 phút Đề số 1 Bài 1 (2,0 điểm). 2 x 2 6 Cho biểu thức: A và B với x 0, x 9. x 9 x 3 x 3 x
1) Tính giá trị B khi x 4.
2) Rút gọn biểu thức A. B 2 x 1
3) Tìm giá trị của x để . A 2
Bài 2 (2,0 điểm). Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một ca nô xuôi dòng 78km và ngược dòng 44 km mất 5 giờ với vận tốc dự định. Biết rằng,
nếu ca nô xuôi dòng 13 km và ngược dòng 11 km, trên cùng dòng sông đó, với cùng vận tốc dự
định đó thì mất 1 giờ; vận tốc của dòng nước không đổi và thời gian để ca nô quay đầu là không
đáng kể. Tính vận tốc riêng của ca nô và vận tốc dòng nước. Bài 3 (2,0 điểm). 1) Cho phương trình 2 x m 2
1 x m m 2 0 , với m là tham số.
a) Chứng minh rằng phương trình đã cho luôn có hai nghiệm trái dấu với mọi m .
b) Gọi hai nghiệm của phương trình đã cho là x , x . Tìm m để biểu thức 1 2 3 3 x x 1 2
A đạt giá trị lớn nhất. x x 2 1 x m y m 1
2) Cho hệ phương trình (m là tham số). m x y 3m 1
Tìm m để hệ phương trình đã cho có nghiệm duy nhất sao cho x y đạt giá trị nhỏ nhất. Bài 4 (3,5 điểm).
Cho đường tròn tâm O , bán kính R , có hai đường kính AB và CD vuông góc với nhau. Lấy
điểm M bất kỳ thuộc đoạn OA ( M khác ,
O A ). Tia DM cắt lại đường tròn ( ) O tại N.
1) Chứng minh rằng bốn điểm ,
O M, N,C cùng thuộc một đường tròn;
2) Chứng minh rằng khi M thay đổi trên đoạn OA, thì tích DM DN không đổi.
3) Đường tròn tâm M bán kính MC cắt C ,
A CB lần lượt tại E, F (E, F C). Tính CE CF theo bán kính R.
4) Nối B với N cắt OC tại .
P Xác định vị trí của điểm M trên đoạn OA sao cho OM OP
đạt giá trị nhỏ nhất. AM CP Bài 5 (0,5 điểm).
1) Xét hai số thực x, y thỏa mãn điều kiện x 2y 3 và x 0.Tìm giá trị nhỏ nhất của biểu 2 2x y thức 2 P y . x 2 2 2 a b c 3 2) Cho a,b,c thỏa mãn 2 2 2
a b c 1. Chứng minh rằng: . 1 2bc 1 2ca 1 2ab 5
--------------- Hết --------------- TRƯỜNG THPT CHUYÊN
ĐỀ ÔN TẬP TỔNG HỢP TUẦN 3 THÁNG 2 NĂM 2020 HÀ NỘI – AMSTERDAM Năm học 2019 – 2020 Tổ Toán – Tin học Môn: Toán 9
Thời gian làm bài: 120 phút Ngày 17/02/2020 x 1 x 2 2 x 3
Bài 1. Cho hai biểu thức A và B , với x 0; x 1. x 1 x 1 x 1
1) Tính giá trị biểu thức B khi x 4. 2) Rút gọn biểu thức . A A
3) Tìm tất cả các giá trị của x để P
nhận giá trị nguyên dương. B
Bài 2. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Một phòng họp có 300 ghế ngồi, được xếp thành một số hàng có số ghế bằng nhau. Buổi họp hôm
đó có 378 người đến dự họp nên ban tổ chức đã kê thêm 3 hàng ghế và mỗi hàng phải xếp thêm 1 ghế
mới đủ chỗ ngồi. Hỏi ban đầu phòng họp có bao nhiêu hàng ghế và mỗi hàng ghế có bao nhiêu ghế, biết
rằng số hàng ghế ban đầu không vượt quá 20. Bài 3. y 4x 1 1 2y 3
1) Giải hệ phương trình . 3 3 4x 1 1 2 y 3 1
2) Trong mặt phẳng tọa độ Oxy cho parabol 2
(P) : y x và đường thẳng (d) : y 2mx 4. 2
a) Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của m.
b) Gọi x , x là hoành độ các giao điểm của (d) và (P). Tìm số dương m để x 2 x 8. 1 2 1 2
Bài 4. Cho đường tròn tâm O có hai đường kính AB, CD vuông góc với nhau. Gọi M là một điểm di động trên đoạn OB ( M ,
O B ). Tia CM cắt BD tại P và đường tròn tại N ( N C ). Gọi Q là giao điểm của AN và CD.
1) Chứng minh rằng tứ giác DQPN nội tiếp và PQ A . B 2) Chứng minh rằng A CQ ~ M
AC và diện tích tứ giác ACMQ không đổi khi M thay đổi trên OB. 2 CQ CN 3) Chứng minh rằng . AM AN
4) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác CQN luôn nằm trên một đường thẳng cố
định khi M thay đổi trên đoạn OB.
Bài 5. Cho các số thực a,b không âm, thỏa mãn a b a 2b.
Tìm giá trị nhỏ nhất và lớn nhất của biểu thức 2 2
P a b 2(a 1)(b 1) 8 4 a b.
-------------------- Hết -------------------- TRƯỜNG THPT CHUYÊN
ĐỀ ÔN TẬP TỔNG HỢP TUẦN 4 THÁNG 2 NĂM 2020 HÀ NỘI – AMSTERDAM Môn : TOÁN LỚP 9 TỔ TOÁN – TIN HỌC
Thời gian làm bài : 120 phút Ngày 24/02/2020 1 x 15 x 2 x 1
Bài 1. Cho các biểu thức A và B : với x 0, x 25. 1 x x 25 x 5 x 5
1) Tính giá trị của biểu thức A khi x 16. 2) Rút gọn biểu thức . B
3) Tìm x để B A nhận giá trị nguyên.
Bài 2. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Trong một kì thi tuyển sinh vào THPT, hai trường A và B có tổng cộng 350 học sinh dự thi. Kết quả hai
trường đó có 338 học sinh trúng tuyển. Theo thống kê, trường A có 97% số học sinh dự thi trúng tuyển và
trường B có 96% số học sinh dự thi trúng tuyển. Hỏi mỗi trường có bao nhiêu học sinh dự thi. Bài 3. 1 6 2 x 1 | y 2 |
1) Giải hệ phương trình: . 3 x 3 9 x 1 | 6 3y | 2) Cho parabol P 2
: y x và đường thẳng d : y mx 3.
a) Chứng minh rằng d luôn cắt P tại hai điểm phân biệt với mọi giá trị của m .
b) Tìm tất cả các giá trị của m để d cắt P tại hai điểm phân biệt có tọa độ (x ; y ) và (x ; y ) sao 1 1 2 2
cho y y 11 4x 4x . 1 2 1 2 Bài 4.
Cho đường tròn O và đường thẳng d, không đi qua O, cắt đường tròn O tại hai điểm A và B phân
biệt. Trên d lấy điểm C nằm bên ngoài đường tròn sao cho CB C .
A Kẻ hai tiếp tuyến CM ,CN với đường
tròn O ( M thuộc cung AB lớn). Gọi H là trung điểm AB. Các đường thẳng OH và CN cắt nhau tại K.
1) Chứng minh 5 điểm M, H, O, N, C cùng nằm trên một đường tròn.
2) Các đường thẳng ON và AB cắt nhau tại J. Chứng minh KN KC KH KO và KJ MN.
3) Đoạn thẳng CO cắt đường tròn O tại I. Chứng minh rằng I cách đều các đường thẳng CM, CN và MN.
4) Vẽ đường thẳng qua O và song song với MN, tương ứng cắt các tia CM và CN tại E và F. Tìm vị trí của C
trên d sao cho diện tích tam giác CEF đạt giá trị nhỏ nhất.
Bài 5. Cho các số dương a, b, c thỏa mãn abc 2. Chứng minh rằng 3 3 3
a b c a b c b c a c a b .
-------------------- HẾT --------------------
Document Outline
- De luyen tap mon Toan lop 9 tuan 10-16 thang 02 nam 2020
- De_on_tong_hop_tuan3_thang2-2020_Toan9
- De_on_tuan_4_thang_2_2020_Toan9