Đề ôn xác suất thống kê | Đại học Kinh tế kỹ thuật công nghiệp

lOMoAR cPSD| 45315597
ĐỀ ÔN TẬP XSTK NO1
Câu 1. Cho hai biến cố A và B. Biết rằng P(A + B) = 0,88; P(A) = 0,6; P(B) = 0,7.
a) Tính P(AB) và chứng tỏ A và B ộc lập với nhau.
b) Tính xác suất ể cả 2 biến cố A, B không xảy ra?
Câu 2.Cho hàm mật ộ của biến ngẫu nhiên X: 𝑓
a)Tìm k ể f(x) là hàm mật ộ. b)Tính P(X > m - 1) biết m = ModX.
Câu 3. Có 10 loại vắc-xin với xác suất sẽ ược ưa vào sử dụng trong tháng ều là 0,8. Gọi X là số vắcxin sẽ ược ưa vào sử dụng.
a)Tính trung bình có bao nhiêu vắc-xin sẽ ược sử dụng? b)Tính P(X2 < 4)?
Câu 4. Thời gian (giờ) ể một loại sơn khô khi sơn tường là một chỉ số quan trọng
khi sản xuất của công ty sơn EXPO. Để ánh giá một mẫu sơn mới sản xuất, hãng
tiến hành lấy mẫu với số liệu: cỡ mẫu n =36; trung bình mẫu là x = 1,428 giờ; ộ
lệch hiệu chỉnh là S’=0,179.
1. Hãy ước lượng thời gian khô trung bình của loại sơn trên với ộ tin cậy 94%.
Giải: Ta có: n = 36; x = 1,428; S’ = 0,179; =94%= 0,94 Vì n = 36 > 30 nên Z =
(x a n− ') ~ N(0; 1) và: = S ' .z , với Φ(zα) = γ/2 = S n
0,94/2 = 0,4700 tra ngược bảng phụ lục 1 ta có zα = 1,88 = 0,179 1, 88 0,056. 36
Vậy thời gian khô trung bình của loại sơn trên là: x− a x+ hay:
1,428 – 0,056 < a < 1,428 + 0,056 giờ.
2. Kỹ sư phụ trách nghiên cứu mẫu sơn mới này cho rằng thời gian khô là < 1,5
(giờ). Hãy kết luận với mức ý nghĩa 5%.
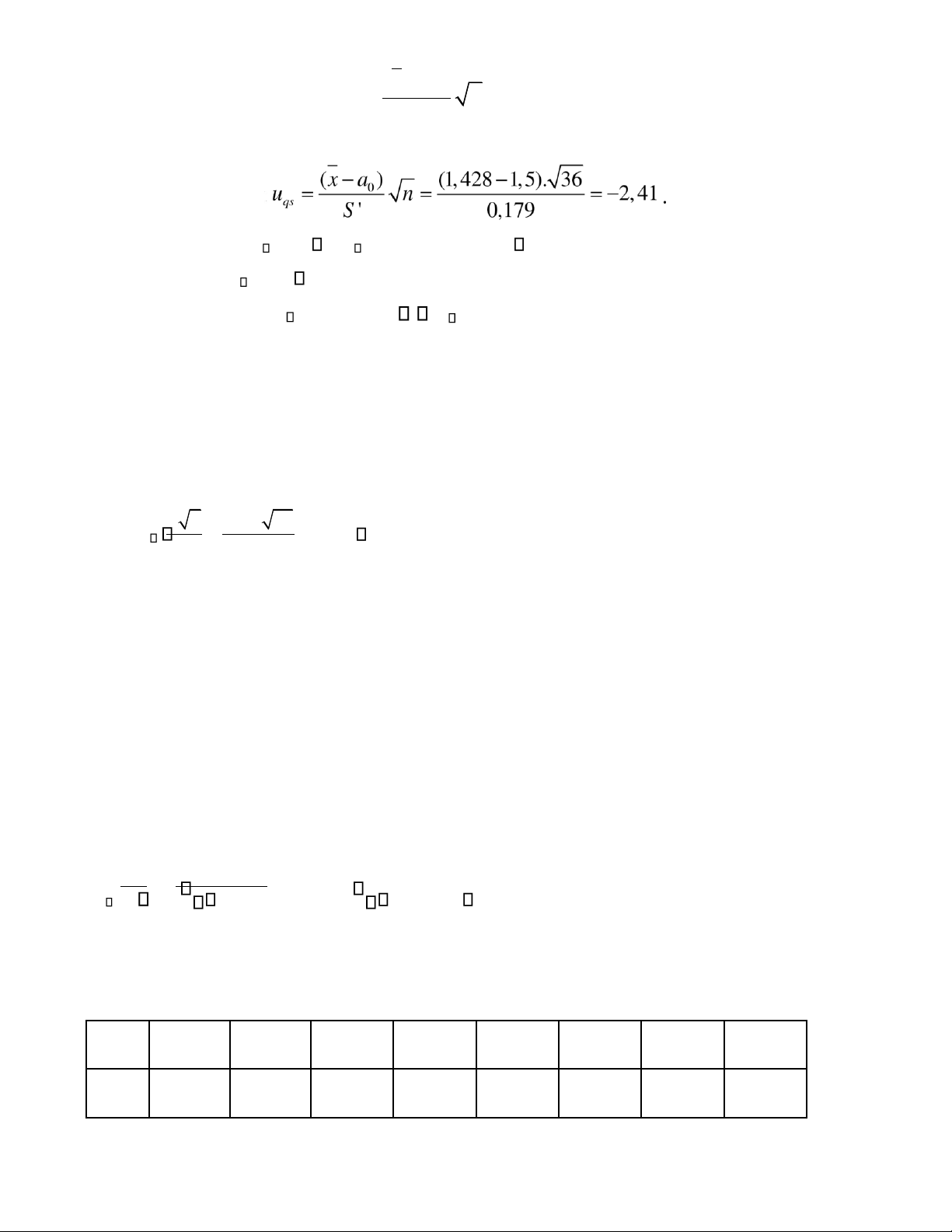
Giải: Ta có a0 = 1,5 giờ; n = 36, x = 1,428; S’ = 0,179; α = 5% = 0,05. + Chọn cặp giả thuyết: H a a0 : 0 H a a1 : 0 VV lOMoAR cPSD| 45315597
+ Tiêu chuẩn kiểm ịnh: = U (x a− )
0 n ~ N(0, 1) vì n ≥ 30. S ' - Giá trị quan sát: =V
+ Miền bác bỏ: W = −( , −u ). Với α = 0,05 uα = u0,05 = 1,645 (tra ngược bảng
phụ lục 2) nên: W = −( ; −1,645).
+ So sánh uqs với W ta thấy uqs W chấp nhận H1.
+ Kết luận: Qua mẫu iều tra trên ta thấy thời gian khô trung bình của loại sơn
trên thực sự nhỏ hơn 1,5 giờ. Vậy tuyên bố của kỹ sư trên là áng tin cậy. 3.
Khi ước lượng thời gian khô trung bình với yêu cầu ộ chính xác là 0,07 thì ộ tin cậy bằng bao nhiêu?
Ta có: ε = 0,07; S’= 0,179; n= 36 thì γ = ? n
0,07. 36 2,35 ; tra bảng PL1 ta ược Φ(2,28) = 0,4906 suy ra ộ Tính: z = = S ' 0,179
tin cậy của ƯL là γ = 2.Φ(zα) = 2.0,4906 = 0,9812 = 98,12%. 4.
Nếu yêu cầu ước lượng thời gian khô trung bình với ộ chính xác 0,065 và ộ
tin cậy 99% thì cần khảo sát thêm bao nhiêu mẫu nữa?
Ta có: ε = 0,065; γ = 99% = 0,99, xác ịnh nthêm = ?
Ta có γ = 2.Φ(zα) → Φ(zα) = γ/2 = 0,99/2 = 0,4950, tra ngược PL1 ta ược zα = 2,575.
Vậy số mẫu sơn cần iều tra là: n = z 2 2. S '2 = 2,575.0,1790,065 2 = 50,28 50 mẫu sơn.
Vậy cần iều tra thêm : nthêm = nmới - ncũ = 50 – 36 = 14 mẫu sơn.
Câu 5. Khảo sát chỉ số chất lượng không khí y ( ơn vị:AQI), và số lượng cây xanh trên ầu người x (m2/người)
tại một số thành phố lớn khu vực Đông Nam Á, người ta thu ược mẫu số liệu như sau: xi 60 55 42 35 28 20 11 5 yi 25 75 124 180 250 300 350 400 lOMoAR cPSD| 45315597
ĐỀ ÔN TẬP XSTK NO2 Câu 1. ni 3 5 2 6 4 3 5 2
Với biến BNN X về lượng cây xanh và Y chỉ số chất lượng không khí ều tuân theo luật chuẩn. a)
Lập phương trình hồi quy tuyến tính thực nghiệm, và cho biết sai số về chỉ số chất lượng không
khí AQI khi khảo sát chất lượng không khí ở thành phố có lượng cây xanh 42 (m2/người) giữa số liệu thực tế và qua hàm hồi quy. b)
Có giả thiết cho rằng XY −0,86 , hãy ưa ra kết luận với mức ý nghĩa 1%.
Cho hai biến cố A và B. Biết rằng P(A + B) = 0,88; P(A) = 0,6; P(B) = 0,7.
a)Tính P(AB) và chứng tỏ A và B ộc lập với nhau. b)
Tính xác suất ể chỉ có biến cố B xảy ra? Câu 2.Cho hàm mật ộ của biến ngẫu nhiên X: ) 𝑓
a)Tìm k ể f(x) là hàm mật ộ. b)Tính P(X < m) biết m = ModX.
Câu 3. Cho 2 BNN X, Y ộc lập nhau. Biết X N(6, 9); Y là số cuộc gọi vào số ĐT 115 trong ngày với trung bình 15 cuộc gọi/ngày.
a) Tính D(2X – Y) ? b) Tính P(Y = 14)?
Câu 4. Điều tra doanh thu/tháng của 200 gia ình kinh doanh iện thoại tại một thành phố, người ta tính ược
doanh thu trung bình/tháng là 45 triệu VNĐ và ộ lệch mẫu hiệu chỉnh là 8,912 triệu VNĐ.
1. Hãy ước lượng doanh thu trung bình/tháng của một gia ình kinh doanh iện thoại với ộ tin cậy 99%.
2. Nếu dùng số liệu trên ể ước lượng doanh thu trung bình/tháng của một gia ình kinh doanh iện thoại và yêu
cầu ộ chính xác là 1,5 triệu VNĐ thì ộ tin cậy bằng bao nhiêu?
3. Có 22 gia ình trong mẫu này có doanh thu/tháng trên 70 triệu VND. Với mức ý nghĩa 0,05, có thể cho rằng
tỷ lệ gia ình kinh doanh iện thoại có doanh thu/tháng trên 70 triệu VND lớn hơn 10% không?
Câu 5. Theo dõi về lượng khách vào cửa hàng (người/ngày) và doanh thu trong ngày của cửa hàng ó
(triệu/ngày) ta có số liệu thống kê như sau: xi 22 24 26 28 30 32 34 36 lOMoAR cPSD| 45315597 yi 12,5 14 15 17 18 18,5 20 15, 5 Số ngày 3 5 7 6 8 4 5 2
Với BNN X về lượng khách trong ngày; Y về doanh thu trong ngày của cửa hàng.
a) Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu lượng khách vào cửa hàng là 40
(người/ngày) thì doanh thu là bao nhiêu?
b) Hãy ước lượng hệ số tương quan ρxy với ộ tin cậy 99%. lOMoAR cPSD| 45315597
ĐỀ ÔN TẬP XSTK NO4 Câu 1.
Cho hệ ầy ủ 3 biến cố {A, B , C } với P(A) = 0,3; P(B) = 2P(A). Biết biến cố F thỏa mãn: P(F/A) =
0,02; P(F/B) = 0,35; P(F/C) = 0,5. a) Tính xác suất P(F)?
b) Tính giá trị P[(A+BC)|F] ?
Câu 2. Cho biến nhẫu nhiên X và Y có bảng phân phối ồng thời như sau: Y -3 0 2 X -2 a 0,5a a 0 0,05 a 1,5a 1 0,15 0,1 0,2
a)Tìm hệ số a từ bảng phân phối? b)Tính E(5X2 - 3)?
Câu 3. Trong một lô 100 sản phẩm có 75 sản phẩm loại I. Lấy ngẫu nhiên 45 sản phẩm ể kiểm tra, gọi X là số
sản phẩm loại I gặp ược khi kiểm tra. Biết Y ~ N(3;4).
a)Tính giá trị của E(4X + 5Y)? b)Tính E(Y2), D(Y) = E(Y2) – [E(Y)]2
Câu 4. Điều tra ngẫu nhiên thu nhập/tháng của 100 gia ình ở ịa phương A tính ược thu nhập trung bình/tháng
là 25,8 triệu VNĐ và ộ lệch mẫu hiệu chỉnh là 1,1055 triệu VNĐ. Có 30 gia ình có thu nhập trên 50 triệu VNĐ/tháng.
1. Với ộ tin cậy 95% hãy ước lượng thu nhập trung bình/ tháng của gia ình ở ịa phương A.
2. Nếu muốn ước lượng thu nhập trung bình/tháng của gia ình ở ịa phương A với ộ tin cậy 99% và ộ chính xác
0,25 thì cần iều tra thêm thu nhập của bao nhiêu gia ình?
3. Với mức ý nghĩa 1%, có thể cho rằng tỉ lệ gia ình có thu nhập trên 50 triệu VNĐ/tháng là 20% không?
Câu 5. Nghiên cứu về mối liên hệ giữa tuổi nghề và năng suất lao ộng (NSLĐ) của một số công nhân ở
một phân xưởng ta có số liệu sau: xi 1 2 3 4 5 6 7 8 yi 6,5 8 10 11 13,5 15 18 20 Số CN 3 5 8 10 7 5 3 2
Với biến BNN X là tuổi nghề (năm) và Y là NSLĐ (kg/giờ). lOMoAR cPSD| 45315597
a) Lập phương trình hồi quy tuyến tính biểu diễn mối quan hệ giữa X và Y và cho biết nếu tuổi nghề là 10
năm thì NSLĐ là bao nhiêu?
b) Có giả thiết cho rằng XY 0,81 , hãy ưa ra kết luận với mức ý nghĩa 5%.
Cho hệ ầy ủ 3 biến cố {A, B , C } với P(A) = 0,3; P(B) = 2P(A). Biết biến cố F thỏa mãn: P(F/A) =
0,02; P(F/B) = 0,35; P(F/C) = 0,5. a) Tính xác suất P(F)?
b) Tính giá trị P AC B F[( + )/ ] ?
Câu 2.Cho biến ngẫu nhiên X và Y có bảng phân phối ồng thời như sau: X 0 1 2 ∑𝑝 = P(Y) Y 2 0.05 0.4 4 0.2 ∑𝑝 = P(X) 0.2 0.5 1
a)Điền các giá trị còn thiếu vào bảng? b)Tính E(X - 3Y2)?
Câu 3. Trong một lô 100 sản phẩm có 75 sản phẩm loại I. Lấy ngẫu nhiên 45 sản phẩm ể kiểm tra, gọi X là số
sản phẩm loại I gặp ược khi kiểm tra. Biết Y ~ N(3;4).
a)Tính giá trị của E(3X – 3Y)? b)Tính xác suất P(X = 40)?
Câu 4. Để ánh giá thời lượng pin/1 lần sạc của một mẫu laptop, người ta tiến hành
theo dõi thời lượng pin/1 lần sạc của n= 100 laptop của mẫu này và thu ược thời
lượng pin trung bình/1 lần sạc của mẫu là x = 4,5 giờ; ộ lệch mẫu hiệu chỉnh là
S’=0,5 giờ. Trong mẫu này, có m=7 laptop có thời lượng pin/1 lần sạc nhiều hơn 5,5 giờ. 1.
Với ộ tin cậy 0,93 hãy ước lượng tỉ lệ laptop có thời lượng pin/1 lần sạc nhiều hơn 5,5 giờ. lOMoAR cPSD| 45315597
ĐỀ ÔN TẬP XSTK NO6 Câu 1.
Giải: Ta có n = 100, m = 7, tỷ lệ laptop có thời lượng pin/1 lần sạc nhiều hơn 5,5
giờ trong mẫu là f = m/n = 7/100 = 0,07.
Có γ = 2.Φ(zα) → Φ(zα) = γ/2 = 0,93/2 = 0,4650, tra ngược PL1 ta ược zα = 1,81. − = f (1 f ) p
z .=1,81. 0,07.(1−0,07) = 0,046 n 100
Vậy tỷ lệ laptop có thời lượng pin/1 lần sạc nhiều hơn 5,5 giờ là: P ∈ (f – ε; f + ε)
= (0,07 – 0,046; 0,07 + 0,046) 2.
Nhà sản xuất cho rằng tỉ lệ laptop có thời lượng pin/1 lần sạc nhiều hơn 5,5
giờ là > 6%. Với mức ý nghĩa 1%, hãy kết luận về thông tin nói trên.
Ta có P0 = 6% = 0,06; n = 100; f = 0,07; α = 5% = 0,05.
+ Chọn cặp giả thuyết: H P P0 : 0 H P P: 0 VV 1 + Tiêu chuẩn ( f − p ). 0 n = ~ N(0, 1). kiểm ịnh: U p (1 − p ) 0 0 - Giá trị quan − − : ( f P ). n (0 ,07 0,06) .100 0 u = = =0,421 qs sát: P (1 −P ) 0,06(1 −0,06) 0 0
+ Miền bác bỏ: W = (u , + ). Với α = 0,05 uα = u0,05 = 1,645 (tra ngược PL2) nên: Wα = (1,645; +∞). =V
+ So sánh uqs với W ta thấy uqs W chấp nhận H0.
+ Kết luận: Qua mẫu iều tra trên ta thấy tỷ lệ laptop có thời lượng pin/1 lần sạc
nhiều hơn 5,5 giờ không nhiều hơn mức 6%. Vậy khẳng ịnh của nhà sản xuất là chưa chính xác. 3.
Nếu sử dụng số liệu trên ể ước lượng tỉ lệ laptop có thời lượng pin/1 lần sạc
nhiều hơn 5,5 giờ với yêu cầu ộ chính xác 0,05 thì ộ tin cậy là bao nhiêu? lOMoAR cPSD| 45315597
Giải: Ta có: εp = 0,05; tìm γ = ? . n = 0,05. 100 =1,96
Tính z = f (1− f ) 0,07.(1− 0,07)
Tra PL1 ta ược: Φ(zα) = Φ(1,96) = 0,4750 → γ = 2.Φ(zα) = 2.0,4750 = 0,9500 = 95%.
Câu 5. Để tìm hiểu mối liên hệ giữa kết quả học tập ở phổ thông và ở năm thứ nhất bậc ại học, ta thống
kê kết quả của 40 sinh viên. Gọi X là kết quả thi tốt nghiệp THPT về môn toán, Y là iểm thi môn toán
ở năm thứ nhất tương ứng: xi 6 6 7 7 7 8 9 9 yi 4 6 4 6 7 4 6 7 ni 8 3 2 6 3 1 4 13
Với biến ngẫu nhiên X ;Y ều tuân theo luật chuẩn.
a) Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết sai số về iểm thi môn toán năm thứ nhất
của những sinh viên có kết quả thi tốt nghiệp THPT ược 9 iểm giữa số liệu thực tế và qua hàm hồi quy?
b) Có giả thiết cho rằng 𝜌𝑋𝑌 > 0,5, hãy ưa ra kết luận với mức ý nghĩa 5%?