Đề tập huấn thi THPT Quốc gia 2019 môn Toán sở GD&ĐT Bắc Ninh

Giới thiệu đến quý thầy, cô giáo và các em học sinh khối 12 nội dung đề tập huấn thi THPT Quốc gia 2019 môn Toán sở GD&ĐT Bắc Ninh

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi THPTQG môn Toán năm 2019

Môn: Toán

Thông tin:

14 trang 8 tháng trước

Tác giả:

Profile Thanh Hoa
Trang 1/7 - Mã đề 101 - https://toanmath.com/
SỞ GDĐT BẮC NINH
PHÒNG QUẢN LÝ CHẤT LƯỢNG
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
ĐỀ TẬP HUẤN THI THPT QUỐC GIA NĂM 2019
Bài thi: Toán
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề có 50 câu trắc nghiệm)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Họ và tên thí sinh:..................................................... Số báo danh :...................
Câu 1. Số giao điểm của đồ thị hàm số
4 2
5 4y x x
với trục hoành là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 2. Hàm số nào sau đây không có điểm cực trị?
A.
3
3 1y x x
. B.
2
2y x x
. C.
4 2
4 1y x x
. D.
3
3 1y x x
.
Câu 3. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
ABCD
có
và
CD
thuộc hai đáy của hình trụ,
4AB a
,
5AC a
. Thể tích khối trụ là
A.
3
16V a
. B.
3
4V a
. C.
3
12V a
. D.
3
8V a
.
Câu 4. Cho hình chóp
.S ABC
có
SA
vuông góc với đáy. Tam giác
ABC
vuông cân tại
B
, biết
2SA AC a
. Thể tích khối chóp
.S ABC
là
A.
3
.
2
.
3
S ABC
V a
B.
3
.
3
S ABC
a
V
. C.
3
.
2
S ABC
V a
. D.
3
.
4
3
S ABC
a
V
.
Câu 5. Cho
,k n
( )k n
là các số nguyên dương. Mệnh đề nào sau đây SAI?
A.
k n k
n n
C C
. B.
!
!.( )!
k
n
n
C
k n k
. C.
!.
k k
n n
A k C
. D.
!.
k k
n n
A n C
.
Câu 6. Cho hình lăng trụ
.ABC A B C
có thể tích bằng
V
. Gọi
M
là trung điểm cạnh
BB
, điểm
N
thuộc cạnh
CC
sao cho
2CN C N
. Tính thể tích khối chóp
.A BCNM
theo
V
.
A.
.
7
12
A BCNM
V
V
. B.
.
7
18
A BCNM
V
V
. C.
.
3
A BCNM
V
V
. D.
.
5
18
A BCNM
V
V
.
Câu 7. Cho hàm số
3
3 1y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho nghịch biến trên khoảng
1;3
.
B. Hàm số đã cho đồng biến trên khoảng
1;1
.
C. Hàm số đã cho đồng biến trên khoảng
; 1
và khoảng
1;
.
D. Hàm số đã cho nghịch biến trên khoảng
2;1
.
Câu 8. Cho tứ diện
ABCD
, gọi
1 2
,G G
lần lượt là trọng tâm các tam giác
BCD
và
ACD
. Mệnh đề nào sau
đây SAI?
A.
1 2
/ /
G G ABD
. B.
1 2
/ /
G G ABC
.
C.
1 2
2
3
G G AB
. D. Ba đường thẳng
1 2
,BG AG
và
CD
đồng quy.
Câu 9. Tìm họ nguyên hàm của hàm số
3
2 1
x
f x x e
.
Mã đề 101
Trang 2/7 - Mã đề 101 - https://toanmath.com/
A.
3
1
d
x
f x x e C
. B.
3
1
d 3
x
f x x e C
.
C.
3
1
1
d
3
x
f x x e C
. D.
3
3
1
d
3
x
x
f x x e C
.
Câu 10. Phương trình
2
2 5 4
7 49
x x
có tổng tất cả các nghiệm bằng
A.
1
. B.
5
2
.
C.
1
. D.
5
2
.
Câu 11. Đường cong như hình vẽ là đồ thị của hàm số nào?
A.
3 2
3 5y x x
. B.
3 2
2 6 5y x x
.
C.
3 2
3 5y x x
. D.
3
3 5y x x
.
Câu 12. Cho hình chóp đều
.S ABCD
có cạnh
AB a
, góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
45º
. Thể tích khối chóp
.S ABCD
là
A.
3
3
a
. B.
3
2
6
a
.
C.
3
6
a
. D.
3
2
3
a
.
Câu 13. Mệnh đề nào sau đây đúng?
A.
d
x x x
xe x e xe C
. B.
d
x x x
xe x xe e C
.
C.
2
d
2
x x
x
xe x e C
. D.
2
d
2
x x x
x
xe x e e C
.
Câu 14. Khối đa diện nào có số đỉnh nhiều nhất?
A. Khối nhị thập diện đều (
20
mặt đều). B. Khối bát diện đều (
8
mặt đều).
C. Khối thập nhị diện đều (
12
mặt đều). D. Khối tứ diện đều.
Câu 15. Họ nguyên hàm của hàm số
1
5 4
f x
x
là
A.
1
ln 5 4
ln 5
x C
. B.
ln 5 4
x C
. C.
1
ln 5 4
5
x C
. D.
1
ln 5 4
5
x C
.
Câu 16. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
SA
vuông góc với mặt phẳng
ABC
và
2, 4, 5AB AC SA
. Mặt cầu đi qua các đỉnh của hình chóp
.S ABC
có bán kính là
A.
5
2
R
. B.
5R
. C.
10
3
R
. D.
25
2
R
.
Câu 17. Số đường tiệm cận của đồ thị hàm số
2
2
1
2
x x
y
x x
là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 18. Cho khối nón có bán kính đáy
3r
và chiều cao
4h
. Tính thể tích
V
của khối nón đã cho.
A.
12V
. B.
4V
. C.
4V
. D.
12V
.
Câu 19. Tìm tập xác định
D
của hàm số
2 3
2
3 4y x x
.
A.
\ 1;4
D
. B.
D
.
5
3
1
2
1
y
x
O
Trang 3/7 - Mã đề 101 - https://toanmath.com/
C.
; 1 4;D
 
. D.
; 1 4;D
 
.
Câu 20. Cho
a
là số thực dương khác
5
. Tính
3
5
log
125
a
a
I
.
A.
1
3
I
. B.
3I
. C.
1
3
I
. D.
3I
.
Câu 21. Cho
0a
,
0b
, giá trị của biểu thức
1
2
2
1
1
2
1
2 . . 1
4
a b
T a b ab
b a
bằng
A.
1
. B.
1
3
. C.
2
3
. D.
1
2
.
Câu 22. Cho
a
,
b
,
c
dương và khác
1
. Các hàm số
log
a
y x
,
log
b
y x
,
log
c
y x
có đồ thị như hình
vẽ
Khẳng định nào dưới đây đúng?
A.
b c a
. B.
a b c
. C.
a c b
. D.
c b a
.
Câu 23. Tập xác định của hàm số
2 siny x
là
A.
0;2
. B.
2;2
. C.
. D.
1;1
.
Câu 24. Cho
0a
,
0b
thỏa mãn
2 2
4 5a b ab
. Khẳng định nào sau đây đúng?
A.
2 log 2 5 log loga b a b
. B.
log 1 log 1
a b
.
C.
2 log log
log
3 2
a b a b
. D.
5 log 2 log loga b a b
.
Câu 25. Cho tập
A
có
26
phần tử. Hỏi
A
có bao nhiêu tập con gồm
6
phần tử?
A.
6
26
A
. B.
26
. C.
6
P
. D.
6
26
C
.
Câu 26. Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
A.
1
. B.
1
3
. C.
2
3
.
D.
1
2
.
Câu 27. Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0
x x
là
A.
11
3;
2
S
. B.
;4
S

.
y = log
b
x
y = log
c
x
1
y = log
a
x
y
x
O
2
-2
-2
-1
21
y
x
O
Trang 4/7 - Mã đề 101 - https://toanmath.com/
C.
1; 4
S
. D.
1;4
S
.
Câu 28. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Mệnh đề nào sau đây SAI?
A. Hàm số
y f x
có hai điểm cực trị.
B. Nếu
2
m
thì phương trình
f x m
có nghiệm duy nhất.
C. Hàm số
y f x
có cực tiểu bằng
1
.
D. Giá trị lớn nhất của hàm số
y f x
trên đoạn
2;2
bằng
2
.
Câu 29. Cho hàm số
2
x
f x x e
. Tìm một nguyên hàm
F x
của hàm số
f x
thỏa mãn
0 2019
F
.
A.
2019
x
F x e
. B.
2
2018
x
F x x e
.
C.
2
2017
x
F x x e
. D.
2
2018
x
F x x e
.
Câu 30. Tập tất cả giá trị của tham số
m
để hàm số
3 2
3 3 1y x mx x
đồng biến trên
là
A.
1;1
. B.
; 1 1;m

.
C.
; 1 1;

. D.
1;1
.
Câu 31. Cho
a
,
b
là các số dương thỏa mãn
9 16 12
5
log log log
2
b a
a b
. Tính giá trị
a
b
.
A.
3 6
4
a
b
. B.
7 2 6
a
b
. C.
7 2 6
a
b
. D.
3 6
4
a
b
.
Câu 32. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và
60ABC
. Hình chiếu vuông
góc của điểm
S
lên mặt phẳng
ABCD
trùng với trọng tâm tam giác
ABC
. Gọi
là góc giữa đường
thẳng
SB
với mặt phẳng
SCD
, tính
sin
biết rằng
SB a
.
A.
1
sin
4
. B.
1
sin
2
. C.
3
sin
2
. D.
2
sin
2
.
Câu 33. Cho hàm số
y f x
liên tục trên
và có đạo hàm
2 2
2 6
f x x x x x m
với mọi
x
. Có bao nhiêu số nguyên
m
thuộc đoạn
2019;2019
để hàm số
1
g x f x
nghịch biến trên
khoảng
; 1
?
A.
2010
. B.
2012
. C.
2011
. D.
2009
.
Câu 34. Cho hình chóp
.S ABC
có
4, 2, 4 3
AB AC BC SA
,
30ºSAB SAC
. Tính thể
tích khối chóp
. .S ABC
A.
.
8
S ABC
V
. B.
.
6
S ABC
V
. C.
.
4
S ABC
V
. D.
.
12
S ABC
V
.
Câu 35. Cho hàm số
y f x
có bảng biến thiên như sau
Trang 5/7 - Mã đề 101 - https://toanmath.com/
Giá trị lớn nhất của
m
để phương trình
3 2
13 3
2 7
2 2
f x f x f x
e m
có nghiệm trên đoạn
0;2
là
A.
4
e
. B.
3
e
. C.
15
13
e
. D.
5
e
.
Câu 36. Cho phương trình
2
2 sin 1 3 tan 2 sin 3 4 cosx x x x
. Tổng tất cả các nghiệm thuộc
đoạn
0;20
của phương trình bằng
A.
1150
3
. B.
570
3
. C.
880
3
. D.
875
3
.
Câu 37. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
3AB a
,
2BC a
, đường thẳng
AC
tạo với mặt phẳng
BCC B
một góc
30
. Diện tích của mặt cầu ngoại tiếp
hình lăng trụ đã cho bằng
A.
2
6 a
. B.
2
3 a
. C.
2
4 a
. D.
2
24 a
.
Câu 38. Cho hàm số
f x
liên tục trên
thỏa mãn các điều kiện:
0 2 2
f
,
0,f x x
và
2
. 2 1 1 ,f x f x x f x x
. Khi đó giá trị
1f
bằng
A.
15
. B.
23
. C.
24
. D.
26
.
Câu 39. Cho hình chóp
.S ABCD
có
SA
vuông góc với mặt phẳng
ABCD
; tứ giác
ABCD
là hình thang
vuông với cạnh đáy
,AD BC
;
3 3 , , 3AD BC a AB a SA a
. Điểm
I
thỏa mãn
3AD AI
 
;
M
là trung điểm
SD
,
H
là giao điểm của
AM
và
SI
. Gọi
E
,
F
lần lượt là hình chiếu của
A
lên
SB
,
Tính thể tích
V
của khối nón có đáy là đường tròn ngoại tiếp tam giác
EFH
và đỉnh thuộc mặt phẳng
ABCD
.
A.
3
2 5
a
V
. B.
3
5
a
V
. C.
3
10 5
a
V
. D.
3
5 5
a
V
.
Câu 40. Cho phương trình
2
ln 1 2 ln 1 2 0
m x x m x x
1
. Tập tất cả giá trị của
tham số
m
để phương trình
1
có hai nghiệm phân biệt thỏa mãn
1 2
0 2 4x x
là khoảng
;a

.
Khi đó,
a
thuộc khoảng
A.
3, 8;3,9
. B.
3,7;3, 8
. C.
3,6;3,7
. D.
3,5;3,6
.
Câu 41. Cho hàm số
4 2
2 2y x x m
có đồ thị
C
. Gọi
S
là tập các giá trị của
m
sao cho đồ thị
C
có đúng một tiếp tuyến song song với trục
.Ox
Tổng tất cả các phần tử của
S
là
A.
3
. B.
8
. C.
5
. D.
2
.
Câu 42. Cho hai số thực
,x y
thỏa mãn
2 2 2 2
4 6 4 6 10 6 4x y x y y y x x
. Gọi
Trang 6/7 - Mã đề 101 - https://toanmath.com/
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
2 2
T x y a
. Có bao nhiêu giá trị
nguyên thuộc đoạn
10;10
của tham số
a
để
2M m
?
A.
17
. B.
16
. C.
15
. D.
18
.
Câu 43. Cho hình chóp
.O ABC
có ba cạnh
, ,OA OB OC
đôi một vuông góc và
OA OB OC a
. Gọi
M
là trung điểm cạnh
. Góc hợp bởi hai véc tơ
và
OM

bằng
A.
120º
. B.
150º
. C.
135º
. D.
60º
.
Câu 44. Cho số nguyên dương
n
thỏa mãn điều kiện
7 7 7 10
7 8 1
1
720 ....
4032
n n
C C C A
. Hệ số của
7
x
trong khai triển
2
1
0
n
x x
x
bằng
A.
560
. B.
120
C.
560
. D.
120
.
Câu 45. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
x m
y
x m
trên đoạn
0; 4
bằng
1.
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 46. Cho hàm số
3 2 2
3
3 2 1
x
y
x mx m x m
. Có bao nhiêu giá trị nguyên thuộc đoạn
6;6
của tham số
m
để đồ thị hàm số có bốn đường tiệm cận?
A.
12
. B.
9
. C.
8
. D.
11
.
Câu 47. Tập nghiệm của bất phương trình
2 2 2
2
log 2 4 2 2 1
x x x x x
là
;
a b
.
Khi đó
ab
bằng
A. . B. . C. . D. .
Câu 48. Cho tứ diện
SABC
và
G
là trọng tâm của tứ diện, mặt phẳng quay quanh
AG
và cắt các cạnh
,SB SC
tương ứng tại
,M N
. Giá trị nhỏ nhất của tỉ số
.
.
S AMN
S ABC
V
V
là
A.
1
2
. B.
1
3
. C.
3
8
. D.
4
9
.
Câu 49. Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là
12 cm
. Giá
trị lớn nhất của thể tích khối trụ là
A.
32
3
cm
. B.
64
3
cm
. C.
8
3
cm
. D.
3
cm
.
Câu 50. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ.
12
5
5
12
15
16
16
15
Trang 7/7 - Mã đề 101 - https://toanmath.com/
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3 sin cos 1
4 4
2 cos sin 4
x x
f f m m
x x
có
nghiệm?
A.
4
. B.
5
. C. Vô số. D.
3
.
------ HẾT ------
Trang 1/7 - Mã đề 101 - https://toanmath.com/
SỞ GDĐT BẮC NINH
PHÒNG QUẢN LÝ CHẤT LƯỢNG
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
ĐỀ TẬP HUẤN THI THPT QUỐC GIA NĂM 2019
Bài thi: Toán
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề có 50 câu trắc nghiệm)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Họ và tên thí sinh:..................................................... Số báo danh :...................
Câu 1. Số giao điểm của đồ thị hàm số
4 2
5 4y x x
với trục hoành là
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 2. Hàm số nào sau đây không có điểm cực trị?
A.
3
3 1y x x
. B.
2
2y x x
. C.
4 2
4 1y x x
. D.
3
3 1y x x
.
Câu 3. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật
ABCD
có
và
CD
thuộc hai đáy của hình trụ,
4AB a
,
5AC a
. Thể tích khối trụ là
A.
3
16V a
. B.
3
4V a
. C.
3
12V a
. D.
3
8V a
.
Câu 4. Cho hình chóp
.S ABC
có
SA
vuông góc với đáy. Tam giác
ABC
vuông cân tại
B
, biết
2SA AC a
. Thể tích khối chóp
.S ABC
là
A.
3
.
2
.
3
S ABC
V a
B.
3
.
3
S ABC
a
V
. C.
3
.
2
S ABC
V a
. D.
3
.
4
3
S ABC
a
V
.
Câu 5. Cho
,k n
( )k n
là các số nguyên dương. Mệnh đề nào sau đây SAI?
A.
k n k
n n
C C
. B.
!
!.( )!
k
n
n
C
k n k
. C.
!.
k k
n n
A k C
. D.
!.
k k
n n
A n C
.
Câu 6. Cho hình lăng trụ
.ABC A B C
có thể tích bằng
V
. Gọi
M
là trung điểm cạnh
BB
, điểm
N
thuộc cạnh
CC
sao cho
2CN C N
. Tính thể tích khối chóp
.A BCNM
theo
V
.
A.
.
7
12
A BCNM
V
V
. B.
.
7
18
A BCNM
V
V
. C.
.
3
A BCNM
V
V
. D.
.
5
18
A BCNM
V
V
.
Câu 7. Cho hàm số
3
3 1y x x
. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho nghịch biến trên khoảng
1;3
.
B. Hàm số đã cho đồng biến trên khoảng
1;1
.
C. Hàm số đã cho đồng biến trên khoảng
; 1
và khoảng
1;
.
D. Hàm số đã cho nghịch biến trên khoảng
2;1
.
Câu 8. Cho tứ diện
ABCD
, gọi
1 2
,G G
lần lượt là trọng tâm các tam giác
BCD
và
ACD
. Mệnh đề nào sau
đây SAI?
A.
1 2
/ /
G G ABD
. B.
1 2
/ /
G G ABC
.
C.
1 2
2
3
G G AB
. D. Ba đường thẳng
1 2
,BG AG
và
CD
đồng quy.
Câu 9. Tìm họ nguyên hàm của hàm số
3
2 1
x
f x x e
.
Mã đề 101
Trang 2/7 - Mã đề 101 - https://toanmath.com/
A.
3
1
d
x
f x x e C
. B.
3
1
d 3
x
f x x e C
.
C.
3
1
1
d
3
x
f x x e C
. D.
3
3
1
d
3
x
x
f x x e C
.
Câu 10. Phương trình
2
2 5 4
7 49
x x
có tổng tất cả các nghiệm bằng
A.
1
. B.
5
2
.
C.
1
. D.
5
2
.
Câu 11. Đường cong như hình vẽ là đồ thị của hàm số nào?
A.
3 2
3 5y x x
. B.
3 2
2 6 5y x x
.
C.
3 2
3 5y x x
. D.
3
3 5y x x
.
Câu 12. Cho hình chóp đều
.S ABCD
có cạnh
AB a
, góc giữa đường thẳng
SA
và mặt phẳng
ABC
bằng
45º
. Thể tích khối chóp
.S ABCD
là
A.
3
3
a
. B.
3
2
6
a
.
C.
3
6
a
. D.
3
2
3
a
.
Câu 13. Mệnh đề nào sau đây đúng?
A.
d
x x x
xe x e xe C
. B.
d
x x x
xe x xe e C
.
C.
2
d
2
x x
x
xe x e C
. D.
2
d
2
x x x
x
xe x e e C
.
Câu 14. Khối đa diện nào có số đỉnh nhiều nhất?
A. Khối nhị thập diện đều (
20
mặt đều). B. Khối bát diện đều (
8
mặt đều).
C. Khối thập nhị diện đều (
12
mặt đều). D. Khối tứ diện đều.
Câu 15. Họ nguyên hàm của hàm số
1
5 4
f x
x
là
A.
1
ln 5 4
ln 5
x C
. B.
ln 5 4
x C
. C.
1
ln 5 4
5
x C
. D.
1
ln 5 4
5
x C
.
Câu 16. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
A
,
SA
vuông góc với mặt phẳng
ABC
và
2, 4, 5AB AC SA
. Mặt cầu đi qua các đỉnh của hình chóp
.S ABC
có bán kính là
A.
5
2
R
. B.
5R
. C.
10
3
R
. D.
25
2
R
.
Câu 17. Số đường tiệm cận của đồ thị hàm số
2
2
1
2
x x
y
x x
là
A.
4
. B.
1
. C.
3
. D.
2
.
Câu 18. Cho khối nón có bán kính đáy
3r
và chiều cao
4h
. Tính thể tích
V
của khối nón đã cho.
A.
12V
. B.
4V
. C.
4V
. D.
12V
.
Câu 19. Tìm tập xác định
D
của hàm số
2 3
2
3 4y x x
.
A.
\ 1;4
D
. B.
D
.
5
3
1
2
1
y
x
O
Trang 3/7 - Mã đề 101 - https://toanmath.com/
C.
; 1 4;D
 
. D.
; 1 4;D
 
.
Câu 20. Cho
a
là số thực dương khác
5
. Tính
3
5
log
125
a
a
I
.
A.
1
3
I
. B.
3I
. C.
1
3
I
. D.
3I
.
Câu 21. Cho
0a
,
0b
, giá trị của biểu thức
1
2
2
1
1
2
1
2 . . 1
4
a b
T a b ab
b a
bằng
A.
1
. B.
1
3
. C.
2
3
. D.
1
2
.
Câu 22. Cho
a
,
b
,
c
dương và khác
1
. Các hàm số
log
a
y x
,
log
b
y x
,
log
c
y x
có đồ thị như hình
vẽ
Khẳng định nào dưới đây đúng?
A.
b c a
. B.
a b c
. C.
a c b
. D.
c b a
.
Câu 23. Tập xác định của hàm số
2 siny x
là
A.
0;2
. B.
2;2
. C.
. D.
1;1
.
Câu 24. Cho
0a
,
0b
thỏa mãn
2 2
4 5a b ab
. Khẳng định nào sau đây đúng?
A.
2 log 2 5 log loga b a b
. B.
log 1 log 1
a b
.
C.
2 log log
log
3 2
a b a b
. D.
5 log 2 log loga b a b
.
Câu 25. Cho tập
A
có
26
phần tử. Hỏi
A
có bao nhiêu tập con gồm
6
phần tử?
A.
6
26
A
. B.
26
. C.
6
P
. D.
6
26
C
.
Câu 26. Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
A.
1
. B.
1
3
. C.
2
3
.
D.
1
2
.
Câu 27. Tập nghiệm của bất phương trình
1 3
3
log 1 log 11 2 0
x x
là
A.
11
3;
2
S
. B.
;4
S

.
y = log
b
x
y = log
c
x
1
y = log
a
x
y
x
O
2
-2
-2
-1
21
y
x
O
Trang 4/7 - Mã đề 101 - https://toanmath.com/
C.
1; 4
S
. D.
1;4
S
.
Câu 28. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Mệnh đề nào sau đây SAI?
A. Hàm số
y f x
có hai điểm cực trị.
B. Nếu
2
m
thì phương trình
f x m
có nghiệm duy nhất.
C. Hàm số
y f x
có cực tiểu bằng
1
.
D. Giá trị lớn nhất của hàm số
y f x
trên đoạn
2;2
bằng
2
.
Câu 29. Cho hàm số
2
x
f x x e
. Tìm một nguyên hàm
F x
của hàm số
f x
thỏa mãn
0 2019
F
.
A.
2019
x
F x e
. B.
2
2018
x
F x x e
.
C.
2
2017
x
F x x e
. D.
2
2018
x
F x x e
.
Câu 30. Tập tất cả giá trị của tham số
m
để hàm số
3 2
3 3 1y x mx x
đồng biến trên
là
A.
1;1
. B.
; 1 1;m

.
C.
; 1 1;

. D.
1;1
.
Câu 31. Cho
a
,
b
là các số dương thỏa mãn
9 16 12
5
log log log
2
b a
a b
. Tính giá trị
a
b
.
A.
3 6
4
a
b
. B.
7 2 6
a
b
. C.
7 2 6
a
b
. D.
3 6
4
a
b
.
Câu 32. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi cạnh
a
và
60ABC
. Hình chiếu vuông
góc của điểm
S
lên mặt phẳng
ABCD
trùng với trọng tâm tam giác
ABC
. Gọi
là góc giữa đường
thẳng
SB
với mặt phẳng
SCD
, tính
sin
biết rằng
SB a
.
A.
1
sin
4
. B.
1
sin
2
. C.
3
sin
2
. D.
2
sin
2
.
Câu 33. Cho hàm số
y f x
liên tục trên
và có đạo hàm
2 2
2 6
f x x x x x m
với mọi
x
. Có bao nhiêu số nguyên
m
thuộc đoạn
2019;2019
để hàm số
1
g x f x
nghịch biến trên
khoảng
; 1
?
A.
2010
. B.
2012
. C.
2011
. D.
2009
.
Câu 34. Cho hình chóp
.S ABC
có
4, 2, 4 3
AB AC BC SA
,
30ºSAB SAC
. Tính thể
tích khối chóp
. .S ABC
A.
.
8
S ABC
V
. B.
.
6
S ABC
V
. C.
.
4
S ABC
V
. D.
.
12
S ABC
V
.
Câu 35. Cho hàm số
y f x
có bảng biến thiên như sau
Trang 5/7 - Mã đề 101 - https://toanmath.com/
Giá trị lớn nhất của
m
để phương trình
3 2
13 3
2 7
2 2
f x f x f x
e m
có nghiệm trên đoạn
0;2
là
A.
4
e
. B.
3
e
. C.
15
13
e
. D.
5
e
.
Câu 36. Cho phương trình
2
2 sin 1 3 tan 2 sin 3 4 cosx x x x
. Tổng tất cả các nghiệm thuộc
đoạn
0;20
của phương trình bằng
A.
1150
3
. B.
570
3
. C.
880
3
. D.
875
3
.
Câu 37. Cho hình lăng trụ đứng
.ABC A B C
có đáy
ABC
là tam giác vuông tại
A
,
3AB a
,
2BC a
, đường thẳng
AC
tạo với mặt phẳng
BCC B
một góc
30
. Diện tích của mặt cầu ngoại tiếp
hình lăng trụ đã cho bằng
A.
2
6 a
. B.
2
3 a
. C.
2
4 a
. D.
2
24 a
.
Câu 38. Cho hàm số
f x
liên tục trên
thỏa mãn các điều kiện:
0 2 2
f
,
0,f x x
và
2
. 2 1 1 ,f x f x x f x x
. Khi đó giá trị
1f
bằng
A.
15
. B.
23
. C.
24
. D.
26
.
Câu 39. Cho hình chóp
.S ABCD
có
SA
vuông góc với mặt phẳng
ABCD
; tứ giác
ABCD
là hình thang
vuông với cạnh đáy
,AD BC
;
3 3 , , 3AD BC a AB a SA a
. Điểm
I
thỏa mãn
3AD AI
 
;
M
là trung điểm
SD
,
H
là giao điểm của
AM
và
SI
. Gọi
E
,
F
lần lượt là hình chiếu của
A
lên
SB
,
Tính thể tích
V
của khối nón có đáy là đường tròn ngoại tiếp tam giác
EFH
và đỉnh thuộc mặt phẳng
ABCD
.
A.
3
2 5
a
V
. B.
3
5
a
V
. C.
3
10 5
a
V
. D.
3
5 5
a
V
.
Câu 40. Cho phương trình
2
ln 1 2 ln 1 2 0
m x x m x x
1
. Tập tất cả giá trị của
tham số
m
để phương trình
1
có hai nghiệm phân biệt thỏa mãn
1 2
0 2 4x x
là khoảng
;a

.
Khi đó,
a
thuộc khoảng
A.
3, 8;3,9
. B.
3,7;3, 8
. C.
3,6;3,7
. D.
3,5;3,6
.
Câu 41. Cho hàm số
4 2
2 2y x x m
có đồ thị
C
. Gọi
S
là tập các giá trị của
m
sao cho đồ thị
C
có đúng một tiếp tuyến song song với trục
.Ox
Tổng tất cả các phần tử của
S
là
A.
3
. B.
8
. C.
5
. D.
2
.
Câu 42. Cho hai số thực
,x y
thỏa mãn
2 2 2 2
4 6 4 6 10 6 4x y x y y y x x
. Gọi
Trang 6/7 - Mã đề 101 - https://toanmath.com/
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
2 2
T x y a
. Có bao nhiêu giá trị
nguyên thuộc đoạn
10;10
của tham số
a
để
2M m
?
A.
17
. B.
16
. C.
15
. D.
18
.
Câu 43. Cho hình chóp
.O ABC
có ba cạnh
, ,OA OB OC
đôi một vuông góc và
OA OB OC a
. Gọi
M
là trung điểm cạnh
. Góc hợp bởi hai véc tơ
và
OM

bằng
A.
120º
. B.
150º
. C.
135º
. D.
60º
.
Câu 44. Cho số nguyên dương
n
thỏa mãn điều kiện
7 7 7 10
7 8 1
1
720 ....
4032
n n
C C C A
. Hệ số của
7
x
trong khai triển
2
1
0
n
x x
x
bằng
A.
560
. B.
120
C.
560
. D.
120
.
Câu 45. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
x m
y
x m
trên đoạn
0; 4
bằng
1.
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 46. Cho hàm số
3 2 2
3
3 2 1
x
y
x mx m x m
. Có bao nhiêu giá trị nguyên thuộc đoạn
6;6
của tham số
m
để đồ thị hàm số có bốn đường tiệm cận?
A.
12
. B.
9
. C.
8
. D.
11
.
Câu 47. Tập nghiệm của bất phương trình
2 2 2
2
log 2 4 2 2 1
x x x x x
là
;
a b
.
Khi đó
ab
bằng
A. . B. . C. . D. .
Câu 48. Cho tứ diện
SABC
và
G
là trọng tâm của tứ diện, mặt phẳng quay quanh
AG
và cắt các cạnh
,SB SC
tương ứng tại
,M N
. Giá trị nhỏ nhất của tỉ số
.
.
S AMN
S ABC
V
V
là
A.
1
2
. B.
1
3
. C.
3
8
. D.
4
9
.
Câu 49. Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là
12 cm
. Giá
trị lớn nhất của thể tích khối trụ là
A.
32
3
cm
. B.
64
3
cm
. C.
8
3
cm
. D.
3
cm
.
Câu 50. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ.
12
5
5
12
15
16
16
15
Trang 7/7 - Mã đề 101 - https://toanmath.com/
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
3 sin cos 1
4 4
2 cos sin 4
x x
f f m m
x x
có
nghiệm?
A.
4
. B.
5
. C. Vô số. D.
3
.
------ HẾT ------
| 1/14
| | Tải xuống

Có thể bạn quan tâm:

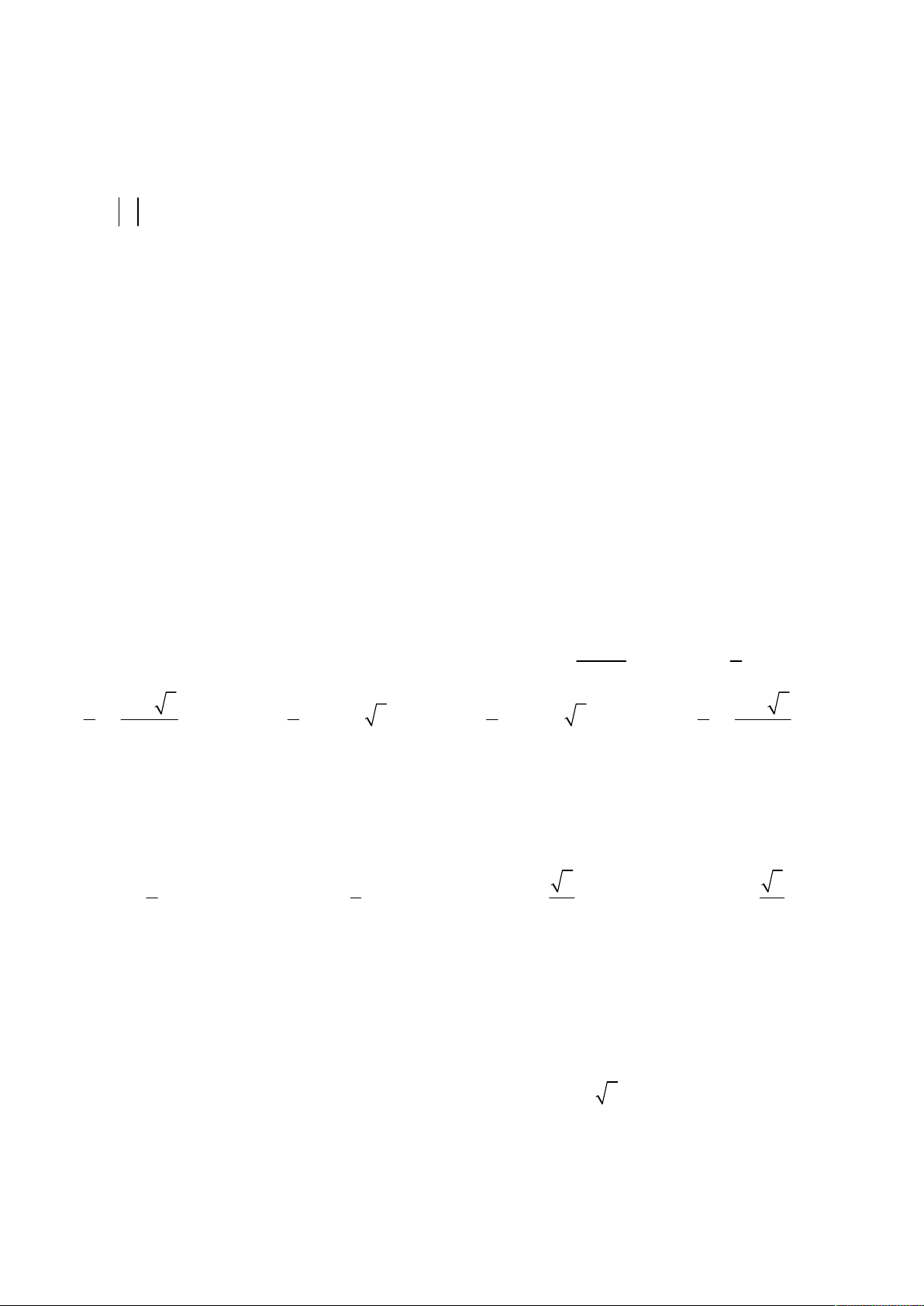
Preview text:

SỞ GDĐT BẮC NINH
ĐỀ TẬP HUẤN THI THPT QUỐC GIA NĂM 2019
PHÒNG QUẢN LÝ CHẤT LƯỢNG Bài thi: Toán
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề có 50 câu trắc nghiệm)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Họ và tên thí sinh:..................................................... Số báo danh :................... Mã đề 101
Câu 1. Số giao điểm của đồ thị hàm số 4 2
y x  5x  4 với trục hoành là A. 3 . B. 2 . C. 4 . D. 1.
Câu 2. Hàm số nào sau đây không có điểm cực trị? A. 3
y x  3x  1 . B. 2
y x  2x . C. 4 2
y x  4x  1 . D. 3
y x  3x  1.
Câu 3. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD
thuộc hai đáy của hình trụ, AB  4a , AC  5a . Thể tích khối trụ là A. 3 V  16 a . B. 3 V  4 a . C. 3 V  12 a . D. 3 V  8 a .
Câu 4. Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B , biết
SA AC  2a . Thể tích khối chóp S.ABC là 2 3 a 3 4a A. 3 Va . B. V  . C. 3 V  2a . D. V  . S .ABC 3 S .ABC 3 S .ABC S .ABC 3
Câu 5. Cho k, n (k n) là các số nguyên dương. Mệnh đề nào sau đây SAI? n k ! A. k n k C C   . B. C  . C. k
A k !. k C . D. k
A n !. k C . n n n
k !.(n k)! n n n n
Câu 6. Cho hình lăng trụ ABC .AB C
  có thể tích bằng V . Gọi M là trung điểm cạnh BB , điểm N
thuộc cạnh CC  sao cho CN  2C N
 . Tính thể tích khối chóp .
A BCNM theo V . 7V 7V V 5V A. V  . B. V  . C. V  . D. V  . . A BCNM 12 . A BCNM 18 . A BCNM 3 . A BCNM 18 Câu 7. Cho hàm số 3
y x  3x  1. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho nghịch biến trên khoảng 1;  3 .
B. Hàm số đã cho đồng biến trên khoảng  1  ;  1 .
C. Hàm số đã cho đồng biến trên khoảng  ;    1 và khoảng 1;   .
D. Hàm số đã cho nghịch biến trên khoảng 2;  1 .
Câu 8. Cho tứ diện ABCD , gọi G ,G lần lượt là trọng tâm các tam giác BCD và ACD . Mệnh đề nào sau 1 2 đây SAI?
A. G G / / ABD .
B. G G / / ABC . 1 2   1 2   2 C. G G AB .
D. Ba đường thẳng BG , AG và CD đồng quy. 1 2 3 1 2
Câu 9. Tìm họ nguyên hàm của hàm số f x  3 2 x 1 x e   .
Trang 1/7 - Mã đề 101 - https://toanmath.com/   A.    3 1 d x f x x eC . B.    3 1 d  3 x f x x eC . 1 3 x C. f  x 3 x 1 dx e   C . D. f  x 3 x 1 dx e   C . 3 3 2
Câu 10. Phương trình 2x 5  x 4 7
 49 có tổng tất cả các nghiệm bằng y 5 5 A. 1. B. . 2 5 C. 1 . D.  . 2 3
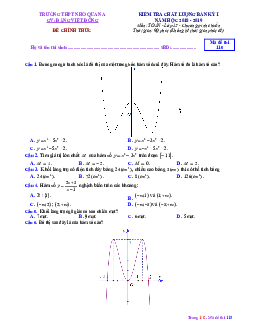
Câu 11. Đường cong như hình vẽ là đồ thị của hàm số nào? A. 3 2 y x   3x  5 . B. 3 2
y  2x  6x  5 . 1 C. 3 2
y x  3x  5 . D. 3
y x  3x  5 .
Câu 12. Cho hình chóp đều S.ABCD có cạnh AB a , góc giữa đường thẳng O 1 2 x
SA và mặt phẳng ABC  bằng 45º . Thể tích khối chóp S.ABCD là 3 a 3 a 2 A. . B. . 3 6 3 a 3 a 2 C. . D. . 6 3
Câu 13. Mệnh đề nào sau đây đúng? A. x d x x
xe x e xe C  . B. x d x x
xe x xe e C  . 2 x 2 x C. x xe d x x e C  . D. x xe d x x x
e e C  . 2 2
Câu 14. Khối đa diện nào có số đỉnh nhiều nhất?
A. Khối nhị thập diện đều ( 20 mặt đều).
B. Khối bát diện đều ( 8 mặt đều).
C. Khối thập nhị diện đều (12 mặt đều). D. Khối tứ diện đều.
Câu 15. Họ nguyên hàm của hàm số f x  1  là 5x  4 1 1 1 A.
ln 5x  4 C .
B. ln 5x  4  C . C.
ln 5x  4 C . D.
ln 5x  4 C . ln 5 5 5
Câu 16. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , SA vuông góc với mặt phẳng
ABCvà AB  2,AC  4,SA  5 . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là 5 10 25 A. R  . B. R  5 . C. R  . D. R  . 2 3 2 2 x x  1
Câu 17. Số đường tiệm cận của đồ thị hàm số y  là 2 x x  2 A. 4 . B. 1. C. 3 . D. 2 .
Câu 18. Cho khối nón có bán kính đáy r
3 và chiều cao h  4 . Tính thể tích V của khối nón đã cho.
A. V  12. B. V  4. C. V  4 . D. V  12 . 
Câu 19. Tìm tập xác định D của hàm số y  x x   2 3 2 3 4 . A. D   \  1  ;4 . B. D   .
Trang 2/7 - Mã đề 101 - https://toanmath.com/ C. D   ;    1  4;. D. D  ; 1      4;     .  3 a   
Câu 20. Cho a là số thực dương khác 5 . Tính I  log  . a   125 5 1 1 A. I   . B. I  3  . C. I  . D. I  3 . 3 3 1  2  2 1   1  1  a b  
Câu 21. Cho a  0 , b  0 , giá trị của biểu thức T  2a b .ab2 . 1          bằng 4  b a         1 2 1 A. 1. B. . C. . D. . 3 3 2
Câu 22. Cho a , b , c dương và khác 1. Các hàm số y  log x , y  log x , y  log x có đồ thị như hình a b c vẽ y y = log x a O 1 x y = log x b y = log x c
Khẳng định nào dưới đây đúng?
A. b c a .
B. a b c .
C. a c b .
D. c b a .
Câu 23. Tập xác định của hàm số y  2 sin x là       A. 0; 2       . B. 2;2     . C.  . D. 1;1     .
Câu 24. Cho a  0 , b  0 thỏa mãn 2 2
a  4b  5ab . Khẳng định nào sau đây đúng?
A. 2 loga  2b  5loga  logb. B. loga   1  logb  1 . a  2b loga  logb C. log  .
D. 5 log a  2b  loga  logb . 3 2
Câu 25. Cho tập A có 26 phần tử. Hỏi A có bao nhiêu tập con gồm 6 phần tử? A. 6 A . B. 26 . C. P . D. 6 C . 26 6 26
Câu 26. Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là 1 2 A. 1. B. . C. . 3 3 y 1 D. . 2 2
Câu 27. Tập nghiệm của bất phương trình log
x  1  log 11  2x  0 là 1   3   3  x 11   A. S  3;  -2 -1 O 1 2  S     . B.  ;4  2   . -2
Trang 3/7 - Mã đề 101 - https://toanmath.com/ C. S 1;4   . D. S  1;4.
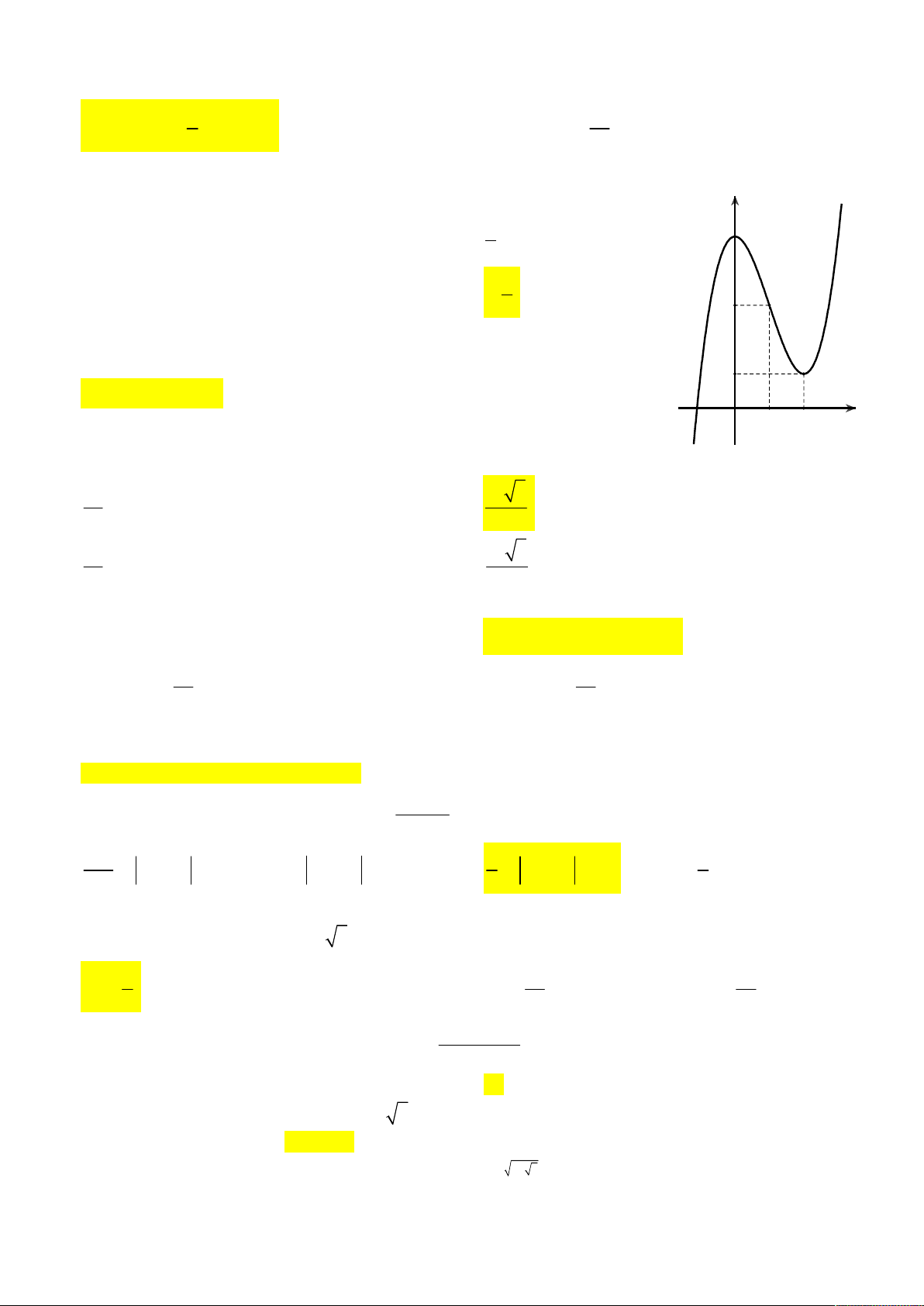
Câu 28. Cho hàm số y f x  liên tục trên  và có đồ thị như hình vẽ. Mệnh đề nào sau đây SAI?
A. Hàm số y f x  có hai điểm cực trị.
B. Nếu m  2 thì phương trình f x   m có nghiệm duy nhất.
C. Hàm số y f x  có cực tiểu bằng 1 .  
D. Giá trị lớn nhất của hàm số y f x  trên đoạn 2  ;2     bằng 2 . Câu 29. Cho hàm số    2 x f x
x e . Tìm một nguyên hàm F x của hàm số f x thỏa mãn F 0  2019 . A.   x
F x e  2019 . B.   2 x
F x x e  2018 . C.   2 x
F x x e  2017 . D.   2 x
F x x e  2018 .
Câu 30. Tập tất cả giá trị của tham số m để hàm số 3 2
y x  3mx  3x  1 đồng biến trên  là     A. 1;1          . B. m  ; 1 1;     . C.  ;    1  1;   . D.  1  ;  1 . 5b a a
Câu 31. Cho a , b là các số dương thỏa mãn log a  log b  log . Tính giá trị . 9 16 12 2 b a 3  6 a a a 3  6 A.  . B.  7  2 6 . C.  7  2 6 . D.  . b 4 b b b 4 
Câu 32. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ABC  60 . Hình chiếu vuông
góc của điểm S lên mặt phẳng ABCD trùng với trọng tâm tam giác ABC . Gọi là góc giữa đường
thẳng SB với mặt phẳng SCD, tính sin biết rằng SB a . 1 1 3 2 A. sin  . B. sin  . C. sin  . D. sin  . 4 2 2 2
Câu 33. Cho hàm số y f x  liên tục trên  và có đạo hàm f x  2
x x   2
2 x  6x m với mọi x    
. Có bao nhiêu số nguyên m thuộc đoạn 2019;2019     
 để hàm số g x
f 1 x nghịch biến trên khoảng  ;    1 ? A. 2010 . B. 2012 . C. 2011 . D. 2009 .  
Câu 34. Cho hình chóp S.ABC có AB AC  4,BC  2,SA  4 3 , SAB SAC  30º . Tính thể
tích khối chóp S.ABC . A. V  8 . B. V  6 . C. V  4 . D. V  12 . S .ABC S .ABC S .ABC S .ABC
Câu 35. Cho hàm số y f x  có bảng biến thiên như sau
Trang 4/7 - Mã đề 101 - https://toanmath.com/ 3 f x 13 2 
f x fx  3 2 7   
Giá trị lớn nhất của m để phương trình 2 2 e
m có nghiệm trên đoạn 0;2     là 15 A. 4 e . B. 3 e . C. 13 e . D. 5 e .
Câu 36. Cho phương trình  x   x x 2 2 sin 1 3 tan 2 sin
 3  4 cos x . Tổng tất cả các nghiệm thuộc   đoạn 0;20   
 của phương trình bằng 1150 570 880 875 A. . B. . C. . D. . 3 3 3 3
Câu 37. Cho hình lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông tại A , AB a 3 ,
BC  2a , đường thẳng AC  tạo với mặt phẳng BCC B
  một góc 30. Diện tích của mặt cầu ngoại tiếp
hình lăng trụ đã cho bằng A. 2 6 a . B. 2 3 a . C. 2 4 a . D. 2 24 a .
Câu 38. Cho hàm số f x  liên tục trên  thỏa mãn các điều kiện: f 0  2 2 , f x   0, x    và
f xf x   x   2 . 2
1 1  f x, x   . Khi đó giá trị f   1 bằng A. 15 . B. 23 . C. 24 . D. 26 .
Câu 39. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD; tứ giác ABCD là hình thang   vuông với cạnh đáy ,
AD BC ; AD  3BC  3 , a AB  ,
a SA a 3 . Điểm I thỏa mãn AD  3AI ; M
là trung điểm SD , H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , SC .
Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng ABCD. 3 a 3 a 3 a 3 a A. V  . B. V  . C. V  . D. V  . 2 5 5 10 5 5 5 Câu 40. Cho phương trình 2
m ln x  
1  x  2  mlnx  
1  x  2  0  
1 . Tập tất cả giá trị của
tham số m để phương trình  
1 có hai nghiệm phân biệt thỏa mãn 0  x  2  4  x là khoảng a;   . 1 2
Khi đó, a thuộc khoảng A. 3, 8;3,9. B. 3,7;3, 8 . C. 3,6;3,7. D. 3,5;3,  6 . Câu 41. Cho hàm số 4 2
y x  2x m  2 có đồ thị C  . Gọi S là tập các giá trị của m sao cho đồ thị
C có đúng một tiếp tuyến song song với trục Ox. Tổng tất cả các phần tử của S là A. 3 . B. 8 . C. 5 . D. 2 .
Câu 42. Cho hai số thực x,y thỏa mãn 2 2 2 2
x y  4x  6y  4  y  6y  10  6  4x x . Gọi
Trang 5/7 - Mã đề 101 - https://toanmath.com/
M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2 T
x y a . Có bao nhiêu giá trị  
nguyên thuộc đoạn 10;10   M m
 của tham số a để 2 ? A. 17 . B. 16 . C. 15 . D. 18 .
Câu 43. Cho hình chóp O.ABC có ba cạnh , OA ,
OB OC đôi một vuông góc và OA OB OC a . Gọi  
M là trung điểm cạnh AB . Góc hợp bởi hai véc tơ BC và OM bằng A. 120º . B. 150º . C. 135º . D. 60º . 1
Câu 44. Cho số nguyên dương n thỏa mãn điều kiện 720 7 7 7
C C  ....CA . Hệ số của 7 x n  10 7 8 n 1 4032  n  1    trong khai triển x    x  0  bằng 2     x  A. 560 . B. 120 C. 560 . D. 120 . 2 x m  2  
Câu 45. Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y  trên đoạn 0; 4 x m   bằng 1  . A. 3 . B. 2 . C. 1. D. 0 . x  3  
Câu 46. Cho hàm số y
. Có bao nhiêu giá trị nguyên thuộc đoạn 6  ;6 3 2  
x  3mx   2 2m   1 x m  
của tham số m để đồ thị hàm số có bốn đường tiệm cận? A. 12 . B. 9 . C. 8 . D. 11.
Câu 47. Tập nghiệm của bất phương trình log  2 2
x x  2  4  x  2
 2x x  2  1là  a; b   2  . Khi đó ab bằng 12 5 15 16 A. . B. . C. . D. . 5 12 16 15
Câu 48. Cho tứ diện SABC và G là trọng tâm của tứ diện, mặt phẳng quay quanh AG và cắt các cạnh V ,
SB SC tương ứng tại M,N . Giá trị nhỏ nhất của tỉ số S.AMN là VS.ABC 1 1 3 4 A. . B. . C. . D. . 2 3 8 9
Câu 49. Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là 12 cm . Giá
trị lớn nhất của thể tích khối trụ là A. 32 3 cm . B. 64 3 cm . C. 8 3 cm . D. 16 3 cm .
Câu 50. Cho hàm số y f x  liên tục trên  và có đồ thị như hình vẽ.
Trang 6/7 - Mã đề 101 - https://toanmath.com/
 3sinx cosx 1    
Có bao nhiêu giá trị nguyên của tham số m để phương trình f    f    2
m  4m  4 có
 2 cosx  sin x  4  nghiệm? A. 4 . B. 5 . C. Vô số. D. 3 . ------ HẾT ------
Trang 7/7 - Mã đề 101 - https://toanmath.com/ SỞ GDĐT BẮC NINH
ĐỀ TẬP HUẤN THI THPT QUỐC GIA NĂM 2019
PHÒNG QUẢN LÝ CHẤT LƯỢNG Bài thi: Toán
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
(Đề có 50 câu trắc nghiệm)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Họ và tên thí sinh:..................................................... Số báo danh :................... Mã đề 101
Câu 1. Số giao điểm của đồ thị hàm số 4 2
y x  5x  4 với trục hoành là A. 3 . B. 2 . C. 4 . D. 1.
Câu 2. Hàm số nào sau đây không có điểm cực trị? A. 3
y x  3x  1 . B. 2
y x  2x . C. 4 2
y x  4x  1 . D. 3
y x  3x  1.
Câu 3. Cắt khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD
thuộc hai đáy của hình trụ, AB  4a , AC  5a . Thể tích khối trụ là A. 3 V  16 a . B. 3 V  4 a . C. 3 V  12 a . D. 3 V  8 a .
Câu 4. Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B , biết
SA AC  2a . Thể tích khối chóp S.ABC là 2 3 a 3 4a A. 3 Va . B. V  . C. 3 V  2a . D. V  . S .ABC 3 S .ABC 3 S .ABC S .ABC 3
Câu 5. Cho k, n (k n) là các số nguyên dương. Mệnh đề nào sau đây SAI? n k ! A. k n k C C   . B. C  . C. k
A k !. k C . D. k
A n !. k C . n n n
k !.(n k)! n n n n
Câu 6. Cho hình lăng trụ ABC .AB C
  có thể tích bằng V . Gọi M là trung điểm cạnh BB , điểm N
thuộc cạnh CC  sao cho CN  2C N
 . Tính thể tích khối chóp .
A BCNM theo V . 7V 7V V 5V A. V  . B. V  . C. V  . D. V  . . A BCNM 12 . A BCNM 18 . A BCNM 3 . A BCNM 18 Câu 7. Cho hàm số 3
y x  3x  1. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho nghịch biến trên khoảng 1;  3 .
B. Hàm số đã cho đồng biến trên khoảng  1  ;  1 .
C. Hàm số đã cho đồng biến trên khoảng  ;    1 và khoảng 1;   .
D. Hàm số đã cho nghịch biến trên khoảng 2;  1 .
Câu 8. Cho tứ diện ABCD , gọi G ,G lần lượt là trọng tâm các tam giác BCD và ACD . Mệnh đề nào sau 1 2 đây SAI?
A. G G / / ABD .
B. G G / / ABC . 1 2   1 2   2 C. G G AB .
D. Ba đường thẳng BG , AG và CD đồng quy. 1 2 3 1 2
Câu 9. Tìm họ nguyên hàm của hàm số f x  3 2 x 1 x e   .
Trang 1/7 - Mã đề 101 - https://toanmath.com/   A.    3 1 d x f x x eC . B.    3 1 d  3 x f x x eC . 1 3 x C. f  x 3 x 1 dx e   C . D. f  x 3 x 1 dx e   C . 3 3 2
Câu 10. Phương trình 2x 5  x 4 7
 49 có tổng tất cả các nghiệm bằng y 5 5 A. 1. B. . 2 5 C. 1 . D.  . 2 3
Câu 11. Đường cong như hình vẽ là đồ thị của hàm số nào? A. 3 2 y x   3x  5 . B. 3 2
y  2x  6x  5 . 1 C. 3 2
y x  3x  5 . D. 3
y x  3x  5 .
Câu 12. Cho hình chóp đều S.ABCD có cạnh AB a , góc giữa đường thẳng O 1 2 x
SA và mặt phẳng ABC  bằng 45º . Thể tích khối chóp S.ABCD là 3 a 3 a 2 A. . B. . 3 6 3 a 3 a 2 C. . D. . 6 3
Câu 13. Mệnh đề nào sau đây đúng? A. x d x x
xe x e xe C  . B. x d x x
xe x xe e C  . 2 x 2 x C. x xe d x x e C  . D. x xe d x x x
e e C  . 2 2
Câu 14. Khối đa diện nào có số đỉnh nhiều nhất?
A. Khối nhị thập diện đều ( 20 mặt đều).
B. Khối bát diện đều ( 8 mặt đều).
C. Khối thập nhị diện đều (12 mặt đều). D. Khối tứ diện đều.
Câu 15. Họ nguyên hàm của hàm số f x  1  là 5x  4 1 1 1 A.
ln 5x  4 C .
B. ln 5x  4  C . C.
ln 5x  4 C . D.
ln 5x  4 C . ln 5 5 5
Câu 16. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , SA vuông góc với mặt phẳng
ABCvà AB  2,AC  4,SA  5 . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là 5 10 25 A. R  . B. R  5 . C. R  . D. R  . 2 3 2 2 x x  1
Câu 17. Số đường tiệm cận của đồ thị hàm số y  là 2 x x  2 A. 4 . B. 1. C. 3 . D. 2 .
Câu 18. Cho khối nón có bán kính đáy r
3 và chiều cao h  4 . Tính thể tích V của khối nón đã cho.
A. V  12. B. V  4. C. V  4 . D. V  12 . 
Câu 19. Tìm tập xác định D của hàm số y  x x   2 3 2 3 4 . A. D   \  1  ;4 . B. D   .
Trang 2/7 - Mã đề 101 - https://toanmath.com/ C. D   ;    1  4;. D. D  ; 1      4;     .  3 a   
Câu 20. Cho a là số thực dương khác 5 . Tính I  log  . a   125 5 1 1 A. I   . B. I  3  . C. I  . D. I  3 . 3 3 1  2  2 1   1  1  a b  
Câu 21. Cho a  0 , b  0 , giá trị của biểu thức T  2a b .ab2 . 1          bằng 4  b a         1 2 1 A. 1. B. . C. . D. . 3 3 2
Câu 22. Cho a , b , c dương và khác 1. Các hàm số y  log x , y  log x , y  log x có đồ thị như hình a b c vẽ y y = log x a O 1 x y = log x b y = log x c
Khẳng định nào dưới đây đúng?
A. b c a .
B. a b c .
C. a c b .
D. c b a .
Câu 23. Tập xác định của hàm số y  2 sin x là       A. 0; 2       . B. 2;2     . C.  . D. 1;1     .
Câu 24. Cho a  0 , b  0 thỏa mãn 2 2
a  4b  5ab . Khẳng định nào sau đây đúng?
A. 2 loga  2b  5loga  logb. B. loga   1  logb  1 . a  2b loga  logb C. log  .
D. 5 log a  2b  loga  logb . 3 2
Câu 25. Cho tập A có 26 phần tử. Hỏi A có bao nhiêu tập con gồm 6 phần tử? A. 6 A . B. 26 . C. P . D. 6 C . 26 6 26
Câu 26. Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là 1 2 A. 1. B. . C. . 3 3 y 1 D. . 2 2
Câu 27. Tập nghiệm của bất phương trình log
x  1  log 11  2x  0 là 1   3   3  x 11   A. S  3;  -2 -1 O 1 2  S     . B.  ;4  2   . -2
Trang 3/7 - Mã đề 101 - https://toanmath.com/ C. S 1;4   . D. S  1;4.
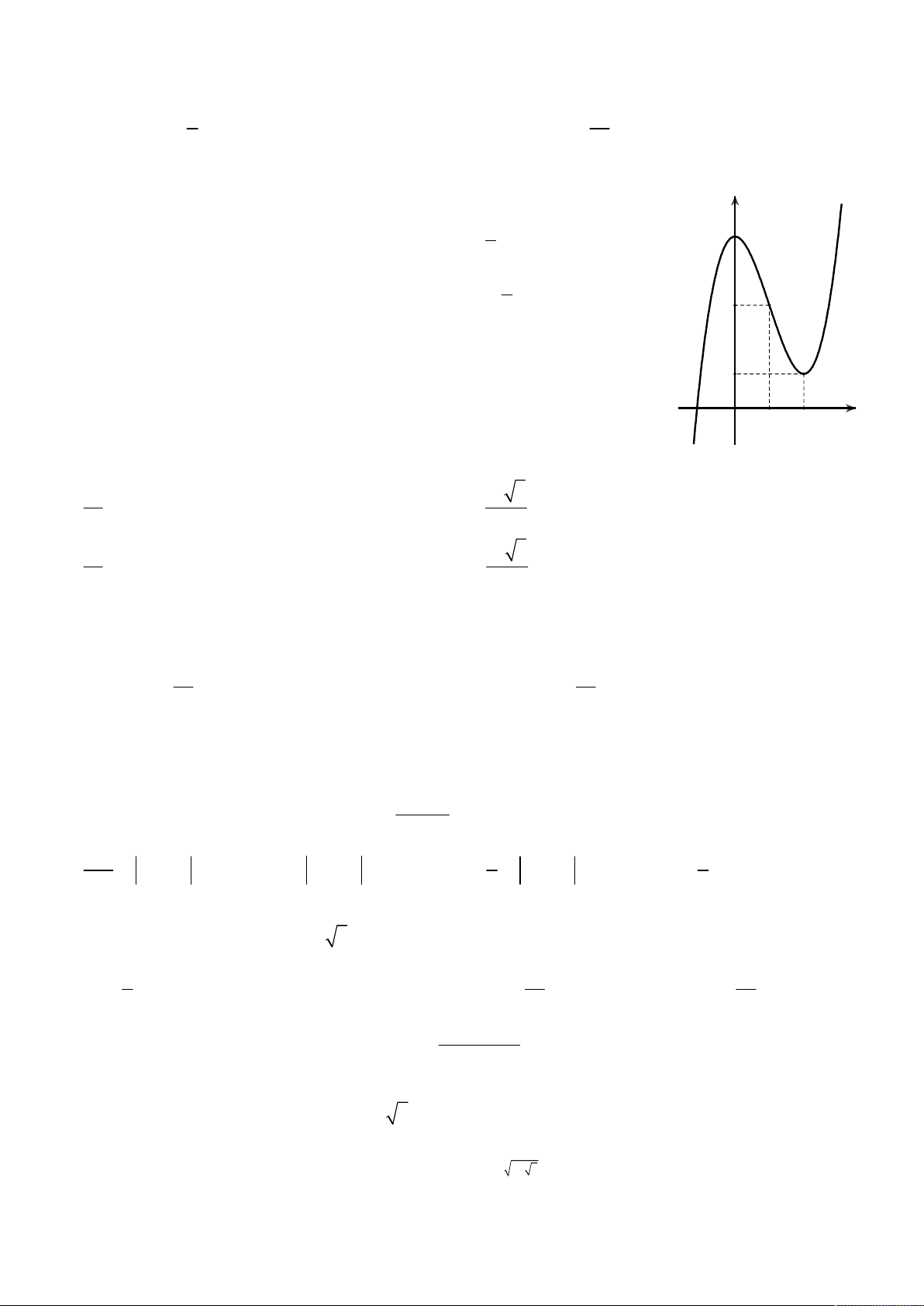
Câu 28. Cho hàm số y f x  liên tục trên  và có đồ thị như hình vẽ. Mệnh đề nào sau đây SAI?
A. Hàm số y f x  có hai điểm cực trị.
B. Nếu m  2 thì phương trình f x   m có nghiệm duy nhất.
C. Hàm số y f x  có cực tiểu bằng 1 .  
D. Giá trị lớn nhất của hàm số y f x  trên đoạn 2  ;2     bằng 2 . Câu 29. Cho hàm số    2 x f x
x e . Tìm một nguyên hàm F x của hàm số f x thỏa mãn F 0  2019 . A.   x
F x e  2019 . B.   2 x
F x x e  2018 . C.   2 x
F x x e  2017 . D.   2 x
F x x e  2018 .
Câu 30. Tập tất cả giá trị của tham số m để hàm số 3 2
y x  3mx  3x  1 đồng biến trên  là     A. 1;1          . B. m  ; 1 1;     . C.  ;    1  1;   . D.  1  ;  1 . 5b a a
Câu 31. Cho a , b là các số dương thỏa mãn log a  log b  log . Tính giá trị . 9 16 12 2 b a 3  6 a a a 3  6 A.  . B.  7  2 6 . C.  7  2 6 . D.  . b 4 b b b 4 
Câu 32. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ABC  60 . Hình chiếu vuông
góc của điểm S lên mặt phẳng ABCD trùng với trọng tâm tam giác ABC . Gọi là góc giữa đường
thẳng SB với mặt phẳng SCD, tính sin biết rằng SB a . 1 1 3 2 A. sin  . B. sin  . C. sin  . D. sin  . 4 2 2 2
Câu 33. Cho hàm số y f x  liên tục trên  và có đạo hàm f x  2
x x   2
2 x  6x m với mọi x    
. Có bao nhiêu số nguyên m thuộc đoạn 2019;2019     
 để hàm số g x
f 1 x nghịch biến trên khoảng  ;    1 ? A. 2010 . B. 2012 . C. 2011 . D. 2009 .  
Câu 34. Cho hình chóp S.ABC có AB AC  4,BC  2,SA  4 3 , SAB SAC  30º . Tính thể
tích khối chóp S.ABC . A. V  8 . B. V  6 . C. V  4 . D. V  12 . S .ABC S .ABC S .ABC S .ABC
Câu 35. Cho hàm số y f x  có bảng biến thiên như sau
Trang 4/7 - Mã đề 101 - https://toanmath.com/ 3 f x 13 2 
f x fx  3 2 7   
Giá trị lớn nhất của m để phương trình 2 2 e
m có nghiệm trên đoạn 0;2     là 15 A. 4 e . B. 3 e . C. 13 e . D. 5 e .
Câu 36. Cho phương trình  x   x x 2 2 sin 1 3 tan 2 sin
 3  4 cos x . Tổng tất cả các nghiệm thuộc   đoạn 0;20   
 của phương trình bằng 1150 570 880 875 A. . B. . C. . D. . 3 3 3 3
Câu 37. Cho hình lăng trụ đứng ABC .AB C
  có đáy ABC là tam giác vuông tại A , AB a 3 ,
BC  2a , đường thẳng AC  tạo với mặt phẳng BCC B
  một góc 30. Diện tích của mặt cầu ngoại tiếp
hình lăng trụ đã cho bằng A. 2 6 a . B. 2 3 a . C. 2 4 a . D. 2 24 a .
Câu 38. Cho hàm số f x  liên tục trên  thỏa mãn các điều kiện: f 0  2 2 , f x   0, x    và
f xf x   x   2 . 2
1 1  f x, x   . Khi đó giá trị f   1 bằng A. 15 . B. 23 . C. 24 . D. 26 .
Câu 39. Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ABCD; tứ giác ABCD là hình thang   vuông với cạnh đáy ,
AD BC ; AD  3BC  3 , a AB  ,
a SA a 3 . Điểm I thỏa mãn AD  3AI ; M
là trung điểm SD , H là giao điểm của AM và SI . Gọi E , F lần lượt là hình chiếu của A lên SB , SC .
Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng ABCD. 3 a 3 a 3 a 3 a A. V  . B. V  . C. V  . D. V  . 2 5 5 10 5 5 5 Câu 40. Cho phương trình 2
m ln x  
1  x  2  mlnx  
1  x  2  0  
1 . Tập tất cả giá trị của
tham số m để phương trình  
1 có hai nghiệm phân biệt thỏa mãn 0  x  2  4  x là khoảng a;   . 1 2
Khi đó, a thuộc khoảng A. 3, 8;3,9. B. 3,7;3, 8 . C. 3,6;3,7. D. 3,5;3,  6 . Câu 41. Cho hàm số 4 2
y x  2x m  2 có đồ thị C  . Gọi S là tập các giá trị của m sao cho đồ thị
C có đúng một tiếp tuyến song song với trục Ox. Tổng tất cả các phần tử của S là A. 3 . B. 8 . C. 5 . D. 2 .
Câu 42. Cho hai số thực x,y thỏa mãn 2 2 2 2
x y  4x  6y  4  y  6y  10  6  4x x . Gọi
Trang 5/7 - Mã đề 101 - https://toanmath.com/
M,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2 T
x y a . Có bao nhiêu giá trị  
nguyên thuộc đoạn 10;10   M m
 của tham số a để 2 ? A. 17 . B. 16 . C. 15 . D. 18 .
Câu 43. Cho hình chóp O.ABC có ba cạnh , OA ,
OB OC đôi một vuông góc và OA OB OC a . Gọi  
M là trung điểm cạnh AB . Góc hợp bởi hai véc tơ BC và OM bằng A. 120º . B. 150º . C. 135º . D. 60º . 1
Câu 44. Cho số nguyên dương n thỏa mãn điều kiện 720 7 7 7
C C  ....CA . Hệ số của 7 x n  10 7 8 n 1 4032  n  1    trong khai triển x    x  0  bằng 2     x  A. 560 . B. 120 C. 560 . D. 120 . 2 x m  2  
Câu 45. Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số y  trên đoạn 0; 4 x m   bằng 1  . A. 3 . B. 2 . C. 1. D. 0 . x  3  
Câu 46. Cho hàm số y
. Có bao nhiêu giá trị nguyên thuộc đoạn 6  ;6 3 2  
x  3mx   2 2m   1 x m  
của tham số m để đồ thị hàm số có bốn đường tiệm cận? A. 12 . B. 9 . C. 8 . D. 11.
Câu 47. Tập nghiệm của bất phương trình log  2 2
x x  2  4  x  2
 2x x  2  1là  a; b   2  . Khi đó ab bằng 12 5 15 16 A. . B. . C. . D. . 5 12 16 15
Câu 48. Cho tứ diện SABC và G là trọng tâm của tứ diện, mặt phẳng quay quanh AG và cắt các cạnh V ,
SB SC tương ứng tại M,N . Giá trị nhỏ nhất của tỉ số S.AMN là VS.ABC 1 1 3 4 A. . B. . C. . D. . 2 3 8 9
Câu 49. Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là 12 cm . Giá
trị lớn nhất của thể tích khối trụ là A. 32 3 cm . B. 64 3 cm . C. 8 3 cm . D. 16 3 cm .
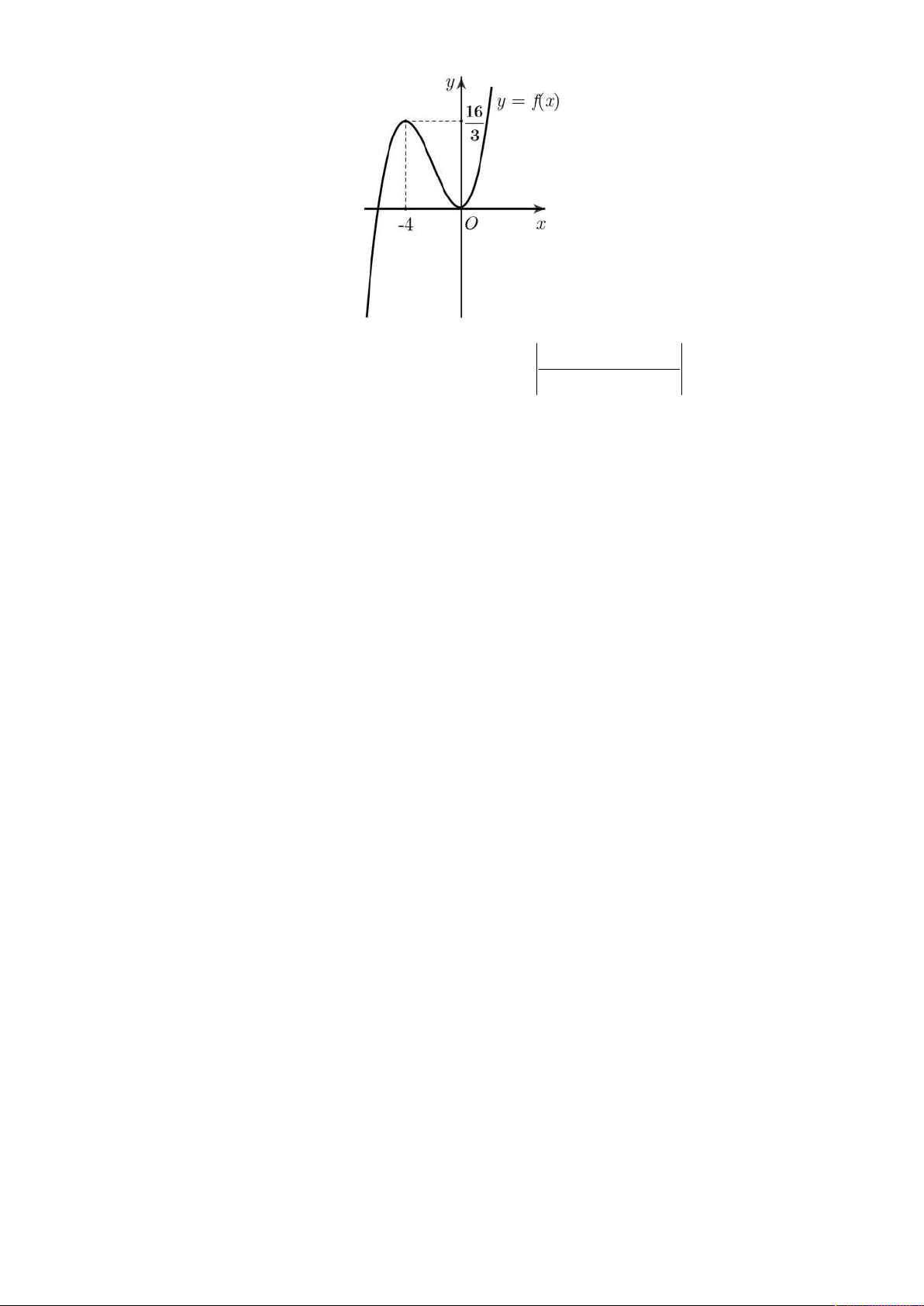
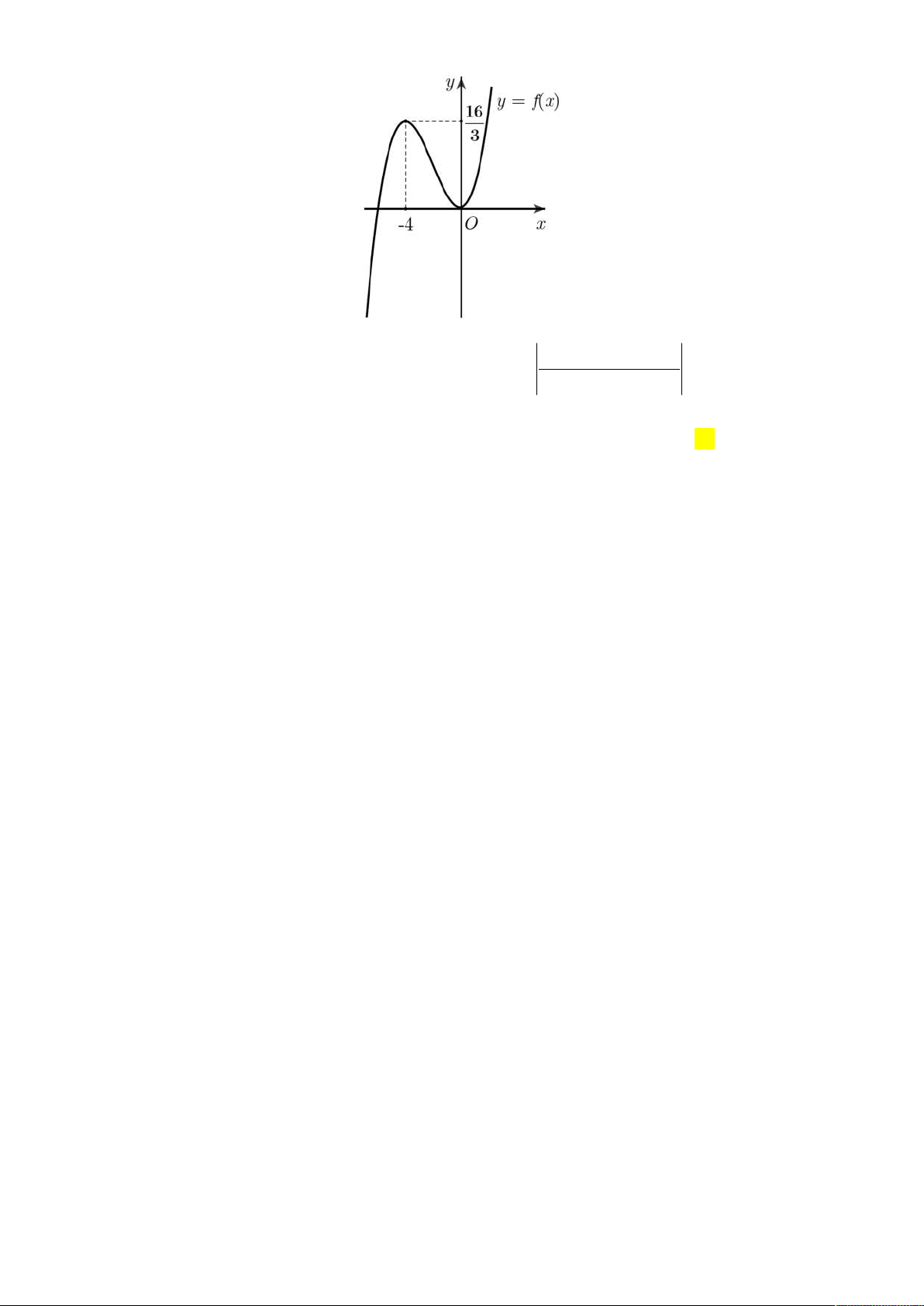
Câu 50. Cho hàm số y f x  liên tục trên  và có đồ thị như hình vẽ.
Trang 6/7 - Mã đề 101 - https://toanmath.com/
 3sinx cosx 1    
Có bao nhiêu giá trị nguyên của tham số m để phương trình f    f    2
m  4m  4 có
 2 cosx  sin x  4  nghiệm? A. 4 . B. 5 . C. Vô số. D. 3 . ------ HẾT ------
Trang 7/7 - Mã đề 101 - https://toanmath.com/
Document Outline

  • aĐỀ TẬP HUẤN SỞ GDĐT BẮC NINH
  • ĐỀ TẬP HUẤN SỞ GDĐT BẮC NINH