Đề tham khảo cuối kì 2 Toán 9 năm 2024 – 2025 phòng GD&ĐT Bình Thạnh – TP HCM có đáp án
Đề tham khảo cuối kì 2 Toán 9 năm 2024 – 2025 phòng GD&ĐT Bình Thạnh – TP HCM có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 91 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem.
Chủ đề: Đề HK2 Toán 9 287 tài liệu
Môn: Toán 9 2.5 K tài liệu
Tác giả:
Preview text:
MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ II – TOÁN 9
A. BẢNG MA TRẬN ĐỀ KIỂM TRA.
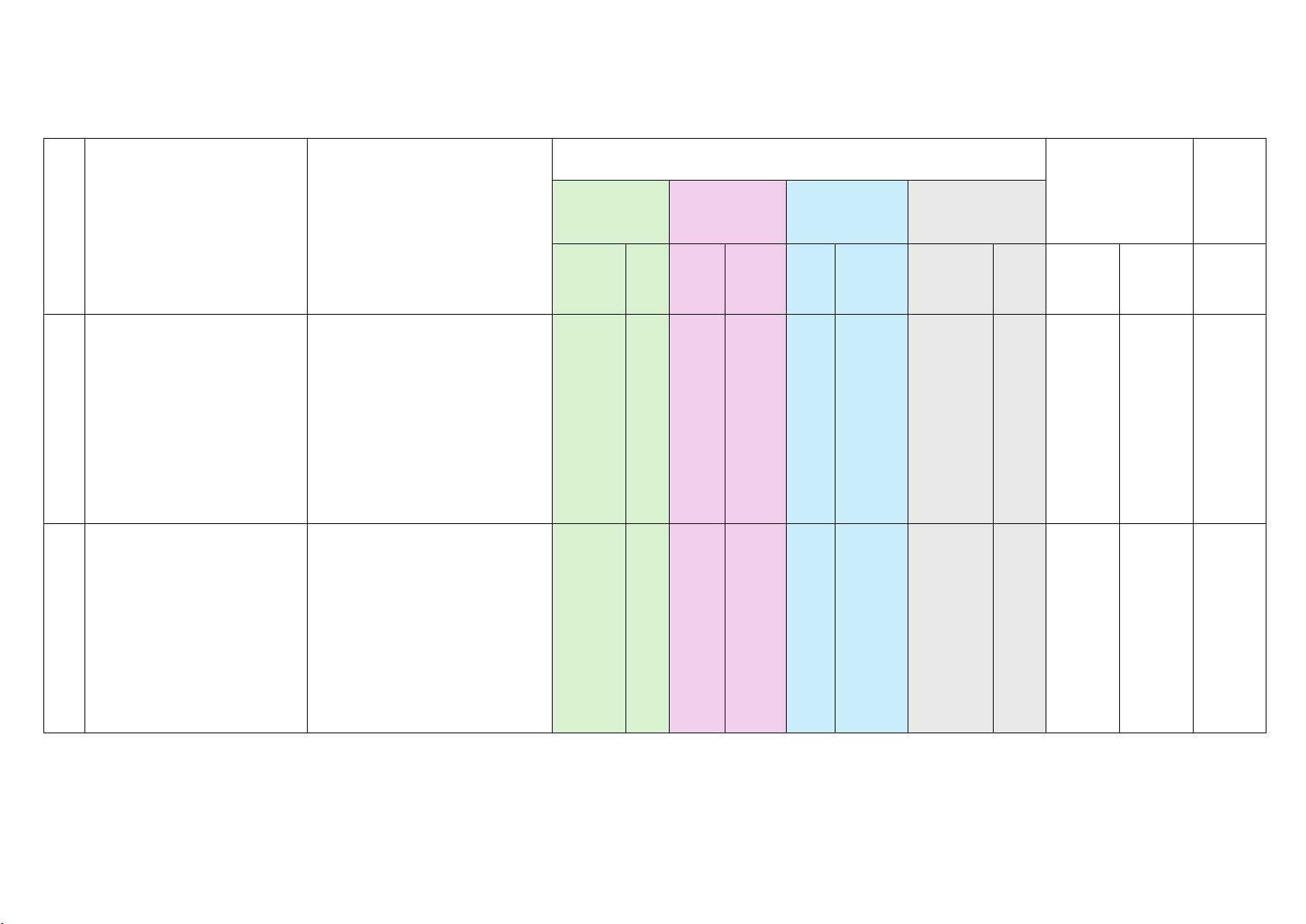
Mức độ đánh giá Tổng T Tổng số câu %
Nhận biết Thông hiểu Vận dụng Vận dụng cao T Chủ đề
Nội dung/Đơn vị kiến thức điểm TNK T TN Q L KQ TL TN KQ TL TNKQ TL TNK Q TL
HÀM SỐ Y = ax2 ( a Hàm số và đồ thị hàm số y = ax2 2 1
≠0) VÀ PHƯƠNG ( a ≠ 0) (Bài
TRÌNH BẬC HAI Phương trình bậc hai một ẩn 5 1a,b) 1 (Bài 2) 5 3 32,5 MỘT ẨN Định lí Vi1ète
Bảng tần số và biểu đồ tần số 2
2 MỘT SỐ YẾU TỐ Bảng tần số tương đối và biểu đồ THỐNG KÊ tần số tương đối 2 ( Bài 2 2 12,5
Biểu diễn số liệu ghép nhóm 3a,b) GIẢI TOÁN BẰNG 1 3 CÁCH LẬP
Lập phương trình bậc hai một ẩn 1 ( Bài 1 1 10,0 PHƯƠNG TRÌNH 4) TỨ GIÁC NỘI
Đường tròn ngoại tiếp tam giác. 1 1 1 4 TIẾP. ĐA GIÁC
Đường tròn nội tiếp tam giác 2 (Bài ( Bài (Bài 2 3 30,0 ĐỀU
Tứ giác nội tiếp
Đa giác đều và phép quay 6a) 6b) 6c)
CÁC HÌNH KHỐI Hình Trụ 2 5 TRONG THỰC Hình nón 2 ( Bài 2 2 15,0 TIỄN Hình cầu 5a,b) Tổng 12 6 4 1 12 12 Tỉ lệ % 30% 35% 25% 10% 100 Tỉ lệ chung 65% 35% 100
BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA ĐÁNH GIÁ CUỐI HKII – TOÁN 9
Số câu hỏi theo mức độ nhận thức
TT Chương/Chủ đề
Nội dung/Đơn vị kiến thức
Mức độ đánh giá Nhận Thông Vận Vận biêt hiểu dụng dụng cao Nhận biết:
- Hàm số và đồ thị hàm số y = ax2 ( a ≠ 0) 5 TN
- Phương trình bậc hai một ẩn
HÀM SỐ Y = ax2 Hàm số và đồ thị hàm - Định lí Viète ( a ≠0) VÀ số y = ax2 ( a ≠ 0) 2TL 1 PHƯƠNG
Phương trình bậc hai Thông hiểu:: TRÌNH BẬC một ẩn
- Vẽ đồ thị hàm số, các bài toán liên quan đến hàm số
HAI MỘT ẨN Định lí vi-et
- Giải phương trình bậc hai một ẩn,..
- Sử dụng định lí Viète Vận dụng: 1TL
- Vận dụng định lí Viète để tính giá trị của biểu thức,..
Bảng tần số và biểu đồ Nhận biết: 2TN tần số
- Bảng tần số và biểu đồ tần số
Bảng tần số tương đối - Bảng tần số tương đối và biểu đồ tần số tương đối 2
MỘT SỐ YẾU và biểu đồ tần số
TỐ THỐNG KÊ tương đối Thông hiểu:: 2TL
Biểu diễn số liệu ghép - Lập được bảng tần số và biểu đồ tần số nhóm
- Lập được bảng tần số tương đối và biểu đồ tần số tương đối
- Biểu diễn số liệu ghép nhóm 1TN GIẢI TOÁN Nhận biết:
- Phương trình bậc hai một ẩn thỏa bài toán. 3
BẰNG CÁCH Lập phương trình bậc
LẬP PHƯƠNG hai một ẩn Thông hiểu:: 1TL TRÌNH
- Lập được phương trình bậc hai một ẩn Nhận biết: 2TN
TỨ GIÁC NỘI Đường tròn ngoại tiếp - Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
4 TIẾP. ĐA GIÁC tam giác. Đường tròn - Tứ giác nội tiếp ĐỀU nội tiếp tam giác
Tứ giác nội tiếp Thông hiểu:: 1TL
- Nhận biết 4 điểm cùng thuộc một đường tròn, tứ giác nội tiếp.
Đa giác đều và phép Vận dụng: 1TL quay
- Vận dụng các kiến thức liên quan để chứng minh đẳng thức,… Vận dụng cao: 1TL
- Vận dụng cá kiến thức liên quan đến đường tròn để chứng minh 4 điểm
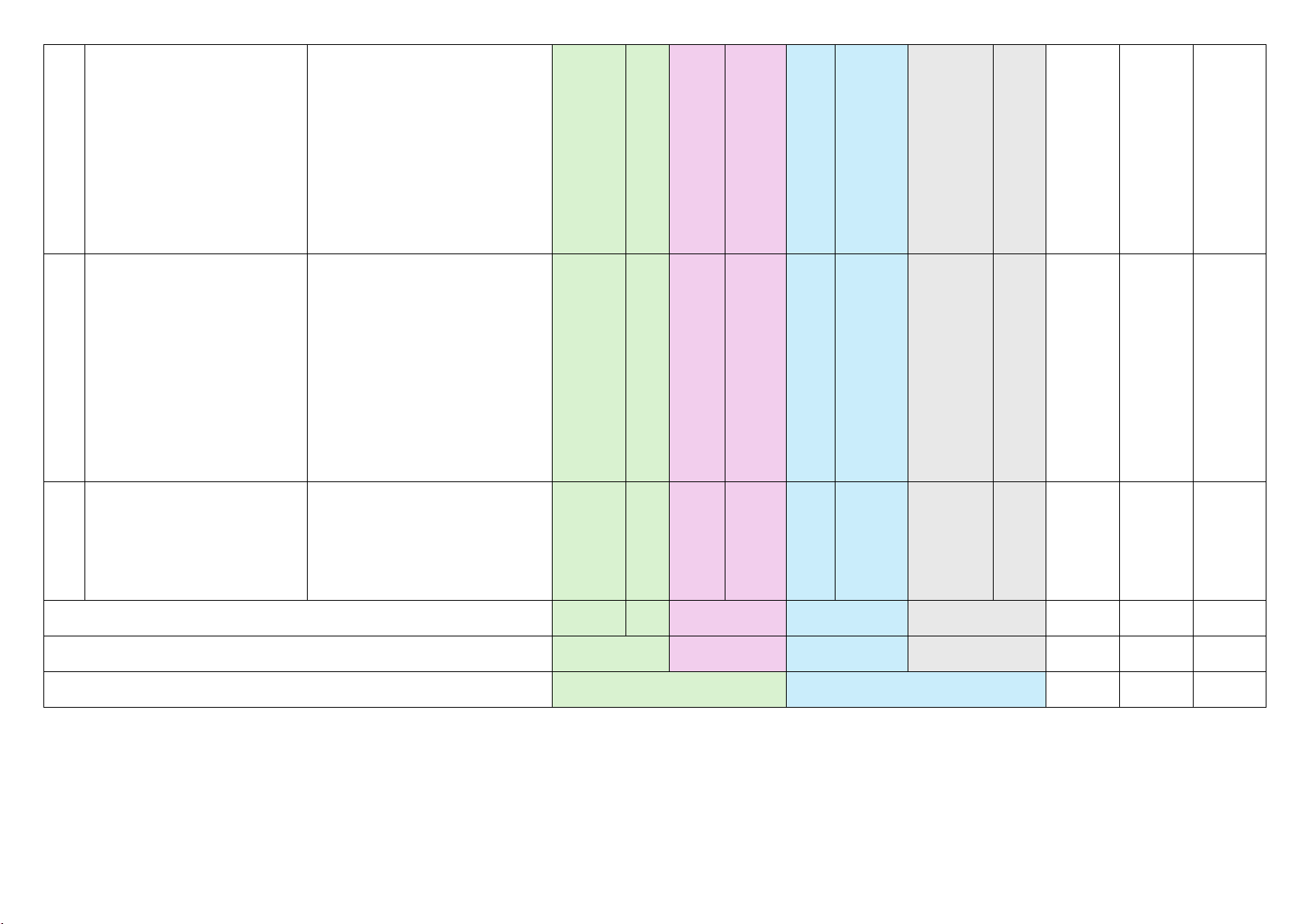
cùng thuộc một đường, chứng minh đẳng thức, ….. Nhận biết: 2TN CÁC HÌNH Hình Trụ
- Nhận biết hình trụ, hình nón, hình cầu và các yếu tố về bán kính, chiều cao, 5
KHỐI TRONG Hình nón đường sinh,… THỰC TIỄN Hình cầu Vận dụng: 2TL
- Vận dụng các công thúc về diện tích, thể tích của các hình khối vào giải
quyết các bài toán trong thực tiễn. Tổng số câu 12 7 4 1 Tỷ lệ (%) 30% 35% 25% 10% Tỷ lệ chung (%) 30% 70%
UBND QUẬN BÌNH THẠNH
ĐỀ KIỂM TRA ĐÁNH GIÁ CUỐI HỌC KÌ II
TRƯỜNG TRUNG HỌC CƠ SỞ
NĂM HỌC: 2024-2025
BÌNH LỢI TRUNG MÔN: TOÁN - LỚP 9
(Đề gồm có 02 trang)
Thời gian 90 phút (không kể thời gian phát đề)
I. Trắc nghiệm khác quan (3 điểm) Chọn đáp án đúng nhất.
Câu 1: Điểm nào sau đây thuộc đồ thị của hàm số 2 y = x ? A. (1; 1) B. (1; -2) C. (-1; 2) D. (2; 1)
Câu 2: Phương trình nào dưới đây không là phương trình bậc hai một ẩn?
A. x2 – 2 x = 0
B. 0x2 + 5x – 2 = 0 C. 4x2 – 5 = 0 D. 7x2 + 5x - 2 = 0
Câu 3: Phương trình 2
ax + bx + c = 0 (a ≠ 0) có hai nghiệm phân biêt khi nào? A. ∆ = 0 B. ∆ > 0 C. ∆ ≥ 0 D. ∆ < 0
Câu 4: Nghiệm của phương trình 2 x − 4x + 3 = 0 là: A. x = 1; − x = 3 x = -1;x = -3 x =1;x = 3 − x =1;x = 3 1 2 . B. 1 2 . C. 1 2 . D. 1 2 .
Câu 5: Cho phương trình 2
x − 2x − 3 = 0 có hai nghiệm x , x . Theo định lý Viète, tổng và tích của hai 1 2 nghiệm lần lượt là:
A. x + x = 2, x x = 3 − B. x + x = 2, − x x = 3 − 1 2 1 2 1 2 1 2
C. x + x = 2, x x = 3 D. x + x = 2, − x x = 3 1 2 1 2 1 2 1 2
Câu 6: Chọn phát biểu SAI:
A. Tập hợp các dữ liệu thu thập được theo tiêu chí cho trước là mẫu dữ liệu.
B. Số lần xuất hiện của một giá trị trong mẫu dữ liệu gọi là tần số của giá trị đó.
C. Biểu đồ biểu diễn tần số của các giá trị trong mẫu dữ liệu gọi là biểu đồ tần số.
D. Bảng dùng để biểu diễn tần số của mỗi giá trị trong mẫu dữ liệu gọi là bảng tần số tương đối.
Câu 7: Quan sát biểu đồ cột:
Hãy cho biết có tổng bao nhiêu y tá? A. 9 B. 28 C. 39 D. 40
Câu 8: Hai xe ô tô khởi hành cùng một lúc từ A đến B cách nhau 120 km. Tốc độ của xe thứ nhất
nhanh hơn tốc độ của xe thứ hai là 10km/h nên đã đến sớm hơn xe thứ hai 24 phút. Gọi x (km/h) là tốc
độ của xe thứ hai (x > 0). Phương trình nào dưới đây phù hợp với yêu cầu bài toán? A. 120 120 − = 24 B. 120 120 2 − = C. 120 120 2 − = D. 120 120 2 − = x x +10 x x +10 5 x x −10 5 x +10 x 5
Câu 9: Cho ∆𝐴𝐴𝐴𝐴𝐴𝐴 vuông cân có AB = AC = 4 cm. Bán kính R của đường tròn ngoại tiếp tam giác có độ dài là: A. 2√2 cm. B. √2 cm. C. 4√2 cm. D. 8√2 cm. Câu 10:
Cho tứ giác MNPQ nội tiếp đường tròn (O;R) và 63o M =
.Số đo của ˆP là: A.630 B.1170 C.600 D.1260
Câu 11: Diện tích xung quanh của hình trụ có bán kính đáy 4 cm và chiều cao 8 cm là A. 32π cm2 B. 48π cm2 C. 64π cm2 D. 128π cm2
Câu 12: Thể tích của hình cầu bán kính là 12cm là: A. 120π cm3 B. 2304π m3 C. 1000π cm3 D. 2304π cm3
II. Tự luận (7 điểm)
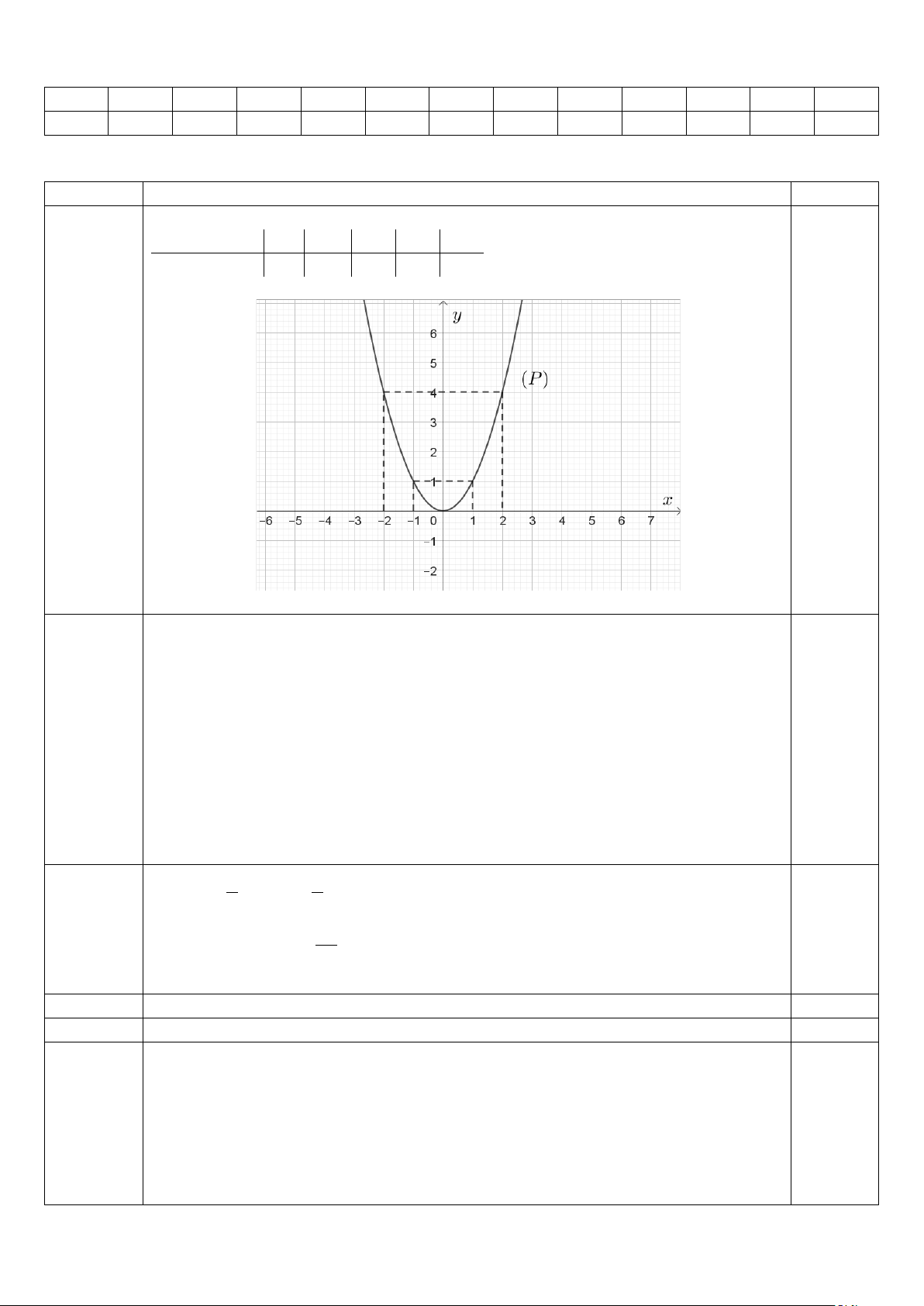
Bài 1. [TH] (1,0 điểm). Cho hàm số: (P) 2 : y = x
a) Vẽ đồ thị (P) của hàm số trên.
b) Tìm tọa độ những điểm M thuộc (P) có tung độ bằng hai lần hoành độ bằng phép toán.
Bài 2. [VD] (1,0 điểm). Cho phương trình: 2
3x − 5x +1 = 0 (1)
Gọi x ; x là 2 nghiệm của phương trình (1). Không giải phương trình, tính giá trị của biểu thức: 1 2
A = (x − x )2 2 2 − 3x .x 1 2 1 2
Bài 3. [TH] (0,75điểm) Số cuộc gọi chăm sóc khách hàng của một tổng đài trong tháng 4 được ghi lại ở bảng sau: 4 2 6 3 6 3 2 5 4 2 5 4 3 3 3 3 5 4 4 3 4 6 5 3 6 3 5 3 5 5
a) Lập bảng tần số cho mẫu số liệu trên.
b) Vẽ biểu đồ tần số dạng đoạn thẳng.
Bài 4. (0,75điểm) [TH]
Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90 km trong một thời gian đã định. Sau
khi đi được 1 giờ, người đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng hẹn, người ấy phải tăng vận tốc
thêm 4 km/h. Tính vận tốc lúc đầu của người đó.
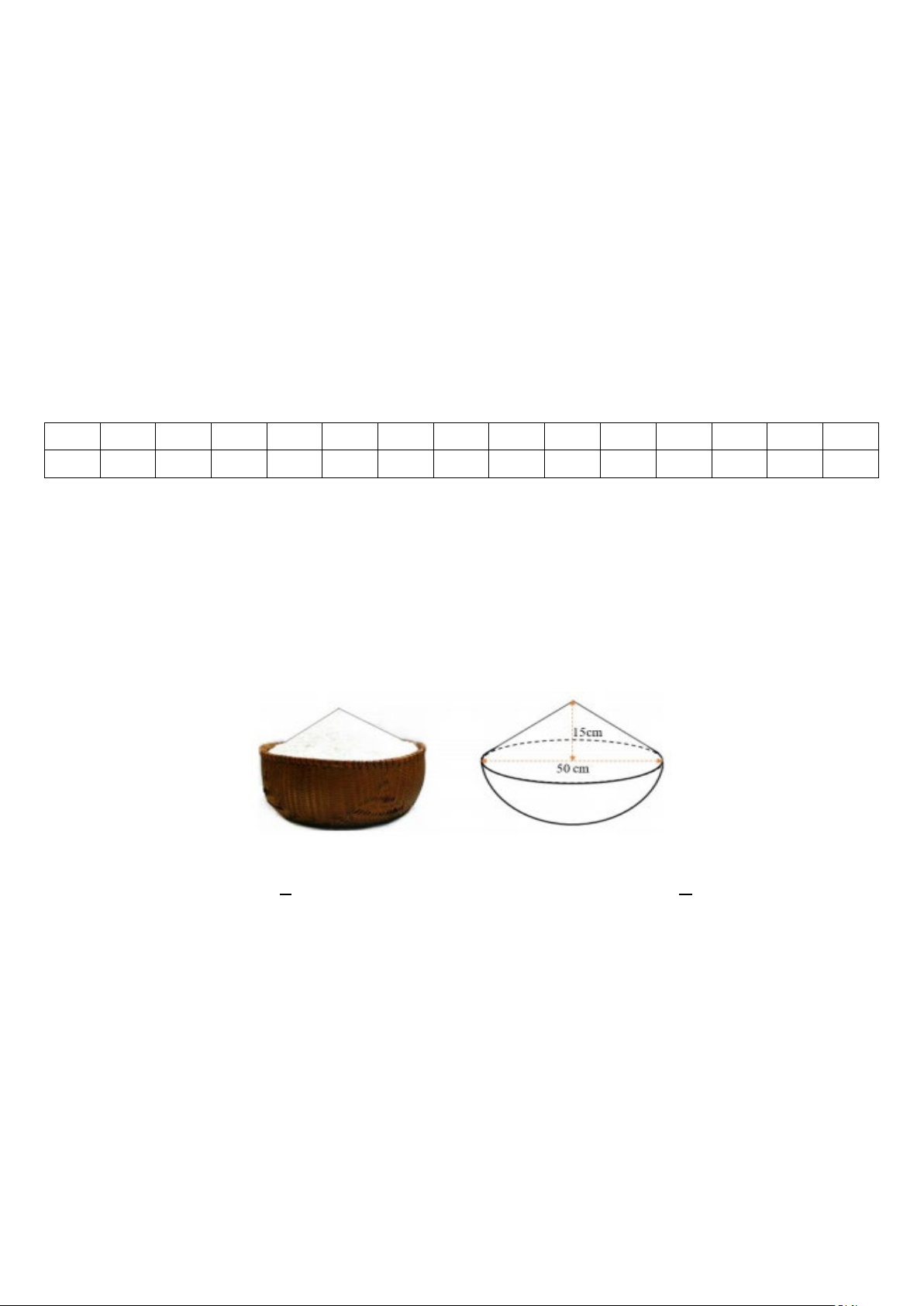
Bài 5: [ VD] (1 điểm) . Cho hình bên là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với
đường kính 50cm , phần gạo vun lên có dạng hình nón cao 15cm.
a) Tính thể tích phần gạo trong thúng. (làm tròn đến hàng đơn vị).
Biết thể tích hình nón là 1 2 V = R π h , hình trụ là 2 V = R
π h và hình cầu là 4 3 V = R π 3 3
b) Nhà Danh dùng lon sữa bò cũ có dạng hình trụ (bán kính đáy bằng 5cm , chiều cao 15cm) để đong
gạo mỗi ngày. Biết mỗi ngày nhà Danh ăn 5 lon gạo và mỗi lần đong thì lượng gạo chiếm 90% thể
tích lon. Hỏi với lượng gạo ở thúng trên thì nhà Danh có thể ăn nhiều nhất là bao nhiêu ngày.
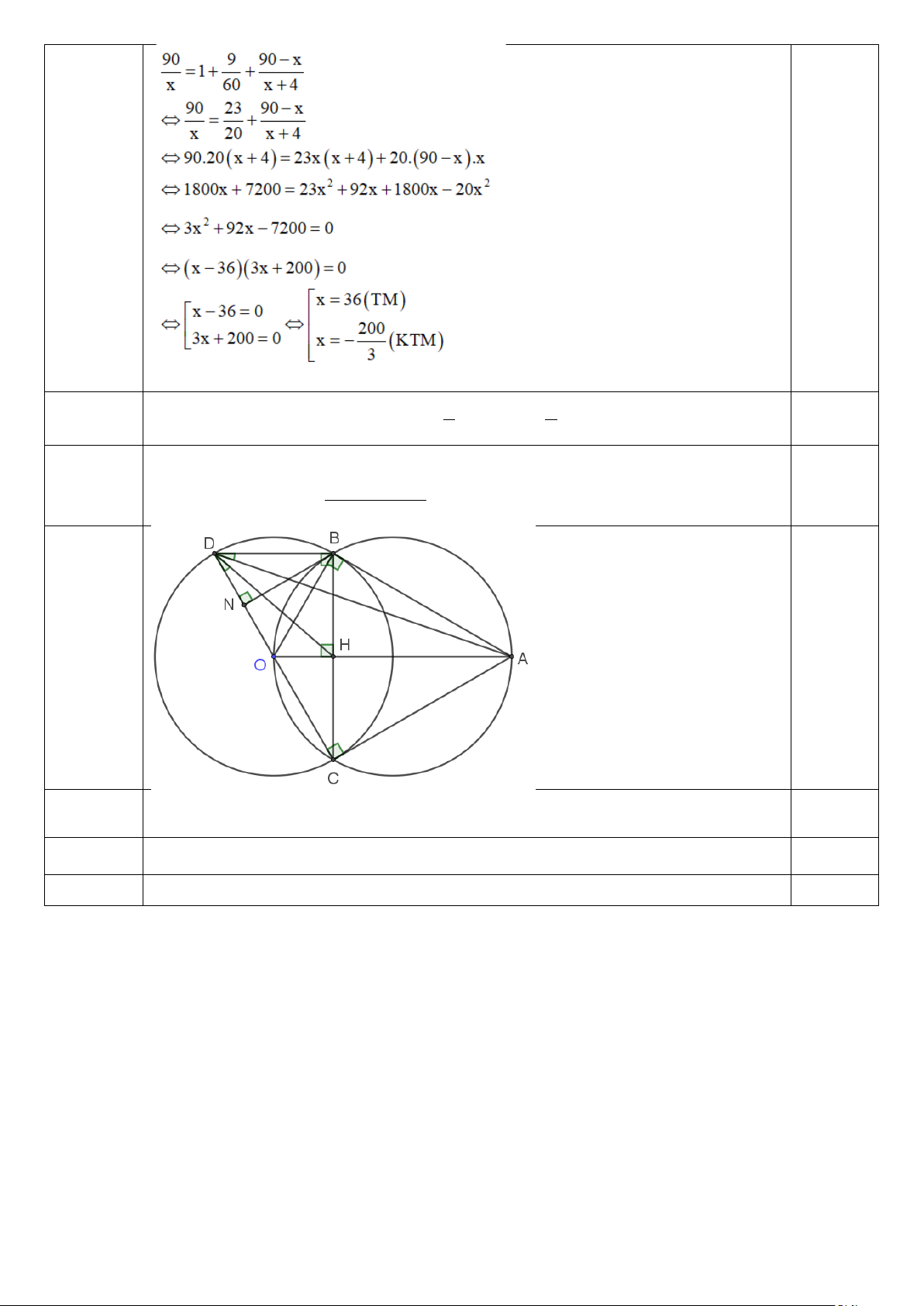
Bài 6. (2,5 điểm) Cho đường tròn (O,R). Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB
và AC đến đường tròn (O) ( B,C là hai tiếp điểm). Vẽ đường kính CD của đường tròn (O).
a) [TH] (1 điểm) Chứng minh tứ giác OBAC nội tiếp và OA / /BD .
b) [VD] ( 0,5 điểm) Gọi H là giao điểm của OA và BC . Chứng minh 2 . OA OH = OB
c) [VDC] ( 1 điểm) Vẽ BN song song với AC (N ∈CD) . Trong trường hợp OA = 2R, tính diện tích
của tứ giác DBAC . ĐÁP ÁN
I. Trắc nghiệm (3 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 ĐA A B B D A D C B A B C B
II. Tự luận (7 điểm) Bài Nội dung Điểm 1a/ 0,25 x -2 -1 0 1 2 (P): y = x2 4 1 0 1 4 0,25 b/ y = 2x 0,25 Ta có: 2 y = x 2 ⇒ 2x = x 2 x − 2x = 0
Giải phương trình ta được: x = 0 và x = 2
Khi x = 0 ⇒ y = 2.0 = 0 ⇒ M (0;0)
Khi x = 2 ⇒ y = 2.2 = 4 ⇒ M (2;4)
Vậy tọa độ những điểm M thuộc (P) có tung độ bằng hai lần hoành độ là: 0,25
M (0;0) và M (2;4) . Bài 2 5 0,5 x + x = ; 1 x .x = 1 2 3 1 2 3 2 2
A = S − 4P − 3P =10 9 0,5
Bài 3 a/ Vẽ đúng bảng tần số 0,5 b/
Vẽ đúng biểu đồ dạng đoạn thẳng 0,25 Bài 4
Gọi vận tốc ban đầu của người đó là x (km/h) (x > 0).
Thời giạn dự định người đó đi hết quãng đường là 90/x (h).
Quãng đường người đó đi được sau 1 giờ là x (km).
Quãng đường còn lại người đó phải tăng tốc là 90 – x (km).
Vận tốc của người đó sau khi tăng tốc là x + 4 (km/h).
Thời gian người đó đi hết quãng đường còn lại là (h).
Theo đề bài ta có phương trình:
Vậy vận tốc lúc đầu của người đó là 36 km/h. Bài 5 a/ 0,5
Thể tích phần gạo trong thúng: 1 2 4 3 3
V = π.25 .15 + π.25 : 2 ≈ 42542cm 3 3 b/ Thể tích lon gạo: 2 V = π.5 .15 = 375π 0,25 0,25 Nhà Danh có thể ăn: 42542 ≈ 8 ngày 375π.90%.5 a/
Chứng minh tứ giác OBAC nội tiếp 0,5
Chứng minh: OA / /BD 0,5 b/ Chứng minh 2 . OA OH = OB 0,5 c/
Tính diện tích của tứ giác DBAC . 1 UBND QUẬN BÌNH THẠNH
ĐỀ KIỂM TRA ĐÁNH GIÁ CUỐI KỲ HỌC KỲ II
TRƯỜNG TRUNG HỌC CƠ SỞ
NĂM HỌC 2024 – 2025 CÙ CHÍNH LAN MÔN TOÁN LỚP 9 Thời gian: 90 phút ĐỀ ĐỀ NGHỊ
(Không kể thời gian phát đề)
PHẦN 1. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm).
I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu 1: Trong những điểm sau đây, điểm nào thuộc đồ thị hàm số y = 2x2 ? A. (2; 4). B. (1; 2). C. ( 2; − 6) . D. ( 1; − − 3) .
Câu 2: Đồ thị hàm số 2
y = ax ,(a ≠ 0) đi qua điểm A(1; 3). Giá trị của a bằng: A. 1. B. - 1. C. 3. D. - 3.
Câu 3: Phương trình nào dưới đây là phương trình bậc hai một ẩn? A. 2 0x +1= 0 B. 2 2x − 5x = 0 C. 2 4
−x + x − 2 = 0 D. 3 x − 2x +1= 0
Câu 4: Nghiệm của phương trình 2
2x − 5x + 3 = 0 là: A. x = –1; 3 x = . B. x =1; 3 x = . 1 2 2 1 2 2 D. x 3 =1; x = − C. x = –1; 3 x = − 1 2 2 1 2 2
Câu 5: Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình 2
x − 3x − 4 = 0.
Khi đó giá trị của S và P là: A. S = 3; P = - 4 B. S = 3; P = 4 C. S = - 3; P = - 4 D. S = 4; P = 3
Câu 6: Cho hình trụ có bán kính đáy R = 4( cm) và chiều cao h = 5( cm). Diện
tích xung quanh của hình trụ là: A. 40π B. 30π C. 20π D. 50π
Câu 7: Lấy ra lần lượt 2 quả bóng từ một hộp chứa 3 quả bóng được đánh số 1;
2; 3. Số các kết quả có thể xảy ra là: A. 3. B. 4. C. 5. D. 6. 3
Câu 8: Cho mặt cầu có thể tích V = 972π (cm ). Tính đường kính mặt cầu: A. 18 3 cm B. 12 cm C. 9 cm D. 16 cm
Câu 9: Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và 0 ˆ
M = 75 . Số đo của ˆP là: A. 1150. B. 750. C. 1050. D. 1800.
Câu 10: Bảng phân bố tần số sau đây ghi lại số vé không bán được trong 62 buổi chiếu phim: Lớp
[0;5) [5;10) [10;15) [15;20) [20;25) [25;30) Cộng Tần số 3 8 15 18 12 6 62
Hỏi có bao nhiêu buổi chiếu phim có nhiều nhất 19 vé không bán được? A. 42 B. 43 C. 44 D. 45
Câu 11: Cho đa giác 9- cạnh đều ABCDEFGKM có O là tâm. Phép quay tâm O
biến đa giác trên thành chính nó là: A. 400. B. 600. C. 900. D. 1000.
Câu 12: Cho tứ giác ABCD có số đo các góc A,B,C,D lần lượt như sau. Truờng
hợp nào thì tứ giác ABCD có thể là tứ giác nội tiếp .
A 50;60;130;140 . .
B 65;85;115;95 .
C. 82;90;98;100 . D. Các câu đều sai
PHẦN 2: TỰ LUẬN (7 điểm)
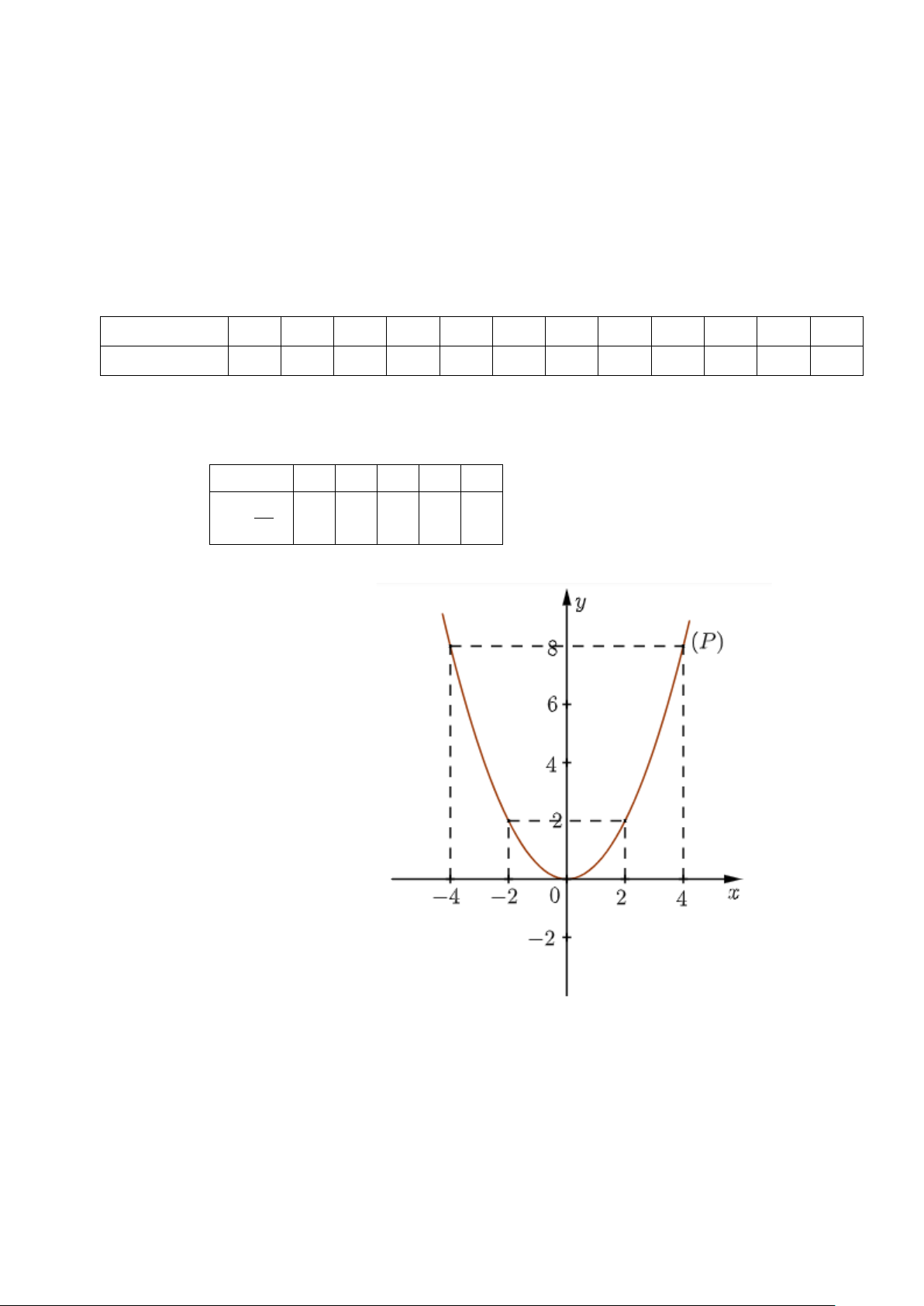
Bài 1. [TH] (1,0 điểm). 2 Cho hàm số x y =
có đồ thị hàm số là Parabol(P). 2
a) Vẽ đồ thị (P) của hàm số trên.
b) Tìm điểm A thuộc (P)sao cho hoành độ gấp hai lần tung độ.
Bài 2. [VD] (1,0 điểm). Cho phương trình: 2
3x −14x −1 = 0 .
a) Chứng tỏ phương trình trên có hai nghiệm phân biệt. b) Gọi 1x; 2
x là hai nghiệm của phương trình trên. Không giải phương
trình, hãy tính giá trị của biểu thức: x x A = 1 + 2 x −1 x . − 2 1 1
Bài 3. [TH] (0,75điểm). Điểm kiểm tra 1 tiết môn tiếng Anh của học sinh lớp
9A được ghi lại trong bảng sau: 7 6 7 6 7 3 5 6 6 4 6 3 4 6 5 3 8 4 4 7 8 10 5 7 7 7 4 7 7 7 9 4 9 6 6 6 6 6 6 7 7 6 8 8 6
a) Lập bảng tần số cho mẫu số liệu trên.
b) Vẽ biểu đồ tần số dạng cột (hay dạng đoạn thẳng).
Bài 4. (0,75điểm) [TH] Một bài toán về xác suất.
Hộp thứ nhất chứa 1 quả bóng màu xanh và 1 quả bóng đỏ. Hộp thứ hai chứa 1
quả bóng màu vàng và 1 quả bóng đỏ. Lấy ra ngẫu nhiên cùng lúc từ mỗi hộp 1 quả bóng.
a) Xác định không gian mẫu và số kết quả có thể xảy ra của phép thử.
b) Biết rằng các quả bóng có cùng kích thước và khối lượng. Hãy tính xác suất của mỗi biến cố sau:
- M: "2 quả bóng lấy ra có cùng màu";
- Q: "Có ít nhất 1 quả bóng màu đỏ trong 2 quả bóng lấy ra".
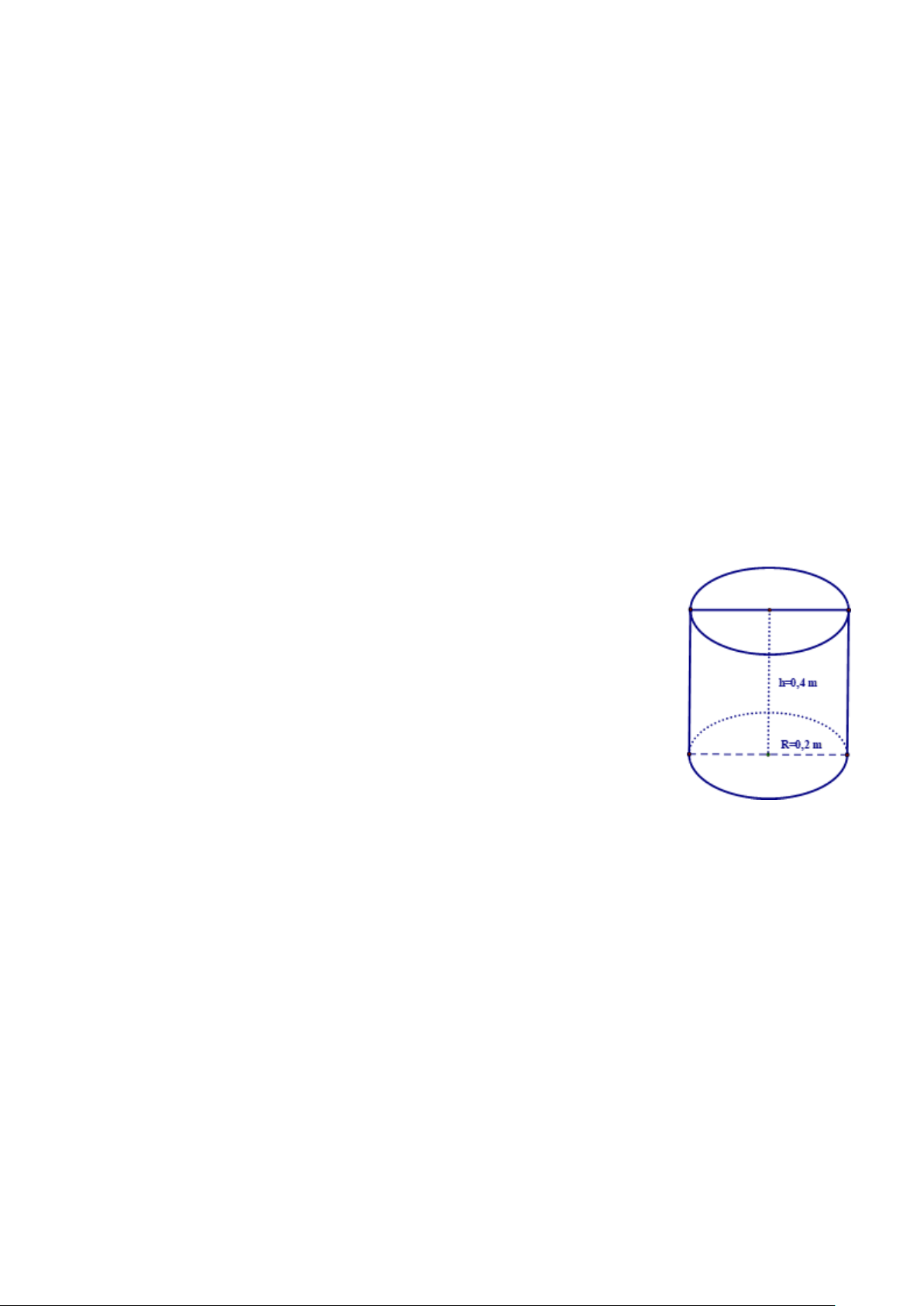
Bài 5: [ VD] (1 điểm) . Anh Minh vừa mới xây một cái hồ
trữ nước cạnh nhà có hình hộp chữ nhật kích thước 2m x
2m x 1m . Hiện hồ chưa có nước nên anh Minh phải ra sông
lấy nước . Mỗi lần ra sông anh gánh được 1 đôi nước đầy
gồm hai thùng hình trụ bằng nhau có kích thước đáy 0,2m , chiều cao 0, 4m.
a) Tính lượng nước (m3) anh Minh đổ vào hồ sau mỗi lần
gánh (ghi kết quả làm tròn đến hai chữ số thập phân). Biết
trong quá trình gánh nước về hao hụt khoảng 10% và công
thức tính thể tích hình trụ là V = πR2h.
b) Hỏi anh Minh phải gánh ít nhất bao nhiêu lần để đầy
hồ? (Bỏ qua thể tích thành hồ).
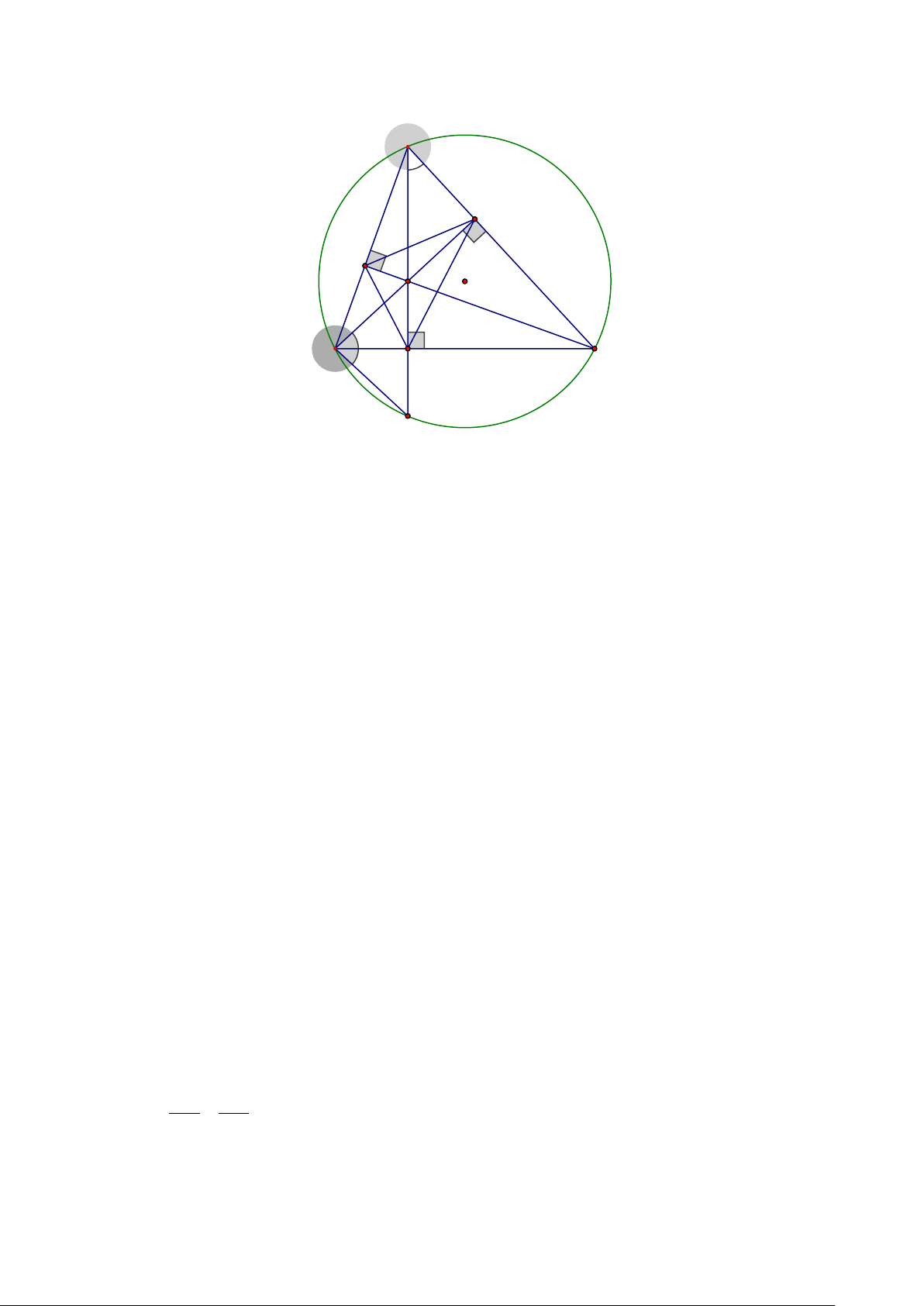
Bài 6. (2,5 điểm)Cho ∆ABC nhọn(AB < AC)nội tiếp đường tròn (O). Vẽ các đường
cao AD,BE,CF của ∆ABC cắt nhau tại H . Đường thẳng AD cắt đường tròn (O)tại R .
a) Chứng minh: Tứ giác CEHD và tứ giác BCEF nội tiếp. b) Chứng minh: .
AE AC = AH.AD và .
AE BC = AH.BE
c) Chứng minh: H và R đối xứng nhau qua BC và xác định tâm đường tròn nội tiếp∆DEF ĐÁP ÁN I.TRẮC NGHIỆM CÂU 1 2 3 4 5 6 7 8 9 10 11 12 ĐÁP ÁN B C B B A A D A C C A B II. TỰ LUẬN
Bài 1:(1 điểm) a) BGT: 0,25 x −4 −2 0 2 4 2 x y = 8 2 0 2 8 2 Vẽ đồ thị: 0,25
a) Điểm A thuộc (P) có hoành độ gấp hai lần tung độ nên có phương trình x = 2y 2 x x = 2. 2 2 x − x = 0 0,25 x(x −1) = 0 x = 0 ⇒ y = 0 1 x = 1 ⇒ y = 2
Vậy toạ độ điểm A cần tìm là (0;0) ; 1 1; . 0,25 2 Bài 2:(1 điểm) a) 2
3x −14x −1 = 0 (a = 3; b = −14; c = −1)
Vì ∆ = b − ac = (− )2 2 4
14 − 4.3.(−1) = 208 > 0 0,25
Nên phương trình có hai nghiệm phân biệt x ,x . 1 2 b (−14) 14
x + x = − = − = 1 2
b) Theo định lí Viète, ta có: a 3 3 0,25 c −1 x .x = = 1 2 a 3 Ta có: x x A = 1 + 2 x −1 x − 2 1 1 x x 1 x x 1 1 ( − 1 )+ 2 ( − 2 ) A = (x −1 x 1 2 )( − 1 ) 2 x − x + 2 x − x A = 1 1 2 2
x x − x − x + 1 2 1 1 2 ( 2 x + 2 x x x 1 2 ) − ( + 1 2 )
A = x x − x x 1 0,25*2 1 2 ( + 1 2 ) + (x + x 2x x x x 1 2 )2 − − 1 2 ( + 1 2 ) A = x x − x x 1 1 2 ( + 1 2 ) + 14 2 −1 14 − 2 − 3 3 3 40 A = = − −1 14 9 − + 1 3 3 Bài 3: (0,75) Điểm 3 4 5 6 7 8 9 10 Tần số 3 6 3 14 12 4 2 1
b)Vẽ biểu đồ tần số 0,5 Bài 4: (0,75)
a) Không gian mẫu {(xanh, vàng); (xanh, đỏ); (đỏ, vàng); (đỏ, đỏ)}
Có 4 kết quả sảy ra cho phép thử
b) Có 1 kết quả thoả mãn điều kiện hai quả bóng cùng màu là hai quả bóng cùng 1 P(M ) 0,25
màu đỏ. Xác suất của biến cố M là 4
Có 3 kết quả lấy ra hai quả bóng khác màu là cặp (xanh, vàng); (xanh, đỏ); (đỏ, vàng) 3 P(N ) 0,75
Xác suất của biến cố N là 4 Bài 5. (1.0 điểm)
a)Thể tích hình trụ là: V = πR2h = π. 0.22.0,4 = 0,05 (m3) 0.25
Lượng nước anh Minh đổ vào hồ sau mỗi lần gánh:
V = 2.0,05.90% = 0,09 (m3) 0.25
b)Thể tích cái hồ là: V = 2.2.1 = 4 (m3)
Số lần gánh của anh Minh để đầy hồ là: 4 : 0,09 = 44,4 0.25
Vậy anh minh cần gánh ít nhất 45 lần 0.25 BÀI 6: (2,5) A E F H O B D C R
a) Ta có: ∆CEH vuông tại E ( BE là đường cao)
⇒ ∆CEH nội tiếp đường tròn, đường kính CH (1)
Ta có: ∆CDH vuông tại D ( AD là đường cao)
⇒ ∆CDH nội tiếp đường tròn, đường kính CH (2)
Từ (1) và (2) ta được 4 điểm C , E , H , D cùng thuộc đường tròn, đường kính CH .
Vậy tứ giác CEHD nội tiếp.
Ta có: ∆BCE vuông tại E ( BE là đường cao)
⇒ ∆BCE nội tiếp đường tròn, đường kính BC (3)
Ta có: ∆BCF vuông tại F (CF là đường cao)
⇒ ∆BCF nội tiếp đường tròn, đường kính BC (4)
Từ (3) và (4) ta được 4 điểm B , C , E , F cùng thuộc đường tròn, đường kính BC .
Vậy tứ giác BCEF nội tiếp.
b) Xét ∆AEH và ∆ADC có: A là góc chung
AEH = ADC(= 90°)
Suy ra ∆AEH” ∆ADC (g.g) AE AD ⇒ = hay .
AE AC = AH.AD AH AC
Xét ∆BEC và ∆ADC có: C là góc chung
BEC = ADC(= 90°)
Suy ra ∆BEC” ∆ADC ( .gg)
Mà ∆AEH” ∆ADC (cmt)
Vậy ∆BEC” ∆AEH BC BE ⇒ = hay .
AE BC = AH.BE AH AE c) Ta có
HBD = RAC (cùng phụ ACB ) và
RAC = RBD (hai góc nội tiếp cùng chắn RC ) ⇒ HBD = RBD
Xét ∆HBD vuông tại D và ∆RBD vuông tại D có: BD là cạnh chung
HBD = RBD(cmt)
Suy ra ∆HBD” ∆RBD (cạnh góc vuông – góc nhọn kề)
⇒ HD = RD (2 cạnh tương ứng)
Mà HR ⊥ BC(gt)
Vậy H và R đối xứng nhau qua BC .
Ta có: ∆BFH vuông tại F (CF là đường cao)
⇒ ∆BFH nội tiếp đường tròn, đường kính BH (5)
Ta có: ∆BDH vuông tại D ( AD là đường cao)
⇒ ∆BDH nội tiếp đường tròn, đường kính BH (6)
Từ (5) và (6) ta được 4 điểm B , F , H , D cùng thuộc đường tròn, đường kính BH .
Vậy tứ giác BFHD nội tiếp.
Tương tự: chứng minh tứ giác ABDE nội tiếp
Xét tứ giác BFHD nội tiếp có 1 FDH = FBH = SdFH 2
Xét tứ giác ABDE nội tiếp có 1 EDH = FBH = SdAE 2 Suy ra FDH = EDH
⇒ DH là đường phân giác của ∆DEF
Chứng minh tương tự, ta có FH , EH là đường phân giác của ∆DEF
Vậy H là tâm của đường tròn nội tiếp ∆DEF
MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ II – TOÁN 9
A. BẢNG MA TRẬN ĐỀ KIỂM TRA.
Mức độ đánh giá Tổng Tổng số câu % T
Nhận biết Thông hiểu Vận dụng Vận dụng cao Chủ đề
Nội dung/Đơn vị kiến thức điểm T TN TN TNKQ TL TL TL TNKQ TL TNKQ TL KQ KQ
HÀM SỐ Y = ax2 ( a Hàm số và đồ thị hàm số y 2 ≠0) VÀ PHƯƠNG = ax2 ( a ≠ 0) (Bài 1 1 5 5 3 32,5 TRÌNH BẬC HAI
Phương trình bậc hai một ẩn 1a,b) (Bài 2) MỘT ẨN Định lí vi-et
Bảng tần số và biểu đồ tần số 2 MỘT SỐ YẾU TỐ 2
Bảng tần số tương đối và 2 ( Bài 2 2 12,5 THỐNG KÊ
biểu đồ tần số tương đối 3a,b)
Biểu diễn số liệu ghép nhóm GIẢI TOÁN BẰNG
Lập phương trình bậc hai 1
3 CÁCH LẬP PHƯƠNG một ẩn 1 ( Bài 1 1 10,0 TRÌNH 4)
Đường tròn ngoại tiếp tam
giác. Đường tròn nội tiếp 1 1 1
TỨ GIÁC NỘI TIẾP. tam giác 4 2 (Bài ( Bài (Bài 2 3 30,0 ĐA GIÁC ĐỀU
Tứ giác nội tiếp 6a) 6b) 6c)
Đa giác đều và phép quay Hình Trụ 2 CÁC HÌNH KHỐI 5 Hình nón 2 ( Bài 2 2 15,0
TRONG THỰC TIỄN Hình cầu 5a,b) Tổng 12 6 4 1 12 12 Tỉ lệ % 30% 35% 25% 10% 100 Tỉ lệ chung 65% 35% 100
ĐỀ THAM KHẢO KIỂM TRA CUỐI KỲ II MÔN TOÁN 9._ CỬU LONG
PHẦN 1. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm).
Câu 1: Hệ số a của hàm số 2 y = 2x − là A.3. B.-2. C.2. D. 2 2x − .
Câu 2: Điểm nào sau đây thuộc hàm số y = 1 2 x ? 2 A. (2; 1) B. (2; 8 ) C. (2; 4) D. (2; 2)
Câu 3: Phương trình nào là phương trình bậc hai một ẩn? A. 0x2 + 5x + 2 = 0 B. 6x2 + y -3 = 0 C. x2 - 2x = 0 D. 2x + y = 3
Câu 4: Phương trình: 2
3x 8x5 0 co biệt thức ∆ bằng: A. 124 B. 4 C. - 4 D. 79
Câu 5: Cho phương trình 2
x 11x 3 0 . Không giải phương trình, hãy tính tổng và tích các nghiệm, hãy chọn câu đúng:
A. x x 11; x x 3
x x 14; x x 33 1 2 1 2 B. 1 2 1 2 ;
C. x x 11; x x 3
x x 14; x x 33 1 2 1 2 D. 1 2 1 2 .
Dựaa vào biểu đồ biểu thị số lượng y tá theo năm công tác; hay trả lời câu 6,7.
Câu 6: Số năm công tác nào có số lượng y tá nhiều nhất. A. 4 năm B.5 năm; C. 6 năm D. 7 năm.
Câu 7: Có bao nhiêu y tá công tác dưới 4 năm? A. 6 B.16 C. 17 D. 23.
Câu 8: Một hình chữ nhật có chu vi là 30 m. Nếu đặt x (m) là chiều dài hình chữ nhật (x>0); thì chiều
rộng hình chữ nhật biểu diễn theo x là: A. 2x (m) B.30 – x (m) C. 15 – x (m) D. 2 x (m)
Câu 9: Tứ giác ABCD nội tiếp đường tròn có A = 1300. Khi đó C bằng: A. 400 B . 500 C . 1000 D . 1300
Câu 10: Lục giác đều là đa giác có: A. 6 cạnh bằng nhau.
B. 8 cạnh bằng nhau, 8 góc bằng nhau.
C. 6 cạnh bằng nhau, 6 góc bằng nhau. D. 8 góc bằng nhau.
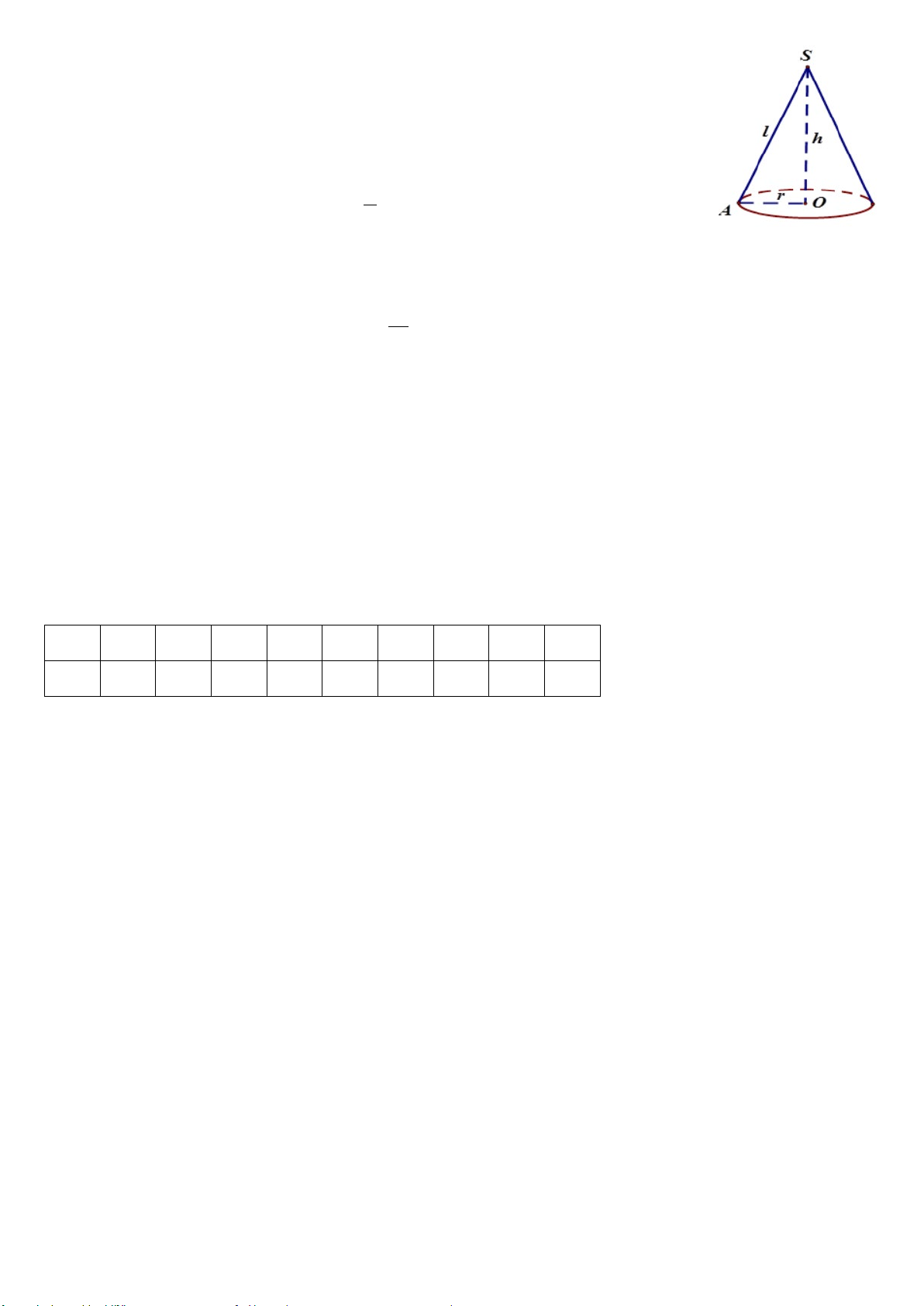
Câu 11: Cho hình nón có bán kính đáy r = 6 cm; đường sinh l = 10 cm. Tính chiều cao hình nón: A. 6 cm B.8 cm C. 15 cm D. 16 cm.
Câu 12: Chọn câu đúng nhất. Tìm thể tích hình cầu có bán kính là 5 cm. Biết
công thức tính thể tích hình cầu là 4 3 V R . 3 A. 523,5 3 cm B. 523,6 3 cm C.523 3 cm D. 65,4 3 cm
PHẦN 2: TỰ LUẬN (7 điểm) 2
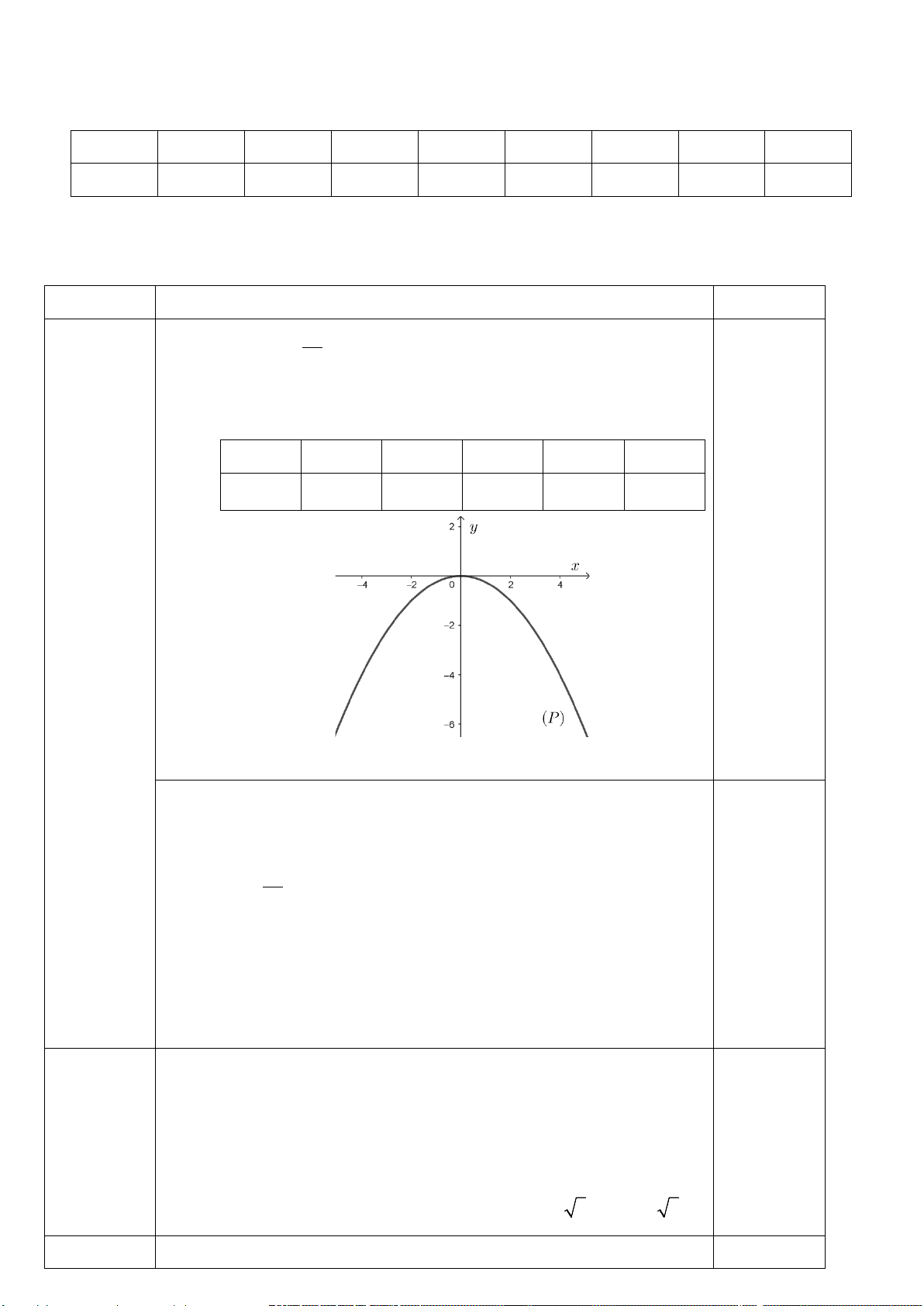
Bài 1. [TH] (1,0 điểm). Cho hàm số x y = − có đồ thị (P). 4
a) Vẽ đồ thị (P) của hàm số trên.
b) Tìm những điểm thuộc (P) có tung độ bằng hoành độ.
Bài 2. [VD] (1,0 điểm). Cho phương trình 2
3x − 6x − 7 = 0.
a) Chứng minh phương trình trên có hai nghiệm phân biệt x , x . 1 2
b) Không giải phương trình, hãy tính giá trị của biểu thức A = (x − 2 x − 2 . 1 )( 2 )
Bài 3. [TH] (0,75điểm). Kết quả điểm bài kiểm tra thường xuyên môn Toán ở lớp 9A được ghi lại như sau. 9 8 8 8 10 5 8 10 7 8 7 7 5 8 8 7 6 6 5 6
a) Lập bảng tần số cho mẫu số liệu trên.
b) Vẽ biểu đồ tần số dạng cột (hay dạng đoạn thẳng).
Bài 4. (0,75điểm) [TH] Bài toán về giải toán bằng cách lập phương trình .
Một tổ may mặc dự định may 320 cái áo trong một thời gian nhất định, nhưng do cải tiến kĩ thuật nên tổ
may thêm được 5 cái áo mỗi ngày, do đó không những rút ngắn được thời gian 3 ngày so với dự định
mà còn may thêm được 5 cái áo. Hỏi năng suất mỗi ngày theo dự định mà tổ may được là bao nhiêu cái áo ?
Bài 5: [ VD] (1 điểm) . Hiện nay các văn phòng thường sử dụng loại thùng rác văn phòng màu sắc, chất
liệu thân thiện với môi trường. Trong ảnh là một thùng rác văn phòng có đường cao 0,8m, đường kính 0,4m.
a) Hãy tính thể tích của thùng rác này? ( Biết 2
V = π.R .h. R bán kính đường tròn)
b) Tính diện tích phần giấy dùng để làm thùng rác tính cả nắp đậy. Biết phần giấy hao hụt cho mối ráp
là 5%. (Làm tròn đến hàng phần mười)
Bài 6. (2,5 điểm) Từ điểm S nằm ngoài đường tròn ( ;
O R) sao cho OS=2R,kẻ hai tiếp tuyến SB và SC
đến (O) ( B , C là các tiếp điểm) . Gọi H là giao điểm của SO và BC .
a) Chứng minh rằng:OS vuông góc với BC và H là trung điểm của BC.
b)Vẽ đường kính BD. SD cắt (O) tại K.Chứng minh:SH.SO=SD.SK .
c) OS cắt đường tròn tại M.Tính theo R diện tích tứ giác SBMC
ĐÁP ÁN ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II – KHỐI 9 MÔN: TOÁN
PHẦN I. TRẮC NGHIỆM (2,0 điểm) Câu 1 2 3 4 5 6 7 8 Đáp án B A C D C B C A
PHẦN I . TỰ LUẬN (8,0 điểm) Đáp án Điểm Câu 1. 2 0,25 ×3 Cho hàm số x y = − có đồ thị (P). (1,5 điểm) 4
a) Vẽ đồ thị (P) của hàm số trên. Bảng giá trị x - 4 - 2 0 2 4 y - 4 - 1 0 -1 - 4
b) Tìm những điểm thuộc (P) có tung độ bằng hoành độ. 0,25 × 3 Gọi M ( ;
x x)∈(P) , ta có 2 x x = − 4 ... x = 0 1 x = 4 − 2
Vậy có hai điểm cần tìm có toạ độ (0;0) và ( 4; − 4 − ). Câu 2.
(2x −3)2 − 4x = 5 0,25 ×3 (0,75 điểm) 2
4x −16x + 4 = 0 2 x − 4x +1 = 0 ∆ = (− )2 4 − 4 =12 > 0
Vậy phương trình có hai nghiệm phân biệt là x = 2 + 3, x = 2 − 3 . 1 2 Câu 3. 0,25x2