Đề tham khảo giữa kì 2 Toán 12 năm 2022 – 2023 THPT Thuận Thành 1 – Bắc Ninh

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giữa học kì 2 môn Toán 12 năm học 2022 – 2023 .Mời bạn đọc đón xem.

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

43 trang 8 tháng trước

Tác giả:

Profile Lan Tường
1
TRƯỜNG THPT THUẬN THÀNH SỐ 1
TỔ TOÁN
-------------
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: Toán lớp 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Thầy Nguyễn Chí Khôi
Câu 1: Cho hàm số
4 2
2y x x
có đồ thị như hình vẽ bên. Tìm
tất cả các giá trị thực của tham số
m
để phương trình
4 2
2
2 logx x m
có bốn nghiệm thực phân biệt.
A.
0 1.
m
B.
0.
m
C.
1 2
m
. D.
2.
m
Câu 2: Thể tích khối chóp có đường cao bằng
và đáy là hình vuông cạnh
2a
bằng
A.
3
4
.
3
a
B.
3
2 .a
C.
3
4 .a
D.
3
2
.
3
a
Câu 3: Trong không gian
Oxyz
, mặt phẳng nào dưới đây song song với mặt phẳng
( )Oxy
?
A.
( ) : 1 0
x
. B.
( ) : 1 0
z
.
C.
( ) : 1 0
x z
. D.
( ) : 1 0
y
.
Câu 4: Biết hàm số
2sin cos
sin cos
x m x
y
x x
đạt giá trị lớn nhất trên
0;
4
bằng 1. Mệnh đề nào sau
đây đúng?
A.
1;0
m
. B.
0;1
m
. C.
1;2
m
. D.
2;3
m
.
Câu 5: Trong không gian tọa độ
Oxyz
, cho mặt phẳng
:4 3 1 0
P x y z
và đường thẳng
1 6 4
:
4 3 1
x y z
d
. Sin của góc giữa đường thẳng
d
và mặt phẳng
P
bằng:
A.
5
13
. B.
1
13
. C.
12
13
. D.
8
13
.
Câu 6: Trong không gian
Oxyz
, cho hai điểm
3; 2;2
A
,
2;2;0
B
và mặt phẳng
: 2 2 3 0
P x y z
. Xét các điểm
,M N
di động trên
P
sao cho
1
MN
. Giá trị nhỏ nhất
của biểu thức
2 2
2 3
MA NB
bằng
A.
45.
B.
53.
C.
49,8.
D.
55,8.
O
x
y
1
1
1
2
Câu 7: Cho hàm số
( )y f x
có đồ thị như hình bên dưới. Hàm
số đã cho nghịch biến trên khoảng nào dưới đây?
A.
2;2 .
B.
1;2 .
C.
1;1 .
D.
2;0 .
Câu 8: Biết
4
0
2 1d 5
ln 2 ln , ,
3
2 3 2 1 3
x x
a b c a b c
x x
. Tính
2
T a b c
.
A.
4T
. B.
2T
. C.
1T
. D.
3
T
.
Câu 9: Đường cong trong hình là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
.
B.
3
3 2y x x
.
C.
1
x
y
x
.
D.
4 2
2 1
y x x
.
Câu 10: Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
, gọi
là góc giữa đường thẳng
A B
và mặt phẳng
BB D D
. Tính
sin
.
A.
3
2
. B.
3
5
. C.
3
4
. D.
1
2
.
Câu 11: Biết
4
2
3
ln 2 ln3 ln 5
dx
I a b c
x x
, trong đó
, ,
a b c Z
. Tính giá trị
T a b c
.
A.
1 T
. B.
5
T
. C.
3
T
. D.
2T
.
Câu 12: Một khối đồ chơi gồm một khối nón (N) xếp chồng
lên một khối trụ (T). Khối trụ (T) có bán kính đáy và chiều
cao lần lượt là
1 1
, r h
. Khối nón (N) có bán kính đáy và chiều
cao lần lượt là
2 2
, r h
thỏa mãn
2 1
2
3
r r
và
2 1
h h
(tham
khảo hình vẽ bên). Biết rằng thể tích của toàn bộ khối đồ
chơi bằng
3
124 cm
, thể tích khối nón (N) bằng
A.
3
62 cm .
B.
3
15 cm .
C.
3
108 cm .
D.
3
16 cm .
O
x
y
1
1
1
1
3
Câu 13: Đáy của một lăng trụ tam giác đều là tam giác
ABC
có cạnh bằng
a
. Trên các cạnh bên
lấy các điểm
1
A
,
1
B
,
1
C
lần lượt cách đáy một khoảng bằng
2
a
,
a
,
3
2
a
(tham khảo hình vẽ bên).
Cosin góc giữa
1 1 1
A B C
và
ABC
bằng
A.
2
2
. B.
3
2
. C.
13
4
. D.
15
5
.
Câu 14: Xét các số thực dương
,x y
thỏa mãn
2 2
3
log 3 3
2
x y
x x y y xy
x y xy
.
Tìm giá trị lớn nhất
max
P
cuả biểu thức
3 2 1
6
x y
P
x y
.
A.
max
3.P
B.
max
2.P
C.
max
1.P
D.
max
4.P
Câu 15: Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
1
: .
1 2 2
x y z
d
Vectơ nào
sau đây là vectơ chỉ phương của đường thẳng
?d
A.
2
1; 2; 2 .u
B.
4
0;1;0 .u
C.
3
1; 2;2 .u
D.
1
1;2; 2 .u
Câu 16: Hàm số
y f x
có đạo hàm
3
4 2
2 ,f x x x x x
. Số điểm cực trị của
hàm số là
A.
3
. B.
2
. C.
1
. D.
4
.
Câu 17: Cho hàm số
y f x
liên tục trên
2;6
và có đồ thị
như hình vẽ dưới. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của hàm số đã cho trên đoạn
2;6
. Hiệu
M m
bằng
A.
4
. B.
8
.
C.
6
. D.
3
.
A
1
C
1
B
1
B
C
A
4
Câu 18: Từ các chữ số
1,2,3, 4,5,6
. Có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số khác
nhau?
A.
. B.
20
. C.
120
. D.
720
.
Câu 19: Tìm số nghiệm của phương trình
2
ln 4 ln 6 .
x x x
A.
2.
B.
1.
C.
3.
D.
0.
Câu 20: Trong không gian
Oxyz
, cho mặt phẳng
( ) : 3 0
P x y z
và đường thẳng
2 1
:
2 1 3
x y z
d
. Hình chiếu vuông góc của đường thẳng
d
trên
( )P
có phương trình là
A.
1 2
2 3 5
x y z
. B.
1 2
2 7 5
x y z
.
C.
1 2
4 3 7
x y z
. D.
1 2
5 8 13
x y z
.
Câu 21: Cho hàm số liên tục trên R, có đồ thị như hình
vẽ bên. Gọi là diện tích hình phẳng được giới hạn bởi đồ thị
hàm số , trục hoành và trục tung. Khẳng định nào sau đây
đúng?
A. .
B. .
C. .
D. .
Câu 22: Tìm tập nghiệm của bất phương trình
2x 1 x 2
2018 2019
2019 2018
.
A.
1;
. B.
;1
. C.
1;

. D.
; 1
.
Câu 23: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
2AB a
,
BC a
, mặt bên
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
E
là trung điểm của
CD
. Tính
theo
khoảng cách giữa hai đường thẳng
BE
và
SC
.
A.
15
5
a
. B.
3
2
a
. C.
.a
D.
30
10
a
.
Câu 24: Phương trình tham số của đường thẳng
d
đi qua hai điểm
1;2; 3
A
và
3; 1;1
B
là
A.
1
2 2
1 3
x t
y t
z t
. B.
1 3
2
3
x t
y t
z t
. C.
1 2
2 3
3 4
x t
y t
z t
. D.
1 2
5 3
7 4
x t
y t
z t
.
f x
S
f x
0
d d
d
c d
S f x x f x x
0
d d
d
c d
S f x x f x x
0
d d
d
c d
S f x x f x x
0
d d
d
c d
S f x x f x x
O
x
y
c
d
y f x
5
Câu 25: Tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2 3
3 3 6y x mx x m
đồng
biến trên khoảng
0;
là:
A.
; 1 .
B.
2; .
C.
; 2 .
D.
; 0 .
Câu 26: Cho cấp số nhân
( )
n
u
thỏa mãn
1
3u
và
5
48u
. Số hạng thứ ba của cấp số nhân bằng
A.
8.
B.
16.
C.
12.
D.
16.
Câu 27: Cho biết đồ thị của hàm số
2
1
x
y
x
cắt đường thẳng
:d y x m
tại hai điểm phân biệt
,A B
. Gọi I là trung điểm của đoạn
AB
. Tìm giá trị của
m
để
I
nằm trên trục hoành.
A.
3m
. B.
4m
. C.
1m
. D.
2m
.
Câu 28: Tích các nghiệm của phương trình
1
1
5
log 6 36 2
x x
bằng
A.
0
. B.
6
log 5
. C.
5
. D.
1
.
Câu 29: Họ nguyên hàm của hàm số
3
x
f x x
là
A.
2
3 ln 3
2
x
x
C . B.
3
1
ln3
x
C . C.
1 3 ln 3
x
C
. D.
2
3
2 ln 3
x
x
C .
Câu 30: Cho hàm số
y f x
có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng
A.
.
B.
.
C.
.
D.
.
Câu 31: Với
5
log 3 a
thì
15
log 45
bằng
A.
2
1
1
a
a
. B.
1 2
1
a
a
. C.
2
1
a
a
. D.
2
a
.
Câu 32: Thể tích V của khối chóp có diện tích đáy B và chiều cao h là:
A.
V Bh
B.
1
2
V Bh
C.
2V Bh
D.
1
3
V Bh
Câu 33: Cho hàm số
f x
có bảng biến thiên như hình vẽ. Khẳng định nào dưới đây là khẳng
định đúng?
3
26
6
1
6
A. Đồ thị của hàm số
f x
có đúng 1 tiệm cận ngang và 1 tiệm cận đứng.
B. Đồ thị của hàm số
f x
không có tiệm cận ngang và có 1 tiệm cận đứng.
C. Đồ thị của hàm số
f x
có đúng 2 tiệm cận ngang và không có tiệm cận đứng.
D. Đồ thị của hàm số
f x
có đúng 2 tiệm cận ngang và 1 tiệm cận đứng.
Câu 34: Cho hình lăng trụ tam giác đều
.ABC A B C
có
AB a
, góc giữa
A C
và mặt phẳng
ABC
bằng
45
. Thể tích khối lăng trụ
.ABC A B C
bằng
A.
3
3
2
a
. B.
3
3
6
a
. C.
3
3
12
a
. D.
3
3
4
a
.
Câu 35: Với mọi
, ,a b x
là các số thực dương thoả mãn
2 2 2
log 5log 3logx a b
. Khẳng định
nào dưới đây đúng ?
A.
5 3
x a b
. B.
5 3x a b
. C.
5 3
x a b
. D.
3 5x a b
.
Câu 36: Biết
2
2
1
ln
d ln 2
x b
x a
x c
( với
a
là số hữu tỉ,
b
,
c
là các số nguyên dương và
b
c
là phân
số tối giản). Tính giá trị của
2 3S a b c
.
A.
4S
. B.
6S
. C.
6S
. D.
5S
.
Câu 37: Cho khối lăng trụ
.ABC A B C
có thể tích bằng
2019
(đvtt). Gọi
M
là trung điểm của
A B
, hai điểm
,N
P
lần lượt nằm trên các cạnh
B C
và
BC
sao cho
3B N NC
,
1
4
BP BC
. Đường thẳng
NP
cắt
BB
tại
E
, đường thẳng
EM
cắt cạnh
AB
tại
Q
. Thể tích khối đa diện
lồi
AQPCA MNC
bằng
A.
39707
24
. B.
63935
36
. C.
15479
12
. D.
88163
48
.
Câu 38: Cho nửa đường tròn đường kính
AB R 2
và điểm
C
thay đổi trên nửa đường tròn đó,
đặt
CAB
và gọi
H
là hình chiếu vuông góc của
C
lên
AB
. Tìm
sao cho thể tích vật thể
tròn xoay tạo thành khi quay tam giác
ACH
quanh trục
AB
đạt giá trị lớn nhất.
A.
0
45
B.
1
arctan
2
C.
0
30
D.
0
60
7
Câu 39: Trong không gian tọa độ
Oxyz
, cho mặt cầu
2 2 2
5
: ( 1) ( 1)
6
S x y z
, mặt phẳng
: 1 0P x y z
và đường thẳng
:
1 1 1
x y z
. Điểm
M
thay đổi trên đường tròn giao tuyến
của
P
và
S
. Giá trị lớn nhất của
,d M
là:
A.
2
. B.
3 2
2
. C.
2
2
. D.
2 2
.
Câu 40: Ông A vay ngân hàng
50
triệu đồng với lãi suất
0,67%
/tháng. Ông ta muốn hoàn nợ cho
ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông ta bắt đầu hoàn nợ; hai lần hoàn nợ
liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ mỗi tháng đều bằng nhau và bằng
3
triệu. Biết
rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi bằng cách hoàn nợ
đó, ông A cần trả ít nhất bao nhiêu tháng kể từ ngày vay đến lúc hoàn hết nợ ngân hàng (giả định
trong thời gian này lãi suất không thay đổi)
A.
17
tháng. B.
19
tháng. C.
18
tháng. D.
20
tháng.
Câu 41: Cho hình nón có bán kính đáy bằng
a
và diện tích xung quanh bằng
2
3 a
. Độ dài đường
sinh của hình nón bằng
A.
3
2
a
. B.
2a
. C.
3a
. D.
9a
.
Câu 42: Một chiếc cổng có hình dạng là một parabol (P) có
kích thước như hình vẽ, biết chiều cao cổng bằng
4 m
,
4 mAB
. Người ta thiết kế cửa đi là một hình chữ nhật
CDEF
(với
, ;C F AB
, ( )D E P
), phần còn lại (phần
gạch chéo) dùng để trang trí. Biết chi phí để trang trí phần
tô đậm là 1.000.000 đồng/
2
m . Hỏi số tiền ít nhất dùng để
trang trí phần tô đậm gần với số tiền nào dưới đây?
A.
4.450.000
đồng. B.
4.605.000
đồng.
C.
4.505.000
đồng. D.
4.509.000
đồng.
Câu 43: Có 3 quyển sách Văn học khác nhau, 4 quyển sách Toán học khác nhau và 7 quyển sách
Tiếng anh khác nhau được xếp lên một kệ ngang. Tính xác suất để hai cuốn sách cùng môn không
ở cạnh nhau.
A.
1
1716
. B.
5
8008
. C.
1
1001
. D.
19
12012
.
Câu 44: Cho hàm số
y f x
. Hàm số
y f x
có bảng biến thiên như sau
8
Bất phương trình
cos
2 3
x
f x m
đúng với mọi
0;
2
x
khi và chỉ khi
A.
1
1 .
3 2
m f
B.
1
1 .
3 2
m f
C.
1
0 2 .
3
m f
D.
1
0 2 .
3
m f
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho
(1;0;0) , B(0;2;0), C(0;0;3)A
, phương trình
nào sau đây là phương trình mặt phẳng .
A.
1
2 3
y z
x
B.
6 3 2 6 0 x y z
C.
6 3 2 6 0 x y z
D.
12 6 4 12 0x y z
Câu 46: Xét tam thức bậc hai
2
f x ax bx c
, với
, ,a b c R
, thỏa mãn điều kiện
1f x
,
với mọi
1;1x
. Gọi
m
là số nguyên dương nhỏ nhất sao cho
2;2
max
x
f x m
. Khi đó
m
bằng
A.
8
. B.
7
. C.
4
. D.
3
.
Câu 47: Cho hàm số
f x
có bảng xét dấu của đạo hàm như sau
Hàm số
3 2
3
3 2 2 3 2019
2
y f x x x x
đồng biến trên khoảng nào dưới đây?
A.
1;
. B.
; 1
. C.
1
1;
2
. D.
0;2
.
Câu 48: Phương trình
2
2 4 5
2 32
x x
có bao nhiêu nghiệm?
A. 3. B. 0. C. 1. D. 2.
Câu 49: Trong không gian với hệ toạ độ
Oxyz
, phương trình mặt cầu đường kính
AB
với
1; 1;2
A
,
3;1;2
B
là:
A.
2 2
2
2 1 5x y z
. B.
2 2
2
2 1 5x y z
.
C.
2 2
2
1 2 5x y z
. D.
2 2
2
1 2 5x y z
.
Câu 50: Hàm số
2
log 1y x
có đạo hàm là
A.
2
2
'
1 ln10
x
y
x
. B.
2
1
'
1 ln10
y
x
. C.
2
2 ln10
'
1
x
y
x
. D.
2
ln10
'
1
y
x
.
----------- HẾT ----------
9
TRƯỜNG THPT THUẬN THÀNH SỐ 1
TỔ TOÁN
-------------
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: Toán lớp 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Thầy Nguyễn Bá Cao
Câu 1: Số cách sắp xếp
6
học sinh theo một hàng dọc bằng
A.
46656
. B.
4320
. C.
720
. D.
360
.
Câu 2 : Cho cấp số nhân
n
u
có số hạng đầu
1
5
u
và công bội
2
q
. Giá trị của
6
u
bằng
A.
160
. B.
320
. C.
160
. D.
320
.
Câu 3: Cho hàm số
y f x
có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng
1; 3
.
B. Hàm số đồng biến trên khoảng
1;
.
C. Hàm số nghịch biến trên khoảng
1;1
.
D. Hàm số đồng biến trên khoảng
;1
.
Câu 4: Hàm số
y f x
liên tục trên
và có bảng biến thiên dưới đây.
.
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại
1
x
. B. Hàm số đạt cực đại tại
0
x
.
C. Hàm số có ba điểm cực trị. D. Hàm số đạt cực đại tại
2
x
.
Câu 5: Hàm số
2 5
1
x
y
x
có bao nhiêu điểm cực trị?
A.
0
. B.
2
. C.
3
. D.
1
.
Câu 6: Tiệm cận ngang của đồ thị hàm số
5
1
y
x
là đường thẳng có phương trình
A.
5
y
. B.
0
x
. C.
1x
. D.
0
y
.
10
Câu 7: Đường cong dưới đây là đồ thị của hàm số nào?
A.
3
3y x x
. B.
3
3 1y x x
.
C.
3
3y x x
. D.
3
3 1y x x
.
Câu 8: Cho hàm số
y f x
có bảng biến thiên như sau:
Tìm tất cả các giá trị của tham số
m
để phương trình
f x m
có ba nghiệm phân biệt.
A.
2
m
. B.
2 4
m
. C.
2 4
m
. D.
4
m
.
Câu 9: Cho
a
là số thực dương khác
1
. Tính
3
log .
a
I a
A.
1
3
I
. B.
3
I
. C.
0
I
. D.
3
I
.
Câu 10: Hàm số nào sau đây đồng biến trên
;
 
?
A.
2021
2
x
y
. B.
5 2
x
y . C.
3
x
y
. D.
0,7
x
y
.
Câu 11: Tập xác định của hàm số
1
5
1
y x
là
A.
0;
. B.
1;
. C.
1;
. D.
.
Câu 12: Số nghiệm của phương trình
2
2 5 3
2 1
x x
là
A.
3
. B.
2
. C.
0
. D.
1
.
Câu 13: Tập nghiệm của bất phương trình
2
log 1 3
x
là
A.
9;
. B.
4;
. C.
1;
. D.
10;
.
Câu 14: Cho hàm số
cosf x x x
.Trong các khẳng định sau, khẳng định nào đúng?
A.
2
d sin
2
x
f x x x C
. B.
d 1 sin
f x x x C
.
C.
d sin cos
f x x x x x C
. D.
2
d sin
2
x
f x x x C
.
Câu 15: Biết
F x
là một nguyên hàm của hàm số
f x
. Trong các khẳng định sau, khẳng định
nào đúng?
O
x
y
11
A.
3 1 d 3 1
f x x F x C
. B.
3 1 d 3 1
f x x xF x C
.
C.
3 1 d 3
f x x xF x x C
. D.
3 1 d 3
f x x F x x C
.
Câu 16: Cho hàm số
f x
liên tục trên
và
F x
là nguyên hàm của
f x
, biết
9
0
d 9
f x x
và
0 3
F
. Giá trị của
9
F
bằng
A.
9 6
F
B.
9 12
F
C.
9 6
F
D.
9 12
F
Câu 17: Cho hàm số
f x
liên tục trên
và
2
0
2 d 5
f x x x
. Tính
2
0
( )df x x
.
A.
9
. B.
1
. C.
9
. D.
1
.
Câu 18: Tập nghiệm của bất phương trình
2
2 1
2
log 3 2 log 1 2
x x x
là
A.
1;6
S
. B.
1;S
. C.
2;S
. D.
2;6
S
.
Câu 19: Từ một tổ gồm
8
nam và
7
nữ chọn ra một đoàn đại biểu gồm
5
người để tham dự hội
nghị. Xác suất để đại biểu được chọn có đúng
2
nữ bằng
A.
140
429
. B.
56
143
. C.
28
715
. D.
1
39
.
Câu 20: Tính diện tích S của hình phẳng giới hạn bởi các đồ thị các hàm số
lny x
,
1y
,
1y x
.
A.
3
2
S e
. B.
1
2
S e
. C.
1
2
S e
. D.
3
2
S e
Câu 21: Cho hình chóp có diện tích mặt đáy là
2
3a
và chiều cao bằng
2a
. Thể tích của khối
chóp bằng
A.
3
6a
. B.
3
2a
. C.
3
3a
. D.
3
a
.
Câu 22: Cho khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng
3
. Thể tích khối lăng trụ
đã cho bằng
A.
9 3
4
. B.
27 3
4
. C.
27 3
2
. D.
9 3
2
.
Câu 23: Cho hình nón có bán kính đáy là
2
r
và độ dài đường sinh
4l
. Diện tích xung quanh
của hình nón đã cho bằng
A.
16
. B.
8 2
. C.
16 2
. D.
4 2
.
Câu 24: Khối trụ có chiều cao bằng bán kính đáy và diện tích xung quanh bằng
2
. Thể tích
khối trụ bằng
A.
. B.
2
. C.
3
. D.
4
.
Câu 25: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
3;0;0
M
,
0;0;4
N
. Độ dài đoạn
thẳng
MN
bằng
12
A.
1
. B.
7
. C.
5
. D.
10
.
Câu 26: Trong không gian với hệ tọa độ
Oxyz
, mặt cầu
2 2 2
: 2 2 4 2 0
S x y z x y z
có bán kính bằng
A.
2 2
. B.
26
. C.
4
. D.
2
.
Câu 27: Trong không gian với hệ tọa độ
Oxyz
, điểm
3;4; 2
M
thuộc mặt phẳng nào trong
các mặt phẳng sau?
A.
: 7 0
R x y
. B.
: 5 0
S x y z
.
C.
: 1 0
Q x
. D.
: 2 0
P z
.
Câu 28: Trong không gian với hệ tọa độ
Oxyz
, vectơ nào dưới đây là một vectơ chỉ phương của
đường thẳng đi qua hai điểm
1;2;2
A
,
3; 2;0
B
?
A.
1
1;2;1
u
. B.
2
1;2; 1
u
. C.
3
2; 4;2
u
. D.
4
2;4; 2
u
.
Câu 29: Một tổ học sinh có
7
nam và
3
nữ. Chọn ngẫu nhiên
2
người. Xác suất sao cho
2
người được chọn có ít nhất một người nữ bằng
A.
2
15
. B.
7
15
. C.
8
15
. D.
1
15
.
Câu 30: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
1
mx
y
x m
đồng biến trên mỗi
khoảng xác định?
A.
4
. B.
6
. C. Vô số. D.
2
.
Câu 31: Gọi
,M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
1
1
x
f x
x
trên
đoạn
3;5
. Khi đó
M m
bằng
A.
7
2
. B.
1
2
. C.
2
. D.
3
8
.
Câu 32: Tập nghiệm của bất phương trình
1
3
3
5 5
x
x
là
A.
; 5
. B.
;0

. C.
5;

. D.
0;

.
Câu 33: Cho hàm số
f x
có đạo hàm liên tục trên
2;3
đồng thời
2 2
f
,
3 5
f
.
3
2
df x
x
bằng
A.
3
B.
7
C.
10
D.
3
Câu 34: Với
a
là số thực dương bất kỳ, mệnh đề nào dưới đây đúng?
A.
log 3 3loga a
. B.
1
log 3 log
3
a a
. C.
3
log 3loga a
.D.
3
1
log log
3
a a
.
Câu 35: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
, 2, 3AB a AD a SA a
và
SA ABCD
( tham khảo hình vẽ) . Góc giữa đường thẳng
SC
và mặt phẳng
ABCD
bằng
13
A.
0
60
. B.
0
120
. C.
0
30
. D.
0
90
.
Câu 36: Cho hình lập phương
. ' ' ' 'ABCD A B C D
có cạnh bằng 1 ( tham khảo hình vẽ). Khoảng
cách giữa hai đường thẳng
'AA
và
'BD
bằng
A.
3
3
. B.
2
2
. C.
2 2
5
. D.
3 5
7
.
Câu 37: Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
1; 0; 2
I
và mặt phẳng
P
có
phương trình:
2 2 4 0
x y z
. Phương trình mặt cầu
S
có tâm
I
và tiếp xúc với
mặt phẳng
P
là
A.
2 2
2
1 2 9
x y z
. B.
2 2
2
1 2 3
x y z
.
C.
2 2
2
1 2 3
x y z
. D.
2 2
2
1 2 9
x y z
.
Câu 38: Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
1;2; 3
A
,
2;3;1
B
đường thẳng
đi qua
1;2; 3
A
và song song với
OB
có phương trình tham số là
A.
1 2
2 3
3
x t
y t
z t
. B.
2
3 2
1 3
x t
y t
z t
. C.
1 2
2 3
3
x t
y t
z t
. D.
1 4
2 6
3 2
x t
y t
z t
.
C
A
B
D
S
D'
C'
A'
DA
B
C
B'
14
Câu 39: Cho hàm số
y f x
có đồ thị
f x
như hình vẽ
Giá trị lớn nhất của hàm số
3
2 24 2
x x x
g x f
trên đoạn
4;2
bằng
A.
2
1
3
f
. B.
1 11
2 24
f
. C.
2
2
3
f
. D.
2
1
3
f
.
Câu 40: Có bao nhiêu giá trị nguyên dương của tham số
m
nhỏ hơn 2021 để bất phương trình
1
4 2 .2 3 0
x x
m m
có nghiệm?
A.
2019.
B.
0.
C.
2020.
D. 2018.
Câu 41: Nếu
1
0
3 1 d 2
f x x
và
2
2
2
2
1
log
log d ln 2
x
f x x
x
thì
4
0
df x x
bằng
A.
4.
B.
7.
C.
8.
D.
4
.
Câu 42: Có bao nhiêu số nguyên dương
m
sao cho ứng với mỗi
m
luôn có ít hơn
4041
số
nguyên
thoả mãn
3 3
log log 4 1 0
x m x
?
A.
. B.
11
. C.
. D.
9
.
Câu 43: Cho hình hộp
.
ABCD A B C D
có đáy
ABCD
là hình thoi cạnh
a
,
3BD a
. Hình
chiếu vuông góc của
B
trên mặt phẳng
A B C D
là giao điểm của
A C
và
' 'B D
(
tham khảo hình vẽ). Góc giữa hai mặt phẳng
' ' ' 'A B C D
và
' 'ADD A
bằng
0
60 .
Thể tích khối hộp
.
ABCD A B C D
bằng
15
A.
3
3
4
a
. B.
3
3 3
4
a
. C.
3
3 3
8
a
. D.
3
3
8
a
.
Câu 44: Một bồn hình trụ đang chứa đầy nước, được đặt nằm ngang, chiều dài bồn là
4m
, bán
kính đáy
1,2m
. Người ta rút nước trong bồn một lượng tương ứng như hình vẽ. Thể tích
của lượng nước còn lại trong bồn xấp xỉ bằng
A.
3
12,637m . B.
3
14,558m . C.
3
12,064m . D.
3
13,571m .
Câu 45 : Trong không gian với hệ tọa độ
Oxyz
, cho hai điểm
2;4;1 , 0; 2;1A B
và mặt phẳng
: 2 4 0P x y z
. Đường thẳng
d
nằm trên
P
sao cho mọi điểm của
d
cách
đều 2 điểm
, A B
có phương trình là
A.
4 3
.
x t
y t
z t
B.
4 3
.
x t
y t
z t
C.
1 3
1 .
1
x t
y t
z t
D.
1
1 3 .
1 3
x t
y t
z t
Câu 46: Cho hàm số
f x
có
2 2
16 1 4 4f x x x x x m
. Có bao nhiêu giá trị
nguyên của tham số
m
thuộc
2021;2021
sao cho hàm số
2
g x f x
có 5 điểm
cực trị?
A.
2025
. B.
2026
. C.
2021
. D.
4043.
Câu 47: Có bao nhiêu số nguyên dương
a
sao cho tồn tại số thực x thỏa mãn
16
2021
2021.ln 1
2021
2021.ln 1
2020 2 2020
x
x
x a
a x
A.
5
. B.
2
. C.
3
. D.
4
Câu 48: Ông An dự định làm một vườn hoa dạng elip được chia ra làm bốn phần bởi hai đường
parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ dưới. Biết độ dài
trục lớn, trục nhỏ của elip lần lượt là
16m
và
8m
,
1 2
,F F
là hai tiêu điểm của elip. Phần
A
,
B
dùng để trồng hoa, phần
C
,
D
dùng để trồng cỏ. Kinh phí để trồng mỗi mét
vuông hoa và cỏ lần lượt là
200.000
đồng và
100.000
đồng. Tính tổng tiền để hoàn thành
vườn hoa trên (làm tròn đến hàng nghìn).
A.
17.679.000
đ. B.
19.526.000
đ. C.
15.831.000
đ. D.
13.547.000
đ.
Câu 49. Cho hàm số
f x
có đạo hàm cấp hai liên tục trên
thỏa mãn
2
1 2021, 1 2 , .
f f x x f x x x
Tính
2
0
d .xf x x
A.
674.
I
B.
673.
I
C.
2021
.
3
I
D.
2020
.
3
I
Câu 50: Trong không gian với hệ tọa độ
Ox ,yz
cho
3; 1;2 , 1;1;8
A B
và mặt phẳng
: 5 0.
P x y z
Mặt cầu
S
đi qua hai điểm
,A B
và tiếp xúc với
P
tại điểm
C
. Biết
C
luôn thuộc một đường tròn
T
cố định, tính bán kính
r
của đường tròn
T
.
A.
33
r . B.
5
r
. C.
37
r . D.
6.
r
--------------------Hết----------------------
17
TRƯỜNG THPT THUẬN THÀNH SỐ 1
TỔ TOÁN
-------------
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: Toán lớp 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Nguyễn Thị Diệp
Câu 1:
Cho với là các số hữu tỷ. Giá trị của bằng
A.
.
B. .
C.
.
D.
.
Câu 2:
Trong không gian
Oxyz
, đường thẳng
đi qua
1;2; 3
M
nhận vectơ
1;2;1
u
làm
vectơ chỉ phương có phương trình là
A.
1 2 3
1 2 1
x y z
.
B.
1 2 3
1 2 1
x y z
.
C.
1 2 3
1 2 1
x y z
.
D.
1 2 3
1 2 1
x y z
.
Câu 3:
Cho hàm số xác định và liên tục trên có , . Biết
. Tìm tất cả giá trị của tham số để phương trình có hai
nghiệm thực phân biệt.
A.
3
4
m e
.
B.
.
C.
.
D.
.
Câu 4:
Cho là hình phẳng giới hạn bởi các đường , và trục hoành (phần
kẻ dọc trong hình vẽ). Diện tích của bằng
A.
.
B.
.
C.
.
D.
.
1
2
0
ln 2 ln 3
2
xdx
a b c
x
, ,a b c
3
a b c
1
2
1
2
y f x
0,f x x
3
1
f e
2 1,
f x
x x
f x
m
f x m
3
4
0
m e
3
4
m e
3
4
1
m e
H
y x
2y x
H
O
x
y
4
2
2
y x
O
x
y
4
2
2
y x
O
x
y
4
2
2
y x
7
3
16
3
8
3
10
3
18
Câu 5:
Trong không gian với hệ tọa độ
Oxyz
cho điểm
1;0;2
A
và đường thẳng
d
có phương
trình:
1 1
1 1 2
x y z
. Viết phương trình đường thẳng
đi qua A, vuông góc và cắt d.
A.
1 2
2 2 1
x y z
B.
1 2
1 3 1
x y z
C.
1 2
1 1 1
x y z
D.
1 2
1 1 1
x y z
Câu 6:
Tính .
A.
.
B.
.
C.
.
D.
.
Câu 7:
Hàm số là một nguyên hàm của hàm số trên khoảng nếu
A.
B.
C.
D.
Câu 8:
Tìm họ tất cả các nguyên hàm của hàm số trên .
A.
.
B.
.
C.
.
D.
.
Câu 9:
Trong không gian , tọa độ của vectơ vuông góc với hai vectơ
là
A. .
B. .
C. .
D. .
Câu 10:
Trong không gian , có bao nhiêu mặt phẳng song song với mặt phẳng
và tiếp xúc với mặt cầu ?
A.
0.
B.
2
C.
3.
D.
1.
Câu 11:
Trong không gian , cho tứ diện có đỉnh ,
. Trên các cạnh lần lượt lấy các điểm sao cho
. Viết phương trình mặt phẳng biết tứ diện có thể
tích nhỏ nhất .
0
sin 3 dx x
1
3
1
3
2
3
2
3
( )F x
( )f x
K
'( ) ( ), .f x F x x K
'( ) ( ), .f x F x x K
'( ) ( ), .F x f x x K
'( ) ( ), .F x f x x K
1
1 2
f x
x
1
;
2
ln 2 1
x C
1
ln 1 2
2
x C
1
ln 1 2
2
x C
1
ln 2 1
2
x C
Oxyz
(2; 1;2), (3; 2;1)
a b
3;4;1
n
3;4; 1
n
3;4; 1
n
3; 4; 1
n
Oxyz
( ) : 6 0
P x y z
12:)(
222
zyxS
Oxyz
ABCD
1;1;1 , 2;0;2
A B
1; 1;0 , 0;3;4
C D
, ,
AB AC AD
', ', 'B C D
4
' ' '
AB AC AD
AB AC AD
' ' 'B C D
' ' 'AB C D
19
A.
.
B.
.
C.
.
D.
.
Câu 12:
Trong không gian , cho mặt cầu , mặt phẳng
. Giá trị của để mặt phẳng cắt mặt cầu .
A.
.
B.
.
C.
.
D.
.
Câu 13:
Trong không gian , mặt cầu có tâm là
A.
B.
C.
D.
Câu 14:
Tích phân bằng
A.
.
B.
.
C.
.
D.
.
Câu 15:
Cho hàm số xác định với mọi . Một nguyên hàm của
hàm số là
A.
.
B.
.
C.
.
D.
.
Câu 16:
Cho hàm số xác định trên thỏa mãn .
Giá trị của biểu thức bằng
A.
.
B.
.
C.
.
D.
.
Câu 17:
Trong không gian , cho ba điểm . Tọa độ trọng
tâm của tam giác là
A. .
B. .
C. .
D. .
16 40 44 39 0
x y z
16 40 44 39 0
x y z
16 40 44 39 0
x y z
16 40 44 39 0
x y z
Oxyz
2 2 2
( ) : 2 2 7 0
S x y z x z
: 4 3 0
P x y m
m
P
S
12 4
m
11
19
m
m
19 11
m
4
12
m
m
Oxyz
2 2 2
: 8 2 1 0
S x y z x y
4; 1;0 .
I
8;2;0 .
I
4;1;0 .
I
8; 2;0 .
I
2
0
d
3
x
x
2
15
5
ln
3
5
log
3
16
225
2
x
f x
cos x
,
2
x k k
f x
x tan x ln cosx
x tan x ln cosx
x tan x ln cosx
x tan x ln sin x
( )f x
1
\
2
2
, 0 1, 1 2
2 1
f x f f
x
1 3
f f
3 ln15
4 ln15
2 ln15
ln15
Oxyz
1;0; 3 , 2;4; 1 , 2; 2;0
A B C
G
ABC
5;2;4
5
;1; 2
2
5 2 4
; ;
3 3 3
5 2 4
; ;
3 3 3
20
Câu 18:
Cho hàm số xác định với mọi . Mệnh đề nào
sau đây
đúng
?
A.
.
B.
.
C.
.
D.
.
Câu 19:
Tìm giá trị của để .
A.
.
B.
.
C.
.
D.
.
Câu 20:
Trong không gian , cho mặt phẳng đi qua , và vuông
góc với mặt phẳng . Phương trình mặt phẳng là
A.
.
B.
.
C.
.
D.
.
Câu 21:
Họ tất cả các nguyên hàm của hàm số là
A. .
B. .
C. .
D. .
Câu 22:
Cho đường thẳng
3
4
y x
và parabol
2
1
2
y x a
, (
a
là tham số thực dương). Gọi
1 2
,S S
lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi
1 2
S S
thì
a
thuộc
khoảng nào dưới đây?
A.
7 1
;
32 4
.
B.
1 9
;
4 32
.
C.
3 7
;
16 32
.
D.
3
0;
16
.
2
2
cos
x
x
e
f x e
x
,
2
x k k
2 tan
x
f x dx e x C
2 tan
x
f x dx e x C
1
2
cos
x
f x dx e C
x
1
2
cos
x
f x dx e C
x
4
3
1
d ln
1 2
x a
x x
3
4
1
3
4
3
12
Oxyz
2; 1;4
A
3;2; 1
B
: 2 3 0
Q x y z
11 7 2 21 0
x y z
5 3 4 0
x y z
2 3 0
x y z
3 5 21 0
x y z
x
f x xe
x
e C
x x
xe e C
2
x
x
e C
2
x x
xe e C
21
Câu 23:
Họ tất cả các nguyên hàm của hàm số là
A.
.
B.
.
C.
.
D.
.
Câu 24:
Gọi là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: , . Tính
.
A.
.
B.
.
C.
.
D.
.
Câu 25:
Biết là một nguyên hàm của hàm số và . Giá trị của
bằng
A.
4.
B.
8.
C.
6.
D.
2.
Câu 26:
Trong không gian , cho hai điểm và . Phương trình mặt cầu
đường kính AB là
A.
B.
C.
D.
Câu 27:
Tính .
A.
.
B.
.
C.
.
D.
.
Câu 28:
Biết ; ; . Mệnh đề nào sau đây
sai
?
A.
.
B.
.
C.
.
D.
.
Câu 29:
Trong không gian , phương trình nào sau đây
không phải
là phương trình mặt
cầu?
A.
B.
cos2f x x
2sin 2
x C
2sin 2
x C
1
sin 2
2
x C
1
sin2
2
x C
S
3
3y x x
y x
S
2
S
8
S
4
S
0
S
F x
2x
f x e
0 0
F
ln3
F
Oxyz
1;0; 3
A
3;2;1
B
2 2 2
4 2 2 6 0.
x y z x y z
2 2 2
4 2 2 0.
x y z x y z
2 2 2
2 6 0.
x y z x y z
2 2 2
4 2 2 0.
x y z x y z
3 d
x
I x
3
x
I C
3 ln 3
x
I C
3
ln3
x
I C
3 ln 3
x
I C
8
1
d 2
f x x
4
1
d 3
f x x
4
1
d 7
g x x
4
1
4 2 d 2
f x g x x
8 4
4 1
d d 8
f x x g x x
4
1
d 10
f x g x x
8
4
d 5
f x x
Oxyz
2 2 2
2 1 2 1 2 1 6.
x y z
2 2 2
1 1 1 6.
x y z
22
C.
D.
Câu 30:
Đường thẳng
là giao của hai mặt phẳng
5 0x z
và
2 3 0x y z
thì có
phương trình là
A.
2 1
1 3 1
x y z
.
B.
2 1
1 2 1
x y z
.
C.
2 1 3
1 1 1
x y z
.
D.
2 1 3
1 2 1
x y z
.
Câu 31:
Tìm .
A.
.
B.
.
C.
.
D.
.
Câu 32:
Tích phân bằng
A.
B.
C.
D.
Câu 33:
Cho hàm số
y f x
có đạo hàm trên
, đồ thị hàm số
y f x
như hình vẽ. Biết
diện tích hình phẳng phần sọc kẻ bằng 3. Tính giá trị của biểu thức:
2 3 4
1 2 3
1 dx 1 dx 2 8 dxT f x f x f x
A.
9
2
T
.
B.
6T
.
C.
0T
.
D.
3
2
T
.
Câu 34:
Bác thợ xây bơm nước vào bể nước. Gọi là thể tích nước bơm được sau giây.
Cho và ban đầu bể không có nước. Sau giây thì thể tích nước trong bể là
, sau giây thì thể tích nước trong bể là . Tính thể tích nước trong bể sau khi
bơm được giây.
2 2 2
1 2 1 1 6.
x y z
2
2
2 3 6 .
x y xy z x
cos dI x x x
sin cos
I x x x C
2
cos
2
x
I x C
sin cos
I x x x C
2
sin
2
x
I x C
1
2
0
2 e d
x
x x
2
5 3e
.
2
2
5 3e
.
4
2
5 3e
.
4
2
5 3e
.
4
h t
t
2
3
h t at bt
5
3
150m
10
3
1100m
20
23
A.
.
B.
.
C.
.
D.
.
Câu 35:
Trong không gian , khoảng cách từ điểm đến mặt phẳng
bằng
A.
.
B.
.
C.
.
D.
.
Câu 36:
Tập nghiệm của bất phương trình là
A.
.
B.
.
C.
.
D.
.
Câu 37:
Trong không gian , mặt cầu tâm và tiếp xúc với mặt phẳng
có phương trình
A.
B.
C.
D.
Câu 38:
Tập nghiệm của bất phương trình là
A.
.
B.
.
C.
.
D.
.
Câu 39:
Trong không gian , cho hình hộp có , ,
, . Toạ độ trọng tâm tam giác là
A.
.
B.
.
C.
.
D.
.
Câu 40:
Viết công thức tính thể tích của khối tròn xoay được tạo ra khi quay hình thang cong,
giới hạn bởi đồ thị hàm số , trục và hai đường thẳng , xung
quanh trục .
A.
.
B.
.
C.
.
D.
.
Câu 41:
Giả sử là hàm liên tục trên khoảng và là ba số bất kì trên khoảng .
Khẳng định nào sau đây sai?
3
4200m
3
2200m
3
8400m
3
600m
Oxyz
0;0;5
A
: 2 2 3 0
P x y z
7
3
8
3
4
3
2 5
x
5
log 2;

2
log 5;

5
;log 2

2
5
;log
Oxyz
S
1;2; 3
I
: 2 2 1 0
P x y z
2 2 2
4
1 2 3 .
9
x y z
2 2 2
16
1 2 3 .
3
x y z
2 2 2
4
1 2 3 .
3
x y z
2 2 2
4
1 2 3 .
9
x y z
2
3
log 18 2
x
; 3 3;

;3

3;3
0;3
Oxyz
.
ABCD A B C D
0; 0; 0
A
3; 0; 0
B
0; 3; 0
D
0; 3; 3
D
A B C
1; 1; 2
1; 2; 1
2; 1; 1
2; 1; 2
V
y f x
Ox
,
x a x b a b
Ox
2
b
a
V f x dx
2
b
a
V f x dx
b
a
V f x dx
b
a
V f x dx
f
K
, ,a b c
K
24
A.
.
B.
.
C.
.
D.
.
Câu 42:
Trong không gian , cho mặt phẳng và mặt cầu
. Giả sử điểm và sao cho cùng
phương với và khoảng cách giữa và là lớn nhất. Tính .
A.
.
B.
.
C.
.
D.
.
Câu 43:
Một chất điểm xuất phát từ , chuyển động thẳng với vận tốc biến thiên theo thời
gian bởi quy luật , trong đó (giây) là khoảng thời gian tính từ lúc
bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm cũng xuất phát từ , chuyển động
thẳng cùng hướng với nhưng chậm hơn giây so với và có gia tốc bằng ( là
hằng số). Sau khi xuất phát được giây thì đuổi kịp . Vận tốc của tại thời điểm đuổi
kịp bằng
A.
.
B.
.
C.
.
D.
.
Câu 44:
Cho hàm số có đạo hàm liên tục trên thỏa mãn
Giá trị của tích phân bằng
A.
B.
C.
D.
Câu 45:
Trong không gian , cho mặt phẳng có phương trình . Mặt
phẳng có một vectơ pháp tuyến là
A.
.
B.
.
C.
.
D.
.
Câu 46:
Trong không gian , cho hai mặt phẳng và
.Tìm để .
( ) ( )
b a
a b
f x dx f x dx
( ) ( ) ( ) , ,
c b b
a c a
f x dx f x dx f x dx c a b
( ) ( )
b b
a a
f x dx f t dt
( ) 1
b
a
f x dx
Oxyz
: 2 2 3 0
P x y z
2 2 2
: 2 4 2 5 0
S x y z x y z
M P
N S
MN
1;0;1
u
M
N
MN
3 2
MN
1 2 2
MN
14
MN
3
MN
A
O
2
1 13
m/s
100 30
v t t t
t
A
B
O
A
10
A
2
m/s
a
B
15
A
B
A
42 m/s
15 m/s
25 m/s
9 m/s
f x
0;1 ,
2
2 3 1 1 .f x f x x
1
0
' df x x
3
.
2
1.
0.
1
.
2
Oxyz
P
2 2 3 0
x y z
P
( 2;2; 3)
n
(0;0; 3)
n
( 4;4;2)
n
( 4;4; 2)
n
Oxyz
( ) : 5 5 0
P x my z
( ) : 3 2 7 0
Q nx y z
,m n
/ /
P Q
25
A.
.
B.
.
C.
.
D.
.
Câu 47:
Cho hàm số xác định và liên tục trên đoạn . Diện tích hình phẳng giới
hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng được tính theo
công thức
A.
.
B.
.
C.
.
D.
.
Câu 48:
Trong không gian
Oxyz
, cho
2;0;0
A
, đường thẳng
d
đi qua
A
cắt chiều âm trục
Oy
tại điểm
B
sao cho diện tích tam giác
OAB
bằng 1. Phương trình tham số đường thẳng
d
là
A.
1 2
0
x t
y t
z
.
B.
2 2
0
x t
y t
z
.
C.
2 2
0
x t
y t
z
.
D.
2 2
1
x t
y t
z
.
Câu 49:
Biết với , , là các số nguyên dương. Tính
.
A.
.
B.
.
C.
.
D.
.
Câu 50:
Trong không gian , mặt phẳng đi qua điểm , , có
phương trình là
A.
.
B.
.
C.
.
D.
.
5; 3
m n
3
; 10
2
m n
5; 3
m n
3
; 10
2
m n
y f x
;a b
y f x
,
x a x b
b
a
S f x dx
a
b
S f x dx
b
a
S f x dx
b
a
S f x dx
2
1
d
1 1
x
I a b c
x x x x
c
P a b c
18
P
12P
24P
46
P
Oxyz
3
1;0;0
A
0;2;0
B
0;0;3
C
0
1 2 3
x y z
1
1 2 3
x y z
1
1 2 3
x y z
1
1 1 3
x y z
26
TRƯỜNG THPT THUẬN THÀNH SỐ 1
TỔ TOÁN
-------------
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: Toán lớp 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Vũ Thị Vui
Câu 1. Mệnh đề nào sau đây sai ?
A.
k.f dx x k f x C
với mọi số thực
0k
.
B.
d d df x g x x f x x g x x
.
C. Nếu
F x
,
G x
đều là nguyên hàm của hàm số
f x
thì
F x G x
.
D.
sin cosdx x x C
.
Câu 2. Họ tất cả các nguyên hàm của hàm số
2cos sinf x x x
là
A.
2sin cosx x C
. B.
2sin cosx x C
.
C.
2sin cosx x C
. D.
2sin cosx x C
.
Câu 3. Hình phẳng
H
được giới hạn bởi đồ thị
C
của hàm đa thức bậc ba và parabol
P
có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng
A.
37
12
. B.
7
12
. C.
11
12
. D.
5
12
.
Câu 4.
1
sin 3 d
3
x x
bằng
A.
1 1
cos 3
3 3
x C
. B.
1
cos 3
3
x C
.
C.
1 1
cos 3
3 3
x C
. D.
1 1
sin 3
3 3
x C
.
27
Câu 5. Trong không gian
Oxyz
, cho điểm
3;2; 1
M
. Hình chiếu vuông góc của điểm
M
lên trục
Oz
là điểm
A.
3
3;0;0
M
. B.
4
0;2;0
M
. C.
1
0;0; 1
M
. D.
2
3;2;0
M
.
Câu 6.
1 3ln .ln
d
x x
x
x
bằng
A.
2 2
2
1 3ln 1 3ln 1
9
x x C
.
B.
1 3ln 1
1 3ln 1 3ln
5 3
x
x x C
.
C.
2 1 3ln 1
1 3ln 1 3ln
9 5 3
x
x x C
.
D.
2 1 3ln 1
1 3ln 1 3ln
3 5 3
x
x x C
.
Câu 7. Cho hàm số
( )f x
thỏa mãn
3
4 ( ) ( ) 2 ( )
, 0
( ) 0
x
e f x f x f x
x
f x
và
(0) 1
f
. Tính
ln 2
0
( )d
I f x x
.
A.
1
12
I
. B.
1
12
I
. C.
209
640
I
. D.
7
640
I
.
Câu 8. Biết rằng
( )g x
là một nguyên hàm của
( 1)sinf x x x
và
(0) 0
g
, tính
( )
g
.
A.
0
. B.
1
. C.
2
. D.
1
.
Câu 9. Cho hai hàm số
y f x
và
y g x
có đạo hàm liên tục trên đoạn [0; 2] và thỏa mãn
2
0
' . 1f x g x dx
,
2
0
. ' 1f x g x dx
. Tính
2
/
0
.
I f x g x dx
.
A.
2I
. B.
0
I
. C.
3
I
. D.
2I
.
Câu 10. Cho
2
1
d 3
f x x
. Khi đó
2
1
d
e
f x
x
bằng
A.
3
e
. B.
2
e
C.
2
3e
. D.
3
e
.
Câu11. Trong không gian
Oxyz
, cho hai mặt phẳng
: 1 0
P x y z
và
: 2 1 0
Q x y mz m
, với
m
là tham số thực. Giá trị của
m
để
P Q
là
A.
1
. B.
0
. C.
1
. D.
4
.
Câu 12. Cho hàm số
f (x)
có đạo hàm liên tục trên đoạn
[a;b]
và
2
f (a)
2
f (b)1
. Tính
f '(x)dx
a
b
A.
I 0
. B.
I 2
. C.
I 1
. D.
I 1
.
28
Câu 13. Biết rằng
3
3
2
0
1 e
d e
e e 1
x
b
x x
x a
với
,a b
, hãy tính
b a
.
A.
1b a
. B.
1
b a
. C.
7
b a
. D.
7
b a
.
Câu 14. Cho hàm số
y f x
sao cho
f x
liên tục trên
,
2
1
d 3 ln 2
f x
x
x
và
2 3.
f
Tính
2
1
.ln dI f x x x
.
A.
4ln2 3
I
. B.
2ln2 3
I
. C.
2ln2 3
I
. D.
3ln2 4
I
.
Câu 15. Biết
2
2
1 ln ln
ln
mx x n px
dx x C
x x
với
, , ,m n p C
là các số thực. Khi đó,
m n p
bằng
A.
1e
. B.
2
e
. C.
2 1e
. D.
2 2
e
.
Câu 16. Giả sử hàm số
( )f x
liên tục và dương trên đoạn
0;3
thỏa mãn
( ). (3 ) 4
f x f x
. Tính tích
phân
3
0
1
d
2
I x
f x
.
A.
3
5
I
. B.
1
2
I
. C.
3
4
I
. D.
1
3
I
.
Câu 17. Cho hàm số
f x
có đồ thị như hình vẽ bên dưới.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số
f x
và trục
Ox
được tính theo công thức
nào sau đây?
A.
2
1
df x x
. B.
2
1
3
df x x
.
C.
1
2
3
1
1
3
d df x x f x x
. D.
1
2
3
1
1
3
d df x x f x x
.
Câu 18.Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
2
1 2 1
f x x x x
và trục
Ox
29
A.
11
20
. B.
1
20
. C.
19
20
. D.
117
20
.
Câu 19. Gọi
S
là diện tích của hình phẳng giới hạn bởi parabol
2
3
2 2
x x
y
và đường thẳng
1.y x
Ta có
A.
3
2
S
B.
11
.
2
S
C.
3
.
4
S
D.
9
.
4
S
Câu 20. Hình vẽ dưới đây là một mảnh vườn hình Elip có bốn đỉnh là
, , , ;I J K L ,ABCD EFGH
là các
hình chữ nhật;
10m, = 6 mIJ KL
,
5m, 3mAB EH
. Biết rằng kinh phí trồng hoa là
50000
đồng/
2
m
, hãy tính số tiền (làm tròn đến hàng đơn vị) dùng để trồng hoa trên phần gạch
sọc.
A.
2869834
đồng. B.
1434917
đồng.
C.
2119834
đồng. D.
684917
đồng.
Câu 21. Cho hàm số
y f x
. Đồ thị của hàm số
y f x
như hình bên. Đặt
2
2 1g x f x x
. Mệnh đề nào dưới đây đúng?
A.
1 3 3g g g
B.
1 3 3g g g
C.
3 3 1g g g
D.
3 3 1g g g
30
Câu 22. Cho hình
H
giới hạn bởi đồ thị hàm số
2
y
x
, trục hoành, các đường thẳng
1, 2x x
.
Biết rằng khối tròn xoay do
H
quay quanh trục
Ox
tạo ra có thể tích là
lna
. Giá trị của
a
là
A.
6
. B.
2
. C.
4
. D.
8
.
Câu 23. Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách
điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên
dưới. Biết rằng
5OO
cm
,
10OA
cm
,
20OB
cm
, đường cong
AB
là một phần của parabol có
đỉnh là điểm
A
. Thể tích của chiếc mũ bằng
A.
2750
3
3
cm
B.
2500
3
3
cm
C.
2050
3
3
cm
D.
2250
3
3
cm
Câu 24. Cho hình thang cong giới hạn bởi đồ thị hàm số
y x
, trục hoành, các đường thẳng
1x
và
4x
. Thể tích của khối tròn xoay được tạo thành khi quay hình thang cong trên quanh trục
Ox
bằng
A.
4
1
dx x
. B.
4
1
dx x
. C.
4
1
dx x
. D.
4
2
1
d
x x .
Câu 25. Cho
,a b
là hai số thực dương. Gọi
H
là hình phẳng giới hạn bởi parabol
2
y ax
và đường
thẳng
y bx
. Quay
H
quanh trục hoành thu được khối có thể tích là
1
V
, quay
H
quanh
trục tung thu được khối có thể tích là
2
V
. Tìm
b
sao cho
1 2
V V
.
A.
5
6
b
. B.
5
3
b
. C.
5
2
b
. D.
5
4
b
.
Câu 26: Vận tốc (tính bằng
m
s
) của một hạt chuyển động theo một đường được xác định bởi công thức
3 2
8 17 10 v t t t t
, trong đó t được tính bằng giây. Tổng quãng đường mà hạt đi được
trong khoảng thời gian
1 5t
là bao nhiêu?
31
A.
32
m
3
. B.
71
m
3
. C.
38
m
3
. D.
71
m
6
.
Câu 27: Biết
F x
là một nguyên hàm của hàm số
3
4 1
f x x
và
0 1
F
. Tính giá trị của
1
F
.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 28: Cho hàm số
f x
xác định trên
\ 2
thỏa mãn
1
2
f x
x
,
1 2020
f
,
3 2021
f
.
Tính
4 0
P f f
.
A.
4P
. B.
ln 2P
. C.
ln4041
P
. D.
1P
.
Câu 29. Trong không gian
Oxyz
, cho
1; 2;5 , 0;2; 1
a b
. Nếu
4c a b
thì
c
có tọa độ là
A.
1;0;4
. B.
1;6;1
. C.
1; 4;6
. D.
1; 10;9
.
Câu 30. Trong không gian
Oxyz
, cho hai điểm
2;1;1
A
,
3;2; 1
B
. Độ dài đoạn thẳng
AB
bằng
A.
30
. B.
10
. C.
22
. D.
2
.
Câu 31. Trong không gian
Oxyz
, cho
2; 3;4
u
,
3; 2;2
v
khi đó
.u v
bằng
A.
20
. B.
8
. C.
46
. D.
2 2
.
Câu 32. Trong không gian
Oxyz
, cho
1;0;6
A
,
0;2; 1
B
,
1;4;0
C
. Bán kính mặt cầu
S
có
tâm
2;2; 1
I
và tiếp xúc với mặt phẳng
ABC
bằng
A.
8 3
3
. B.
8 77
77
. C.
16 77
77
. D.
16 3
3
.
Câu 33. Trong không gian
Oxyz
, cho mặt cầu
2 2 2
: 1 2 1 4
S x y z
. Tìm tọa độ tâm
I
và bán kính
R
của mặt cầu
S
.
A.
1;2;1
I
và
2R
. B.
1; 2; 1
I
và
2R
.
C.
1;2;1
I
và
4R
. D.
1; 2; 1
I
và
4R
.
Câu 34. Trong không gian
Oxyz
cho hai điểm
( 2;1;0)
A
,
(2; 1;2)
B
. Phương trình mặt cầu
S
có tâm
B
và đi qua
A
là
A.
2 2
2
2 1 ( 2) 24
x y z
. B.
2 2
2
2 1 ( 2) 24
x y z
.
C.
2 2
2
2 1 24
x y z
. D.
2 2
2
2 1 ( 2) 24
x y z
.
Câu 35. Trong không gian
,Oxyz
tọa độ nào sau đây là tọa độ của một véctơ chỉ phương của đường
thẳng
2 4
: 1 6 , ?
9
x t
y t t
z t
A.
1 1 3
; ;
3 2 4
. B.
1 1 3
; ;
3 2 4
. C.
2;1;0
. D.
4; 6;0
.
32
Câu 36. Trong không gian với hệ trục tọa độ
Oxyz
, phương trình nào dưới đây là phương trình mặt
phẳng đi qua
1; 1;2
M
và vuông góc với đường thẳng
1 2
:
2 1 3
x y z
.
A.
2 3 9 0
x y z
. B.
2 3 9 0
x y z
.
C.
2 3 9 0
x y z
. D.
2 3 6x y z
.
Câu 37. Trong không gian
Oxyz
, cho mặt cầu
S
có tâm thuộc trục
Ox
và đi qua hai điểm
1;2; 1
A
và
2;1;3
B
. Phương trình của
S
là
A.
2
2 2
4 14.
x y z
B.
2
2 2
4 14.
x y z
C.
2 2 2
( 4) 14.
x y z
D.
2 2 2
( 4) 14.
x y z
Câu 38. Trong không gian
Oxyz
, cho mặt cầu
S
có tâm
1; 2;3
I
và tiếp xúc với mặt phẳng
: 2 2 3 0
P x y z
. Phương trình của
S
là
A.
2 2 2
1 2 3 16.
x y z
B.
2 2 2
1 2 3 9.
x y z
C.
2 2 2
1 2 3 16.
x y z
D.
2 2 2
1 2 3 4.
x y z
Câu 39. Trong không gian
Oxyz
cho các điểm
1; 1;3
A
,
2;1;0
B
,
3; 1; 3
C
và mặt phẳng
: 4 0
P x y z
. Gọi
, ,M a b c
là điểm thuộc mặt phẳng
P
sao cho biểu thức
3 2
T MA MB MC
đạt giá trị nhỏ nhất. Tính giá trị của biểu thức
S a b c
.
A.
3
S
. B.
1
S
. C.
2
S
. D.
1
S
.
Câu 40. Trong không gian
Oxyz
, cho điểm
2; 5; 3
A
và đường thẳng
d
:
1 2
2 1 2
x y z
. Biết rằng
P
:
3 0
ax by cz
, ,a b c
là mặt phẳng chứa
d
và khoảng cách từ
A
đến
P
lớn nhất.
Khi đó tổng
T a b c
bằng
A.
3
. B.
3
. C.
2
. D.
5
.
Câu 41. Trong không gian
Oxyz
, cho hai đường thẳng
1
3 3 2
:
1 2 1
x y z
d
;
2
5 1 2
:
3 2 1
x y z
d
và mặt phẳng
: 2 3 5 0
P x y z
. Đường thẳng vuông góc với
P
, cắt
1
d
và
2
d
có phương trình là
A.
1 1
3 2 1
x y z
B.
2 3 1
1 2 3
x y z
C.
3 3 2
1 2 3
x y z
D.
1 1
1 2 3
x y z
Câu 42.
Trong không gian
Oxyz
, mặt phẳng đi qua điểm
1;2;4
A
và song song với mặt phẳng
: 4 5 0
P x y z
có phương trình là
A.
4 5 0
x y z
. B.
4 2 0
x y z
.
33
C.
4 0
x y z
. D.
4 6 0
x y z
.
Câu 43. Trong không gian Oxyz, cho mặt phẳng
: 3 0
x yP z
và đường thẳng
1 2
:
1 2 1
x y z
d
. Hình chiếu vuông góc của
d
trên
P
có phương trình là
A.
1 1 1
1 4 5
x y z
B.
1 4 5
1 1 1
x y z
C.
1 1 1
1 4 5
x y z
D.
1 1 1
3 2 1
x y z
Câu 44. Trong không gian
Oxyz
, cho mặt cầu
S
:
2 2 2
1 2 1 9
x y z
. Mặt phẳng
P
tiếp xúc với
S
tại điểm
1;3; 1
A
có phương trình là
A.
2 2 7 0
x y z
. B.
2 2 7 0
x y z
.
C.
2 10 0
x y z
. D.
2 2 2 0
x y z
.
Câu 45. Trong không gian
O
xyz
, cho mặt phẳng
:2 2 1 0
P x y z
và hai điểm
1;0; 2 , 1; 1;3
A B
. Mặt phẳng
Q
đi qua hai điểm
,A B
và vuông góc với
P
có
phương trình dạng
5 0
ax by cz
. Khẳng định nào sau đây đúng?
A.
21
a b c
. B.
7a b c
. C.
21
a b c
. D.
7
a b c
.
Câu 46. Trong không gian
Oxyz
, cho điểm
4;2;3
M
.Viết phương trình mặt phẳng đi qua ba điểm
, ,A B C
lần lượt là hình chiếu của điểm
M
trên các trục
, , .Ox Oy Oz
A.
3 6 4 12 0
x y z
. B.
4 2 3 1 0
x y z
.
C.
3 6 4 12 0
x y z
. D.
4 2 3 1 0
x y z
.
Câu 47. Trong không gian
Oxyz
, cho mặt phẳng
Q
song song mặt phẳng
: 2 2 17 0
P x y z
.
Biết mặt phẳng
Q
cắt mặt cầu
2 2
2
: 2 1 25
S x y z
theo giao tuyến là một
đường tròn có bán kính
3.
r
Khi đó mặt phẳng
Q
có phương trình là
A.
2 2 7 0
x y z
. B.
2 2 17 0
x y z
.
C.
2 2 17 0
x y z
. D.
2 7 0
x y z
.
Câu 48. Trong không gian với hệ tọa độ
Oxyz
, cho đường thẳng
3 1
:
2 1 1
x y z
d
và điểm
(2; 1;0)
A
. Khoảng cách từ điểm
A
đến đường thẳng
d
bằng
A.
7
. B.
7
2
. C.
21
3
. D.
7
3
.
Câu 49. Trong không gian
Oxyz
, cho mặt phẳng
: 3 0
P x y z
và đường thẳng
1 2
:
1 2 1
x y z
d
. Đường thẳng
'd
đối xứng với
d
qua mặt phẳng
P
có phương trình
là
34
A.
1 1 1
1 2 7
x y z
. B.
1 1 1
1 2 7
x y z
.
C.
1 1 1
1 2 7
x y z
. D.
1 1 1
1 2 7
x y z
.
Câu 50: Trong không gian
Oxyz
, cho hai điểm
1;2;4 , 0;0;1
A B
và mặt cầu
2 2
2
: 1 1 4
S x y z
. Mặt phẳng
: a 4 0
P x by cz
đi qua
,A B
và cắt
S
theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính
?T a b c
A.
1
5
T
. B.
3
4
T
. C.
1T
. D.
2T
.
35
TRƯỜNG THPT THUẬN THÀNH SỐ 1
TỔ TOÁN
-------------
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II
NĂM HỌC 2022 - 2023
MÔN: Toán lớp 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề : Cô Hà Thị San
Câu 1. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số
f x
nghịch biến trên khoảng nào sau đây?
A.
1;3
. B.
1;3
. C.
1;1
. D.
3;1
.
Câu 2. Hàm số
2
3
log 3
f x x
có đạo hàm là
A.
2
2 ln 3
3
x
f x
x
. B.
2
2
3 ln3
x
f x
x
.
C.
2
ln 3
3
f x
x
. D.
2
1
3 ln 3
f x
x
.
Câu 3. Nghiệm của phương trình
log 2 3 1
x
là
A.
3
x
. B.
3
2
x
. C.
2
x
. D.
13
2
x
.
Câu 4. Cho hàm số
sin3f x x
. Trong các khẳng định dưới đây, khẳng định nào đúng?
A.
1
cos 3
3
f x x x C
d
. B.
cos3
f x x x C
d
.
C.
1
cos3
3
f x x x C
d
D.
3cos3
f x x x C
d
.
36
Câu 5. Tiệm cận ngang của đồ thị hàm số
2 1
2
x
y
x
là đường thẳng
A.
2
x
. B.
2
y
. C.
1
y
. D.
1
x
.
Câu 6. Cho hình nón có bán kính đáy bằng
5
và góc ở đỉnh bằng
60
. Diện tích xung quanh của
hình nón đã cho bằng
A.
55
. B.
100
. C.
75
. D.
50
.
Câu 7. Cho hàm số
f x
liên tục trên đoạn
1; 2
thỏa mãn
2
1
6
f x dx
. Giá trị
1
0
3 1
f x dx
bằng
A.
18
. B.
1
. C.
2
. D.
3
.
Câu 8. Cho khối nón đỉnh
S
có đáy là hình tròn tâm
O
, độ dài đường sinh là
.l
Biết
.SO h
Độ
dài bán kính đáy của khối nón bằng
A.
2 2
l h
. B.
2 2
2
l h
. C.
2 2
l h
. D.
2 2
h l
.
Câu 9. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ?
A.
4 2
2 2
y x x
. B.
3 2
2 2
y x x
.
C.
3 2
2 2
y x x
. D.
4 2
2 2
y x x
.
Câu 10. Trong không gian
yzOx
, phương trình đường thẳng đi qua hai điểm
(3; 1;2)
A
và
(4;1;0)
B
là
A.
3 1 2
1 2 2
x y z
. B.
1 2 2
3 1 2
x y z
.
C.
1 2 2
3 1 2
x y z
. D.
3 1 2
1 2 2
x y z
.
Câu 11.Nếu
2
2
9
f x dx
và
2
1
2
f x dx
thì
1
2
f x dx
bằng
A.
7
. B.
3
. C.
10
. D.
7
.
37
Câu 12. Biết
3
2
2
2
2 14
ln2 ln3 ,( , , )
1
x x
dx a b c a b c
x
. Giá trị của
2
a b c
bằng
A. 494 B. 484. C. 474. D. 464.
Câu 13. Tập xác định của hàm số
3
2y x
là
A.
2; 
. B.
. C.
}\{2
. D.
2;
.
Câu 14. Cho hàm số
y f x
có bảng biến thiên như sau
Đồ thị hàm số có đường tiệm cận đứng là
A.
1y
. B.
2x
. C.
2y
. D.
1x
.
Câu 15. Trong không gian
Oxyz
, cho hai véctơ
1;2;1a
và
2; 4;2b
. Khi đó tích
.ab
bằng
A.
12
B.
4
C.
12
D.
4
Câu 16. Cho hình cầu bán kính
R
. Thể tích của khối cầu tương ứng là
A.
3
4
3
R
. B.
3
4 R
. C.
2
4
3
R
. D.
3
4
3
R
.
Câu 17. Trong không gian
Oxyz
, cho mặt cầu
2 2
2
: 1 2 16S x y z
. Tâm của
S
có
tọa độ là
A.
1;2;1
. B.
1;2;0
. C.
1; 2;0
. D.
1; 2;1
.
Câu 18. Trong không gian
Oxyz
, khoảng cách từ gốc tọa độ
O
đến mặt phẳng
2 2 12 0x y z
bằng
A.
12
. B.
4
3
. C.
4
. D.
4
3
.
Câu 19. [Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh
2a
. Thể
tích khối trụ bằng
38
A.
3
2
a
. B.
3
2
a
. C.
3
2
3
a
. D.
3
4
a
.
Câu 20. Trong không gian
Oxyz
, phương trình mặt phẳng đi qua
1; 2;2
A
và có vectơ pháp
tuyến
3; 1; 2
n
là
A.
3 2 1 0
x y z
. B.
2 2 1 0
x y z
.
C.
3 2 1 0
x y z
. D.
2 2 1 0
x y z
.
Câu 21. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
x m
nghịch biến trên
khoảng
15;

?
A.
3
. B.
4
. C.
5
. D. Vô số.
Câu 22. Với
a
là số thực dương tùy ý
7
4
a
bằng
A.
7
4
a
. B.
7
a
. C.
28
a
. D.
4
7
a
.
Câu 23. Họ các nguyên hàm của hàm số
2
1
x
f x e
là
A.
2
1
2
x
e C
. B.
2
2
x
e x C
. C.
2
2
x
e C
. D.
2
1
2
x
e x C
.
Câu 24. Tập nghiệm của bất phương trình
2
5
1 1
2 16
x
là
A.
; 3 3;

. B.
3;3
. C.
;3

. D.
3;

.
Câu 25. Trong không gian
Oxyz
, cho điểm
7; 1;2
A
và mặt phẳng
: 2 2 6 0
P x y z
.
Mặt cầu
S
tâm
A
và tiếp xúc với mặt phẳng
P
có phương trình là
A.
2 2 2
49
7 1 2
9
x y z
. B.
2 2 2
7
7 1 2
3
x y z
.
C.
2 2 2
49
7 1 2
9
x y z
. D.
2 2 2
7
7 1 2
3
x y z
.
39
Câu 26. Trong không gian
Oxyz
, cho điểm
8; 4;3M
và đường thẳng
1 3
: 2 2
x t
d y t
z t
. Gọi
H
là hình chiếu vuông góc của
M
lên
d
. Khi đó tọa độ của điểm
H
là
A.
7; 6;2H
. B.
9; 2;4H
. C.
2;0; 1H
. D.
1; 2;1H
.
Câu 27. Trong không gian
Oxyz
, cho điểm
0; 1;2M
và mặt phẳng
: 4x 3z 2 0P y
.
Đường thẳng
đi qua điểm
M
và vuông góc với mặt phẳng
P
có phương trình tham
số là
A.
4
3 2
x
y t
z t
. B.
4
1
2 3
x t
y t
z t
. C.
4
1
3 2
x
y t
z t
. D.
4
1
2 3
x t
y
z t
.
Câu 28. Cho hàm số
y f x
có bảng biến thiên như sau
Số nghiệm của phương trình
3 7 0f x
là
A. 2. B. 3. C. 1. D. 4.
Câu 29. Cho phương trình
2
log 2 4
x
x m m
với
m
là tham số thực. Có bao nhiêu giá trị
nguyên của
27;27 m
sao cho phương trình trên có nghiệm?
A.
10
. B.
26
. C.
1
. D.
53
.
Câu 30. Có một khối gỗ hình lăng trụ đứng có chiều cao 200 cm và đáy là hình tam giác có độ
dài ba cạnh là 50 cm, 120 cm và 130 cm. Người ta tiện khối gỗ này thành một khối trụ.
Thể tích lớn nhất của khối trụ gần nhất với giá trị nào sau đây?
A.
3
2654645,79 cm . B.
3
62831,85 cm .
C.
3
251327,41 cm . D.
3
83775,81 cm .
Câu 31. Tập nghiệm của phương trình
2
2
log 4 8 3x x
là
40
A.
0;4
. B.
0
. C.
4
. D.
0; 4
.
Câu 32. Cho tích phân
0
1
1dx x
, với cách đặt
1t x
thì tích phân đã cho bằng tích phân
nào sau đây?
A.
1
2
0
2 dt t
. B.
1
2
0
dt t
. C.
1
3
0
3 dt t
. D.
0
3
1
3 dt t
.
Câu 33. Tìm giá trị nhỏ nhất
m
của hàm số
3 1
3
x
y
x
trên đoạn
0;2
.
A.
5
m
. B.
1
3
m
. C.
1
3
m
. D.
5
m
.
Câu 34. Cho khối lăng trụ đứng
. ' ' 'ABC A B C
có
'BB a
, đáy
ABC
là tam giác vuông cân tại
B
,
2AC a
. Thể tích lăng trụ đã cho bằng
A.
3
2
a
. B.
3
a
. C.
3
3
a
. D.
3
6
a
.
Câu 35. Tìm giá trị thực của tham số
m
để hàm số
3 2 2
1
4 3
3
y x mx m x
đạt cực tiểu tại
3
x
.
A.
7
m
. B.
1
m
. C.
5
m
. D.
1
m
.
Câu 36. Tập nghiệm
S
của bất phương trình
3 3
2log 4 3 log 18 27
x x
là
A.
3;S
. B.
3
;3
8
S
. C.
3
;
4
S
. D.
3
;3
4
S
.
Câu 37. Cho hình chóp
.
S ABCD
có đáy là hình vuông cạnh bằng
2a
, cạnh bên
SA
vuông góc
với đáy và
3SA a
. Góc giữa hai mặt phẳng
SBD
và
ABCD
bằng
A.
90
. B.
60
. C.
30
. D.
45
.
Câu 38. Trong không gian với hệ trục toạ độ
Oxyz
, cho bốn điểm
;0;0
A a
,
0; ;0B b
,
0;0;C c
và
1;2; 1
D
; với
, ,a b c
là các số thực khác
0
. Biết rằng bốn điểm
, , ,A B C D
đồng phẳng khi khoảng cách từ gốc toạ độ
O
đến mặt phẳng
ABC
là lớn
nhất. Giá trị biểu thức
a b c
bằng
41
A.
2
. B.
4
. C.
3
. D.
15
.
Câu 39. Cho
4
1
( )
4
f x
dx
x
và
2
2
0
1 4sin sin 2 5
f x xdx
. Tích phân
5
2
f x dx
bằng
A.
18
B.
22
. C.
12
. D.
1
.
Câu 40. Cho hình thang cong
H
giới hạn bởi các đường
y x
,
0
y
,
0
x
,
4
x
.
Đường thẳng
x k
0 4
k
chia
H
thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ.
Để
1 2
3S S
thì giá trị
k
thuộc khoảng nào sau đây ?
A.
3,3; 3,5
. B.
3,5;3,8
. C.
3,1;3,3
. D.
3,8;3,9
.
Câu 41. Trong không gian
,Oxyz
cho mặt cầu
S
có tâm là điểm
2;1; 3
A
và tiếp xúc với mặt
phẳng
.Oxy
Mặt cầu
S
có phương trình là
A.
2 2 2
2 1 3 5
x y z
. B.
2 2 2
2 1 3 9
x y z
.
C.
2 2 2
2 1 3 5
x y z
. D.
2 2 2
2 1 3 9
x y z
.
Câu 42. Cho hàm số
y f x
, biết
3
3 1.
f x x x
Có bao nhiêu giá trị nguyên của tham số
m
thuộc đoạn
8;8
sao cho hàm số
2 1 6
g x f x m x
nghịch biết trên
khoảng
2;3
?
A.
11
. B.
12
. C.
9
D.
10
.
42
Câu 43. Cho hàm số
,
f x g x
là hai hàm số liên tục trên
0; 3
thỏa mãn điều kiện
3
0
10
f x g x dx
và
3
0
3 6
f x g x dx
. Tính
3
2021
2
2018 0
2021 3 2 ?f x dx g x dx
A.
5
. B.
7
. C.
13
. D.
6
.
Câu 44. Trong không gian
Oxyz
, cho hai điểm
1;1; 1
A
,
7; 2;2
B
và đường thẳng
1 3
: 2 2
2 2
x t
y t
z t
. Gọi
P
là mặt phẳng chứa đường thẳng
, khoảng cách từ
A
đến
P
gấp đôi khoảng cách từ
B
đến
P
và
,A B
nằm khác phía so với
P
. Biết rằng phương
trình
P
có dạng
28 0.
zax by c
Giá trị của
a b c
bằng
A.
26
. B.
26
. C.
34
. D.
34
.
Câu 45. Cho hàm số
f x
có đạo hàm và liên tục trên
, thỏa mãn
2
' 2 e
x
f x xf x x
và
0 2
f
. Tính
1f
.
A.
2
1
e
f
. B.
1
1
e
f
. C.
2
1
e
f
. D.
1 e
f
.
Câu 46. Cho hai số thực
,x y
thỏa mãn
2 2
1
log 2 4 1
x y
x y
. Tính
.P x y
khi biểu thức
4 3 5S x y
đạt giá trị lớn nhất.
A.
52
25
P
. B.
13
25
P
C.
52
25
P
. D.
13
25
P
Câu 47. Trong không gian
Oxyz
, cho hai đường thẳng
1
1 1
1
: 4
3
x t
d y t
z t
và
2
2 2
2
1 2
: 3
4
x t
d y t
z t
.
Đưởng thẳng vuông góc với mặt phẳng
Oxz
cắt hai đường thẳng
1
d
và
2
d
có phương
trình là
43
A.
1
3
7
3
10
3
x
y t
z
B.
1
7
7
1
3
10
3
x t
y t
z t
.
C.
3
7
25
1
7
18
7
x t
y t
z t
. D.
3
7
25
7
18
7
x
y t
z
.
Câu 48. Gọi tập
X
là tập hợp tất cả các số nguyên
2021;2021
m
sao cho đồ thị của hàm số
3 2
2 1
y x m x mx m
có 5 điểm cực trị. Tính tổng các phần tử của tập
X
.
A.
0
. B.
1
. C.
4036
. D.
1
.
Câu 49. Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số
siny x
, trục hoành và các đường thẳng
0;x x
quanh trục
Ox
bằng
A.
4
. B.
2
. C.
2
4
. D.
2
2
.
Câu 50. Cho hàm số
y x
có đồ thị
C
và điểm
M
thuộc
C
có hoành độ dương. Gọi
1
S
là diện tích hình phẳng giới hạn bởi
C
, trục hoành và đường thẳng đi qua
M
và vuông
góc với trục hoành;
2
S
là diện tích hình phẳng giới hạn bởi
C
và đường thẳng
.OM
Biết
2
1
S
a
S b
(với
*
,a b
và
a
b
là phân số tối giản), giá trị của
a b
bằng
A.
6
. B.
5
. C.
19
. D.
21
.
| 1/43
| | Tải xuống

Có thể bạn quan tâm:

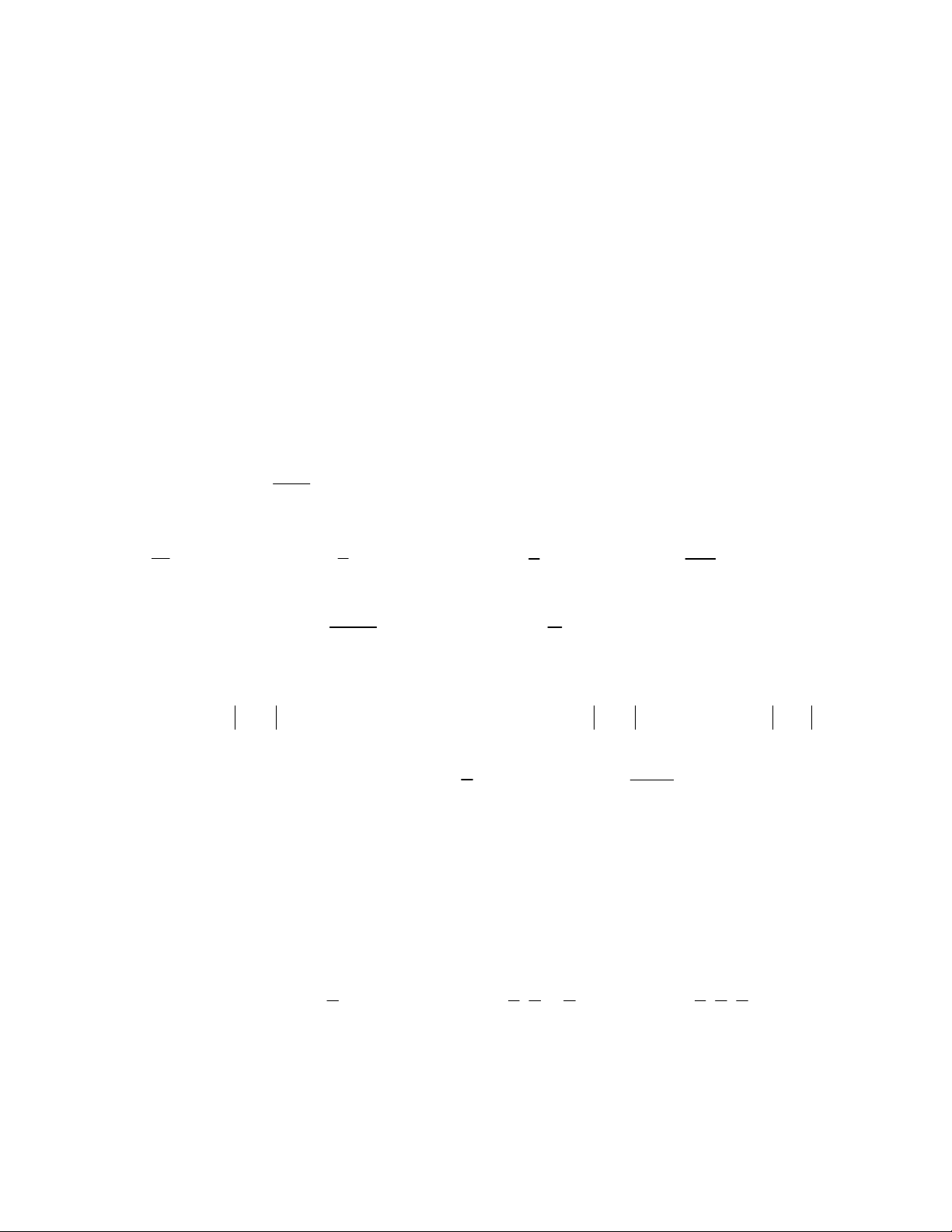
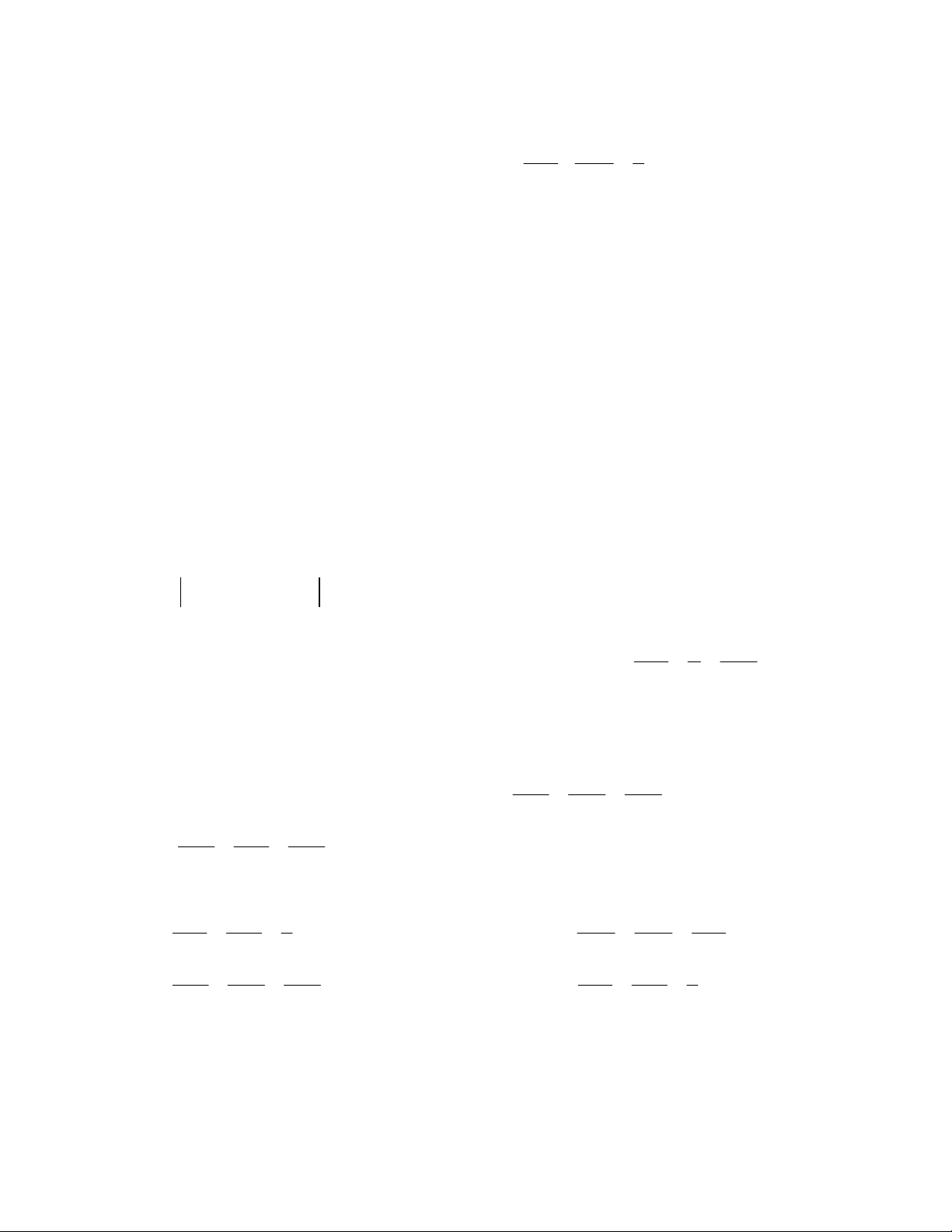
Preview text:

TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 12 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
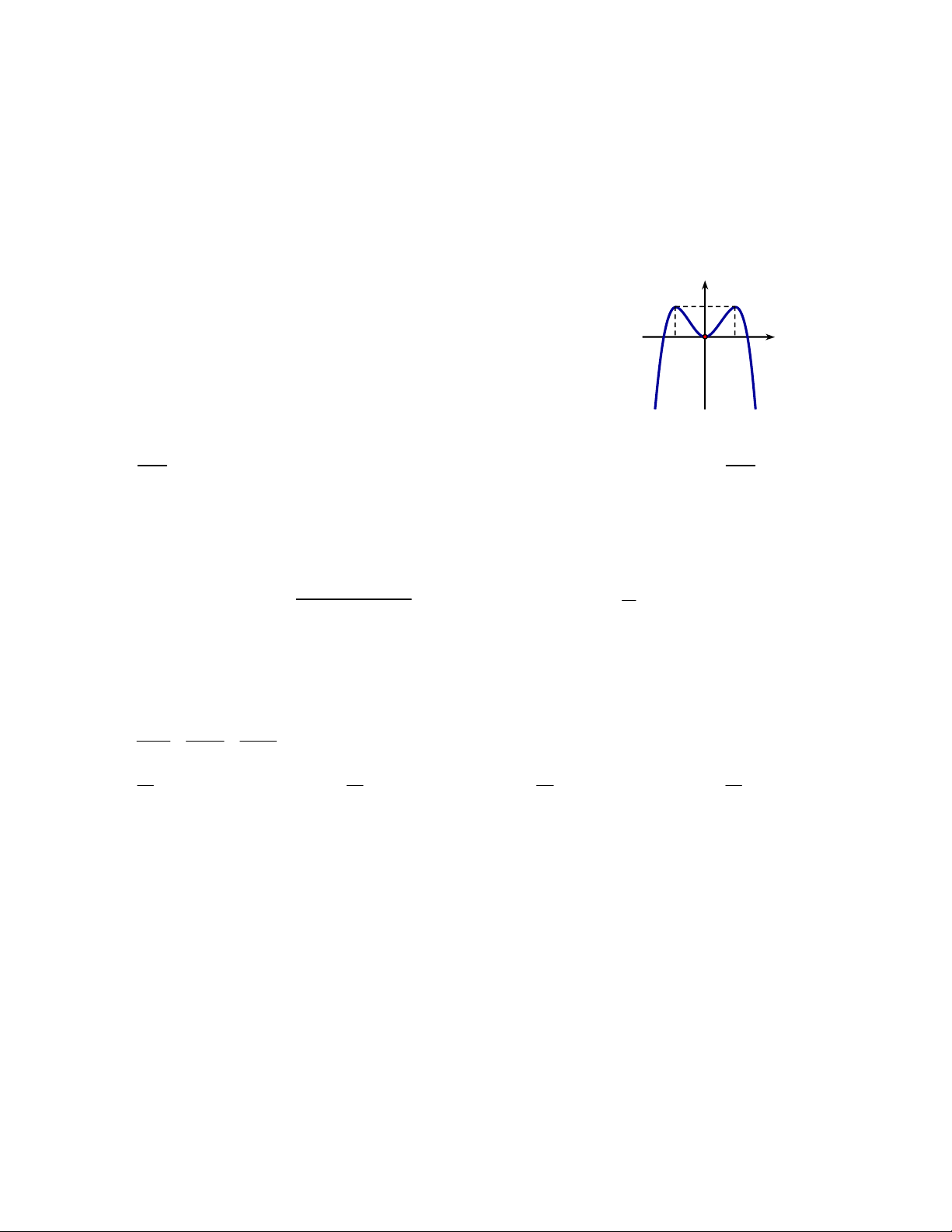
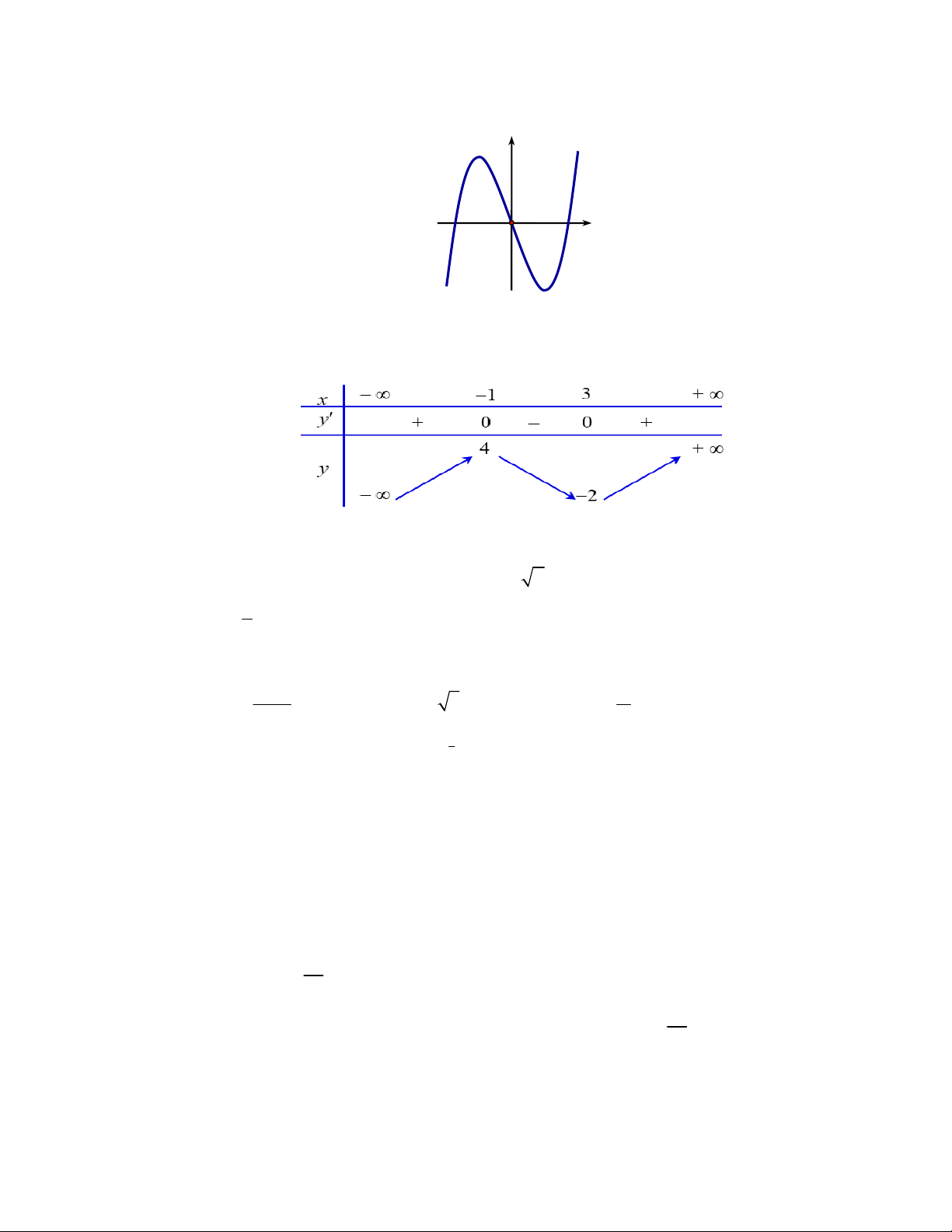
Giáo viên soạn đề: Thầy Nguyễn Chí Khôi y Câu 1: Cho hàm số 4 2
y  x  2x có đồ thị như hình vẽ bên. Tìm 1
tất cả các giá trị thực của tham số m để phương trình 4 2
x  2x  log m có bốn nghiệm thực phân biệt. 2 1 O 1 x
A. 0  m  1. B. m  0.
C. 1  m  2 . D. m  2.
Câu 2: Thể tích khối chóp có đường cao bằng a và đáy là hình vuông cạnh 2a bằng 3 4a 3 2a A. . B. 3 2a . C. 3 4a . D. . 3 3
Câu 3: Trong không gian Oxyz , mặt phẳng nào dưới đây song song với mặt phẳng (Oxy) ?
A. ( ) : x  1  0 .
B. ( ) : z  1  0 .
C. ( ) : x z  1  0 .
D. ( ) : y  1  0 .
2sin x mcos x   
Câu 4: Biết hàm số y
đạt giá trị lớn nhất trên 0;
bằng 1. Mệnh đề nào sau sin x  cos x  4    đây đúng? A. m  1  ; 0 . B. m 0  ;1 .
C. m 1; 2 .
D. m 2;3 .
Câu 5: Trong không gian tọa độ O xyz , cho mặt phẳng  P : 4x  3y z 1  0 và đường thẳng x  1 y  6 z  4 d :  
. Sin của góc giữa đường thẳng d và mặt phẳng  P bằng: 4 3 1 5 1 12 8 A. . B. . C. . D. . 13 13 13 13
Câu 6: Trong không gian Oxyz , cho hai điểm A3;  2; 2 , B  2
 ; 2;0 và mặt phẳng
P : 2x y  2z  3  0 . Xét các điểm M , N di động trên  P sao cho MN 1. Giá trị nhỏ nhất của biểu thức 2 2
2MA  3NB bằng A. 45. B. 53. C. 49,8. D. 55,8. 1
Câu 7: Cho hàm số y f ( )
x có đồ thị như hình bên dưới. Hàm
số đã cho nghịch biến trên khoảng nào dưới đây? A.  2  ; 2. B.  1;  2. C. 1;  1 . D. 2; 0. 4 2x 1dx 5 Câu 8: Biết
a b ln 2  c ln a, , b c   
 . Tính T  2a b c .
2x  3 2x 1  3 3 0 A. T  4 . B. T  2 . C. T  1 . D. T  3 .
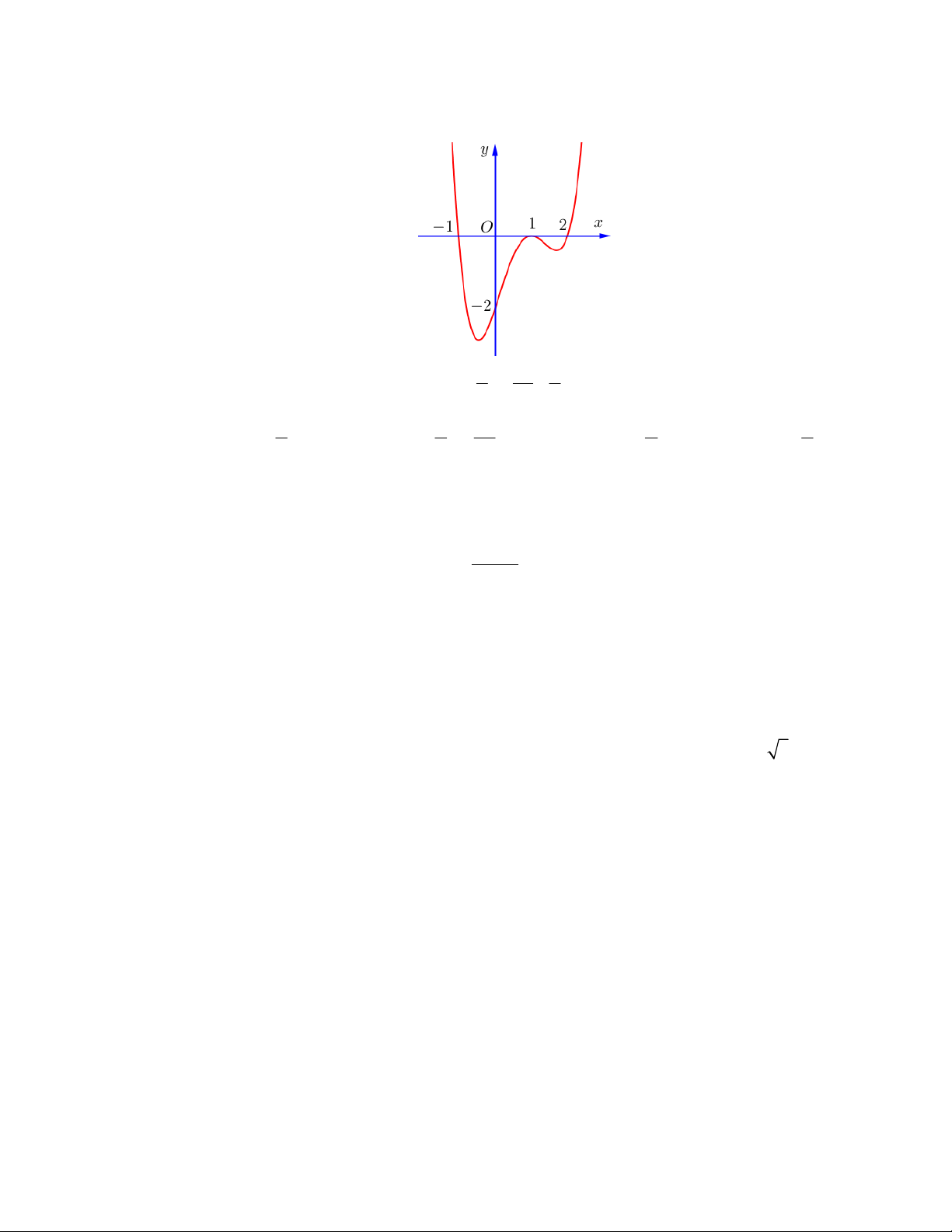
Câu 9: Đường cong trong hình là đồ thị của hàm số nào dưới đây? x 1 y A. y  . x 1 1 B. 3
y x  3x  2 . 1 1 xx O C. y  . 1 x 1 D. 4 2
y x  2x 1.
Câu 10: Cho hình lập phương ABC . D A BCD
  có cạnh bằng a , gọi  là góc giữa đường thẳng A B
 và mặt phẳng  BB DD   . Tính sin . 3 3 3 1 A. . B. . C. . D. . 2 5 4 2 4 dx
Câu 11: Biết I
a ln 2  b ln 3  c ln 5 
, trong đó a, b, c Z . Tính giá trị T a b c . 2 3 x x A. T  1  . B. T  5 . C. T  3. D. T  2 .
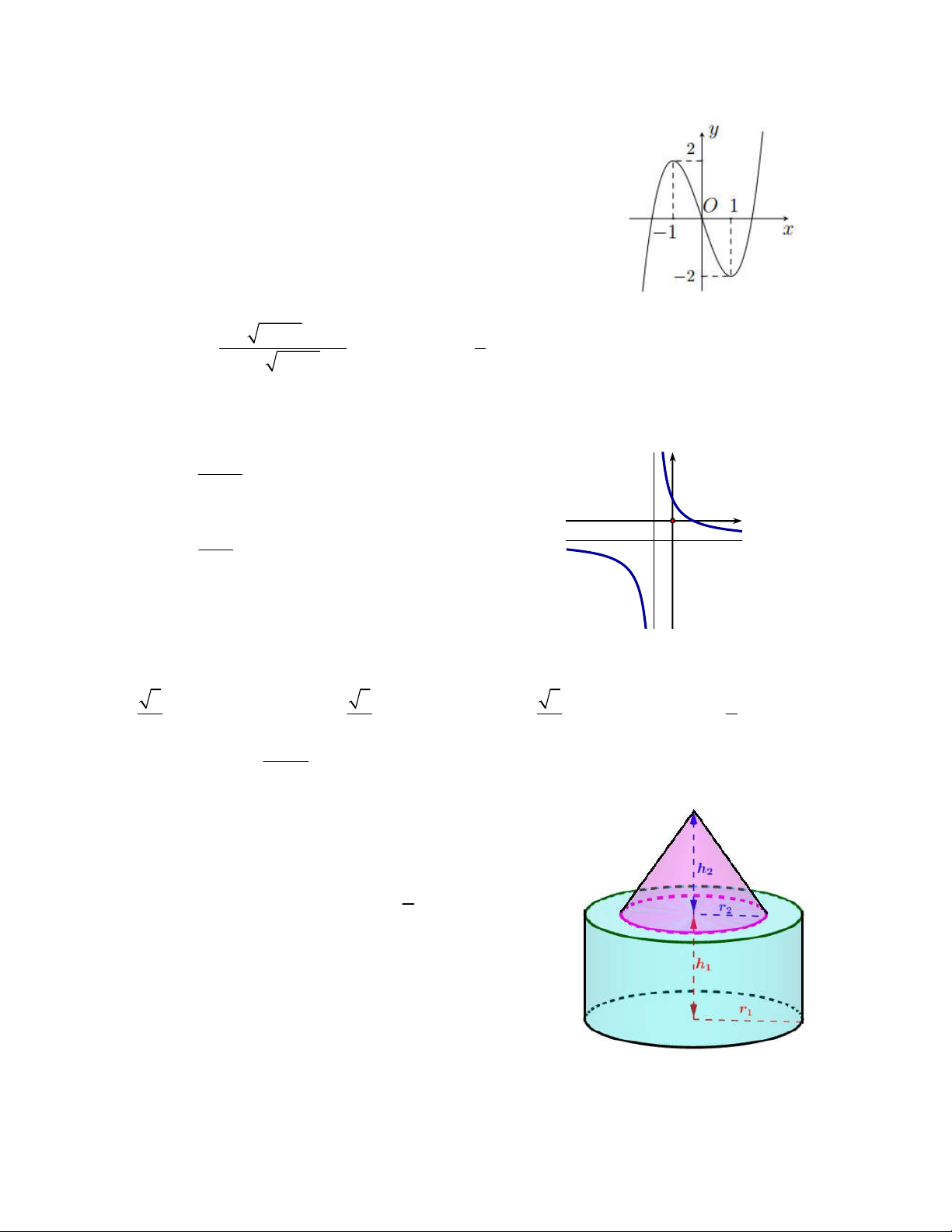
Câu 12: Một khối đồ chơi gồm một khối nón (N) xếp chồng
lên một khối trụ (T). Khối trụ (T) có bán kính đáy và chiều
cao lần lượt là r , h . Khối nón (N) có bán kính đáy và chiều 1 1 2
cao lần lượt là r , h thỏa mãn r
r và h h (tham 2 2 2 1 3 2 1
khảo hình vẽ bên). Biết rằng thể tích của toàn bộ khối đồ chơi bằng 3
124 cm , thể tích khối nón (N) bằng A. 3 62 cm . B. 3 15 cm . C. 3 108 cm . D. 3 16 cm . 2
Câu 13: Đáy của một lăng trụ tam giác đều là tam giác ABC có cạnh bằng a . Trên các cạnh bên a 3a
lấy các điểm A , B , C lần lượt cách đáy một khoảng bằng , a ,
(tham khảo hình vẽ bên). 1 1 1 2 2
Cosin góc giữa  A B C và ABC bằng 1 1 1  B1 C A 1 1 A B C 2 3 13 15 A. . B. . C. . D. . 2 2 4 5 x y
Câu 14: Xét các số thực dương x, y thỏa mãn log
x x  3  y y  3  xy . 3 2 2
x y xy  2 3x  2 y 1
Tìm giá trị lớn nhất P
cuả biểu thức P  . max x y  6 A. P  3. B. P  2. C. P  1. D. P  4. max max max max x y 1 z
Câu 15: Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d :   . Vectơ nào 1 2 2
sau đây là vectơ chỉ phương của đường thẳng d ?   A. u  1; 2  ; 2  .
B. u  0;1; 0 . 4   2     C. u  1; 2  ; 2 . D. u  1; 2; 2  . 1   3  
Câu 16: Hàm số y f x có đạo hàm f  x   x x  x  3 4 2 2 , x
   . Số điểm cực trị của hàm số là A. 3 . B. 2 . C. 1. D. 4 .
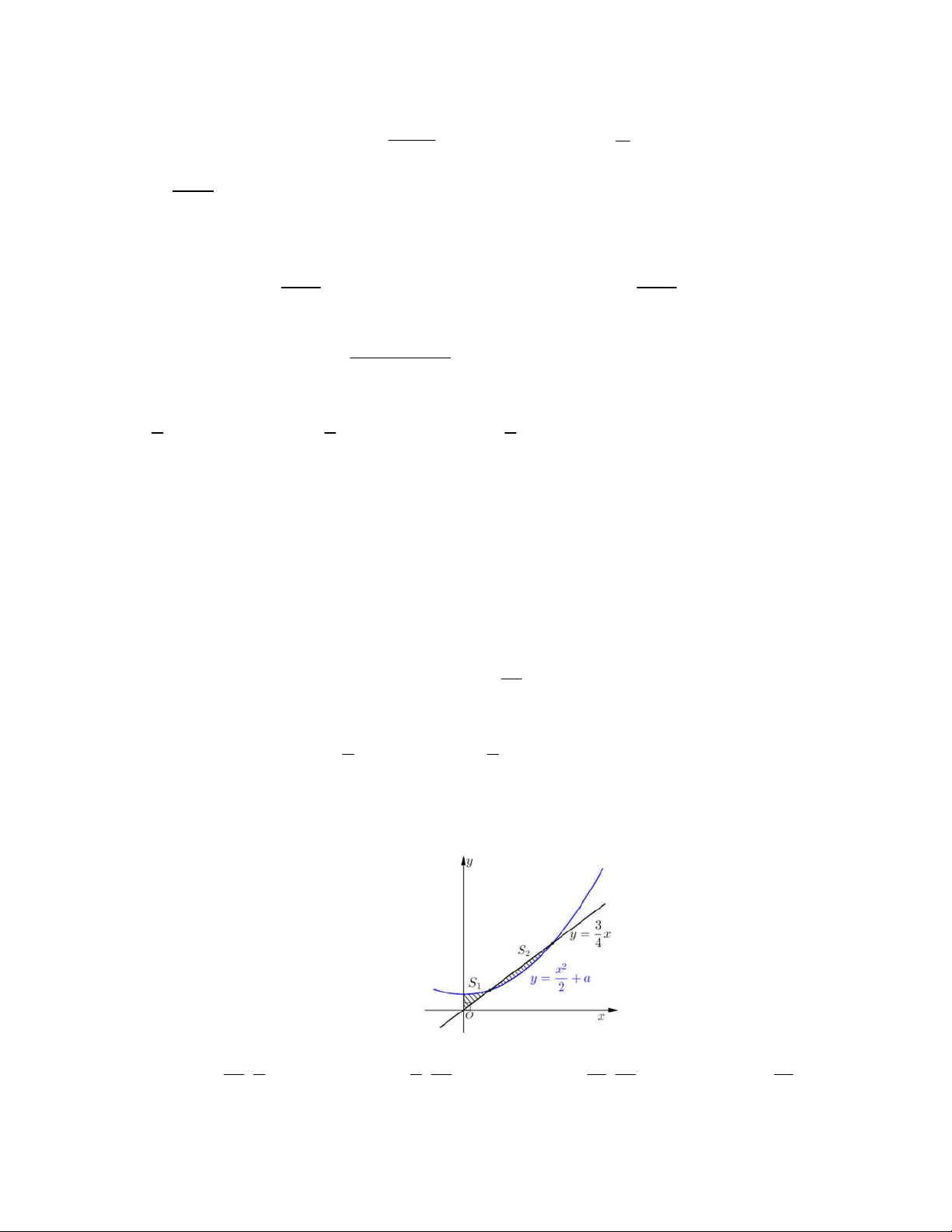
Câu 17: Cho hàm số y f x liên tục trên  2  ;6 và có đồ thị
như hình vẽ dưới. Gọi M và m lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của hàm số đã cho trên đoạn  2
 ;6 . Hiệu M m bằng A. 4 . B. 8 . C. 6 . D. 3 . 3
Câu 18: Từ các chữ số 1, 2, 3, 4, 5, 6 . Có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số khác nhau? A. 6 . B. 20 . C. 120 . D. 720 .
Câu 19: Tìm số nghiệm của phương trình  2
ln x  4x   ln  x  6. A. 2. B. 1. C. 3. D. 0.
Câu 20: Trong không gian Oxyz , cho mặt phẳng (P) : x y z  3  0 và đường thẳng x  2 y 1 z d :  
. Hình chiếu vuông góc của đường thẳng d trên ( )
P có phương trình là 2 1  3 x y 1 z  2 x y 1 z  2 A.   . B.   . 2 3 5  2 7  5 x y 1 z  2 x y 1 z  2 C.   . D.   . 4 3 7  5 8 1  3 y
Câu 21: Cho hàm số f x liên tục trên R, có đồ thị như hình
vẽ bên. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị
hàm số f x , trục hoành và trục tung. Khẳng định nào sau đây c d O x đúng? d 0 A. S
f x dx f x dx .  
y f x c d d 0
B. S   f x dx f x dx .   c d d 0
C. S   f x dx f x dx .   c d d 0 D. S
f x dx f x dx .   c d 2 x 1  x 2  2018   2019 
Câu 22: Tìm tập nghiệm của bất phương trình      .  2019   2018  A. 1;  . B.   ;1 . C.  1  ;  . D.  ;    1 .
Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  2a , BC a , mặt bên SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E là trung điểm của CD . Tính
theo a khoảng cách giữa hai đường thẳng BE và SC . a 15 a 3 a 30 A. . B. . C. a. D. . 5 2 10
Câu 24: Phương trình tham số của đường thẳng d  đi qua hai điểm A1;2; 3   và B3; 1  ;  1 là x  1  t
x  1  3tx  1   2tx  1   2t     A.y  2
  2t . B.y  2
  t . C.y  2
  3t . D.y  5  3t . z  1   3t     z  3   tz  3  4tz  7   4t  4
Câu 25: Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2 3
y x  3mx  3x  6m đồng
biến trên khoảng 0;   là: A.  ;   1 . B. 2;  . C.  ;  2. D.  ;  0.
Câu 26: Cho cấp số nhân (u ) thỏa mãn u  3 và u  48 . Số hạng thứ ba của cấp số nhân bằng n 1 5 A. 8. B. 1  6. C. 12. D. 16. x  2
Câu 27: Cho biết đồ thị của hàm số y
cắt đường thẳng d : y x m tại hai điểm phân biệt x 1 ,
A B . Gọi I là trung điểm của đoạn AB . Tìm giá trị của m để I nằm trên trục hoành.
A. m  3 .
B. m  4 .
C. m  1.
D. m  2 .
Câu 28: Tích các nghiệm của phương trình log  x 1 6   36x  2  bằng 1  5 A. 0 . B. log 5 . C. 5 . D. 1. 6
Câu 29: Họ nguyên hàm của hàm số     3x f x x là 2 x 3x 2 3x x A.
 3x ln 3  C . B. 1  C .
C. 1  3x ln 3  C . D.   C . 2 ln 3 2 ln 3
Câu 30: Cho hàm số y f x có bảng biến thiên như sau
Giá trị cực tiểu của hàm số đã cho bằng A. 3 . B. 26 . C. 6 . D. 1  .
Câu 31: Với log 3  a thì log 45 bằng 5 15 2 1 a 1 2a 2  a 2 A. . B. . C. . D. . 1 a 1 a 1 a a
Câu 32: Thể tích V của khối chóp có diện tích đáy B và chiều cao h là: 1 1
A. V Bh B. V Bh
C. V  2Bh D. V Bh 2 3
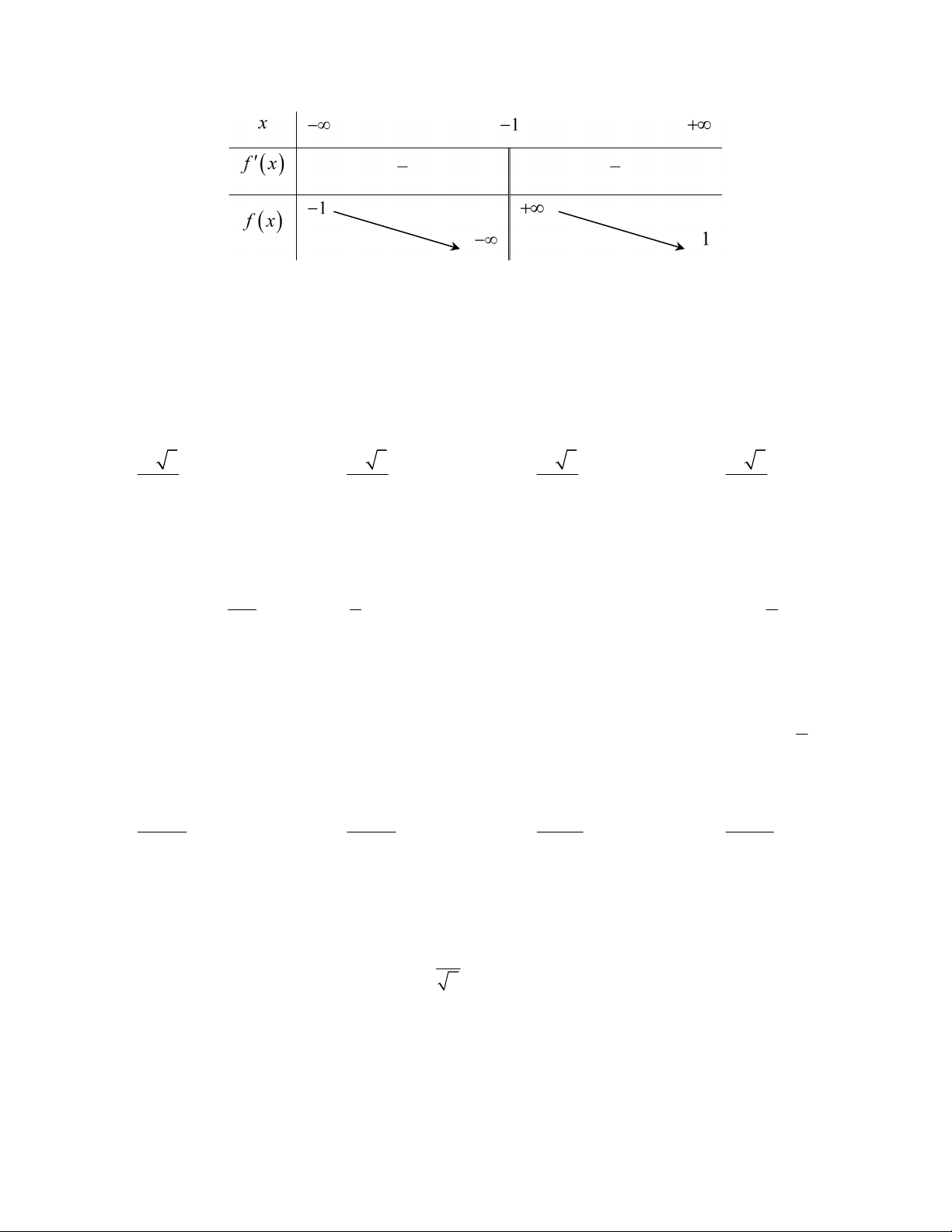
Câu 33: Cho hàm số f x có bảng biến thiên như hình vẽ. Khẳng định nào dưới đây là khẳng định đúng? 5
A. Đồ thị của hàm số f x có đúng 1 tiệm cận ngang và 1 tiệm cận đứng.
B. Đồ thị của hàm số f x không có tiệm cận ngang và có 1 tiệm cận đứng.
C. Đồ thị của hàm số f x có đúng 2 tiệm cận ngang và không có tiệm cận đứng.
D. Đồ thị của hàm số f x có đúng 2 tiệm cận ngang và 1 tiệm cận đứng.
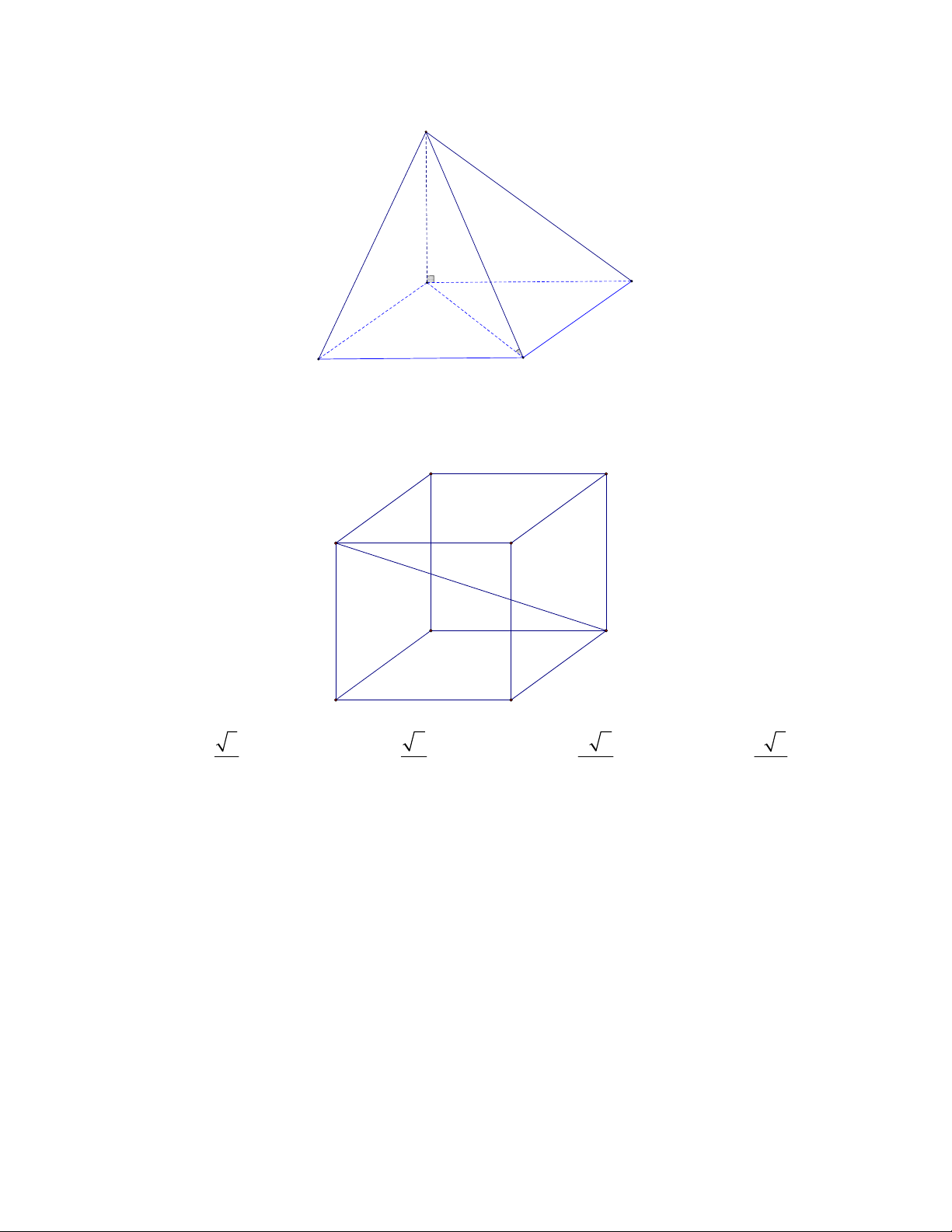
Câu 34: Cho hình lăng trụ tam giác đều ABC.A BC
  có AB a , góc giữa AC và mặt phẳng
ABC bằng 45. Thể tích khối lăng trụ ABC.A BC   bằng 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 2 6 12 4
Câu 35: Với mọi a, b, x là các số thực dương thoả mãn log x  5log a  3log b . Khẳng định 2 2 2
nào dưới đây đúng ? A. 5 3
x a b .
B. x  5a  3b . C. 5 3 x a b .
D. x  3a  5b . 2 ln x b b Câu 36: Biết
dx a ln 2  
( với a là số hữu tỉ, b , c là các số nguyên dương và là phân 2 x c c 1
số tối giản). Tính giá trị của S  2a  3b c . A. S  4 . B. S  6  . C. S  6 . D. S  5.
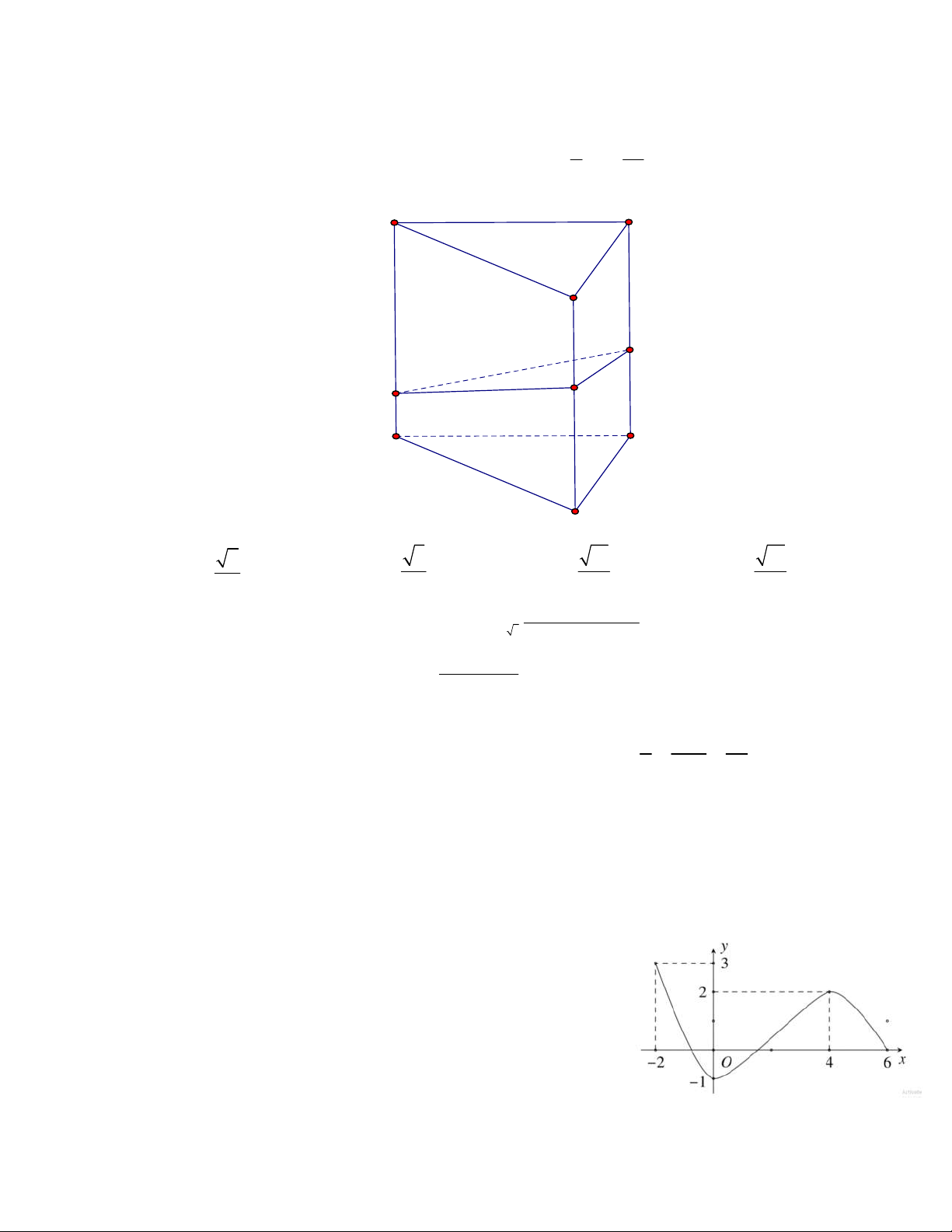
Câu 37: Cho khối lăng trụ ABC.A BC
  có thể tích bằng 2019 (đvtt). Gọi M là trung điểm của 1 A B
  , hai điểm N , P lần lượt nằm trên các cạnh B C
  và BC sao cho B N
 3NC , BP BC 4
. Đường thẳng NP cắt BB tại E , đường thẳng EM cắt cạnh AB tại Q . Thể tích khối đa diện
lồi AQPCAMNC bằng 39707 63935 15479 88163 A. . B. . C. . D. . 24 36 12 48
Câu 38: Cho nửa đường tròn đường kính AB  2R và điểm C thay đổi trên nửa đường tròn đó, đặt 
CAB   và gọi H là hình chiếu vuông góc của C lên AB . Tìm  sao cho thể tích vật thể
tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất. 1 A.   0 45 B.   arctan C.   0 30 D.   0 60 2 6 5
Câu 39: Trong không gian tọa độ Oxyz , cho mặt cầu S  2 2 2
: (x 1)  ( y 1)  z  , mặt phẳng 6  x y z
P : x y z 1  0 và đường thẳng  :  
. Điểm M thay đổi trên đường tròn giao tuyến 1 1 1
của  P và  S  . Giá trị lớn nhất của d M ,  là: 3 2 2 A. 2 . B. . C. . D. 2 2 . 2 2
Câu 40: Ông A vay ngân hàng 50 triệu đồng với lãi suất 0, 67% /tháng. Ông ta muốn hoàn nợ cho
ngân hàng theo cách: Sau đúng một tháng kể từ ngày vay, ông ta bắt đầu hoàn nợ; hai lần hoàn nợ
liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ mỗi tháng đều bằng nhau và bằng 3 triệu. Biết
rằng mỗi tháng ngân hàng chỉ tính lãi trên số dư nợ thực tế của tháng đó. Hỏi bằng cách hoàn nợ
đó, ông A cần trả ít nhất bao nhiêu tháng kể từ ngày vay đến lúc hoàn hết nợ ngân hàng (giả định
trong thời gian này lãi suất không thay đổi) A. 17 tháng. B. 19 tháng. C. 18 tháng. D. 20 tháng.
Câu 41: Cho hình nón có bán kính đáy bằng a và diện tích xung quanh bằng 2
3 a . Độ dài đường sinh của hình nón bằng 3a A. . B. 2a . C. 3a . D. 9a . 2
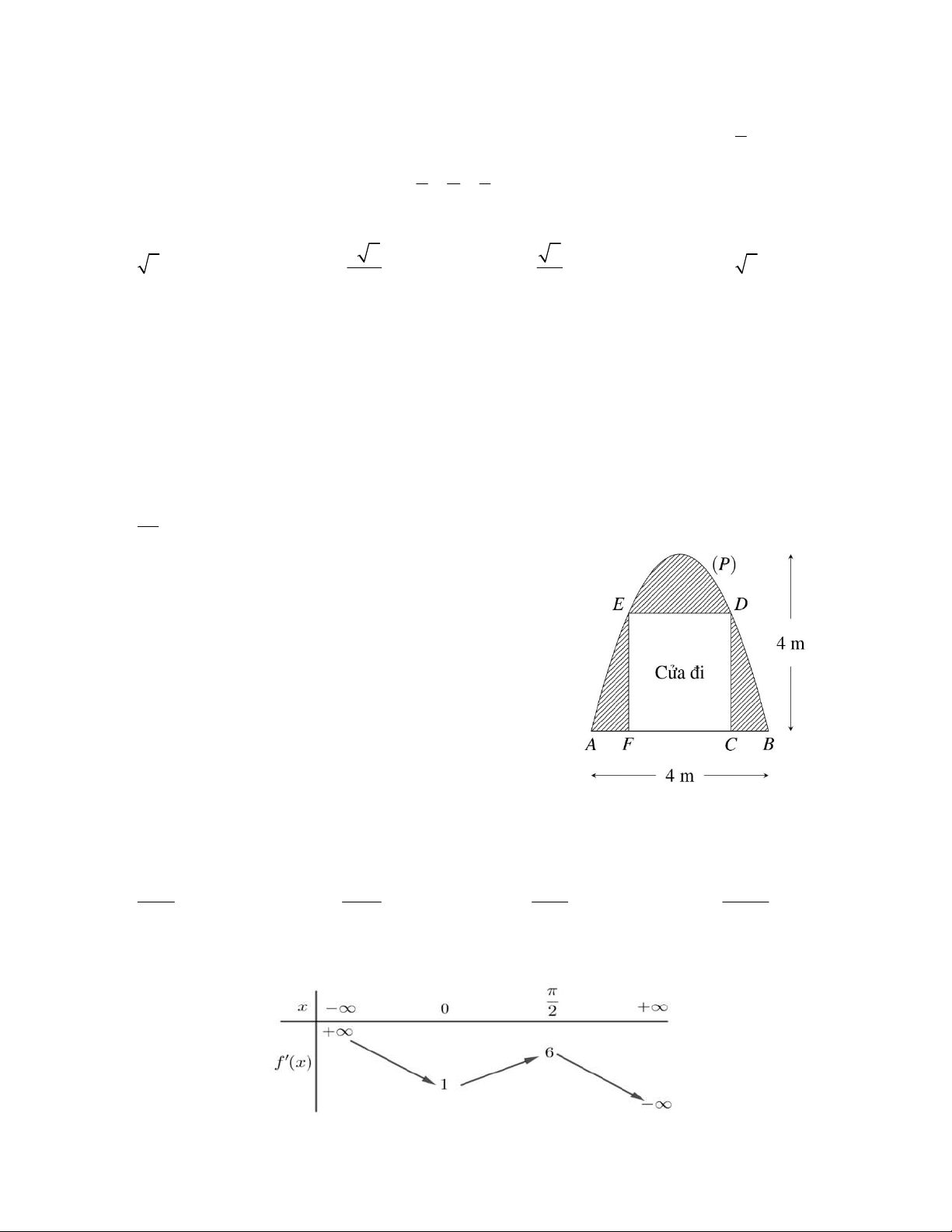
Câu 42: Một chiếc cổng có hình dạng là một parabol (P) có
kích thước như hình vẽ, biết chiều cao cổng bằng 4 m ,
AB  4 m . Người ta thiết kế cửa đi là một hình chữ nhật
CDEF (với C, F AB; D, E  (P) ), phần còn lại (phần
gạch chéo) dùng để trang trí. Biết chi phí để trang trí phần
tô đậm là 1.000.000 đồng/ 2
m . Hỏi số tiền ít nhất dùng để
trang trí phần tô đậm gần với số tiền nào dưới đây? A. 4.450.000 đồng. B. 4.605.000 đồng. C. 4.505.000 đồng. D. 4.509.000 đồng.
Câu 43: Có 3 quyển sách Văn học khác nhau, 4 quyển sách Toán học khác nhau và 7 quyển sách
Tiếng anh khác nhau được xếp lên một kệ ngang. Tính xác suất để hai cuốn sách cùng môn không ở cạnh nhau. 1 5 1 19 A. . B. . C. . D. . 1716 8008 1001 12012
Câu 44: Cho hàm số y f x . Hàm số y f  x có bảng biến thiên như sau 7    Bất phương trình   cos  2 x f x
 3m đúng với mọi x  0;   khi và chỉ khi  2  1      1      A. m f 1 .    B. m f 1 .    3 2       3   2   1 1 C. m   f 0  2. m   f 0  2 . 3   D.   3  
Câu 45: Trong không gian với hệ tọa độ Oxyz, cho (
A 1; 0; 0) , B(0;2;0), C(0;0;3) , phương trình
nào sau đây là phương trình mặt phẳng . y z A. x    1
B. 6x  3 y  2z  6  0 2 3
C. 6x  3 y  2z  6  0
D. 12 x  6 y  4z  12  0
Câu 46: Xét tam thức bậc hai   2
f x ax bx c , với a, b, c R , thỏa mãn điều kiện f x  1, với mọi x  1  ; 
1 . Gọi m là số nguyên dương nhỏ nhất sao cho max f x  m . Khi đó m bằng x   2;2 A. 8 . B. 7 . C. 4 . D. 3 .
Câu 47: Cho hàm số f x có bảng xét dấu của đạo hàm như sau 3
Hàm số y  3 f x  2 3 2  2x
x  3x  2019 đồng biến trên khoảng nào dưới đây? 2  1  A. 1;  . B.  ;    1 . C. 1;   . D. 0; 2 .  2  2
Câu 48: Phương trình 2x 4x5 2
 32 có bao nhiêu nghiệm? A. 3. B. 0. C. 1. D. 2.
Câu 49: Trong không gian với hệ toạ độ Oxyz , phương trình mặt cầu đường kính AB với A1; 1  ; 2 , B  3  ;1; 2 là: 2 2 2 2
A. x     y   2 2 1  z  5 .
B. x     y   2 2 1  z  5 . 2 2 2 2 C. x   2 1
y   z  2  5 . D. x   2 1
y   z  2  5 .
Câu 50: Hàm số y   2 log x   1 có đạo hàm là 2x 1 2x ln10 ln10 A. y '  . B. y '  . C. y '  . D. y '  .  2 x   1 ln10  2 x   1 ln10 2 x  1 2 x  1
----------- HẾT ---------- 8
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 12 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Thầy Nguyễn Bá Cao
Câu 1: Số cách sắp xếp 6 học sinh theo một hàng dọc bằng A. 46656 . B. 4320 . C. 720 . D. 360 .
Câu 2 : Cho cấp số nhân u có số hạng đầu u  5 và công bội q  2
 . Giá trị của u bằng n  1 6 A. 160 . B. 320 . C. 160 . D. 320 .
Câu 3: Cho hàm số y f x có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng  1  ; 3 .
B. Hàm số đồng biến trên khoảng 1;   .
C. Hàm số nghịch biến trên khoảng 1;  1 .
D. Hàm số đồng biến trên khoảng  ;   1 .
Câu 4: Hàm số y f x liên tục trên  và có bảng biến thiên dưới đây. .
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại x  1 .
B. Hàm số đạt cực đại tại x  0 .
C. Hàm số có ba điểm cực trị.
D. Hàm số đạt cực đại tại x  2 . 2x  5
Câu 5: Hàm số y
có bao nhiêu điểm cực trị? x 1 A. 0 . B. 2 . C. 3 . D. 1. 5
Câu 6: Tiệm cận ngang của đồ thị hàm số y
là đường thẳng có phương trình x 1 A. y  5 . B. x  0 . C. x  1 . D. y  0 . 9
Câu 7: Đường cong dưới đây là đồ thị của hàm số nào? y O x A. 3
y x  3x . B. 3
y x  3x 1. C. 3
y x  3x . D. 3
y x  3x 1.
Câu 8: Cho hàm số y f x có bảng biến thiên như sau:
Tìm tất cả các giá trị của tham số m để phương trình f x  m có ba nghiệm phân biệt.
A. m  2 .
B. 2  m  4 .
C. 2  m  4 . D. m  4 .
Câu 9: Cho a là số thực dương khác 1. Tính 3 I  log a. a 1 A. I  . B. I  3 . C. I  0 . D. I  3 . 3
Câu 10: Hàm số nào sau đây đồng biến trên  ;   ? x x  2021  x  3  x A. y    .
B. y   5  2 .
C. y    .
D. y  0, 7 .  2     1
Câu 11: Tập xác định của hàm số y   x  5 1 là A. 0;   . B. 1;   . C. 1;   . D.  . 2
Câu 12: Số nghiệm của phương trình 2x 5x3 2  1 là A. 3 . B. 2 . C. 0 . D. 1. log x 1  3 2  
Câu 13: Tập nghiệm của bất phương trình là A. 9;   . B. 4;   . C. 1;   . D. 10;   .
Câu 14: Cho hàm số f x  x  cos x .Trong các khẳng định sau, khẳng định nào đúng? 2 x A.
f x dx   sin x C  . B.
f x dx  1 sin x C  . 2 2 x C.
f x dx x sin x  cos x C  . D.
f x dx   sin x C  . 2
Câu 15: Biết F x là một nguyên hàm của hàm số f x . Trong các khẳng định sau, khẳng định nào đúng? 10
A. 3 f x 1 dx  3F x 1 C    .
B. 3 f x 1 dx  3xF x 1 C    .
C. 3 f x 1 dx  3xF x  x C    .
D. 3 f x 1 dx  3F x  x C    . 9
Câu 16: Cho hàm số f x liên tục trên  và F x là nguyên hàm của f x , biết f x dx  9 0
và F 0  3. Giá trị của F 9 bằng
A. F 9  6
B. F 9  12
C. F 9  6 D. F 9  12 2 2
Câu 17: Cho hàm số f x liên tục trên  và  f x  2x dx  5    . Tính f (x)dx  . 0 0 A. 9 . B. 1  . C. 9 . D. 1.
Câu 18: Tập nghiệm của bất phương trình log  2
x  3x  2  log x 1  2 là 2  1   2
A. S  1;6 .
B. S  1;   .
C. S  2;   .
D. S  2; 6 .
Câu 19: Từ một tổ gồm 8 nam và 7 nữ chọn ra một đoàn đại biểu gồm 5 người để tham dự hội
nghị. Xác suất để đại biểu được chọn có đúng 2 nữ bằng 140 56 28 1 A. . B. . C. . D. . 429 143 715 39
Câu 20: Tính diện tích S của hình phẳng giới hạn bởi các đồ thị các hàm số y  ln x , y  1, y  1 x . 3 1 1 3
A. S e
. B. S e  .
C. S e  .
D. S e  2 2 2 2
Câu 21: Cho hình chóp có diện tích mặt đáy là 2
3a và chiều cao bằng 2a . Thể tích của khối chóp bằng A. 3 6a . B. 3 2a . C. 3 3a . D. 3 a .
Câu 22: Cho khối lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng 9 3 27 3 27 3 9 3 A. . B. . C. . D. . 4 4 2 2
Câu 23: Cho hình nón có bán kính đáy là r
2 và độ dài đường sinh l  4 . Diện tích xung quanh
của hình nón đã cho bằng A. 16 . B. 8 2 . C. 16 2 . D. 4 2 .
Câu 24: Khối trụ có chiều cao bằng bán kính đáy và diện tích xung quanh bằng 2 . Thể tích khối trụ bằng A.  . B. 2 . C. 3 . D. 4 .
Câu 25: Trong không gian với hệ tọa độ Oxyz , cho hai điểm M 3; 0;0 , N 0; 0; 4 . Độ dài đoạn thẳng MN bằng 11 A. 1. B. 7 . C. 5 . D. 10 .
Câu 26: Trong không gian với hệ tọa độ Oxyz , mặt cầu S  2 2 2
: x y z  2x  2 y  4z  2  0 có bán kính bằng A. 2 2 . B. 26 . C. 4 . D. 2 .
Câu 27: Trong không gian với hệ tọa độ Oxyz , điểm M 3; 4; 2
  thuộc mặt phẳng nào trong các mặt phẳng sau?
A.R : x y  7  0 .
B.S  : x y z  5  0 .
C.Q : x 1  0 .
D.P : z  2  0 .
Câu 28: Trong không gian với hệ tọa độ Oxyz , vectơ nào dưới đây là một vectơ chỉ phương của
đường thẳng đi qua hai điểm A1;2; 2 , B 3; 2  ; 0 ?    A. u1   1  ; 2  ;1 .
B. u2  1; 2;   1 .
C. u3  2; 4  ; 2 . D.  u  2; 4; 2  . 4  
Câu 29: Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Xác suất sao cho 2
người được chọn có ít nhất một người nữ bằng 2 7 8 1 A. . B. . C. . D. . 15 15 15 15 mx  2
Câu 30: Có bao nhiêu giá trị nguyên của tham số m để hàm số y  đồng biến trên mỗi x m 1 khoảng xác định? A. 4 . B. 6 . C. Vô số. D. 2 . x 1
Câu 31: Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x  trên x 1
đoạn 3;5. Khi đó M m bằng 7 1 3 A. . B. . C. 2 . D. . 2 2 8 x
Câu 32: Tập nghiệm của bất phương trình  3 5 1 x3  5 là A.  ;  5 . B.  ;  0 .
C. 5;  . D. 0;  .
Câu 33: Cho hàm số f x có đạo hàm liên tục trên 2; 
3 đồng thời f 2  2 , f 3  5 . 3 f
  xdx bằng 2 A. 3 B. 7 C. 10 D. 3
Câu 34: Với a là số thực dương bất kỳ, mệnh đề nào dưới đây đúng? 1 1
A. log 3a  3log a .
B. log 3a  log a . C. 3
log a  3log a .D. 3 log a  log a . 3 3
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB a, AD a 2, SA  3a
và SA   ABCD ( tham khảo hình vẽ) . Góc giữa đường thẳng SC và mặt phẳng  ABCD bằng 12 S B A D C A. 0 60 . B. 0 120 . C. 0 30 . D. 0 90 .
Câu 36: Cho hình lập phương ABC .
D A ' B 'C ' D ' có cạnh bằng 1 ( tham khảo hình vẽ). Khoảng
cách giữa hai đường thẳng AA' và BD ' bằng A D B C A' D' B' C' 3 2 2 2 3 5 A. . B. . C. . D. . 3 2 5 7
Câu 37: Trong không gian với hệ trục tọa độ Oxyz , cho điểm I 1; 0;  2 và mặt phẳng  P có
phương trình: x  2 y  2z  4  0 . Phương trình mặt cầu S  có tâm I và tiếp xúc với
mặt phẳng  P là 2 2 2 2 A. x   2
1  y   z  2  9 . B. x   2
1  y   z  2  3 . 2 2 2 2 C. x   2
1  y   z  2  3 . D. x   2
1  y   z  2  9 .
Câu 38: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A1; 2; 3 , B  2  ;3  ;1 đường thẳng
đi qua A1; 2; 3 và song song với OB có phương trình tham số là
x  1 2tx  2   t
x  1 2t
x  1 4t    
A. y  2  3t .
B. y  3  2t .
C. y  2  3t . D. y  2  6t .
z  3 t     z  1 3tz  3  t
z  3  2t  13
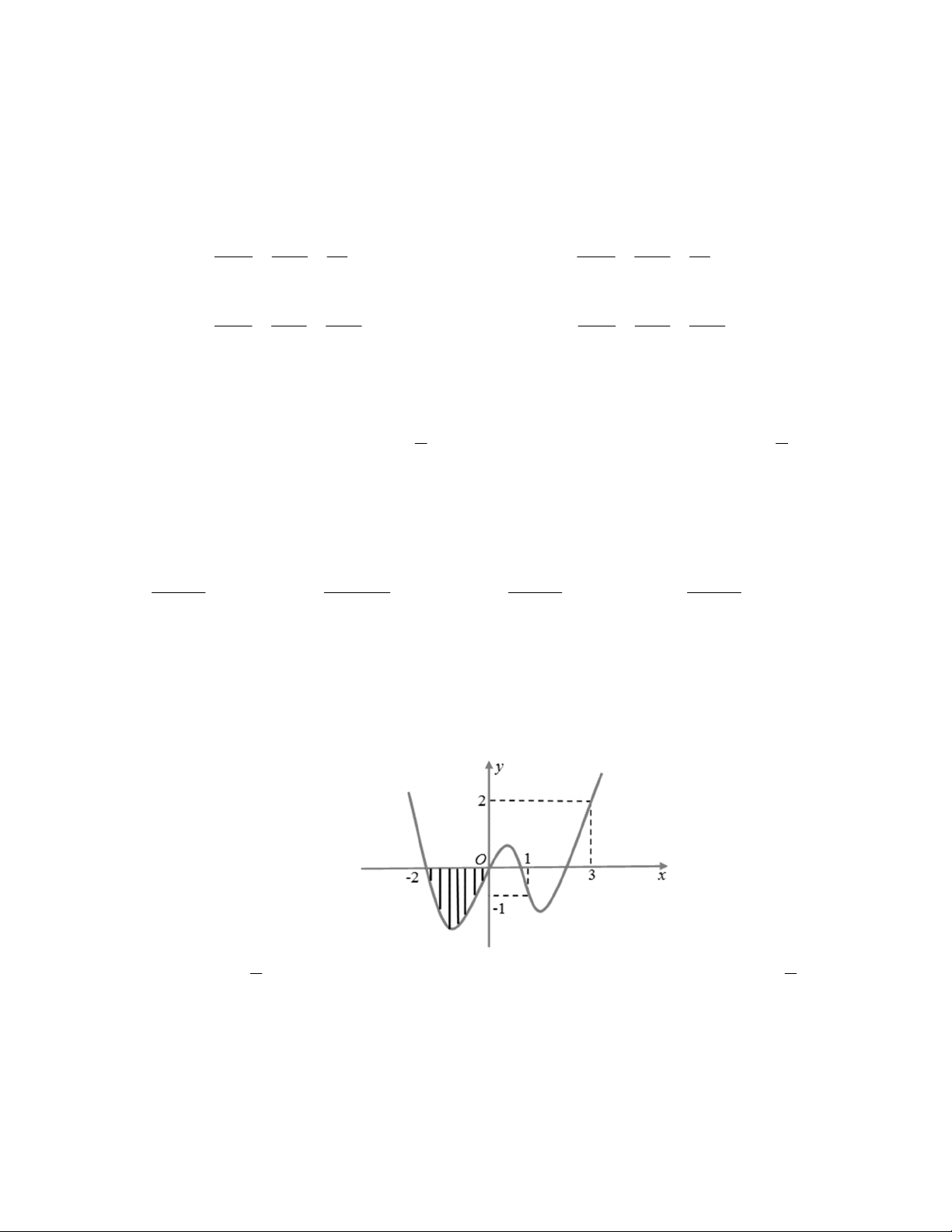
Câu 39: Cho hàm số y f x có đồ thị f  x như hình vẽ 3  x x x
Giá trị lớn nhất của hàm số g x  f     trên đoạn  4  ;  2 bằng  2  24 2 2  1  11 2 2 A. f   1  . B. f     .
C. f 2  . D. f   1  . 3  2  24 3 3
Câu 40: Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để bất phương trình x x 1 4 2 .2 m  
 3  m  0 có nghiệm? A. 2019. B. 0. C. 2020. D. 2018. 1 2 log x 4 Câu 41: Nếu f 3x   1 dx  2  và f   2 log x 2 dx  ln 2 thì
f x dx 2  bằng x 0 1 0 A. 4. B. 7. C. 8. D. 4 .
Câu 42: Có bao nhiêu số nguyên dương m sao cho ứng với mỗi m luôn có ít hơn 4041 số
nguyên x thoả mãn log x m log x  4 1  0 3   3    ? A. 6 . B. 11. C. 7 . D. 9 .
Câu 43: Cho hình hộp ABC . D AB CD
  có đáy ABCD là hình thoi cạnh a , BD a 3 . Hình
chiếu vuông góc của B trên mặt phẳng  AB CD
  là giao điểm của AC và B ' D ' (
tham khảo hình vẽ). Góc giữa hai mặt phẳng  A' B 'C ' D ' và  ADD ' A' bằng 0 60 .
Thể tích khối hộp ABC . D AB CD   bằng 14 3 3a 3 3a 3 3 3a 3 3 a 3 A. . B. . C. . D. . 4 4 8 8
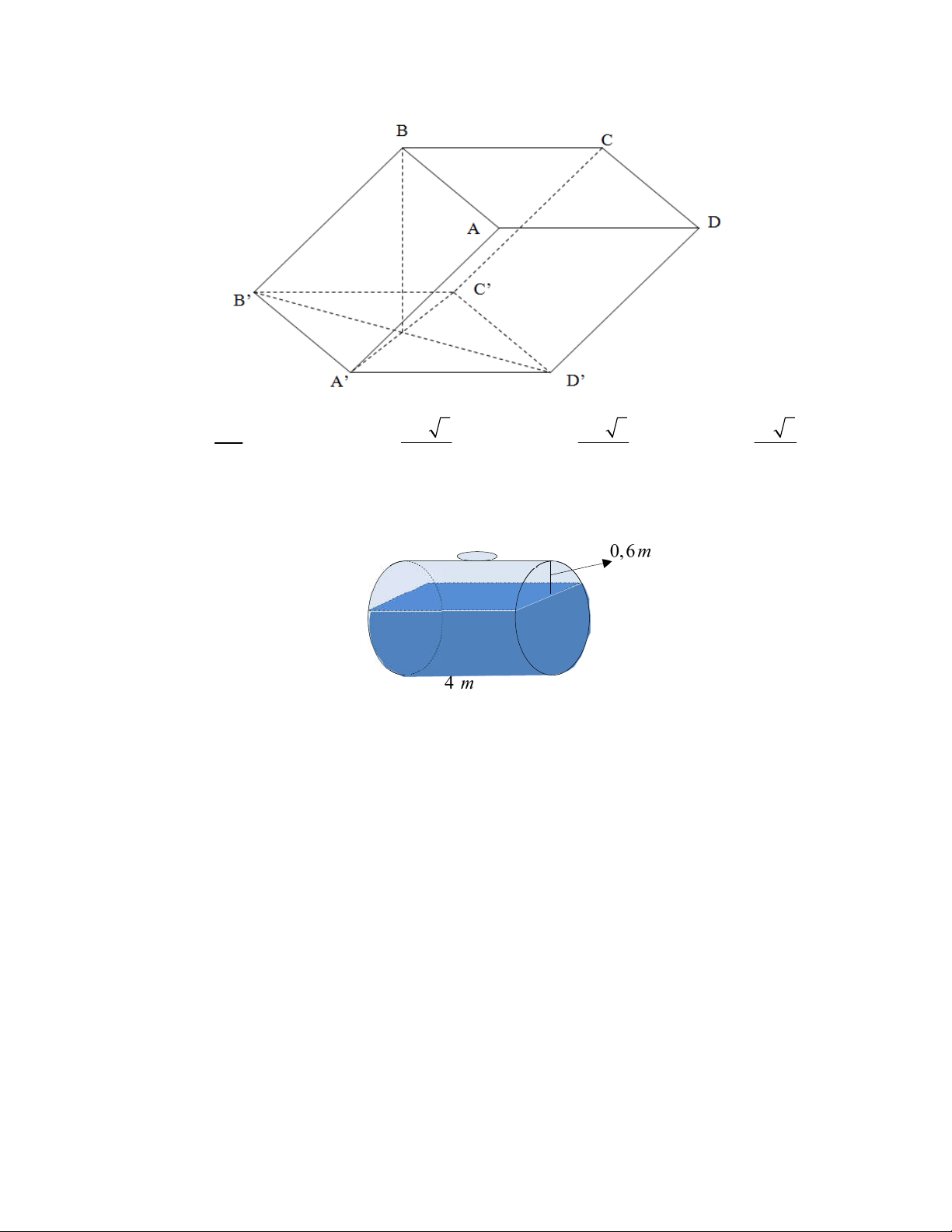
Câu 44: Một bồn hình trụ đang chứa đầy nước, được đặt nằm ngang, chiều dài bồn là 4m , bán
kính đáy 1, 2m . Người ta rút nước trong bồn một lượng tương ứng như hình vẽ. Thể tích
của lượng nước còn lại trong bồn xấp xỉ bằng A. 3 12, 637m . B. 3 14, 558m . C. 3 12, 064m . D. 3 13,571m .
Câu 45 : Trong không gian với hệ tọa độ Oxyz , cho hai điểm A2; 4  ;1 , B 0; 2  ;1 và mặt phẳng
P : x  2y z  4  0 . Đường thẳng d nằm trên  P sao cho mọi điểm của d cách đều 2 điểm ,
A B có phương trình là
x  4  3t
x  4  3tx  1 3tx  1 t    
A. y t .
B. y t .
C. y  1 t .
D. y  1 3t . z t     z tz  1 tz  1 3t
Câu 46: Cho hàm số f x có f x   2 x  x  2 16
1 x  4x m  4 . Có bao nhiêu giá trị
nguyên của tham số m thuộc  20  21; 202 
1 sao cho hàm số     2 g x f x  có 5 điểm cực trị? A. 2025 . B. 2026 . C. 2021 . D. 4043.
Câu 47: Có bao nhiêu số nguyên dương a sao cho tồn tại số thực x thỏa mãn 15   x  2021.lnx  1 2021 2021.ln
1  2020  2x a a  2021 x  2020 A. 5 . B. 2 . C. 3 . D. 4
Câu 48: Ông An dự định làm một vườn hoa dạng elip được chia ra làm bốn phần bởi hai đường
parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ dưới. Biết độ dài
trục lớn, trục nhỏ của elip lần lượt là 16m và 8m , F , F là hai tiêu điểm của elip. Phần 1 2
A , B dùng để trồng hoa, phần C , D dùng để trồng cỏ. Kinh phí để trồng mỗi mét
vuông hoa và cỏ lần lượt là 200.000 đồng và 100.000 đồng. Tính tổng tiền để hoàn thành
vườn hoa trên (làm tròn đến hàng nghìn). A. 17.679.000 đ. B. 19.526.000 đ. C. 15.831.000 đ. D. 13.547.000 đ.
Câu 49. Cho hàm số f x có đạo hàm cấp hai liên tục trên  thỏa mãn 2 f    f   x 2 1 2021, 1
x f   x  2 , x x   .
 Tính xf xd . x  0 2021 2020
A. I  674.
B. I  673. C. I  . D. I  . 3 3
Câu 50: Trong không gian với hệ tọa độ Oxyz, cho A3; 1; 2, B 1;1;8 và mặt phẳng
P : x y z  5  0. Mặt cầu S  đi qua hai điểm ,
A B và tiếp xúc với  P tại điểm C
. Biết C luôn thuộc một đường tròn T  cố định, tính bán kính r của đường tròn T  . A. r  33 . B. r  5 . C. r  37 . D. r  6.
--------------------Hết---------------------- 16
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 12 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Nguyễn Thị Diệp 1 xdx Câu 1: Cho
a b ln 2  c ln 3  , a , b c 2 với
là các số hữu tỷ. Giá trị của 3a b c bằng x  2 0   A. 1. B. 2 . C. 1 . D. 2 . 
Câu 2: Trong không gian Oxyz , đường thẳng  đi qua M 1; 2; 3
  nhận vectơ u   1  ; 2  ;1 làm
vectơ chỉ phương có phương trình là x 1 y  2 z  3 x 1 y  2 z  3 A.   . B.   . 1  2 1 1 2  1 x 1 y  2 z  3 x 1 y  2 z  3 C.   . D.   . 1 2 1  1  2 1
Câu 3: Cho hàm số y f x xác định và liên tục trên  có f x  0, x   , f   3 1  e . Biết
f  x  2x 1, x . Tìm tất cả giá trị của tham số m để phương trình f x  m có hai f x nghiệm thực phân biệt. 3 3 3 3 A. 4 m e . B. 4 . C. 4 . D. 4 . 0  m e m e 1  m e
Câu 4: Cho  H  là hình phẳng giới hạn bởi các đường y x , y x  2 và trục hoành (phần
kẻ dọc trong hình vẽ). Diện tích của  H  bằng y 2 y x O 2 4 x 7 16 8 10 A. . B. . C. . D. . 3 3 3 3 17
Câu 5: Trong không gian với hệ tọa độ Oxyz cho điểm A1; 0; 2 và đường thẳng d có phương x 1 y z 1 trình:  
. Viết phương trình đường thẳng  đi qua A, vuông góc và cắt d. 1 1 2 x 1 y z  2 x 1 y z  2 A.   B.   2 2 1 1 3  1 x 1 y z  2 x 1 y z  2 C.   D.   1 1 1 1 1 1  
Câu 6: Tính sin 3xdx . 0 1 1 2 2 A. . B.  . C.  . D. . 3 3 3 3
Câu 7: Hàm số F ( x) là một nguyên hàm của hàm số f ( x) trên khoảng K nếu
A. f '(x)  F (x), x K.
B. f '( x)   F ( x), x K .
C. F '(x)  f (x), x K.
D. F '(x)   f ( x), x K . 1  1 
Câu 8: Tìm họ tất cả các nguyên hàm của hàm số f x  trên ;   . 1 2x  2  1 1 1
A. ln 2x 1  C .
B.  ln 1 2x  C . C.
ln 1 2x  C . D.
ln 2x 1  C . 2 2 2 
Câu 9: Trong không gian Oxyz , tọa độ của vectơ n vuông góc với hai vectơ  
a  (2; 1; 2), b  (3; 2;1) là    
A. n  3; 4  ;1 . B. n   3  ; 4;   1 .
C. n  3; 4;   1 . D. n  3; 4  ;   1 .
Câu 10: Trong không gian Oxyz , có bao nhiêu mặt phẳng song song với mặt phẳng
(P) : x y z  6  0 và tiếp xúc với mặt cầu (S ) : 2 2 2
x y z  12 ? A. 0. B. 2 C. 3. D. 1.
Câu 11: Trong không gian Oxyz , cho tứ diện ABCD có đỉnh A1;1;  1 , B2;0;2 , C  1  ; 1
 ;0, D0;3;4 . Trên các cạnh AB, AC, AD lần lượt lấy các điểm B ',C ', D ' sao cho AB AC AD  
 4 . Viết phương trình mặt phẳng  B 'C ' D' biết tứ diện AB'C ' D' có thể AB ' AC ' AD ' tích nhỏ nhất . 18
A. 16x  40 y  44z  39  0 .
B. 16x  40 y  44z  39  0 .
C. 16x  40 y  44z  39  0 .
D. 16x  40 y  44z  39  0 .
Câu 12: Trong không gian Oxyz , cho mặt cầu 2 2 2
(S) : x y z  2x  2z  7  0 , mặt phẳng
P : 4x 3y m  0 . Giá trị của m để mặt phẳng P cắt mặt cầu S  . m  11 m  4 A. 1  2  m  4 . B. . C. 1  9  m 1 . 1 D. .   m  19   m  12  
Câu 13: Trong không gian Oxyz , mặt cầu  S  2 2 2
: x y z  8x  2y 1  0 có tâm là A. I 4; 1  ;0. B. I  8  ; 2;0. C. I  4  ;1;0. D. I 8; 2  ;0. 2 dx Câu 14: Tích phân bằng  x3 0 2 5 5 16 A. . B. ln . C. log . D. . 15 3 3 225 x 
Câu 15: Cho hàm số f  x 
xác định với mọi x
k , k   . Một nguyên hàm của 2 cos x 2 hàm số f  x là
A. x tan x  ln cos x . B. x tan x  ln cos x . C. x tan x  ln cos x . D. x tan x  ln sin x . 1  2
Câu 16: Cho hàm số f (x) xác định trên  \   thỏa mãn f  x 
, f 0  1, f   1  2 . 2 2x 1
Giá trị của biểu thức f   1  f   3 bằng A. 3  ln 15 . B. 4  ln 15 . C. 2  ln 15 . D. ln 15 .
Câu 17: Trong không gian Oxyz , cho ba điểm A1;0;   3 , B2;4;  1 ,C 2; 2
 ;0 . Tọa độ trọng
tâm G của tam giác ABC là  5   5 2 4   5 2 4 
A. 5;2;4 . B. ;1; 2  . C. ; ;  . D. ; ; .        2   3 3 3   3 3 3  19  xe   x
Câu 18: Cho hàm số f x   e 2  
 xác định với mọi x
k , k   . Mệnh đề nào 2 cos x   2 sau đây đúng? A.   2 x f x dx
e  tan x C . B. x f x dx e x C .    2 tan  x 1 x 1 C.
f xdx 2e   C . D. f x dx 2e   C .     cos x cos x 4 1
Câu 19: Tìm giá trị của a để d  ln .  x a x 1 x  2 3    3 1 4 A. . B. . C. . D. 12 . 4 3 3
Câu 20: Trong không gian Oxyz , cho mặt phẳng   đi qua A2; 1
 ;4 , B3;2;  1 và vuông
góc với mặt phẳng Q : x y  2z  3  0 . Phương trình mặt phẳng   là
A. 11x  7 y  2z  21  0 . B. 5x  3y  4z  0 . C. x y  2z  3  0 . D. x  3y  5z  21  0 .
Câu 21: Họ tất cả các nguyên hàm của hàm số   x f x  xe là 2 x A. x e  C . B. x x xe  e  C . C. x e  C . D. x x xe  e  C . 2 3 1
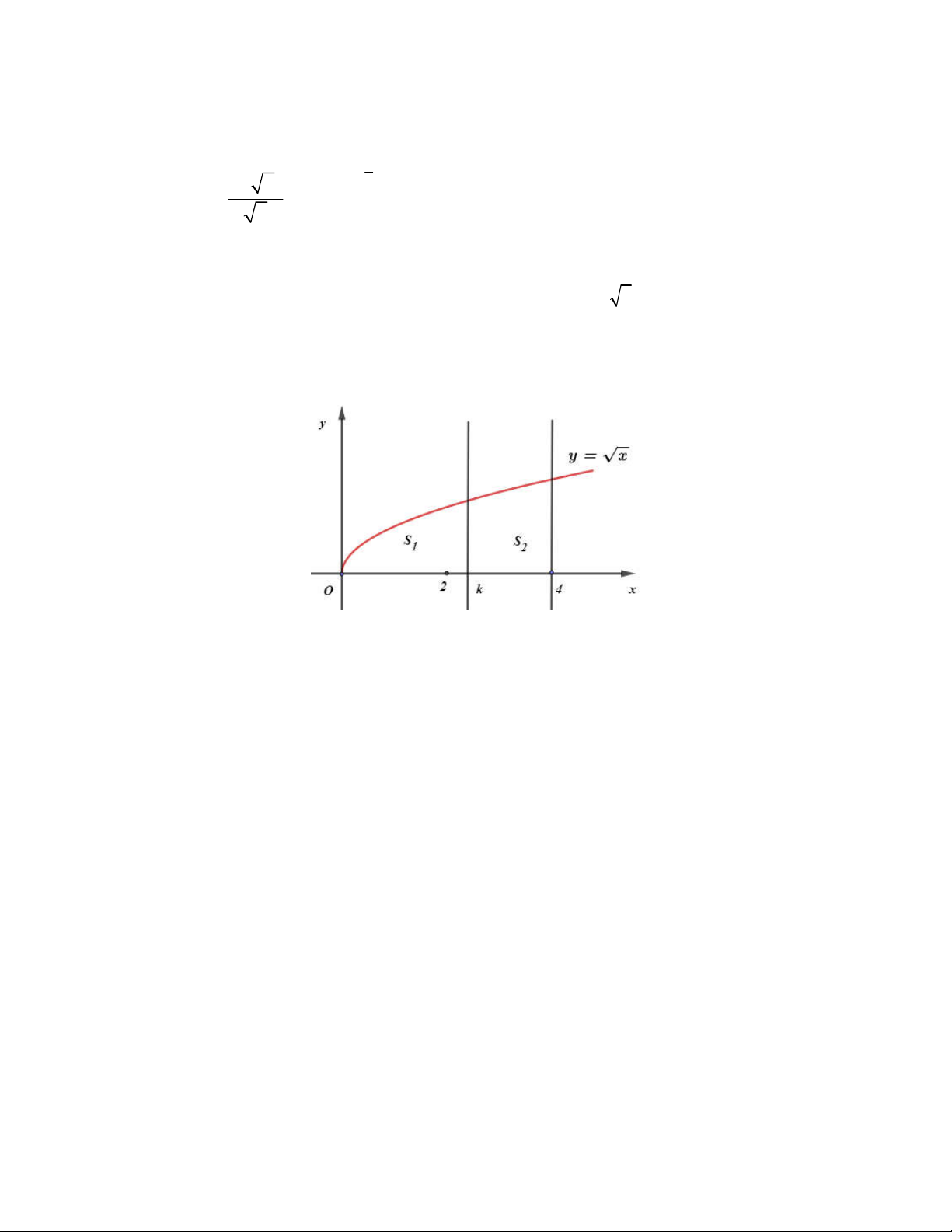
Câu 22: Cho đường thẳng y x và parabol 2 y
x a , ( a là tham số thực dương). Gọi S , S 1 2 4 2
lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi S S thì a thuộc 1 2
khoảng nào dưới đây?  7 1   1 9   3 7   3  A. ;   . B. ;   . C. ;   . D. 0;   .  32 4   4 32   16 32   16  20
Câu 23: Họ tất cả các nguyên hàm của hàm số f x  cos 2x là 1 1 A. 2
 sin 2x C .
B. 2sin 2x C .
C.  sin 2x C . D. sin 2x C . 2 2
Câu 24: Gọi S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số: 3
y x  3x , y x . Tính S . A. S  2 . B. S  8. C. S  4 . D. S  0 .
Câu 25: Biết F x là một nguyên hàm của hàm số   2 x
f x e và F 0  0 . Giá trị của F ln 3 bằng A. 4. B. 8. C. 6. D. 2.
Câu 26: Trong không gian Oxyz , cho hai điểm A1;0; 3   và B3;2 
;1 . Phương trình mặt cầu đường kính AB là A. 2 2 2
x y z  4x  2 y  2z  6  0. B. 2 2 2
x y z  4x  2 y  2z  0. C. 2 2 2
x y z  2x y z  6  0. D. 2 2 2
x y z  4x  2 y  2z  0. x
Câu 27: Tính I  3 dx .  3x A.  3x IC . B.  3x I ln 3  C . C. I   C . D.  3x I  ln 3  C . ln 3 8 4 4 Câu 28: Biết
f x dx  2
 ; f x dx  3 ; g x dx  7 . Mệnh đề nào sau đây sai?        1 1 1 4 8 4
A. 4 f x  2g x dx  2  . B.
f x dx g x dx  8 .      1 4 1 4 8
C. f x  g x dx  10 . D.
f x dx  5  .     1 4
Câu 29: Trong không gian Oxyz , phương trình nào sau đây không phải là phương trình mặt cầu? 2 2 2 2 2 2
A. 2x   1  2y   1  2z   1  6. B. x   1   y   1   z   1  6. 21 2 2 2
C. x   1  2y   1   z   1  6.
D. x y2 2
 2xy z  3  6 . x
Câu 30: Đường thẳng  là giao của hai mặt phẳng x z  5  0 và x  2 y z  3  0 thì có phương trình là A. x  2 y 1 z . B. x  2 y 1 z .     1 3 1 1 2 1 C. x  2 y 1 z  3 . D. x  2 y 1 z  3 .     1 1 1 1 2 1
Câu 31: Tìm I x cos d x x .  x x
A. I x sin x  cosx C . B. 2 I x cos
C . C. I x sin x  cosx C . D. 2 I x s in  C . 2 2 1 2 x
Câu 32: Tích phân  x  2 e dx bằng 0 2 5  3e 2 5   3e 2 5  3e 2 5  3e A. . B. . C. . D. . 2 4 4 4
Câu 33: Cho hàm số y f x có đạo hàm trên  , đồ thị hàm số y f x như hình vẽ. Biết
diện tích hình phẳng phần sọc kẻ bằng 3. Tính giá trị của biểu thức: 2 3 4 T
f  x   1 dx 
f  x   1 dx 
f 2x  8 dx    1 2 3 9 3 A. T  . B. T  6 . C. T  0 . D. T  . 2 2
Câu 34: Bác thợ xây bơm nước vào bể nước. Gọi h t  là thể tích nước bơm được sau t giây. Cho ht  2
 3at bt và ban đầu bể không có nước. Sau 5 giây thì thể tích nước trong bể là 3
150 m , sau 10 giây thì thể tích nước trong bể là 3
1100 m . Tính thể tích nước trong bể sau khi bơm được 20 giây. 22 A. 3 4200 m . B. 3 2200 m . C. 3 8400 m . D. 3 600 m .
Câu 35: Trong không gian Oxyz , khoảng cách từ điểm A0;0;5 đến mặt phẳng
P : x  2y  2z  3  0 bằng 7 8 4 A. 3 . B. . C. . D. . 3 3 3
Câu 36: Tập nghiệm của bất phương trình 2x  5 là A. log 2; log 5;  ;  log 2 ;log 5 2  5  2  5  . B. . C. . D. .
Câu 37: Trong không gian Oxyz , mặt cầu S  tâm I  1  ; 2; 3
  và tiếp xúc với mặt phẳng
P : x  2y  2z 1 0 có phương trình 2 2 2 4 2 2 2 16
A. x  
1   y  2   z  3  . B. x  
1   y  2   z  3  . 9 3 2 2 2 4 2 2 2 4
C. x  
1   y  2   z  3  . D. x  
1   y  2   z  3  . 3 9 2
Câu 38: Tập nghiệm của bất phương trình log 18  x  2 3   là
A.  ;  3  3;   . B. ;  3 . C. 3; 3. D. 0;  3 .
Câu 39: Trong không gian Oxyz , cho hình hộp ABC . D AB CD
  có A0; 0; 0 , B 3; 0; 0 ,
D 0; 3; 0 , D0; 3;  3 . Toạ độ trọng tâm tam giác A BC  là
A. 1; 1;  2 . B. 1; 2;   1 . C. 2; 1;   1 . D. 2; 1;  2 .
Câu 40: Viết công thức tính thể tích V của khối tròn xoay được tạo ra khi quay hình thang cong,
giới hạn bởi đồ thị hàm số y f x , trục Ox và hai đường thẳng x  ,
a x b a b , xung quanh trục Ox . b b b b 2 2 A. V  
f xdx . B. V f x dx . C. V f x dx . D. V   f x dx .           a a a a
Câu 41: Giả sử f là hàm liên tục trên khoảng K và , a ,
b c là ba số bất kì trên khoảng K .
Khẳng định nào sau đây sai? 23 b a c b b A.
f (x)dx   f (x)dx . B.
f (x)dx f (x)dx f (x)d ,
x c a,b .        a b a c a b b b C.
f (x)dx f (t)dt . D. f x dx  .   ( ) 1  a a a
Câu 42: Trong không gian Oxyz , cho mặt phẳng  P : x  2 y  2z  3  0 và mặt cầu  S  2 2 2
: x y z  2x  4 y  2z  5  0 . Giả sử điểm M  P và N S  sao cho MN cùng 
phương với u  1;0 
;1 và khoảng cách giữa M và N là lớn nhất. Tính MN .
A. MN  3 2 .
B. MN  1 2 2 . C. MN  14 . D. MN  3.
Câu 43: Một chất điểm A xuất phát từ O , chuyển động thẳng với vận tốc biến thiên theo thời 1 13
gian bởi quy luật v t  2  t t
 m/s , trong đó t (giây) là khoảng thời gian tính từ lúc A 100 30
bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O , chuyển động thẳng cùng hướng với 2
A nhưng chậm hơn 10 giây so với A và có gia tốc bằng a   m/s  ( a là
hằng số). Sau khi B xuất phát được 15 giây thì đuổi kịp A . Vận tốc của B tại thời điểm đuổi kịp A bằng A. 42   m/s . B. 15   m/s . C. 25   m/s . D. 9  m/s .
Câu 44: Cho hàm số f x có đạo hàm liên tục trên 0;  1 , thỏa mãn 1
f x f   x 2 2 3 1
 1 x . Giá trị của tích phân
f 'xdx  bằng 0 3 1 A. . B. 1. C. 0. D. . 2 2
Câu 45: Trong không gian Oxyz , cho mặt phẳng  P có phương trình 2x  2 y z  3  0 . Mặt
phẳng  P có một vectơ pháp tuyến là     A. n( 2  ; 2; 3  ) . B. ( n 0;0; 3  ) . C. ( n 4  ;4; 2) . D. n( 4  ; 4; 2  ) .
Câu 46: Trong không gian Oxyz , cho hai mặt phẳng (P) : 5x my z  5  0 và
(Q) : nx  3 y  2z  7  0 .Tìm ,
m n để P / / Q . 24 3 3
A. m  5; n  3 . B. m  ; n  1  0 .
C. m  5; n  3 .
D. m   ; n  10 . 2 2
Câu 47: Cho hàm số y f x xác định và liên tục trên đoạn  ;
a b . Diện tích hình phẳng giới
hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng x a, x b được tính theo công thức b a b b
A. S   f xdx . B. S f x dx . C. S f x dx . D. S f x dx .           a b a a
Câu 48: Trong không gian Oxyz , cho , đường thẳng A2;0;0
d đi qua A cắt chiều âm trục Oy
tại điểm B sao cho diện tích tam giác OAB bằng 1. Phương trình tham số đường thẳng d là A. . B. . C. . D. . x  1 2t
x  2  2t
x  2  2t
x  2  2t      y ty t   y t   y tz  0     z  0  z  0  z  1  2 dx
Câu 49: Biết I
a b c với , , là các số nguyên dương. Tính  a b c x 1 x x x 1 1  
P a b c . A. P 18. B. P  12 . C. P  24 . D. P  46 .
Câu 50: Trong không gian Oxyz , mặt phẳng đi qua 3 điểm A1;0;0 , B0; 2;0 , C 0;0;  3 có phương trình là x y z x y z x y z x y z A.    0 . B.    1. C.    1  . D.    1. 1 2 3 1 2 3 1 2 3 1 1 3 25
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 12 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Vũ Thị Vui
Câu 1. Mệnh đề nào sau đây sai ?
A. k.f  x dx k f xC   
với mọi số thực k  0 .
B.f x  g x dx f x dx g x dx      .
C. Nếu F x , G x đều là nguyên hàm của hàm số f x thì F x  G x .
D. sin x dx   cos x C  .
Câu 2. Họ tất cả các nguyên hàm của hàm số f x  2cos x  sin x là
A. 2sin x  cos x C . B. 2
 sin x cos x C .
C. 2sin x  cos x C . D. 2
 sin x cos x C .
Câu 3. Hình phẳng  H  được giới hạn bởi đồ thị C  của hàm đa thức bậc ba và parabol
P có trục đối xứng vuông góc với trục hoành. Phần tô đậm của hình vẽ có diện tích bằng 37 7 11 5 A. . B. . C. . D. . 12 12 12 12  1 
Câu 4. sin 3x  d    x bằng  3  1  1   1  A. cos 3x   C   .
B.  cos 3x   C   . 3  3   3  1  1  1  1 
C.  cos 3x   C   .
D.  sin 3x   C   . 3  3  3  3  26
Câu 5. Trong không gian Oxyz , cho điểm M 3; 2;  
1 . Hình chiếu vuông góc của điểm M lên trục Oz là điểm A. M 3; 0; 0 . B. M 0; 2;0 . C. M 0; 0; 1 . D. M 3; 2; 0 . 2   1   4   3   1 3ln x.ln x Câu 6. d  x bằng x 2 2 2 A.
1 3ln x 1 3ln x 1     C . 9   1 3ln x 1 
B. 1 3ln x 1 3ln x     C .  5 3  2 1 3ln x 1  C.
13ln x 13ln x     C . 9  5 3  2 1 3ln x 1  D.
13ln x 13ln x     C . 3  5 3  3   x
e 4 f (x)  f (
x)  2 f (x)
Câu 7. Cho hàm số f (x) thỏa mãn 
, x  0 và f (0)  1. Tính  f (x)  0  ln 2 I f (x)d  x . 0 1 1 209 7 A. I  . B. I   . C. I . D. I  . 12 12 640 640
Câu 8. Biết rằng g(x) là một nguyên hàm của f x  (x 1)sin x và g(0)  0 , tính g( ) . A. 0 . B.  1. C.  2. D. 1.
Câu 9. Cho hai hàm số y f x và y g x có đạo hàm liên tục trên đoạn [0; 2] và thỏa mãn 2 2 2 /
f ' x.g xdx  1  ,
f x.g ' xdx  1 
. Tính I   f x.g x dx    . 0 0 0 A. I  2  .
B. I  0.
C. I  3 . D. I  2 . 2 2 f xCâu 10. Cho
f x dx  3  . Khi đó dx  bằng e 1 1 3 3 A. . B. 2 e C. 2 3e . D. . e e Câu11. Trong không gian Oxyz , cho hai mặt phẳng
P : x y z 1  0 và
Q : 2x y mz m 1  0, với m là tham số thực. Giá trị của m để P  Q là A. 1 . B. 0. C. 1 . D. 4 . b
Câu 12. Cho hàm số f (x)có đạo hàm liên tục trên đoạn [a;b]và 2 f (a)  2 f (b)1. Tính f '(x) dx a
A. I  0.
B. I  2 . C. I  1. D. I  1. 27 3 3 1 e x Câu 13. Biết rằng
dx a  eb
với a, b   , hãy tính b a . 2 e x  ex 1 0
A. b a 1.
B. b a  1  .
C. b a  7 .
D. b a  7  . 2 f x
Câu 14. Cho hàm số y f x sao cho f  x liên tục trên  , dx  3  ln 2 
và f 2  3. Tính x 1 2 I
f  x.ln d x x  . 1
A. I  4ln 2 3. B. I  2ln 2 3.
C. I  2ln 2  3.
D. I  3ln 2  4. mx   1 ln x n ln px 2   Câu 15. Biết dx  ln x    C với , m ,
n p,C là các số thực. Khi đó, m n p 2 x x bằng A. e 1. B. e  2 . C. 2e 1. D. 2e  2 .
Câu 16. Giả sử hàm số f (x) liên tục và dương trên đoạn 0; 
3 thỏa mãn f (x). f (3  x)  4 . Tính tích 3 1 phân I  dx  . 2  f x 0   3 1 3 1 A. I  . B. I  . C. I  . D. I  . 5 2 4 3
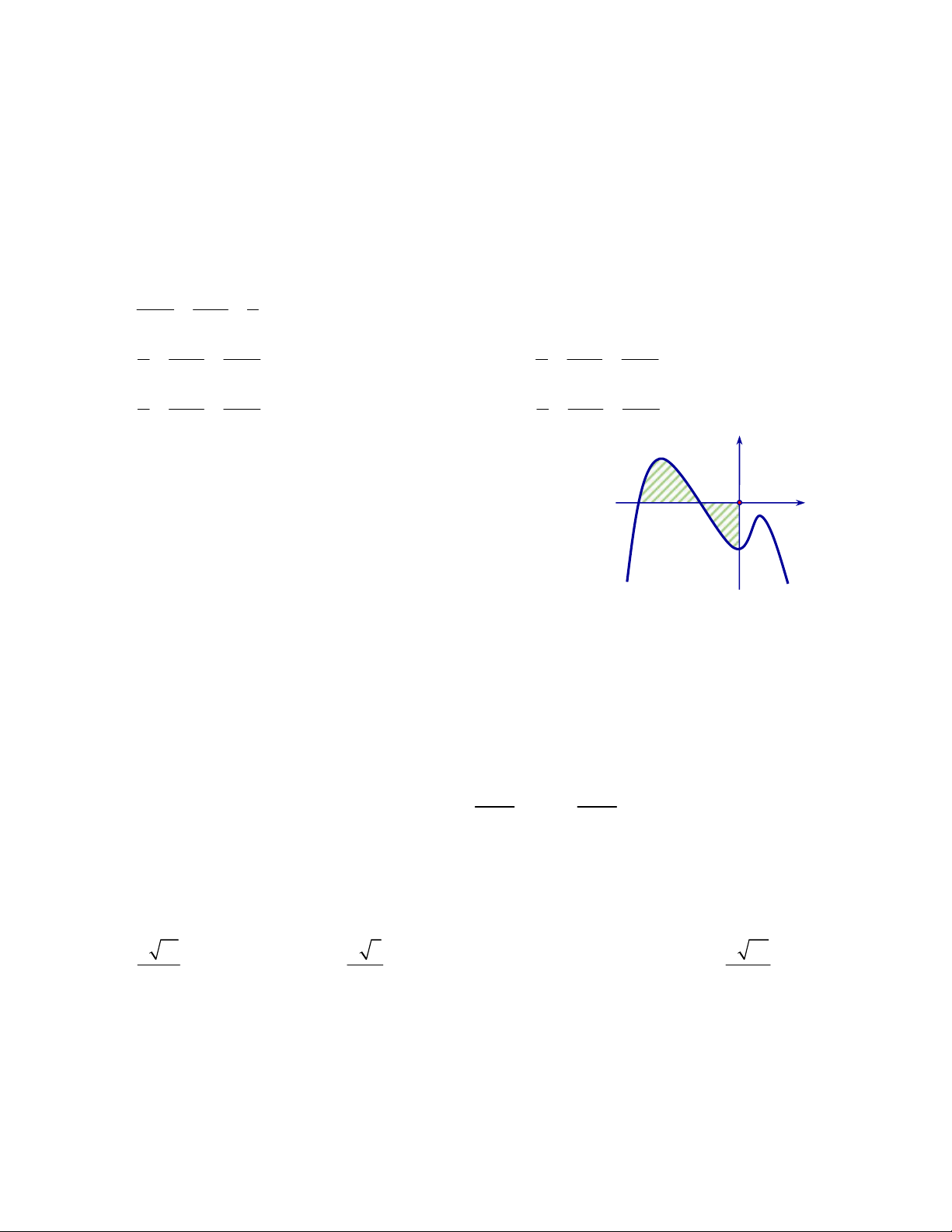
Câu 17. Cho hàm số f x  có đồ thị như hình vẽ bên dưới.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số f x  và trục Ox được tính theo công thức nào sau đây? 2 2 A.
f xdx  . B.
f xdx  . 1  1 3 1 1 3 2 3 2 C.
f xdx f xdx   .
D. f xdx f xdx   . 1  1 1  1 3 3
Câu 18.Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số f x    x    x  2 1 2
x  1 và trục Ox 28 11 1 19 117 A. . B. . C. . D. . 20 20 20 20 2 x 3x
Câu 19. Gọi S là diện tích của hình phẳng giới hạn bởi parabol y  
và đường thẳng y x 1. 2 2 Ta có 3 11 3 9 A. S B. S  . C. S  . D. S  . 2 2 4 4
Câu 20. Hình vẽ dưới đây là một mảnh vườn hình Elip có bốn đỉnh là I , J , K , L; ABCD, EFGH là các
hình chữ nhật; IJ  10 m, KL= 6 m , AB  5 m, EH  3 m . Biết rằng kinh phí trồng hoa là 50000 đồng/ 2
m , hãy tính số tiền (làm tròn đến hàng đơn vị) dùng để trồng hoa trên phần gạch sọc. A. 2869834 đồng. B. 1434 917 đồng.
C. 2119 834 đồng. D. 684 917 đồng.
Câu 21. Cho hàm số y f x . Đồ thị của hàm số y f  x như hình bên. Đặt
g x  f x   x  2 2
1 . Mệnh đề nào dưới đây đúng? A. g   1  g   3  g   3 B. g   1  g   3  g   3 C. g   3  g   3  g   1 D. g   3  g   3  g   1 29 2
Câu 22. Cho hình H giới hạn bởi đồ thị hàm số y
, trục hoành, các đường thẳng x  1, x  2 . x
Biết rằng khối tròn xoay do H quay quanh trục Ox tạo ra có thể tích là  ln a . Giá trị của a là A. 6 . B. 2 . C. 4 . D. 8 .
Câu 23. Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách
điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên
dưới. Biết rằng OO  5 cm , OA  10 cm , OB  20 cm , đường cong AB là một phần của parabol có
đỉnh là điểm A . Thể tích của chiếc mũ bằng 2750 2500 2050 2250 A. 3 3 3 3 cm  B. cm  C. cm  D. cm  3 3 3 3
Câu 24. Cho hình thang cong giới hạn bởi đồ thị hàm số y x , trục hoành, các đường thẳng x 1 và
x  4. Thể tích của khối tròn xoay được tạo thành khi quay hình thang cong trên quanh trục Ox bằng 4 4 4 4 A. x dx  .
B.x dx  . C.x dx  . D. 2  d  x x . 1 1 1 1 2
Câu 25. Cho a, b là hai số thực dương. Gọi  
H là hình phẳng giới hạn bởi parabol y ax và đường
thẳng y  bx . Quay H quanh trục hoành thu được khối có thể tích là V , quay   H quanh 1
trục tung thu được khối có thể tích là V . Tìm b sao cho V V . 2 1 2 5 5 5 5 A. b  . B. b  . C. b  . D. b  . 6 3 2 4 m
Câu 26: Vận tốc (tính bằng
) của một hạt chuyển động theo một đường được xác định bởi công thức s v t 3 2
t 8t 17t 10 , trong đó t được tính bằng giây. Tổng quãng đường mà hạt đi được
trong khoảng thời gian 1 t  5 là bao nhiêu? 30 32 71 38 71 A. m. B. m . C. m. D. m . 3 3 3 6
Câu 27: Biết F x là một nguyên hàm của hàm số f x 3
 4x 1 và F 0  1. Tính giá trị của F   1 . A. 0 . B. 1. C. 2 . D. 3 . 1
Câu 28: Cho hàm số f x xác định trên  \  
2 thỏa mãn f  x  , f  
1  2020 , f 3  2021. x  2
Tính P f 4  f 0 . A. P  4 . B. P  ln 2 .
C. P  ln 4041. D. P  1 .      
Câu 29. Trong không gian Oxyz , cho a  1;  2;5,b  0; 2;  
1 . Nếu c a  4b thì c có tọa độ là A. 1; 0; 4 . B. 1;6;  1 . C. 1; 4;6 . D. 1;10;9 .
Câu 30. Trong không gian O xyz , cho hai điểm A 2;1;  1 , B 3;2; 
1 . Độ dài đoạn thẳng AB bằng A. 30 . B. 10 . C. 22 . D. 2 .    
Câu 31. Trong không gian O xyz , cho u  2; 3; 4 , v   3
 ;  2; 2 khi đó u.v bằng A. 20 . B. 8 . C. 46 . D. 2 2 .
Câu 32. Trong không gian O xyz , cho A 1; 0; 6 , B0;2; 
1 , C 1; 4;0 . Bán kính mặt cầu  S  có tâm I 2; 2;  
1 và tiếp xúc với mặt phẳng  ABC bằng 8 3 8 77 16 77 16 3 A. . B. . C. . D. . 3 77 77 3
Câu 33. Trong không gian Oxyz , cho mặt cầu S   x  2   y  2   z  2 : 1 2 1
 4 . Tìm tọa độ tâm I
và bán kính R của mặt cầu  S  . A. I  1  ; 2;  1 và R  2 . B. I 1; 2  ;   1 và R  2 . C. I  1  ; 2;  1 và R  4 . D. I 1; 2  ;   1 và R  4 .
Câu 34. Trong không gian Oxyz cho hai điểm A(2;1; 0) , B(2; 1; 2) . Phương trình mặt cầu  S  có tâm
B và đi qua A là A.  2 2
x  2   y  2 2 2 1  ( z  2)  24 .
B. x     y   2 2 1
 ( z  2)  24 . C.  2 2
x  2   y  2 2 2 1  z  24 .
D. x     y   2 2 1
 ( z  2)  24 .
Câu 35. Trong không gian Oxyz, tọa độ nào sau đây là tọa độ của một véctơ chỉ phương của đường
x  2  4t
thẳng  :  y  1 6t ,t  ?  z  9t   1 1 3   1 1 3  A. ; ;   . B. ; ;   . C. 2;1; 0 . D. 4;  6; 0 .  3 2 4   3 2 4  31
Câu 36. Trong không gian với hệ trục tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt x 1 y  2 z
phẳng đi qua M 1; 1
 ; 2 và vuông góc với đường thẳng  :   . 2 1 3
A. 2x y  3z  9  0 .
B. 2x y  3z  9  0 .
C. 2x y  3z  9  0 .
D. 2x y  3z  6 .
Câu 37. Trong không gian Oxyz , cho mặt cầu  S  có tâm thuộc trục Ox và đi qua hai điểm A1; 2;   1
và B 2;1;3 . Phương trình của  S  là
A. x  2 2 2 4
y z  14.
B. x  2 2 2 4
y z  14. 2 2 2 2 2 2
C. x (y 4)  z 14.
D. x y (z 4) 14.
Câu 38. Trong không gian Oxyz , cho mặt cầu  S  có tâm I 1; 2;3 và tiếp xúc với mặt phẳng
P : 2x  2y z  3  0 . Phương trình của S  là A.  2 2 2
x  2   y  2   z  2 1 2 3  16.
B. x 1   y  2   z  3  9. C.  2 2 2
x  2   y  2   z  2 1 2 3  16.
D. x 1   y  2   z  3  4.
Câu 39. Trong không gian Oxyz cho các điểm A1; 1;3 , B 2;1;0 , C 3; 1; 3 và mặt phẳng
P : x y z  4  0 . Gọi M a,b,c là điểm thuộc mặt phẳng P sao cho biểu thức   
T  3MA  2MB MC đạt giá trị nhỏ nhất. Tính giá trị của biểu thức S a b c .
A. S  3 . B. S  1  .
C. S  2 .
D. S  1 . x 1 y z  2
Câu 40. Trong không gian Oxyz , cho điểm A2; 5; 3 và đường thẳng d :   . Biết rằng 2 1 2
P : ax by cz  3  0 a,b,c   là mặt phẳng chứa d và khoảng cách từ A đến  P lớn nhất.
Khi đó tổng T a b c bằng A. 3 . B. 3 . C. 2  . D. 5 . x  3 y  3 z  2
Câu 41. Trong không gian Oxyz , cho hai đường thẳng d :   ; 1 1  2  1 x  5 y 1 z  2 d :  
và mặt phẳng  P : x  2y  3z 5  0 . Đường thẳng vuông góc với 2 3  2 1
P , cắt d và d có phương trình là 1 2 x 1 y 1 z x  2 y  3 z 1 A.   B.   3 2 1 1 2 3 x  3 y  3 z  2 x 1 y 1 z C.   D.   1 2 3 1 2 3
Câu 42. Trong không gian Oxyz , mặt phẳng đi qua điểm A 1
 ; 2; 4 và song song với mặt phẳng
P : 4x y z  5  0 có phương trình là
A. 4x y z  5  0 .
B. 4x y z  2  0 . 32
C. 4x y z  0 .
D. 4x y z  6  0 .
Câu 43. Trong không gian Oxyz, cho mặt phẳng  P : x y z  3  0 và đường thẳng x y 1 z  2 d :  
. Hình chiếu vuông góc của d trên  P có phương trình là 1 2 1  x 1 y 1 z 1 x 1 y  4 z  5 A.   B.   1 4 5  1 1 1 x 1 y 1 z 1 x 1 y 1 z 1 C.   D.   1  4  5 3 2  1  2 2 2
Câu 44. Trong không gian Oxyz , cho mặt cầu  S  :  x  
1   y  2   z   1
 9 . Mặt phẳng  P
tiếp xúc với  S  tại điểm A1;3;   1 có phương trình là
A. 2x y  2z  7  0 .
B. 2x y  2z  7  0 .
C. 2x y z 10  0 .
D. 2x y  2z  2  0 .
Câu 45. Trong không gian Oxyz , cho mặt phẳng  P:2x y  2z 1 0 và hai điểm
A1;0;  2, B 1
 ; 1;3 . Mặt phẳng Q đi qua hai điểm A, B và vuông góc với P có
phương trình dạng ax by cz  5  0 . Khẳng định nào sau đây đúng?
A. a b c  21 . B. a b c  7 . C. a b c   21.
D. a b c   7 .
Câu 46. Trong không gian Oxyz , cho điểm M 4; 2;3 .Viết phương trình mặt phẳng đi qua ba điểm ,
A B, C lần lượt là hình chiếu của điểm M trên các trục Ox, Oy, Oz.
A. 3x  6 y  4z 12  0 .
B. 4x  2 y  3z 1  0 .
C. 3x  6 y  4z 12  0 .
D. 4x  2 y  3z  1  0 .
Câu 47. Trong không gian Oxyz , cho mặt phẳng Q song song mặt phẳng  P : 2x  2 y z 17  0 . 2 2
Biết mặt phẳng Q cắt mặt cầu S  2
: x   y  2   z   1
 25 theo giao tuyến là một
đường tròn có bán kính r  3. Khi đó mặt phẳng Q có phương trình là
A. 2x  2 y z  7  0 .
B. 2 x  2 y z 17  0 .
C. 2x  2 y z  17  0 .
D. x y  2z  7  0 . x  3 y z 1
Câu 48. Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d  :   và điểm 2  1  1 ( A 2; 1
 ;0) . Khoảng cách từ điểm A đến đường thẳng d  bằng 7 21 7 A. 7 . B. . C. . D. . 2 3 3
Câu 49. Trong không gian O xyz , cho mặt phẳng P: x y z 3  0 và đường thẳng x y 1 z  2 d :  
. Đường thẳng d ' đối xứng với d qua mặt phẳng P có phương trình 1 2 1 là 33 x 1  y 1 z 1 x 1 y 1 z 1 A.   . B.   . 1 2 7 1 2 7 x 1 y 1 z 1 x 1 y 1 z 1 C.   . D.   . 1 2 7 1 2 7
Câu 50: Trong không gian Oxyz , cho hai điểm
A1; 2; 4, B 0;0  ;1 và mặt cầu
S   x  2   y  2 2 : 1
1  z  4 . Mặt phẳng  P : ax by cz  4  0 đi qua ,
A B và cắt S
theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tính T a b c? 1 3 A. T  . B. T  . C. T  1. D. T  2  . 5 4 34
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 12 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề : Cô Hà Thị San
Câu 1. Cho hàm số y f x có bảng biến thiên như sau:
Hàm số f x nghịch biến trên khoảng nào sau đây? A. 1;  3 . B.  1  ;3 . C.  1  ;  1 . D.  3  ;  1 .
Câu 2. Hàm số f x   log  2
x  3 có đạo hàm là 3  2x ln 3 2x
A. f  x  .
B. f  x  . 2 x  3  2 x  3ln 3 ln 3 1
C. f  x  .
D. f  x  .  2 x  3  2 x  3ln 3
Câu 3. Nghiệm của phương trình log 2x  3  1 là 3 13
A. x  3 . B. x  .
C. x  2 . D. x  . 2 2
Câu 4. Cho hàm số f x  sin 3x . Trong các khẳng định dưới đây, khẳng định nào đúng? 1 A. f   xx d  cos 3x C . B. f   xx
d   cos 3x C . 3 1 C. f   xx
d   cos 3x C D. f   xx
d  3 cos 3x C . 3 35 2x 1
Câu 5. Tiệm cận ngang của đồ thị hàm số y  là đường thẳng x  2
A. x  2 .
B. y  2 .
C. y  1. D. x  1 .
Câu 6. Cho hình nón có bán kính đáy bằng 5 và góc ở đỉnh bằng 60 . Diện tích xung quanh của hình nón đã cho bằng A. 55 . B. 100 . C. 75 . D. 50 . 2 1
Câu 7. Cho hàm số f x liên tục trên đoạn 1; 2 thỏa mãn f xdx  6 
. Giá trị f 3x   1 dx  1  0 bằng A. 18 . B. 1. C. 2 . D. 3.
Câu 8. Cho khối nón đỉnh S có đáy là hình tròn tâm O , độ dài đường sinh là l. Biết SO  . h Độ
dài bán kính đáy của khối nón bằng A. 2 2 l h . B. 2 2 2 l h . C. 2 2 l h . D. 2 2 h l .
Câu 9. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ? A. 4 2
y  x  2x  2 . B. 3 2
y x  2x  2 . C. 3 2
y  x  2x  2 . D. 4 2
y x  2x  2 .
Câu 10. Trong không gian y
Ox z , phương trình đường thẳng đi qua hai điểm (3 A ; 1  ; 2) và B(4;1; 0) là x  3 y 1 z  2 x 1 y  2 z  2 A.   . B.   . 1 2 2 3 1 2 x 1 y  2 z  2 x  3 y 1 z  2 C.   . D.   . 3 1 2 1 2 2  2 2 1 Câu 11.Nếu
f xdx  9  và
f xdx  2 thì
f xdx bằng   2  1 2  A. 7 . B. 3 . C. 10 . D. 7 . 36 3 2 2  x 14x Câu 12. Biết
dx a ln 2  b ln 3  c , (a, , b c  )   . Giá trị của 2
a b c bằng 2 x 1 2 A. 494 B. 484. C. 474. D. 464.
Câu 13. Tập xác định của hàm số y   x   3 2 là A.  2  ;  . B.  . C.  \ { } 2 . D. 2;  .
Câu 14. Cho hàm số y f x có bảng biến thiên như sau
Đồ thị hàm số có đường tiệm cận đứng là A. y  1  . B. x  2 . C. y  2 . D. x  1  .    
Câu 15. Trong không gian Oxyz , cho hai véctơ a  1;2;  1 và b  2; 4  ;  2 . Khi đó tích . a b bằng A. 12 B. 4 C. 12 D. 4
Câu 16. Cho hình cầu bán kính R . Thể tích của khối cầu tương ứng là 3 4 R 4 3 4R A. . B. 3 4 R . C. 2  R . D. . 3 3 3 2 2
Câu 17. Trong không gian Oxyz , cho mặt cầu S   x     y   2 : 1 2
z  16 . Tâm của S  có tọa độ là A.  1  ; 2  ;1 . B.  1  ; 2; 0 . C. 1; 2  ; 0 . D. 1; 2   ;1 .
Câu 18. Trong không gian Oxyz , khoảng cách từ gốc tọa độ O đến mặt phẳng 2x y  2z 12  0 bằng 4  4 A. 12 . B. . C. 4 . D. . 3 3
Câu 19. [Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh 2a . Thể tích khối trụ bằng 37 3  a 3 2 a A. . B. 3 2 a . C. . D. 3 4 a . 2 3
Câu 20. Trong không gian Oxyz , phương trình mặt phẳng đi qua A1; 2
 ;2 và có vectơ pháp  tuyến n  3; 1  ; 2   là
A. 3x y  2z 1  0 .
B. x  2 y  2z 1  0 .
C. 3x y  2z 1  0 .
D. x  2 y  2z 1  0 . x  6
Câu 21. Có bao nhiêu giá trị nguyên của tham số m để hàm số y  nghịch biến trên
x  5m khoảng 15;  ? A. 3 . B. 4 . C. 5 . D. Vô số.
Câu 22. Với a là số thực dương tùy ý 4 7 a bằng 7 4 A. 4 a . B. 7 a . C. 28 a . D. 7 a .
Câu 23. Họ các nguyên hàm của hàm số   2x
f x e 1là 1 1 A. 2 x e C . B. 2 2 x
e x C . C. 2 2 x
e C . D. 2 x
e x C . 2 2 2 x 5  1  1
Câu 24. Tập nghiệm của bất phương trình    là  2  16
A. ; 3  3;  . B. 3;3 . C. ;3 . D. 3;  .
Câu 25. Trong không gian Oxyz , cho điểm A7; 1; 2 và mặt phẳng  P : x  2y  2z  6  0 .
Mặt cầu S  tâm A và tiếp xúc với mặt phẳng  P có phương trình là 2 2 2 49 2 2 2 7
A. x  7   y  
1   z  2  .
B. x  7   y  
1   z  2  . 9 3 2 2 2 49 2 2 2 7
C. x  7   y  
1   z  2  .
D. x  7   y  
1   z  2  . 9 3 38 x  1 3t
Câu 26. Trong không gian Oxyz , cho điểm M 8;  4;3 và đường thẳng d : y  2
  2t . Gọi H z t
là hình chiếu vuông góc của M lên d . Khi đó tọa độ của điểm H là
A. H 7;  6; 2 .
B. H 9;  2; 4 . C. H  2  ; 0;  
1 . D. H 1;  2  ;1 .
Câu 27. Trong không gian Oxyz , cho điểm M 0; 1
 ; 2 và mặt phẳng  P : 4x  y  3z  2  0 .
Đường thẳng  đi qua điểm M và vuông góc với mặt phẳng  P có phương trình tham số là x  4 x  4tx  4 x  4t    
A. y t  . B. y  1   t .
C. y  1 t . D. y  1  . z  3   2t     z  2  3tz  3   2tz  2  3t
Câu 28. Cho hàm số y f x có bảng biến thiên như sau
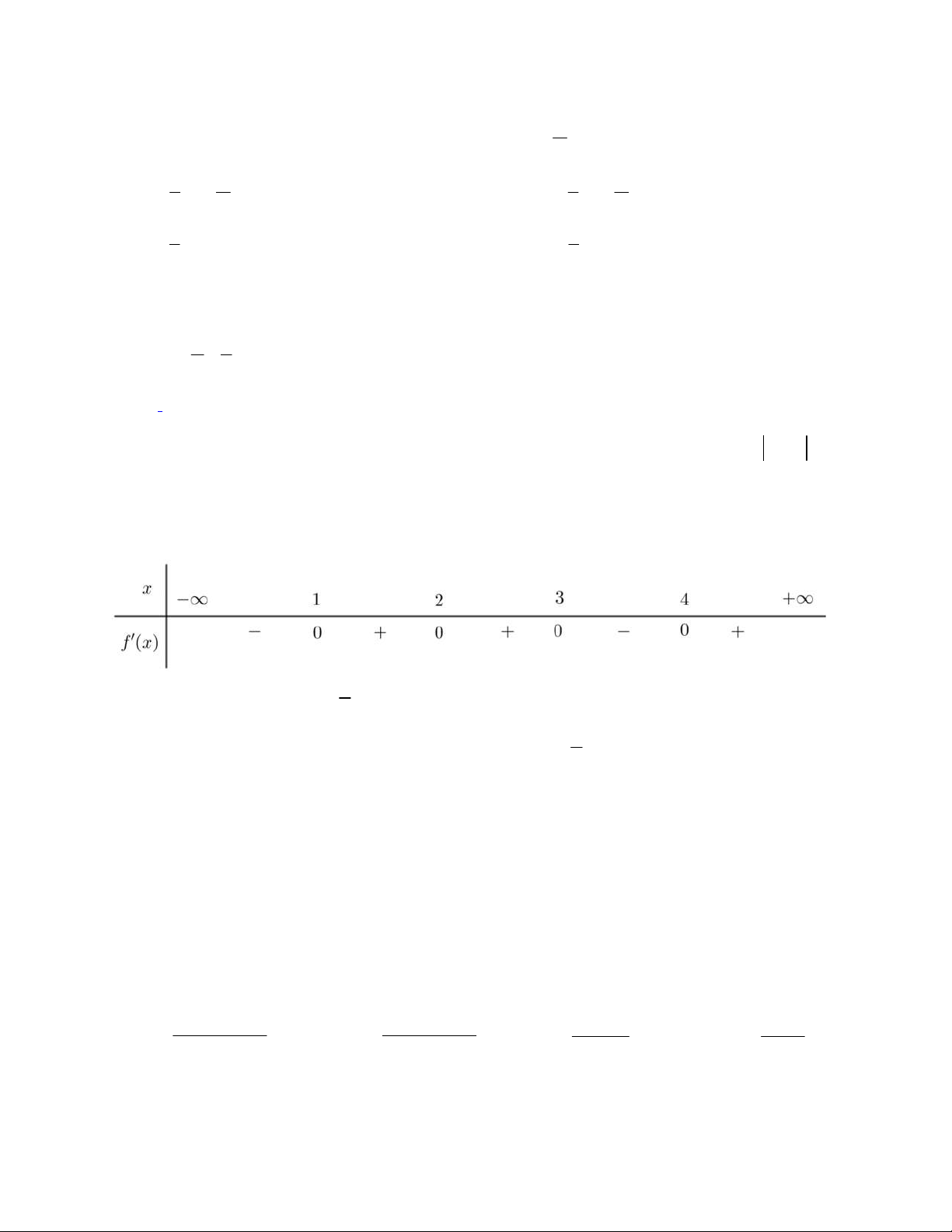
Số nghiệm của phương trình 3 f x  7  0 là A. 2. B. 3. C. 1. D. 4.
Câu 29. Cho phương trình log 2   4x x m
m với m là tham số thực. Có bao nhiêu giá trị 2  
nguyên của m   27 
; 27 sao cho phương trình trên có nghiệm? A. 10 . B. 26 . C. 1. D. 53 .
Câu 30. Có một khối gỗ hình lăng trụ đứng có chiều cao 200 cm và đáy là hình tam giác có độ
dài ba cạnh là 50 cm, 120 cm và 130 cm. Người ta tiện khối gỗ này thành một khối trụ.
Thể tích lớn nhất của khối trụ gần nhất với giá trị nào sau đây? A. 3 2654645, 79 cm . B. 3 62831,85 cm . C. 3 251327,41 cm . D. 3 83775,81 cm .
Câu 31. Tập nghiệm của phương trình log  2
x  4x  8  3 là 2  39 A. 0;  4 . B.   0 . C.   4 . D. 0;  4 . 0
Câu 32. Cho tích phân x 1 dx
, với cách đặt t
x 1 thì tích phân đã cho bằng tích phân 1  nào sau đây? 1 1 1 0 A. 2 2 t dt  . B. 2 t dt  . C. 3 3 t dt  . D. 3 3 t dt  . 0 0 0 1 3x 1
Câu 33. Tìm giá trị nhỏ nhất m của hàm số y  trên đoạn 0;  2 . x  3 1 1 A. m  5  . B. m  . C. m   . D. m  5 . 3 3
Câu 34. Cho khối lăng trụ đứng ABC.A' B 'C ' có BB '  a , đáy ABC là tam giác vuông cân tại B
, AC a 2 . Thể tích lăng trụ đã cho bằng 3 a 3 a 3 a A. . B. 3 a . C. . D. . 2 3 6 1
Câu 35. Tìm giá trị thực của tham số m để hàm số 3 2 y
x mx   2
m  4 x  3 đạt cực tiểu tại 3 x  3 . A. m  7  . B. m  1  . C. m  5 . D. m  1.
Câu 36. Tập nghiệm S của bất phương trình 2 log
4x  3  log 18x  27 là 3   3    3  3  3
A. S 3;   . B.    S   ; 3 . C. . D. .  S  ;    S  ; 3  8      4   4 
Câu 37. Cho hình chóp .
S ABCD có đáy là hình vuông cạnh bằng a 2 , cạnh bên SA vuông góc
với đáy và SA a 3 . Góc giữa hai mặt phẳng  SBD và  ABCD bằng A. 90 . B. 60 . C. 30 . D. 45.
Câu 38. Trong không gian với hệ trục toạ độ Oxyz , cho bốn điểm Aa;0;0 , B0;b;0 ,
C 0;0;c và D1;2; 
1 ; với a, b , c là các số thực khác 0 . Biết rằng bốn điểm ,
A B, C, D đồng phẳng khi khoảng cách từ gốc toạ độ O đến mặt phẳng  ABC là lớn
nhất. Giá trị biểu thức abc bằng 40 A. 2 . B. 4 . C. 3 . D. 15 .  4 5 f ( x ) 2 Câu 39. Cho dx  4  và f   2
1 4sin xsin 2xdx  5 . Tích phân f xdxx bằng 1 0 2 A. 18 B. 22 . C. 12 . D. 1 .
Câu 40. Cho hình thang cong  H  giới hạn bởi các đường y x , y  0 , x  0 , x  4 .
Đường thẳng x k 0  k  4 chia  H  thành hai phần có diện tích là S S 1 và 2 như hình vẽ. Để S  3S 1
2 thì giá trị k thuộc khoảng nào sau đây ? A. 3,3; 3,  5 . B. 3,5;3,  8 . C. 3,1;3,3 . D. 3,8;3,9 .
Câu 41. Trong không gian Oxyz, cho mặt cầu S  có tâm là điểm A 2;1; 3 và tiếp xúc với mặt
phẳng Oxy . Mặt cầu S  có phương trình là 2 2 2 2 2 2
A. x  2   y  
1   z  3  5 .
B. x  2   y  
1   z  3  9 . 2 2 2 2 2 2
C. x  2   y  
1   z  3  5 .
D. x  2   y  
1   z  3  9 .
Câu 42. Cho hàm số y f x , biết f  x 3
x  3x 1. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  8  ; 
8 sao cho hàm số g x  f 2  x 1 mx  6 nghịch biết trên khoảng 2;  3 ? A. 11. B. 12 . C. 9 D. 10 . 41
Câu 43. Cho hàm số f x, g x là hai hàm số liên tục trên 0;  3 thỏa mãn điều kiện 3 3
f x  g xdx   10    và
3 f x  g xdx  6    . Tính 0 0 3 2021 2
f 2021 xdx  3 g 2xdx ?   2018 0 A. 5 . B. 7 . C. 13 . D. 6 .
Câu 44. Trong không gian Oxyz , cho hai điểm A1;1;  
1 , B 7; 2;2 và đường thẳng x  1   3t
 :  y  2  2t . Gọi  P là mặt phẳng chứa đường thẳng , khoảng cách từ A đến  P
z  2  2t
gấp đôi khoảng cách từ B đến  P và ,
A B nằm khác phía so với  P . Biết rằng phương
trình  P có dạng ax by  z
c  28  0. Giá trị của a b c bằng A. 26. B. 26 . C. 34 . D. 34 .
Câu 45. Cho hàm số f x có đạo hàm và liên tục trên  , thỏa mãn     2 ' 2 e x f x xf x x    và f 0  2  . Tính f   1 . 2 1 2 A. f   1  . B. f   1  . C. f   1   . D. f   1  e . e e e
Câu 46. Cho hai số thực , x y thỏa mãn log
2x  4 y  1. Tính P  . x y khi biểu thức 2 2   x y 1 
S  4x  3y  5 đạt giá trị lớn nhất. 52 13 52 13 A. P   . B. P   C. P  . D. P  25 25 25 25 x tx  1 2t 1 2  
Câu 47. Trong không gian Oxyz , cho hai đường thẳng d :  y  4
  t và d :  y  3   t . 1 1 2 2 z  3  t   z  4  t 1  2
Đưởng thẳng vuông góc với mặt phẳng Oxz cắt hai đường thẳng d và d có phương 1 2 trình là 42  1  1 x    x   t 3  7    7  7
A. y    t
B. y  1 t . 3  3   10  10 z   z t   3  3  3  3 x tx  7  7    25  25 C. y  1 t . D. y    t . 7  7   18  18 z tz    7  7
Câu 48. Gọi tập X là tập hợp tất cả các số nguyên m  202  1; 202 
1 sao cho đồ thị của hàm số 3
y x   m   2 2
1 x mx m có 5 điểm cực trị. Tính tổng các phần tử của tập X . A. 0 . B. 1  . C. 4036 . D. 1.
Câu 49. Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đồ thị hàm số
y  sin x , trục hoành và các đường thẳng x  0; x   quanh trục Ox bằng   2  2  A. . B. . C. . D. . 4 2 4 2
Câu 50. Cho hàm số y
x có đồ thị C  và điểm M thuộc C  có hoành độ dương. Gọi S 1
là diện tích hình phẳng giới hạn bởi C  , trục hoành và đường thẳng đi qua M và vuông
góc với trục hoành; S là diện tích hình phẳng giới hạn bởi C  và đường thẳng OM. 2 S a a Biết 2  (với * a,b   và
là phân số tối giản), giá trị của a b bằng S b b 1 A. 6 . B. 5. C. 19. D. 21 . 43