Đề tham khảo giữa kỳ 1 Toán 9 năm 2023 – 2024 trường THCS Trương Công Định – TP HCM
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề tham khảo kiểm tra giữa học kỳ 1 môn Toán 9 năm học 2023 – 2024 trường THCS Trương Công Định, quận Bình Thạnh, thành phố Hồ Chí Minh; đề thi có đáp án và biểu điểm. Mời bạn đọc đón xem.
Preview text:
UBND QUẬN BÌNH THẠNH ĐỀ KIỂM TRA
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
GIỮA HỌC KỲ 1 NĂM HỌC 2023 - 2024
TRƯỜNG THCS TRƯƠNG CÔNG ĐỊNH MÔN TOÁN LỚP 9
Thời gian: 90 phút (không kể thời gian phát đề)
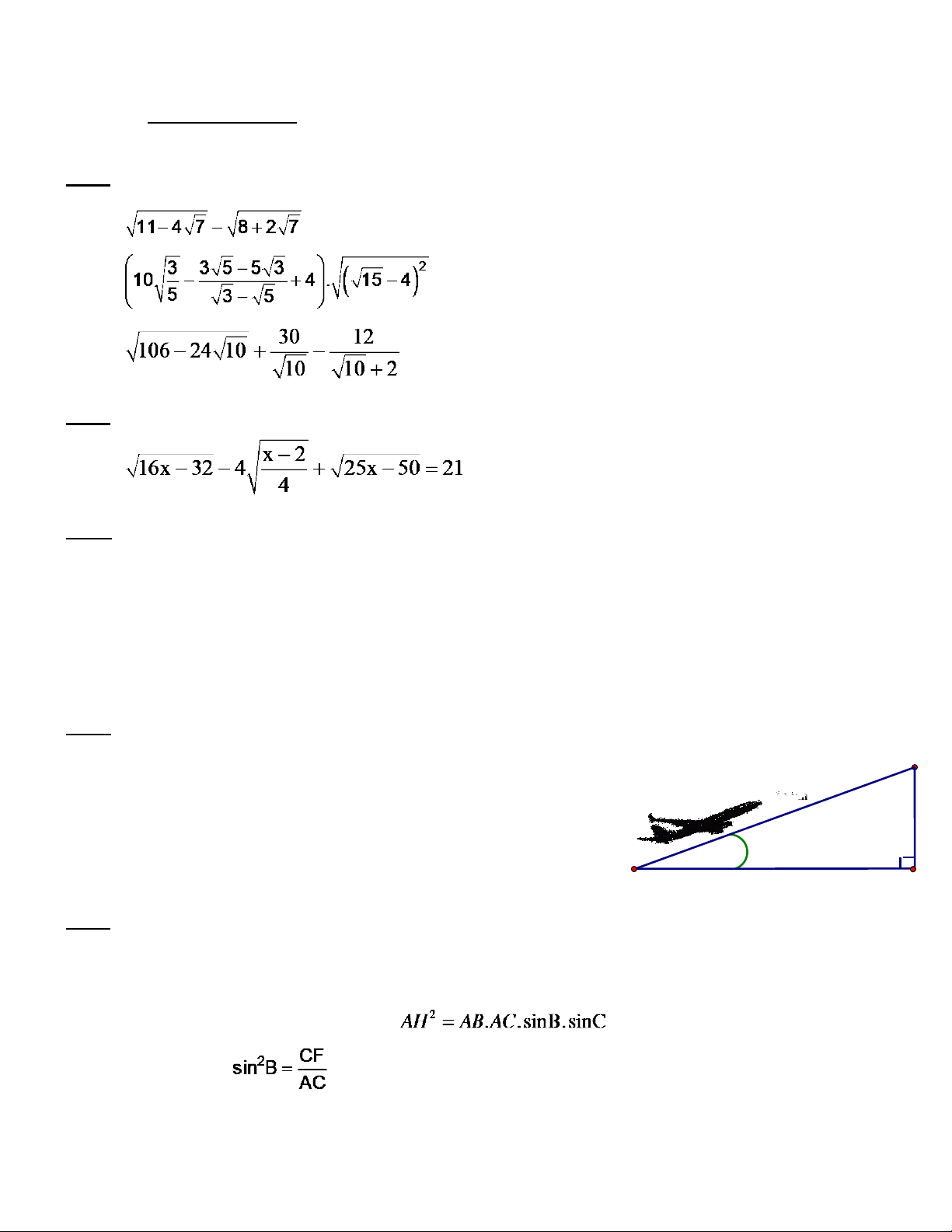
Bài 1. (3 điểm). Tính: a) . b) . c) .
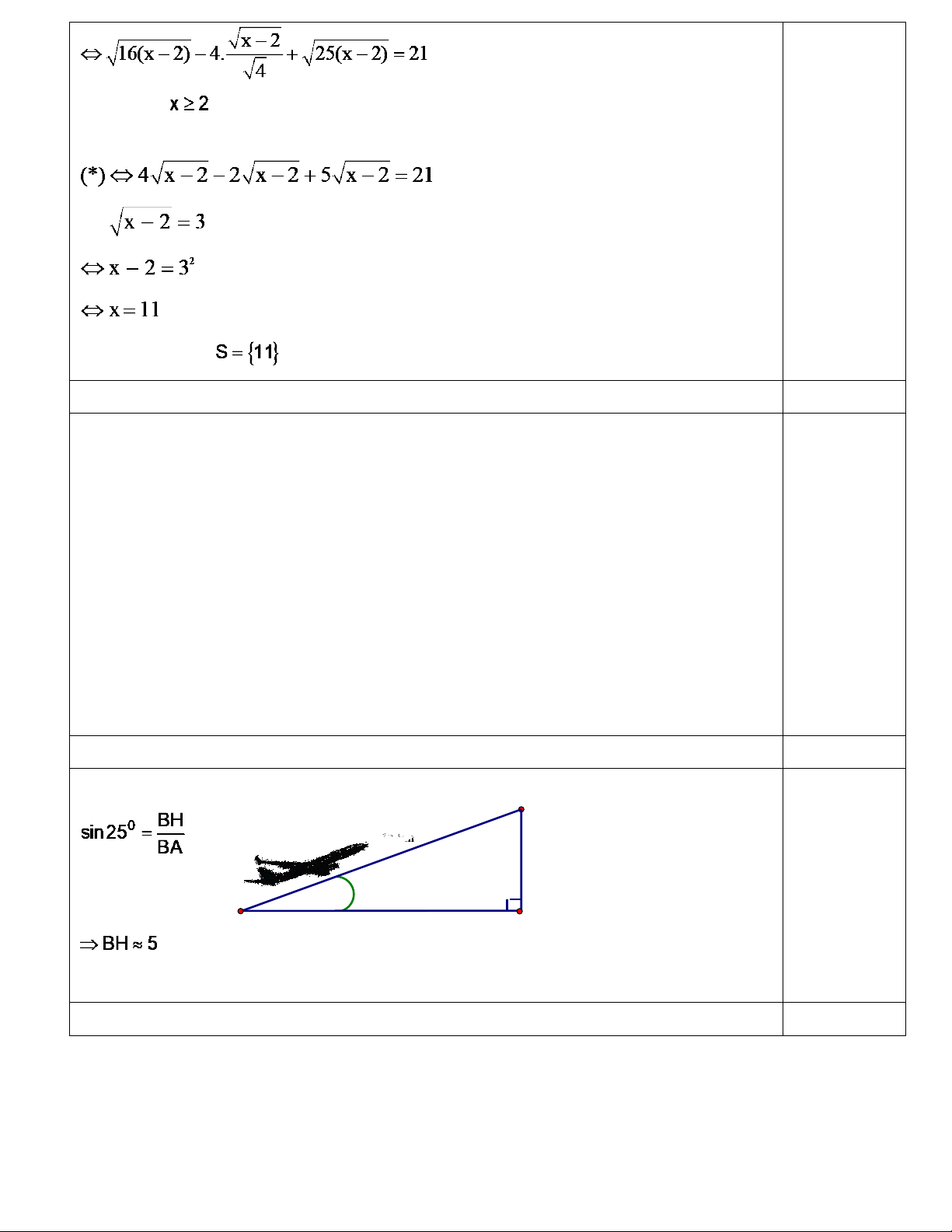
Bài 2. (1,5 điểm). Giải các phương trình: .
Bài 3. (1,5 điểm). Giá niêm yết của một cái tivi loại A là 10 000 000 đồng. Nhân dịp khai trương, cửa
hàng giảm giá 10% trên giá niêm yết đối với mỗi sản phẩm. Kết thúc ngày khuyến mãi thứ nhất, cửa
hàng bán được 30 cái tivi loại A. Nhẩm tính có lời, cửa hàng quyết định bán 20 cái tivi loại A còn lại
với giá bằng 70% giá của ngày thứ nhất. Em hãy cho biết, sau khi bán hết 50 cái tivi trên thì cửa hàng
lãi bao nhiêu tiền? Biết cửa hàng mua lô hàng 50 cái tivi loại A với giá 6 000 000 đồng/cái.
Bài 4. (1 điểm). Một chiếc máy bay xuất phát từ vị trí A bay lên theo đường thẳng tạo với phương
ngang một góc 200 (xem hình bên). Nếu máy bay chuyển B
động theo hướng đó đi được 12 km đến vị trí B thì khi đó máy 12 km
bay sẽ ở độ cao bao nhiêu kilômét so với mặt đất (BH là độ 25 0
cao)? (độ cao làm tròn đến hàng đơn vị). A H
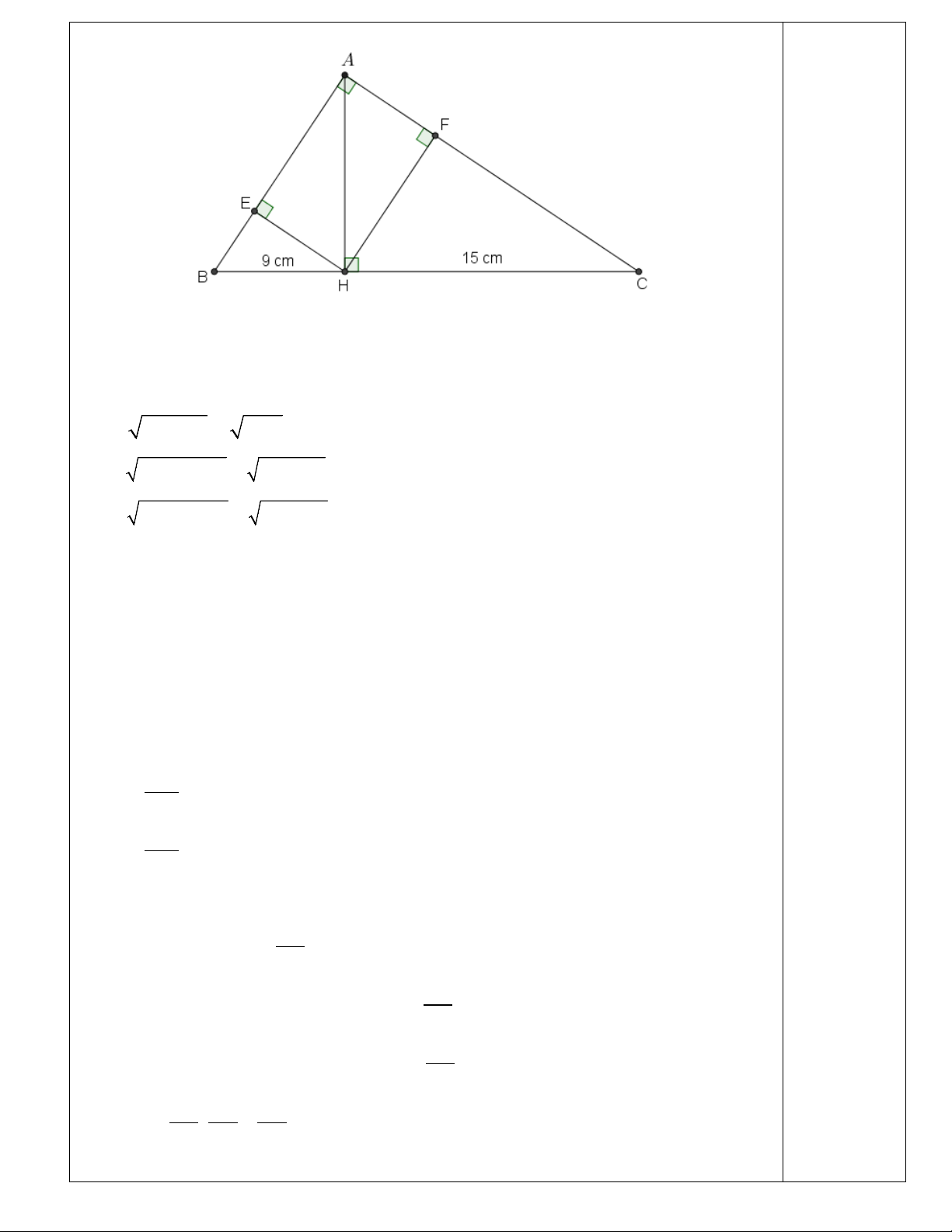
Bài 5. (3 điểm). Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH.
a) Cho HB = 9 cm, HC = 16 cm. Tính AH, AB, BC, AC.
b) Gọi E, F lần lượt là hình chiếu của H trên AB, AC.
Chứng minh AE.AB = AF.AC và . c) Chứng minh .
-------------------- HẾT --------------------
UBND QUẬN BÌNH THẠNH ĐÁP ÁN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN TOÁN LỚP 9
TRƯỜNG THCS TRƯƠNG CÔNG ĐỊNH HƯỚNG DẪN CHẤM ĐIỂM Bài 1) Tính: 3 a) 11− 4 7 − 8 + 2 7 1 2 2 = ( 7 − 2) − ( 7 + ) 1 0.5 = 7 − 2 − 7 −1 0.25 = −3 . 0.25 − 2 3 3 5 5 3 b)10 − + 4 . ( 15 − 4) 5 3 − 5 1 3 5 ( 3 − 5) = 2 15 − + 4 . 15 − 4 3 − 5 0.5
= (2 15 − 15 + 4).(4 − 15) = (4 + 15).(4 − 15) 0.25 = 1 0.25 2 12 c) 106 − 24 10 +15 − 1 1 5 10 + 2 0.5 ( − = 3 10 − 4)2 12.( 10 2 2. 5 ) +15. − 5. 5 ( 10 + 2).( 10 − 2) 0.25
= 3 10 − 4 + 3 10 − 2.( 10 − 2)
= 3 10 − 4 + 3 10 − 2 10 + 4 0.25 = 4 10 .
Bài 2) Giải các phương trình: 1,5 x − 2 16x − 32 − 4 + 25x − 50 = 21 4 0.25 0.25 Điều kiện: Phương trình trở thành: 0.25 0. 25 0.25 ⇔ 0.25 (Nhận) Vậy tập nghiệm . Bài 3) 1,5
Tiền vốn của 50 cái tivi:
6 000 000 . 50 = 300 000 000 (đồng) 0.25
Giá tiền một cái tivi trong ngày khuyến mãi thứ nhất:
10 000 000 . 90% = 9 000 000 (đồng) 0.25
Giá tiền một cái tivi trong ngày khuyến mãi thứ hai:
9 000 000 . 70% = 6 300 000 (đồng) 0.5
Số tiền thu về khi bán hết 50 cái tivi:
9 000 000 . 30 + 6 300 000 . 20 = 396 000 000 (đồng) 0.25
Sau khi bán hết 50 cái tivi trên thì cửa hàng lãi: 0.25
396 000 000 - 300 000 000 = 96 000 000 (đồng). Bài 4) 1 ∆ABH vuông tại H: B 0.25 12 km BH = BA . sịn250 0.25 25 0 BH = 12 . sịn250 A H 0.25
Vậy máy bay đạt độ cao 5 km so với mặt đất. 0.25 Bài 5) 3 a) Tính AH, AB, BC, AC 0.25
∆ABC vuông tại A có đường cao AH: 0.25 BC = 9 + 16 = 25 0.25 AH = HB.HC = 9.16 =12 0.25 = 2 + 2 = 2 + 2 AB HA HB 9 12 = 15 (Định lí Pytago) = 2 + 2 = 2 + 2 AC HA HC 9 16 = 20 (Định lí Pytago)
b) Chứng minh AE.AB = AF.AC và 2 AH = A . B A . C sinB.sinC
• Chứng minh AE.AB = AF.AC 0.25
AE.AB = AH2 (∆AHB vuông tại H, đường cao HE) 0.25
AF.AC = AH2 (∆AHC vuông tại H, đường cao HF) ⇒ AE.AB = AF.AC • Chứng minh 2 AH = A . B A . C sinB.sinC AH sin B = ⇒ AH = AB.sin B AB AH sinC = ⇒ AH = AC.sinC 0.25 AC 0.25 2 AH = AB.AC.sin B.sinC c) Chứng minh 2 = CF sin B AC Chứng minh = ⇒ = = CF B FHC sinB sinFHC CH Chứng minh = ⇒ = = CH B CAH sinB sinCAH 0.25 AC 0.25 ⇒ 2 = CF ⋅ CH = CF sin B . CH AC AC 0.25 0.25