Đề thi 8 tuần HK2 Toán 12 năm 2018 – 2019 trường chuyên Lê Hồng Phong – Nam Định

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giữa học kì 2 môn Toán 12 năm học 2018 – 2019 .Mời bạn đọc đón xem.

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 12

Môn: Toán 12

Thông tin:

66 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trường THPT Chuyên Lê Hồng Phong
ĐỀ CHÍNH THỨC
(Đề thi có 6 trang)
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019
Môn: Toán - Lớp 12 - Khối ABCD
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 638
Câu 1. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a
√
2 bằng
A. 4πa
3
√
2. B. πa
3
√
2. C. 2πa
3
. D.
πa
3
√
2
3
.
Câu 2. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả
cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng.
A.
3
14
. B.
1
35
. C.
3
7
. D.
2
5
.
Câu 3. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
x
f
0
(x)
f(x)
−∞
−1
2
+∞
+ −
0
+
−∞−∞
1 1
−2−2
+∞+∞
A. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
B. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2.
C. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
D. Giá trị cực đại của hàm số bằng 1.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC.
A. G(3; −6; 12). B. G(1; −2; −4). C. G(−1; 2; −4). D. G(1; −2; 4).
Câu 5. Số phức liên hợp của số phức z = 5 + 6i là
A. z = −5 + 6i. B. z = −5 − 6i. C. z = 6 − 5i. D. z = 5 − 6i.
Câu 6. Cho cấp số nhân (u
n
) có công bội q, số hạng đầu u
1
= −2 và số hạng thứ tư u
4
= 54. Giá trị
của q bằng
A.
√
3. B. −6. C. 6. D. −3.
Câu 7. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ?
A. y + 5 = 0. B. z + 20 = 0. C. x − 2019 = 0. D. 2x + 5y − 8z = 0.
Câu 8. Tập xác định của hàm số y =
2x − 1
2x − 4
là
A. D = R \ {2}. B. D = R \ {−4}. C. D = R \ {4}. D. D = R \ {−2}.
Câu 9. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng?
A. log(ab) = log a. log b. B. log
a
b
= log b −log a.
C. log
a
b
=
log a
log b
. D. log(ab) = log a + log b.
Câu 10. Cho hình lăng trụ đứng ABC.A
0
B
0
C
0
có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA
0
= 3a. Tính thể tích V của lăng trụ đó.
A. V = 3a
3
. B. V = 3a
2
. C. V = a
3
. D. V = 6a
3
.
Trang 1/6 − Mã đề 638
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ
−→
a = (3; 2; 1),
−→
b = (−2; 0; 1) . Độ dài
của véc-tơ
−→
a +
−→
b bằng
A. 2. B. 1. C.
√
2. D. 3.
Câu 12. Tìm tập xác định D của hàm số y = (2 − x)
1
3
.
A. D = (−∞; 2] . B. D = (2; +∞). C. D = (−∞; 2) . D. D = (−∞; +∞) .
Câu 13. Cho hàm số f(x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định
sai.
A.
a
Z
a
f(x) dx = 0. B.
b
Z
a
f(x) dx = F (b) − F (a).
C.
b
Z
a
f(x) dx = −
a
Z
b
f(x) dx. D.
b
Z
a
f(x) dx = F (a) − F (b).
Câu 14. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là
A. 36π. B.
9π
2
. C.
7π
√
14
3
. D.
9π
8
.
Câu 15. Viết phương trình tiếp tuyến của đồ thị hàm số y =
2x − 1
2x + 1
tại điểm có hoành độ x
0
= 0.
A. y = −4x + 1. B. y = 4x + 1. C. y = 4x. D. y = 4x − 1.
Câu 16.
Hàm số nào cho dưới đây có đồ thị như hình bên?
A. y = log
3
x. B. y = log
2
x + 1.
C. y = log
2
(x + 1). D. y = log
3
(x + 1).
O
x
1 2
y
1
2
−1
Câu 17. Cho hàm số y =
x
3
3
− x
2
+ x + 2019. Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên R.
B. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
C. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1).
D. Hàm số đã cho nghịch biến trên (−∞; 1).
Câu 18.
Gọi z
1
, z
2
lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên.
Tính |z
1
+ z
2
|.
A. 2
√
29. B. 20. C. 2
√
5. D. 116.
x
y
O
3
M
2
1
N
−4
Câu 19. Cho bất phương trình 4
x
−5.2
x+1
+16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a
2
+ b
2
).
A. 2. B. 1. C. 0. D. 10.
Câu 20. Gọi z
1
và z
2
là hai nghiệm phức của phương trình z
2
+ 4z + 29 = 0. Tính giá trị biểu thức
|z
1
|
4
+ |z
2
|
4
.
A. 841. B. 1682. C. 1282. D. 58.
Trang 2/6 − Mã đề 638
Câu 21.
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f
0
(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau:
1) Hàm số y = f(x) có hai cực trị.
2) Hàm số y = f(x) đồng biến trên khoảng (1; +∞).
3) f(1) > f (2) > f (4).
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f(x) là f(1).
Số mệnh đề đúng trong bốn mệnh đề trên là:
A. 1. B. 4. C. 2. D. 3.
x
y
O
−1
1 4
y = f
0
(x)
Câu 22. Cho
5
Z
0
f(x) dx = −2. Tích phân
5
Z
0
[4f( x) − 3x
2
] dx bằng
A. −140. B. −130. C. −120. D. −133.
Câu 23. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f(x) = m có đúng hai nghiệm phân
biệt?
A. 2018. B. 4016. C. 2019. D. 2020.
Câu 24. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền
ra.
A. 9 năm. B. 10 năm. C. 11 năm. D. 12 năm.
Câu 25. Cho hình phẳng giới hạn bởi các đường y =
√
x −2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành.
A. V =
7
6
. B. V =
5π
6
. C. V =
7π
11
. D. V =
11π
6
.
Câu 26. Họ nguyên hàm của hàm số f (x) = x
4
+ xe
x
là
A.
1
5
x
5
+ (x + 1)e
x
+ C. B.
1
5
x
5
+ (x − 1)e
x
+ C.
C.
1
5
x
5
+ xe
x
+ C. D. 4x
3
+ (x + 1)e
x
C.
Câu 27. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1)
là
A.
x − 5
2
=
y − 4
1
=
z + 1
2
. B.
x + 1
4
=
y + 2
2
=
z + 3
−4
.
C.
x − 1
4
=
y − 2
2
=
z − 3
4
. D.
x − 3
−2
=
y − 3
−1
=
z − 1
2
.
Câu 28. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của
hình chóp đó.
A. h =
a
√
28
3
. B. V = h =
a
√
14
3
. C. h =
a
√
33
3
. D. h =
a
√
11
3
.
Trang 3/6 − Mã đề 638
Câu 29.
Đường cong trong hình bên là đồ thị của hàm số nào?
A. y = −x
4
+ 1. B. y = x
4
+ 2x
2
+ 1.
C. y = x
4
+ 1. D. y = −x
4
+ 2x
2
+ 1.
x
y
O
−2 −1 1 2
−1
1
2
Câu 30. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q): x − 2y + z − 5 = 0 và mặt cầu
(S): (x − 1)
2
+ y
2
+ (z + 2)
2
= 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây?
A. (2; −2; 1). B. (1; −2; 0). C. (0; −1; −5). D. (−2; 2; −1).
Câu 31. Tập hợp các giá trị thực của tham số m để phương trình log
2019
(4−x
2
)+log
1
2019
(2x+m−1) =
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b.
A. 20. B. 8. C. 18. D. 16.
Câu 32. Cho hàm số y =
x − 2
mx
2
− 2x + 4
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 1. B. 3. C. 0. D. 2.
Câu 33. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x
4
− 8x
3
− 6x
2
+ 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S.
A. 42. B. 50. C. 30. D. 63.
Câu 34.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM.
A.
2
5
. B.
1
2
. C.
4
5
. D. −
2
5
.
S
A
B C
D
M
Câu 35. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện.
A.
4a
√
6
3
. B.
3a
√
2
2
. C.
4a
√
3
3
. D.
a
√
3
2
.
Câu 36. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
√
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60
◦
chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm).
A. V ≈ 1,42 cm
3
. B. V ≈ 2,36 cm
3
. C. V ≈ 1,53 cm
3
. D. V ≈ 2,47 cm
3
.
Câu 37. Trong không gian Oxyz, điểm M
0
đối xứng với điểm M(1; 2; 4) qua mặt phẳng
(α): 2x + y + 2z −3 = 0 có tọa độ là
A. (−3; 0; 0). B. (−1; 1; 2). C. (−1; −2; −4). D. (2; 1; 2).
Câu 38. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2).
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức
# »
IA − 2
# »
IB + 3
# »
IC
đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0
A.
17
5
. B. 6. C.
12
5
. D. 9.
Trang 4/6 − Mã đề 638
Câu 39. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực.
Tính a + b.
A. z = −2. B. 0. C. z = 2. D. 4.
Câu 40. Biết
4
Z
1
x
3
+ x
2
+ 7x + 3
x
2
− x + 3
dx =
a
b
+ c ln 5 với a, b, c là các số nguyên dương và
a
b
là phân số
tối giản. Tính P = a − b
2
− c
3
.
A. −5. B. −4. C. 5. D. 0.
Câu 41. Cho hàm số y = f(x) có đạo hàm liên tục trên [2; 4] và f
0
(x) > 0, ∀x ∈ [2; 4]. Biết 4x
3
f(x) =
[f
0
(x)]
3
− x
3
, ∀x ∈ [2; 4], f (2) =
7
4
. Giá trị f(4) bằng:
A.
40
√
5 − 1
2
. B.
20
√
5 − 1
4
. C.
20
√
5 − 1
2
. D.
40
√
5 − 1
4
.
Câu 42. Cho hàm số y = f(x) có đạo hàm liên tục trên R. Biết hàm số y = f
0
(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử?
x
y
O
−1 1 3
A. 4. B. 3. C. 6. D. 5.
Câu 43. Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm
số g(x) = f (4x − x
2
) +
1
3
x
3
− 3x
2
+ 8x +
1
3
trên đoạn [1;3].
x
f
0
(x)
f(x)
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−3−3
55
−∞−∞
A. 15. B.
25
3
. C.
19
3
. D. 12.
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3),
D(2; 0;
√
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)
2
+ (y − 4)
2
+ z
2
= 39 thỏa mãn M A
2
+
2 ·
−−→
MB ·
−−→
MC = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó.
A. 2
√
7. B.
√
7. C. 3
√
7. D. 4
√
7.
Câu 45. Cho hàm số y = f (x). Đồ thị hàm số y = f
0
(x) như hình bên.
Hàm số g(x) =
1
2
f(1−2x)
nghịch biến trên khoảng nào trong các khoảng
sau?
A. (0; 1). B. (−∞; 0). C. (−1; 0). D. (1; +∞).
x
y
O
−1 1 2 4
Trang 5/6 − Mã đề 638
Câu 46. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F
1
, F
2
là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
A. 5.676.000 đ. B. 4.766.000 đ.
C. 4.656.000 đ. D. 5.455.000 đ.
F
1
F
2
A
B
C D
Câu 47. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
có cạnh bằng a. Gọi E và F lần lượt là các điểm trên
các cạnh A
0
D
0
và A
0
B
0
sao cho A
0
E =
2
3
A
0
D
0
và A
0
F =
2
3
A
0
B
0
. Tính thể tích khối chóp A.BDEF .
A. V =
a
3
√
3
8
. B. V =
5a
3
18
. C. V =
a
3
8
. D. V =
3a
3
√
3
8
.
Câu 48. Cho hai số phức z
1
;z
2
thỏa mãn |z
1
+ 2 − i|+ |z
1
− 4 − 7i| = 6
√
2 và |iz
2
−1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z
1
+ z
2
|.
A.
√
2 − 1. B.
√
2 + 1. C. 2
√
2 + 1. D. 2
√
2 − 1.
Câu 49. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 720. B. 860. C. 984. D. 1228.
Câu 50. Gọi m
0
là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của
đồ thị hàm số y = x
3
−6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
√
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
A. m
0
∈ (2; 3). B. m
0
∈ (3; 4). C. m
0
∈ (0; 1). D. m
0
∈ (1; 2).
HẾT
Trang 6/6 − Mã đề 638
ĐÁP ÁN MÃ ĐỀ 638
1 B
2 C
3 A
4 D
5 D
6 D
7 D
8 A
9 D
10 A
11 D
12 C
13 D
14 C
15 D
16 C
17 A
18 C
19 B
20 B
21 C
22 D
23 C
24 C
25 D
26 B
27 D
28 C
29 D
30 D
31 D
32 A
33 A
34 A
35 A
36 A
37 A
38 B
39 B
40 B
41 D
42 D
43 D
44 A
45 D
46 A
47 B
48 D
49 C
50 C
Trang 1/1 −Đáp án mã đề 638
Trường THPT Chuyên Lê Hồng Phong
ĐỀ CHÍNH THỨC
(Đề thi có 6 trang)
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019
Môn: Toán - Lớp 12 - Khối ABCD
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 752
Câu 1. Số phức liên hợp của số phức z = 5 + 6i là
A. z = −5 − 6i. B. z = 5 − 6i. C. z = −5 + 6i. D. z = 6 − 5i.
Câu 2. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ?
A. y + 5 = 0. B. 2x + 5y − 8z = 0. C. x − 2019 = 0. D. z + 20 = 0.
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC.
A. G(−1; 2; −4). B. G(1; −2; −4). C. G(1; −2; 4). D. G(3; −6; 12).
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
x
f
0
(x)
f(x)
−∞
−1
2
+∞
+ −
0
+
−∞−∞
1 1
−2−2
+∞+∞
A. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
B. Giá trị cực đại của hàm số bằng 1.
C. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
D. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2.
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ
−→
a = (3; 2; 1),
−→
b = (−2; 0; 1). Độ dài
của véc-tơ
−→
a +
−→
b bằng
A. 3. B.
√
2. C. 2. D. 1.
Câu 6. Cho cấp số nhân (u
n
) có công bội q, số hạng đầu u
1
= −2 và số hạng thứ tư u
4
= 54. Giá trị
của q bằng
A. 6. B. −6. C.
√
3. D. −3.
Câu 7. Cho hình lăng trụ đứng ABC.A
0
B
0
C
0
có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA
0
= 3a. Tính thể tích V của lăng trụ đó.
A. V = a
3
. B. V = 3a
3
. C. V = 3a
2
. D. V = 6a
3
.
Câu 8. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a
√
2 bằng
A. 2πa
3
. B. 4πa
3
√
2. C.
πa
3
√
2
3
. D. πa
3
√
2.
Câu 9. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng?
A. log
a
b
= log b −log a. B. log
a
b
=
log a
log b
.
C. log(ab) = log a. log b. D. log(ab) = log a + log b.
Câu 10. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4
quả cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng.
A.
2
5
. B.
3
7
. C.
3
14
. D.
1
35
.
Trang 1/6 − Mã đề 752
Câu 11. Cho hàm số f(x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định
sai.
A.
b
Z
a
f(x) dx = F (a) − F (b). B.
b
Z
a
f(x) dx = F (b) − F (a).
C.
a
Z
a
f(x) dx = 0. D.
b
Z
a
f(x) dx = −
a
Z
b
f(x) dx.
Câu 12. Tìm tập xác định D của hàm số y = (2 − x)
1
3
.
A. D = (−∞; 2] . B. D = (−∞; 2) . C. D = (−∞; +∞) . D. D = (2; +∞).
Câu 13. Tập xác định của hàm số y =
2x − 1
2x − 4
là
A. D = R \ {−2}. B. D = R \ {4}. C. D = R \ {−4}. D. D = R \ {2}.
Câu 14. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1)
là
A.
x − 1
4
=
y − 2
2
=
z − 3
4
. B.
x − 5
2
=
y − 4
1
=
z + 1
2
.
C.
x + 1
4
=
y + 2
2
=
z + 3
−4
. D.
x − 3
−2
=
y − 3
−1
=
z − 1
2
.
Câu 15. Viết phương trình tiếp tuyến của đồ thị hàm số y =
2x − 1
2x + 1
tại điểm có hoành độ x
0
= 0.
A. y = 4x + 1. B. y = −4x + 1. C. y = 4x − 1. D. y = 4x.
Câu 16. Cho hàm số y =
x
3
3
− x
2
+ x + 2019. Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1).
B. Hàm số đã cho đồng biến trên R.
C. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
D. Hàm số đã cho nghịch biến trên (−∞; 1).
Câu 17. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f(x) = m có đúng hai nghiệm phân
biệt?
A. 2018. B. 4016. C. 2020. D. 2019.
Câu 18.
Đường cong trong hình bên là đồ thị của hàm số nào?
A. y = x
4
+ 2x
2
+ 1. B. y = −x
4
+ 2x
2
+ 1.
C. y = x
4
+ 1. D. y = −x
4
+ 1.
x
y
O
−2 −1 1 2
−1
1
2
Trang 2/6 − Mã đề 752
Câu 19. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền
ra.
A. 12 năm. B. 11 năm. C. 10 năm. D. 9 năm.
Câu 20. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là
A.
9π
2
. B.
7π
√
14
3
. C.
9π
8
. D. 36π.
Câu 21. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q): x − 2y + z − 5 = 0 và mặt cầu
(S): (x − 1)
2
+ y
2
+ (z + 2)
2
= 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây?
A. (2; −2; 1). B. (1; −2; 0). C. (−2; 2; −1). D. (0; −1; −5).
Câu 22. Gọi z
1
và z
2
là hai nghiệm phức của phương trình z
2
+ 4z + 29 = 0. Tính giá trị biểu thức
|z
1
|
4
+ |z
2
|
4
.
A. 1282. B. 841. C. 58. D. 1682.
Câu 23. Cho bất phương trình 4
x
−5.2
x+1
+16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a
2
+ b
2
).
A. 10. B. 0. C. 2. D. 1.
Câu 24. Cho hình phẳng giới hạn bởi các đường y =
√
x −2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành.
A. V =
11π
6
. B. V =
7π
11
. C. V =
7
6
. D. V =
5π
6
.
Câu 25. Họ nguyên hàm của hàm số f (x) = x
4
+ xe
x
là
A.
1
5
x
5
+ xe
x
+ C. B.
1
5
x
5
+ (x − 1)e
x
+ C.
C. 4x
3
+ (x + 1)e
x
C. D.
1
5
x
5
+ (x + 1)e
x
+ C.
Câu 26. Cho
5
Z
0
f(x) dx = −2. Tích phân
5
Z
0
[4f( x) − 3x
2
] dx bằng
A. −133. B. −130. C. −140. D. −120.
Câu 27.
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f
0
(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau:
1) Hàm số y = f(x) có hai cực trị.
2) Hàm số y = f(x) đồng biến trên khoảng (1; +∞).
3) f(1) > f (2) > f (4).
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f(x) là f(1).
Số mệnh đề đúng trong bốn mệnh đề trên là:
A. 3. B. 2. C. 1. D. 4.
x
y
O
−1
1 4
y = f
0
(x)
Câu 28.
Gọi z
1
, z
2
lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên.
Tính |z
1
+ z
2
|.
A. 20. B. 2
√
29. C. 116. D. 2
√
5.
x
y
O
3
M
2
1
N
−4
Trang 3/6 − Mã đề 752
Câu 29.
Hàm số nào cho dưới đây có đồ thị như hình bên?
A. y = log
2
x + 1. B. y = log
3
x.
C. y = log
2
(x + 1). D. y = log
3
(x + 1).
O
x
1 2
y
1
2
−1
Câu 30. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của
hình chóp đó.
A. h =
a
√
33
3
. B. V = h =
a
√
14
3
. C. h =
a
√
11
3
. D. h =
a
√
28
3
.
Câu 31. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực.
Tính a + b.
A. 0. B. z = −2. C. z = 2. D. 4.
Câu 32. Biết
4
Z
1
x
3
+ x
2
+ 7x + 3
x
2
− x + 3
dx =
a
b
+ c ln 5 với a, b, c là các số nguyên dương và
a
b
là phân số
tối giản. Tính P = a − b
2
− c
3
.
A. 5. B. −4. C. −5. D. 0.
Câu 33. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2).
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức
# »
IA − 2
# »
IB + 3
# »
IC
đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0
A. 9. B. 6. C.
17
5
. D.
12
5
.
Câu 34. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện.
A.
4a
√
6
3
. B.
4a
√
3
3
. C.
a
√
3
2
. D.
3a
√
2
2
.
Câu 35. Cho hàm số y =
x − 2
mx
2
− 2x + 4
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 0. B. 1. C. 2. D. 3.
Câu 36.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM.
A.
4
5
. B. −
2
5
. C.
2
5
. D.
1
2
.
S
A
B C
D
M
Câu 37. Trong không gian Oxyz, điểm M
0
đối xứng với điểm M(1; 2; 4) qua mặt phẳng
(α): 2x + y + 2z −3 = 0 có tọa độ là
A. (2; 1; 2). B. (−3; 0; 0). C. (−1; −2; −4). D. (−1; 1; 2).
Trang 4/6 − Mã đề 752
Câu 38. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
√
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60
◦
chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm).
A. V ≈ 2,47 cm
3
. B. V ≈ 1,42 cm
3
. C. V ≈ 2,36 cm
3
. D. V ≈ 1,53 cm
3
.
Câu 39. Tập hợp các giá trị thực của tham số m để phương trình log
2019
(4−x
2
)+log
1
2019
(2x+m−1) =
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b.
A. 18. B. 16. C. 8. D. 20.
Câu 40. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x
4
− 8x
3
− 6x
2
+ 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S.
A. 42. B. 30. C. 63. D. 50.
Câu 41. Gọi m
0
là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của
đồ thị hàm số y = x
3
−6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
√
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
A. m
0
∈ (2; 3). B. m
0
∈ (0; 1). C. m
0
∈ (1; 2). D. m
0
∈ (3; 4).
Câu 42. Cho hàm số y = f(x) có đạo hàm liên tục trên R. Biết hàm số y = f
0
(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử?
x
y
O
−1 1 3
A. 5. B. 6. C. 4. D. 3.
Câu 43. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 984. B. 1228. C. 720. D. 860.
Câu 44. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
có cạnh bằng a. Gọi E và F lần lượt là các điểm trên
các cạnh A
0
D
0
và A
0
B
0
sao cho A
0
E =
2
3
A
0
D
0
và A
0
F =
2
3
A
0
B
0
. Tính thể tích khối chóp A.BDEF .
A. V =
5a
3
18
. B. V =
a
3
√
3
8
. C. V =
3a
3
√
3
8
. D. V =
a
3
8
.
Câu 45. Cho hai số phức z
1
;z
2
thỏa mãn |z
1
+ 2 − i|+ |z
1
− 4 − 7i| = 6
√
2 và |iz
2
−1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z
1
+ z
2
|.
A.
√
2 + 1. B.
√
2 − 1. C. 2
√
2 − 1. D. 2
√
2 + 1.
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3),
D(2; 0;
√
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)
2
+ (y − 4)
2
+ z
2
= 39 thỏa mãn M A
2
+
2 ·
−−→
MB ·
−−→
MC = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó.
A. 4
√
7. B. 2
√
7. C.
√
7. D. 3
√
7.
Câu 47. Cho hàm số y = f (x). Đồ thị hàm số y = f
0
(x) như hình bên.
Hàm số g(x) =
1
2
f(1−2x)
nghịch biến trên khoảng nào trong các khoảng
sau?
A. (−∞; 0). B. (−1; 0). C. (0; 1). D. (1; +∞).
x
y
O
−1 1 2 4
Trang 5/6 − Mã đề 752
Câu 48. Cho hàm số y = f(x) có đạo hàm liên tục trên [2; 4] và f
0
(x) > 0, ∀x ∈ [2; 4]. Biết 4x
3
f(x) =
[f
0
(x)]
3
− x
3
, ∀x ∈ [2; 4], f (2) =
7
4
. Giá trị f(4) bằng:
A.
20
√
5 − 1
4
. B.
40
√
5 − 1
2
. C.
40
√
5 − 1
4
. D.
20
√
5 − 1
2
.
Câu 49. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F
1
, F
2
là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
A. 5.455.000 đ. B. 4.766.000 đ.
C. 4.656.000 đ. D. 5.676.000 đ.
F
1
F
2
A
B
C D
Câu 50. Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm
số g(x) = f (4x − x
2
) +
1
3
x
3
− 3x
2
+ 8x +
1
3
trên đoạn [1;3].
x
f
0
(x)
f(x)
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−3−3
55
−∞−∞
A. 12. B.
25
3
. C. 15. D.
19
3
.
HẾT
Trang 6/6 − Mã đề 752
ĐÁP ÁN MÃ ĐỀ 752
1 B
2 B
3 C
4 C
5 A
6 D
7 B
8 D
9 D
10 B
11 A
12 B
13 D
14 D
15 C
16 B
17 D
18 B
19 B
20 B
21 C
22 D
23 D
24 A
25 B
26 A
27 B
28 D
29 C
30 A
31 A
32 B
33 B
34 A
35 B
36 C
37 B
38 B
39 B
40 A
41 B
42 A
43 A
44 A
45 C
46 B
47 D
48 C
49 D
50 A
Trang 1/1 −Đáp án mã đề 752
Trường THPT Chuyên Lê Hồng Phong
ĐỀ CHÍNH THỨC
(Đề thi có 6 trang)
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019
Môn: Toán - Lớp 12 - Khối ABCD
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 843
Câu 1. Số phức liên hợp của số phức z = 5 + 6i là
A. z = 6 − 5i. B. z = 5 − 6i. C. z = −5 − 6i. D. z = −5 + 6i.
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC.
A. G(1; −2; −4). B. G(3; −6; 12). C. G(1; −2; 4). D. G(−1; 2; −4).
Câu 3. Cho hình lăng trụ đứng ABC.A
0
B
0
C
0
có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA
0
= 3a. Tính thể tích V của lăng trụ đó.
A. V = 3a
3
. B. V = a
3
. C. V = 6a
3
. D. V = 3a
2
.
Câu 4. Tìm tập xác định D của hàm số y = (2 − x)
1
3
.
A. D = (−∞; 2) . B. D = (−∞; 2] . C. D = (−∞; +∞) . D. D = (2; +∞).
Câu 5. Cho cấp số nhân (u
n
) có công bội q, số hạng đầu u
1
= −2 và số hạng thứ tư u
4
= 54. Giá trị
của q bằng
A.
√
3. B. −6. C. 6. D. −3.
Câu 6. Tập xác định của hàm số y =
2x − 1
2x − 4
là
A. D = R \ {−4}. B. D = R \ {−2}. C. D = R \ {4}. D. D = R \ {2}.
Câu 7. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả
cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng.
A.
3
14
. B.
3
7
. C.
1
35
. D.
2
5
.
Câu 8. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
x
f
0
(x)
f(x)
−∞
−1
2
+∞
+ −
0
+
−∞−∞
1 1
−2−2
+∞+∞
A. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
B. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
C. Giá trị cực đại của hàm số bằng 1.
D. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2.
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ
−→
a = (3; 2; 1),
−→
b = (−2; 0; 1). Độ dài
của véc-tơ
−→
a +
−→
b bằng
A. 1. B.
√
2. C. 3. D. 2.
Câu 10. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a
√
2 bằng
A. 2πa
3
. B. 4πa
3
√
2. C. πa
3
√
2. D.
πa
3
√
2
3
.
Câu 11. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng?
A. log(ab) = log a. log b. B. log
a
b
=
log a
log b
.
C. log
a
b
= log b −log a. D. log(ab) = log a + log b.
Trang 1/6 − Mã đề 843
Câu 12. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ?
A. x − 2019 = 0. B. 2x + 5y − 8z = 0. C. y + 5 = 0. D. z + 20 = 0.
Câu 13. Cho hàm số f(x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định
sai.
A.
b
Z
a
f(x) dx = F (b) − F (a). B.
b
Z
a
f(x) dx = F (a) − F (b).
C.
b
Z
a
f(x) dx = −
a
Z
b
f(x) dx. D.
a
Z
a
f(x) dx = 0.
Câu 14.
Gọi z
1
, z
2
lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên.
Tính |z
1
+ z
2
|.
A. 20. B. 2
√
5. C. 116. D. 2
√
29.
x
y
O
3
M
2
1
N
−4
Câu 15. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q): x − 2y + z − 5 = 0 và mặt cầu
(S): (x − 1)
2
+ y
2
+ (z + 2)
2
= 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây?
A. (1; −2; 0). B. (2; −2; 1). C. (−2; 2; −1). D. (0; −1; −5).
Câu 16. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f(x) = m có đúng hai nghiệm phân
biệt?
A. 2018. B. 2019. C. 4016. D. 2020.
Câu 17.
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f
0
(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau:
1) Hàm số y = f(x) có hai cực trị.
2) Hàm số y = f(x) đồng biến trên khoảng (1; +∞).
3) f(1) > f (2) > f (4).
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f(x) là f(1).
Số mệnh đề đúng trong bốn mệnh đề trên là:
A. 1. B. 4. C. 2. D. 3.
x
y
O
−1
1 4
y = f
0
(x)
Câu 18. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền
ra.
A. 11 năm. B. 9 năm. C. 10 năm. D. 12 năm.
Trang 2/6 − Mã đề 843
Câu 19. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của
hình chóp đó.
A. V = h =
a
√
14
3
. B. h =
a
√
11
3
. C. h =
a
√
33
3
. D. h =
a
√
28
3
.
Câu 20. Gọi z
1
và z
2
là hai nghiệm phức của phương trình z
2
+ 4z + 29 = 0. Tính giá trị biểu thức
|z
1
|
4
+ |z
2
|
4
.
A. 841. B. 1282. C. 1682. D. 58.
Câu 21. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1)
là
A.
x − 1
4
=
y − 2
2
=
z − 3
4
. B.
x − 3
−2
=
y − 3
−1
=
z − 1
2
.
C.
x − 5
2
=
y − 4
1
=
z + 1
2
. D.
x + 1
4
=
y + 2
2
=
z + 3
−4
.
Câu 22. Họ nguyên hàm của hàm số f (x) = x
4
+ xe
x
là
A.
1
5
x
5
+ (x + 1)e
x
+ C. B.
1
5
x
5
+ xe
x
+ C.
C.
1
5
x
5
+ (x − 1)e
x
+ C. D. 4x
3
+ (x + 1)e
x
C.
Câu 23. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là
A.
9π
2
. B.
9π
8
. C.
7π
√
14
3
. D. 36π.
Câu 24. Cho
5
Z
0
f(x) dx = −2. Tích phân
5
Z
0
[4f( x) − 3x
2
] dx bằng
A. −140. B. −120. C. −133. D. −130.
Câu 25. Cho hình phẳng giới hạn bởi các đường y =
√
x −2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành.
A. V =
5π
6
. B. V =
11π
6
. C. V =
7
6
. D. V =
7π
11
.
Câu 26.
Đường cong trong hình bên là đồ thị của hàm số nào?
A. y = x
4
+ 1. B. y = x
4
+ 2x
2
+ 1.
C. y = −x
4
+ 2x
2
+ 1. D. y = −x
4
+ 1.
x
y
O
−2 −1 1 2
−1
1
2
Câu 27.
Hàm số nào cho dưới đây có đồ thị như hình bên?
A. y = log
3
x. B. y = log
2
x + 1.
C. y = log
3
(x + 1). D. y = log
2
(x + 1).
O
x
1 2
y
1
2
−1
Câu 28. Cho bất phương trình 4
x
−5.2
x+1
+16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a
2
+ b
2
).
A. 2. B. 0. C. 10. D. 1.
Trang 3/6 − Mã đề 843
Câu 29. Viết phương trình tiếp tuyến của đồ thị hàm số y =
2x − 1
2x + 1
tại điểm có hoành độ x
0
= 0.
A. y = 4x. B. y = 4x − 1. C. y = −4x + 1. D. y = 4x + 1.
Câu 30. Cho hàm số y =
x
3
3
− x
2
+ x + 2019. Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên R.
B. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
C. Hàm số đã cho nghịch biến trên (−∞; 1).
D. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1).
Câu 31. Biết
4
Z
1
x
3
+ x
2
+ 7x + 3
x
2
− x + 3
dx =
a
b
+ c ln 5 với a, b, c là các số nguyên dương và
a
b
là phân số
tối giản. Tính P = a − b
2
− c
3
.
A. −5. B. −4. C. 5. D. 0.
Câu 32. Trong không gian Oxyz, điểm M
0
đối xứng với điểm M(1; 2; 4) qua mặt phẳng
(α): 2x + y + 2z −3 = 0 có tọa độ là
A. (2; 1; 2). B. (−1; 1; 2). C. (−1; −2; −4). D. (−3; 0; 0).
Câu 33. Cho hàm số y =
x − 2
mx
2
− 2x + 4
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 3. B. 0. C. 1. D. 2.
Câu 34.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM.
A.
2
5
. B.
1
2
. C. −
2
5
. D.
4
5
.
S
A
B C
D
M
Câu 35. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện.
A.
4a
√
3
3
. B.
3a
√
2
2
. C.
a
√
3
2
. D.
4a
√
6
3
.
Câu 36. Tập hợp các giá trị thực của tham số m để phương trình log
2019
(4−x
2
)+log
1
2019
(2x+m−1) =
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b.
A. 20. B. 18. C. 8. D. 16.
Câu 37. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực.
Tính a + b.
A. z = −2. B. 0. C. 4. D. z = 2.
Câu 38. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x
4
− 8x
3
− 6x
2
+ 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S.
A. 50. B. 63. C. 42. D. 30.
Câu 39. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2).
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức
# »
IA − 2
# »
IB + 3
# »
IC
đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0
A.
17
5
. B. 9. C. 6. D.
12
5
.
Trang 4/6 − Mã đề 843
Câu 40. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
√
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60
◦
chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm).
A. V ≈ 1,53 cm
3
. B. V ≈ 2,47 cm
3
. C. V ≈ 1,42 cm
3
. D. V ≈ 2,36 cm
3
.
Câu 41. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F
1
, F
2
là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
A. 4.766.000 đ. B. 4.656.000 đ.
C. 5.455.000 đ. D. 5.676.000 đ.
F
1
F
2
A
B
C D
Câu 42. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 860. B. 984. C. 720. D. 1228.
Câu 43. Cho hàm số y = f(x) có đạo hàm liên tục trên R. Biết hàm số y = f
0
(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử?
x
y
O
−1 1 3
A. 5. B. 3. C. 4. D. 6.
Câu 44. Cho hàm số y = f (x). Đồ thị hàm số y = f
0
(x) như hình bên.
Hàm số g(x) =
1
2
f(1−2x)
nghịch biến trên khoảng nào trong các khoảng
sau?
A. (−1; 0). B. (−∞; 0). C. (0; 1). D. (1; +∞).
x
y
O
−1 1 2 4
Câu 45. Cho hai số phức z
1
;z
2
thỏa mãn |z
1
+ 2 − i|+ |z
1
− 4 − 7i| = 6
√
2 và |iz
2
−1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z
1
+ z
2
|.
A.
√
2 + 1. B. 2
√
2 + 1. C.
√
2 − 1. D. 2
√
2 − 1.
Câu 46. Cho hàm số y = f(x) có đạo hàm liên tục trên [2; 4] và f
0
(x) > 0, ∀x ∈ [2; 4]. Biết 4x
3
f(x) =
[f
0
(x)]
3
− x
3
, ∀x ∈ [2; 4], f (2) =
7
4
. Giá trị f(4) bằng:
A.
20
√
5 − 1
4
. B.
40
√
5 − 1
2
. C.
40
√
5 − 1
4
. D.
20
√
5 − 1
2
.
Câu 47. Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm
số g(x) = f (4x − x
2
) +
1
3
x
3
− 3x
2
+ 8x +
1
3
trên đoạn [1;3].
Trang 5/6 − Mã đề 843
x
f
0
(x)
f(x)
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−3−3
55
−∞−∞
A. 15. B.
25
3
. C.
19
3
. D. 12.
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3),
D(2; 0;
√
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)
2
+ (y − 4)
2
+ z
2
= 39 thỏa mãn M A
2
+
2 ·
−−→
MB ·
−−→
MC = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó.
A. 2
√
7. B. 4
√
7. C.
√
7. D. 3
√
7.
Câu 49. Gọi m
0
là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của
đồ thị hàm số y = x
3
−6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
√
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
A. m
0
∈ (2; 3). B. m
0
∈ (0; 1). C. m
0
∈ (3; 4). D. m
0
∈ (1; 2).
Câu 50. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
có cạnh bằng a. Gọi E và F lần lượt là các điểm trên
các cạnh A
0
D
0
và A
0
B
0
sao cho A
0
E =
2
3
A
0
D
0
và A
0
F =
2
3
A
0
B
0
. Tính thể tích khối chóp A.BDEF .
A. V =
5a
3
18
. B. V =
3a
3
√
3
8
. C. V =
a
3
√
3
8
. D. V =
a
3
8
.
HẾT
Trang 6/6 − Mã đề 843
ĐÁP ÁN MÃ ĐỀ 843
1 B
2 C
3 A
4 A
5 D
6 D
7 B
8 A
9 C
10 C
11 D
12 B
13 B
14 B
15 C
16 B
17 C
18 A
19 C
20 C
21 B
22 C
23 C
24 C
25 B
26 C
27 D
28 D
29 B
30 A
31 B
32 D
33 C
34 A
35 D
36 D
37 B
38 C
39 C
40 C
41 D
42 B
43 A
44 D
45 D
46 C
47 D
48 A
49 B
50 A
Trang 1/1 −Đáp án mã đề 843
Trường THPT Chuyên Lê Hồng Phong
ĐỀ CHÍNH THỨC
(Đề thi có 6 trang)
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019
Môn: Toán - Lớp 12 - Khối ABCD
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 926
Câu 1. Cho hình lăng trụ đứng ABC.A
0
B
0
C
0
có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA
0
= 3a. Tính thể tích V của lăng trụ đó.
A. V = a
3
. B. V = 6a
3
. C. V = 3a
3
. D. V = 3a
2
.
Câu 2. Cho cấp số nhân (u
n
) có công bội q, số hạng đầu u
1
= −2 và số hạng thứ tư u
4
= 54. Giá trị
của q bằng
A. −6. B.
√
3. C. −3. D. 6.
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ
−→
a = (3; 2; 1),
−→
b = (−2; 0; 1). Độ dài
của véc-tơ
−→
a +
−→
b bằng
A. 1. B. 3. C.
√
2. D. 2.
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng?
x
f
0
(x)
f(x)
−∞
−1
2
+∞
+ −
0
+
−∞−∞
1 1
−2−2
+∞+∞
A. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2.
B. Giá trị cực đại của hàm số bằng 1.
C. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
D. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
Câu 5. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ?
A. z + 20 = 0. B. x − 2019 = 0. C. y + 5 = 0. D. 2x + 5y − 8z = 0.
Câu 6. Số phức liên hợp của số phức z = 5 + 6i là
A. z = 5 − 6i. B. z = −5 − 6i. C. z = 6 − 5i. D. z = −5 + 6i.
Câu 7. Tìm tập xác định D của hàm số y = (2 − x)
1
3
.
A. D = (−∞; 2) . B. D = (−∞; 2] . C. D = (−∞; +∞) . D. D = (2; +∞).
Câu 8. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả
cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng.
A.
3
14
. B.
2
5
. C.
1
35
. D.
3
7
.
Câu 9. Tập xác định của hàm số y =
2x − 1
2x − 4
là
A. D = R \ {2}. B. D = R \ {−2}. C. D = R \ {−4}. D. D = R \ {4}.
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC.
A. G(1; −2; −4). B. G(−1; 2; −4). C. G(1; −2; 4). D. G(3; −6; 12).
Câu 11. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng?
A. log(ab) = log a. log b. B. log
a
b
= log b −log a.
C. log
a
b
=
log a
log b
. D. log(ab) = log a + log b.
Trang 1/6 − Mã đề 926
Câu 12. Cho hàm số f(x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định
sai.
A.
b
Z
a
f(x) dx = −
a
Z
b
f(x) dx. B.
b
Z
a
f(x) dx = F (a) − F (b).
C.
b
Z
a
f(x) dx = F (b) − F (a). D.
a
Z
a
f(x) dx = 0.
Câu 13. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a
√
2 bằng
A.
πa
3
√
2
3
. B. 2πa
3
. C. πa
3
√
2. D. 4πa
3
√
2.
Câu 14. Cho hàm số y =
x
3
3
− x
2
+ x + 2019. Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho đồng biến trên R.
B. Hàm số đã cho nghịch biến trên (−∞; 1).
C. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
D. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1).
Câu 15. Viết phương trình tiếp tuyến của đồ thị hàm số y =
2x − 1
2x + 1
tại điểm có hoành độ x
0
= 0.
A. y = 4x. B. y = −4x + 1. C. y = 4x + 1. D. y = 4x − 1.
Câu 16. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền
ra.
A. 10 năm. B. 11 năm. C. 9 năm. D. 12 năm.
Câu 17. Cho
5
Z
0
f(x) dx = −2. Tích phân
5
Z
0
[4f( x) − 3x
2
] dx bằng
A. −133. B. −120. C. −130. D. −140.
Câu 18. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q): x − 2y + z − 5 = 0 và mặt cầu
(S): (x − 1)
2
+ y
2
+ (z + 2)
2
= 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây?
A. (2; −2; 1). B. (1; −2; 0). C. (−2; 2; −1). D. (0; −1; −5).
Câu 19. Cho hình phẳng giới hạn bởi các đường y =
√
x −2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành.
A. V =
5π
6
. B. V =
11π
6
. C. V =
7π
11
. D. V =
7
6
.
Câu 20.
Đường cong trong hình bên là đồ thị của hàm số nào?
A. y = x
4
+ 1. B. y = x
4
+ 2x
2
+ 1.
C. y = −x
4
+ 1. D. y = −x
4
+ 2x
2
+ 1.
x
y
O
−2 −1 1 2
−1
1
2
Câu 21. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là
A.
9π
8
. B.
9π
2
. C. 36π. D.
7π
√
14
3
.
Trang 2/6 − Mã đề 926
Câu 22. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f(x) = m có đúng hai nghiệm phân
biệt?
A. 2020. B. 2018. C. 4016. D. 2019.
Câu 23. Gọi z
1
và z
2
là hai nghiệm phức của phương trình z
2
+ 4z + 29 = 0. Tính giá trị biểu thức
|z
1
|
4
+ |z
2
|
4
.
A. 841. B. 58. C. 1682. D. 1282.
Câu 24.
Hàm số nào cho dưới đây có đồ thị như hình bên?
A. y = log
3
x. B. y = log
2
(x + 1).
C. y = log
2
x + 1. D. y = log
3
(x + 1).
O
x
1 2
y
1
2
−1
Câu 25. Cho bất phương trình 4
x
−5.2
x+1
+16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a
2
+ b
2
).
A. 2. B. 1. C. 0. D. 10.
Câu 26.
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f
0
(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau:
1) Hàm số y = f(x) có hai cực trị.
2) Hàm số y = f(x) đồng biến trên khoảng (1; +∞).
3) f(1) > f (2) > f (4).
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f(x) là f(1).
Số mệnh đề đúng trong bốn mệnh đề trên là:
A. 3. B. 1. C. 4. D. 2.
x
y
O
−1
1 4
y = f
0
(x)
Câu 27. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của
hình chóp đó.
A. h =
a
√
28
3
. B. h =
a
√
33
3
. C. h =
a
√
11
3
. D. V = h =
a
√
14
3
.
Câu 28.
Gọi z
1
, z
2
lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên.
Tính |z
1
+ z
2
|.
A. 2
√
29. B. 2
√
5. C. 20. D. 116.
x
y
O
3
M
2
1
N
−4
Trang 3/6 − Mã đề 926
Câu 29. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1)
là
A.
x − 3
−2
=
y − 3
−1
=
z − 1
2
. B.
x − 5
2
=
y − 4
1
=
z + 1
2
.
C.
x + 1
4
=
y + 2
2
=
z + 3
−4
. D.
x − 1
4
=
y − 2
2
=
z − 3
4
.
Câu 30. Họ nguyên hàm của hàm số f (x) = x
4
+ xe
x
là
A.
1
5
x
5
+ (x − 1)e
x
+ C. B.
1
5
x
5
+ xe
x
+ C.
C.
1
5
x
5
+ (x + 1)e
x
+ C. D. 4x
3
+ (x + 1)e
x
C.
Câu 31. Tập hợp các giá trị thực của tham số m để phương trình log
2019
(4−x
2
)+log
1
2019
(2x+m−1) =
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b.
A. 18. B. 8. C. 20. D. 16.
Câu 32. Trong không gian Oxyz, điểm M
0
đối xứng với điểm M(1; 2; 4) qua mặt phẳng
(α): 2x + y + 2z −3 = 0 có tọa độ là
A. (−1; −2; −4). B. (−3; 0; 0). C. (−1; 1; 2). D. (2; 1; 2).
Câu 33. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện.
A.
4a
√
6
3
. B.
3a
√
2
2
. C.
4a
√
3
3
. D.
a
√
3
2
.
Câu 34. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực.
Tính a + b.
A. 0. B. 4. C. z = −2. D. z = 2.
Câu 35. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x
4
− 8x
3
− 6x
2
+ 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S.
A. 42. B. 30. C. 50. D. 63.
Câu 36. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2).
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức
# »
IA − 2
# »
IB + 3
# »
IC
đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0
A. 9. B.
17
5
. C.
12
5
. D. 6.
Câu 37. Cho hàm số y =
x − 2
mx
2
− 2x + 4
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 0. B. 2. C. 3. D. 1.
Câu 38. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
√
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60
◦
chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm).
A. V ≈ 1,53 cm
3
. B. V ≈ 2,47 cm
3
. C. V ≈ 1,42 cm
3
. D. V ≈ 2,36 cm
3
.
Câu 39.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM.
A. −
2
5
. B.
1
2
. C.
2
5
. D.
4
5
.
S
A
B C
D
M
Trang 4/6 − Mã đề 926
Câu 40. Biết
4
Z
1
x
3
+ x
2
+ 7x + 3
x
2
− x + 3
dx =
a
b
+ c ln 5 với a, b, c là các số nguyên dương và
a
b
là phân số
tối giản. Tính P = a − b
2
− c
3
.
A. −5. B. 5. C. 0. D. −4.
Câu 41. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3),
D(2; 0;
√
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)
2
+ (y − 4)
2
+ z
2
= 39 thỏa mãn M A
2
+
2 ·
−−→
MB ·
−−→
MC = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó.
A.
√
7. B. 2
√
7. C. 3
√
7. D. 4
√
7.
Câu 42. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 1228. B. 720. C. 860. D. 984.
Câu 43. Cho hình lập phương ABCD.A
0
B
0
C
0
D
0
có cạnh bằng a. Gọi E và F lần lượt là các điểm trên
các cạnh A
0
D
0
và A
0
B
0
sao cho A
0
E =
2
3
A
0
D
0
và A
0
F =
2
3
A
0
B
0
. Tính thể tích khối chóp A.BDEF .
A. V =
3a
3
√
3
8
. B. V =
a
3
√
3
8
. C. V =
a
3
8
. D. V =
5a
3
18
.
Câu 44. Cho hàm số y = f(x) có đạo hàm liên tục trên [2; 4] và f
0
(x) > 0, ∀x ∈ [2; 4]. Biết 4x
3
f(x) =
[f
0
(x)]
3
− x
3
, ∀x ∈ [2; 4], f (2) =
7
4
. Giá trị f(4) bằng:
A.
20
√
5 − 1
4
. B.
40
√
5 − 1
2
. C.
20
√
5 − 1
2
. D.
40
√
5 − 1
4
.
Câu 45. Cho hàm số y = f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm
số g(x) = f (4x − x
2
) +
1
3
x
3
− 3x
2
+ 8x +
1
3
trên đoạn [1;3].
x
f
0
(x)
f(x)
−∞
0 4
+∞
−
0
+
0
−
+∞+∞
−3−3
55
−∞−∞
A.
25
3
. B. 15. C.
19
3
. D. 12.
Câu 46. Cho hàm số y = f (x). Đồ thị hàm số y = f
0
(x) như hình bên.
Hàm số g(x) =
1
2
f(1−2x)
nghịch biến trên khoảng nào trong các khoảng
sau?
A. (−∞; 0). B. (0; 1). C. (−1; 0). D. (1; +∞).
x
y
O
−1 1 2 4
Câu 47. Gọi m
0
là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của
đồ thị hàm số y = x
3
−6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
√
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
A. m
0
∈ (0; 1). B. m
0
∈ (3; 4). C. m
0
∈ (1; 2). D. m
0
∈ (2; 3).
Câu 48. Cho hàm số y = f(x) có đạo hàm liên tục trên R. Biết hàm số y = f
0
(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử?
Trang 5/6 − Mã đề 926
x
y
O
−1 1 3
A. 6. B. 5. C. 4. D. 3.
Câu 49. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F
1
, F
2
là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).
A. 5.676.000 đ. B. 4.656.000 đ.
C. 4.766.000 đ. D. 5.455.000 đ.
F
1
F
2
A
B
C D
Câu 50. Cho hai số phức z
1
;z
2
thỏa mãn |z
1
+ 2 − i|+ |z
1
− 4 − 7i| = 6
√
2 và |iz
2
−1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z
1
+ z
2
|.
A. 2
√
2 + 1. B.
√
2 − 1. C. 2
√
2 − 1. D.
√
2 + 1.
HẾT
Trang 6/6 − Mã đề 926
ĐÁP ÁN MÃ ĐỀ 926
1 C
2 C
3 B
4 C
5 D
6 A
7 A
8 D
9 A
10 C
11 D
12 B
13 C
14 A
15 D
16 B
17 A
18 C
19 B
20 D
21 D
22 D
23 C
24 B
25 B
26 D
27 B
28 B
29 A
30 A
31 D
32 B
33 A
34 A
35 A
36 D
37 D
38 C
39 C
40 D
41 B
42 D
43 D
44 D
45 D
46 D
47 A
48 B
49 A
50 C
Trang 1/1 −Đáp án mã đề 926
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 1 Mã đề 638
ĐỀ 8 TUẦN HKII
TRƯỜNG CHUYÊN LÊ HỒNG PHONG NĂM 2019
MÔN TOÁN
THỜI GIAN: 90 PHÚT
Bản quyền thuộc về tập thể thầy cô nhóm STRONG.
Tổng biên tập tài liệu: Admin Lưu Thêm
Gv THPT Yên Phong 1 - Bắc Ninh
Câu 1: [2H2-2.3-1] Thể tích khối trụ có bán kính đáy
ra=
và chiều cao
2ha=
bằng
A.
3
42a
. B.
. C.
3
2 a
. D.
3
2
3
a
.
Câu 2: [1D2-4.3-2] Một hộp đựng
6
quả cầu màu trắng và
4
quả cầu màu vàng. Lấy ngẫu nhiên từ
hộp ra
4
quả cầu. Tính xác suất để trong
4
quả cầu lấy được có đúng
2
quả cầu vàng.
A.
3
14
. B.
1
35
. C.
3
7
. D.
2
5
.
Câu 3: [2D1-2.3-1] Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
2x =
và không có điểm cực đại.
B. Hàm số đạt cực tiểu tại
1x =−
và đạt cực đại tại
2x =
.
C. Hàm số đạt cực đại tại
1x =−
và đạt cực tiểu tại
2x =
.
D. Giá trị cực đại của hàm số bằng 1.
Câu 4: [2H3-1.1-1] Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
0;2;5A
,
( )
2;0;1B −
,
( )
5; 8;6C −
. Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
( )
3; 6;12G −
. B.
( )
1; 2; 4G −−
. C.
( )
1;2; 4G −−
. D.
( )
1; 2;4G −
.
Câu 5: [2D4-1.3-1] Số phức liên hợp của số phức
56zi=+
là
A.
56zi= − +
. B.
56zi= − −
. C.
65zi=−
. D.
56zi=−
.
Câu 6: [1D3-4.2-1] Cho cấp số nhân
( )
n
u
có công bội
q
, số hạng đầu
1
2u =−
và số hạng thứ tư
4
54u =
. Giá trị của
q
bằng
A.
3
. B.
6−
. C.
6
. D.
3−
.
Câu 7: [2H3-3.4-1] Trong không gian
Oxyz
, mặt phẳng nào dưới đây đi qua gốc tọa độ?
A.
50y +=
. B.
20 0z +=
. C.
2019 0x−=
. D.
2 5 8 0x y z+ − =
.
Câu 8:
[2D1-1.0-1] Tập xác định của hàm số
21
24
x
y
x
−
=
−
là
A.
\2D =
. B.
\4D =−
. C.
\4D =
. D.
\2D =−
.
+
+
f(x)
2
1
1
∞
+
∞
0
2
1
+
∞
∞
f
/
(x)
x
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 2 Mã đề 638
Câu 9: [2D2-3.2-1] Với các số thực dương
a
,
b
bất kì. Mệnh đề nào sau đây đúng?
A.
( )
log log .logab a b=
. B.
log log log
a
ba
b
=−
.
C.
log
log
log
aa
bb
=
. D.
( )
log log logab a b=+
.
Câu 10: [2H1-3.1-1] Cho hình lăng trụ đứng
' ' '
.ABC A BC
có đáy là tam giác vuông tại
,A
,AB a=
2,AC a=
'
3AA a=
. Tính thể tích của khối lăng trụ đó.
A.
3
3Va=
. B.
2
3Va=
. C.
3
Va=
. D.
3
6Va=
.
Câu 11: [2H3-1.1-1] Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( )
3;2;1a =
,
( )
2;0;1b =−
. Độ
dài của vectơ
ab+
bằng
A.
2
. B.
1
. C.
2
. D.
3
.
Câu 12: [2D2-2.1-1] Tìm tập xác định
D
của hàm số
( )
1
3
2yx=−
.
A.
(
;2D = −
. B.
( )
2;D = +
. C.
( )
;2D = −
. D.
( )
;D = − +
.
Câu 13: [2D3-3.1-1] Cho hàm số
( )
fx
liên tục trên đoạn
;ab
và
( )
Fx
là một nguyên hàm của hàm
( )
fx
. Tìm khẳng định sai.
A.
( )
d0
a
a
f x x =
. B.
( ) ( ) ( )
d
b
a
f x x F b F a=−
.
C.
( ) ( )
d d .
ba
ab
f x x f x x=−

. D.
( ) ( ) ( )
d
b
a
f x x F a F b=−
.
Câu 14: [2H2-3.5-1] Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước
1
,
2
,
3
là
A.
36
. B.
9
2
. C.
7 14
3
. D.
9
8
.
Câu 15: [2D1-7.1-1] Viết phương trình tiếp tuyến của đồ thị hàm số
21
21
x
y
x
−
=
+
tại điểm có hoành độ
0
0x =
.
A.
41yx= − +
. B.
41yx=+
. C.
4yx=
. D.
41yx=−
.
Câu 16: [2D2-4.7-1] Hàm số nào sau đây có đồ thị như hình bên?
A.
3
logyx=
. B.
2
log 1yx=+
. C.
( )
2
log 1yx=+
. D.
( )
3
log 1yx=+
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 3 Mã đề 638
Câu 17: [2D1-1.4-1] Cho hàm số
3
2
2019
3
x
y x x= − + +
. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho đồng biến trên .
B. Hàm số đã cho đồng biến trên
( )
;1−
và nghịch biến trên
( )
1; +
.
C. Hàm số đã cho đồng biến trên
( )
1; +
và nghịch biến trên
( )
;1−
.
D. Hàm số đã cho nghịch biến trên
( )
;1−
.
Câu 18: [2D4-1.4-2] Gọi
1
z
,
2
z
lần lượt có điểm biểu diễn là
M
và
N
trên mặt phẳng phức ở hình bên.
Tính
12
zz+
.
A.
2 29
. B.
20
. C.
25
. D.
116
.
Câu 19: [2D2-5.3-2] Cho bất phương trình
1
4 5.2 16 0
xx+
− +
có tập nghiệm là đoạn
;ab
. Tính
( )
22
log ab+
.
A.
2
. B.
1
. C.
0
. D.
10
.
Câu 20: [2D4-1.4-2] Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
4 29 0zz+ + =
.Tính giá trị của
biểu thức
44
12
zz+
.
A.
841
. B.
1682
. C.
1282
. D.
58
.
Câu 21: [2D1-5.4-2] Cho hàm số
( )
y f x=
có đạo hàm liên tục trên . Hàm số
( )
y f x
=
có đồ thị
như hình vẽ dưới đây:
Cho bốn mệnh đề sau:
1) Hàm số
( )
y f x=
có hai điểm cực trị.
2) Hàm số
( )
y f x=
đồng biến trên khoảng
( )
1; +
.
3)
( ) ( ) ( )
1 2 4f f f
.
4) Trên đoạn
1;4−
, giá trị lớn nhất của hàm số
( )
y f x=
là
( )
1f
.
x
y
-4
3
2
O
1
M
N
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 4 Mã đề 638
Số mệnh đề đúng trong bốn mệnh đề trên là:
A.
1
. B.
4
. C.
2
. D.
3
.
Câu 22: [2D3-3.3-2] Cho
( )
5
0
d2f x x =−
. Tích phân
( )
5
2
0
4 3 df x x x

−

bằng
A.
140−
. B.
130−
. C.
120−
. D.
133−
.
Câu 23: [2D3-3.3-2] Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như hình
sau:
Có bao nhiêu giá trị nguyên
2019;2019m−
để phương trình
( )
f x m=
có hai nghiệm phân
biệt.
A.
2018
. B.
4016
. C.
2019
. D.
2020
.
Câu 24: [2D2-4.8-2] Một người gửi
300
triệu đồng vào một ngân hàng với lãi suất
7%/
năm. Biết rằng
nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính
lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn
600
triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và
người đó không rút tiền ra.
A.
9
năm. B.
10
năm. C.
11
năm. D.
12
năm.
Câu 25: [2D3-5.9-2] Cho hình phẳng giới hạn bởi các đường
2yx=−
,
0y =
và
9x =
quay xung
quanh trục
Ox
. Tính thể tích khối tròn xoay tạo thành.
A.
7
6
V =
. B.
5
6
V
=
. C.
7
11
V
=
. D.
11
6
V
=
.
Câu 26: [2D3-1.3-2] Họ nguyên hàm của hàm số
( )
4
e
x
f x x x=+
là
A.
( )
5
1
1e
5
x
x x C+ + +
. B.
( )
5
1
1e
5
x
x x C+ − +
. C.
5
1
e
5
x
x x C++
. D.
( )
3
4 1 e
x
x x C+ + +
.
Câu 27: [2H3-5.2-2] Trong không gian
Oxyz
, phương trình đường thẳng đi qua hai điểm
( )
1;2;3A
và
( )
5;4; 1B −
là
A.
5 4 1
2 1 2
x y z− − +
==
. B.
1 2 3
4 2 4
x y z+ + +
==
−
.
C.
1 2 3
4 2 4
x y z− − −
==
. D.
3 3 1
2 1 2
x y z− − −
==
−−
.
Câu 28: [2H1-2.3-2] Cho hình chóp tam giác đều có cạnh đáy bằng
a
, cạnh bên
2a
. Tính chiều cao
h
của hình chóp đó
A.
28
3
a
h =
. B.
14
3
a
h =
. C.
33
3
a
h =
. D.
11
3
a
h =
.
Câu 29: [2D1-5.6-1] Đường cong trong hình bên là đồ thị của hàm số nào?
x
−
1−
0
1
+
( )
'fx
+
0
−
0
+
0
−
( )
fx
−
3
1−
3
−
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 5 Mã đề 638
A.
4
1yx= − +
. B.
42
21y x x= + +
. C.
4
1yx=+
. D.
42
21y x x= − + +
.
Câu 30: [2H3-3.6-2] Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
( )
: 2 5 0Q x y z− + − =
và
mặt cầu
( ) ( ) ( )
22
2
: 1 2 15S x y z− + + + =
. Mặt phẳng
( )
P
song song với mặt phẳng
( )
Q
và cắt
mặt cầu
( )
S
theo giao tuyến là một đường tròn có chu vi bằng
6
đi qua điểm nào sau đây?
A.
( )
2; 2;1−
. B.
( )
1; 2;0−
. C.
( )
0; 1; 5−−
. D.
( )
2;2; 1−−
.
Câu 31: [2D2-6.2-3] Tập hợp các giá trị thực của tham số
m
để phương trình
( )
( )
2
2019 1
2019
log 4 log 2 1 0x x m− + + − =
có hai nghiệm thực phân biệt là
( )
;T a b=
. Tính
2S a b=+
.
A. 20. B. 8. C. 18. D. 16.
Câu 32: [2D1-4.7-2] Cho hàm số
2
2
24
x
y
mx x
−
=
−+
. Có tất cả bao nhiêu giá trị của tham số
m
để đồ thị
hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 1. B. 3. C. 0. D. 2.
Câu 33: [2D1-2.7-3] Gọi
S
là tập hợp các giá trị nguyên
m
để đồ thị hàm số
4 3 2
3 8 6 24y x x x x m= − − + −
có
7
điểm cực trị. Tính tổng các phần tử của
S
.
A.
42
. B.
50
. C.
30
. D.
63
.
Câu 34: [1H3-2.4-2] ] Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh là
2a
; cạnh
SA a=
và vuông
góc với đáy. Gọi
M
là trung điểm của
CD
. Tính
cos
với
là góc tạo bởi hai đường thẳng
SB
và
AM
.
A.
2
5
. B.
1
2
. C.
4
5
. D.
2
5
−
.
Câu 35: [2H1-4.2-3] Cho hình bát diện đều có cạnh
a
và điểm
I
nằm trong hình bát diện. Tính tổng
khoảng cách từ
I
đến tất cả các mặt của bát diện.
A.
46
3
a
. B.
32
2
a
. C.
43
3
a
. D.
3
2
a
.
Câu 36: [2H2-1.4-3] Một khối nón có bán kính đáy bằng
2 cm
, chiều cao bằng
3cm
. Một mặt phẳng
đi qua đỉnh và tạo với đáy một góc
0
60
chia khối nón làm
2
phần. Tính thể tích
V
phần nhỏ
hơn (Tính gần đúng đến hàng phần trăm).
A.
3
1,42cmV
. B.
3
2,36cmV
. C.
3
1,53cmV
. D.
3
2,47cmV
.
Câu 37: [2H3-6.17-2] Trong không gian
Oxyz
, điểm
M
đối xứng với điểm
( )
1;2;4M
qua mặt phẳng
( )
:2 2 3 0x y z
+ + − =
có tọa độ là
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 6 Mã đề 638
A.
( )
3;0;0−
. B.
( )
1;1;2−
. C.
( )
1; 2; 4− − −
. D.
( )
2;1;2
.
Câu 38: [2H3-6.18-3] Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1;2;5A −
,
( )
3; 1;0B −
,
( )
4;0; 2C −−
. Gọi
I
là điểm trên mặt phẳng
( )
Oxy
sao cho biểu thức
23IA IB IC−+
đạt giá
trị nhỏ nhất. Tính khoảng cách từ
I
đến mặt phẳng
( )
:4 3 2 0P x y+ + =
.
A.
17
5
. B.
6
. C.
12
5
. D.
9
.
Câu 39: [2D4-1.4-3] Cho số phức
z a bi=+
( )
,ab
thỏa mãn
31zz− = −
và
( )
( )
2z z i+−
là số
thực. Tính
ab+
.
A.
2−
. B. 0. C. 2. D. 4.
Câu 40: [2D3-4.3-3] Biết
4
32
2
1
73
d ln5
3
x x x a
xc
x x b
+ + +
=+
−+
với
a
,
b
,
c
là các số nguyên dương và
a
b
là
phân số tối giản. Tính
23
P a b c= − −
.
A.
5−
. B.
4−
. C. 5. D. 0.
Câu 41: [2D3-4.12-3] Cho hàm số
( )
y f x=
có đạo hàm liên tục trên
2;4
và
( )
0, 2;4f x x
.
Biết
( ) ( )
( )
3
33
7
4 , 2;4 , 2
4
x f x f x x x f
= − =


. Giá trị của
( )
4f
bằng
A.
40 5 1
2
−
. B.
20 5 1
4
−
. C.
20 5 1
2
−
. D.
40 5 1
4
−
.
Câu 42: [2D1-1.3-3] Cho hàm số
( )
y f x=
có đạo hàm liên tục trên . Biết hàm số
( )
y f x
=
có đồ
thị như hình vẽ. Gọi
S
là tập hợp các giá trị nguyên
5;5m −
để hàm số
( ) ( )
g x f x m=+
nghịch biến trên khoảng
( )
1;2
. Hỏi
S
có bao nhiêu phần tử?
A.
4
. B.
3
. C.
6
. D.
5
.
Câu 43: [2D1-3.1-3] Cho hàm số
( )
y f x=
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất
của hàm số
( )
( )
2 3 2
11
4 3 8
33
g x f x x x x x= − + − + +
trên đoạn
1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 7 Mã đề 638
Câu 44: [2H3-2.13-3] Trong không gian với hệ tọa độ
Oxyz
cho bốn điểm
(1;0;0)A
,
(2;1;3)B
,
(0;2; 3)C −
,
(2;0; 7)D
. Gọi
M
là điểm thuộc mặt cầu
2 2 2
( ) : ( 2) ( 4) 39S x y z+ + − + =
thỏa
mãn:
2
2 . 8MA MB MC+=
. Biết độ dài đoạn thẳng
MD
đạt giá trị lớn nhất. Tính giá trị lớn nhất
đó.
A.
27
. B.
7
. C.
37
. D.
47
.
Câu 45: [2D1-1.4-3] Cho hàm số
( )
y f x=
. Đồ thị
( )
y f x
=
như hình bên. Hàm số
( )
( )
12
1
2
fx
gx
−

=


nghịch biến trên khoảng nào trong các khoảng sau?
A.
( )
0;1
. B.
( )
;0−
. C.
( )
1;0−
. D.
( )
1;+
.
Câu 46: [2D3-5.13-3] Nhà trường dự định làm một vườn hoa dạng elip được chia ra làm bốn phần bởi
hai đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ
dài trục lớn, trục nhỏ của elip lần lượt là
8
m
và
4
m
,
1
,F
2
F
là hai tiêu điểm của elip. Phần
A
,
B
dùng để trồng hoa, phần
C
,
D
dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa
và cỏ lần lượt là
250.000
đ và
150.000
đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm
tròn đến hàng nghìn).
A.
5.676.000
đ. B.
4.766.000
đ. C.
4.656.000
đ. D.
5.455.000
đ.
Câu 47: [2H1-2.5-3] Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
. Gọi
E
và
F
lần lượt là
các điểm trên các cạnh
AD

và
AB

sao cho
2
3
A E A D
=
và
2
3
A F A B
=
. Tính thể tích
khối chóp
.A BDEF
.
A.
3
3
8
a
. B.
3
5
18
a
. C.
3
8
a
. D.
3
33
8
a
.
Câu 48: [2D4-4.1-4] Cho hai số phức
12
,zz
thoả mãn
11
2 4 7 6 2z i z i+ − + − − =
và
2
1 2 1iz i− + =
.
Tìm giá trị nhỏ nhất của biểu thức
12
T z z=+
.
A.
21−
. B.
21+
. C.
2 2 1+
. D.
2 2 1−
.
Câu 49: [1D2-2.2-4] Từ các chữ số thuộc tập
0;1;2;3;4;5;6;7X =
có thể lập được bao nhiêu số tự
nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 720. B. 860. C. 984. D. 1228.
Câu 50: [2D1-2.11-4] Gọi
0
m
là giá trị của tham số
m
để đường thẳng đi qua điểm cực đại và cực tiểu
của đồ thị hàm số
3
64y x mx= − +
cắt đường tròn tâm
( )
1;0I
, bán kính bằng
2
tại hai điểm
phân biệt
A
,
B
sao cho diện tích tam giác
IAB
đạt giá trị lớn nhất. Mệnh đề nào sau đây
đúng:
A.
( )
0
2;3m
. B.
( )
0
3;4m
. C.
( )
0
0;1m
. D.
( )
0
1;2m
.
HẾT
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 8 Mã đề 638
BẢNG ĐÁP ÁN
1.B
2.C
3.A
4.D
5.D
6.D
7.D
8.A
9.D
10.A
11.D
12.C
13.D
14.C
15.D
16.C
17.A
18.C
19.B
20.B
21.C
22.D
23.C
24.C
25.D
26.B
27.D
28.C
29.D
30.D
31.D
32.A
33.A
34.A
35.A
36.A
37.A
38.B
39.B
40.B
41.D
42.D
43.D
44.A
45.D
46.A
47.B
48.D
49.C
50.C
GIẢI CHI TIẾT ĐỀ 8 TUẦN HKII
TRƯỜNG CHUYÊN LÊ HỒNG PHONG NĂM 2019
MÔN TOÁN
THỜI GIAN: 90 PHÚT
Huyenmi232@gmail.com.
Câu 1: [2H2-2.3-1] Thể tích khối trụ có bán kính đáy
ra=
và chiều cao
2ha=
bằng
A.
3
42a
. B.
. C.
3
2 a
. D.
3
2
3
a
.
Lời giải
Tác giả: Nguyễn Huyền; Fb:Huyen Nguyen
Chọn B
Thể tích khối trụ là:
2
V r h
=
2
. . 2aa
=
3
2a
=
.
Câu 2: [1D2-4.3-2] Một hộp đựng
6
quả cầu màu trắng và
4
quả cầu màu vàng. Lấy ngẫu nhiên từ
hộp ra
4
quả cầu. Tính xác suất để trong
4
quả cầu lấy được có đúng
2
quả cầu vàng.
A.
3
14
. B.
1
35
. C.
3
7
. D.
2
5
.
Lời giải
Tác giả: Nguyễn Huyền; Fb: Huyen Nguyen
Chọn C
Chọn
4
quả cầu từ
10
quả cầu có
4
10
C
(cách )
( )
4
10
nC =
.
Gọi
A
là biến cố “
4
quả cầu lấy được có đúng
2
quả màu vàng”.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 9 Mã đề 638
Chọn
4
quả cầu trong đó có đúng
2
quả màu vàng có
22
46
.CC
(cách)
( )
22
46
.n A C C=
.
Xác suất của biến cố
A
là:
( )
( )
( )
nA
PA
n
=
22
46
4
10
.CC
C
=
3
7
=
.
Câu 3: [2D1-2.3-1] Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
2x =
và không có điểm cực đại.
B. Hàm số đạt cực tiểu tại
1x =−
và đạt cực đại tại
2x =
.
C. Hàm số đạt cực đại tại
1x =−
và đạt cực tiểu tại
2x =
.
D. Giá trị cực đại của hàm số bằng 1.
Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức
Chọn A
Từ bảng biến thiên ta có:
+) Hàm số
( )
y f x=
có tập xác định là
\1DR=−
. Suy ra hàm số không đạt cực trị tại
1x =−
. Do đó các mệnh đề ở đáp án
B
và
C
là các mệnh đề sai.
+) Hàm số không có điểm cực đại nên không có giá trị cực đại bằng
1
. Do đó mệnh đề ở đáp án
D
là mệnh đề sai.
+) Tại
2x =
thì
( )
'0fx=
và đổi dấu từ âm sang dương nên
2x =
là điểm cực tiểu của hàm số
và dễ thấy hàm số không có điểm cực đại. Suy ra mệnh để ở đáp án
A
đúng.
Vậy mệnh đề của đáp án
A
là đúng.
Câu 4: [2H3-1.1-1] Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
0;2;5A
,
( )
2;0;1B −
,
( )
5; 8;6C −
. Tìm tọa độ trọng tâm
G
của tam giác
ABC
.
A.
( )
3; 6;12G −
. B.
( )
1; 2; 4G −−
. C.
( )
1;2; 4G −−
. D.
( )
1; 2;4G −
.
Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức
Chọn D
Gọi
( )
;;
G G G
G x y z
là trọng tâm của tam giác
ABC
.
+
+
f(x)
2
1
1
∞
+
∞
0
2
1
+
∞
∞
f
/
(x)
x
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 10 Mã đề 638
Công thức tọa độ trọng tâm
G
của tam giác
ABC
là:
3
3
3
A B C
G
A B C
G
A B C
G
xxx
x
yyy
y
zzz
x
++
=
++
=
++
=
1
2
4
G
G
G
x
y
x
=
= −
=
Vậy
( )
1; 2;4G −
.
Câu 5: [2D4-1.3-1] Số phức liên hợp của số phức
56zi=+
là
A.
56zi= − +
. B.
56zi= − −
. C.
65zi=−
. D.
56zi=−
.
Lời giải
Tác giả: Võ Thanh Hải; Fb: Võ Thanh Hải
Chọn D
Số phức liên hợp của số phức
z x yi=+
,
,xy
là số phức
z x yi=−
. Do đó số phức liên
hợp của số phức
56zi=+
là
56zi=−
.
Câu 6: [1D3-4.2-1] Cho cấp số nhân
( )
n
u
có công bội
q
, số hạng đầu
1
2u =−
và số hạng thứ tư
4
54u =
. Giá trị của
q
bằng
A.
3
. B.
6−
. C.
6
. D.
3−
.
Lời giải
Tác giả: Võ Thanh Hải; Fb: Võ Thanh Hải
Chọn D
Với cấp số nhân
( )
n
u
có công bội
q
ta có:
3 3 3
4
41
1
. 27 3
u
u u q q q q
u
= = = − = −
.
Câu 7: [2H3-3.4-1] Trong không gian
Oxyz
, mặt phẳng nào dưới đây đi qua gốc tọa độ?
A.
50y +=
. B.
20 0z +=
. C.
2019 0x−=
. D.
2 5 8 0x y z+ − =
.
Lời giải
Tác giả:Nguyễn Văn Diệu; Fb:dieuptnguyen
Chọn D
Phương trình tổng quát của mặt phẳng có dạng
Ax 0By Cz D+ + + =
, trong đó
A
,
B
,
C
không
đồng thời bằng
0
.
Nếu
0D =
thì mặt phẳng đi qua gốc tọa độ. Từ đó ta chọn đáp án
D
.
Câu 8:
[2D1-1.0-1] Tập xác định của hàm số
21
24
x
y
x
−
=
−
là
A.
\2D =
. B.
\4D =−
. C.
\4D =
. D.
\2D =−
.
Lời giải
Tác giả:Nguyễn Văn Diệu; Fb:dieuptnguyen
Chọn A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 11 Mã đề 638
Hàm số
21
24
x
y
x
−
=
−
xác định khi và chỉ khi
2 4 0x −
2x
.
Vậy tập xác định của hàm số đã cho là
\2D =
.
Câu 9: [2D2-3.2-1] Với các số thực dương
a
,
b
bất kì. Mệnh đề nào sau đây đúng?
A.
( )
log log .logab a b=
. B.
log log log
a
ba
b
=−
.
C.
log
log
log
aa
bb
=
. D.
( )
log log logab a b=+
.
Lời giải
Tác giả: Nguyễn Thị Phương; Fb: Hộp Thư
Chọn D
Với các số thực dương
a
,
b
bất kì ta có:
)log log log
a
ab
b
−+ =
nên B, C sai.
( )
)log log logab a b++ =
nên A sai, D đúng.
Vậy chọn D.
Câu 10: [2H1-3.1-1] Cho hình lăng trụ đứng
' ' '
.ABC A BC
có đáy là tam giác vuông tại
,A
,AB a=
2,AC a=
'
3AA a=
. Tính thể tích của khối lăng trụ đó.
A.
3
3Va=
. B.
2
3Va=
. C.
3
Va=
. D.
3
6Va=
.
Lời giải
Tác giả: Nguyễn Thị Phương; Fb: Hộp Thư
Chọn A
Vì
( )
'AA ABC⊥
nên thể tích của khối lăng trụ
' ' '
.ABC AB C
là
3
11
'. '. . . 3 . .2 3 .
22
ABC
V AA S AA AB AC a a a a= = = =
Câu 11: [2H3-1.1-1] Trong không gian với hệ tọa độ
Oxyz
, cho hai vectơ
( )
3;2;1a =
,
( )
2;0;1b =−
. Độ
dài của vectơ
ab+
bằng
A.
2
. B.
1
. C.
2
. D.
3
.
Lời giải
Tác giả: Trần Quốc Khang; Fb: BiTran
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 12 Mã đề 638
Chọn D
Ta có
( )
1;2;2ab+=
1 4 4 3ab + = + + =
.
Câu 12: [2D2-2.1-1] Tìm tập xác định
D
của hàm số
( )
1
3
2yx=−
.
A.
(
;2D = −
. B.
( )
2;D = +
. C.
( )
;2D = −
. D.
( )
;D = − +
.
Lời giải
Tác giả: Trần Quốc Khang; Fb: BiTran
Chọn C
ĐKXĐ:
2 0 2xx−
. Suy ra TXĐ:
( )
;2D = −
.
Câu 13: [2D3-3.1-1] Cho hàm số
( )
fx
liên tục trên đoạn
;ab
và
( )
Fx
là một nguyên hàm của hàm
( )
fx
. Tìm khẳng định sai.
A.
( )
d0
a
a
f x x =
. B.
( ) ( ) ( )
d
b
a
f x x F b F a=−
.
C.
( ) ( )
d d .
ba
ab
f x x f x x=−

. D.
( ) ( ) ( )
d
b
a
f x x F a F b=−
.
Lời giải
Tác giả:Nguyễn Tuyết Lê; Fb: Nguyen Tuyet Le.
Chọn D
Theo định nghĩa tích phân ta có:
( ) ( ) ( )
d
b
a
f x x F b F a=−
. Đáp án B đúng, D sai.
( )
d
a
a
f x x
( ) ( )
0F a F a=−=
. Đáp án A đúng.
( )
d
b
a
f x x
( ) ( )
F b F a=−
( )
d
a
b
f x x=−
. Đáp án C đúng.
Câu 14: [2H2-3.5-1] Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước
1
,
2
,
3
là
A.
36
. B.
9
2
. C.
7 14
3
. D.
9
8
.
Lời giải
Tác giả:Nguyễn Tuyết Lê; Fb: Nguyen Tuyet Le.
Chọn C
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 13 Mã đề 638
Gọi
R
là bán kính khối cầu ngoại tiếp hình hộp chữ nhật.
Ta có
1
2
R BD
=
2 2 2
1
1 2 3
2
= + +
14
2
=
.
Vậy thể tích khối cầu là:
3
4
3
VR
=
3
4 14
32

==



7 14
3
.
Câu 15: [2D1-7.1-1] Viết phương trình tiếp tuyến của đồ thị hàm số
21
21
x
y
x
−
=
+
tại điểm có hoành độ
0
0x =
.
A.
41yx= − +
. B.
41yx=+
. C.
4yx=
. D.
41yx=−
.
Lời giải
Tác giả: Trần Bạch Mai; Fb: Bạch Mai
Chọn D
Ta có:
( )
( )
2
4
04
21
yy
x

= =
+
;
( )
01y =−
.
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ
0
0x =
:
( )( ) ( )
0 0 0 4 1y y x y y x
= − + = −
.
Vậy phương trình tiếp tuyến cần tìm là:
41yx=−
.
Câu 16: [2D2-4.7-1] Hàm số nào sau đây có đồ thị như hình bên?
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 14 Mã đề 638
A.
3
logyx=
. B.
2
log 1yx=+
. C.
( )
2
log 1yx=+
. D.
( )
3
log 1yx=+
Lời giải
Tác giả: Bạch Mai; Fb: Bạch Mai
Chọn C
Đồ thị hàm số đi qua điểm
( )
0;0
nên loại đáp án A và B.
Đồ thị hàm số đi qua điểm
( )
1;1
nên loại D.
Vậy đáp án C thỏa mãn.
Câu 17: [2D1-1.4-1] Cho hàm số
3
2
2019
3
x
y x x= − + +
. Mệnh đề nào sau đây đúng?
A. Hàm số đã cho đồng biến trên .
B. Hàm số đã cho đồng biến trên
( )
;1−
và nghịch biến trên
( )
1; +
.
C. Hàm số đã cho đồng biến trên
( )
1; +
và nghịch biến trên
( )
;1−
.
D. Hàm số đã cho nghịch biến trên
( )
;1−
.
Lời giải
Tác giả: LêHoa; Fb:LêHoa
Chọn A
Tập xác định:
D =
.
Ta có
( )
2
'2
2 1 1 0y x x x= − + = −
với
x
, đẳng thức xảy ra tại
1x =
.
Vậy hàm số đã cho đồng biến trên .
Câu 18: [2D4-1.4-2] Gọi
1
z
,
2
z
lần lượt có điểm biểu diễn là
M
và
N
trên mặt phẳng phức ở hình bên.
Tính
12
zz+
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 15 Mã đề 638
A.
2 29
. B.
20
. C.
25
. D.
116
.
Lời giải
Tác giả: LêHoa; Fb:LêHoa
Chọn C
Từ hình bên ta có tọa độ
( )
3;2M
biểu diễn số phức
1
32zi=+
.
Tọa độ
( )
1; 4N −
biểu diễn
2
14zi=−
.
Ta có
12
42z z i+ = −
( ) ( )
22
12
4 2 2 5zz+ = + − =
.
Câu 19: [2D2-5.3-2] Cho bất phương trình
1
4 5.2 16 0
xx+
− +
có tập nghiệm là đoạn
;ab
. Tính
( )
22
log ab+
.
A.
2
. B.
1
. C.
0
. D.
10
.
Lời giải
Tác giả:Vũ Thị Thúy; Fb: Vũ Thị Thúy
Chọn B
Bất phương trình
1
4 5.2 16 0
xx+
− +
4 10.2 16 0 2 2 8
x x x
− +
13x
.
Vậy tập nghiệm của bất phương trình là
1;3
.
Suy ra
1; 3ab==
nên
( ) ( )
2 2 2 2
log log 1 3 1ab+ = + =
.
Câu 20: [2D4-1.4-2] Gọi
1
z
và
2
z
là hai nghiệm phức của phương trình
2
4 29 0zz+ + =
.Tính giá trị của
biểu thức
44
12
zz+
.
A.
841
. B.
1682
. C.
1282
. D.
58
.
Lời giải
Tác giả:Vũ Thị Thúy; Fb: Vũ Thị Thúy
Chọn B
Phương trình
( ) ( ) ( )
2 2 2
1
2
2
25
4 29 0 2 25 2 5
25
zi
z z z z i
zi
= − −
+ + = + = − + =
= − +
.
x
y
-4
3
2
O
1
M
N
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 16 Mã đề 638
Suy ra
( )
2
2
12
2 5 29zz= = − + =
.
Vậy
( ) ( )
44
44
12
29 29 1682zz+ = + =
.
Câu 21: [2D1-5.4-2] Cho hàm số
( )
y f x=
có đạo hàm liên tục trên . Hàm số
( )
y f x
=
có đồ thị
như hình vẽ dưới đây:
Cho bốn mệnh đề sau:
1) Hàm số
( )
y f x=
có hai điểm cực trị.
2) Hàm số
( )
y f x=
đồng biến trên khoảng
( )
1; +
.
3)
( ) ( ) ( )
1 2 4f f f
.
4) Trên đoạn
1;4−
, giá trị lớn nhất của hàm số
( )
y f x=
là
( )
1f
.
Số mệnh đề đúng trong bốn mệnh đề trên là:
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc
Chọn C
Từ đồ thị của hàm số
( )
y f x
=
ta có bảng biến thiên của hàm số
( )
y f x=
như sau:
Khi đó dựa vào bảng biến thiên ta thấy:
+) Hàm số có ba điểm cực trị nên mệnh đề 1) sai.
+) Hàm số đồng biến trên các khoảng
( )
1;1−
và
( )
4; +
nên mệnh đề 2) sai.
+) Hàm số nghịch biến trên khoảng
( )
1;4
nên
( ) ( ) ( )
1 2 4f f f
suy ra mệnh đề 3) đúng.
+) Trên đoạn
1;4−
, giá trị lớn nhất của hàm số
( )
y f x=
là
( )
1f
suy ra mệnh đề 4) đúng.
Vậy có tất cả
2
mệnh đề đúng.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 17 Mã đề 638
Câu 22: [2D3-3.3-2] Cho
( )
5
0
d2f x x =−
. Tích phân
( )
5
2
0
4 3 df x x x

−

bằng
A.
140−
. B.
130−
. C.
120−
. D.
133−
.
Lời giải
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc
Chọn D
( ) ( )
5 5 5
5
2 2 3
0
0 0 0
4 3 d 4 d 3 d 8 8 125 133f x x x f x x x x x

− = − = − − = − − = −

.
Câu 23: [2D3-3.3-2] Cho hàm số
( )
y f x=
xác định, liên tục trên và có bảng biến thiên như hình
sau:
Có bao nhiêu giá trị nguyên
2019;2019m−
để phương trình
( )
f x m=
có hai nghiệm phân
biệt.
A.
2018
. B.
4016
. C.
2019
. D.
2020
.
Lời giải
Tác giả:Vũ Thị Thanh Huyền; Fb: Vu Thi Thanh Huyen
Chọn C
Số nghiệm của phương trình
( ) ( )
1f x m=
là số giao điểm của đường thẳng
:d y m=
và đồ thị
( )
C
của hàm số
( )
y f x=
. Do đó phương trình
( )
1
có hai nghiệm phân biệt khi và chỉ khi
d
cắt
( )
C
tại hai điểm phân biệt
3
1
m
m
=
−
.
Mà
2019;2019 ,mm −
nên
2019; 2018; 2017;...; 2;3m − − − −
.
Vậy có
2019
giá trị nguyên của
m
thỏa mãn.
Câu 24: [2D2-4.8-2] Một người gửi
300
triệu đồng vào một ngân hàng với lãi suất
7%/
năm. Biết rằng
nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính
lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn
600
triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và
người đó không rút tiền ra.
A.
9
năm. B.
10
năm. C.
11
năm. D.
12
năm.
Lời giải
Tác giả:Vũ Thị Thanh Huyền; Fb: Vu Thi Thanh Huyen
Chọn C
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 18 Mã đề 638
Kí hiệu số tiền gửi ban đầu là
A
, lãi suất một kì hạn là
m
thì số tiền cả gốc và lãi có được sau
n
kì hạn là
( )
.1
n
Am+
.
Do đó, số tiền cả gốc và lãi người đó nhận được sau
n
năm là
300.1,07
n
triệu đồng.
Số tiền cả gốc và lãi nhận được nhiều hơn
600
triệu đồng
300.1,07 600
n

1,07
log 2 10,245n
.
Vậy sau ít nhất
11
năm thì người đó nhận được số tiền nhiều hơn
600
triệu đồng bao gồm cả
gốc và lãi.
Câu 25: [2D3-5.9-2] Cho hình phẳng giới hạn bởi các đường
2yx=−
,
0y =
và
9x =
quay xung
quanh trục
Ox
. Tính thể tích khối tròn xoay tạo thành.
A.
7
6
V =
. B.
5
6
V
=
. C.
7
11
V
=
. D.
11
6
V
=
.
Lời giải
Tác giả: Trần Thị Thúy; Fb: Thúy Minh
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số
2yx=−
và trục hoành:
20x −=
2x=
4x=
.
Thể tích của khối tròn xoay tạo thành là:
( )
9
2
4
2dV x x
=−
( )
9
4
4 4 dx x x
= − +
9
2
4
8
4
23
x x x
x

= − +



81 16 64 11
72 36 16
2 2 3 6

= − + − − + =
.
Câu 26: [2D3-1.3-2] Họ nguyên hàm của hàm số
( )
4
e
x
f x x x=+
là
A.
( )
5
1
1e
5
x
x x C+ + +
. B.
( )
5
1
1e
5
x
x x C+ − +
.
C.
5
1
e
5
x
x x C++
. D.
( )
3
4 1 e
x
x x C+ + +
.
Lời giải
Tác giả: Trần Thị Thúy; Fb: Minh Thúy.
Chọn B
Ta có:
( )
44
e dx dx e dx
xx
x x x x+ = +
.
+)
45
1
1
dx=
5
x x C+
.
+) Đặt
du dx
.
dv e dx e
xx
ux
v
==


==

Suy ra:
e dx
x
x
2
e e dx e e
x x x x
x x C= − = − +
( )
2
1e
x
xC= − +
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 19 Mã đề 638
Vậy
( )
( )
45
1
e dx 1 e
5
xx
x x x x C+ = + − +
.
Câu 27: [2H3-5.2-2] Trong không gian
Oxyz
, phương trình đường thẳng đi qua hai điểm
( )
1;2;3A
và
( )
5;4; 1B −
là
A.
5 4 1
2 1 2
x y z− − +
==
. B.
1 2 3
4 2 4
x y z+ + +
==
−
.
C.
1 2 3
4 2 4
x y z− − −
==
. D.
3 3 1
2 1 2
x y z− − −
==
−−
.
Lời giải
Tác giả: Phùng Hoàng Cúc; Fb: Phùng Hoàng Cúc
Chọn D
Ta có
( )
4;2; 4AB −
. Suy ra
AB
cùng phương với
( )
2; 1;2u −−
.
Phương trình đường thẳng
AB
đi qua
( )
5;4; 1B −
nhận
( )
2; 1;2u −−
làm vectơ chỉ phương là:
( )
5 4 1
,1
2 1 2
x y z− − +
==
−−
. Do đó loại A, C.
Có tọa độ
( )
1; 2; 3C − − −
không thỏa mãn phương trình
( )
1
nên phương án B.
Lại có tọa độ
( )
3;3;1D
thỏa mãn phương trình
( )
1
nên phương trình đường thẳng
AB
cũng
được viết là:
3 3 1
2 1 2
x y z− − −
==
−−
.
Câu 28: [2H1-2.3-2] Cho hình chóp tam giác đều có cạnh đáy bằng
a
, cạnh bên
2a
. Tính chiều cao
h
của hình chóp đó
A.
28
3
a
h =
. B.
14
3
a
h =
. C.
33
3
a
h =
. D.
11
3
a
h =
.
Lời giải
Tác giả: Phùng Hoàng Cúc; Fb: Phùng Hoàng Cúc
Chọn C
Gọi chóp tam giác đều là
.S ABC
có
M
,
F
lần lượt là trung điểm
BC
,
AB
và
O
là trọng tâm
của
ABC
. Ta có
( )
SO ABC⊥
.
Ta có
3
2
a
AM =
2 2 3 3
.
3 3 2 3
aa
OA AM = = =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 20 Mã đề 638
Xét tam giác vuông
SOA
ta có
22
h SO SA AO= = −
( )
2
2
3
2
3
a
a

=−



33
3
a
=
.
Vậy chiều cao cần tìm của hình chóp là
33
3
a
h =
.
Câu 29: [2D1-5.6-1] Đường cong trong hình bên là đồ thị của hàm số nào?
A.
4
1yx= − +
. B.
42
21y x x= + +
. C.
4
1yx=+
. D.
42
21y x x= − + +
.
Lời giải
Tác giả: Bùi Thị Kim Oanh; Fb: Bùi Thị Kim Oanh
Chọn D
Vì đường cong có hướng đi xuống khi
x → +
nên hệ số
0a
, đồng thời đồ thị đi qua điểm
( )
1;2
. Do đó đường cong này là đồ thị của hàm số
42
21y x x= − + +
.
Chú ý: Đồ thị hàm số
42
,0y ax bx c a= + +
có 3 điểm cực trị khi và chỉ khi
.0ab
. Do đó
loại A, B, C.
Câu 30: [2H3-3.6-2] Trong không gian với hệ tọa độ
Oxyz
cho mặt phẳng
( )
: 2 5 0Q x y z− + − =
và
mặt cầu
( ) ( ) ( )
22
2
: 1 2 15S x y z− + + + =
. Mặt phẳng
( )
P
song song với mặt phẳng
( )
Q
và cắt
mặt cầu
( )
S
theo giao tuyến là một đường tròn có chu vi bằng
6
đi qua điểm nào sau đây?
A.
( )
2; 2;1−
. B.
( )
1; 2;0−
. C.
( )
0; 1; 5−−
. D.
( )
2;2; 1−−
.
Lời giải
Tác giả: Bùi Thị Kim Oanh; Fb: Bùi Thị Kim Oanh
Chọn D
Mặt cầu
( )
S
có tâm
( )
1;0; 2I −
và bán kính
15R =
.
Đường tròn có chu vi bằng
6
nên có bán kính
6
3
2
r
==
.
Mặt phẳng
( )
P
song song với mặt phẳng
( )
Q
nên phương trình mặt phẳng
( )
P
có dạng:
20x y z D− + + =
,
5D −
.
Vì mặt phẳng
( )
P
cắt mặt cầu
( )
S
theo giao tuyến là một đường tròn có chu vi bằng
6
nên
( )
( )
( )
( )
22
; ; 6d I P R r d I P= − =
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 21 Mã đề 638
( )
2
22
1 6 7
1 2.0 2
6 1 6
1 6 5
1 2 1
DD
D
D
DD
− = =
− − +

= − =

− = − = −

+ − +
.
Đối chiếu điều kiện ta được
7D =
. Do đó phương trình mặt phẳng
( )
: 2 7 0P x y z− + + =
.
Nhận thấy điểm có tọa độ
( )
2;2; 1−−
thuộc mặt phẳng
( )
P
.
Câu 31: [2D2-6.2-3] Tập hợp các giá trị thực của tham số
m
để phương trình
( )
( )
2
2019 1
2019
log 4 log 2 1 0x x m− + + − =
có hai nghiệm thực phân biệt là
( )
;T a b=
. Tính
2S a b=+
.
A. 20. B. 8. C. 18. D. 16.
Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham
Chọn D
Ta có:
( )
( ) ( )
2
2019 1
2019
log 4 log 2 1 0 1x x m− + + − =
( )
( )
2
2019 2019
log 4 log 2 1 0x x m − − + − =
( )
( )
2
2019 2019
log 4 log 2 1x x m − = + −
2
2
4 2 1
40
x x m
x
− = + −
−
( )
2
25
2
22
x x m
x
− − + =
−
.
Phương trình
( )
1
có hai nghiệm thực phân biệt
hệ phương trình
( )
2
có hai nghiệm phân
biệt
đường thẳng
ym=
cắt đồ thị hàm số
2
25y x x= − − +
tại
2
điểm phân biệt có hoành
độ
1
x
;
2
x
( )
2;2−
.
Xét hàm số
2
25y x x= − − +
trên
( )
2;2−
.
22yx
= − −
;
( )
0 2 2 0 1 2;2y x x
= − − = = − −
.
BBT
Từ BBT ta thấy
( )
5;6m
thỏa mãn yêu cầu bài toán. Vậy
5a =
;
6 2 16b S a b= = + =
.
Câu 32: [2D1-4.7-2] Cho hàm số
2
2
24
x
y
mx x
−
=
−+
. Có tất cả bao nhiêu giá trị của tham số
m
để đồ thị
hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 1. B. 3. C. 0. D. 2.
Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham
Chọn A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 22 Mã đề 638
ĐK:
2
2 4 0mx x− +
Trường hợp 1:
0m =
Hàm số trở thành
2
24
x
y
x
−
=
−+
. Đồ thị hàm số không có đường TCĐ
loại
0m =
.
Trường hợp 2:
0m
Ta có:
lim 0
x
y
→+
=
,
lim 0
x
y
→−
=
. Suy ra đồ thị hàm số có
1
đường TCN
0y =
.
Do đó đồ thị hàm số có đúng
2
đường tiệm cận
đồ thị hàm số có đứng
1
đường tiệm cận
đứng
phương trình
2
2 4 0mx x− + =
có nghiệm kép hoặc có
2
nghiệm phân biệt trong đó
có
1
nghiệm
2x =
.
0 4 16 0
1
0 1 4 0
4
4 2.2 4 0 0
m
m
m
mm
= − =


=
−




− + = =


.
Vậy có 1 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 33: [2D1-2.7-3] Gọi
S
là tập hợp các giá trị nguyên
m
để đồ thị hàm số
4 3 2
3 8 6 24y x x x x m= − − + −
có
7
điểm cực trị. Tính tổng các phần tử của
S
.
A.
42
. B.
50
. C.
30
. D.
63
.
Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn.
Chọn A
Xét hàm số
( )
4 3 2
3 8 6 24f x x x x x m= − − + −
trên .
Ta có
( )
32
12 24 12 24f x x x x
= − − +
.
( )
1
02
1
x
f x x
x
=−
= =
=
.
Bảng biến thiên của hàm số
Dựa vào BBT suy ra đồ thị hàm số
4 3 2
3 8 6 24y x x x x m= − − + −
có 7 điểm cực trị khi và chỉ
khi đồ thị của hàm số
( )
4 3 2
3 8 6 24f x x x x x m= − − + −
cắt trục hoành tại 4 điểm phân biệt
13 0
8 13
80
m
m
m
−
−
.
Mà
m
nguyên nên
9;10;11;12mS=
. Suy ra tổng tất cả các phần tử của tập
S
là
42
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 23 Mã đề 638
Câu 34: [1H3-2.4-2] ] Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh là
2a
; cạnh
SA a=
và vuông
góc với đáy. Gọi
M
là trung điểm của
CD
. Tính
cos
với
là góc tạo bởi hai đường thẳng
SB
và
AM
.
A.
2
5
. B.
1
2
. C.
4
5
. D.
2
5
−
.
Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn
Chọn A
Cách 1:
Gọi
N
,
P
lần lượt là trung điểm của
AB
và
SA
.
Ta có
//
//
SB NP
AM NC
( ) ( )
,AM ,SB NP NC
= =
.
Xét
NPC
có
5
2
a
NP =
,
33
2
a
PC =
,
5NC a=
.
Khi đó
2 2 2
2
cos cos
2 . 5
NP NC PC
PNC
NP NC
+−
= = =
.
Cách 2: Trương Hồng Hà
Chọn hệ trục toạ độ
Oxyz
sao cho
( )
0;0;0A
,
( )
0;0;Sa
,
( )
2 ;0;0Ba
,
( )
0;2 ;0Da
.
Ta có
( )
;2 ;0M a a
,
( )
;2 ;0AM a a=
,
( )
2 ;0;SB a a=−
.
Do đó
( )
2
2 2 2 2
2
2
cos cos ,
5
4 . 4
a
AM SB
a a a a
= = =
++
.
Câu 35: [2H1-4.2-3] Cho hình bát diện đều có cạnh
a
và điểm
I
nằm trong hình bát diện. Tính tổng
khoảng cách từ
I
đến tất cả các mặt của bát diện.
A.
46
3
a
. B.
32
2
a
. C.
43
3
a
. D.
3
2
a
.
Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly
P
N
M
D
C
B
A
S
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 24 Mã đề 638
Chọn A
Hình 1 Hình 2
Thể tích khối bát diện
ABCDEF
là
3
2
.
1 1 2 2
2.V 2. . . 2. . .
3 3 2 3
ABCDEF E ABCD ABCD
aa
V EO S a= = = =
Gọi
1
d
,
2
d
, …,
8
d
lần lượt là khoảng cách từ
I
đến các mặt của bát diện. Gọi
1
V
,
2
V
,…,
8
V
lần lượt là thể tích của các khối chóp tam giác có đỉnh
I
và có đáy là các mặt bên ứng với các
đường cao
1
d
,
2
d
, …,
8
d
.
Ta có
( )
1 2 8 1 2 8
1
... . ... .
3
ABCDEF
V V V V d d d S= + + + = + + +
, trong đó
2
3
4
a
S =
là diện tích một
mặt của khối bát diện
ABCDEF
.
Suy ra
3
1 2 8
2
2
3.
3.
46
3
...
3
3
4
ABCDEF
a
V
a
d d d
S
a
+ + + = = =
.
Vậy tổng khoảng cách từ
I
đến tất cả các mặt của bát diện là
46
3
a
.
Câu 36: [2H2-1.4-3] Một khối nón có bán kính đáy bằng
2 cm
, chiều cao bằng
3cm
. Một mặt phẳng
đi qua đỉnh và tạo với đáy một góc
0
60
chia khối nón làm
2
phần. Tính thể tích
V
phần nhỏ
hơn (Tính gần đúng đến hàng phần trăm).
A.
3
1,42cmV
. B.
3
2,36cmV
. C.
3
1,53cmV
. D.
3
2,47cmV
.
Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly
Chọn A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 25 Mã đề 638
Cách 1:
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc
60
cắt khối nón theo thiết diện là tam giác
SMN
như hình vẽ.
Gọi
I
là trung điểm
MN
. Khi đó
OI MN⊥
và
SI MN⊥
, suy ra góc giữa mặt phẳng
( )
SMN
và mặt đáy là góc
60SIO =
.
Xét tam giác
SIO
ta có:
0
3
1
tan 60
tan
SO
OI
SIO
= = =
.
22
3IN ON OI= − =
,
2 2 3MN IN==
.
1
. . 3
2
OMN
S OI MN
==
.
.
1
. . 1
3
S OMN OMN
V SO S
==
.
2
/
1 4 3
. .2 . 3
33
k non
V

==
.
3
sin
2
IN
ION
ON
==
. Suy ra
60ION =
,
2. 120MON ION= =
.
Gọi
V
là thể tích cần tính.
Ta có
3
/.
1 4 3
1 1,42cm
39
k non S OMN
V V V
= − = −
.
Cách 2: Ngọc Toàn
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc
60
cắt khối nón theo thiết diện là tam giác
SMN
như hình vẽ.
Gọi
I
là trung điểm
MN
. Khi đó
OI MN⊥
và
SI MN⊥
, suy ra góc giữa mặt phẳng
( )
SMN
và mặt đáy là góc
0
60SIO =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 26 Mã đề 638
Xét tam giác
SIO
ta có:
0
3
1
tan 60
tan
SO
OI
SIO
= = =
.
22
3IN ON OI= − =
2 2 3MN IN = =
.
1
. . 3
2
OMN
S OI MN
==
.
Ta có
3
sin
2
IN
ION
ON
==
suy ra
60ION =
,
2. 120MON ION= =
.
Gọi
V
S
là diện tích hình viên phân tạo bởi dây
MN
và cung nhỏ
MN
.
Ta có
2
14
3
33
V OMN
S R S
= − = −
Thể tích phần nhỏ cần tính là:
3
1 4 3
. 1 1,42cm
39
V
V SO S
= = −
.
Câu 37: [2H3-6.17-2] Trong không gian
Oxyz
, điểm
M
đối xứng với điểm
( )
1;2;4M
qua mặt phẳng
( )
:2 2 3 0x y z
+ + − =
có tọa độ là
A.
( )
3;0;0−
. B.
( )
1;1;2−
. C.
( )
1; 2; 4− − −
. D.
( )
2;1;2
.
Lời giải
Tác giả: Nguyễn Tình; Fb: Gia Sư Toàn Tâm
Chọn A
Mặt phẳng
( )
có vectơ pháp tuyến là
( )
2;1;2n =
.
MM
vuông góc với mặt phẳng
( )
nên đường thẳng
MM
nhận
( )
2;1;2n =
làm vectơ chỉ
phương. Phương trình đường thẳng
MM
là:
12
2
42
xt
yt
zt
=+
=+
=+
.
Gọi
H
là giao điểm của đường thẳng
MM
và mặt phẳng
( )
.
H MM
( )
1 2 ;2 ;4 2H t t t + + +
.
( )
H
( ) ( )
2 1 2 2 2 4 2 3 0t t t + + + + + − =
9 9 0t + =
1t = −
( )
1;1;2H−
.
M
đối xứng với điểm
M
qua mặt phẳng
( )
nên
H
là trung điểm của
MM
( )
3;0;0M
−
.
Câu 38: [2H3-6.18-3] Trong không gian với hệ tọa độ
Oxyz
, cho ba điểm
( )
1;2;5A −
,
( )
3; 1;0B −
,
( )
4;0; 2C −−
. Gọi
I
là điểm trên mặt phẳng
( )
Oxy
sao cho biểu thức
23IA IB IC−+
đạt giá
trị nhỏ nhất. Tính khoảng cách từ
I
đến mặt phẳng
( )
:4 3 2 0P x y+ + =
.
A.
17
5
. B.
6
. C.
12
5
. D.
9
.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 27 Mã đề 638
Tác giả: Nguyễn Tình; Fb: Gia Sư Toàn Tâm
Chọn B
Gọi
( )
;;M a b c
là điểm thỏa mãn
2 3 0MA MB MC− + =
.
Khi đó:
( ) ( )
( ) ( )
( ) ( )
1 2 3 3 4 0
2 2 1 3 0 0
5 2 0 3 2 0
a a a
b b b
c c c
− − − − + − − =
− − − − + − =
− − − + − − =
19
2
2
1
2
a
b
c
=−
=
=−
19 1
;2;
22
M

− −


.
Ta có:
23IA IB IC−+
2 2 3 3IM MA IM MB IM MC= + − − + +
( )
2 2 3IM MA MB MC= + − +
22IM IM==
.
Biểu thức
23IA IB IC−+
đạt giá trị nhỏ nhất
IM
nhỏ nhất
I
là hình chiếu vuông góc
của
M
lên
( )
Oxy
19
;2;0
2
I

−


.
Khoảng cách từ điểm
I
đến mặt phẳng
( )
P
là:
( )
( )
22
19
4. 3.2 2
2
;6
43
d I P

− + +


==
+
.
Câu 39: [2D4-1.4-3] Cho số phức
z a bi=+
( )
,ab
thỏa mãn
31zz− = −
và
( )
( )
2z z i+−
là số
thực. Tính
ab+
.
A.
2−
. B. 0. C. 2. D. 4.
Lời giải
Tác giả: Trần Thơm; Fb: Kem LY
Chọn B
Ta có
z a bi=+
( )
,ab
.
+)
31zz− = −
31a bi a bi − + = − +
( ) ( )
22
22
31a b a b − + = − +
( ) ( )
22
22
31a b a b − + = − +
4 8 0a − + =
2a=
.
+)
( )
( )
( )( ) ( ) ( )
2 2 2 1z z i a bi a bi i a bi a b i+ − = + + − − = + + − +
( ) ( ) ( )
2 1 2 2a a b b a b i= + + + − + +
.
( )
( )
2z z i+−
là số thực
2 2 0ab + + =
.
Thay
2a =
tìm được
2b =−
. Vậy
0ab+=
.
Câu 40: [2D3-4.3-3] Biết
4
32
2
1
73
d ln5
3
x x x a
xc
x x b
+ + +
=+
−+
với
a
,
b
,
c
là các số nguyên dương và
a
b
là
phân số tối giản. Tính
23
P a b c= − −
.
A.
5−
. B.
4−
. C. 5. D. 0.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 28 Mã đề 638
Lời giải
Tác giả: Trần Thơm; Fb: Kem LY
Chọn B
Cách 1:
Ta có
4
32
2
1
73
d
3
x x x
x
xx
+ + +
=
−+
( )
4
2
1
3 2 1
2d
3
x
xx
xx
−

++

−+

( )
4
2
4
4
22
2
1
1
1
d3
1 27 27
2 3 3ln 3 3ln 5
2 3 2 2
xx
x x x x
xx
−+

= + + = + − + = +

−+

.
Mà
4
32
2
1
73
d ln5
3
x x x a
xc
x x b
+ + +
=+
−+
, suy ra
27a =
,
2b =
,
3c =
.
Vậy
23
4P a b c= − − = −
.
Cách 2: Sử dụng máy tính cầm tay
Ta có
4
32
2
1
73
d ln5
3
x x x a
xc
x x b
+ + +
=+
−+
4
32
2
1
73
d ln5
3
a x x x
xc
b x x
+ + +
=−
−+
.
Đặt
( )
4
32
2
1
73
f X d Xln5
3
a x x x
x
b x x
+ + +
= = −
−+
với
X c=
.
Vì
a
,
b
,
c
là các số nguyên dương và
a
b
là phân số tối giản nên ta có thể tìm giá trị của
X
nguyên dương để
( )
fX
a
b
=
là số hữu tỉ.
Bước 1: Bấm tích phân
4
32
2
1
73
d
3
x x x
x
xx
+ + +
−+
→
Shift
→
STO
→
A.
Bước 2: MODE
→
7
→
Nhập
( )
f X A Xln5=−
→
X chạy từ 1 đến 20, STEP = 1.
Bước 3: Ta thấy chỉ có một giá trị duy nhất
X3=
để
( )
f X 13,5=
là số hữu tỉ.
Vậy
3c =
và
27
13,5
2
a
b
==
nên
27a =
,
2b =
. Do đó
23
4P a b c= − − = −
.
Câu 41: [2D3-4.12-3] Cho hàm số
( )
y f x=
có đạo hàm liên tục trên
2;4
và
( )
0, 2;4f x x
.
Biết
( ) ( )
( )
3
33
7
4 , 2;4 , 2
4
x f x f x x x f
= − =


. Giá trị của
( )
4f
bằng
A.
40 5 1
2
−
. B.
20 5 1
4
−
. C.
20 5 1
2
−
. D.
40 5 1
4
−
.
Lời giải
Tác giả: Nguyễn Hoàng Hưng; Fb: Nguyễn Hưng
Chọn D
Ta có:
( )
0, 2;4f x x
nên hàm số
( )
y f x=
đồng biến trên
2;4
( ) ( )
2f x f
mà
( )
7
2
4
f =
. Do đó:
( )
0, 2;4f x x
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 29 Mã đề 638
Từ giả thiết ta có:
( ) ( ) ( ) ( )
33
3 3 3
4 4 1x f x f x x x f x f x

= − + =
( ) ( )
( )
( )
3
3
. 4 1
41
fx
x f x f x x
fx
+ = =
+
.
Suy ra:
( )
( )
( )
( )
2
33
d 4 1
1
dd
42
4 1 4 1
fx
fx
x
x x x C
f x f x
+


= = +
++
( )
2
2
3
3
41
82
x
f x C + = +


.
( )
7 3 1
22
4 2 2
f C C= = + = −
.
Vậy:
( )
( )
3
2
4
11
3
4
x
fx

−−


=
( )
40 5 1
4
4
f
−
=
.
Câu 42: [2D1-1.3-3] Cho hàm số
( )
y f x=
có đạo hàm liên tục trên . Biết hàm số
( )
y f x
=
có đồ
thị như hình vẽ. Gọi
S
là tập hợp các giá trị nguyên
5;5m −
để hàm số
( ) ( )
g x f x m=+
nghịch biến trên khoảng
( )
1;2
. Hỏi
S
có bao nhiêu phần tử?
A.
4
. B.
3
. C.
6
. D.
5
.
Lời giải
Tác giả: Hoàng Thị Minh Tuấn; Fb: Minh Tuấn Hoàng Thị
Chọn D
Ta có
( ) ( )
g x f x m

=+
. Vì
( )
y f x
=
liên tục trên nên
( ) ( )
g x f x m

=+
cũng liên tục
trên . Căn cứ vào đồ thị hàm số
( )
y f x
=
ta thấy
( ) ( )
00g x f x m

+
11
1 3 1 3
x m x m
x m m x m
+ − − −



+ − −

.
Hàm số
( ) ( )
g x f x m=+
nghịch biến trên khoảng
( )
1;2
21
32
11
m
m
m
− −
−
−
3
01
m
m
−

.
Mà
m
là số nguyên thuộc đoạn
5;5−
nên ta có
5; 4; 3;0;1S = − − −
.
Vậy
S
có 5 phần tử.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 30 Mã đề 638
Câu 43: [2D1-3.1-3] Cho hàm số
( )
y f x=
có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất
của hàm số
( )
( )
2 3 2
11
4 3 8
33
g x f x x x x x= − + − + +
trên đoạn
1;3
.
A. 15. B.
25
3
. C.
19
3
. D. 12.
Lời giải
Tác giả: Lưu Thị Thủy; Fb: thuy.luu.33886
Chọn D
( ) ( )
( )
22
4 2 4 6 8g x x f x x x x

= − − + − +
( )
( )
2
2 2 4 4x f x x x

= − − + −

.
Với
1;3x
thì
40x−
;
2
3 4 4xx −
nên
( )
2
40f x x
−
.
Suy ra
( )
2
2 4 4 0f x x x
− + −
,
1;3x
.
Bảng biến thiên
Suy ra
( ) ( )
1;3
max 2g x g=
( )
4 7 12f= + =
.
Câu 44: [2H3-2.13-3] Trong không gian với hệ tọa độ
Oxyz
cho bốn điểm
(1;0;0)A
,
(2;1;3)B
,
(0;2; 3)C −
,
(2;0; 7)D
. Gọi
M
là điểm thuộc mặt cầu
2 2 2
( ) : ( 2) ( 4) 39S x y z+ + − + =
thỏa
mãn:
2
2 . 8MA MB MC+=
. Biết độ dài đoạn thẳng
MD
đạt giá trị lớn nhất. Tính giá trị lớn nhất
đó.
A.
27
. B.
7
. C.
37
. D.
47
.
Lời giải
Tác giả: Nguyễn Thị Ngọc Lan; Fb:Ngoclan nguyen
Chọn A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 31 Mã đề 638
+) Mặt cầu
2 2 2
( ) : ( 2) ( 4) 39S x y z+ + − + =
có tâm là
( )
2;4;0I −
, bán kính
39R =
.
Gọi
( , , ) ( )M x y z S
. Ta có:
2 2 2
19 4 8x y z x y+ + = − +
.
2 2 2 2
( 1) 20 6 8MA x y z x y= − + + = − +
.
(2 ;1 ;3 )MB x y z= − − −
;
( ;2 ; 3 )MC x y z= − − − −
.
2 2 2
. 2 2 3 9MB MC x x y y z= − + + − + − +
19 4 8 2 3 7x y x y= − + − − −
6 5 12xy= − + +
.
Suy ra
2
2.MA MB MC+
18 18 44xy= − + +
.
Theo giả thiết
2
2 . 8MA MB MC+=
18 18 44 8xy − + + =
20xy − + + =
.
Do đó
( ) : 2 0M P x y − + + =
.
Ta có
8
( ;( )) 32 39
2
d I P = =
nên mặt phẳng
()P
cắt mặt cầu
()S
theo giao tuyến là
đường tròn
( )
C
có bán kính
1
R
với
22
1
39 32 7R R d= − = − =
.
Mặt khác ta có
( )
( )
,
,
D M P
D M S
, (C)DM
. Do đó độ dài
MD
lớn nhất bằng
1
2 2 7R =
.
Vậy chọn A.
Câu 45: [2D1-1.4-3] Cho hàm số
( )
y f x=
. Đồ thị
( )
y f x
=
như hình bên. Hàm số
( )
( )
12
1
2
fx
gx
−

=


nghịch biến trên khoảng nào trong các khoảng sau?
A.
( )
0;1
. B.
( )
;0−
. C.
( )
1;0−
. D.
( )
1;+
.
Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến
Chọn D
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 32 Mã đề 638
Từ đồ thị hàm số
( )
y f x
=
ta có
( )
1
0
12
x
fx
x
−


.
Xét hàm số
( )
( )
12
1
2
fx
gx
−

=


.
Ta có
( )
( )
( ) ( )
12
11
. 2 . 1 2 .ln
22
fx
g x f x
−

= − −
( )
( )
12
1
2ln 2. . 1 2
2
fx
fx
−

=−


.
( ) ( )
0 1 2 0g x f x

−
1
1 2 1
1
1 1 2 2
0
2
x
x
x
x
− −

−
−
.
Vậy hàm số
( )
gx
nghịch biến trên khoảng
( )
1;+
. Chọn D.
Câu 46: [2D3-5.13-3] Nhà trường dự định làm một vườn hoa dạng elip được chia ra làm bốn phần bởi
hai đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ
dài trục lớn, trục nhỏ của elip lần lượt là
8
m
và
4
m
,
1
,F
2
F
là hai tiêu điểm của elip. Phần
A
,
B
dùng để trồng hoa, phần
C
,
D
dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa
và cỏ lần lượt là
250.000
đ và
150.000
đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm
tròn đến hàng nghìn).
A.
5.676.000
đ. B.
4.766.000
đ. C.
4.656.000
đ. D.
5.455.000
đ.
Lời giải
Tác giả: Ngô Quốc Tuấn; Fb: Quốc Tuấn
Chọn A
Gắn hệ trục tọa độ như hình vẽ.
Do elip có độ dài trục lớn
2 8 4aa= =
, độ dài trục nhỏ
2 4 2bb= =
.
Diện tích của
( )
E
là:
( )
8
E
S ab

==
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 33 Mã đề 638
Phương trình chính tắc
( )
E
là:
22
1
16 4
xy
+=
. Suy ra
2
1
16
2
yx= −
.
Ta có
22
23c a b= − =
( )
2
2 3; 0F
.
Do
N
và
2
F
có cùng hoành độ
( )
2 3; 1N
.
Gọi
( )
2
:P y kx=
là parabol nằm ở phía trên trục
Ox
.
Do
( )
NP
ta có
( )
2
1
1 2 3
12
kk= =
. Suy ra
( )
2
1
:
12
P y x=
.
Diện tích phần
A
là
23
22
23
11
16 d
2 12
A
S x x x
−

= − −


23
22
0
11
2 16 d
2 12
x x x

= − −


2 3 2 3
22
00
1
16 d d
6
x x x x= − −

.
* Xét
23
2
1
0
16 dI x x=−
. Đặt
4sin d 4cos dx t x t t= =
.
Đổi cận:
Khi đó
3
2
1
0
16 16sin .4cos dI t t t
=−
3
2
0
16 cos dtt
=
( )
3
0
8 1 cos2 dtt
=+
3
0
1
8 sin 2
2
tt

=+


3
8
34

=+



.
* Ta có
23
2
2
0
1
d
6
I x x=
23
3
0
1
18
x=
43
3
=
.
Suy ra:
12
8 2 3
3
A
S I I
+
= − =
16 4 3
2
3
A B A
S S S
+
+ = =
.
Tổng diện tích phần
C
,
D
là:
CD
SS+=
( )
( )
AB
E
S S S− + =
8 4 3
3
−
.
Khi đó tổng số tiền để hoàn thành vườn hoa trên là:
16 4 3 8 4 3
.250000 .150000 5676000
33

+−
+
đ.
Câu 47: [2H1-2.5-3] Cho hình lập phương
.ABCD A B C D
có cạnh bằng
a
. Gọi
E
và
F
lần lượt là
các điểm trên các cạnh
AD

và
AB

sao cho
2
3
A E A D
=
và
2
3
A F A B
=
. Tính thể tích
khối chóp
.A BDEF
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 34 Mã đề 638
A.
3
3
8
a
. B.
3
5
18
a
. C.
3
8
a
. D.
3
33
8
a
.
Lời giải
Tác giả: Đàm Văn Thượng; Fb:Thượng Đàm
Chọn B
Cách 1:
Ta có
. . .A EFBD E ABD E ABF
V V V=+
.
Gọi
S
là diện tích một mặt của hình lập phương,
1
S
là diện tích tam giác
ABD
và
2
S
là diện
tích tam giác
ABF
.
Do
2
1
1
22
a
SS==
và
( )
( )
d,E ABCD AA a
==
suy ra
23
.
1
..
3 2 6
E ABD
aa
Va==
.
Lại có
2
2
1
.
22
a
S AB BB
==
và
( )
( )
2
d,
3
E AA B B EA a
==
suy ra
( )
( )
23
.2
1 1 2
.d , .
3 3 2 3 9
E ABF
aa
V S E AA B B a

= = =
.
Vậy
3 3 3
. . .
5
6 9 18
A EFBD E ABD E ABF
a a a
V V V= + = + =
.
Cách 2:
O
F
E
A'
D'
A
B'
B
D
C'
C
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 35 Mã đề 638
Trong tam giác
ABD
có
A E A F
A D A B

=
suy ra
//EF B D

mà
//BD B D

nên
//EF BD
.
Suy ra tứ giác
EFBD
là hình thang.
Trong mặt phẳng
( )
A ADD

dựng
//EH DD
suy ra
( )
EH ABCD⊥
( )
1EH BD⊥
, trong
mặt phẳng
( )
ABCD
dựng
HI BD⊥
tại
I
( )
2
Từ
( )
1
và
( )
2
suy ra
( )
BD EHI⊥
( ) ( )
EBD EHI⊥
,
( ) ( )
EBD EHI EI=
.
Trong mặt phẳng
( )
EHI
, kẻ
( )
,HK EI K EI HK EBD⊥ ⊥
hay
( )
( )
d,H EBD HK=
.
Ta thấy
( )
( )
( )
( )
d,
3
d,
A EBD
AD
HD
H EBD
==
( )
( )
( )
( )
d , 3d , 3A EBD H EBD HK = =
.
Trong tam giác
ABD
, có
2
3
EF A E
B D A D
==
22
3
a
EF=
.
Trong tam giác
DOA
, có
1
3
HI DH
AO DA
==
12
36
a
HI AO = =
.
Trong tam giác
EHI
, có
EH AA a
==
,
22
38
6
a
EI HE HI= + =
,
. 19
19
HE HI a
HK
EI
==
.
Diện tích hình thang
EFBD
là
( )
2
.
5 19
2 18
EF BD EI
a
S
+
==
và
( )
( )
3 19
d,
19
a
A EBD =
.
Vậy thể tích khối
.A EFBD
là
( )
( )
3
15
.d ,
3 18
a
V S A EBD==
.
Câu 48: [2D4-4.1-4] Cho hai số phức
12
,zz
thoả mãn
11
2 4 7 6 2z i z i+ − + − − =
và
2
1 2 1iz i− + =
.
Tìm giá trị nhỏ nhất của biểu thức
12
T z z=+
.
A.
21−
. B.
21+
. C.
2 2 1+
. D.
2 2 1−
.
Lời giải
Tác giả: Đào Văn Tiến; Fb: Đào Văn Tiến
Chọn D
O
I
H
F
E
A'
D'
A
B'
B
D
C'
C
K
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 36 Mã đề 638
Gọi
M
là điểm biểu diễn số phức
1
z
và
( )
2;1A −
;
( )
4;7B
lần lượt là hai điểm biểu diễn hai số
phức
2 i−+
,
47i+
. Ta có
62AB =
. Phương trình đường thẳng
AB
là
: 3 0d x y− + =
.
+)
11
2 4 7 6 2z i z i+ − + − − =
62MA MB + =
MA MB AB + =
. Do đó tập hợp các
điểm biểu diễn số phức
1
z
là đoạn thẳng
AB
.
+)
2 2 2
1 2 1 1 2 1 2 1iz i iz i i z i− + = − + = − − − =
.
Gọi
N
là điểm biểu diễn số phức
2
z−
và
( )
2;1I
là điểm biểu diễn số phức
2 i+
. Ta có
1IN =
Suy ra tập hợp các điểm biểu diễn số phức
2
z−
là đường tròn
( )
C
có phương trình:
( ) ( )
22
2 1 1xy− + − =
.
( )
, 2 2 1d I AB =
, suy ra
AB
không cắt đường tròn.
Gọi
K
là hình chiếu của
( )
2;1I
lên
AB
. Dễ thấy
K
nằm trên đoạn thẳng
AB
.
Gọi
H
là giao điểm của đoạn
IK
với đường tròn
( )
C
.
Ta có
( )
12
, 2 2 1z z MN KH d I AB R+ = = − = −
.
Suy ra
12
2 2 1.min z z+ = −
Câu 49: [1D2-2.2-4] Từ các chữ số thuộc tập
0;1;2;3;4;5;6;7X =
có thể lập được bao nhiêu số tự
nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.
A. 720. B. 860. C. 984. D. 1228.
Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Nguyễn Thị Thu Trang
Chọn C
Giả sử số lập được có dạng
1 2 3 4 5 6
a a a a a a
,
1
0a
,
ij
aa
với
ij
,
1;6i =
,
1;6j =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 37 Mã đề 638
Ta có
1 2 3 4 5 6
18a a a a a a
1 2 3 4 5 6
1 2 3 4 5 6
9
2
a a a a a a
a a a a a a
( )
1 2 3 4 5 6
6
9
2
a a a a a a
a
+ + + + +
.
Vì
( )
1 2 3 4 5 6
9a a a a a a+ + + + +
nên ta có các trường hợp sau
Trường hợp 1:
1
a
,
2
a
,
3
a
,
4
a
,
5
a
,
6
a
được chọn từ
1
2;3;4;5;6;7X =
+ Có 3 cách chọn chọn
6
a
.
+ Có
5!
cách chọn chọn bộ 5 số
( )
1 2 3 4 5
; ; ; ;a a a a a
.
Suy ra có
3.5! 360=
số.
Trường hợp 2:
1
a
,
2
a
,
3
a
,
4
a
,
5
a
,
6
a
được chọn từ
2
0;1;2;4;5;6X =
+
6
0a =
, có
5!
cách chọn bộ 5 số
( )
1 2 3 4 5
; ; ; ;a a a a a
.
+
6
0a
khi đó
6
a
có 3 cách chọn,
1
a
có 4 cách chọn và có
4!
cách chọn bộ 4 số
( )
2345
; ; ;a a a a
. Suy ra có
5! 3.4.4! 408+=
số.
Trường hợp 3:
1
a
,
2
a
,
3
a
,
4
a
,
5
a
,
6
a
được chọn từ
3
0;1;2;3;5;7X =
+
6
0a =
, có
5!
cách chọn bộ 5 số
( )
1 2 3 4 5
; ; ; ;a a a a a
.
+
6
0a
khi đó
6
a
có 1 cách chọn,
1
a
có 4 cách chọn và có
4!
cách chọn bộ 4 số
( )
2345
; ; ;a a a a
.
Suy ra có
5! 1.4.4! 216+=
số.
Vậy có
360 408 216 984+ + =
số.
Câu 50: [2D1-2.11-4] Gọi
0
m
là giá trị của tham số
m
để đường thẳng đi qua điểm cực đại và cực tiểu
của đồ thị hàm số
3
64y x mx= − +
cắt đường tròn tâm
( )
1;0I
, bán kính bằng
2
tại hai điểm
phân biệt
A
,
B
sao cho diện tích tam giác
IAB
đạt giá trị lớn nhất. Mệnh đề nào sau đây
đúng:
A.
( )
0
2;3m
. B.
( )
0
3;4m
. C.
( )
0
0;1m
. D.
( )
0
1;2m
.
Lời giải
Tác giả: Hà Lê; Fb: Ha Le
Chọn C
Ta có
2
36y x m
=−
,
2
02y x m
= =
. Đồ thị hàm số có điểm cực đại, điểm cực tiểu khi và
chỉ khi
0y
=
có hai nghiệm phân biệt. Do đó
0m
.
Ta có
( )
2
. 3 6 4 4
3
x
y x m mx= − − +
phương trình đường thẳng
( )
đi qua điểm cực đại và
cực tiểu của đồ thị hàm số đã cho là:
44y mx= − +
4 4 0mx y+ − =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 38 Mã đề 638
Đường thẳng
( )
cắt đường tròn đã cho tại hai điểm phân biệt
A
,
B
sao cho
I
,
A
,
B
là ba
đỉnh của một tam giác
( )
( )
0 ; 2dI
( )
2
44
02
16 1
m
m
−
+
.
Gọi
H
là trung điểm đoạn
AB
1
.
2
IAB
S IH AB=
.IH AH=
22
.IH R IH=−
2
.2IH IH=−
( )
( )
22
22
2
. 2 1
2
IH IH
IH IH
+−
= − =
1
IAB
S
.
Vậy diện tích tam giác
IAB
đạt giá trị lớn nhất bằng
1
22
2IH IH=−
1IH =
2
4 4 16 1mm− = +
( )
2
2
4 4 16 1mm− = +
15
32
m =
(thỏa mãn điều kiện
( )
).
Vậy
0
15
32
m =
nên
( )
0
0;1m
.
| 1/66
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Trường THPT Chuyên Lê Hồng Phong
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019 ĐỀ CHÍNH THỨC
Môn: Toán - Lớp 12 - Khối ABCD (Đề thi có 6 trang)
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 638 √
Câu 1. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a 2 bằng √ √ √ πa3 2 A. 4πa3 2. B. πa3 2. C. 2πa3. D. . 3
Câu 2. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả
cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng. 3 1 3 2 A. . B. . C. . D. . 14 35 7 5
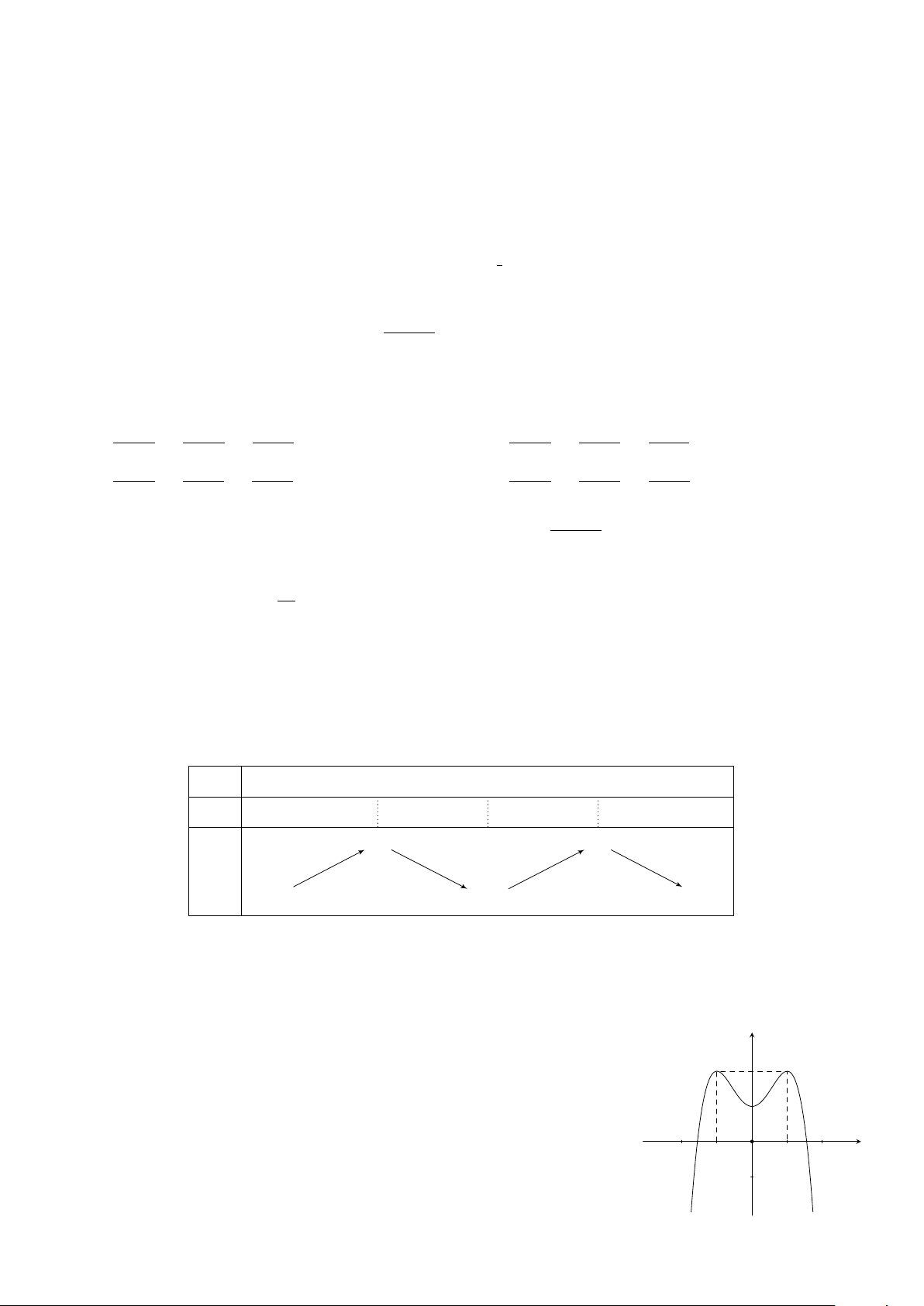
Câu 3. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng? x −∞ −1 2 +∞ f 0(x) + − 0 + 1 1 +∞ + f (x) −∞ −2 −
A. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
B. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2.
C. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
D. Giá trị cực đại của hàm số bằng 1.
Câu 4. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC. A. G(3; −6; 12). B. G(1; −2; −4). C. G(−1; 2; −4). D. G(1; −2; 4).
Câu 5. Số phức liên hợp của số phức z = 5 + 6i là A. z = −5 + 6i. B. z = −5 − 6i. C. z = 6 − 5i. D. z = 5 − 6i.
Câu 6. Cho cấp số nhân (un) có công bội q, số hạng đầu u1 = −2 và số hạng thứ tư u4 = 54. Giá trị của q bằng √ A. 3. B. −6. C. 6. D. −3.
Câu 7. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ? A. y + 5 = 0. B. z + 20 = 0. C. x − 2019 = 0. D. 2x + 5y − 8z = 0. 2x − 1
Câu 8. Tập xác định của hàm số y = là 2x − 4 A. D = R \ {2}. B. D = R \ {−4}. C. D = R \ {4}. D. D = R \ {−2}.
Câu 9. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng? a A. log(ab) = log a. log b. B. log = log b − log a. b a log a C. log = . D. log(ab) = log a + log b. b log b
Câu 10. Cho hình lăng trụ đứng ABC.A0B0C0 có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA0 = 3a. Tính thể tích V của lăng trụ đó. A. V = 3a3. B. V = 3a2. C. V = a3. D. V = 6a3. Trang 1/6 − Mã đề 638 − → − →
Câu 11. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ a = (3; 2; 1), b = (−2; 0; 1). Độ dài − → − → của véc-tơ a + b bằng √ A. 2. B. 1. C. 2. D. 3. 1
Câu 12. Tìm tập xác định D của hàm số y = (2 − x)3 . A. D = (−∞; 2] . B. D = (2; +∞). C. D = (−∞; 2) . D. D = (−∞; +∞) .
Câu 13. Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai. a b Z Z A. f (x) dx = 0. B. f (x) dx = F (b) − F (a). a a b a b Z Z Z C. f (x) dx = − f (x) dx. D. f (x) dx = F (a) − F (b). a b a
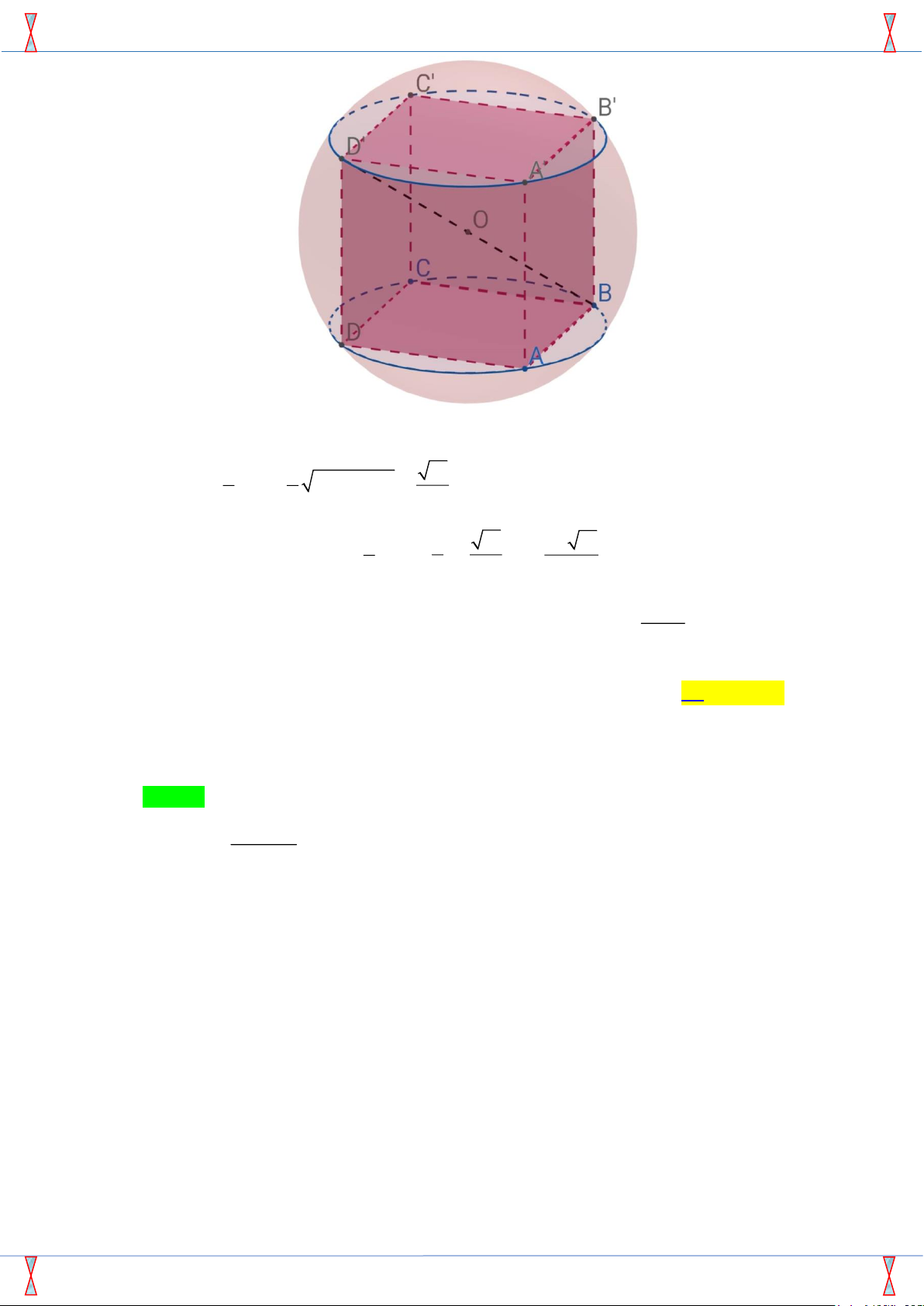
Câu 14. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là √ 9π 7π 14 9π A. 36π. B. . C. . D. . 2 3 8 2x − 1
Câu 15. Viết phương trình tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ x0 = 0. 2x + 1 A. y = −4x + 1. B. y = 4x + 1. C. y = 4x. D. y = 4x − 1. Câu 16.
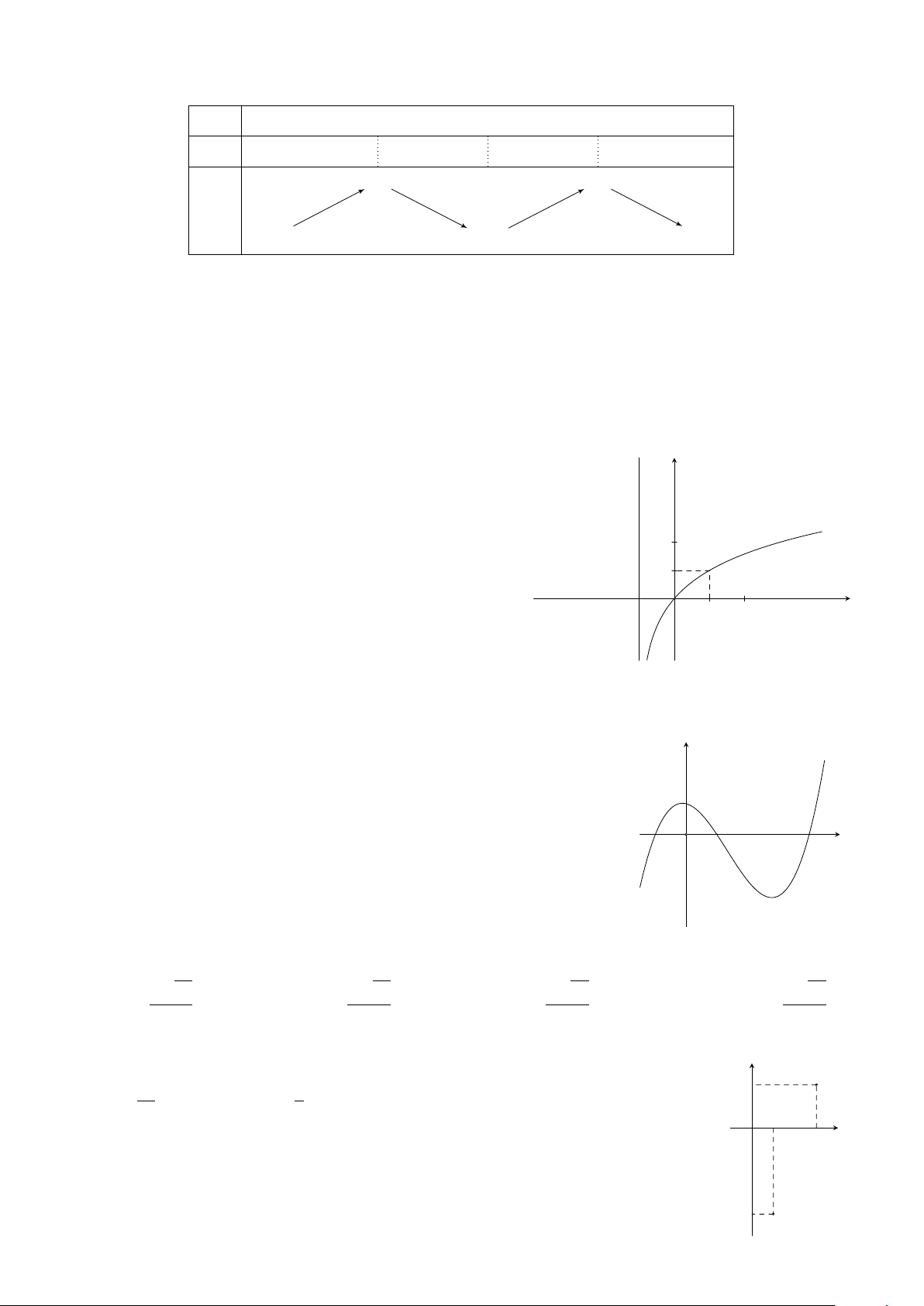
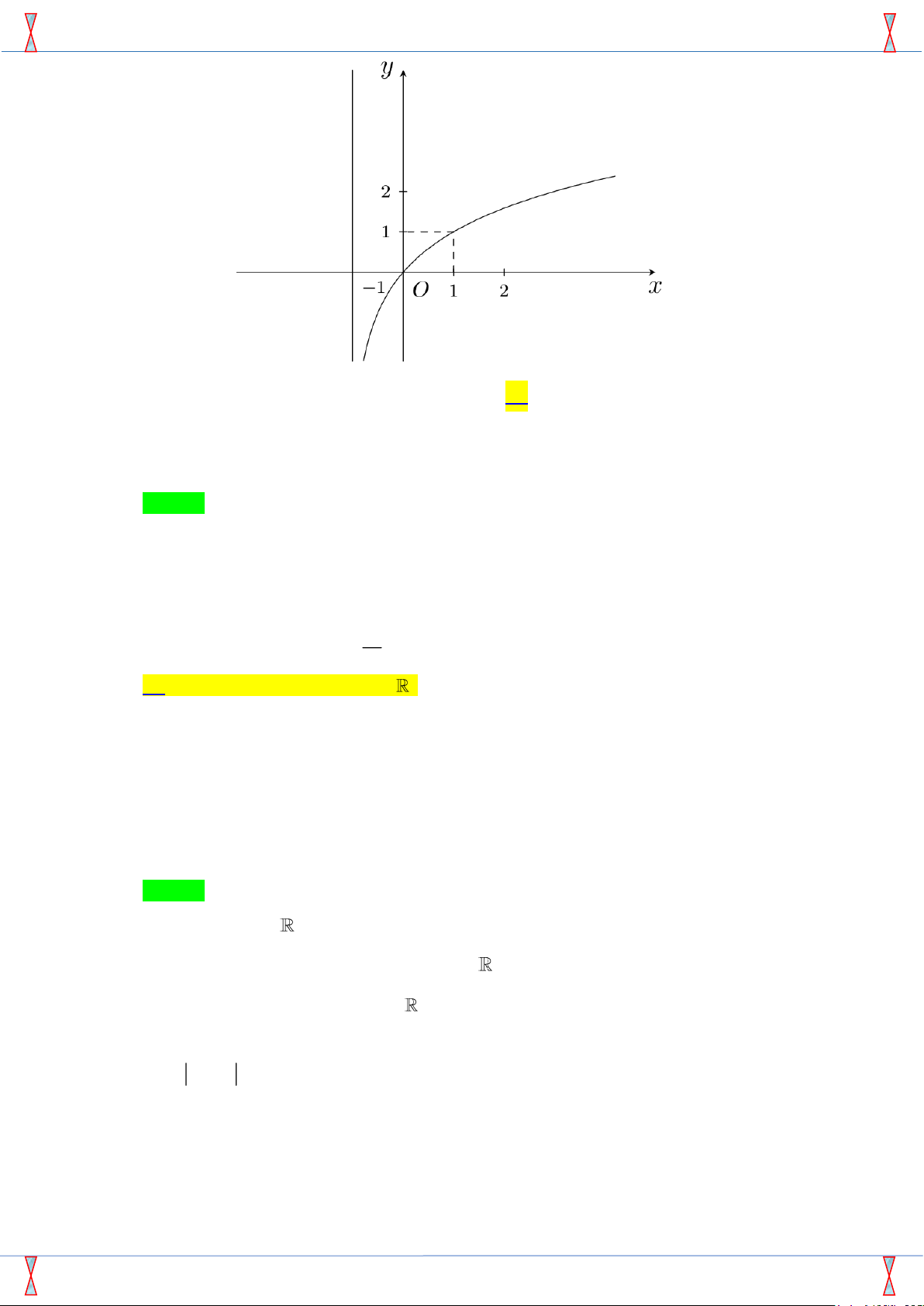
Hàm số nào cho dưới đây có đồ thị như hình bên? y A. y = log x. B. y = log x + 1. 3 2 C. y = log (x + 1). D. y = log (x + 1). 2 3 2 1 −1 O 1 2 x x3 Câu 17. Cho hàm số y =
− x2 + x + 2019. Mệnh đề nào sau đây là đúng? 3
A. Hàm số đã cho đồng biến trên R.
B. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
C. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1).
D. Hàm số đã cho nghịch biến trên (−∞; 1). Câu 18. Gọi z y
1, z2 lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. M Tính |z 2 1 + z2|. √ √ A. 2 29. B. 20. C. 2 5. D. 116. 1 x O 3 −4 N
Câu 19. Cho bất phương trình 4x −5.2x+1 +16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a2 + b2). A. 2. B. 1. C. 0. D. 10.
Câu 20. Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + 4z + 29 = 0. Tính giá trị biểu thức |z1|4 + |z2|4. A. 841. B. 1682. C. 1282. D. 58. Trang 2/6 − Mã đề 638 Câu 21. y
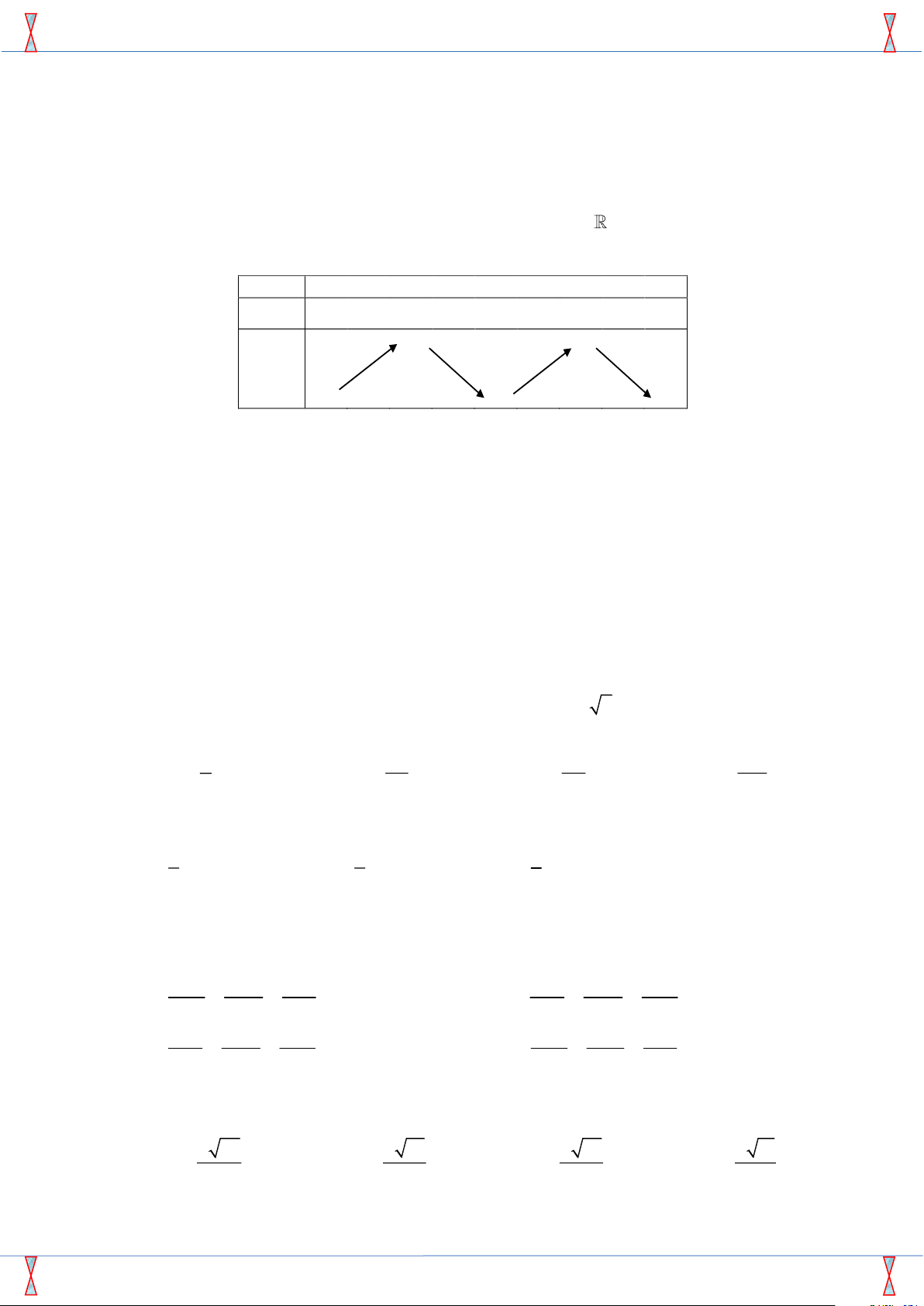
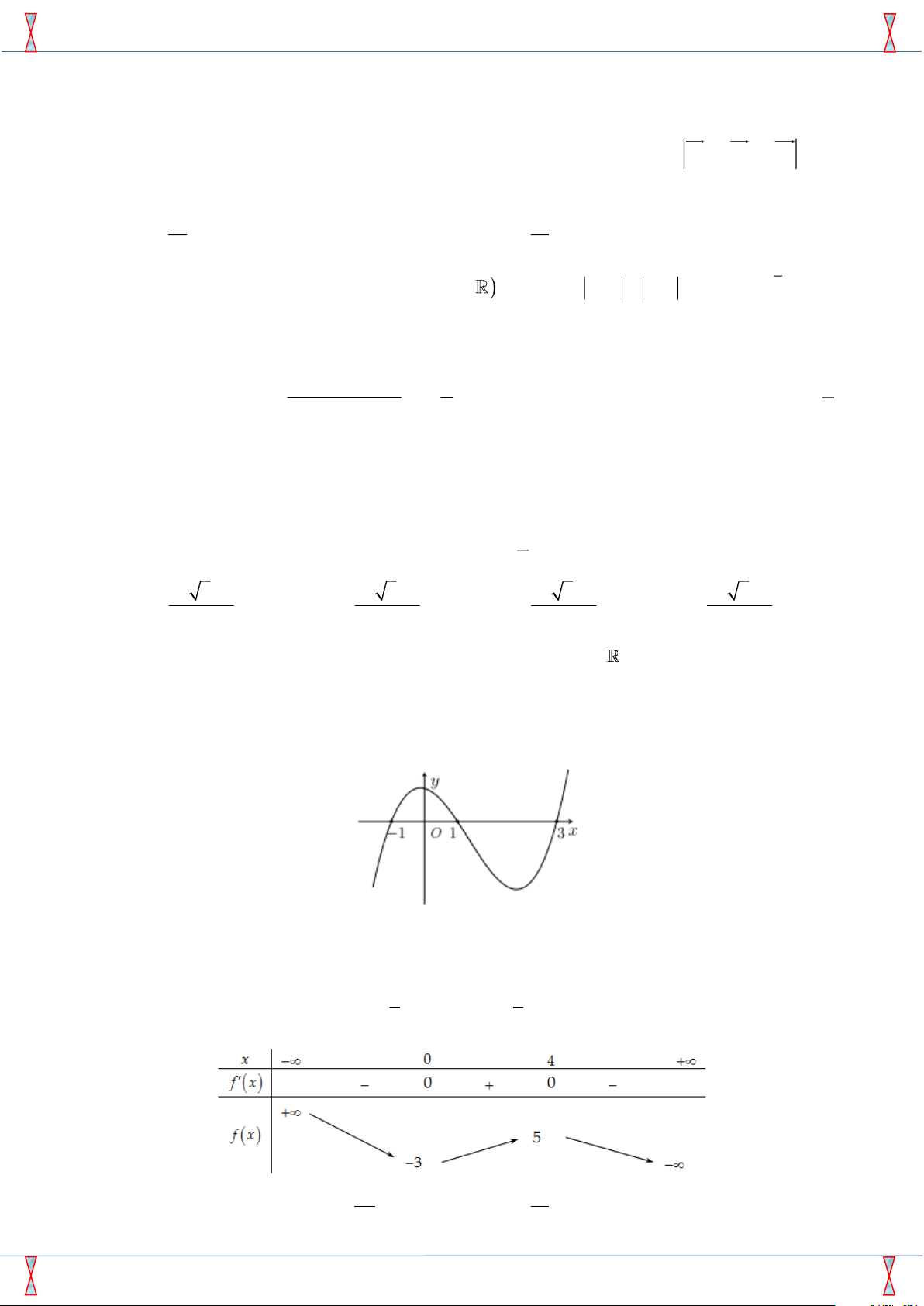
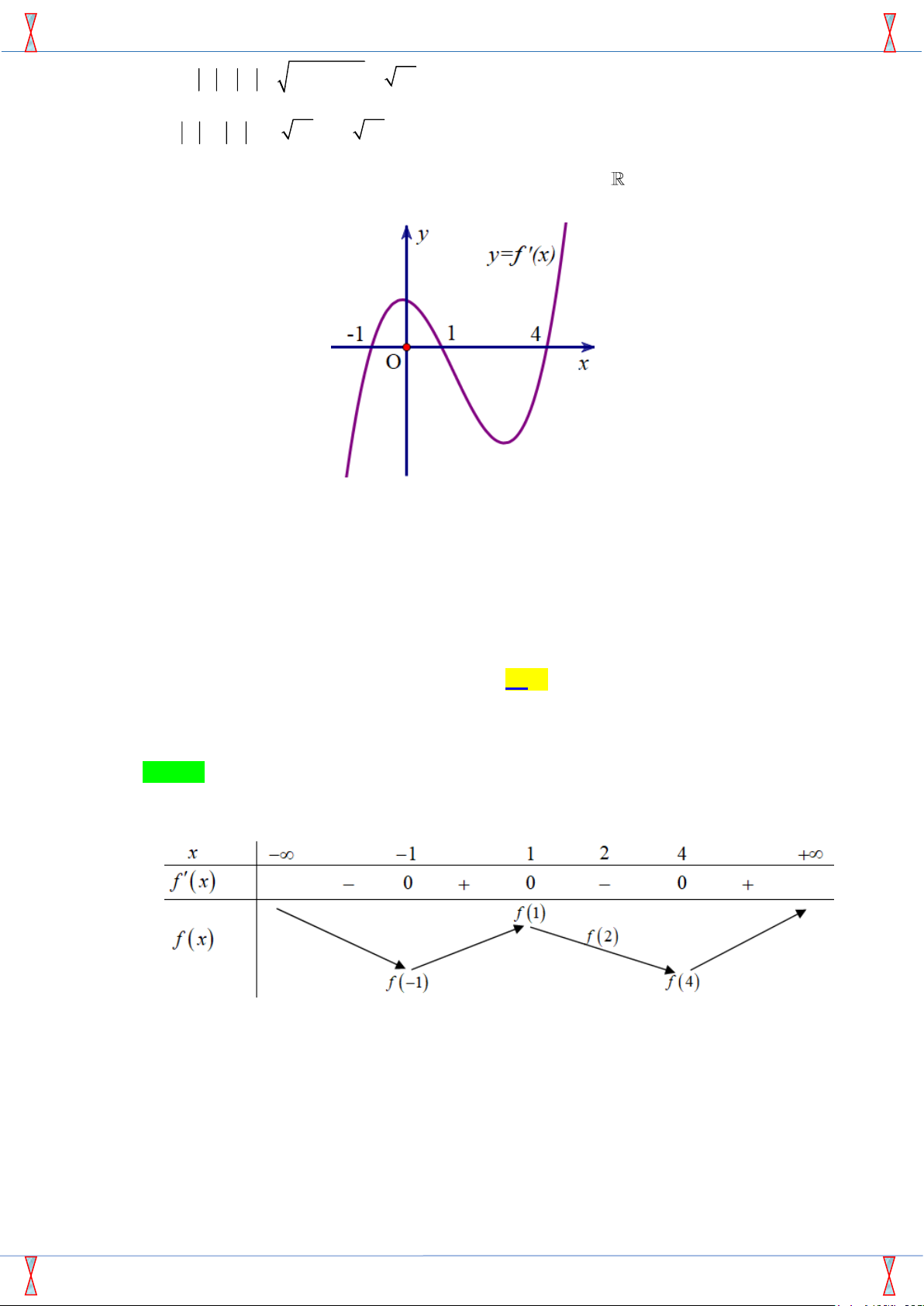
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f 0(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau: y = f 0(x)
1) Hàm số y = f (x) có hai cực trị.
2) Hàm số y = f (x) đồng biến trên khoảng (1; +∞). −1 1 4
3) f (1) > f (2) > f (4). x O
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f (x) là f (1).
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 1. B. 4. C. 2. D. 3. 5 5 Z Z Câu 22. Cho f (x) dx = −2. Tích phân [4f (x) − 3x2] dx bằng 0 0 A. −140. B. −130. C. −120. D. −133.
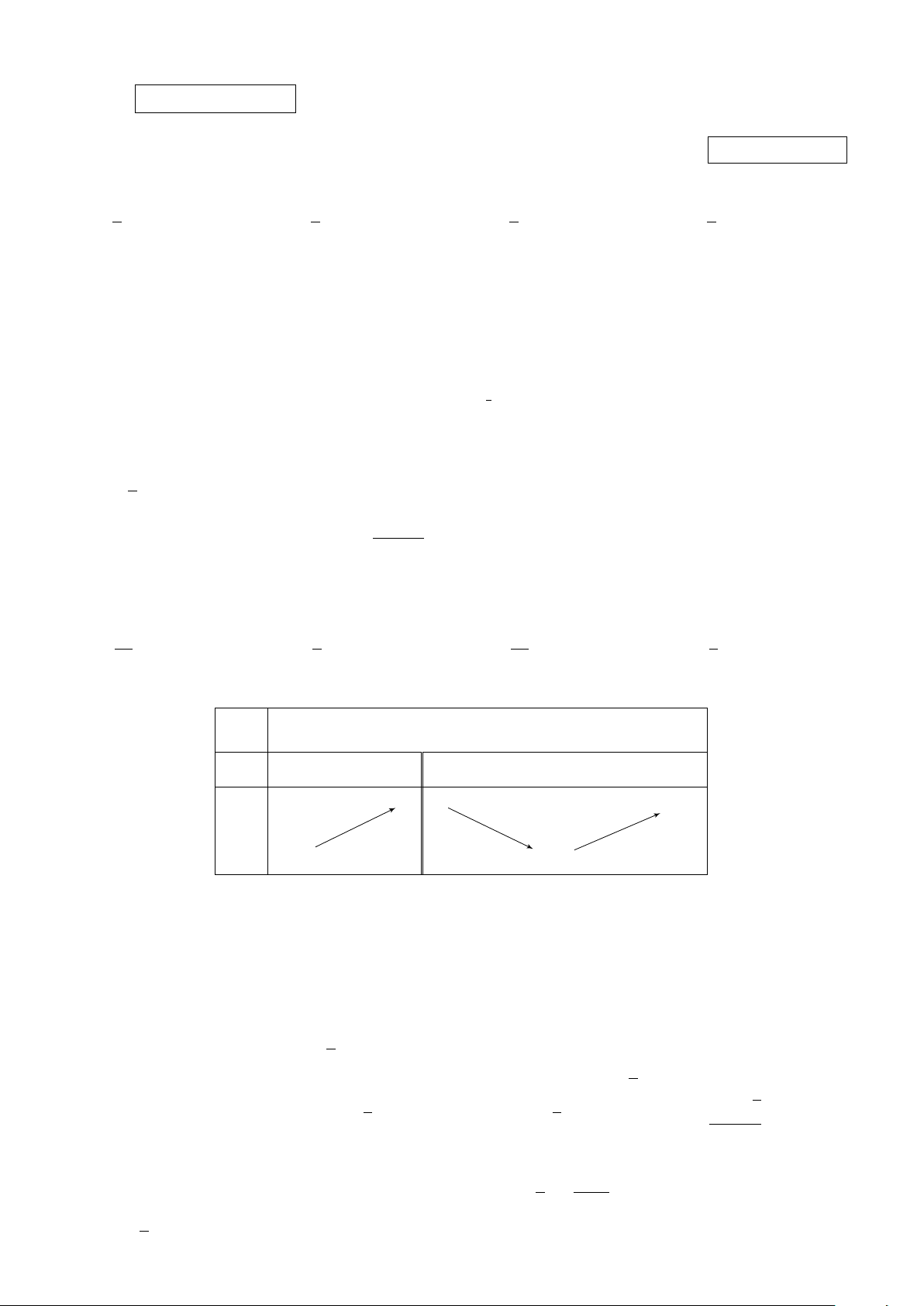
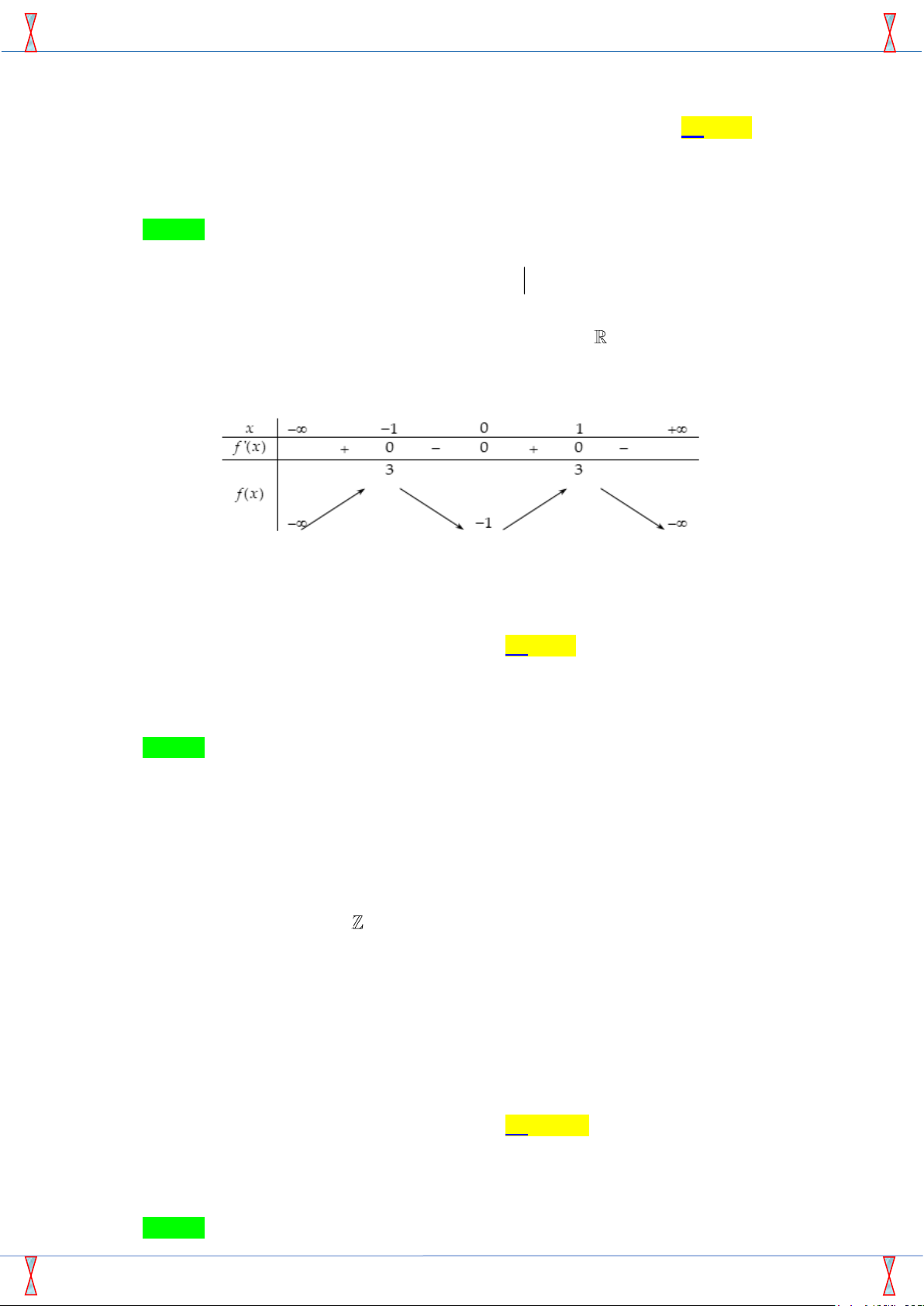
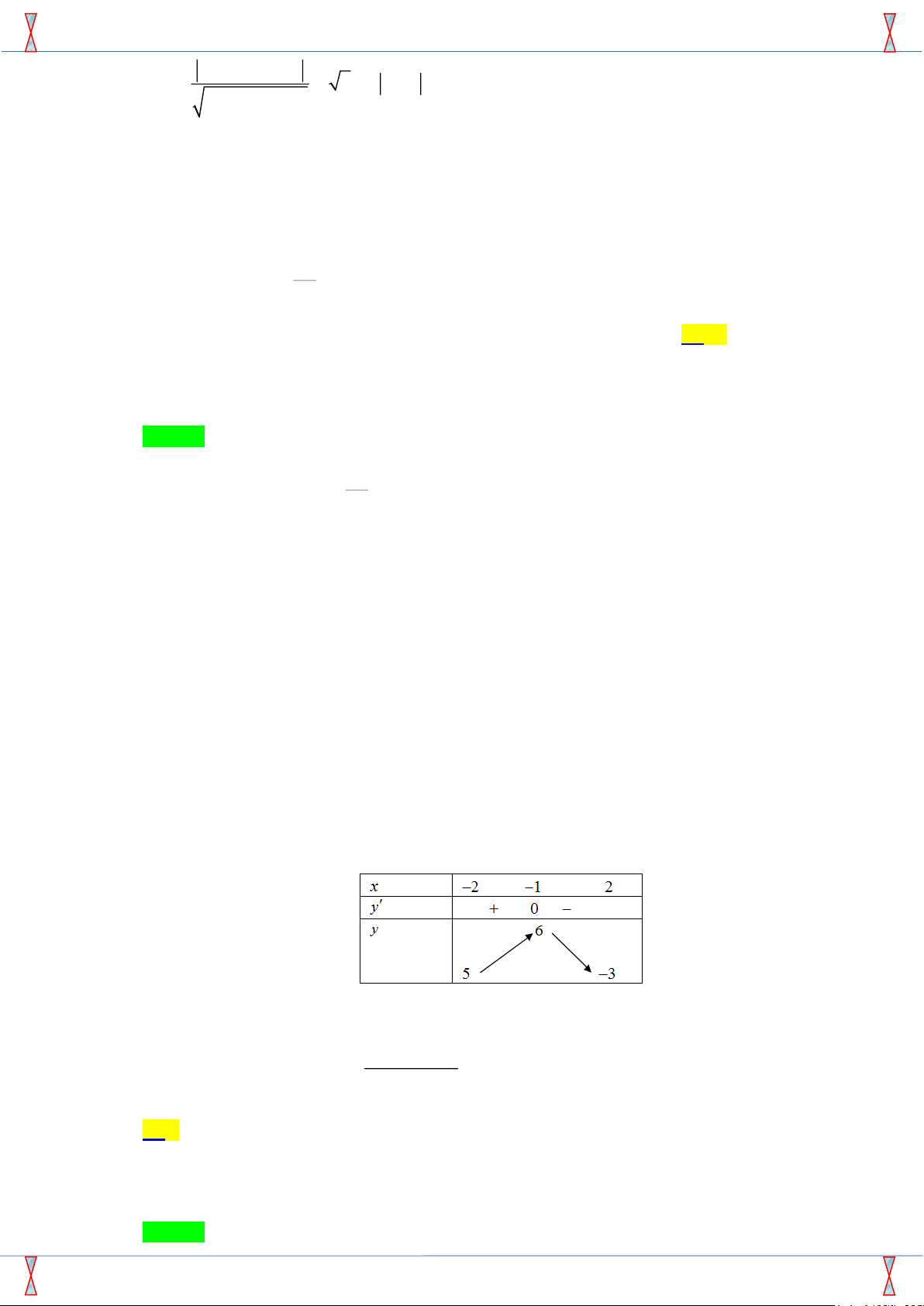
Câu 23. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau: x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 3 3 f (x) −∞ −1 − −∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f (x) = m có đúng hai nghiệm phân biệt? A. 2018. B. 4016. C. 2019. D. 2020.
Câu 24. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra. A. 9 năm. B. 10 năm. C. 11 năm. D. 12 năm. √
Câu 25. Cho hình phẳng giới hạn bởi các đường y =
x − 2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành. 7 5π 7π 11π A. V = . B. V = . C. V = . D. V = . 6 6 11 6
Câu 26. Họ nguyên hàm của hàm số f (x) = x4 + xex là 1 1 A. x5 + (x + 1)ex + C. B. x5 + (x − 1)ex + C. 5 5 1 C. x5 + xex + C. D. 4x3 + (x + 1)exC. 5
Câu 27. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1) là x − 5 y − 4 z + 1 x + 1 y + 2 z + 3 A. = = . B. = = . 2 1 2 4 2 −4 x − 1 y − 2 z − 3 x − 3 y − 3 z − 1 C. = = . D. = = . 4 2 4 −2 −1 2
Câu 28. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của hình chóp đó. √ √ √ √ a 28 a 14 a 33 a 11 A. h = . B. V = h = . C. h = . D. h = . 3 3 3 3 Trang 3/6 − Mã đề 638 Câu 29.
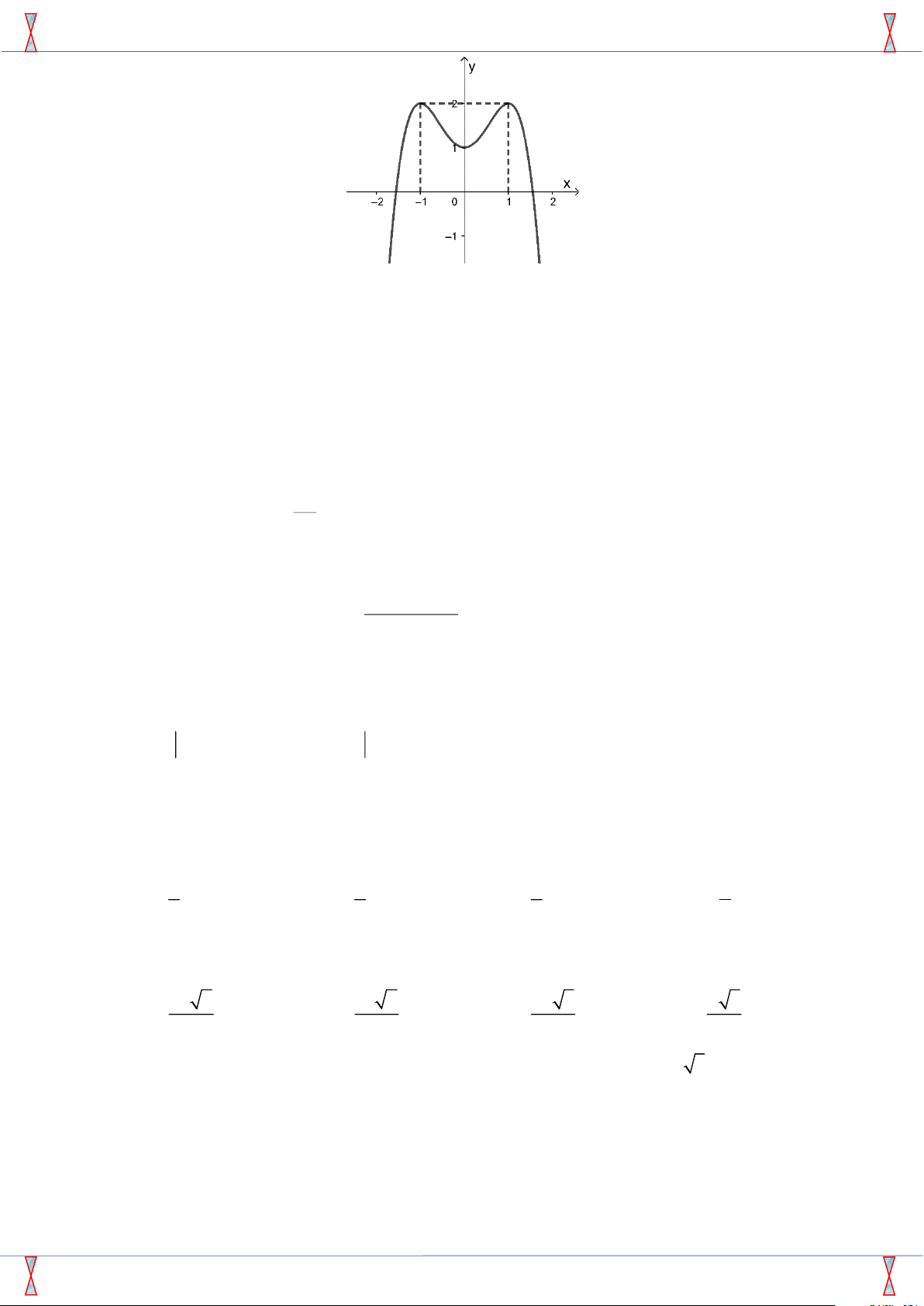
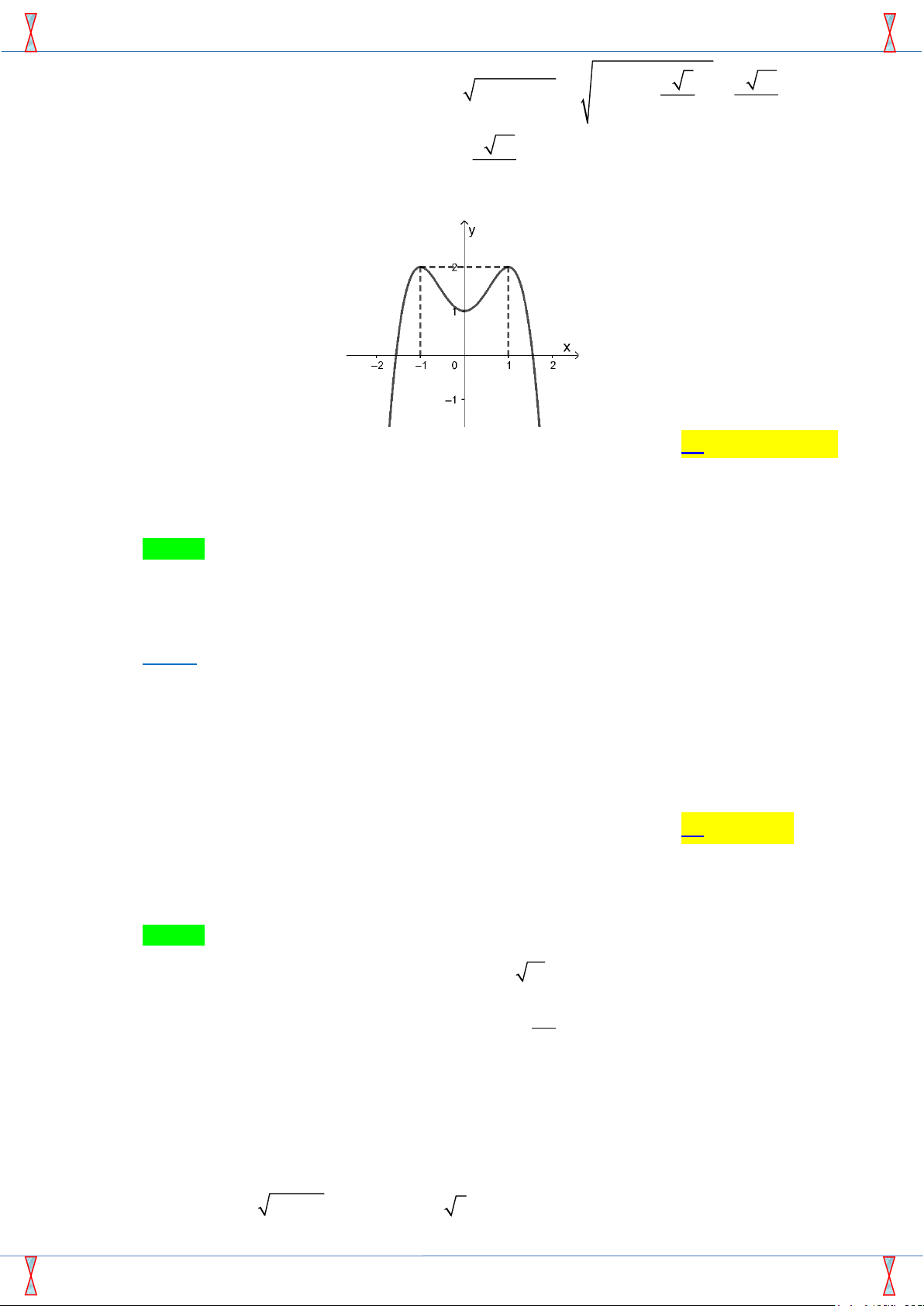
Đường cong trong hình bên là đồ thị của hàm số nào? y 2 A. y = −x4 + 1. B. y = x4 + 2x2 + 1. C. y = x4 + 1. D. y = −x4 + 2x2 + 1. 1 x −2 −1 O 1 2 −1
Câu 30. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q) : x − 2y + z − 5 = 0 và mặt cầu
(S) : (x − 1)2 + y2 + (z + 2)2 = 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây? A. (2; −2; 1). B. (1; −2; 0). C. (0; −1; −5). D. (−2; 2; −1).
Câu 31. Tập hợp các giá trị thực của tham số m để phương trình log (4−x2)+log (2x+m−1) = 2019 1 2019
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b. A. 20. B. 8. C. 18. D. 16. x − 2 Câu 32. Cho hàm số y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm mx2 − 2x + 4
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)? A. 1. B. 3. C. 0. D. 2.
Câu 33. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x4 − 8x3 − 6x2 + 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S. A. 42. B. 50. C. 30. D. 63. Câu 34.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a S
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM . 2 1 4 2 A. . B. . C. . D. − . 5 2 5 5 D A M B C
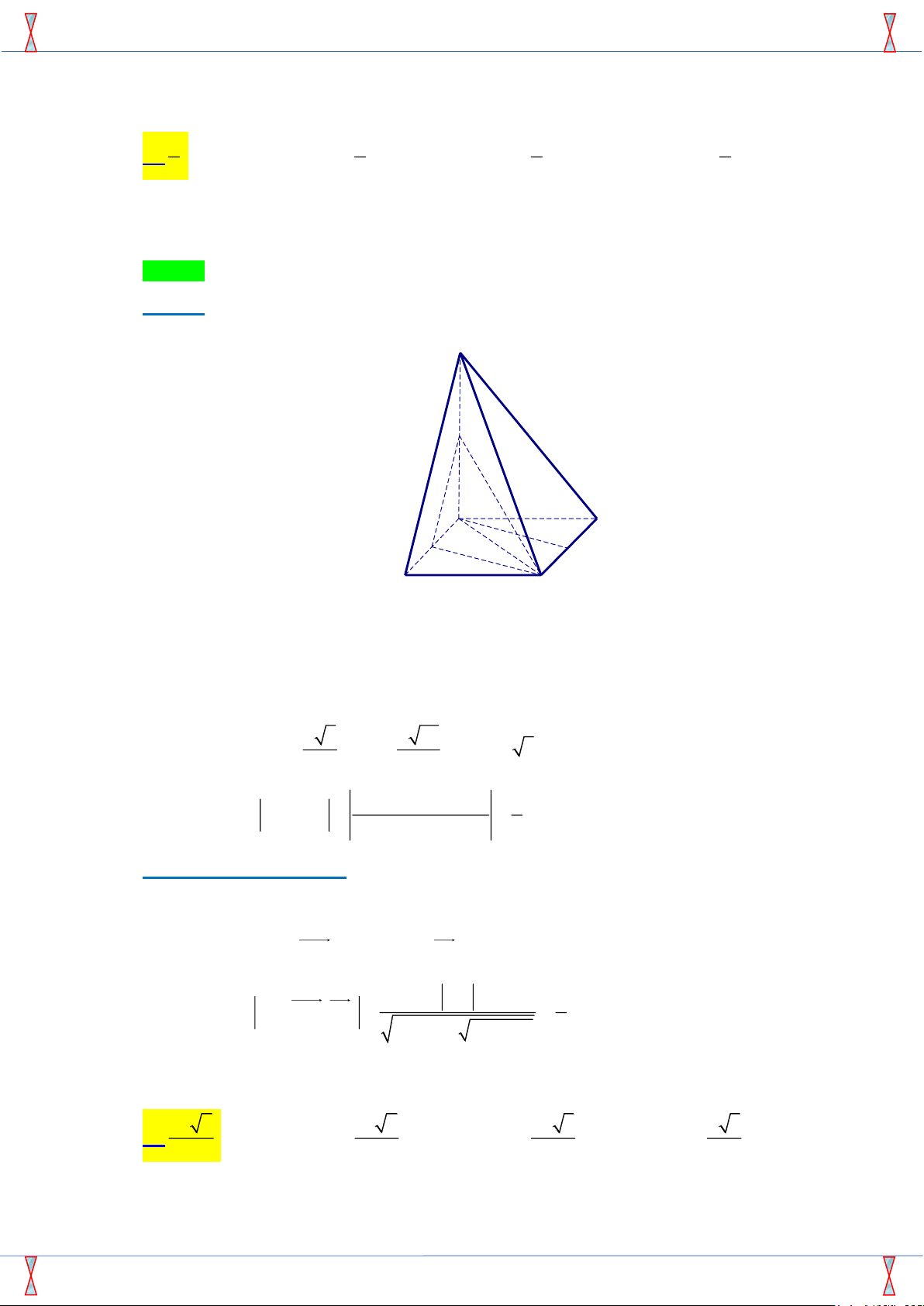
Câu 35. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện. √ √ √ √ 4a 6 3a 2 4a 3 a 3 A. . B. . C. . D. . 3 2 3 2 √
Câu 36. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60◦ chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm). A. V ≈ 1,42 cm3. B. V ≈ 2,36 cm3. C. V ≈ 1,53 cm3. D. V ≈ 2,47 cm3.
Câu 37. Trong không gian Oxyz, điểm M 0 đối xứng với điểm M (1; 2; 4) qua mặt phẳng
(α) : 2x + y + 2z − 3 = 0 có tọa độ là A. (−3; 0; 0). B. (−1; 1; 2). C. (−1; −2; −4). D. (2; 1; 2).
Câu 38. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2). # » # » # »
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức IA − 2IB + 3IC đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0 17 12 A. . B. 6. C. . D. 9. 5 5 Trang 4/6 − Mã đề 638
Câu 39. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực. Tính a + b. A. z = −2. B. 0. C. z = 2. D. 4. 4 Z x3 + x2 + 7x + 3 a a Câu 40. Biết dx =
+ c ln 5 với a, b, c là các số nguyên dương và là phân số x2 − x + 3 b b 1
tối giản. Tính P = a − b2 − c3. A. −5. B. −4. C. 5. D. 0.
Câu 41. Cho hàm số y = f (x) có đạo hàm liên tục trên [2; 4] và f 0(x) > 0, ∀x ∈ [2; 4]. Biết 4x3f (x) = 7
[f 0(x)]3 − x3, ∀x ∈ [2; 4], f (2) = . Giá trị f (4) bằng: √ 4√ √ √ 40 5 − 1 20 5 − 1 20 5 − 1 40 5 − 1 A. . B. . C. . D. . 2 4 2 4
Câu 42. Cho hàm số y = f (x) có đạo hàm liên tục trên R. Biết hàm số y = f 0(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử? y −1 O 1 3 x A. 4. B. 3. C. 6. D. 5.
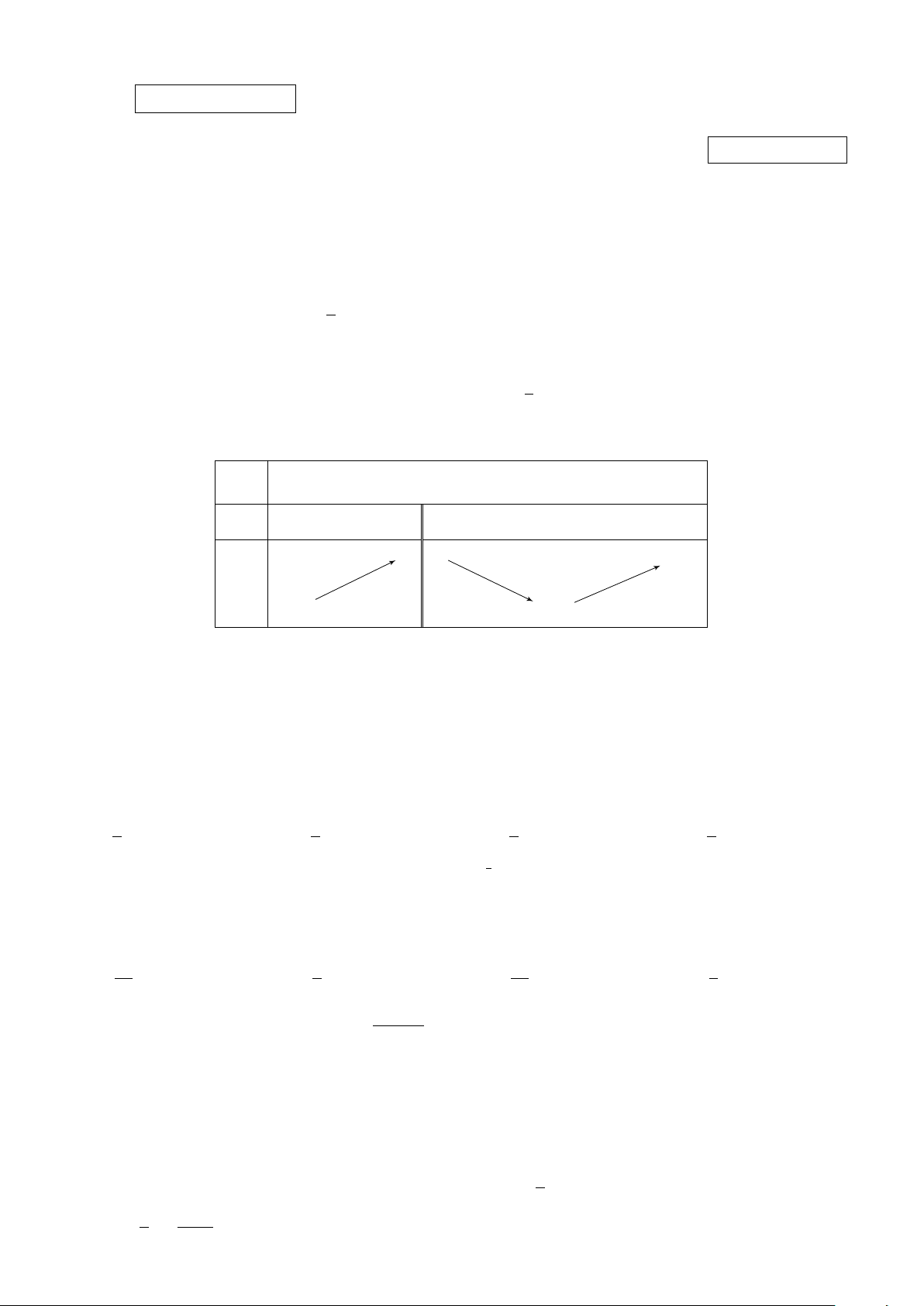
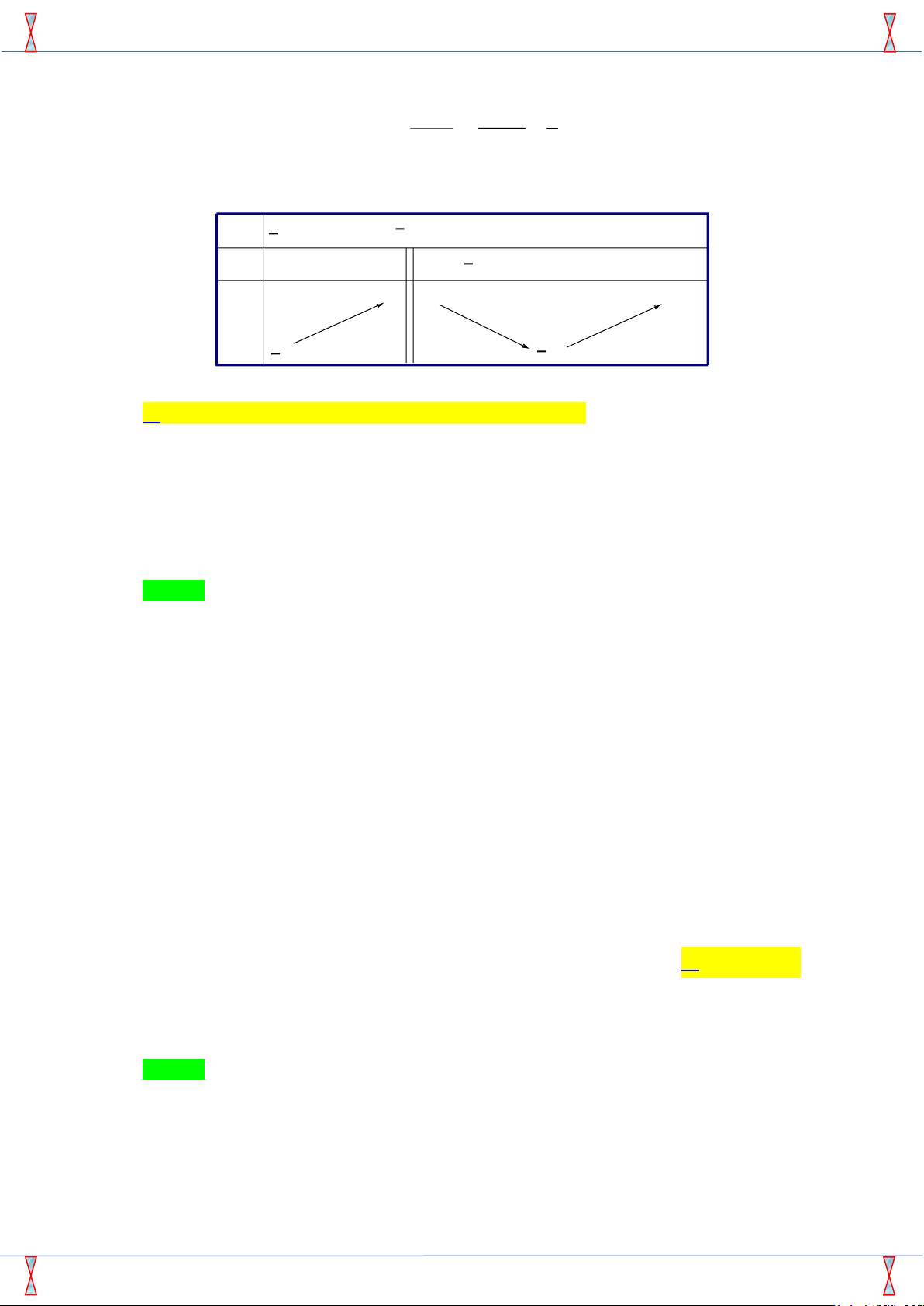
Câu 43. Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm 1 1 số g(x) = f (4x − x2) + x3 − 3x2 + 8x + trên đoạn [1;3]. 3 3 x −∞ 0 4 +∞ f 0(x) − 0 + 0 − +∞ + 5 f (x) −3 − −∞ 25 19 A. 15. B. . C. . D. 12. 3 3
Câu 44. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3), √ D(2; 0;
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)2 + (y − 4)2 + z2 = 39 thỏa mãn M A2 + −−→ −−→
2 · M B · M C = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó. √ √ √ √ A. 2 7. B. 7. C. 3 7. D. 4 7.
Câu 45. Cho hàm số y = f (x). Đồ thị hàm số y = f 0(x) như hình bên. 1 f(1−2x) Hàm số g(x) =
nghịch biến trên khoảng nào trong các khoảng y 2 sau? A. (0; 1). B. (−∞; 0). C. (−1; 0). D. (1; +∞). O x −1 1 2 4 Trang 5/6 − Mã đề 638
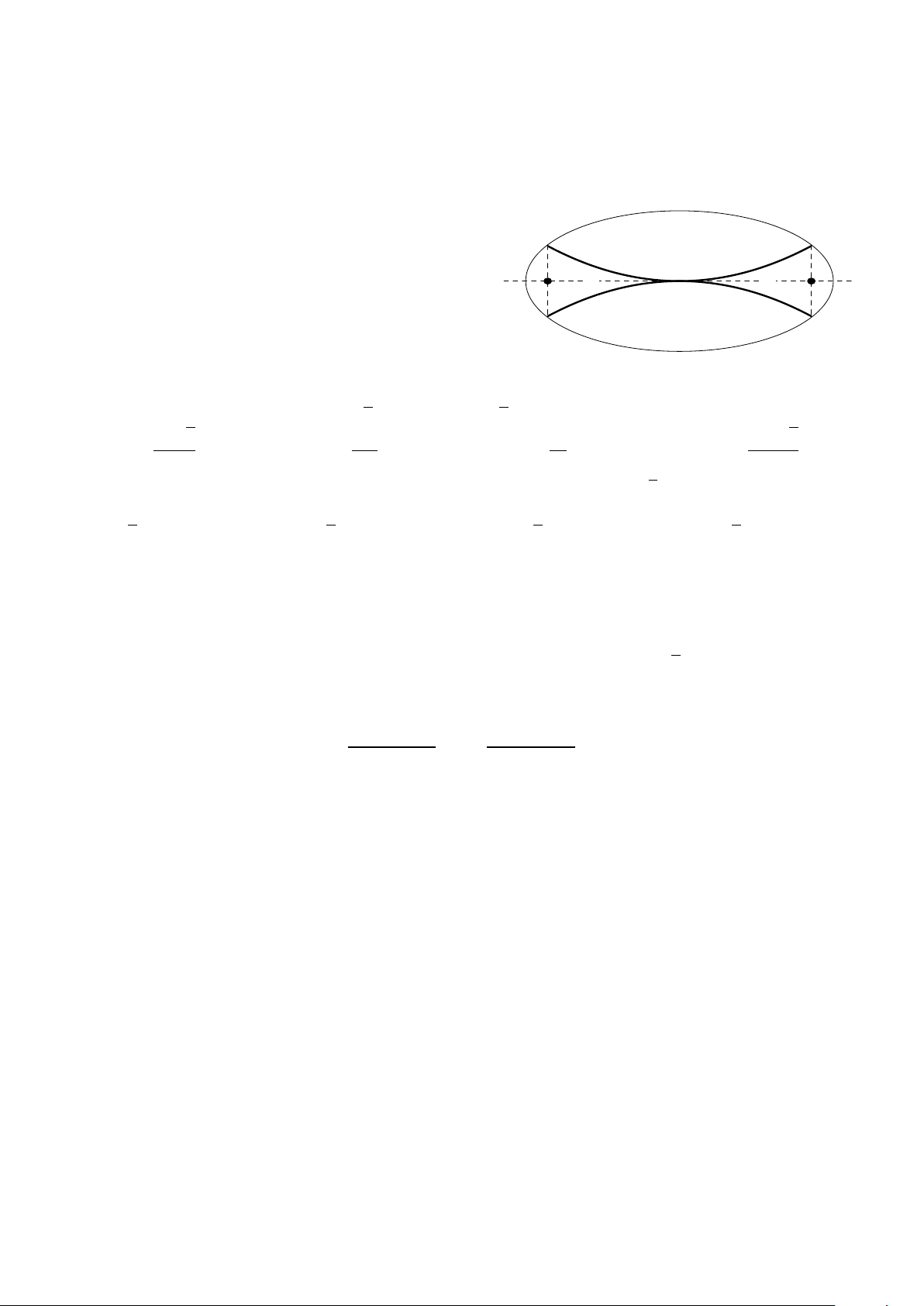
Câu 46. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F1, F2 là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 5.676.000 đ. B. 4.766.000 đ. C. 4.656.000 đ. D. 5.455.000 đ. A F1 F2 C D B
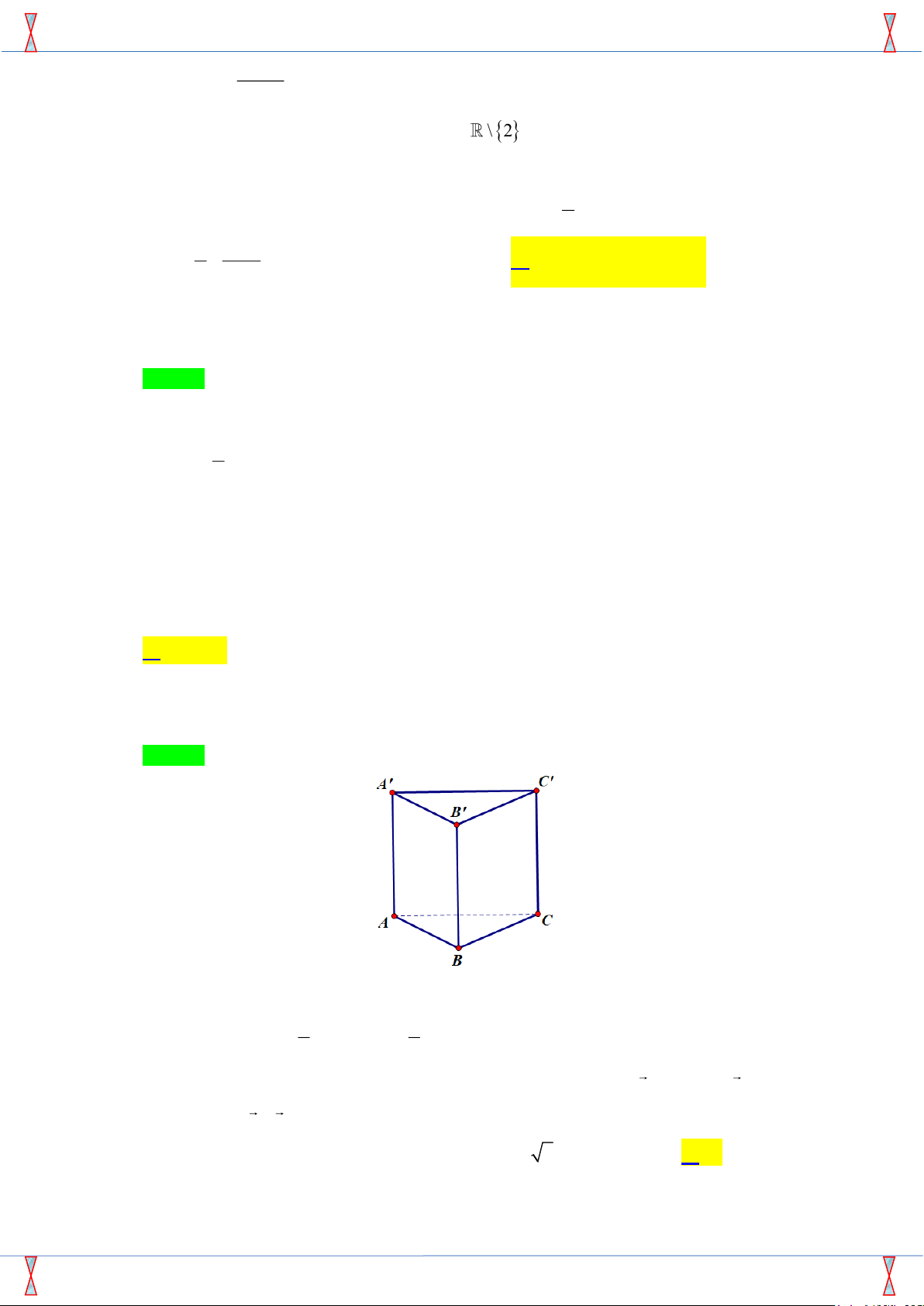
Câu 47. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng a. Gọi E và F lần lượt là các điểm trên 2 2
các cạnh A0D0 và A0B0 sao cho A0E = A0D0 và A0F =
A0B0. Tính thể tích khối chóp A.BDEF . √ 3 3 √ a3 3 5a3 a3 3a3 3 A. V = . B. V = . C. V = . D. V = . 8 18 8 8 √
Câu 48. Cho hai số phức z1;z2 thỏa mãn |z1 + 2 − i| + |z1 − 4 − 7i| = 6 2 và |iz2 − 1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z1 + z2|. √ √ √ √ A. 2 − 1. B. 2 + 1. C. 2 2 + 1. D. 2 2 − 1.
Câu 49. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18. A. 720. B. 860. C. 984. D. 1228.
Câu 50. Gọi m0 là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của √
đồ thị hàm số y = x3 − 6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng: A. m0 ∈ (2; 3). B. m0 ∈ (3; 4). C. m0 ∈ (0; 1). D. m0 ∈ (1; 2). HẾT Trang 6/6 − Mã đề 638 ĐÁP ÁN MÃ ĐỀ 638 1 B 6 D 11 D 16 C 21 C 26 B 31 D 36 A 41 D 46 A 2 C 7 D 12 C 17 A 22 D 27 D 32 A 37 A 42 D 47 B 3 A 8 A 13 D 18 C 23 C 28 C 33 A 38 B 43 D 48 D 4 D 9 D 14 C 19 B 24 C 29 D 34 A 39 B 44 A 49 C 5 D 10 A 15 D 20 B 25 D 30 D 35 A 40 B 45 D 50 C
Trang 1/1 − Đáp án mã đề 638
Trường THPT Chuyên Lê Hồng Phong
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019 ĐỀ CHÍNH THỨC
Môn: Toán - Lớp 12 - Khối ABCD (Đề thi có 6 trang)
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 752
Câu 1. Số phức liên hợp của số phức z = 5 + 6i là A. z = −5 − 6i. B. z = 5 − 6i. C. z = −5 + 6i. D. z = 6 − 5i.
Câu 2. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ? A. y + 5 = 0. B. 2x + 5y − 8z = 0. C. x − 2019 = 0. D. z + 20 = 0.
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC. A. G(−1; 2; −4). B. G(1; −2; −4). C. G(1; −2; 4). D. G(3; −6; 12).
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng? x −∞ −1 2 +∞ f 0(x) + − 0 + 1 1 +∞ + f (x) −∞ −2 −
A. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
B. Giá trị cực đại của hàm số bằng 1.
C. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
D. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2. − → − →
Câu 5. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ a = (3; 2; 1), b = (−2; 0; 1). Độ dài − → − → của véc-tơ a + b bằng √ A. 3. B. 2. C. 2. D. 1.
Câu 6. Cho cấp số nhân (un) có công bội q, số hạng đầu u1 = −2 và số hạng thứ tư u4 = 54. Giá trị của q bằng √ A. 6. B. −6. C. 3. D. −3.
Câu 7. Cho hình lăng trụ đứng ABC.A0B0C0 có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA0 = 3a. Tính thể tích V của lăng trụ đó. A. V = a3. B. V = 3a3. C. V = 3a2. D. V = 6a3. √
Câu 8. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a 2 bằng √ √ πa3 2 √ A. 2πa3. B. 4πa3 2. C. . D. πa3 2. 3
Câu 9. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng? a a log a A. log = log b − log a. B. log = . b b log b C. log(ab) = log a. log b. D. log(ab) = log a + log b.
Câu 10. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4
quả cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng. 2 3 3 1 A. . B. . C. . D. . 5 7 14 35 Trang 1/6 − Mã đề 752
Câu 11. Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai. b b Z Z A. f (x) dx = F (a) − F (b). B. f (x) dx = F (b) − F (a). a a a b a Z Z Z C. f (x) dx = 0. D. f (x) dx = − f (x) dx. a a b 1
Câu 12. Tìm tập xác định D của hàm số y = (2 − x)3 . A. D = (−∞; 2] . B. D = (−∞; 2) . C. D = (−∞; +∞) . D. D = (2; +∞). 2x − 1
Câu 13. Tập xác định của hàm số y = là 2x − 4 A. D = R \ {−2}. B. D = R \ {4}. C. D = R \ {−4}. D. D = R \ {2}.
Câu 14. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1) là x − 1 y − 2 z − 3 x − 5 y − 4 z + 1 A. = = . B. = = . 4 2 4 2 1 2 x + 1 y + 2 z + 3 x − 3 y − 3 z − 1 C. = = . D. = = . 4 2 −4 −2 −1 2 2x − 1
Câu 15. Viết phương trình tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ x0 = 0. 2x + 1 A. y = 4x + 1. B. y = −4x + 1. C. y = 4x − 1. D. y = 4x. x3 Câu 16. Cho hàm số y =
− x2 + x + 2019. Mệnh đề nào sau đây là đúng? 3
A. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1).
B. Hàm số đã cho đồng biến trên R.
C. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
D. Hàm số đã cho nghịch biến trên (−∞; 1).
Câu 17. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau: x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 3 3 f (x) −∞ −1 − −∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f (x) = m có đúng hai nghiệm phân biệt? A. 2018. B. 4016. C. 2020. D. 2019. Câu 18.
Đường cong trong hình bên là đồ thị của hàm số nào? y 2 A. y = x4 + 2x2 + 1. B. y = −x4 + 2x2 + 1. C. y = x4 + 1. D. y = −x4 + 1. 1 x −2 −1 O 1 2 −1 Trang 2/6 − Mã đề 752
Câu 19. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra. A. 12 năm. B. 11 năm. C. 10 năm. D. 9 năm.
Câu 20. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là √ 9π 7π 14 9π A. . B. . C. . D. 36π. 2 3 8
Câu 21. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q) : x − 2y + z − 5 = 0 và mặt cầu
(S) : (x − 1)2 + y2 + (z + 2)2 = 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây? A. (2; −2; 1). B. (1; −2; 0). C. (−2; 2; −1). D. (0; −1; −5).
Câu 22. Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + 4z + 29 = 0. Tính giá trị biểu thức |z1|4 + |z2|4. A. 1282. B. 841. C. 58. D. 1682.
Câu 23. Cho bất phương trình 4x −5.2x+1 +16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a2 + b2). A. 10. B. 0. C. 2. D. 1. √
Câu 24. Cho hình phẳng giới hạn bởi các đường y =
x − 2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành. 11π 7π 7 5π A. V = . B. V = . C. V = . D. V = . 6 11 6 6
Câu 25. Họ nguyên hàm của hàm số f (x) = x4 + xex là 1 1 A. x5 + xex + C. B. x5 + (x − 1)ex + C. 5 5 1 C. 4x3 + (x + 1)exC. D. x5 + (x + 1)ex + C. 5 5 5 Z Z Câu 26. Cho f (x) dx = −2. Tích phân [4f (x) − 3x2] dx bằng 0 0 A. −133. B. −130. C. −140. D. −120. Câu 27. y
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f 0(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau: y = f 0(x)
1) Hàm số y = f (x) có hai cực trị.
2) Hàm số y = f (x) đồng biến trên khoảng (1; +∞). −1 1 4
3) f (1) > f (2) > f (4). x O
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f (x) là f (1).
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 3. B. 2. C. 1. D. 4. Câu 28. Gọi z y
1, z2 lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. M Tính |z 2 1 + z2|. √ √ A. 20. B. 2 29. C. 116. D. 2 5. 1 x O 3 −4 N Trang 3/6 − Mã đề 752 Câu 29.
Hàm số nào cho dưới đây có đồ thị như hình bên? y A. y = log x + 1. B. y = log x. 2 3 C. y = log (x + 1). D. y = log (x + 1). 2 3 2 1 −1 O 1 2 x
Câu 30. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của hình chóp đó. √ √ √ √ a 33 a 14 a 11 a 28 A. h = . B. V = h = . C. h = . D. h = . 3 3 3 3
Câu 31. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực. Tính a + b. A. 0. B. z = −2. C. z = 2. D. 4. 4 Z x3 + x2 + 7x + 3 a a Câu 32. Biết dx =
+ c ln 5 với a, b, c là các số nguyên dương và là phân số x2 − x + 3 b b 1
tối giản. Tính P = a − b2 − c3. A. 5. B. −4. C. −5. D. 0.
Câu 33. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2). # » # » # »
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức IA − 2IB + 3IC đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0 17 12 A. 9. B. 6. C. . D. . 5 5
Câu 34. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện. √ √ √ √ 4a 6 4a 3 a 3 3a 2 A. . B. . C. . D. . 3 3 2 2 x − 2 Câu 35. Cho hàm số y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm mx2 − 2x + 4
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)? A. 0. B. 1. C. 2. D. 3. Câu 36.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a S
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM . 4 2 2 1 A. . B. − . C. . D. . 5 5 5 2 D A M B C
Câu 37. Trong không gian Oxyz, điểm M 0 đối xứng với điểm M (1; 2; 4) qua mặt phẳng
(α) : 2x + y + 2z − 3 = 0 có tọa độ là A. (2; 1; 2). B. (−3; 0; 0). C. (−1; −2; −4). D. (−1; 1; 2). Trang 4/6 − Mã đề 752 √
Câu 38. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60◦ chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm). A. V ≈ 2,47 cm3. B. V ≈ 1,42 cm3. C. V ≈ 2,36 cm3. D. V ≈ 1,53 cm3.
Câu 39. Tập hợp các giá trị thực của tham số m để phương trình log (4−x2)+log (2x+m−1) = 2019 1 2019
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b. A. 18. B. 16. C. 8. D. 20.
Câu 40. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x4 − 8x3 − 6x2 + 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S. A. 42. B. 30. C. 63. D. 50.
Câu 41. Gọi m0 là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của √
đồ thị hàm số y = x3 − 6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng: A. m0 ∈ (2; 3). B. m0 ∈ (0; 1). C. m0 ∈ (1; 2). D. m0 ∈ (3; 4).
Câu 42. Cho hàm số y = f (x) có đạo hàm liên tục trên R. Biết hàm số y = f 0(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử? y −1 O 1 3 x A. 5. B. 6. C. 4. D. 3.
Câu 43. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18. A. 984. B. 1228. C. 720. D. 860.
Câu 44. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng a. Gọi E và F lần lượt là các điểm trên 2 2
các cạnh A0D0 và A0B0 sao cho A0E = A0D0 và A0F =
A0B0. Tính thể tích khối chóp A.BDEF . 3√ 3 √ 5a3 a3 3 3a3 3 a3 A. V = . B. V = . C. V = . D. V = . 18 8 8 8 √
Câu 45. Cho hai số phức z1;z2 thỏa mãn |z1 + 2 − i| + |z1 − 4 − 7i| = 6 2 và |iz2 − 1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z1 + z2|. √ √ √ √ A. 2 + 1. B. 2 − 1. C. 2 2 − 1. D. 2 2 + 1.
Câu 46. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3), √ D(2; 0;
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)2 + (y − 4)2 + z2 = 39 thỏa mãn M A2 + −−→ −−→
2 · M B · M C = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó. √ √ √ √ A. 4 7. B. 2 7. C. 7. D. 3 7.
Câu 47. Cho hàm số y = f (x). Đồ thị hàm số y = f 0(x) như hình bên. 1 f(1−2x) Hàm số g(x) =
nghịch biến trên khoảng nào trong các khoảng y 2 sau? A. (−∞; 0). B. (−1; 0). C. (0; 1). D. (1; +∞). O x −1 1 2 4 Trang 5/6 − Mã đề 752
Câu 48. Cho hàm số y = f (x) có đạo hàm liên tục trên [2; 4] và f 0(x) > 0, ∀x ∈ [2; 4]. Biết 4x3f (x) = 7
[f 0(x)]3 − x3, ∀x ∈ [2; 4], f (2) = . Giá trị f (4) bằng: √ 4√ √ √ 20 5 − 1 40 5 − 1 40 5 − 1 20 5 − 1 A. . B. . C. . D. . 4 2 4 2
Câu 49. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F1, F2 là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 5.455.000 đ. B. 4.766.000 đ. C. 4.656.000 đ. D. 5.676.000 đ. A F1 F2 C D B
Câu 50. Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm 1 1 số g(x) = f (4x − x2) + x3 − 3x2 + 8x + trên đoạn [1;3]. 3 3 x −∞ 0 4 +∞ f 0(x) − 0 + 0 − +∞ + 5 f (x) −3 − −∞ 25 19 A. 12. B. . C. 15. D. . 3 3 HẾT Trang 6/6 − Mã đề 752 ĐÁP ÁN MÃ ĐỀ 752 1 B 6 D 11 A 16 B 21 C 26 A 31 A 36 C 41 B 46 B 2 B 7 B 12 B 17 D 22 D 27 B 32 B 37 B 42 A 47 D 3 C 8 D 13 D 18 B 23 D 28 D 33 B 38 B 43 A 48 C 4 C 9 D 14 D 19 B 24 A 29 C 34 A 39 B 44 A 49 D 5 A 10 B 15 C 20 B 25 B 30 A 35 B 40 A 45 C 50 A
Trang 1/1 − Đáp án mã đề 752
Trường THPT Chuyên Lê Hồng Phong
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019 ĐỀ CHÍNH THỨC
Môn: Toán - Lớp 12 - Khối ABCD (Đề thi có 6 trang)
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 843
Câu 1. Số phức liên hợp của số phức z = 5 + 6i là A. z = 6 − 5i. B. z = 5 − 6i. C. z = −5 − 6i. D. z = −5 + 6i.
Câu 2. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC. A. G(1; −2; −4). B. G(3; −6; 12). C. G(1; −2; 4). D. G(−1; 2; −4).
Câu 3. Cho hình lăng trụ đứng ABC.A0B0C0 có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA0 = 3a. Tính thể tích V của lăng trụ đó. A. V = 3a3. B. V = a3. C. V = 6a3. D. V = 3a2. 1
Câu 4. Tìm tập xác định D của hàm số y = (2 − x)3 . A. D = (−∞; 2) . B. D = (−∞; 2] . C. D = (−∞; +∞) . D. D = (2; +∞).
Câu 5. Cho cấp số nhân (un) có công bội q, số hạng đầu u1 = −2 và số hạng thứ tư u4 = 54. Giá trị của q bằng √ A. 3. B. −6. C. 6. D. −3. 2x − 1
Câu 6. Tập xác định của hàm số y = là 2x − 4 A. D = R \ {−4}. B. D = R \ {−2}. C. D = R \ {4}. D. D = R \ {2}.
Câu 7. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả
cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng. 3 3 1 2 A. . B. . C. . D. . 14 7 35 5
Câu 8. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng? x −∞ −1 2 +∞ f 0(x) + − 0 + 1 1 +∞ + f (x) −∞ −2 −
A. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
B. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
C. Giá trị cực đại của hàm số bằng 1.
D. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2. − → − →
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ a = (3; 2; 1), b = (−2; 0; 1). Độ dài − → − → của véc-tơ a + b bằng √ A. 1. B. 2. C. 3. D. 2. √
Câu 10. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a 2 bằng √ √ √ πa3 2 A. 2πa3. B. 4πa3 2. C. πa3 2. D. . 3
Câu 11. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng? a log a A. log(ab) = log a. log b. B. log = . b log b a C. log = log b − log a. D. log(ab) = log a + log b. b Trang 1/6 − Mã đề 843
Câu 12. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ? A. x − 2019 = 0. B. 2x + 5y − 8z = 0. C. y + 5 = 0. D. z + 20 = 0.
Câu 13. Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai. b b Z Z A. f (x) dx = F (b) − F (a). B. f (x) dx = F (a) − F (b). a a b a a Z Z Z C. f (x) dx = − f (x) dx. D. f (x) dx = 0. a b a Câu 14. Gọi z y
1, z2 lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. M Tính |z 2 1 + z2|. √ √ A. 20. B. 2 5. C. 116. D. 2 29. 1 x O 3 −4 N
Câu 15. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q) : x − 2y + z − 5 = 0 và mặt cầu
(S) : (x − 1)2 + y2 + (z + 2)2 = 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây? A. (1; −2; 0). B. (2; −2; 1). C. (−2; 2; −1). D. (0; −1; −5).
Câu 16. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau: x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 3 3 f (x) −∞ −1 − −∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f (x) = m có đúng hai nghiệm phân biệt? A. 2018. B. 2019. C. 4016. D. 2020. Câu 17. y
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f 0(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau: y = f 0(x)
1) Hàm số y = f (x) có hai cực trị.
2) Hàm số y = f (x) đồng biến trên khoảng (1; +∞). −1 1 4
3) f (1) > f (2) > f (4). x O
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f (x) là f (1).
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 1. B. 4. C. 2. D. 3.
Câu 18. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra. A. 11 năm. B. 9 năm. C. 10 năm. D. 12 năm. Trang 2/6 − Mã đề 843
Câu 19. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của hình chóp đó. √ √ √ √ a 14 a 11 a 33 a 28 A. V = h = . B. h = . C. h = . D. h = . 3 3 3 3
Câu 20. Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + 4z + 29 = 0. Tính giá trị biểu thức |z1|4 + |z2|4. A. 841. B. 1282. C. 1682. D. 58.
Câu 21. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1) là x − 1 y − 2 z − 3 x − 3 y − 3 z − 1 A. = = . B. = = . 4 2 4 −2 −1 2 x − 5 y − 4 z + 1 x + 1 y + 2 z + 3 C. = = . D. = = . 2 1 2 4 2 −4
Câu 22. Họ nguyên hàm của hàm số f (x) = x4 + xex là 1 1 A. x5 + (x + 1)ex + C. B. x5 + xex + C. 5 5 1 C. x5 + (x − 1)ex + C. D. 4x3 + (x + 1)exC. 5
Câu 23. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là √ 9π 9π 7π 14 A. . B. . C. . D. 36π. 2 8 3 5 5 Z Z Câu 24. Cho f (x) dx = −2. Tích phân [4f (x) − 3x2] dx bằng 0 0 A. −140. B. −120. C. −133. D. −130. √
Câu 25. Cho hình phẳng giới hạn bởi các đường y =
x − 2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành. 5π 11π 7 7π A. V = . B. V = . C. V = . D. V = . 6 6 6 11 Câu 26.
Đường cong trong hình bên là đồ thị của hàm số nào? y 2 A. y = x4 + 1. B. y = x4 + 2x2 + 1. C. y = −x4 + 2x2 + 1. D. y = −x4 + 1. 1 x −2 −1 O 1 2 −1 Câu 27.
Hàm số nào cho dưới đây có đồ thị như hình bên? y A. y = log x. B. y = log x + 1. 3 2 C. y = log (x + 1). D. y = log (x + 1). 3 2 2 1 −1 O 1 2 x
Câu 28. Cho bất phương trình 4x −5.2x+1 +16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a2 + b2). A. 2. B. 0. C. 10. D. 1. Trang 3/6 − Mã đề 843 2x − 1
Câu 29. Viết phương trình tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ x0 = 0. 2x + 1 A. y = 4x. B. y = 4x − 1. C. y = −4x + 1. D. y = 4x + 1. x3 Câu 30. Cho hàm số y =
− x2 + x + 2019. Mệnh đề nào sau đây là đúng? 3
A. Hàm số đã cho đồng biến trên R.
B. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
C. Hàm số đã cho nghịch biến trên (−∞; 1).
D. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1). 4 Z x3 + x2 + 7x + 3 a a Câu 31. Biết dx =
+ c ln 5 với a, b, c là các số nguyên dương và là phân số x2 − x + 3 b b 1
tối giản. Tính P = a − b2 − c3. A. −5. B. −4. C. 5. D. 0.
Câu 32. Trong không gian Oxyz, điểm M 0 đối xứng với điểm M (1; 2; 4) qua mặt phẳng
(α) : 2x + y + 2z − 3 = 0 có tọa độ là A. (2; 1; 2). B. (−1; 1; 2). C. (−1; −2; −4). D. (−3; 0; 0). x − 2 Câu 33. Cho hàm số y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm mx2 − 2x + 4
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)? A. 3. B. 0. C. 1. D. 2. Câu 34.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a S
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM . 2 1 2 4 A. . B. . C. − . D. . 5 2 5 5 D A M B C
Câu 35. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện. √ √ √ √ 4a 3 3a 2 a 3 4a 6 A. . B. . C. . D. . 3 2 2 3
Câu 36. Tập hợp các giá trị thực của tham số m để phương trình log (4−x2)+log (2x+m−1) = 2019 1 2019
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b. A. 20. B. 18. C. 8. D. 16.
Câu 37. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực. Tính a + b. A. z = −2. B. 0. C. 4. D. z = 2.
Câu 38. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x4 − 8x3 − 6x2 + 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S. A. 50. B. 63. C. 42. D. 30.
Câu 39. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2). # » # » # »
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức IA − 2IB + 3IC đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0 17 12 A. . B. 9. C. 6. D. . 5 5 Trang 4/6 − Mã đề 843 √
Câu 40. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60◦ chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm). A. V ≈ 1,53 cm3. B. V ≈ 2,47 cm3. C. V ≈ 1,42 cm3. D. V ≈ 2,36 cm3.
Câu 41. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F1, F2 là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 4.766.000 đ. B. 4.656.000 đ. C. 5.455.000 đ. D. 5.676.000 đ. A F1 F2 C D B
Câu 42. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18. A. 860. B. 984. C. 720. D. 1228.
Câu 43. Cho hàm số y = f (x) có đạo hàm liên tục trên R. Biết hàm số y = f 0(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử? y −1 O 1 3 x A. 5. B. 3. C. 4. D. 6.
Câu 44. Cho hàm số y = f (x). Đồ thị hàm số y = f 0(x) như hình bên. 1 f(1−2x) Hàm số g(x) =
nghịch biến trên khoảng nào trong các khoảng y 2 sau? A. (−1; 0). B. (−∞; 0). C. (0; 1). D. (1; +∞). O x −1 1 2 4 √
Câu 45. Cho hai số phức z1;z2 thỏa mãn |z1 + 2 − i| + |z1 − 4 − 7i| = 6 2 và |iz2 − 1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z1 + z2|. √ √ √ √ A. 2 + 1. B. 2 2 + 1. C. 2 − 1. D. 2 2 − 1.
Câu 46. Cho hàm số y = f (x) có đạo hàm liên tục trên [2; 4] và f 0(x) > 0, ∀x ∈ [2; 4]. Biết 4x3f (x) = 7
[f 0(x)]3 − x3, ∀x ∈ [2; 4], f (2) = . Giá trị f (4) bằng: √ 4√ √ √ 20 5 − 1 40 5 − 1 40 5 − 1 20 5 − 1 A. . B. . C. . D. . 4 2 4 2
Câu 47. Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm 1 1 số g(x) = f (4x − x2) + x3 − 3x2 + 8x + trên đoạn [1;3]. 3 3 Trang 5/6 − Mã đề 843 x −∞ 0 4 +∞ f 0(x) − 0 + 0 − +∞ + 5 f (x) −3 − −∞ 25 19 A. 15. B. . C. . D. 12. 3 3
Câu 48. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3), √ D(2; 0;
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)2 + (y − 4)2 + z2 = 39 thỏa mãn M A2 + −−→ −−→
2 · M B · M C = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó. √ √ √ √ A. 2 7. B. 4 7. C. 7. D. 3 7.
Câu 49. Gọi m0 là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của √
đồ thị hàm số y = x3 − 6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng: A. m0 ∈ (2; 3). B. m0 ∈ (0; 1). C. m0 ∈ (3; 4). D. m0 ∈ (1; 2).
Câu 50. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng a. Gọi E và F lần lượt là các điểm trên 2 2
các cạnh A0D0 và A0B0 sao cho A0E = A0D0 và A0F =
A0B0. Tính thể tích khối chóp A.BDEF . 3 √ 3 √ 5a3 3a3 3 a3 3 a3 A. V = . B. V = . C. V = . D. V = . 18 8 8 8 HẾT Trang 6/6 − Mã đề 843 ĐÁP ÁN MÃ ĐỀ 843 1 B 6 D 11 D 16 B 21 B 26 C 31 B 36 D 41 D 46 C 2 C 7 B 12 B 17 C 22 C 27 D 32 D 37 B 42 B 47 D 3 A 8 A 13 B 18 A 23 C 28 D 33 C 38 C 43 A 48 A 4 A 9 C 14 B 19 C 24 C 29 B 34 A 39 C 44 D 49 B 5 D 10 C 15 C 20 C 25 B 30 A 35 D 40 C 45 D 50 A
Trang 1/1 − Đáp án mã đề 843
Trường THPT Chuyên Lê Hồng Phong
ĐỀ THI 8 TUẦN HỌC KÌ II, NĂM HỌC 2018-2019 ĐỀ CHÍNH THỨC
Môn: Toán - Lớp 12 - Khối ABCD (Đề thi có 6 trang)
Thời gian làm bài 90 phút (50 câu trắc nghiệm)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Mã đề thi 926
Câu 1. Cho hình lăng trụ đứng ABC.A0B0C0 có đáy là tam giác vuông tại A, AB = a, AC = 2a,
AA0 = 3a. Tính thể tích V của lăng trụ đó. A. V = a3. B. V = 6a3. C. V = 3a3. D. V = 3a2.
Câu 2. Cho cấp số nhân (un) có công bội q, số hạng đầu u1 = −2 và số hạng thứ tư u4 = 54. Giá trị của q bằng √ A. −6. B. 3. C. −3. D. 6. − → − →
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho hai véc-tơ a = (3; 2; 1), b = (−2; 0; 1). Độ dài − → − → của véc-tơ a + b bằng √ A. 1. B. 3. C. 2. D. 2.
Câu 4. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Mệnh đề nào sau đây đúng? x −∞ −1 2 +∞ f 0(x) + − 0 + 1 1 +∞ + f (x) −∞ −2 −
A. Hàm số đạt cực tiểu tại x = −1 và đạt cực đại tại x = 2.
B. Giá trị cực đại của hàm số bằng 1.
C. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
D. Hàm số đạt cực đại tại x = −1 và đạt cực tiểu tại x = 2.
Câu 5. Trong không gian Oxyz, mặt phẳng nào dưới đây đi qua gốc tọa độ? A. z + 20 = 0. B. x − 2019 = 0. C. y + 5 = 0. D. 2x + 5y − 8z = 0.
Câu 6. Số phức liên hợp của số phức z = 5 + 6i là A. z = 5 − 6i. B. z = −5 − 6i. C. z = 6 − 5i. D. z = −5 + 6i. 1
Câu 7. Tìm tập xác định D của hàm số y = (2 − x)3 . A. D = (−∞; 2) . B. D = (−∞; 2] . C. D = (−∞; +∞) . D. D = (2; +∞).
Câu 8. Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ hộp ra 4 quả
cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng. 3 2 1 3 A. . B. . C. . D. . 14 5 35 7 2x − 1
Câu 9. Tập xác định của hàm số y = là 2x − 4 A. D = R \ {2}. B. D = R \ {−2}. C. D = R \ {−4}. D. D = R \ {4}.
Câu 10. Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0; 2; 5), B(−2; 0; 1), C(5; −8; 6). Tìm
tọa độ trọng tâm G của tam giác ABC. A. G(1; −2; −4). B. G(−1; 2; −4). C. G(1; −2; 4). D. G(3; −6; 12).
Câu 11. Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng? a A. log(ab) = log a. log b. B. log = log b − log a. b a log a C. log = . D. log(ab) = log a + log b. b log b Trang 1/6 − Mã đề 926
Câu 12. Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai. b a b Z Z Z A. f (x) dx = − f (x) dx. B. f (x) dx = F (a) − F (b). a b a b a Z Z C. f (x) dx = F (b) − F (a). D. f (x) dx = 0. a a √
Câu 13. Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a 2 bằng √ πa3 2 √ √ A. . B. 2πa3. C. πa3 2. D. 4πa3 2. 3 x3 Câu 14. Cho hàm số y =
− x2 + x + 2019. Mệnh đề nào sau đây là đúng? 3
A. Hàm số đã cho đồng biến trên R.
B. Hàm số đã cho nghịch biến trên (−∞; 1).
C. Hàm số đã cho đồng biến trên (−∞; 1) và nghịch biến trên (1; +∞).
D. Hàm số đã cho đồng biến trên (1; +∞) và nghịch biến trên (−∞; 1). 2x − 1
Câu 15. Viết phương trình tiếp tuyến của đồ thị hàm số y =
tại điểm có hoành độ x0 = 0. 2x + 1 A. y = 4x. B. y = −4x + 1. C. y = 4x + 1. D. y = 4x − 1.
Câu 16. Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7%/năm. Biết rằng nếu không
rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm
tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn 600 triệu đồng bao
gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra. A. 10 năm. B. 11 năm. C. 9 năm. D. 12 năm. 5 5 Z Z Câu 17. Cho f (x) dx = −2. Tích phân [4f (x) − 3x2] dx bằng 0 0 A. −133. B. −120. C. −130. D. −140.
Câu 18. Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q) : x − 2y + z − 5 = 0 và mặt cầu
(S) : (x − 1)2 + y2 + (z + 2)2 = 15. Mặt phẳng (P ) song song với mặt phẳng (Q) và cắt mặt cầu (S)
theo giao tuyến là một đường tròn có chu vi bằng 6π đi qua điểm nào sau đây? A. (2; −2; 1). B. (1; −2; 0). C. (−2; 2; −1). D. (0; −1; −5). √
Câu 19. Cho hình phẳng giới hạn bởi các đường y =
x − 2, y = 0 và x = 9 quay xung quanh trục
Ox. Tính thể tích khối tròn xoay tạo thành. 5π 11π 7π 7 A. V = . B. V = . C. V = . D. V = . 6 6 11 6 Câu 20.
Đường cong trong hình bên là đồ thị của hàm số nào? y 2 A. y = x4 + 1. B. y = x4 + 2x2 + 1. C. y = −x4 + 1. D. y = −x4 + 2x2 + 1. 1 x −2 −1 O 1 2 −1
Câu 21. Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2, 3 là √ 9π 9π 7π 14 A. . B. . C. 36π. D. . 8 2 3 Trang 2/6 − Mã đề 926
Câu 22. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình sau: x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 3 3 f (x) −∞ −1 − −∞
Có bao nhiêu giá trị nguyên m ∈ [−2019; 2019] để phương trình f (x) = m có đúng hai nghiệm phân biệt? A. 2020. B. 2018. C. 4016. D. 2019.
Câu 23. Gọi z1 và z2 là hai nghiệm phức của phương trình z2 + 4z + 29 = 0. Tính giá trị biểu thức |z1|4 + |z2|4. A. 841. B. 58. C. 1682. D. 1282. Câu 24.
Hàm số nào cho dưới đây có đồ thị như hình bên? y A. y = log x. B. y = log (x + 1). 3 2 C. y = log x + 1. D. y = log (x + 1). 2 3 2 1 −1 O 1 2 x
Câu 25. Cho bất phương trình 4x −5.2x+1 +16 ≤ 0 có tập nghiệm là đoạn [a; b]. Tính log (a2 + b2). A. 2. B. 1. C. 0. D. 10. Câu 26. y
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f 0(x)
có đồ thị như hình bên. Cho bốn mệnh đề sau: y = f 0(x)
1) Hàm số y = f (x) có hai cực trị.
2) Hàm số y = f (x) đồng biến trên khoảng (1; +∞). −1 1 4
3) f (1) > f (2) > f (4). x O
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f (x) là f (1).
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 3. B. 1. C. 4. D. 2.
Câu 27. Cho hình chóp tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính chiều cao h của hình chóp đó. √ √ √ √ a 28 a 33 a 11 a 14 A. h = . B. h = . C. h = . D. V = h = . 3 3 3 3 Câu 28. Gọi z y
1, z2 lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. M Tính |z 2 1 + z2|. √ √ A. 2 29. B. 2 5. C. 20. D. 116. 1 x O 3 −4 N Trang 3/6 − Mã đề 926
Câu 29. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm A (1; 2; 3) , B (5; 4; −1) là x − 3 y − 3 z − 1 x − 5 y − 4 z + 1 A. = = . B. = = . −2 −1 2 2 1 2 x + 1 y + 2 z + 3 x − 1 y − 2 z − 3 C. = = . D. = = . 4 2 −4 4 2 4
Câu 30. Họ nguyên hàm của hàm số f (x) = x4 + xex là 1 1 A. x5 + (x − 1)ex + C. B. x5 + xex + C. 5 5 1 C. x5 + (x + 1)ex + C. D. 4x3 + (x + 1)exC. 5
Câu 31. Tập hợp các giá trị thực của tham số m để phương trình log (4−x2)+log (2x+m−1) = 2019 1 2019
0 có hai nghiệm thực phân biệt là T = (a; b). Tính S = 2a + b. A. 18. B. 8. C. 20. D. 16.
Câu 32. Trong không gian Oxyz, điểm M 0 đối xứng với điểm M (1; 2; 4) qua mặt phẳng
(α) : 2x + y + 2z − 3 = 0 có tọa độ là A. (−1; −2; −4). B. (−3; 0; 0). C. (−1; 1; 2). D. (2; 1; 2).
Câu 33. Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng khoảng
cách từ I đến tất cả các mặt của bát diện. √ √ √ √ 4a 6 3a 2 4a 3 a 3 A. . B. . C. . D. . 3 2 3 2
Câu 34. Cho số phức z = a + bi, (a, b ∈ R) thỏa mãn |z − 3| = |z − 1| và (z + 2)(z − i) là số thực. Tính a + b. A. 0. B. 4. C. z = −2. D. z = 2.
Câu 35. Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số y = |3x4 − 8x3 − 6x2 + 24x − m|
có 7 điểm cực trị. Tính tổng các phần tử của S. A. 42. B. 30. C. 50. D. 63.
Câu 36. Trong không gian với hệ tọa độ Oxyz cho ba điểm A(−1; 2; 5), B(3; −1; 0), C(−4; 0; −2). # » # » # »
Gọi I là điểm trên mặt phẳng (Oxy) sao cho biểu thức IA − 2IB + 3IC đạt giá trị nhỏ nhất. Tính
khoảng cách từ I đến mặt phẳng P : 4x + 3y + 2 = 0 17 12 A. 9. B. . C. . D. 6. 5 5 x − 2 Câu 37. Cho hàm số y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm mx2 − 2x + 4
số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)? A. 0. B. 2. C. 3. D. 1. √
Câu 38. Một khối nón có bán kính đáy bằng 2 cm, chiều cao bằng
3 cm. Một mặt phẳng đi qua
đỉnh và tạo với đáy một góc 60◦ chia khối nón thành 2 phần. Tính thể tích V phần nhỏ hơn (tính gần
đúng đến hàng phần trăm). A. V ≈ 1,53 cm3. B. V ≈ 2,47 cm3. C. V ≈ 1,42 cm3. D. V ≈ 2,36 cm3. Câu 39.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a; cạnh SA = a S
và vuông góc với đáy. Gọi M là trung điểm của CD. Tính cos α với α là
góc tạo bởi hai đường thẳng SB và AM . 2 1 2 4 A. − . B. . C. . D. . 5 2 5 5 D A M B C Trang 4/6 − Mã đề 926 4 Z x3 + x2 + 7x + 3 a a Câu 40. Biết dx =
+ c ln 5 với a, b, c là các số nguyên dương và là phân số x2 − x + 3 b b 1
tối giản. Tính P = a − b2 − c3. A. −5. B. 5. C. 0. D. −4.
Câu 41. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3), √ D(2; 0;
7). Gọi M là điểm thuộc mặt cầu (S) : (x + 2)2 + (y − 4)2 + z2 = 39 thỏa mãn M A2 + −−→ −−→
2 · M B · M C = 8. Biết độ dài đoạn thẳng M D đạt giá trị lớn nhất. Tính giá trị lớn nhất đó. √ √ √ √ A. 7. B. 2 7. C. 3 7. D. 4 7.
Câu 42. Từ các chữ số thuộc tập X = {0; 1; 2; 3; 4; 5; 6; 7} có thể lập được bao nhiêu số tự nhiên gồm
6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18. A. 1228. B. 720. C. 860. D. 984.
Câu 43. Cho hình lập phương ABCD.A0B0C0D0 có cạnh bằng a. Gọi E và F lần lượt là các điểm trên 2 2
các cạnh A0D0 và A0B0 sao cho A0E = A0D0 và A0F =
A0B0. Tính thể tích khối chóp A.BDEF . √ 3√ 3 3a3 3 a3 3 a3 5a3 A. V = . B. V = . C. V = . D. V = . 8 8 8 18
Câu 44. Cho hàm số y = f (x) có đạo hàm liên tục trên [2; 4] và f 0(x) > 0, ∀x ∈ [2; 4]. Biết 4x3f (x) = 7
[f 0(x)]3 − x3, ∀x ∈ [2; 4], f (2) = . Giá trị f (4) bằng: √ 4√ √ √ 20 5 − 1 40 5 − 1 20 5 − 1 40 5 − 1 A. . B. . C. . D. . 4 2 2 4
Câu 45. Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm 1 1 số g(x) = f (4x − x2) + x3 − 3x2 + 8x + trên đoạn [1;3]. 3 3 x −∞ 0 4 +∞ f 0(x) − 0 + 0 − +∞ + 5 f (x) −3 − −∞ 25 19 A. . B. 15. C. . D. 12. 3 3
Câu 46. Cho hàm số y = f (x). Đồ thị hàm số y = f 0(x) như hình bên. 1 f(1−2x) Hàm số g(x) =
nghịch biến trên khoảng nào trong các khoảng y 2 sau? A. (−∞; 0). B. (0; 1). C. (−1; 0). D. (1; +∞). O x −1 1 2 4
Câu 47. Gọi m0 là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của của √
đồ thị hàm số y = x3 − 6mx + 4 cắt đường tròn tâm I(1; 0), bán kính bằng
2 tại hai điểm phân biệt
A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng: A. m0 ∈ (0; 1). B. m0 ∈ (3; 4). C. m0 ∈ (1; 2). D. m0 ∈ (2; 3).
Câu 48. Cho hàm số y = f (x) có đạo hàm liên tục trên R. Biết hàm số y = f 0(x) có đồ thị như
hình vẽ. Gọi S là tập hợp các giá trị nguyên m ∈ [−5; 5] để hàm số g(x) = f (x + m) nghịch biến trên
(1; 2). Hỏi tập S có tất cả bao nhiêu phần tử? Trang 5/6 − Mã đề 926 y −1 O 1 3 x A. 6. B. 5. C. 4. D. 3.
Câu 49. Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai
đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục
lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F1, F2 là hai tiêu điểm của elip. Phần A, B dùng để trồng
hoa, phần C, D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ
và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 5.676.000 đ. B. 4.656.000 đ. C. 4.766.000 đ. D. 5.455.000 đ. A F1 F2 C D B √
Câu 50. Cho hai số phức z1;z2 thỏa mãn |z1 + 2 − i| + |z1 − 4 − 7i| = 6 2 và |iz2 − 1 + 2i| = 1. Tìm
giá trị nhỏ nhất của biểu thức T = |z1 + z2|. √ √ √ √ A. 2 2 + 1. B. 2 − 1. C. 2 2 − 1. D. 2 + 1. HẾT Trang 6/6 − Mã đề 926 ĐÁP ÁN MÃ ĐỀ 926 1 C 6 A 11 D 16 B 21 D 26 D 31 D 36 D 41 B 46 D 2 C 7 A 12 B 17 A 22 D 27 B 32 B 37 D 42 D 47 A 3 B 8 D 13 C 18 C 23 C 28 B 33 A 38 C 43 D 48 B 4 C 9 A 14 A 19 B 24 B 29 A 34 A 39 C 44 D 49 A 5 D 10 C 15 D 20 D 25 B 30 A 35 A 40 D 45 D 50 C
Trang 1/1 − Đáp án mã đề 926
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 ĐỀ 8 TUẦN HKII
TRƯỜNG CHUYÊN LÊ HỒNG PHONG NĂM 2019 MÔN TOÁN THỜI GIAN: 90 PHÚT
Bản quyền thuộc về tập thể thầy cô nhóm STRONG.
Tổng biên tập tài liệu: Admin Lưu Thêm
Gv THPT Yên Phong 1 - Bắc Ninh
Câu 1: [2H2-2.3-1] Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a 2 bằng 3 A.  3 a 2 4 a 2 . B. 3 a 2 . C. 3 2 a . D. . 3
Câu 2: [1D2-4.3-2] Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ
hộp ra 4 quả cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng. A. 3 . B. 1 . C. 3 . D. 2 . 14 35 7 5
Câu 3: [2D1-2.3-1] Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. x ∞ 1 2 + ∞ f /(x) + 0 + 1 1 f(x) + ∞ ∞ 2
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
B. Hàm số đạt cực tiểu tại x = 1
− và đạt cực đại tại x = 2 .
C. Hàm số đạt cực đại tại x = 1
− và đạt cực tiểu tại x = 2 .
D. Giá trị cực đại của hàm số bằng 1.
Câu 4: [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(0;2;5) , B( 2 − ;0; ) 1 ,
C (5; − 8;6) . Tìm tọa độ trọng tâm G của tam giác ABC .
A. G(3;− 6;12) .
B. G (1;− 2;− 4). C. G( 1; − 2;− 4) .
D. G (1;− 2;4) .
Câu 5: [2D4-1.3-1] Số phức liên hợp của số phức z = 5+ 6i là A. z = 5 − + 6i . B. z = 5 − − 6i .
C. z = 6 −5i .
D. z = 5− 6i .
Câu 6: [1D3-4.2-1] Cho cấp số nhân (u
có công bội q , số hạng đầu u = 2 − và số hạng thứ tư n ) 1
u = 54 . Giá trị của 4 q bằng A. 3 . B. 6 − . C. 6 . D. 3 − .
Câu 7: [2H3-3.4-1] Trong không gian Oxyz , mặt phẳng nào dưới đây đi qua gốc tọa độ? A. y + 5 = 0 . B. z + 20 = 0.
C. x − 2019 = 0.
D. 2x + 5y −8z = 0 .
[2D1-1.0-1] Tập xác định của hàm số 2x −1 = là Câu 8: y 2x − 4 A. D = \  2 .
B. D = \−  4 . C. D = \  4 .
D. D = \−  2 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 1 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Câu 9: [2D2-3.2-1] Với các số thực dương a , b bất kì. Mệnh đề nào sau đây đúng? A. log( a ab) = log . a log b .
B. log =logb − log a . b C. a log log a = .
D. log(ab)=log a + logb . b log b
Câu 10: [2H1-3.1-1] Cho hình lăng trụ đứng ' ' '
ABC.A B C có đáy là tam giác vuông tại A, AB = a, AC = 2a, '
AA =3a . Tính thể tích của khối lăng trụ đó. A. 3 V = 3a . B. 2 V = 3a . C. 3 V = a . D. 3 V = 6a .
Câu 11: [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a = (3;2; ) 1 , b = ( 2 − ;0 ) ;1 . Độ
dài của vectơ a + b bằng A. 2 . B. 1. C. 2 . D. 3.
Câu 12: [2D2-2.1-1] Tìm tập xác định D của hàm số y = ( − x)13 2 . A. D = (− ;2  .
B. D = (2;+) . C. D = (− ;2  ) .
D. D = (−;+).
Câu 13: [2D3-3.1-1] Cho hàm số f (x) liên tục trên đoạn a;b và F (x) là một nguyên hàm của hàm
f ( x) . Tìm khẳng định sai. a b A. f  (x)dx = 0. B. f
 (x)dx = F (b)−F (a). a a b a b C. f
 (x)dx = − f  (x)d .x. D. f
 (x)dx = F (a)−F (b). a b a
Câu 14: [2H2-3.5-1] Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2 , 3 là A. 36 . B. 9 . C. 7 14 . D. 9 . 2 3 8
Câu 15: [2D1-7.1-1] Viết phương trình tiếp tuyến của đồ thị hàm số 2x −1 y =
tại điểm có hoành độ 2x +1 x = 0 . 0 A. y = 4 − x +1.
B. y = 4x +1.
C. y = 4x .
D. y = 4x −1.
Câu 16: [2D2-4.7-1] Hàm số nào sau đây có đồ thị như hình bên? A. y = log .
B. y = log x +1.
C. y = log x +1 y = log x +1 2 ( ). D. 3 ( ) 3 x 2
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 2 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 3
Câu 17: [2D1-1.4-1] Cho hàm số x 2 y =
− x + x + 2019 . Mệnh đề nào sau đây đúng? 3
A. Hàm số đã cho đồng biến trên .
B. Hàm số đã cho đồng biến trên ( ) ;1
− và nghịch biến trên (1;+) .
C. Hàm số đã cho đồng biến trên (1;+) và nghịch biến trên ( ) ;1 − .
D. Hàm số đã cho nghịch biến trên ( ) ;1 − .
Câu 18: [2D4-1.4-2] Gọi 1z , z lần lượt có điểm biểu diễn là 2
M và N trên mặt phẳng phức ở hình bên. Tính + . 1 z z2 y 2 M O 1 3 x -4 N A. 2 29 . B. 20 . C. 2 5 . D. 116.
Câu 19: [2D2-5.3-2] Cho bất phương trình x x 1 4 5.2 + −
+16  0 có tập nghiệm là đoạn a;b . Tính ( 2 2 log a + b ) . A. 2 . B. 1. C. 0 . D. 10.
Câu 20: [2D4-1.4-2] Gọi + + = .Tính giá trị của 1
z và z là hai nghiệm phức của phương trình 2 z 4z 29 0 2 biểu thức 4 4 + . 1 z z2 A. 841. B. 1682. C. 1282. D. 58.
Câu 21: [2D1-5.4-2] Cho hàm số y = f (x) có đạo hàm liên tục trên . Hàm số y = f ( x) có đồ thị
như hình vẽ dưới đây: Cho bốn mệnh đề sau:
1) Hàm số y = f (x) có hai điểm cực trị.
2) Hàm số y = f (x) đồng biến trên khoảng (1;+). 3) f ( )
1  f (2)  f (4) .
4) Trên đoạn −1;4, giá trị lớn nhất của hàm số y = f (x) là f ( ) 1 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 3 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 1. B. 4 . C. 2 . D. 3. 5 5
Câu 22: [2D3-3.3-2] Cho f (x)dx = 2 −  . Tích phân 4 f  (x) 2 − 3x  dx   bằng 0 0 A. 140 − . B. 130 − . C. 120 − . D. 133 − .
Câu 23: [2D3-3.3-2] Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên như hình sau: x − −1 0 1 + f '( x) + 0 − 0 + 0 − 3 3 f ( x) − −1 −
Có bao nhiêu giá trị nguyên m 201 −
9; 2019 để phương trình f ( x) = m có hai nghiệm phân biệt. A. 2018 . B. 4016 . C. 2019 . D. 2020 .
Câu 24: [2D2-4.8-2] Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7% / năm. Biết rằng
nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính
lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn
600 triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và
người đó không rút tiền ra. A. 9 năm. B. 10 năm. C. 11 năm. D. 12 năm.
Câu 25: [2D3-5.9-2] Cho hình phẳng giới hạn bởi các đường y = x − 2, y = 0 và x = 9 quay xung
quanh trục Ox . Tính thể tích khối tròn xoay tạo thành. A. 7    V = . B. 5 V = . C. 7 V = . D. 11 V = . 6 6 11 6
Câu 26: [2D3-1.3-2] Họ nguyên hàm của hàm số ( ) 4 = + ex f x x x là A. 1 1 1 5 + ( + ) 1 ex x x + C . B. 5 + ( − ) 1 ex x x + C . C. 5 + ex x x + C . D. 3 4 + ( + ) 1 ex x x + C . 5 5 5
Câu 27: [2H3-5.2-2] Trong không gian Oxyz , phương trình đường thẳng đi qua hai điểm A(1;2;3) và B (5; 4; − ) 1 là
A. x −5 y − 4 z +1 + + + = = .
B. x 1 y 2 z 3 = = . 2 1 2 4 2 4 −
C. x −1 y − 2 z −3 − − − = = .
D. x 3 y 3 z 1 = = . 4 2 4 2 − 1 − 2
Câu 28: [2H1-2.3-2] Cho hình chóp tam giác đều có cạnh đáy bằng a , cạnh bên 2a . Tính chiều cao h của hình chóp đó A. a 28 a a a h = . B. 14 h = . C. 33 h = . D. 11 h = . 3 3 3 3
Câu 29: [2D1-5.6-1] Đường cong trong hình bên là đồ thị của hàm số nào?
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 4 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 A. 4 y = −x +1. B. 4 2
y = x + 2x +1 . C. 4 y = x +1. D. 4 2
y = −x + 2x +1.
Câu 30: [2H3-3.6-2] Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q) : x − 2y + z − 5 = 0 và
mặt cầu (S) (x − )2 + y + (z + )2 2 : 1 2
=15. Mặt phẳng (P) song song với mặt phẳng (Q) và cắt
mặt cầu (S ) theo giao tuyến là một đường tròn có chu vi bằng 6 đi qua điểm nào sau đây? A. (2;− 2; ) 1 . B. (1;− 2;0) . C. (0;−1;−5) . D. (−2;2;− ) 1 .
Câu 31: [2D2-6.2-3] Tập hợp các giá trị thực của tham số m để phương trình log ( 2 4 − x + log
2x + m −1 = 0 có hai nghiệm thực phân biệt là T = (a ;b) . Tính 2019 ) 1 ( ) 2019
S = 2a + b . A. 20. B. 8. C. 18. D. 16.
Câu 32: [2D1-4.7-2] Cho hàm số x − 2 y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị 2 mx − 2x + 4
hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)? A. 1. B. 3. C. 0. D. 2.
Câu 33: [2D1-2.7-3] Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số 4 3 2
y = 3x − 8x − 6x + 24x − m có 7 điểm cực trị. Tính tổng các phần tử của S . A. 42 . B. 50. C. 30. D. 63.
Câu 34: [1H3-2.4-2] ] Cho hình chóp S.ABCD có đáy là hình vuông cạnh là 2a ; cạnh SA = a và vuông
góc với đáy. Gọi M là trung điểm của CD. Tính cos với  là góc tạo bởi hai đường thẳng SB và AM . A. 2 . B. 1 . C. 4 . D. 2 − . 5 2 5 5
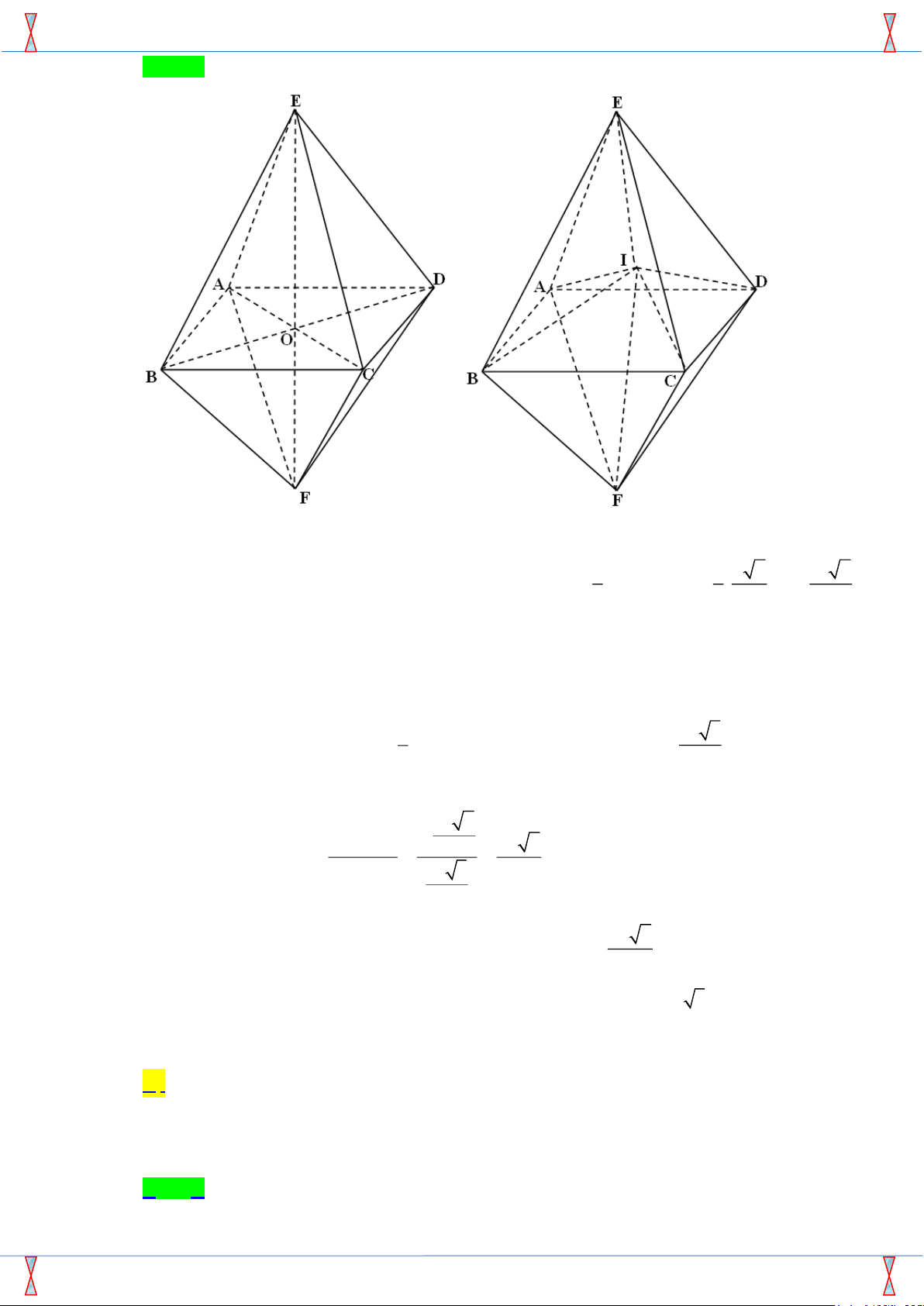
Câu 35: [2H1-4.2-3] Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng
khoảng cách từ I đến tất cả các mặt của bát diện. A. 4a 6 . B. 3a 2 . C. 4a 3 . D. a 3 . 3 2 3 2
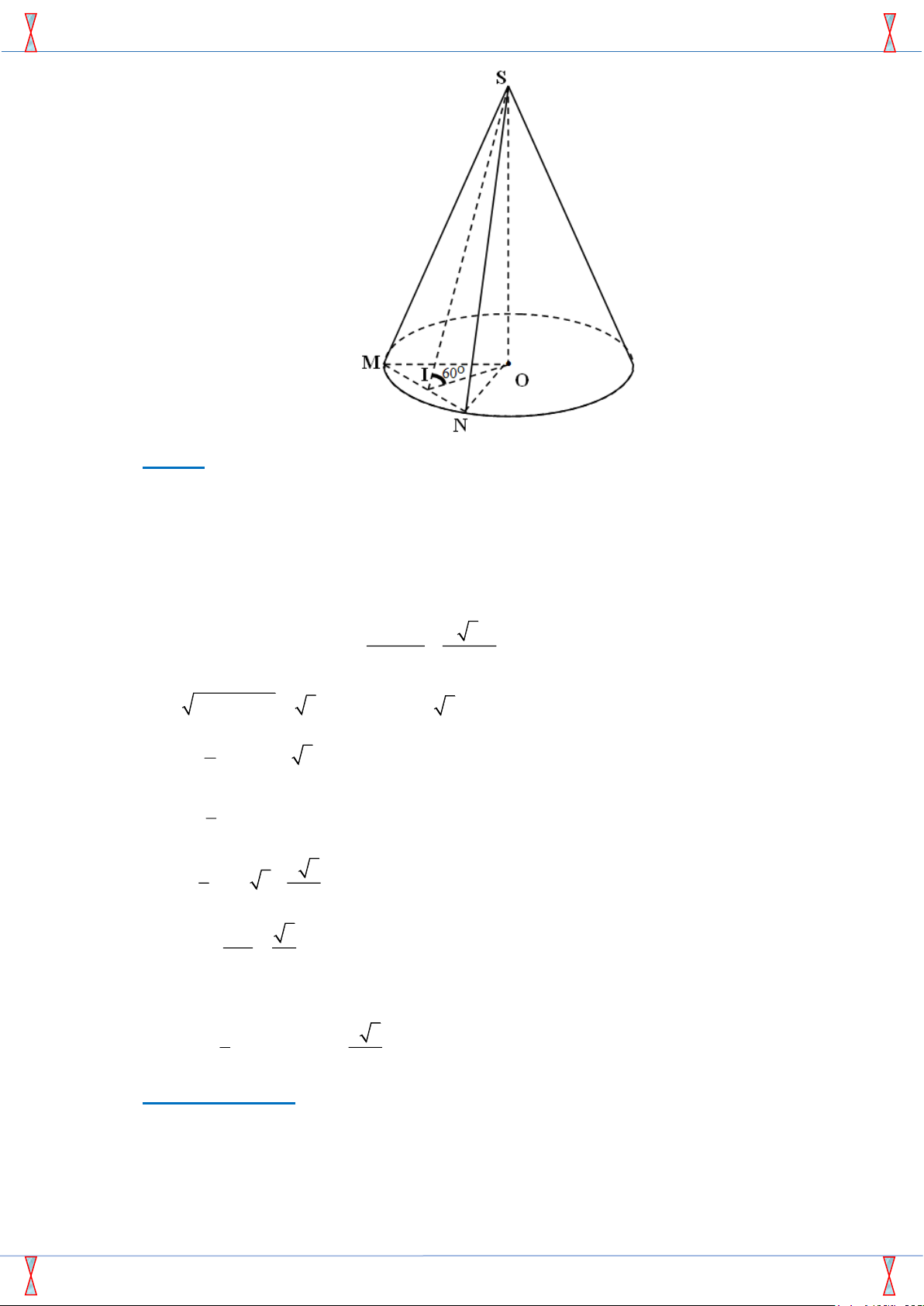
Câu 36: [2H2-1.4-3] Một khối nón có bán kính đáy bằng 2 cm , chiều cao bằng 3cm . Một mặt phẳng
đi qua đỉnh và tạo với đáy một góc 0
60 chia khối nón làm 2 phần. Tính thể tích V phần nhỏ
hơn (Tính gần đúng đến hàng phần trăm). A. 3 V 1, 42 cm . B. 3 V  2,36 cm . C. 3 V 1,53cm . D. 3 V  2, 47 cm .
Câu 37: [2H3-6.17-2] Trong không gian Oxyz , điểm M  đối xứng với điểm M (1;2;4) qua mặt phẳng
( ):2x + y + 2z −3 = 0 có tọa độ là
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 5 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 A. (−3;0;0). B. ( 1 − ;1;2) . C. (−1;−2;−4). D. (2;1;2).
Câu 38: [2H3-6.18-3] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(−1;2;5) , B(3;−1;0) ,
C (−4;0; −2) . Gọi I là điểm trên mặt phẳng (Oxy ) sao cho biểu thức IA − 2IB + 3IC đạt giá
trị nhỏ nhất. Tính khoảng cách từ I đến mặt phẳng (P) : 4x + 3y + 2 = 0 . A. 17 . B. 6 . C. 12 . D. 9. 5 5
Câu 39: [2D4-1.4-3] Cho số phức z = a +bi (a,b ) thỏa mãn z −3 = z −1 và (z + 2)(z −i) là số
thực. Tính a + b . A. 2 − . B. 0. C. 2. D. 4. 4 3 2
Câu 40: [2D3-4.3-3] Biết x + x + 7x + 3 a dx = + c ln 5 
với a , b , c là các số nguyên dương và a là 2 x − x + 3 b b 1
phân số tối giản. Tính 2 3
P = a − b − c . A. 5 − . B. 4 − . C. 5. D. 0.
Câu 41: [2D3-4.12-3] Cho hàm số y = f (x) có đạo hàm liên tục trên 2;4 và f (x)  0, x  2;4.
Biết 4x f (x) =  f   ( x) 3 7 3 3  − x , x   
2;4, f (2) = . Giá trị của f (4) bằng 4 A. 40 5 −1 . B. 20 5 −1 . C. 20 5 −1 . D. 40 5 −1 . 2 4 2 4
Câu 42: [2D1-1.3-3] Cho hàm số y = f (x) có đạo hàm liên tục trên . Biết hàm số y = f ( x) có đồ
thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên m−5;5 để hàm số g (x) = f (x + m)
nghịch biến trên khoảng (1;2). Hỏi S có bao nhiêu phần tử? A. 4 . B. 3. C. 6 . D. 5.
Câu 43: [2D1-3.1-3] Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất
của hàm số g (x) = f ( 1 1 2 4x − x ) 3 2
+ x − 3x + 8x + trên đoạn 1;  3 . 3 3 A. 15. B. 25 . C. 19 . D. 12. 3 3
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 6 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Câu 44: [2H3-2.13-3] Trong không gian với hệ tọa độ Oxyz cho bốn điểm (
A 1;0;0) , B(2;1;3) , C(0; 2; − 3) , (
D 2;0; 7) . Gọi M là điểm thuộc mặt cầu 2 2 2
(S) :(x + 2) + (y − 4) + z = 39 thỏa mãn: 2 MA + 2M .
B MC = 8 . Biết độ dài đoạn thẳng MD đạt giá trị lớn nhất. Tính giá trị lớn nhất đó. A. 2 7 . B. 7 . C. 3 7 . D. 4 7 . f (1−2x)
Câu 45: [2D1-1.4-3] Cho hàm số  1 
y = f ( x) . Đồ thị y = f ( x) như hình bên. Hàm số g ( x) =  2  
nghịch biến trên khoảng nào trong các khoảng sau? A. (0; ) 1 . B. (−;0) . C. (−1;0) . D. (1;+ ) .
Câu 46: [2D3-5.13-3] Nhà trường dự định làm một vườn hoa dạng elip được chia ra làm bốn phần bởi
hai đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ
dài trục lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F ,1 2
F là hai tiêu điểm của elip. Phần
A , B dùng để trồng hoa, phần C , D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa
và cỏ lần lượt là 250.000 đ và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 5.676.000 đ. B. 4.766.000 đ. C. 4.656.000 đ. D. 5.455.000 đ.
Câu 47: [2H1-2.5-3] Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Gọi E và F lần lượt là
các điểm trên các cạnh A D   và A B   sao cho 2 AE =   và 2  =   . Tính thể tích 3 A D A F 3 A B khối chóp . A BDEF . 3 3 3 3 A. a 3 . B. 5a . C. a . D. 3a 3 . 8 18 8 8
Câu 48: [2D4-4.1-4] Cho hai số phức z ,
z + 2 − i + z − 4 − 7i = 6 2 và iz −1+ 2i = 1 . 1 z thoả mãn 2 1 1 2
Tìm giá trị nhỏ nhất của biểu thức T = + 1 z z2 . A. 2 −1. B. 2 +1. C. 2 2 +1. D. 2 2 −1.
Câu 49: [1D2-2.2-4] Từ các chữ số thuộc tập X = 0;1;2;3;4;5;6; 
7 có thể lập được bao nhiêu số tự
nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18. A. 720. B. 860. C. 984. D. 1228.
Câu 50: [2D1-2.11-4] Gọi 0
m là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số 3
y = x − 6mx + 4 cắt đường tròn tâm I (1;0) , bán kính bằng 2 tại hai điểm
phân biệt A , B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng: A. m  2;3 m  3; 4 m  0;1 m  1; 2 0 ( ). B. 0 ( ). C. 0 ( ) . D. 0 ( ) .  HẾT
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 7 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 BẢNG ĐÁP ÁN 1.B 2.C 3.A 4.D 5.D 6.D 7.D 8.A 9.D 10.A 11.D 12.C 13.D 14.C 15.D 16.C 17.A 18.C 19.B 20.B 21.C 22.D 23.C 24.C 25.D 26.B 27.D 28.C 29.D 30.D 31.D 32.A 33.A 34.A 35.A 36.A 37.A 38.B 39.B 40.B 41.D 42.D 43.D 44.A 45.D 46.A 47.B 48.D 49.C 50.C
GIẢI CHI TIẾT ĐỀ 8 TUẦN HKII
TRƯỜNG CHUYÊN LÊ HỒNG PHONG NĂM 2019 MÔN TOÁN THỜI GIAN: 90 PHÚT
Huyenmi232@gmail.com.
Câu 1: [2H2-2.3-1] Thể tích khối trụ có bán kính đáy r = a và chiều cao h = a 2 bằng 3 A.  3 a 2 4 a 2 . B. 3 a 2 . C. 3 2 a . D. . 3 Lời giải
Tác giả: Nguyễn Huyền; Fb:Huyen Nguyen Chọn B Thể tích khối trụ là: 2 V =  r h 2 = .a .a 2 3 =  a 2 .
Câu 2: [1D2-4.3-2] Một hộp đựng 6 quả cầu màu trắng và 4 quả cầu màu vàng. Lấy ngẫu nhiên từ
hộp ra 4 quả cầu. Tính xác suất để trong 4 quả cầu lấy được có đúng 2 quả cầu vàng. A. 3 . B. 1 . C. 3 . D. 2 . 14 35 7 5 Lời giải
Tác giả: Nguyễn Huyền; Fb: Huyen Nguyen Chọn C
Chọn 4 quả cầu từ 10 quả cầu có 4
C (cách )  n () 4 = C . 10 10
Gọi A là biến cố “ 4 quả cầu lấy được có đúng 2 quả màu vàng”.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 8 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Chọn 4 quả cầu trong đó có đúng 2 quả màu vàng có 2 2 C .  n A = C . . 4 6 C (cách) ( ) 2 2 4 6 C 2 2 Xác suất của biến cố n A C .C
A là: P ( A) ( ) = 4 6 = 3 = . n () 4 7 10 C
Câu 3: [2D1-2.3-1] Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. x ∞ 1 2 + ∞ f /(x) + 0 + 1 1 f(x) + ∞ ∞ 2
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x = 2 và không có điểm cực đại.
B. Hàm số đạt cực tiểu tại x = 1
− và đạt cực đại tại x = 2 .
C. Hàm số đạt cực đại tại x = 1
− và đạt cực tiểu tại x = 2 .
D. Giá trị cực đại của hàm số bằng 1. Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức Chọn A
Từ bảng biến thiên ta có:
+) Hàm số y = f (x) có tập xác định là D = R \− 
1 . Suy ra hàm số không đạt cực trị tại x = 1
− . Do đó các mệnh đề ở đáp án B và C là các mệnh đề sai.
+) Hàm số không có điểm cực đại nên không có giá trị cực đại bằng 1. Do đó mệnh đề ở đáp án D là mệnh đề sai.
+) Tại x = 2 thì f '( x) = 0 và đổi dấu từ âm sang dương nên x = 2 là điểm cực tiểu của hàm số
và dễ thấy hàm số không có điểm cực đại. Suy ra mệnh để ở đáp án A đúng.
Vậy mệnh đề của đáp án A là đúng.
Câu 4: [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(0;2;5) , B( 2 − ;0; ) 1 ,
C (5; − 8;6) . Tìm tọa độ trọng tâm G của tam giác ABC .
A. G(3;− 6;12) .
B. G (1;− 2;− 4). C. G( 1; − 2;− 4) .
D. G (1;− 2;4) . Lời giải
Tác giả: Giáp Minh Đức; Fb: Giáp Minh Đức Chọn D
Gọi G (x y z
là trọng tâm của tam giác ABC . G ; G ; G )
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 9 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 x + x + x A B C x =  G 3  x = G 1
Công thức tọa độ trọng tâm  y + y + y
G của tam giác ABC là: A B Cy =  y = − G 2 G 3    x =  G 4 z + z + z A B C x =  G  3 Vậy G (1;− 2;4) .
Câu 5: [2D4-1.3-1] Số phức liên hợp của số phức z = 5+ 6i là A. z = 5 − + 6i . B. z = 5 − − 6i .
C. z = 6 −5i .
D. z = 5− 6i . Lời giải
Tác giả: Võ Thanh Hải; Fb: Võ Thanh Hải Chọn D
Số phức liên hợp của số phức z = x + yi , x, y  là số phức z = x − yi . Do đó số phức liên
hợp của số phức z = 5+ 6i là z = 5− 6i .
Câu 6: [1D3-4.2-1] Cho cấp số nhân (u có công bội q , số hạng đầu u = 2 − và số hạng thứ tư n ) 1
u = 54 . Giá trị của 4 q bằng A. 3 . B. 6 − . C. 6 . D. 3 − . Lời giải
Tác giả: Võ Thanh Hải; Fb: Võ Thanh Hải Chọn D Với cấp số nhân ( u u có công bội q 4
u = u .q q =
q = −27  q = 3 − . n ) ta có: 3 3 3 4 1 1 u
Câu 7: [2H3-3.4-1] Trong không gian Oxyz , mặt phẳng nào dưới đây đi qua gốc tọa độ? A. y + 5 = 0 . B. z + 20 = 0.
C. x − 2019 = 0.
D. 2x + 5y −8z = 0 . Lời giải
Tác giả:Nguyễn Văn Diệu; Fb:dieuptnguyen Chọn D
Phương trình tổng quát của mặt phẳng có dạng Ax + By + Cz + D = 0, trong đó A , B ,C không đồng thời bằng 0 .
Nếu D = 0 thì mặt phẳng đi qua gốc tọa độ. Từ đó ta chọn đáp án D .
[2D1-1.0-1] Tập xác định của hàm số 2x −1 = là Câu 8: y 2x − 4 A. D = \  2 .
B. D = \−  4 . C. D = \  4 .
D. D = \−  2 . Lời giải
Tác giả:Nguyễn Văn Diệu; Fb:dieuptnguyen Chọn A
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 10 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 Hàm số 2x −1 y =
xác định khi và chỉ khi 2x − 4  0  x  2 . 2x − 4
Vậy tập xác định của hàm số đã cho là D = \  2 .
Câu 9: [2D2-3.2-1] Với các số thực dương a , b bất kì. Mệnh đề nào sau đây đúng? A. log( a ab) = log . a log b .
B. log =logb − log a . b C. a log log a = .
D. log(ab)=log a + logb . b log b Lời giải
Tác giả: Nguyễn Thị Phương; Fb: Hộp Thư Chọn D
Với các số thực dương a , b bất kì ta có:
+)log a =log a − logb nên B, C sai. b
+)log(ab)=log a + logb nên A sai, D đúng. Vậy chọn D.
Câu 10: [2H1-3.1-1] Cho hình lăng trụ đứng ' ' '
ABC.A B C có đáy là tam giác vuông tại A, AB = a, AC = 2a, '
AA =3a . Tính thể tích của khối lăng trụ đó. A. 3 V = 3a . B. 2 V = 3a . C. 3 V = a . D. 3 V = 6a . Lời giải
Tác giả: Nguyễn Thị Phương; Fb: Hộp Thư Chọn A
Vì AA' ⊥ ( ABC) nên thể tích của khối lăng trụ ' ' ' ABC.A B C là 1 1 3 V = AA'.S = AA AB AC = a a a = a ABC '. . . 3 . .2 3 . 2 2
Câu 11: [2H3-1.1-1] Trong không gian với hệ tọa độ Oxyz , cho hai vectơ a = (3;2; ) 1 , b = ( 2 − ;0 ) ;1 . Độ
dài của vectơ a + b bằng A. 2 . B. 1. C. 2 . D. 3. Lời giải
Tác giả: Trần Quốc Khang; Fb: BiTran
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 11 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 Chọn D
Ta có a + b = (1;2;2)  a +b = 1+ 4+ 4 = 3.
Câu 12: [2D2-2.1-1] Tìm tập xác định D của hàm số y = ( − x)13 2 . A. D = (− ;2  .
B. D = (2;+) . C. D = (− ;2  ) .
D. D = (−;+). Lời giải
Tác giả: Trần Quốc Khang; Fb: BiTran Chọn C
ĐKXĐ: 2− x  0  x  2. Suy ra TXĐ: D = (− ;2  ) .
Câu 13: [2D3-3.1-1] Cho hàm số f (x) liên tục trên đoạn a;b và F (x) là một nguyên hàm của hàm
f ( x) . Tìm khẳng định sai. a b A. f  (x)dx = 0. B. f
 (x)dx = F (b)−F (a). a a b a b C. f
 (x)dx = − f  (x)d .x. D. f
 (x)dx = F (a)−F (b). a b a Lời giải
Tác giả:Nguyễn Tuyết Lê; Fb: Nguyen Tuyet Le. Chọn D
Theo định nghĩa tích phân ta có: b f
 (x)dx = F (b)−F (a). Đáp án B đúng, D sai. a a f ( x) dx
= F (a) − F (a) = 0 . Đáp án A đúng. a b a f ( x) dx
= F (b) − F (a) = − f
 (x)dx. Đáp án C đúng. a b
Câu 14: [2H2-3.5-1] Thể tích khối cầu ngoại tiếp hình hộp chữ nhật có ba kích thước 1, 2 , 3 là A. 36 . B. 9 . C. 7 14 . D. 9 . 2 3 8 Lời giải
Tác giả:Nguyễn Tuyết Lê; Fb: Nguyen Tuyet Le. Chọn C
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 12 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Gọi R là bán kính khối cầu ngoại tiếp hình hộp chữ nhật. Ta có 1 1 14 R = 2 2 2 = 1 + 2 + 3 = . 2 BD 2 2 3  
Vậy thể tích khối cầu là: 4  3 4 14 V =  =    = 7 14 . 3 R 3  2    3
Câu 15: [2D1-7.1-1] Viết phương trình tiếp tuyến của đồ thị hàm số 2x −1 y =
tại điểm có hoành độ 2x +1 x = 0 . 0 A. y = 4 − x +1.
B. y = 4x +1.
C. y = 4x .
D. y = 4x −1. Lời giải
Tác giả: Trần Bạch Mai; Fb: Bạch Mai Chọn D Ta có: 4 y =
y 0 = 4 ; y (0) = −1. 2 ( ) (2x + ) 1
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 0 : 0
y = y(0)( x − 0) + y (0)  y = 4x −1.
Vậy phương trình tiếp tuyến cần tìm là: y = 4x −1.
Câu 16: [2D2-4.7-1] Hàm số nào sau đây có đồ thị như hình bên?
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 13 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 A. y = log .
B. y = log x +1.
C. y = log x +1 y = log x +1 2 ( ). D. 3 ( ) 3 x 2 Lời giải
Tác giả: Bạch Mai; Fb: Bạch Mai Chọn C
Đồ thị hàm số đi qua điểm (0;0) nên loại đáp án A và B.
Đồ thị hàm số đi qua điểm (1; )
1 nên loại D.
Vậy đáp án C thỏa mãn. 3
Câu 17: [2D1-1.4-1] Cho hàm số x 2 y =
− x + x + 2019 . Mệnh đề nào sau đây đúng? 3
A. Hàm số đã cho đồng biến trên .
B. Hàm số đã cho đồng biến trên ( ) ;1 −
và nghịch biến trên (1;+) .
C. Hàm số đã cho đồng biến trên (1;+) và nghịch biến trên ( ) ;1 − .
D. Hàm số đã cho nghịch biến trên ( ) ;1 − . Lời giải
Tác giả: LêHoa; Fb:LêHoa Chọn A
Tập xác định: D = . Ta có ' 2
y = x − 2x +1 = ( x − )2 1  0 với x
  , đẳng thức xảy ra tại x =1.
Vậy hàm số đã cho đồng biến trên .
Câu 18: [2D4-1.4-2] Gọi 1z , z lần lượt có điểm biểu diễn là 2
M và N trên mặt phẳng phức ở hình bên. Tính + 1 z z2 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 14 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 y 2 M O 1 3 x -4 N A. 2 29 . B. 20 . C. 2 5 . D. 116. Lời giải
Tác giả: LêHoa; Fb:LêHoa Chọn C
Từ hình bên ta có tọa độ M ( 3;2 ) biểu diễn số phức z = 3+ 2 . 1 i
Tọa độ N ( 1;− 4 ) biểu diễn z =1− 4 . 2 i Ta có 2 2
z + z = 4 − 2  z + z = 4 + 2 − = 2 5 . 1 2 ( ) ( ) 1 2 i
Câu 19: [2D2-5.3-2] Cho bất phương trình x x 1 4 5.2 + −
+16  0 có tập nghiệm là đoạn a;b . Tính ( 2 2 log a + b ) . A. 2 . B. 1. C. 0 . D. 10. Lời giải
Tác giả:Vũ Thị Thúy; Fb: Vũ Thị Thúy Chọn B Bất phương trình x x 1 4 5.2 + − +16  0 4x 10.2x 16 0 2 2x  − +     8 1 x  3.
Vậy tập nghiệm của bất phương trình là 1;  3 .
Suy ra a =1;b = 3 nên ( 2 2 a + b ) = ( 2 2 log log 1 + 3 ) =1.
Câu 20: [2D4-1.4-2] Gọi + + = .Tính giá trị của 1
z và z là hai nghiệm phức của phương trình 2 z 4z 29 0 2 biểu thức 4 4 + . 1 z z2 A. 841. B. 1682. C. 1282. D. 58. Lời giải
Tác giả:Vũ Thị Thúy; Fb: Vũ Thị Thúy Chọn B z = 2 − − 5
Phương trình 2 + 4 + 29 = 0  ( + 2)2 = −25  ( + 2)2 = (5 )2 1 i z z z z i   . z = 2 − +  5 2 i
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 15 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Suy ra z = z = ( 2 − )2 2 + 5 = 29 . 1 2
Vậy z + z = ( 29)4 +( 29)4 4 4 =1682 . 1 2
Câu 21: [2D1-5.4-2] Cho hàm số y = f (x) có đạo hàm liên tục trên . Hàm số y = f ( x) có đồ thị
như hình vẽ dưới đây: Cho bốn mệnh đề sau:
1) Hàm số y = f (x) có hai điểm cực trị.
2) Hàm số y = f (x) đồng biến trên khoảng (1;+). 3) f ( )
1  f (2)  f (4) .
4) Trên đoạn −1;4, giá trị lớn nhất của hàm số y = f (x) là f ( ) 1 .
Số mệnh đề đúng trong bốn mệnh đề trên là: A. 1. B. 4 . C. 2 . D. 3. Lời giải
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc Chọn C
Từ đồ thị của hàm số y = f ( x) ta có bảng biến thiên của hàm số y = f (x) như sau:
Khi đó dựa vào bảng biến thiên ta thấy:
+) Hàm số có ba điểm cực trị nên mệnh đề 1) sai.
+) Hàm số đồng biến trên các khoảng (−1; )
1 và (4;+) nên mệnh đề 2) sai.
+) Hàm số nghịch biến trên khoảng (1;4) nên f ( )
1  f (2)  f (4) suy ra mệnh đề 3) đúng.
+) Trên đoạn −1;4, giá trị lớn nhất của hàm số y = f (x) là f ( )
1 suy ra mệnh đề 4) đúng.
Vậy có tất cả 2 mệnh đề đúng.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 16 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 5 5
Câu 22: [2D3-3.3-2] Cho f (x)dx = 2 −  . Tích phân 4 f  (x) 2 − 3x  dx   bằng 0 0 A. 140 − . B. 130 − . C. 120 − . D. 133 − . Lời giải
Tác giả: Minh Anh Phuc; Fb: Minh Anh Phuc Chọn D 5 5 5 4 f
(x)−3x dx = 4 f  (x) 5 2 2 3
dx − 3x dx = 8 − − x = 8 − −125 = 1 − 33    . 0 0 0 0
Câu 23: [2D3-3.3-2] Cho hàm số y = f (x) xác định, liên tục trên và có bảng biến thiên như hình sau:
Có bao nhiêu giá trị nguyên m 201 −
9; 2019 để phương trình f ( x) = m có hai nghiệm phân biệt. A. 2018 . B. 4016 . C. 2019 . D. 2020 . Lời giải
Tác giả:Vũ Thị Thanh Huyền; Fb: Vu Thi Thanh Huyen Chọn C
Số nghiệm của phương trình f (x) = m ( )
1 là số giao điểm của đường thẳng d : y = m và đồ thị
(C) của hàm số y = f (x) . Do đó phương trình ( )
1 có hai nghiệm phân biệt khi và chỉ khi dm = 3
cắt (C) tại hai điểm phân biệt   . m  1 −
Mà m−2019;2019,m nên m 201 −
9;− 2018;− 2017;...;− 2;  3 .
Vậy có 2019 giá trị nguyên của m thỏa mãn.
Câu 24: [2D2-4.8-2] Một người gửi 300 triệu đồng vào một ngân hàng với lãi suất 7% / năm. Biết rằng
nếu không rút tiền khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính
lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm, người đó nhận được số tiền nhiều hơn
600 triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và
người đó không rút tiền ra. A. 9 năm. B. 10 năm. C. 11 năm. D. 12 năm. Lời giải
Tác giả:Vũ Thị Thanh Huyền; Fb: Vu Thi Thanh Huyen Chọn C
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 17 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Kí hiệu số tiền gửi ban đầu là A , lãi suất một kì hạn là m thì số tiền cả gốc và lãi có được sau n n kì hạn là . A (1+ m) .
Do đó, số tiền cả gốc và lãi người đó nhận được sau n năm là 300.1,07n triệu đồng.
Số tiền cả gốc và lãi nhận được nhiều hơn 600 triệu đồng 300.1,07n   600
n  log 2 10,245. 1,07
Vậy sau ít nhất 11 năm thì người đó nhận được số tiền nhiều hơn 600 triệu đồng bao gồm cả gốc và lãi.
Câu 25: [2D3-5.9-2] Cho hình phẳng giới hạn bởi các đường y = x − 2, y = 0 và x = 9 quay xung
quanh trục Ox . Tính thể tích khối tròn xoay tạo thành. A. 7    V = . B. 5 V = . C. 7 V = . D. 11 V = . 6 6 11 6 Lời giải
Tác giả: Trần Thị Thúy; Fb: Thúy Minh Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số y = x − 2 và trục hoành: x − 2 = 0
x = 2  x = 4.
Thể tích của khối tròn xoay tạo thành là: 9 9 9 2  x 8x x
V =  ( x − 2)2 dx =  (x − 4 x + 4)dx =   − + 4  2 3 x    4 4  4  81  16 64  11 =  − 72 + 36 − − +   16 =  . 2 2 3      6
Câu 26: [2D3-1.3-2] Họ nguyên hàm của hàm số ( ) 4 = + ex f x x x là A. 1 1 5 + ( + ) 1 ex x x + C . B. 5 + ( − ) 1 ex x x + C . 5 5 C. 1 5 + ex x x + C . D. 3 4 + ( + ) 1 ex x x + C . 5 Lời giải
Tác giả: Trần Thị Thúy; Fb: Minh Thúy. Chọn B Ta có: ( 4 x + ) 4 e dx = dx + ex x x x x dx   . +) 4 1 5 x dx= x +  . 1 5 C u  = x du = dx +) Đặt    . dv = exdx v = ex Suy ra: ex x dx 
= ex − exdx = ex − ex x x +  = (x − ) 1 ex + . 2 C C2
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 18 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 Vậy ( 4 + ex ) 1 5
dx = x + (x − ) 1 ex x x +  . 5 C
Câu 27: [2H3-5.2-2] Trong không gian Oxyz , phương trình đường thẳng đi qua hai điểm A(1;2;3) và B (5; 4; − ) 1 là
A. x −5 y − 4 z +1 + + + = = .
B. x 1 y 2 z 3 = = . 2 1 2 4 2 4 −
C. x −1 y − 2 z −3 − − − = = .
D. x 3 y 3 z 1 = = . 4 2 4 2 − 1 − 2 Lời giải
Tác giả: Phùng Hoàng Cúc; Fb: Phùng Hoàng Cúc Chọn D Ta có AB(4;2; 4
− ) . Suy ra AB cùng phương với u ( 2 − ; 1 − ;2).
Phương trình đường thẳng AB đi qua B(5;4;− ) 1 nhận u ( 2 − ; 1
− ;2) làm vectơ chỉ phương là: x − 5 y − 4 z +1 = = ,( ) 1 . Do đó loại 2
A, C. − 1 − 2
Có tọa độ C (−1;−2;−3) không thỏa mãn phương trình ( ) 1 nên phương án B.
Lại có tọa độ D(3;3; )
1 thỏa mãn phương trình ( )
1 nên phương trình đường thẳng AB cũng
được viết là: x −3 y −3 z −1 = = . 2 − 1 − 2
Câu 28: [2H1-2.3-2] Cho hình chóp tam giác đều có cạnh đáy bằng a , cạnh bên 2a . Tính chiều cao h của hình chóp đó A. a 28 a a a h = . B. 14 h = . C. 33 h = . D. 11 h = . 3 3 3 3 Lời giải
Tác giả: Phùng Hoàng Cúc; Fb: Phùng Hoàng Cúc Chọn C
Gọi chóp tam giác đều là S.ABC có M , F lần lượt là trung điểm BC , AB và O là trọng tâm của ABC
. Ta có SO ⊥ ( ABC) . Ta có a 3 a a AM = 2 2 3 3  OA = AM = . = . 2 3 3 2 3
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 19 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 2   Xét tam giác vuông 2 a 3 a 33 SOA ta có 2 2 h = SO =
SA − AO = (2a) −  = . 3      3
Vậy chiều cao cần tìm của hình chóp là a 33 h = . 3
Câu 29: [2D1-5.6-1] Đường cong trong hình bên là đồ thị của hàm số nào? A. 4 y = −x +1. B. 4 2
y = x + 2x +1 . C. 4 y = x +1. D. 4 2
y = −x + 2x +1. Lời giải
Tác giả: Bùi Thị Kim Oanh; Fb: Bùi Thị Kim Oanh Chọn D
Vì đường cong có hướng đi xuống khi x → + nên hệ số a  0 , đồng thời đồ thị đi qua điểm
(1;2). Do đó đường cong này là đồ thị của hàm số 4 2
y = −x + 2x +1.
Chú ý: Đồ thị hàm số 4 2
y = ax + bx + ,
c a  0 có 3 điểm cực trị khi và chỉ khi . a b  0 . Do đó
loại A, B, C.
Câu 30: [2H3-3.6-2] Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (Q) : x − 2y + z − 5 = 0 và
mặt cầu (S) (x − )2 + y + (z + )2 2 : 1 2
=15. Mặt phẳng (P) song song với mặt phẳng (Q) và cắt
mặt cầu (S ) theo giao tuyến là một đường tròn có chu vi bằng 6 đi qua điểm nào sau đây? A. (2;− 2; ) 1 . B. (1;− 2;0) . C. (0;−1;−5) . D. (−2;2;− ) 1 . Lời giải
Tác giả: Bùi Thị Kim Oanh; Fb: Bùi Thị Kim Oanh Chọn D
Mặt cầu (S ) có tâm I (1;0;− 2) và bán kính R = 15 .
Đường tròn có chu vi bằng 6 nên có bán kính 6 r = = 3. 2
Mặt phẳng (P) song song với mặt phẳng (Q) nên phương trình mặt phẳng (P) có dạng:
x − 2 y + z + D = 0 , D  5 − .
Vì mặt phẳng (P) cắt mặt cầu (S ) theo giao tuyến là một đường tròn có chu vi bằng 6 nên d (I (P)) 2 2 ;
= R − r d (I ;(P)) = 6
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 20 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 1− 2.0 − 2 + DD −1 = 6 D = 7  = 6  D −1 = 6     . 2 + (− )2 2 + D −1 = 6 − D = 5 1 2 1 −
Đối chiếu điều kiện ta được D = 7 . Do đó phương trình mặt phẳng (P) : x − 2y + z + 7 = 0 .
Nhận thấy điểm có tọa độ (−2;2;− )
1 thuộc mặt phẳng (P) .
Câu 31: [2D2-6.2-3] Tập hợp các giá trị thực của tham số m để phương trình log ( 2 4 − x + log
2x + m −1 = 0 có hai nghiệm thực phân biệt là T = (a ;b) . Tính 2019 ) 1 ( ) 2019
S = 2a + b . A. 20. B. 8. C. 18. D. 16. Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham Chọn D Ta có: log ( 2 4 − x + log
2x + m −1 = 0 1 2019 ) 1 ( ) ( ) 2019  log ( 2 4 − x − log
2x + m −1 = 0  log ( 2 4 − x = log 2x + m −1 2019 ) 2019 ( ) 2019 ) 2019 ( ) 2
4 − x = 2x + m −1 2
−x − 2x + 5 =  m    (2) . 2 4 − x  0  2 −  x  2 Phương trình ( )
1 có hai nghiệm thực phân biệt  hệ phương trình (2) có hai nghiệm phân
biệt  đường thẳng y = m cắt đồ thị hàm số 2
y = −x − 2x + 5 tại 2 điểm phân biệt có hoành độ  −2;2 . 1 x ; 2 x ( ) Xét hàm số 2
y = −x − 2x + 5 trên (−2; 2) . y = 2
− x − 2 ; y = 0  2
− x − 2 = 0  x = −1(−2;2) . BBT
Từ BBT ta thấy m(5;6) thỏa mãn yêu cầu bài toán. Vậy a = 5 ; b = 6  S = 2a +b =16.
Câu 32: [2D1-4.7-2] Cho hàm số x − 2 y =
. Có tất cả bao nhiêu giá trị của tham số m để đồ thị 2 mx − 2x + 4
hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)? A. 1. B. 3. C. 0. D. 2. Lời giải
Tác giả: Phạm Thị Phương Thúy; Fb: thuypham Chọn A
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 21 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 ĐK: 2
mx − 2x + 4  0
Trường hợp 1: m = 0 Hàm số trở thành x − 2 y =
. Đồ thị hàm số không có đường TCĐ  loại m = 0. 2 − x + 4
Trường hợp 2: m  0
Ta có: lim y = 0 , lim y = 0 . Suy ra đồ thị hàm số có 1 đường TCN y = 0. x→+ x→−
Do đó đồ thị hàm số có đúng 2 đường tiệm cận  đồ thị hàm số có đứng 1 đường tiệm cận đứng  phương trình 2
mx − 2x + 4 = 0 có nghiệm kép hoặc có 2 nghiệm phân biệt trong đó có 1 nghiệm x = 2 .  = 0 4 −16m = 0   1    0  1
 − 4m  0  m =   .   4
4m − 2.2+ 4 = 0 m = 0
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 33: [2D1-2.7-3] Gọi S là tập hợp các giá trị nguyên m để đồ thị hàm số 4 3 2
y = 3x − 8x − 6x + 24x − m có 7 điểm cực trị. Tính tổng các phần tử của S . A. 42 . B. 50. C. 30. D. 63. Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn. Chọn A
Xét hàm số f (x) 4 3 2
= 3x −8x − 6x + 24x − m trên . Ta có f (x) 3 2
= 12x − 24x −12x + 24 . x = −1 
f ( x) = 0  x = 2  . x =  1
Bảng biến thiên của hàm số
Dựa vào BBT suy ra đồ thị hàm số 4 3 2
y = 3x − 8x − 6x + 24x − m có 7 điểm cực trị khi và chỉ
khi đồ thị của hàm số f (x) 4 3 2
= 3x −8x − 6x + 24x − m cắt trục hoành tại 4 điểm phân biệt 1  3− m  0    8  m 13. 8  − m  0
Mà m nguyên nên m9;10;11; 
12 = S . Suy ra tổng tất cả các phần tử của tập S là 42 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 22 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Câu 34: [1H3-2.4-2] ] Cho hình chóp S.ABCD có đáy là hình vuông cạnh là 2a ; cạnh SA = a và vuông
góc với đáy. Gọi M là trung điểm của CD. Tính cos với  là góc tạo bởi hai đường thẳng SB và AM . A. 2 . B. 1 . C. 4 . D. 2 − . 5 2 5 5 Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn Chọn A Cách 1: S P A D N M B C
Gọi N , P lần lượt là trung điểm của AB và SA. SB // Ta có NP
 (SB,AM) = (NP, NC) =  . AM // NC Xét a a NPC có 5 NP = , 33 = . 2 PC = , NC a 5 2 2 2 2 + − Khi đó NP NC PC 2 cos = cos PNC = = . 2N . P NC 5
Cách 2: Trương Hồng Hà
Chọn hệ trục toạ độ Oxyz sao cho A(0;0;0), S (0;0;a) , B(2a;0;0) , D(0;2a;0) .
Ta có M (a;2a;0) , AM = (a;2a;0), SB = (2a;0;− a) . 2a Do đó  = (AM SB) 2 2 cos cos , = = . 2 2 2 2 5
a + 4a . 4a + a
Câu 35: [2H1-4.2-3] Cho hình bát diện đều có cạnh a và điểm I nằm trong hình bát diện. Tính tổng
khoảng cách từ I đến tất cả các mặt của bát diện. A. 4a 6 . B. 3a 2 . C. 4a 3 . D. a 3 . 3 2 3 2 Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 23 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 Chọn A Hình 1 Hình 2 3
Thể tích khối bát diện 1 1 a 2 a 2 ABCDEF là 2 V = = EO S = a = ABCDEF
2.VE ABCD 2. . . ABCD 2. . . . 3 3 2 3 Gọi 1 d , d , …, 2
d lần lượt là khoảng cách từ 8
I đến các mặt của bát diện. Gọi 1 V , 2 V ,…, 8 V
lần lượt là thể tích của các khối chóp tam giác có đỉnh I và có đáy là các mặt bên ứng với các đường cao 1 d , d , …, 2 d . 8 2 Ta có 1 a 3 V
= V +V + +V = d + d +
+ d S , trong đó S = là diện tích một ABCDEF . . . . . . 1 2 8 ( 1 2 8 ) 3 4
mặt của khối bát diện ABCDEF . 3 a 2 3. Suy ra 3.V a ABCDEF 3 4 6 d + d + ... + = = = . 1 2 d8 2 S a 3 3 4
Vậy tổng khoảng cách từ a
I đến tất cả các mặt của bát diện là 4 6 . 3
Câu 36: [2H2-1.4-3] Một khối nón có bán kính đáy bằng 2 cm , chiều cao bằng 3cm . Một mặt phẳng
đi qua đỉnh và tạo với đáy một góc 0
60 chia khối nón làm 2 phần. Tính thể tích V phần nhỏ
hơn (Tính gần đúng đến hàng phần trăm). A. 3 V 1, 42 cm . B. 3 V  2,36 cm . C. 3 V 1,53cm . D. 3 V  2, 47 cm . Lời giải
Tác giả: Trần Lê Hương Ly; Fb: Trần Lê Hương Ly Chọn A
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 24 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 Cách 1:
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc 60 cắt khối nón theo thiết diện là tam giác SMN như hình vẽ.
Gọi I là trung điểm MN . Khi đó OI ⊥ MN và SI ⊥ MN , suy ra góc giữa mặt phẳng (SMN )
và mặt đáy là góc SIO = 60. Xét tam giác SO 3
SIO ta có: OI = = = 1. 0 tan SIO tan 60 2 2
IN = ON − OI = 3 , MN = 2IN = 2 3 . 1 S = OI MN = . OMN . . 3 2 1 V = SO S = . S OMN . . OMN 1 . 3 1 2 4 3 V =  =  . k non . .2 . 3 / 3 3 IN 3 sin ION = =
. Suy ra ION = 60 , MON = 2.ION =120. ON 2
Gọi V là thể tích cần tính. Ta có 1 4 3 3 V = V −V =  −  . k non S OMN 1 1,42cm / . 3 9 Cách 2: Ngọc Toàn
Gọi mặt phẳng đi qua đỉnh và tạo với đáy một góc 60 cắt khối nón theo thiết diện là tam giác SMN như hình vẽ.
Gọi I là trung điểm MN . Khi đó OI ⊥ MN và SI ⊥ MN , suy ra góc giữa mặt phẳng (SMN ) và mặt đáy là góc 0 SIO = 60 .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 25 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 Xét tam giác SO 3
SIO ta có: OI = = = 1. 0 tan SIO tan 60 2 2
IN = ON − OI = 3  MN = 2IN = 2 3 . 1 S = OI MN = . OMN . . 3 2 Ta có IN 3 sin ION = =
suy ra ION = 60 , MON = 2.ION =120. ON 2
Gọi S là diện tích hình viên phân tạo bởi dây MN và cung nhỏ MN . V Ta có 1 2 4
S =  R − S = − V OMN 3 3 3
Thể tích phần nhỏ cần tính là: 1 4 3 3 V = . SO S =  −  . V 1 1,42cm 3 9
Câu 37: [2H3-6.17-2] Trong không gian Oxyz , điểm M  đối xứng với điểm M (1;2;4) qua mặt phẳng
( ):2x + y + 2z −3 = 0 có tọa độ là A. (−3;0;0). B. ( 1 − ;1;2) . C. (−1;−2;−4). D. (2;1;2). Lời giải
Tác giả: Nguyễn Tình; Fb: Gia Sư Toàn Tâm Chọn A
Mặt phẳng ( ) có vectơ pháp tuyến là n = (2;1;2).
MM  vuông góc với mặt phẳng ( ) nên đường thẳng MM nhận n = (2;1; 2) làm vectơ chỉ x = 1+ 2t
phương. Phương trình đường thẳng 
MM  là:  y = 2 + t . z = 4+  2t
Gọi H là giao điểm của đường thẳng MM  và mặt phẳng ( ) .
H MM   H (1+ 2t; 2 + t; 4 + 2t ) .
H  ( )  2(1+ 2t ) + 2 + t + 2(4 + 2t ) − 3 = 0  9t + 9 = 0  t = 1 −  H (−1;1;2) .
M  đối xứng với điểm M qua mặt phẳng ( ) nên H là trung điểm của MM   M (−3;0;0) .
Câu 38: [2H3-6.18-3] Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(−1;2;5) , B(3;−1;0) ,
C (−4;0; −2) . Gọi I là điểm trên mặt phẳng (Oxy ) sao cho biểu thức IA − 2IB + 3IC đạt giá
trị nhỏ nhất. Tính khoảng cách từ I đến mặt phẳng (P) : 4x + 3y + 2 = 0 . A. 17 . B. 6 . C. 12 . D. 9. 5 5 Lời giải
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 26 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Tác giả: Nguyễn Tình; Fb: Gia Sư Toàn Tâm Chọn B Gọi M (a; ;
b c) là điểm thỏa mãn MA − 2MB + 3MC = 0 .  19  1 − − = −
a − 2(3 − a) + 3( 4 − − a) = 0 a   2  Khi đó:  19 1  2 − b − 2( 1
− − b) + 3(0 − b) = 0  b  = 2  M − ;2;−  . 2 2    5  −  c − 2  (0−c)+3( 2 − − c) = 0 1 c = −  2
Ta có: IA− 2IB +3IC = IM + MA− 2IM − 2MB +3IM +3MC
= 2IM + (MA− 2MB +3MC) = 2 IM = 2IM .
Biểu thức IA− 2IB +3IC đạt giá trị nhỏ nhất  IM nhỏ nhất  I là hình chiếu vuông góc của  19 
M lên (Oxy )  I −  ;2;0 . 2     19 4.  − + 3.2 +   2 Khoảng cách từ điểm  2 
I đến mặt phẳng ( P) là: d ( I;( P)) = = 6 . 2 2 4 + 3
Câu 39: [2D4-1.4-3] Cho số phức z = a +bi (a,b ) thỏa mãn z −3 = z −1 và (z + 2)(z −i) là số
thực. Tính a + b . A. 2 − . B. 0. C. 2. D. 4. Lời giải
Tác giả: Trần Thơm; Fb: Kem LY Chọn B
Ta có z = a + bi (a,b ) . +) 2 2 2
z − 3 = z −1  a − 3 + bi = a −1+ bi  (a − ) + b = (a − ) 2 3 1 + b  (a − )2 2 + b = (a − )2 2 3 1 + b  4
− a +8 = 0  a = 2 .
+) (z + 2)(z −i) = (a +bi + 2)(a −bi −i) = (a + 2)+bi a −(b+ ) 1 i    
= a (a + 2) + b(b + )
1 − (a + 2b + 2)i .
(z + 2)(z −i) là số thực  a+2b+2 = 0.
Thay a = 2 tìm được b = 2
− . Vậy a +b = 0. 4 3 2
Câu 40: [2D3-4.3-3] Biết x + x + 7x + 3 a dx = + c ln 5 
với a , b , c là các số nguyên dương và a là 2 x − x + 3 b b 1
phân số tối giản. Tính 2 3
P = a − b − c . A. 5 − . B. 4 − . C. 5. D. 0.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 27 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 Lời giải
Tác giả: Trần Thơm; Fb: Kem LY Chọn B Cách 1: 4 3 2 4  3(2x − ) 1 
Ta có x + x + 7x + 3 d =  x+ 2+ d 2 2 x x − x + 3 x x − x +  3 1 1  4 4 1 d( 2 x − x +   3) 4 2 27 2 27 = x + 2x + 3 =
+ 3ln x − x + 3 = +   3ln 5  . 2   − + 1 2 x x 3 2 2 1 1 4 3 2
Mà x + x + 7x + 3 d a x = + c ln 5 
, suy ra a = 27 , b = 2 , c = 3. 2 x − x + 3 1 b Vậy 2 3
P = a − b − c = 4 − .
Cách 2: Sử dụng máy tính cầm tay 4 3 2 4 3 2
Ta có x + x + 7x + 3 d a a
x + x + 7x + 3 x = + c ln 5   = dx − cln5 2  . x − x + 3 2 b x − x + 3 1 b 1 4 3 2 Đặt ( ) a
x + x + 7x + 3 f X = = dx − Xln5  với X = . 2 c b x − x + 3 1
Vì a , b , c là các số nguyên dương và a là phân số tối giản nên ta có thể tìm giá trị của X b
nguyên dương để f (X) a = là số hữu tỉ. b 4 3 2
Bước 1: Bấm tích phân x + x + 7x + 3 d  → Shift → STO→ A. 2 x − x + 3 x 1
Bước 2: MODE → 7 → Nhập f (X) = A − Xln5 → X chạy từ 1 đến 20, STEP = 1.
Bước 3: Ta thấy chỉ có một giá trị duy nhất X = 3 để f (X) =13,5 là số hữu tỉ. Vậy a c = 3 và 27 =13,5 =
nên a = 27 , b = 2 . Do đó 2 3
P = a − b − c = 4 − . b 2
Câu 41: [2D3-4.12-3] Cho hàm số y = f (x) có đạo hàm liên tục trên 2;4 và f (x)  0, x  2;4.
Biết 4x f (x) =  f   ( x) 3 7 3 3  − x , x   
2;4, f (2) = . Giá trị của f (4) bằng 4 A. 40 5 −1 . B. 20 5 −1 . C. 20 5 −1 . D. 40 5 −1 . 2 4 2 4 Lời giải
Tác giả: Nguyễn Hoàng Hưng; Fb: Nguyễn Hưng Chọn D
Ta có: f (x)  0, x
 2;4 nên hàm số y = f (x) đồng biến trên 2;4  f (x)  f (2) mà f ( ) 7
2 = . Do đó: f (x)  0, x  2;4. 4
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 28 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Từ giả thiết ta có: x f (x) =  f (x) 3
 − x x f (x) +  =  f (x) 3 3 3 3 4 4 1        f x 3  .
x 4 f ( x) +1 = f ( x) ( )  = x . 3 4 f ( x) +1 f ( x) 1 d 4 f  (x) 2 +1 2 Suy ra: d = d  x 3 2 x x x x  = + C    3  4 f  (x)+1 = +C  . 3 4 f ( x) +1 4 3 4 f ( x) +1 2 8 2 f ( ) 7 3 1 2 =  = 2 +  = − . 4 2 C C 2 4  (  x − ) 3 2 1 −1  Vậy:   − f ( x) 3 =  f ( ) 40 5 1 4 = . 4 4
Câu 42: [2D1-1.3-3] Cho hàm số y = f (x) có đạo hàm liên tục trên . Biết hàm số y = f ( x) có đồ
thị như hình vẽ. Gọi S là tập hợp các giá trị nguyên m−5;5 để hàm số g (x) = f (x + m)
nghịch biến trên khoảng (1;2). Hỏi S có bao nhiêu phần tử? A. 4 . B. 3. C. 6 . D. 5. Lời giải
Tác giả: Hoàng Thị Minh Tuấn; Fb: Minh Tuấn Hoàng Thị Chọn D
Ta có g(x) = f (x + m) . Vì y = f ( x) liên tục trên nên g(x) = f (x + m) cũng liên tục
trên . Căn cứ vào đồ thị hàm số y = f ( x) ta thấy x + m  1 − x  1 − − m
g( x)  0  f ( x + m)  0   . 1  
  x + m  3 1
 − m x  3− m
Hàm số g (x) = f (x + m) nghịch biến trên khoảng (1;2) 2  −1− m  m  3 −  3− m  2    . 0  m 1  1   − m 1
Mà m là số nguyên thuộc đoạn −5;5 nên ta có S = −5;−4;−3;0;  1 .
Vậy S có 5 phần tử.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 29 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Câu 43: [2D1-3.1-3] Cho hàm số y = f (x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất
của hàm số g (x) = f ( 1 1 2 4x − x ) 3 2
+ x − 3x + 8x + trên đoạn 1;  3 . 3 3 A. 15. B. 25 . C. 19 . D. 12. 3 3 Lời giải
Tác giả: Lưu Thị Thủy; Fb: thuy.luu.33886 Chọn D
g( x) = ( − x) f ( 2 x − x ) 2 4 2 4
+ x − 6x +8 = ( − x) f   ( 2 2 2
4x − x )+ 4− x . Với x 1;  3 2 thì 4 − x  0; 2
3  4x − x  4 nên f (4x − x )  0. Suy ra f ( 2 2
4x − x )+ 4− x  0, x1;3 . Bảng biến thiên
Suy ra max g (x) = g (2) = f (4) + 7 =12 . 1;  3
Câu 44: [2H3-2.13-3] Trong không gian với hệ tọa độ Oxyz cho bốn điểm (
A 1;0;0) , B(2;1;3) , C(0; 2; − 3) , (
D 2;0; 7) . Gọi M là điểm thuộc mặt cầu 2 2 2
(S) :(x + 2) + (y − 4) + z = 39 thỏa mãn: 2 MA + 2M .
B MC = 8 . Biết độ dài đoạn thẳng MD đạt giá trị lớn nhất. Tính giá trị lớn nhất đó. A. 2 7 . B. 7 . C. 3 7 . D. 4 7 . Lời giải
Tác giả: Nguyễn Thị Ngọc Lan; Fb:Ngoclan nguyen Chọn A
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 30 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 +) Mặt cầu 2 2 2
(S) :(x + 2) + (y − 4) + z = 39 có tâm là I ( 2
− ;4;0) , bán kính R = 39 .
Gọi M (x, y , z)(S) . Ta có: 2 2 2
x + y + z = 19 − 4x + 8y . 2 2 2 2
MA = (x −1) + y + z = 20 − 6x + 8y .
MB = (2 − x;1− y;3 − z) ; MC = (−x; 2 − y ; − 3− z) . 2 2 2 M . B MC = 2
− x + x + 2 −3y + y −9 + z =19 − 4x + 8y − 2x − 3y − 7 = −6x + 5y +12 . Suy ra 2 MA + 2M . B MC = 18
− x +18y + 44 . Theo giả thiết 2 MA + 2M .
B MC = 8  −18x +18y + 44 = 8  −x + y + 2 = 0 .
Do đó M (P) : −x + y + 2 = 0 . 8
Ta có d(I;(P)) =
= 32  39 nên mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là 2
đường tròn (C) có bán kính R =
R − d = 39 − 32 = 7 . 1 R với 2 2 1 D  , M (P) Mặt khác ta có 
D, M (C) . Do đó độ dài MD lớn nhất bằng 2R = 2 7 .  1 D, M   (S)
Vậy chọn A. f (1−2x)
Câu 45: [2D1-1.4-3] Cho hàm số  1 
y = f ( x) . Đồ thị y = f ( x) như hình bên. Hàm số g ( x) =  2  
nghịch biến trên khoảng nào trong các khoảng sau? A. (0; ) 1 . B. (−;0) . C. (−1;0) . D. (1;+ ) . Lời giải
Tác giả: Vũ Việt Tiến, FB: Vũ Việt Tiến Chọn D
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 31 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019   − Từ đồ thị hàm số x
y = f ( x) ta có f ( x) 1  0  . 1    x  2 f (1−2x) Xét hàm số   g ( x) 1 =  . 2    f (1−2x) f (1−2x) Ta có      1  g( x) 1 =  
(− ) f ( − x) 1 . 2 . 1 2 .ln = 2ln 2. . f (1−   2x). 2  2      2  x 1 1  − 2x  1 −
g( x)  0  f (1− 2x)  0     1 . 1  1− 2x  2 −  x  0  2
Vậy hàm số g ( x) nghịch biến trên khoảng (1;+ ) . Chọn D.
Câu 46: [2D3-5.13-3] Nhà trường dự định làm một vườn hoa dạng elip được chia ra làm bốn phần bởi
hai đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ
dài trục lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, F ,1 2
F là hai tiêu điểm của elip. Phần
A , B dùng để trồng hoa, phần C , D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa
và cỏ lần lượt là 250.000 đ và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn). A. 5.676.000 đ. B. 4.766.000 đ. C. 4.656.000 đ. D. 5.455.000 đ. Lời giải
Tác giả: Ngô Quốc Tuấn; Fb: Quốc Tuấn Chọn A
Gắn hệ trục tọa độ như hình vẽ.
Do elip có độ dài trục lớn 2a = 8  a = 4, độ dài trục nhỏ 2b = 4  b = 2 .
Diện tích của (E) là: S =  =  ( ) ab 8 . E
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 32 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 2 2 Phương trình chính tắc ( x y 1 E ) là: + = 1. Suy ra 2 y =  16 − . 16 4 2 x Ta có 2 2 c =
a − b = 2 3  F 2 3; 0 . 2 ( ) Do N và N 2 3; 1 . 2
F có cùng hoành độ  ( ) Gọi (P) 2
: y = kx là parabol nằm ở phía trên trục Ox . Do 1
N  ( P) ta có = k ( )2 1 1 2 3  k = . Suy ra (P) 2 : = . 12 y 12 x 2 3 2 3 Diện tích phần  1 1   1 2 1 2  A là 2 2 S = − x − x x
= 2   16− x − x dxA  16 d 2 12     2 12  2 − 3 0 2 3 2 3 2 1 2 = 16 − x dx − x d  6 x  . 0 0 2 3 * Xét 2 I = 16 − x d =  = . 1 x  . Đặt x 4sint dx 4cos d t t 0 Đổi cận:     3 3 3 3 Khi đó 2  1  I = 16 −16sin t.4cos d 2
=16 cos d = 8 1+ cos2t d = 8 t +  sin 2 1 t tt t  ( ) t 2 t    0 0 0 0   3  = 8 + . 3 4      2 3 2 3 * Ta có 1 2 1 I = x d 3 = 4 3 = . 2 6 x  18 x 3 0 0 Suy ra: 8 + 2 3  +
S = I − I = 16 4 3
S + S = S = . A B 2 A 1 2 3 A 3 Tổng diện tích phần  −
C , D là: S + S = S − S + S = 8 4 3 . E ( A B ) C D ( ) 3
Khi đó tổng số tiền để hoàn thành vườn hoa trên là: 16 + 4 3 8 − 4 3 .250000 + .150000  5676000 đ. 3 3
Câu 47: [2H1-2.5-3] Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Gọi E và F lần lượt là
các điểm trên các cạnh A D   và A B   sao cho 2 AE =   và 2  =   . Tính thể tích 3 A D A F 3 A B khối chóp . A BDEF .
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 33 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 3 3 3 3 A. a 3 . B. 5a . C. a . D. 3a 3 . 8 18 8 8 Lời giải
Tác giả: Đàm Văn Thượng; Fb:Thượng Đàm Chọn B Cách 1: A' F B' E C' D' A B O D C Ta có V = + . . V V A EFBD E.ABD E.ABF
Gọi S là diện tích một mặt của hình lập phương, 1S là diện tích tam giác ABD và S là diện 2 tích tam giác ABF . 2 2 3 Do 1 a = = và d( 1 a a E,( ABCD)) =  = suy ra V = a = . E ABD . . 1 S 2 S 2 AA a . 3 2 6 2 Lại có 1 = A . a S = và (E ( AA BB  )) 2 d , =  = suy ra 2 2 B BB 2 EA 3 a 1 a a V = S E AA BB  = a = . E ABF ( ( )) 2 3 1 2 .d , . . 2 3 3 2 3 9 3 3 3 Vậy a a 5a V = + = + = . . V V A EFBD E.ABD E.ABF 6 9 18 Cách 2:
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 34 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 A' F B' E C' D' A B K O H I D C   Trong tam giác A BD   có A E A F = suy ra EF//B D
  mà BD//B D
  nên EF//BD. ADAB
Suy ra tứ giác EFBD là hình thang.
Trong mặt phẳng ( AADD) dựng EH //DD suy ra EH ⊥ ( ABCD)  EH ⊥ BD ( ) 1 , trong
mặt phẳng ( ABCD) dựng HI ⊥ BD tại I (2) Từ ( )
1 và (2) suy ra BD ⊥ (EHI )  (EBD) ⊥ (EHI ), (EBD) (EHI ) = EI .
Trong mặt phẳng (EHI ) , kẻ HK ⊥ EI, K EI HK ⊥ (EBD) hay d(H,(EBD)) = HK . d( , A ( EBD)) Ta thấy AD ( = =  d( ,
A ( EBD)) = 3d ( H ,( EBD)) = 3HK . H ( EBD)) 3 d , HD  Trong tam giác EF A E 2a 2 A BD   , có 2 = =  EF = . B D   A D   3 3 Trong tam giác HI DH a DOA, có 1 = = 1 2  HI = AO = . AO DA 3 3 6 Trong tam giác a HE HI a
EHI , có EH = AA = a , 2 2 38 EI = HE + HI = , . 19 = = . 6 HK EI 19 (EF + BD) 2 . Diện tích hình thang EI 5a 19 a EFBD là S = =
và ( A (EBD)) 3 19 d , = . 2 18 19 Vậy thể tích khối . a
A EFBD là V = S ( A (EBD)) 3 1 5 .d , = . 3 18
Câu 48: [2D4-4.1-4] Cho hai số phức z ,
z + 2 − i + z − 4 − 7i = 6 2 và iz −1+ 2i = 1 . 1 z thoả mãn 2 1 1 2
Tìm giá trị nhỏ nhất của biểu thức T = + 1 z z2 . A. 2 −1. B. 2 +1. C. 2 2 +1. D. 2 2 −1. Lời giải
Tác giả: Đào Văn Tiến; Fb: Đào Văn Tiến Chọn D
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 35 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Gọi M là điểm biểu diễn số phức
A −2;1 ; B (4;7) lần lượt là hai điểm biểu diễn hai số 1 z và ( ) phức 2
− + i , 4 + 7i . Ta có AB = 6 2 . Phương trình đường thẳng AB là d : x − y + 3 = 0 .
+) z + 2 −i + z − 4 − 7i = 6 2  MA+ MB = 6 2  + = . Do đó tập hợp các 1 1 MA MB AB
điểm biểu diễn số phức 1z là đoạn thẳng AB .
+) iz −1+ 2i =1  iz −1+ 2i i =1  −z − 2 − i =1 2 2 2 .
Gọi N là điểm biểu diễn số phức −z và I (2; )
1 là điểm biểu diễn số phức 2 + . Ta có IN =1 2 i
Suy ra tập hợp các điểm biểu diễn số phức −z là đường tròn (C) có phương trình: 2
(x − )2 +( y − )2 2 1 =1.
d ( I, AB) = 2 2  1 , suy ra AB không cắt đường tròn.
Gọi K là hình chiếu của I (2; )
1 lên AB . Dễ thấy K nằm trên đoạn thẳng AB .
Gọi H là giao điểm của đoạn IK với đường tròn (C) .
Ta có z + z = MN KH = d I, AB − R = 2 2 −1. 1 2 ( )
Suy ra min z + z = 2 2 −1. 1 2
Câu 49: [1D2-2.2-4] Từ các chữ số thuộc tập X = 0;1;2;3;4;5;6; 
7 có thể lập được bao nhiêu số tự
nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18. A. 720. B. 860. C. 984. D. 1228. Lời giải
Tác giả: Nguyễn Thị Thu Trang; Fb: Nguyễn Thị Thu Trang Chọn C
Giả sử số lập được có dạng   1 a a2 3 a a4 5 a 6 a , a  0 , với , , j =1;6 . 1 a a i j i = 1;6 i j
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 36 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019 a a a a a a 9 (
 a + a + a + a + a + a 9 1 2 3 4 5 6 ) Ta có a a a a a a 18 1 2 3 4 5 6   . 1 2 3 4 5 6   a a a a a a  2 a  2 1 2 3 4 5 6 6
Vì (a + a + a + a + a + a 9 nên ta có các trường hợp sau 1 2 3 4 5 6 ) Trường hợp 1: X = 2;3; 4;5;6;7 1 a , 2 a , 3 a , 4 a , 5 a , 6
a được chọn từ 1   + Có 3 cách chọn chọn 6 a .
+ Có 5! cách chọn chọn bộ 5 số (a ;a ;a ;a ; . 1 2 3 4 5 a ) Suy ra có 3.5!= 360 số. Trường hợp 2: X = 0;1; 2; 4;5;6 1 a , 2 a , 3 a , 4 a , 5 a , 6
a được chọn từ 2  
+ a = 0, có 5! cách chọn bộ 5 số (a ;a ;a ;a ; 1 2 3 4 5 a ) . 6 + a  0 khi đó 6 6 a
có 3 cách chọn, 1a có 4 cách chọn và có 4! cách chọn bộ 4 số
(a ;a ;a ; + = 2 3 4 5
a ) . Suy ra có 5! 3.4.4! 408 số. Trường hợp 3: X = 0;1; 2;3;5; 7 1 a , 2 a , 3 a , 4 a , 5 a , 6
a được chọn từ 3  
+ a = 0, có 5! cách chọn bộ 5 số (a ;a ;a ;a ; 1 2 3 4 5 a ) . 6 + a  0 khi đó 6 6 a
có 1 cách chọn, 1a có 4 cách chọn và có 4! cách chọn bộ 4 số
(a ;a ;a ; 2 3 4 5 a ) .
Suy ra có 5!+1.4.4!= 216 số.
Vậy có 360+ 408+ 216 = 984 số.
Câu 50: [2D1-2.11-4] Gọi 0
m là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số 3
y = x − 6mx + 4 cắt đường tròn tâm I (1;0) , bán kính bằng 2 tại hai điểm
phân biệt A , B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng: A. m  2;3 m  3; 4 m  0;1 m  1; 2 0 ( ). B. 0 ( ). C. 0 ( ) . D. 0 ( ) . Lời giải
Tác giả: Hà Lê; Fb: Ha Le Chọn C Ta có 2
y = 3x − 6m , 2
y = 0  x = 2m . Đồ thị hàm số có điểm cực đại, điểm cực tiểu khi và
chỉ khi y = 0 có hai nghiệm phân biệt. Do đó m  0. Ta có x y = ( 2
. 3x − 6m) − 4mx + 4  phương trình đường thẳng () đi qua điểm cực đại và 3
cực tiểu của đồ thị hàm số đã cho là: y = 4
− mx + 4  4mx + y −4 = 0.
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 37 Mã đề 638
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề HKII Trường Chuyên Lê Hồng Phong Năm 2019
Đường thẳng () cắt đường tròn đã cho tại hai điểm phân biệt A , B sao cho I , A , B là ba 4m − 4
đỉnh của một tam giác  0  d (I;())  2  0   2 () . 2 16m +1
Gọi H là trung điểm đoạn AB  1 S
= IH AB = IH.AH 2 2
= IH. R − IH 2 = IH. 2 − IH IAB . 2 2 2 IH + 2 − IH 2 = IH .( 2 2 − IH ) ( )  =1  S  . IAB 1 2
Vậy diện tích tam giác IAB đạt giá trị lớn nhất bằng 1  2 2 IH = 2 − IHIH =1  2
4m − 4 = 16m +1  ( m − )2 2 4 4 =16m +1  15 m =
(thỏa mãn điều kiện () ). 32 Vậy 15 m  0;1 . 0 m = nên 0 ( ) 32
Hãy tham gia STRONG TEAM TOÁN VD-VDC- Làm 2 câu nhận lại hơn 600 câu 1 tuần Page 38 Mã đề 638
Document Outline

  • [toanmath.com] - Đề thi 8 tuần HK2 Toán 12 năm 2018 – 2019 trường chuyên Lê Hồng Phong – Nam Định
  • [STRONG TEAM TOÁN VD-VDC]-Giải Chi Tiết Chuyên-Lê-Hồng-Phong-Nam-Định_L1_1819