Đề thi chọn học sinh giỏi cấp tỉnh Toán 12 năm 2018 – 2019 sở GD và ĐT Thái Nguyên

Nhóm toán VD - VDC
ĐỀ THI HSG LỚP 12 TỈNH THÁI NGUYÊN NĂM HỌC: 2018-2019
THỜI GIAN : 180 PHÚT
Bài 1(4 điểm). Cho hàm số 3 2
y = x −3x + 4 có đồ thị (C) , đường thẳng (d ) đi qua A(1; 2) và có
hệ số góc m . Tìm m để (d ) cắt (C) tại ba điểm phân biệt ,
A B, C sao cho BC = 4 2 .
Bài 2(4 điểm). Giải phương trình 3 2
x − 7x + 9x +12 = (x − )
3 (x−2 +5 x−3)( x−3 − ) 1
Bài 3 (4 điểm). u = 2 ∞ 1 Cho dãy số (u thỏa mãn  . n )  n 1 = 2
u + u +...+ u
+ u = n u , n ≥1  1 2 n 1  − n n Tìm giới hạn ( 2 lim n u . n )
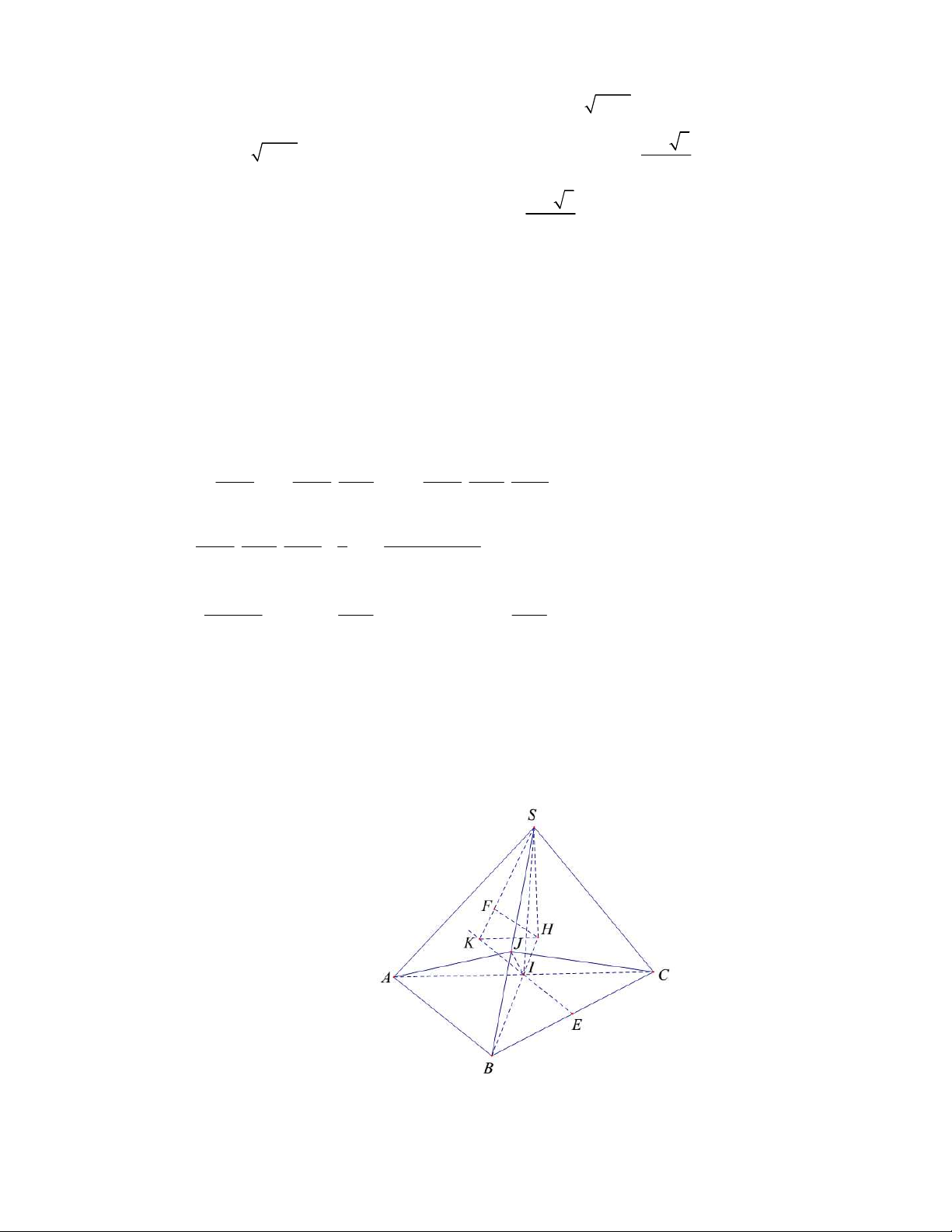
Bài 4 (4 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = a . Gọi I
là trung điểm của AC . Biết hình chiếu của S lên mặt phẳng ABC là điểm H thỏa mãn BI = 3IH
và góc giữa hai mặt phẳng(SAB) ;(SBC) bằng 60ο . Tính thể tích khối chóp S.ABC đã cho và tính
khoảng cách giữa hai đường thẳng AB , SI theo a . Bài 5 8
(4 điểm). Cho các số thực dương x, y thỏa mãn điều kiện 2 2 x + 2 y =
. Tìm giá trị lớn nhất 3 của biểu thức
P = (x + y) 2 2 7 2
− 4 x + 2xy +8y . HẾT Nhóm toán VD - VDC HƯỚNG DẪN GIẢI
Bài 1(4 điểm). Cho hàm số 3 2
y = x −3x + 4 có đồ thị (C) , đường thẳng (d ) đi qua A(1; 2) và có
hệ số góc m . Tìm m để (d ) cắt (C) tại ba điểm phân biệt ,
A B, C sao cho BC = 4 2 . Lời giải
+) Phương trình đường thẳng (d ) : y = m(x − ) 1 + 2
+) Phương trình hoành độ giao điểm 3 2 3 2
x −3x + 4 = m(x −1) + 2 ⇔ x −3x − mx + m + 2 = 0  x = 1 ⇔ (x − ) 1 ( 2
x − 2x − m − 2) = 0 ⇔  2
g(x) = x −2x − m−2 = 0 
Giả sử g (x) = 0 có hai nghiệm x , x , khi đó B(x ; m x −1 + 2 ;C x ;m x −1 + 2 1 ( 1 ) ) ( 2 ( 2 ) ) 1 2 BC (m ) 1 (x x )2 (m ) 1 (  x x )2 2 2 2 4  = + − = + + − x x 1 2  1 2 1 2    =( 2 m + ) 1 (4 + 4m + ) 8 = 32 ⇔ m = 1 Thay m = 1 vào 2
g(x) = x − 2x −3 = 0 ⇔ x = −1; x = 3 (thỏa mãn). Vậy m = 1.
Bài 2(4 điểm). Giải phương trình 3 2
x − 7x + 9x +12 = (x − )
3 (x−2 +5 x−3)( x−3 − ) 1 Lời giải
Điều kiện: x−3 ≥ 0 ⇔ x ≥ 3.
Phương trình đã cho tương đương với (x − )( 2 4 x −3x − ) 3 = (x − )
3 (x−2 +5 x−3)( x−3 − ) 1
⇔ ( x− − )( x− + )( 2 3 1 3 1 x −3x − ) 3 = (x − )
3 (x−2+5 x−3)( x−3 − ) 1
 x−3 −1= 0  →
x −3 = 1 ⇔ x = 4  ⇔  . ( 2
 x −3x − ) 3 ( x−3 + ) 1 = (x − )
3 (x−2 +5 x−3) ( ) ∗ 
Dễ thấy x = 3 không là nghiệm của phương trình đã cho. 2 x −3x −3
x − 2 + 5 x −3
Với x > 3, giải phương trình ( ) ∗ , ta được = x −3 x −3 +1 (x − )2 4 + 5(x − 4)+1
x −3+ 5 x −3 +1 ⇔ =
⇔ f (x − 4) = f ( x−3). x − 4 +1 x −3 +1 2 t + 5t +1 3
Xét hàm số f (t) = trên ( 1 − ;+ )
∞ , có f ′(t) =1+ > 0; ∀t > 1 − . t +1 (t + )2 1 Nhóm toán VD - VDC
Suy ra f (t) là hàm số đồng biến trên f (t) mà f (x − 4) = f ( x−3) x − 4 ≥ 0 x ≥ 4 9 + 5 Do đó x 4 x 3   − = − ⇔  ⇔  ⇔ x = . (  x − 4  )2 2 = x −3
x −9x +19 = 0 2   9 + 5
Vậy phương trình đã cho có hai nghiệm là x = 4; x = . 2
Bài 3 (4 điểm). u = 2 ∞ 1 Cho dãy số (u thỏa mãn  . Tìm giới hạn ( 2 lim n u . n ) n )  n 1 = 2
u + u +...+ u
+ u = n u , n ≥1  1 2 n 1  − n n Lời giải Theo giả thiết ta có: (n + )2 1 u
= u + u + + u + u = n u + u ⇒ n + n u = n u ⇒ n + u = nu n+ ( ... n ) 2 n+ n n+ ( 2 2 ) 2 2 1 1 2 1 1 n 1 + n ( ) n 1 + n n n n −1 n n −1 n − 2 ⇒ u = u = . u = . . .u n 1 + n n 1 − n 2 n + 2 n + 2 n +1 n + 2 n +1 − n n n 1 − n − 2 1 4 = ... = . . ... u = 1 n + 2 n +1 n 3 (n + 2)(n + ) 1 4 4n 4n 2 ⇒ u = ⇒ n u = ⇒ lim n u . n n ( 2 n)= lim = 4 n(n + ) 1 n +1 n +1
Bài 4 (4 điểm). Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB = a . Gọi I
là trung điểm của AC . Biết hình chiếu của S lên mặt phẳng ABC là điểm H thỏa mãn BI = 3IH
và góc giữa hai mặt phẳng(SAB) ;(SBC) bằng 60ο . Tính thể tích khối chóp S.ABC đã cho và tính
khoảng cách giữa hai đường thẳng AB , SI theo a . Lời giải BH ⊥ AC
a) Từ giả thiết của bài toán ta có  
⇒ AC ⊥ (SBH ) ⇒ AC ⊥ SB . SH ⊥  AC Nhóm toán VD - VDC AJ ⊥ SB Kẻ 
IJ ⊥ SB ⇒ 
⇒ góc giữa hai mặt phẳng (SAB) và (SCB) bằng góc giữa CJ ⊥  SB
hai đường thẳng AJ và CJ .
Dễ thấy ∆AIJ là tam giác cân tại J , kết hợp với giả thiết góc giữa hai mặt phẳng (SAB)
và (SCB) bằng 60ο ta có hai trường hợp sau:
TH1: AJC = 60ο ⇒ AJI = 30ο . ο a 6 Ta có 2 2 IJ = AI.tan 60 =
⇒ BJ = BI + IJ = 2 . a 2 IJ.BH AC a 4a
∆BIJ ∼∆BSH ⇒ SH = . Mặt khác IB = = ⇒ BH = . BJ 2 2 3 2 3 a 6 1 6a Nên ta có SH = ⇒ V = SH .S = (đvtt). S . 3 ABC 3 ABC 18
TH2: AJC =120ο ⇒ AJI = 60ο . ο a 2a Ta có 2 2 IJ = AI.tan 30 =
⇒ BJ = BI + IJ = . 6 6 3 2a 1 2a
Làm tương tự TH1 ta có SH = ⇒ V = SH.S = (đvtt). S . 3 ABC 3 ABC 18
b) Gọi E là trung điểm của BC ⇒ IE AB . Do vậy ta có
d (AB, SI ) = d (AB,(SIE)) = d (B,(SIE)) .
Do BI = 3IH ⇒ d (B,(SIE)) = 3d (H ,(SIE)).
Kẻ HK ⊥ IE ( K thuộc IE ).
Mặt khác ta lại có SH ⊥ ( ABC) nên SH ⊥ IE ⇒ IE ⊥ (SHK ) ⇒ (SIE) ⊥ (SHK ) .
Kẻ HF ⊥ SK ⇒ HF ⊥ (SIE) ⇒ d (H ,(SIE)) = HJ . 1 1 1 SH .HK
Xét tam giác vuông SHK ta có: = + ⇒ HF = . 2 2 2 2 2 HF HK SH SH + HK HK IH 1 1 a Mặt khác = = ⇒ HK = BE = . BE IB 3 3 6 a 6 6a - Khi SH = ta có HF = . 3 15 Nhóm toán VD - VDC 2a 2a - Khi SH = ta có HF = . 3 9 Bài 5 8
(4 điểm). Cho các số thực dương x, y thỏa mãn điều kiện 2 2 x + 2 y =
. Tìm giá trị lớn nhất 3 của biểu thức
P = (x + y) 2 2 7 2
− 4 x + 2xy +8y . Lời giải 2 2 Ta có: 2 2 2 2
4 x + 2xy + 8 y = 16x + 32xy +128y = 7(x − 2 y) +(3x +10 y) ≥ 3x +10 y( ) 1
Suy ra: P = (x + y) 2 2 7 2
− 4 x + 2xy +8y ≤ 7x +14 y −(3x +10y) = 4(x + y) .  1   1
Mặt khác: x + y = 1  .  x + 2  y ≤ 1   +  ( 2 2
x + 2 y ) = 2 ⇒ P ≤ 4.2 = 8(2).  2     2
7(x−2y)2=0   4    x =   Đẳ x 2  y  3 ng thức xảy ra ở ( ) 1 &( ) 2 khi và chỉ khi  = ⇔  . 1 1  2    y =  2    3  8  2 2 x + 2 y =  3  4 x =  3
Vậy GTLN P = 8 đạt được khi  .  2 y =  3