

Preview text:
SỞ GD&ĐT NINH BÌNH
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS
Năm học 2013 – 2014 ĐỀ THI C HÍNH THỨC MÔN: TOÁN
Ngày thi: 1 5/3/2014
(Thời gian 150 phút không kể thời gian phát đề)
Đề thi gồm 05 câu, trong 01 trang Câu 1 (6,0 điểm): 2 a) Rút gọn biểu thức: 2 ab 1 a b M = 1+ − a b 4 b a + 2 b) Giải phương trình: x 1 5 x 1 + = − 2 9 x 3 3 x 1 1 + 2 − = 2 x y
c) Giải hệ phương trình: 1 1 + 2 − = 2 y x Câu 2 (3,0 điểm):
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) có phương trình y = mx – 2 và 2
parabol (P) có phương trình y = −x . Chứng minh rằng với mọi giá trị của m đường thẳng 4
(d) luôn cắt parabol (P) tại hai điểm phân biệt A, B. Tìm các giá trị của m để đoạn AB có độ dài nhỏ nhất. Câu 3 (2,0 điểm):
Cho các số thực a, b, c đôi một khác nhau thỏa mãn 0 ≤ a;b;c ≤ 2 Chứng minh rằng: 1 1 1 9 + + ≥ . (a − 2 b) (b − 2 c) (c − 2 a) 4
Câu 4 (6,0 điểm):
Cho đường tròn tâm O đường kính MN, dây cung AB vuông góc với MN tại điểm I nằm
giữa O, N. Gọi K là một điểm thuộc dây AB nằm giữa A, I. Các tia MK, NK cắt đường tròn
tâm O theo thứ tự tại C, D. Gọi E, F, H lần lượt là hình chiếu của C trên các đường thẳng
AD, AB, BD. Chứng minh rằng: a) AC.HF = AD.CF
b) F là trung điểm của EH
c) Hai đường thẳng DC và DI đối xứng với nhau qua đường thẳng DN. Câu 5 (3,0 điểm):
Cho n và k là các số tự nhiên, 4 2k 1 A n 4 + = + .
a) Tìm k, n để A là số nguyên tố. b) Chứng minh rằng:
+ Nếu n không chia hết cho 5 thì A chia hết cho 5.
+ Với p là ước nguyên tố lẻ của A ta luôn có p – 1 chia hết cho 4. HẾT
Họ và tên thí sinh :....................................................... Số báo danh .......................................
Họ và tên, chữ ký: Giám thị 1:..................................................................................................
Giám thị 2:..................................................................................................
SỞ GD&ĐT NINH BÌNH
HDC ĐỀ THI CHỌN HSG LỚP 9 THCS
Năm học 2013 – 2014 MÔN: TOÁN
(hướng dẫn chấm gồm 04 trang) Câu Đáp án Điểm a. (2 điểm) Điều kiện: a;b > 0. 2 2 M = 2 ab 4ab + a + b − 2ab 0,5 a + b 4ab 2 = 2 ab (a + b) a + b . = 1 a + b 2 ab a + b
Nếu a > 0, b > 0 thì M=1
Nếu a < 0, b < 0 thì M= –1 0,5 b. (2 điểm)
Điều kiện xác định: x ≠ 0 0,25 2 Đặt x 1 x 1 2 2 t = − ⇒ + = t + 2 3 x 9 x 3 0,5 t =1
Phương trình đã cho trở thành: 3t2 – 5t + 2 =0 ⇔ 2 0,5 t = 3 1 + t = 1 ± ⇔ x2 – 3x – 3 = 0 3 21 ⇔ x = 0,25 (6 2 điểm) + t = 2/3 = − ⇔ x2 – 2x – 3 =0 x 1 ⇔ 0,25 x = 3
Kết luận: Tập nghiệm của phương trình là: 3+ 21 3− 21 ; ; 1;3 − 2 2 0,25 c. (2 điểm) Điều kiện xác định: 1 x; y ≥ 0,25 2 Từ hệ suy ra 1 1 1 1 + 2 − = + 2 − (2) x y y x + x > y ≥ 1 1 1 ⇒ < và 1 1 2 − < 2 − 2 x y y x ⇒ 1 1 1 1 + 2 − <
+ 2 − ⇒ với x > y ≥ 1 : (x; y) không là x y y x 2 0,5 nghiệm của HPT + y > x ≥ 1 ⇒ 1 1 1 1 + 2 − > + 2 − 2 x y y x 0,5
⇒ với x > y ≥ 1 :(x;y) không là nghiệm của HPT 2
+ x = y: thay vào hệ ta giải được x = 1, y = 1 0,5
Kết luận: Hệ phương trình có nghiệm duy nhất. 0,25
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình 2 −x mx − 2 = (*) 0,5 4 2 (*) ⇔ x + 4mx −8 = 0 Ta có: 2
∆′ = 4m + 8 ⇒ ∆′ > 0 m ∀ ∈ 0,5
Suy ra với mọi giá trị của m phương trình (*) có 2 nghiệm phân
biệt, tức là với mọi giá trị của m (d) luôn cắt (P) tại hai điểm phân biệt A, B. 0,5 2
Giả sử: A(x ;y ),B(x ;y ),y = mx − 2,y = mx − 2 A A B B A A B B (3
Theo định lí Viét có x + x = 4m − A B 0,5 điểm) x .x = 8 − A B Khi đó: AB2=(x
A − xB)2+(yA − yB)2=(xA − xB)2+m2(xB − xA)2=(xB − xA)2(1+m2) 2 2 2 2
= (x + x ) − 4x x (1+ m ) = ( 4 − m) − 4.( 8 − ) (1+ m ) A B A B 2 2 = (16m + 32)(1+ m ) 0,5 2 2
⇒ AB = (16m + 32)(1+ m ) ≥ 32 = 4 2
Đẳng thức xảy ra khi và chỉ khi m = 0.
Vậy độ dài đoạn AB nhỏ nhất khi và chỉ khi m = 0 0,5
Sử dụng BĐT Cô-si với x > 0, y > 0, ta có: 1 1 2 1 + (x + y) ≥ 2. .4xy = 8 . 2 2 x y xy Suy ra: 1 1 8 + ≥
(1). Đẳng thức xảy ra ⇔ x = y. 0,5 2 2 x y (x + 2 y)
Do vai trò của a, b, c là như nhau nên có thể giả sử a > b > c. 3
Áp dụng BĐT (1) cho cặp số dương a – b và b – c, ta có: 1 1 8 8 (2 + ≥ = . (a − 2 b) (b − 2 c) (a − b + b − 2 c) (a − 2 c) điểm) 0,5
Đẳng thức xảy ra ⇔ a – b = b – c. Suy ra: 1 1 1 8 1 9 + + ≥ + = . (a − 2 b) (b − 2 c) (c − 2 a) (a − 2 c) (c − 2 a) (a − 2 c) 0,25
Mặt khác, do a, c ∈ [0; 2] và a > c nên 0 < a – c ≤ 2. Đẳng thức xảy ra ⇔ a = 2 và c = 0. 0,25 Do đó: 1 1 1 9 9 + + ≥ ≥ . 0,25 (a − 2 b) (b − 2 c) (c − 2 a) (a − 2 c) 4
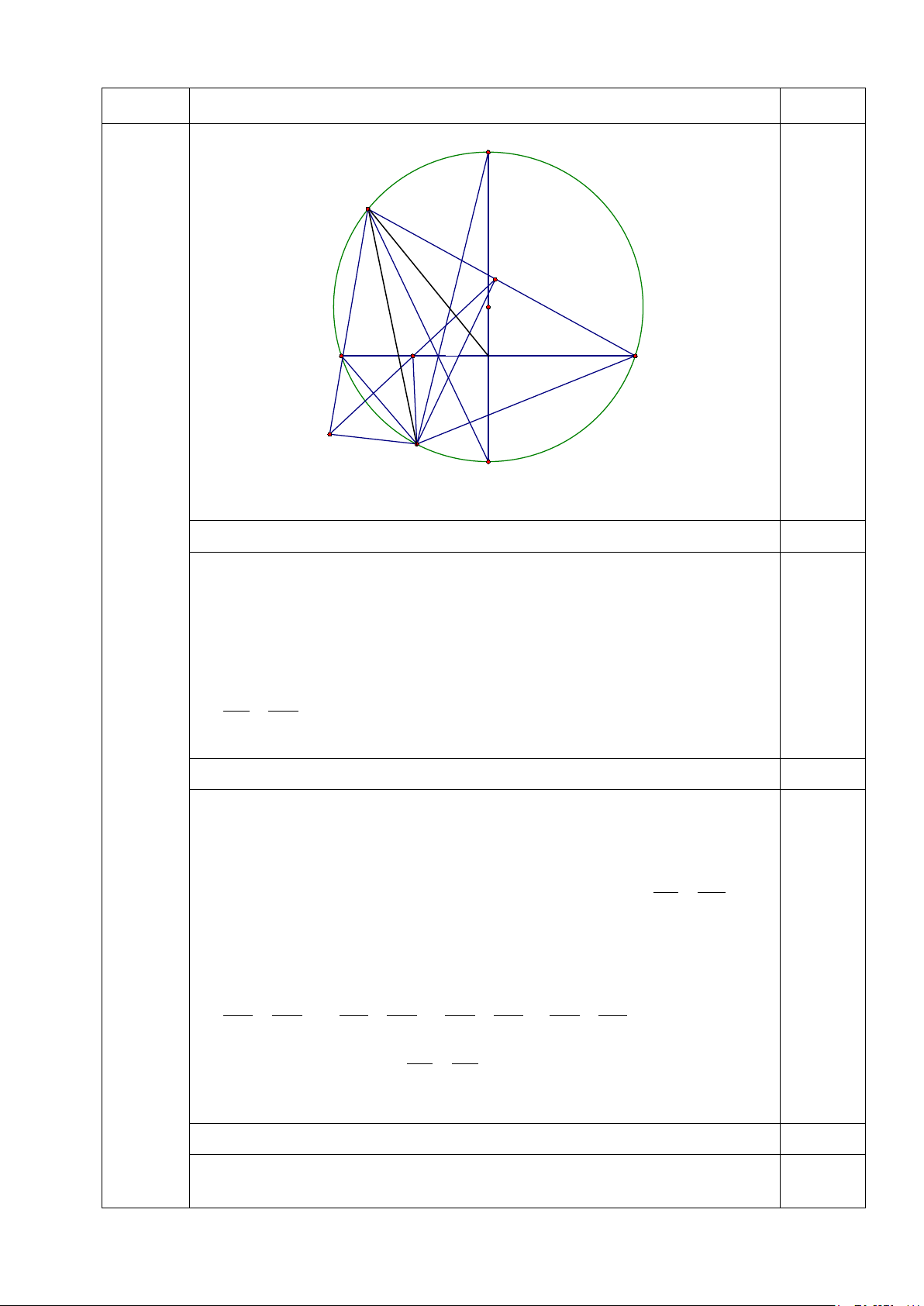
Đẳng thức xảy ra khi (a; b; c) = (2; 1; 0) và các hoán vị. 0,25 M D H O f IK J A B I E C N a. (3 điểm)
Từ giả thiết ta có các tứ giác CBHF nội tiếp. Theo tính chất của 1
tứ giác nội tiếp và góc nội tiếp ta có : = = = FCH FBH ABD ACD 0,5 4 = = = FHC FBC ABC ADC 0,5 (6 ⇒ HF ∆ C DA ∆ C(g.g) 0,5 điểm) HF DA ⇒ = (1) FC AC 0,25 ⇒ AC.HF = AD.CF 0,25 b. (2 điểm)
Các tứ giác AECF, CBHF, ADBC nội tiếp, suy ra: = = 0 = − ⇒ + 0 EFC EAC CBD 180 CFH EFC CFH =180 Suy ra E, F, H thẳng hàng. 0,5
Chứng minh tương tự ý a ta có EF DB E ∆ FC D ∆ BC(g.g) ⇒ = (2) FC BC 0,25
Do đường kính MN vuông góc với dây AB nên N, M lần lượt là
các điểm chính giữa của các cung AB. Suy ra DK là đường phân 0,25 giác của AD ∆
B , CK là đường phân giác của AC ∆ B DA KA ⇒ = và CA KA = DA CA DA DB ⇒ = ⇒ = (3) DB KB CB KB DB CB CA CB 0,5
Từ(1), (2) và (3) suy ra FE FH = ⇒ FE = FH FC FC 0,25
Suy ra F là trung điểm của EH (đpcm) 0,25 c. (1 điểm)
Lấy J trên đoạn AB sao cho DN là phân giác góc CDJ ta có ADC JDB,ADJ C DB 0,25
⇒ AC.BD = DC.BJ,AD.BC = DC.AJ 0,25 Mà DA DB = ⇒ AD.BC = AC.BD ⇒ AJ=BJ CA CB 0,25
⇒ J trùng với I ⇒ Điều phải chứng minh 0,25 a. (1,5 điểm) + Khi n = 0: A là hợp số
+ Khi n = 1 và k = 0, ta có A = 5 là số nguyên tố. 0,25
+ Khi n ≥1 và k ≥1, ta chứng minh M không là số nguyên tố: 2 2k 1 + 2 k 1 + 2 2 2k 1 + k 1 + 2 2k 1 + k 1 A (n 2 ) (n.2 ) (n 2 n.2 )(n 2 n.2 + = + − = + + + − ) 0,5 Ta có : 2 2k 1 + k 1 n 2 n.2 + + +
là số nguyên lớn hơn 1 và 2 2k 1 + k 1 n 2 n.2 + + − là số nguyên Mặt khác 2 2k 1 + 2 2k 1 + k n + 2 ≥ 2 n .2 ≥ 2n.2 2 2 2k 1 + k 1 + k k 1 + k 1 n 2 n.2 2n.2 2 n.2 n.2 + ⇒ + − ≥ − = ( 2 −1) >1 0,5 Suy ra M là hợp số. Kết luận: 4 2k 1 n 4 + +
là số nguyên tố khi và chỉ khi n =1 và k = 0. 0,25 5 b. (1,5 điểm) (3 (n, 5) = 1 ⇒ 4 n −15 điểm) 0,25 mà 2k 1+ 2k 2k 1 4 1 5(4 4 − + = − + ... +1)5 ⇒ A5 0,25 4 2k 1 Ap ⇔ n ≡ 4 + − (modp) ⇒ ( − − n )p 1 ≡ ( 4 + − )p 1 4 2k 1 0,25 2 2 (mod p) ⇒ ( − n ) − ≡ (− )p 1 p 1 1 (2 + )p 1 2 2k 1 − 2 (modp) 0,25 Mà ( )p 1− ( )p 1 2 2k 1 n 2 − + ≡
≡1(modp) (Định lí Fermat nhỏ) ⇒ ≡ (− )p 1−2 1 1 (modp) 0,25 p −1 ⇒ 2 ⇒ p −14 2 0,25 -----------Hết-----------
Document Outline
- TOAN_DE_HSG9_2013-2014
- HẾT
- TOAN_HDC_HSG9_2013-2014




