Đề thi chọn HSG cấp huyện lớp 12 THPT năm học 2017 – 2018 môn Toán sở GD và ĐT Cao Bằng

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN CAO BẰNG
LỚP 12 THPT NĂM HỌC 2017 – 2018 MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian: 180 phút (không kể thời gian giao đề) (Đề gồm 01 trang) Câu 1: (4,0 điểm) 3 x
a. Tìm các giá trị của tham số m để hàm số 2 y =
− 2x + mx −1 có hai điểm 3 cực trị ,
x x thỏa mãn: x − x = 2. 1 2 1 2 x + 3 b. Cho hàm số y =
C . Tìm các giá trị của tham số m để đường x + có đồ thị ( ) 1
thẳng d : y = 2x + m cắt đồ thị (C) tại hai điểm phân biệt ,
A B sao cho AB = 5. Câu 2: (4,0 điểm) a. Giải phương trình: 2
x + x + 1 − x + x = 1 3 2
y + y − 2 = x(x + 3x + 4)
b. Giải hệ phương trình:  2 2 x + y = 5 Câu 3: (2,0 điểm)
Giải phương trình: cos x(4sin x + 3) = sin x Câu 4: (2,0 điểm)
Một trường trung học phổ thông có 12 học sinh giỏi gồm ba học sinh khối 10, bốn
học sinh khối 11 và năm học sinh khối 12. Chọn sáu học sinh trong số học sinh giỏi đó,
tính xác suất sao cho cả ba khối đều có học sinh được chọn. Câu 5: (4,0 điểm)
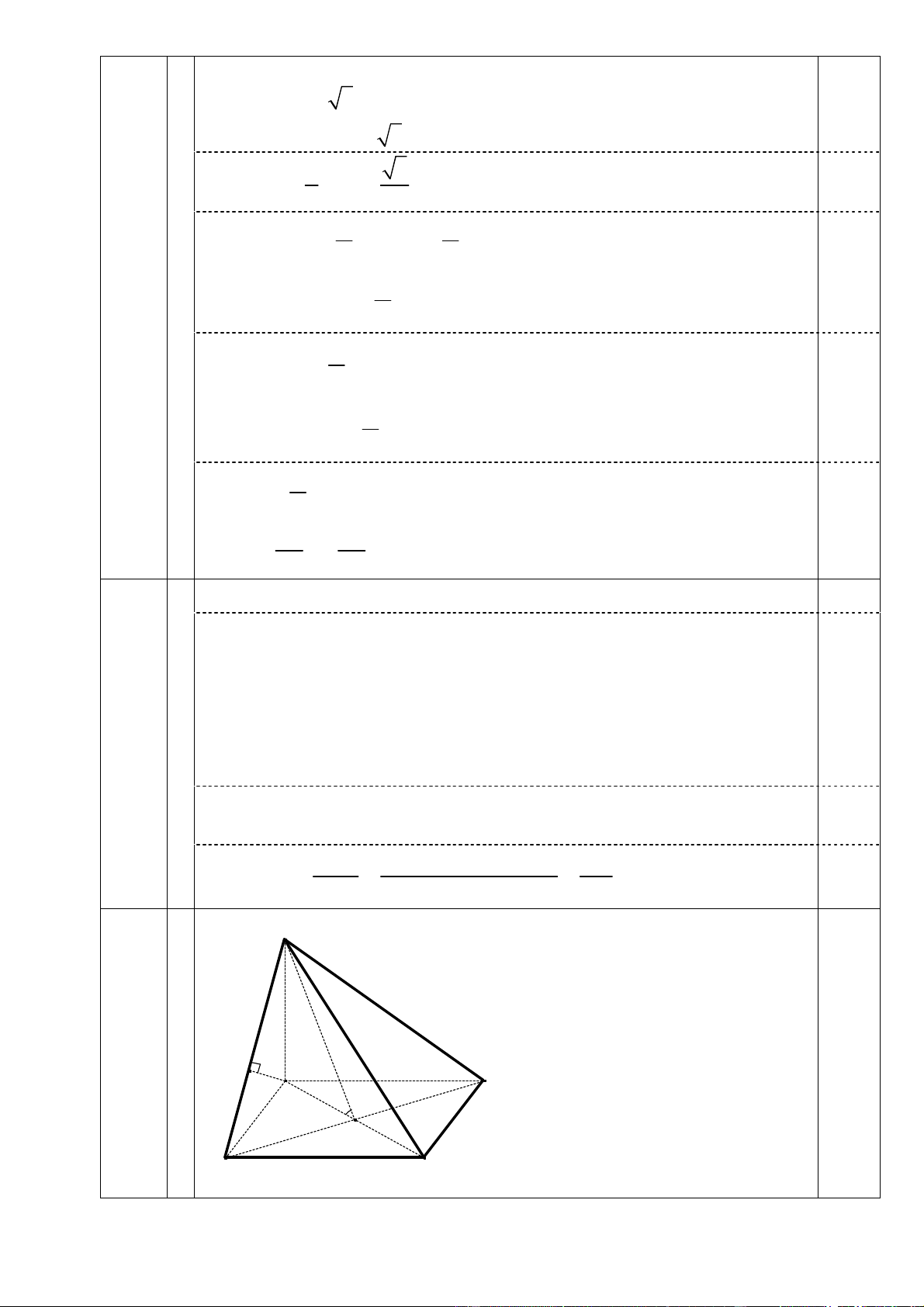
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA o
vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBD) và mặt phẳng đáy bằng 60 .
a. Tính thể tích khối chóp S.ABCD .
b. Tính khoảng cách từ điểm D đến mặt phẳng (SBC) . Câu 6: (2,0 điểm)
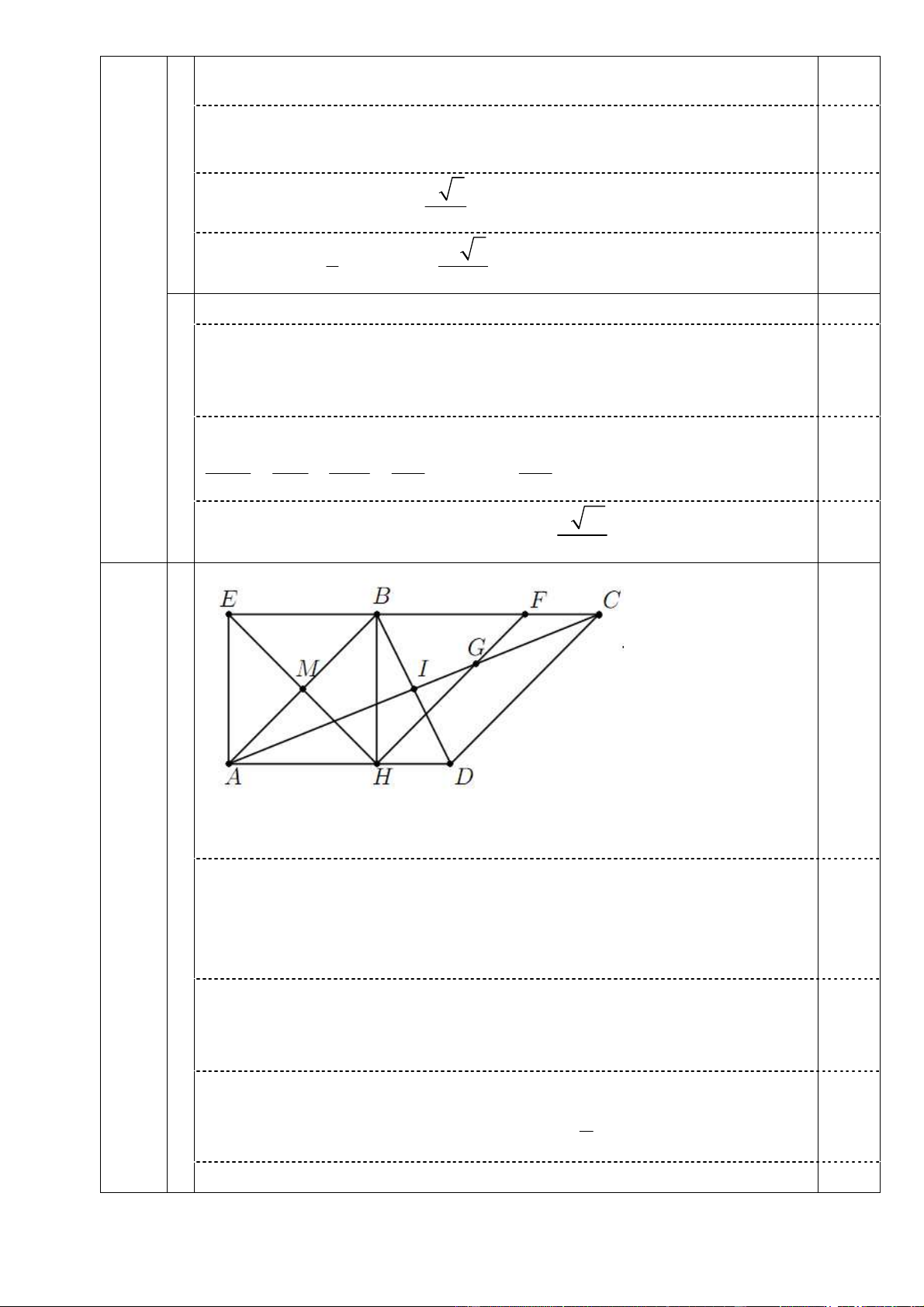
Trong mặt phẳng với hệ tọa độ Oxy, cho hình bình hành ABC . D Điểm
M (−3;0) là trung điểm của cạnh AB, điểm H (0;−1) là hình chiếu vuông góc của B  4 
trên AD và điểm G  ;3 là trọng tâm của tam giác BC .
D Tìm tọa độ các điểm , B . D  3  Câu 7: (2,0 điểm) 1 1 1 Cho , ,
x y z là các số thực dương thỏa mãn
+ + ≤ 3. Chứng minh rằng: x y z 1 1 1 3 + + ≤
2x + y + z
x + 2 y + z x + y + . 2z 4
______________________________Hết_______________________________
(Thí sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm)
Họ và tên thí sinh:…………………………………….. Số báo danh:…..............…………
Họ tên, chữ ký của giám thị 1:………………………………………….........….....…….…
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ THI CHỌN HỌC SINH GIỎI CẤP CAO BẰNG
HUYỆN LỚP 12 THPT NĂM HỌC 2017 - 2018 Môn: TOÁN ĐỀ CHÍNH THỨC
(Hướng dẫn chấm có 05 trang)
I. Hướng dẫn chung:
1. Điểm của bài thi theo thang điểm 20, phần lẻ được tính đến 0,25 điểm.
Giám khảo giữ nguyên điểm lẻ, không được làm tròn điểm.
2. Việc chi tiết hóa (nếu có) thang điểm trong hướng dẫn chấm phải đảm bảo
không làm sai lệch hướng dẫn chấm.
3. Nếu thí sinh làm bài không theo cách nêu trong hướng dẫn chấm nhưng giải
theo cách khác mà lập luận chặt chẽ, tính toán chính xác thì vẫn cho đủ số điểm từng
phần như hướng dẫn quy định.
II. Đáp án và thang điểm: Câu ý Đáp án Điểm 1
a Tập xác định: D = ℝ . 0,25 (4,0đ) 2
y ' = x − 4x + m ; 2 ' = 0 ⇔ − 4 + = 0 y x x m (*) 0,25
Hàm số đã cho có hai điểm cực trị , x x 1 2
⇔ Phương trình (*) có hai nghiệm phân biệt 0,5
⇔ ∆' > 0 ⇔ 4 − m > 0 ⇔ m < 4. Ta có: 2
x − x = 2 ⇔ (x − x ) = 4 1 2 1 2 0,5 2
⇔ (x + x ) − 4x x − 4 = 0 1 2 1 2
⇔ 12 − 4m = 0 ⇔ m = 3 (thỏa mãn điều kiện). 0,5
Vậy giá trị cần tìm là m = 3 .
b Phương trình hoành độ giao điểm:
x + 3 = 2x + m x + 1 0,5 . 2
−2x − (m +1)x + 3 − m = 0 ⇔  (*) x ≠ −1
Đường thẳng (d ) cắt đồ thị (C) tại hai điểm phân biệt ⇔ (*) có hai nghiệm phân biệt. 2
∆ = m − 6m + 25 > 0 0,5 Ta có:  ⇔ m ∀ ∈ℝ . 2  2
− .(−1) − (m +1).(−1) + 3 − m ≠ 0
Suy ra (d ) và (C) luôn cắt nhau tại 2 điểm phân biệt , A B . 1 Khi đó: (
A x ; 2x + m), B(x ;2x + m) . A A B B Ta có: 0,25 AB = 5 2 2
⇔ (x − x ) + 4(x − x ) = 5 B A B A 2 2
⇔ (x − x ) + 4(x − x ) = 25 B A B A 2
⇔ (x − x ) = 5 B A 0,25 2
⇔ (x + x ) − 4x x − 5 = 0 A B A B 2 (m + 1) ⇔ + 2(3 − m) − 5 = 0 4 m =1 2
⇔ m − 6m + 5 = 0 ⇔ 0,5  m = 5
Vậy giá trị cần tìm là =1; m m = 5. 2
a Điều kiện: x ≥ 0 . 0,25 (4,0đ) Ta có: 2
x + x + 1 − x + x = 1 0,5
⇔ ( x −1)(1− x +1) = 0  x =1 ⇔  0,5  x +1 =1 x =1 ⇔  0,5 x = 0
Kết hợp với điều kiện ta có nghiệm của phương trình đã cho là = 0,25 0; x x = 1. b Ta có: 3 2 3 3 0,5
y + y − 2 = x(x + 3x + 4) ⇔ y + y = (x +1) + (x + 1) Xét hàm số 3
f (t) = t + t trên ℝ . Với mọi t ∈ ℝ , 2
f '(t) = 3t + 1 > 0 . 0,25
Suy ra f (t) đồng biến trên ℝ . Do đó 3 3
y + y = (x + 1) + (x +1) ⇔ f ( y) = f (x + 1) ⇔ y = x +1. 0,25
Thế y = x + 1 vào phương trình thứ hai của hệ ta được: x =1 0,5 2 2 2
x + (x + 1) = 5 ⇔ 2x + 2x − 4 = 0 ⇔  x = −2
Với x = 1⇒ y = 2 Với x = 2 − ⇒ y = −1 0,5
Vậy hệ đã cho có nghiệm là (1;2); ( 2 − ; 1 − ). 2 3 Ta có: (2,0đ)
cos x(4sin x + 3) = sin x 0,5
⇔ 2sin 2x = sin x − 3cos x 1 3
⇔ sin 2x = sin x − cos x 0,25 2 2 π π
⇔ sin 2x = cos sin x − sin cos x 3 3 0,25  π 
⇔ sin 2x = sin x −   3    π 
2x =  x −  + k 2π  3   ⇔ 0,5   π 
2x = π −  x −  + k 2π   3   π x = − + k2  π 3  ⇔
(k ∈ Z) . 0,5  4π 2π x = + k  9 3 4
Chọn 6 học sinh giỏi bất kì có 6 C cách 6 ⇒ n(Ω) = C . 0,5 12 12 (2,0đ)
Số cách chọn 6 học sinh giỏi mà trong đó không có học sinh khối 10 là 6 C . 9
Số cách chọn 6 học sinh giỏi mà trong đó không có học sinh khối 11 0,5 là 6 C . 8
Số cách chọn 6 học sinh giỏi mà trong đó không có học sinh khối 12 là 6 C . 7
Gọi A:"Cả ba khối đều có học sinh được chọn" 6 6 6 6 ⇒ n( )
A = C − (C + C + 0,5 C ) 12 9 8 7 6 6 6 6 n( ) A
C − (C + C + C ) 115 Vậy 12 9 8 7 P( ) A = = = . 0,5 6 n(Ω) C 132 12 5 a S (4,0đ) 0,25 H A D I B C 3
+ Diện tích hình vuông ABCD là 2 S = a . ABCD 0,25  AI ⊥ BD o
+ Gọi I là giao điểm của AC và BD ⇒  ⇒ SIA = 60 0,5 SI ⊥ BD a Suy ra 6
SA = AI.tan SIA = . 0,5 2 3 1 a 6 Vậy V = S .SA = . 0,5 S . ABCD 3 ABCD 6
b Ta có: AD / /(SBC) ⇒ d (D,(SBC)) = d ( , A (SBC)) . 0,5
Gọi H là hình chiếu vuông góc của A trên SB , suy ra  AH ⊥ SB  ⇒ 0,5
AH ⊥ (SBC) ⇒ AH = d ( , A (SBC)) .  AH ⊥ BC
Trong tam giác vuông SAB có: 2 1 1 1 5 3a 2 = + = ⇒ 0,5 AH = . 2 2 2 2 AH SA AB 3a 5 a 15
Vậy d (D,(SBC)) = d ( ,
A (SBC)) = AH = . 0,5 5 6 (2,0đ) 0,5
Gọi E và F lần lượt là giao điểm của HM và HG với BC . Suy ra
HM = ME và HG = 2GF . Do đó E(−6;1) và F (2;5) .
Đường thẳng BC đi qua E và nhận EF làm vectơ chỉ phương, nên
phương trình đường thẳng BC là x − 2 y + 8 = 0 . Đường thẳng BH 0,25
đi qua H và nhận EF làm vectơ pháp tuyến, nên phương trình
đường thẳng BH là 2x + y +1 = 0 .
Do B là giao điểm của BH và BC nên tọa độ điểm B thỏa mãn hệ
x − 2y + 8 = 0 0,25 phương trình  ⇒ B(−2;3) .
2x + y + 1 = 0
Do M là trung điểm của AB nên (
A −4;−3) . Gọi I là giao điểm của  3  0,5
AC và BD , suy ra GA = 4GI . Do đó I  0;  .  2 
Do I là trung điểm của đoạn BD , nên D(2;0) . 0,5 4 7
Với a,b > 0 ta có: (2,0đ) 1 a + b 1 1  1 1  2
4ab ≤ (a + b) ⇔ ≤ ⇔ ≤  + . 0,5 a + b 4ab a + b 4  a b 
Dấu "=" xảy ra khi và chỉ khi a = b .
Áp dụng kết quả trên ta có: 1 1  1 1  1  1 1  1 1  1  1 1 1  ≤  +  ≤  +  +  =  + + .
2x + y + z 4  2x y + z  4  2x 4  y z  8  x 2 y 2z  1 1  1 1 1  ⇔ ≤ 0,5  + +  (1)
2x + y + z 8  x 2 y 2z 
2x = y + z Dấu "=" xảy ra khi 
⇔ x = y = z .  y = z Tương tự: 1 1  1 1 1  ≤  + + 
(2) Dấu "=" xảy ra khi x = y = z .
x + 2 y + z 8  y 2z 2x  0,5 1 1  1 1 1  ≤  + + 
(3) Dấu "=" xảy ra khi x = y = z .
x + y + 2z 8  z 2x 2 y  Từ (1), (2) và (3) ta có: 1 1 1 1  1 1 1  3 + + ≤  + +  ≤ .
2x + y + z
x + 2 y + z
x + y + 2z 4  x y z  4
x = y = z  Dấu "=" xảy ra khi  1 1 1
⇔ x = y = z =1 + + = . 3   x y z 0,5 1 1 1 Vậy với , ,
x y z là các số thực dương thỏa mãn + + ≤ 3 ta luôn có: x y z 1 1 1 3 + + ≤
2x + y + z
x + 2 y + z x + y + . 2z 4
Đẳng thức xảy ra khi x = y = z = 1.
______________________Hết________________________ 5