Đề thi chọn HSG cấp tỉnh lớp 12 THPT năm học 2017 – 2018 môn Toán sở GD và ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 THPT HẢI DƯƠNG
NĂM HỌC 2017 – 2018 MÔN THI: TOÁN
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 180 phút(không kể thời gian giao đề) (Đề thi gồm 01 trang) Câu 1( 2,0 điểm): 1) Cho I2; 
1 . Tìm tất cả các giá trị của m để đồ thị hàm số 3
y  x  3mx 1 có hai điểm cực trị A, B sao
cho diện tích ΔIAB bằng 8 2 .
2) Một công ty muốn làm một đường ống dẫn dầu từ một kho B
A ở trên bờ biển đến một vị trí B trên một hòn đảo. Hòn đảo
cách bờ biển 6 km. Gọi C là điểm trên bờ sao cho BC vuông
góc với bờ biển. Khoảng cách từ A đến C là 9 km. Người ta
cần xác định một vị trí D trên AC để lắp ống dẫn theo đường 6km
gấp khúc ADB. Tính khoảng cách AD để số tiền chi phí thấp D A
nhất, biết rằng giá để lắp đặt mỗi km đường ống trên bờ là C
100.000.000 đồng và dưới nước là 260.000.000 đồng. 9km Câu 2 (2,0 điểm): 8 1) Giải phương trình 3  tan x  cot . x 3 sin 2x 3 2 3
x  6x 13x  y  y 10
2) Giải hệ phương trình  . 3 2
 2x  y  2  5  x  y  x  3x 10y 8  Câu 3 (2,0 điểm): u
1) Cho dãy số (u ) có * u  7,u
 5u 12 (n   ) . Tìm lim n . n 1 n 1  n 5n
2) Trong mặt phẳng Oxy, cho đường tròn (I) có hai đường kính AB và MN với ( A 1;3), B(3; 1  ) . Tiếp
tuyến của (I) tại B cắt các đường thẳng AM và AN lần lượt tại E và F. Tìm tọa độ trực tâm H của MEF 
sao cho H nằm trên đường thẳng d : x  y  6  0 và có hoành độ dương. Câu 4 (3,0 điểm):
Cho hình chóp S.ABC có SA  SB  SC  a ,  0  0  0
ASB  60 ,CSB  90 , ASC  120 .
1) Tính thể tích khối chóp S.ABC theo a.
2) Gọi I, J, G lần lượt là trung điểm SC, AB, IJ. Mặt phẳng (P) đi qua G cắt các cạnh SA, SB, SC lần
lượt tại A’, B’, C’. Gọi V ,V ,V
lần lượt là thể tích các khối chóp .
A A' B 'C ' , .
B A' B 'C ' , .
A A'B 'C '
B.A'B'C '
C.A'B 'C '
C.A' B 'C '. Tìm giá trị nhỏ nhất của biểu thức P  V V V theo a. .
A A'B 'C '
B.A'B 'C '
C.A'B 'C ' CN AM
3) Gọi M, N là hai điểm thay đổi lần lượt trên cạnh AB và SC sao cho 
. Tìm giá trị nhỏ nhất SC AB của đoạn thẳng MN. Câu 5 (1,0 điểm):
Với các số thực dương a, ,
b c . Tìm giá trị nhỏ nhất của biểu thức 1 8 P   . 2 2
2a  b  8bc
2b  2(a  c)  5
..............................HẾT..................................
- Thí sinh không được sử dụng tài liệu
- Giám thị không giải thích gì thêm
Họ và tên thí sinh:............................................................ Số báo danh:............................................
Chữ ký của giám thị 1:......................................Chữ ký của giám thị 2:............................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH HẢI DƯƠNG
LỚP 12 THPT NĂM HỌC 2017 – 2018 MÔN THI: TOÁN HƯỚNG DẪN CHẤM
Ngày thi: 04 tháng 10 năm 2017
(Hướng dẫn chấm gồm 05 trang)
(Điểm toàn bài lấy điểm lẻ đến 0,25; thí sinh làm cách khác mà đúng vẫn cho điểm tối đa) Câu Nội dung Điểm
1) Tìm tất cả các giá trị của m để (C ) 3
y  x  3mx 1 có hai điểm cực trị A, B sao cho m (1,0đ)
diện tích ΔIAB bằng 8 2 với I(2;1). TXĐ: D=  ; ' 2 ' 2 y  3x  3 ;
m y  0  x  m (1) 0,25
(C ) có hai điểm cực trị A, B  PT (1) có 2 nghiệm phân biệt  m  0 m
Khi đó: A m; 2  m m  
1 , B  m;2m m   1
I.1 Phương trình AB: y  2
 mx 1 hay 2mx  y 1  0 0,25 4m 4m
Ta có: AB  4m 2 4m  
1 , d I; AB   (Do m  0) 2 2 4m 1 4m 1 1 1 4m S  .A . B d I AB  m m    ABI  ;  . 4  2 4 1. 8 2 0,25 2 2 2 4m 1
 4m m  8 2  m m  2 2  m  2(TM ) 0,25 Kết luận: m = 2
2) Một công ty muốn làm một đường ống dẫn dầu từ một kho A ở trên bờ đến một vị
trí B trên một hòn đảo. Hòn đảo cách bờ biển 6 km. Gọi C là điểm trên bờ sao cho BC
vuông góc với bờ biển. Khoảng cách từ A đến C là 9 km. Người ta cần xác định một vị (1,0đ)
trí D trên AC để lắp ống dẫn theo đường gấp khúc ADB. Tính khoảng cách AD để số
tiền chi phí thấp nhất, biết rằng giá để lắp đặt mỗi km đường ống trên bờ là
100.000.000 đồng và dưới nước là 260.000.000 đồng.
+ Đặt CD  x km, x [0;9] B   2 CD
x  36 ; AD  9  x nên chi phí
xây dựng đường ống là : 6km 0,25 D C A 9km I.2   2
T x  260000000 x  36 100000000(9  x) đồng
+ Xét hàm số T(x) trên đoạn [0 ; 9] ta có :  13x  T '(x)  20000000   5   T’(x) = 0  2 13x  5 x  36 2   x  36  0,25 25 5  2   2 168x 25 x  36  2 x   x  . 4 2 5
+ Lại có T(0)  2460000000 ; T( )  2340000000; T(9)  260000000 117 2 0,25 5
Suy ra T(x) đạt giá trị nhỏ nhất trên đoạn [0 ; 9] bằng 2340000000 khi x = . 2 5
+ Vậy chi phí lắp đặt thấp nhất bằng 2340000000 đồng khi x = hay điểm D cách A một 0,25 2 khoảng bằng 6,5 km. 8 1) Giải phương trình 3  tan x  cot . x (1,0đ) 3 sin 2x 4 4 8 o
c s x  sin x
Điều kiện: sin 2x ¹ 0 . PT tương đương với  0,25 3 3 sin 2x sin x cos x II.1 1 2 2 2   os c
x  sin x  1  os c 2 . x os c x 0,25 2 os c x 2  os c 2x  o
c s2x  2  0 0,25  os c 2x  1  
kết hợp với điều kiện : phương trình vô nghiệm 0,25  os c 2x  2 3 2 3
x  6x 13x  y  y 10 (1)
2) Giải hệ phương trình  (1,0đ) 3 2
 2x  y  2  5  x  y  x  3x 10y  8 (2) 
2x  y  2  0 * ĐK:  5
  x  y  0 0,25
   x  3 3 1
2  x  2  y  y (*) Xét hàm số   3
f t  t  t . Ta có ' f t 2
 3t 1  0 t
    f t đồng biến trên  0,25
Do đó (*)  y  x  2 .
Thay y  x  2 vào (2) ta được : 3 2
3x  7  2x  x  3x 10x  28 II.2 3 x  3 2 x  3 3 2
 3x  3 1 7  2x  x  3x 10x  30    x  3 2 x 10
3x  3 1 7  2x 0,25 x  3   3 2 2    x 10 (3)
 3x  3 1 7  2x 7 3 2
PT (3) vô nghiệm vì với 0  x  thì 2 
1 2  3, x 10 10 . Vậy hệ 2
3x  3 1 7  2x x  3 0,25 có nghiệm duy nhất  . y 1 u
1) Cho dãy số (u ) có * u  7,
 u  5u 12 (n   ) . Tìm lim n . (1,0đ) n 1 n 1  n 5n u
 5u 12  u  3  5(u  3) n 1  n n 1  n 0,25 Đặt *
v  u  3  v  5v n
    dãy số (v ) lập thành cấp số nhân có công bội n n n 1  n n III.1 0,25
q  5,v  u  3  1  0 1 1 n 1  n 1 v v q 10.5       u  2  .5n  3 0,25 n 1 n u 2.5   3  1 n n   lim n  lim  lim[  2  3 ]=-2   0,25 5n 5n  5 
3) 2) Trong mặt phẳng Oxy, cho đường tròn (I) có hai đường kính AB và MN với (1,0đ) ( A 1;3), B(3; 1
 ) . Tiếp tuyến của (I) tại B cắt các đường thẳng AM và AN lần lượt tại E
III.2 và F. Tìm tọa độ trực tâm H của MEF 
sao cho H nằm trên đường thẳng
d : x  y  6  0 và có hoành độ dương.
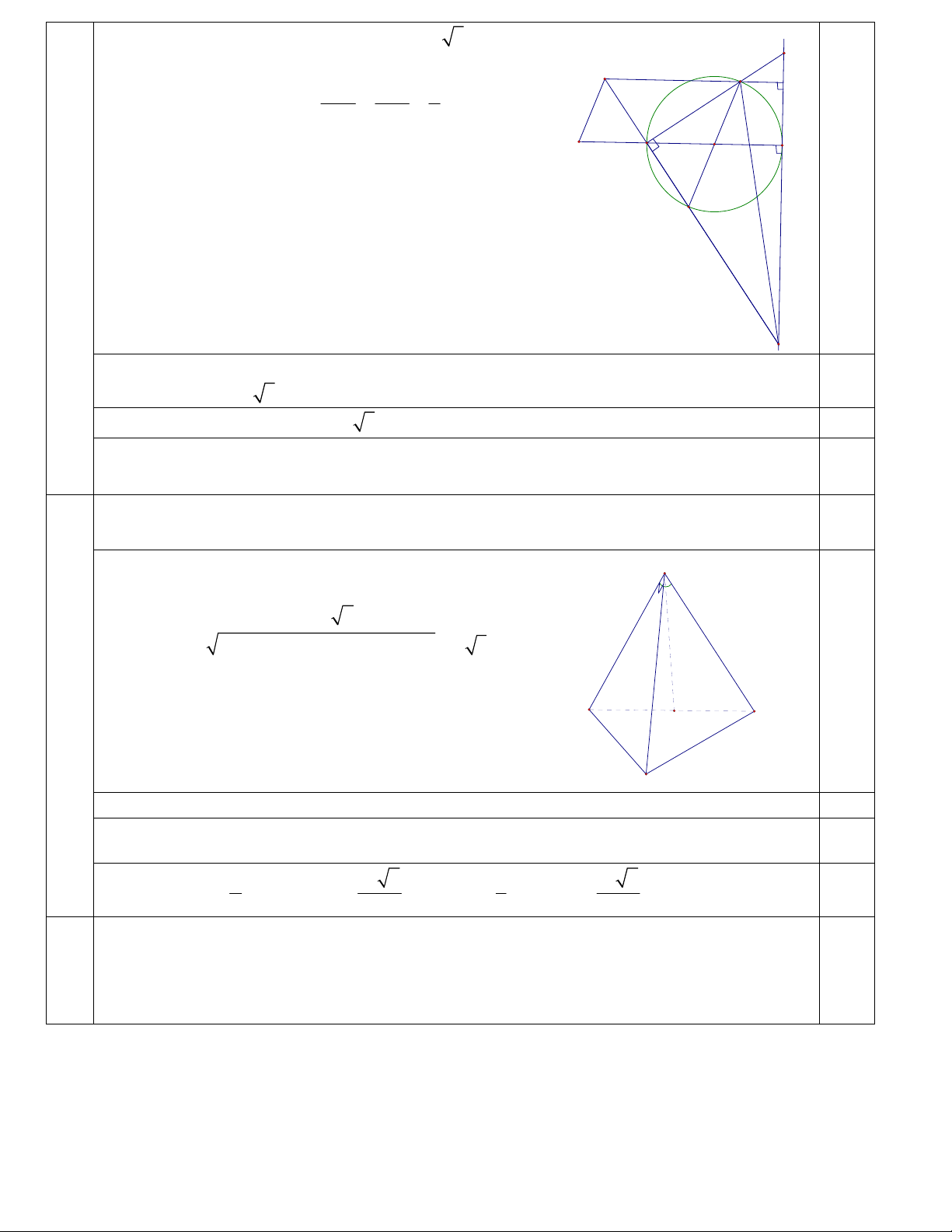
Đường tròn (I) có tâm I2; 
1 ,bán kính r  5 . AF là E
đường cao tam giác MEF nên H,A,F thẳng hàng H M AI NI 1 AI song song với HM nên    HM  2AI HM NM 2 B I' A I 0,25 N F
Gọi I’đối xứng với I qua A nên I '(0;5) . I I’  2AI  HM, I I’ / /HM nên HMI I’ là hình bình 0,25 hành  I’H=IM=r= 5
H  d  H (t;t  6),t  0 ; 2 2
I ' H  5  (t  0)  (t  6  5)  5 0,25 t 1 2
 2t  2t  4  0   . Vậy H (1;7) . 0,25 t  2(  l)
Cho hình chóp S.ABC có SA  SB  SC  a ,  0  0  0
ASB  60 ,CSB  90 , ASC  120 . (1,0đ)
1) Tính thể tích khối chóp S.ABC theo a.
Xét tứ diện SABC có : SA  SB  SC  a S  ABS đều :do SA=SB,  0
ASB  60  AB  a 120
 SBC vuông tại S BC  a 2 a 2 2 0 SAC 
: AC  SA  SC  2S .
A SC.Cos120  a 3 a a 0,25 IV.1 C H A B Có : 2 2 2
AC  AB  BC  ABC  vuông tại B 0,25
Hình chóp S.ABC có SA  SB  SC  a . Hạ SH  (ABC)  H là tâm đường tròn ngoại tiếp
tam giác ABC  H là trung điểm của AC 0,25 a 2 a 2 3 1 a 2
Xét  SAC:SH= ; Có : S   V  SH.S  0,25 2 AB  C 2 S.ABC 3 ABC 12
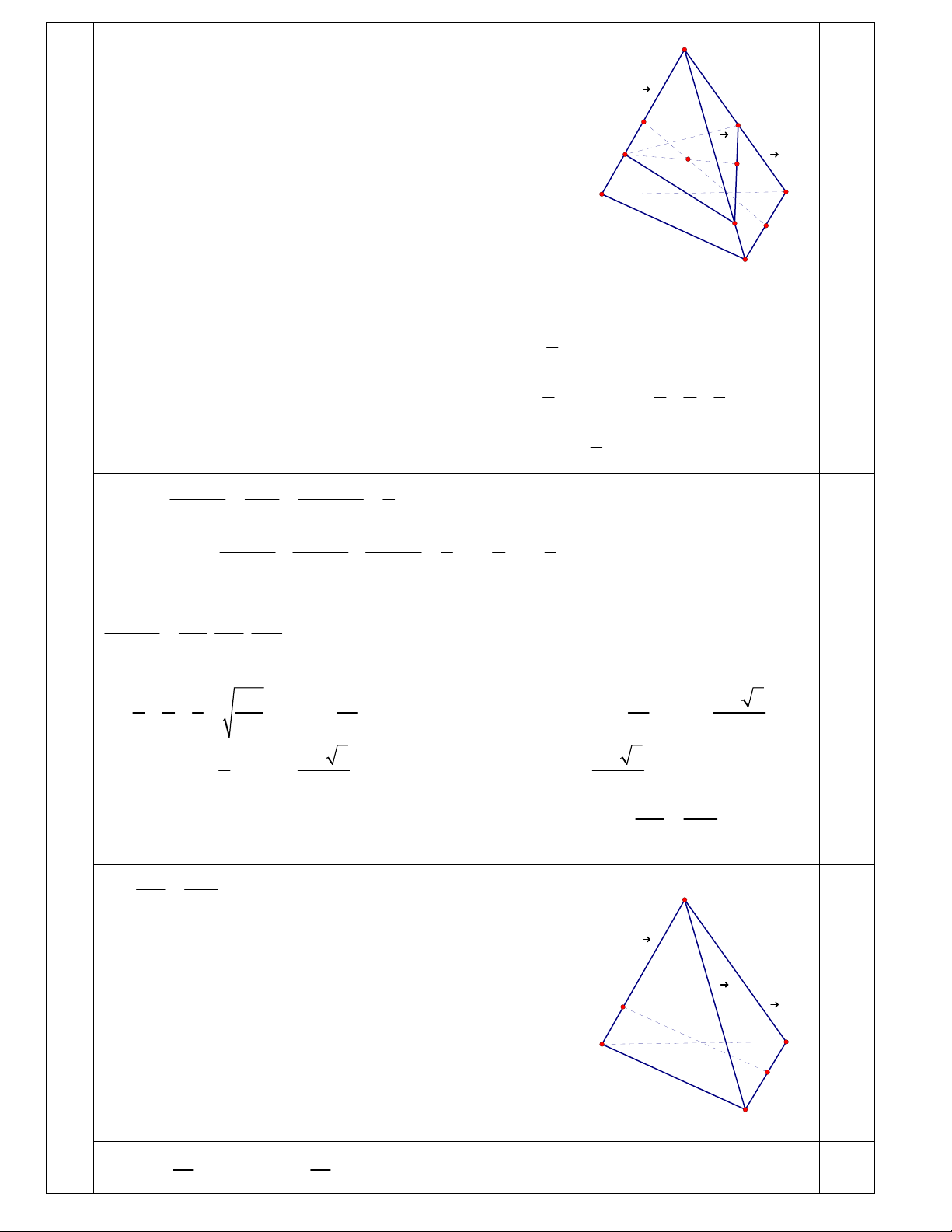
2) Gọi I, J, G lần lượt là trung điểm SC, AB, IJ. Mặt phẳng (P) đi qua G cắt các cạnh
SA, SB, SC lần lượt tại A’, B’, C’. Gọi V ,V ,V
lần lượt là thể tích các IV.2 .
A A'B 'C '
B.A'B'C ' .
A A'B 'C ' khối chóp (1,0đ) .
A A' B 'C ', .
B A' B 'C ', .
A A' B 'C ' . Tìm giá trị nhỏ nhất của biểu thức P  V V V theo a. .
A A'B 'C '
B.A'B 'C '
C.A'B 'C '
         Đặt a  S ,
A b  SB,c  SC, SA'  xSA  xa,       S
SB '  ySB  y ,
b SC '  zSC  zc(0  x, y, z  1)
   
     
C ' A'  SA'  SC '  xa  zc,C ' B '  SB '  SC '  yb  zc c
      
GA  GB  GC  GS  2GI  2GJ  0 I A'
     b
 C ' A  C ' B  C 'C  C 'S  4C 'G C' 0,25 a G 
1     1  1   1
 C 'G  (SA  SB  SC  4SC ')  a  b  c(  z)(1) C A 4 4 4 4 B' J B      
Do A’, B’, C’, G đồng phẳng nên C 'G  mC ' A'  nC ' B '  mxa  nyb  c(mz  nz)(2)  1 mx   4      1 1 1 1 0,25 Mà a, ,
b c không đồng phẳng nên từ (1) và (2) ta có ny      4 4 x y z   1
mz  nz   z  4 V AA ' SA  SA' 1 Ta có .
A A'B 'C '    1 V SA' SA' x
S.A'B 'C ' V V V 1 1 1
Tương tự ta có .AA'B'C'
B.A'B 'C '
C.A'B 'C '  
 1 1 1  1 V V V x y z
S.A'B 'C '
S.A'B 'C '
S.A'B 'C ' 0,25  V V V  V .
A A'B 'C '
B.A'B 'C '
C.A'B 'C '
S.A'B 'C ' V
SA' SB ' SC '
S.A'B 'C '  . .  y x z  V  xyzV
S.A'B 'C ' S.ABC V SA SB SC S.ABC
Theo bất đẳng thức giữa trung bình cộng và trung bình nhân 3 1 1 1 1 27 27 9a 2 4     3  xyz   P  V V V  V  .
A A'B 'C '
B.A'B 'C '
C.A'B 'C ' S. x y z xyz 64 64 ABC 256 0,25 3 3 9a 2 3 9a 2
khi x  y  z  thì P 
nên giá trị nhỏ nhất của P là 4 256 256 CN AM (1,0đ)
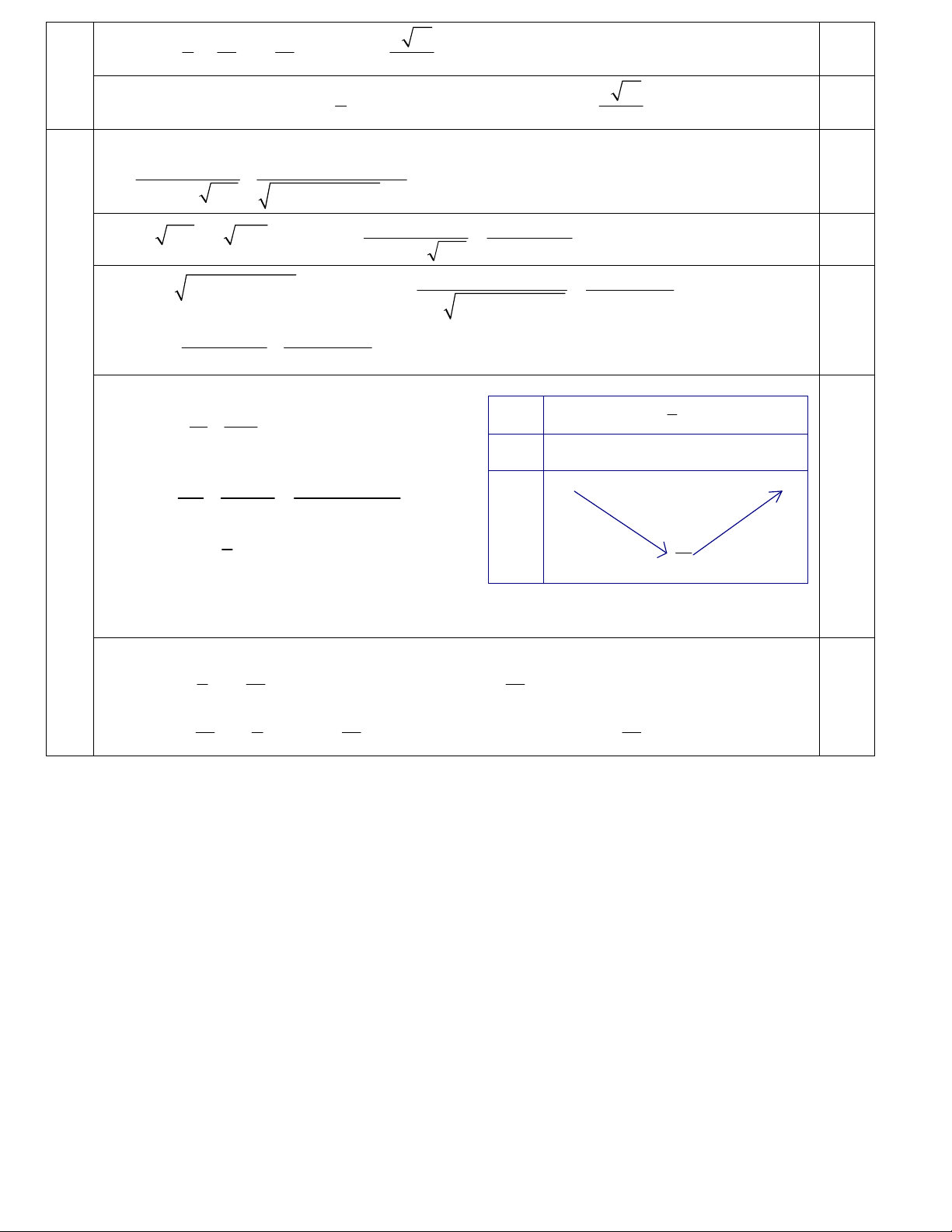
3)Gọi M, N là hai điểm thay đổi lần lượt trên cạnh AB và SC sao cho  . Tìm giá trị SC AB
nhỏ nhất của đoạn thẳng MN. CN AM Đặt 
 m(0  m  1) SC AB S       
 NC  mSC  mc, AM  mAB  m(b  a)
          0,25
MN  MA  AS  SC  CN  m(b  a)  a  c  mc c   
IV.3  (m 1)a  mb  (1 m)c N b a A C M B 2 2   a     a Do . a b  , . b c  0, . a c   nên 2 2 2
MN  (3m  5m  3)a 2 2 0,25 5 11 11 a 33 0,25 2 2 2
 3a (m  )  a  a  MN  m  [0;1] 6 12 12 6 5 a 33 0,25
Dấu đẳng thức xẩy ra khi m  . Vậy giá trị nhỏ nhất của MN là 6 6 V
Với các số thức dương a,b,c . Tìm giá trị nhỏ nhất của biểu thức 1,0 1 8 P   . 2 2
2a  b  8bc
2b  2(a  c)  5 0,25 Ta có 1 1 8bc  2 .
b 2c  b  2c   .
2a  b  8bc (
2 a  b  c) 8 8 0,25 Mặt khác 2 2
2(a  c)  2b  (a  c)  b   . 2 2
5  2(a  c)  2b
5  a  b  c 1 8 Do đó P   .
2(a  b  c) 5  a  b  c
Đặt t  a  b  c, t  0. 0,25 1 8 5 Xét f (t)   , t  0. 0 t + 3 2t 5  t Ta có f'(t) - 0 + 1 8
(3t  5)(5t  5) f '(t)     , t  0. 2 2 2 2 2t (5  t) 2t (5  t) 5 f(t)
f '(t)  0  t  9 3 - 10 Bảng biến thiên Từ bảng biến thiên 0,25 5 9
 f (t)  f ( )   t   9
0  P  f (a  b  c)   3 10 10 5 5 9 9 Khi a  c 
,b  thì P  
.Vậy giá trị nhỏ nhất của P là  12 6 10 10