Đề thi chọn HSG cấp tỉnh Toán 12 năm học 2017 – 2018 sở GD và ĐT Bình Phước

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 12 BÌNH PHƯỚC NĂM HỌC 2017-2018 MÔN THI: TOÁN ĐỀ CHÍ NH THỨC
Thời gian: 180 phút (không kể thời gian giao đề)
(Đề thi gồm có 01 trang) Ngày thi: 28/09/2017 x −
Câu 1. (THPT 4,0 điểm; GDTX 5,0 điểm). Cho hàm số 2 2 y = . x +1
a) Khảo sát sự biến thiên và vẽ đồ thị (C ) của hàm số.
b) Tìm điểm M thuộc (C ) sao cho khoảng cách từ M đến đường thẳng ∆ : 2x − y + 4 = 0 1 bằng 2 lần 3
khoảng cách từ M đến đường thẳng ∆ : x − 2y + 5 = 0 2 .
Câu 2. (THPT 6,0 điểm; GDTX 6,0 điểm). 3 2
4 cos x + 2 cos x (2sin x − )
1 − sin 2x − 2 (sin x + cos x)
a) Giải phương trình: = 0 2 2sin x − . 1  3 6 2 2 y  (x 1)  3 (
y x  2)  3 y  4  0 
b) Giải hệ phương trình:    x y    4x    3  4  xy   , . 2 x   3  
1  3x  8 1  9     n+
c) Tìm hệ số của số hạng chứa 8
x trong khai triển thành đa thức của  + x ( − x) 2 2 1 1    . Biết rằng 0 2 2 C + C + ... n + C = 2048. 2n 2n 2n
Câu 3. (THPT 4,0 điểm; Thí sinh hệ GDTX không phải làm câu 3b, GDTX 3,0 điểm).
a) Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có A1;2. Gọi M, N lần lượt là trung điểm
của các cạnh CD và AD , K là giao điểm của BM với CN . Viết phương trình của đường tròn ngoại tiếp
tam giác BNK , biết đường thẳng BM có phương trình 2x  y  8  0 và điểm B có hoành độ lớn hơn 2 .
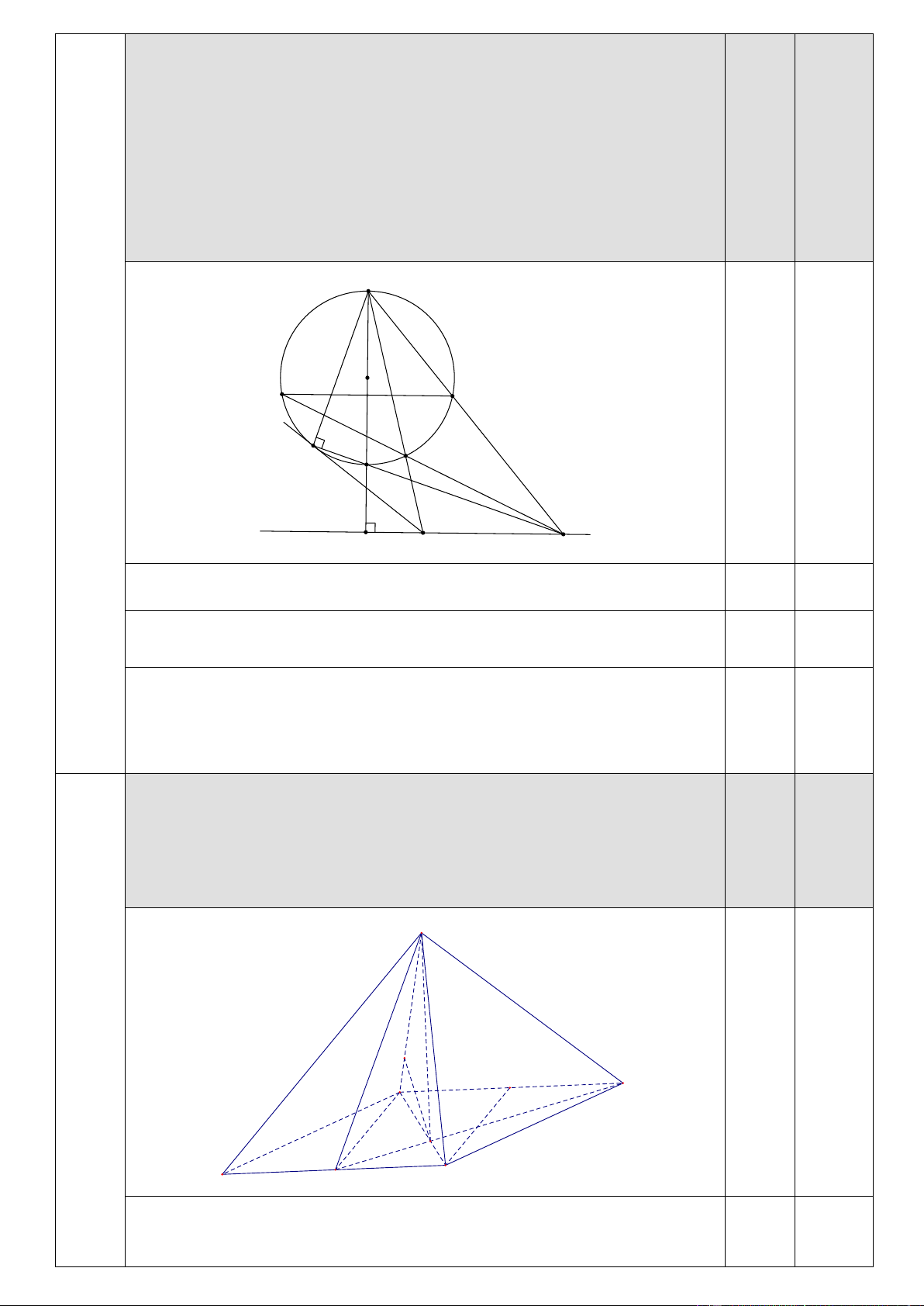
b) Cho đường tròn (O) đường kính AB , một đường thẳng d không có điểm chung với đường tròn (O) và
d vuông góc với AB kéo dài tại K ( B nằm giữa A và K ). Gọi C là một điểm nằm trên đường tròn (O),
( C khác A và B ). Gọi D là giao điểm của AC và d , từ D kẻ tiếp tuyến DE với đường tròn ( E là tiếp điểm và ,
E C nằm về hai phía của đường kính AB ). Gọi F là giao điểm của EB và d , G là giao điểm của
AF và (O), H là điểm đối xứng của G qua AB . Chứng minh ba điểm F, ,
C H thẳng hàng.
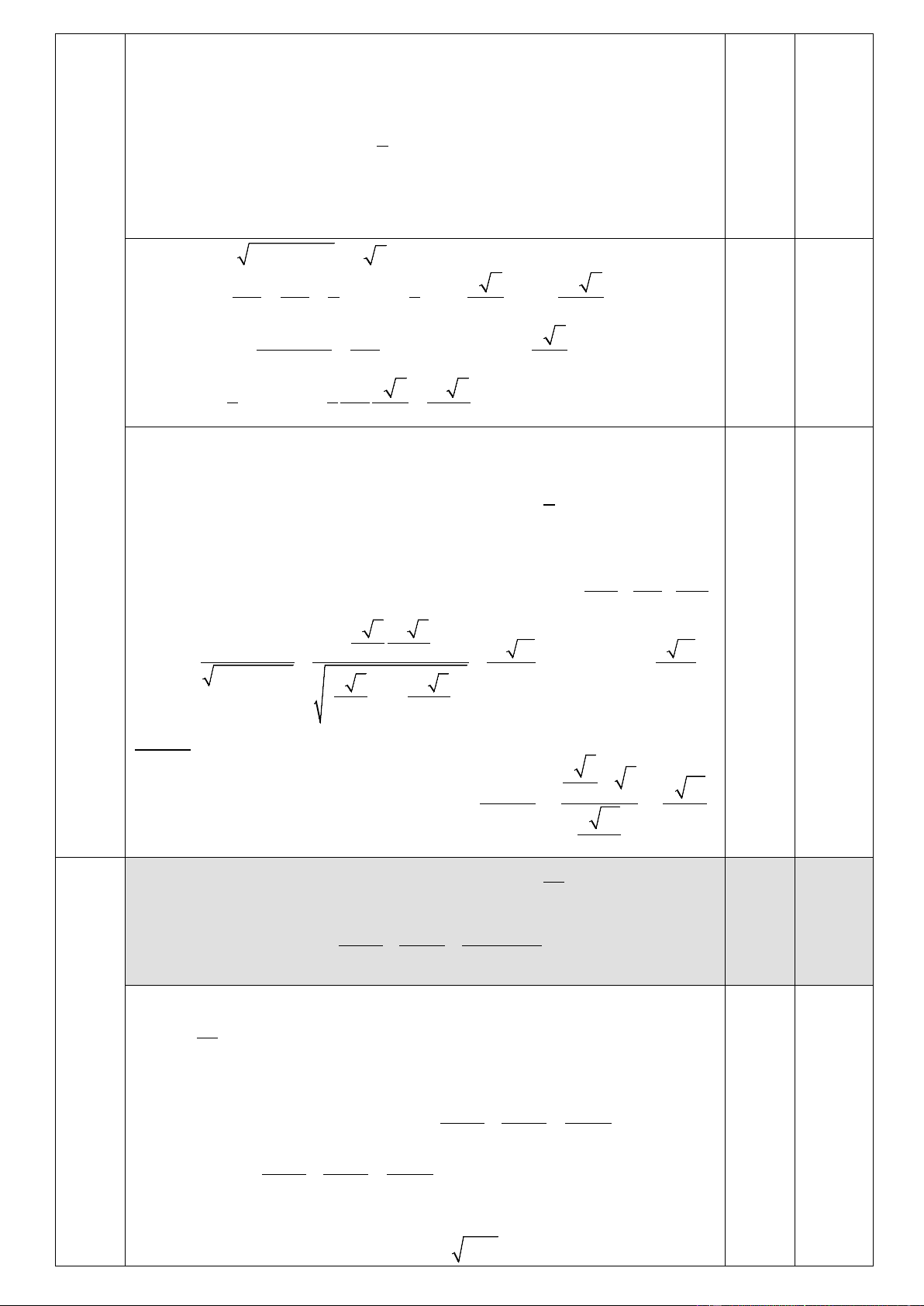
Câu 4. (THPT 3,0 điểm; GDTX 4,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thang với ,
AB  AD  a, CD  2a. Biết rằng hai mặt phẳng SAC  và SBD cùng vuông góc với mặt phẳng đáy,
góc giữa mặt phẳng (SBC) và mặt đáy bằng 0
45 . Tính theo a thể tích của khối chóp S.ABCD và khoảng
cách giữa hai đường thẳng SD và BC.
Câu 5. (THPT 2,0 điểm; GDTX 2,0 điểm). 6 1 1 3 − 2xy
Cho x > 0, y > 0 thỏa 4 4 x + y + 4 =
. Tìm giá trị nhỏ nhất của biểu thức P = + + . xy 2 2 1+ 2x 1+ 2 y 5 − x − y
Câu 6. (THPT 1,0 điểm; Thí sinh hệ GDTX không phải làm câu 6). Cho dãy số (un) được xác định R R   u = a ≥1  2017 2017 2017  1 u u u như sau:  ,∀n∈N *  1 2 n  lim + + ... + 2017 . Tìm . u = u u +  u u u  + 1 n 1 n ( n )  2 3 n+ u + u + u +  1 2 3 n+1   u u u 1 2 n  Hết U
Lưu ý: Thí sinh không được sử dụng tài liệu và máy tính bỏ túi, giám thị coi thi không giải thích gì thêm. U U
Họ và tên thí sinh:.....................................................Số báo danh:...................................................
Chữ ký của giám thị 1:..............................................Chữ ký của giám thị 2:....................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KÌ THI CHỌN HỌC SINH GIỎI BÌNH PHƯỚC
CẤP TỈNH LỚP 12 NĂM HỌC 2017-2018
Hướng dẫn chấm gồm 07 trang MÔN THI: TOÁN
Lưu ý: Điểm toàn bài lấy điểm lẻ đến 0,25; thí sinh làm cách khác đúng vẫn cho điểm tối đa. Điểm Câu Nội dung THPT GDTX Cho hàm số 2x − 2 y = x +1
a) Khảo sát và vẽ đồ thị (C) của hàm số. 1
b) Tìm điểm M thuộc (C) sao cho khoảng cách từ M đến đường thẳng 4,0 5,0
∆ : 2x − y + 4 = 0 bằng 2 lần khoảng cách từ M đến đường thẳng 1 3
∆ : x − 2y + 5 = 0 . 2
⊕ TXĐ: D =  \{− } 1 ⊕ Sự biến thiên 0,5 0.5 4 y′ = > ∀ ≠ − (
nên hàm số đồng biến trên từng khoảng xác định. x + ) 0, x 1 2 1 − − ⊕ 2x 2 2x 2 Ta có lim = ; +∞ lim
= −∞ ⇒ Đồ thị của hàm số nhận − + x→ 1 − + x→ 1 x 1 − x +1
đường thẳng có phương trình x = 1 − là tiệm cận đứng. − − 0,5 0.5  2x 2 2x 2 Ta có lim = 2; lim
= 2 ⇒ Đồ thị của hàm số nhận đường x→−∞ x +1 x→+∞ x +1
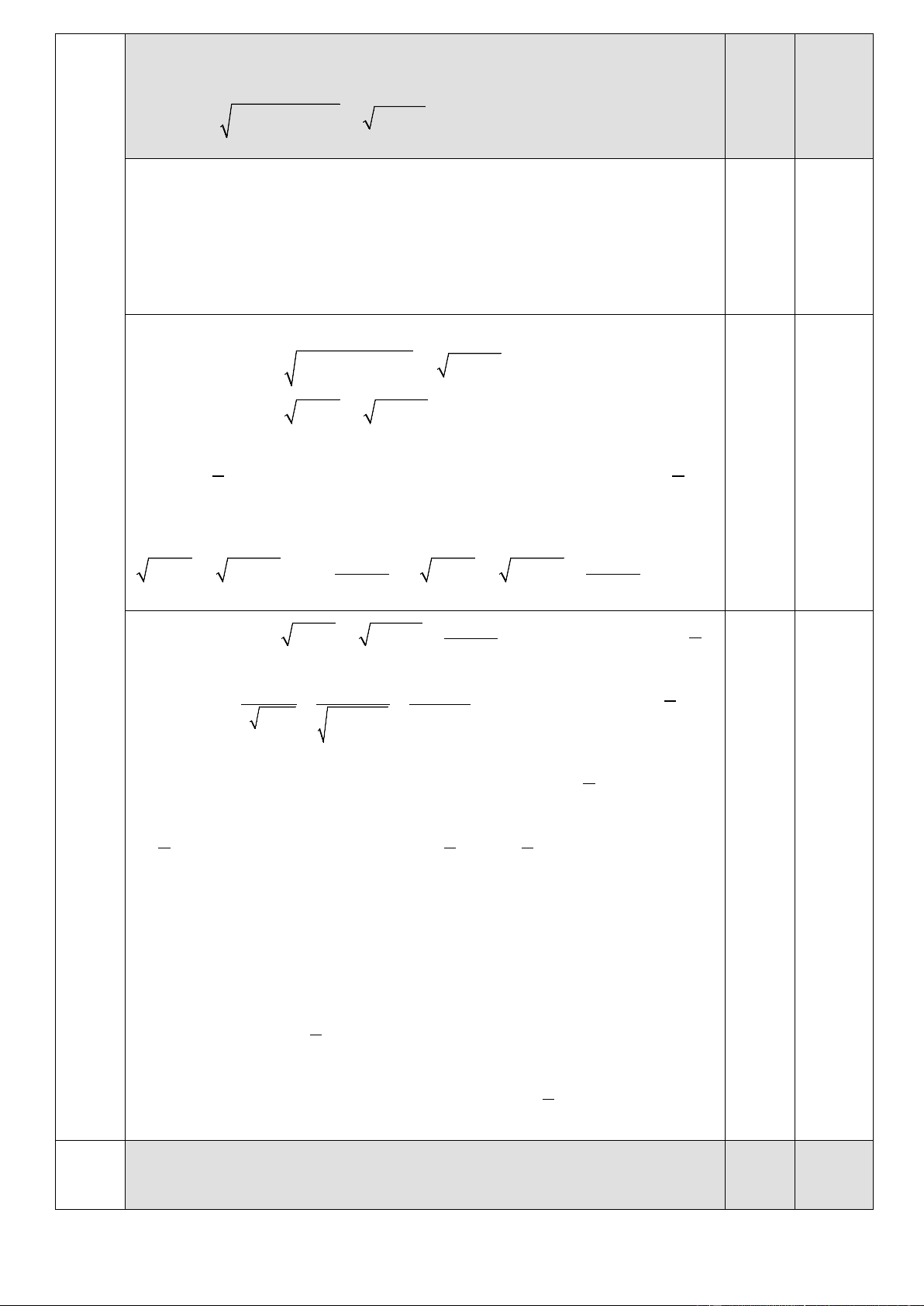
thẳng có phương trình y = 2 là tiệm cận ngang. Bảng biến thiên 0,5 0.5  Điểm đặc biệt: ( 2 − ;6),( 3 − ;4)(0; 2 − ),(1;0). 1a
 Đồ thị hàm số nhận giao điểm hai tiệm cận I(1;2) là tâm đối xứng.  Đồ thị: 0,5 1,0  2x − 2   Giả sử 0 M  x ;
 ∈ (C); x ≠ 1. −  Ta có: 0  0 x + 1  0  2 2x − 2 2x + 4x + 6 0 0 0 2x − + 4 x + 1 x + 1 d = d M, ∆ = = 0,5 0,5 1 ( 1 ) 0 0 0 5 5 2 2x − 2 x + 2x + 9 0 0 0 x − 2 + 5 0 x + 1 x + 1 0 0 1b d = d M, ∆ = = . 2 ( 2) 5 5 2 2 2x + 4x + 6 x + 2x + 9 0 0 0 0  2 2 + 1 + 1 2x +  4x + 6 2 2 = ( 2x + 2x x x + 9 (*) 0 0 0 0 0 0 ) 3 ⊕ d = d ⇔ = ⇔  1 2 0,5 0,5 3 5 3 2 2 5 2
 x + 4x + 6 = − ( 2x + 2x + 9 (**) 0 0 0 0 )  3 x = 0  Ta có 2 0
(*) ⇔ x + 2x = 0 ⇔  và (**) 2
⇔ 2x + 4x + 9 = 0 vô nghiệm. 0 0 0,5 0,75 x = 2 −  0 0 0 
 Với x  0  M 0;2 ;x  2  M 2;6 . 0   0   0,5 0,75 3 2
4 cos x  2 cos x 2 sinx  
1  sin 2x  2sinx  cosx Giải PT:  0 2,0 2,0 2 2 sin x  1  k  ĐK: 2
2 sin x  1  0  cos 2x  0  x   ,k  .  4 2 0,25 0,25  3 2
PT  4 cos x  2 cos x 2 sinx  
1  sin 2x  2sinx  cosx  0 3 2
 4 cos x  2 cos x 2sinx  
1  sin 2x  2sinx  cosx  0 3 2 2
 4 cos x  4 cos x sin x  2 cos x  2 sin x cos x  2sinx  cosx  0 2
 4 cos x sinx  cosx 2cosx sinx  cosx 2sinx  cosx  0
 sinx  cosx 2
4 cos x  2 cos x   2  0 0,75 0,75  
sin x  cos x  0   cosx  1  2a  1 cos x    2     
 Với sin x  cosx  0  2 sinx    0  x    k ,  k     .  4  4
 Với cosx  1  x  k2 ,  k     Với 1 2
cos x    x    k2 ,  k   . 2 3 1,0 1,0
Đối chiếu với điều kiện phương trình có các họ nghiệm là: 2 x  k2 ,  k  ,  x    k2 ,  k   . 3 m 
Chú ý: Viết gộp các họ nghiệm ta được họ nghiệm 2 x  ,m   . U U 3 Giải hệ phương trình: 3 6 2 2
y (x 1)  3 (
y x  2)  3 y  4  0     x y   2,0 2,0  4x  3   4  xy   , . 2 x   3  
1  3x  8  1  9      ĐK:  xy 2 4 x   1  0
 Ta có PT (1)  6 3 x y + 3 2 3 x y = y − 3 2 y + 3y −1+ ( 3 y − ) 1 ⇔ ( 2 x y)3 + 3 2 x y = ( y − ) 1 3 + ( 3 y − ) 1 1,0 1,0
Xét hàm số f t() = t3 + t 3 có f t = 2
'( ) 3t + 3 > 0,∀t ∈  ⇒ f (t) đồng biến trên  . Mặt khác PT 2 2 2
(1) ⇔ f (x y) = f ( y −1) ⇔ x y = y −1 ⇔ x y − y = 1 − .  Thay 2
x y  y  1 vào phương trình (2) ta có:   PT
  x    x 
 2xy  y 3 (2) 4 3 4
 3x  8  1  9   PT   x   3 (2) 4 3
4  x  3x  8   1  9 3 3 0,25 0,25
Vì x   không phải là nghiệm của phương trình nên xét x   , 4 4
chia 2 vế phương trình cho 4x  3 ta có: 9 9 3 3
4  x  3x  8  1 
 4  x  3x  8   1  0 . 2b 4x  3 4x  3 Xét hàm số 9   3
g(x)  4  x  3x  8 
 1, với x ∈(− +∞) 3 4; \ −  4x  3  4   Ta có 1 1 36 g '( ) x   
 0 với x ∈(− +∞) 3 4; \ −  . 2 4  x   4 3x  8 4x  32 2 3 ⇒ Hàm số  
y  g(x), đồng biến trên từng khoảng 3 4; − −   và  4   3  −    3  ; +∞   ⇒ Trên mỗi khoảng 3 4; − −   và − ;+∞   phương trình có  4   4   4  0,75 0,75
tối đa một nghiệm. Mà g(0)  g(3)  0  phương trình chỉ có hai
nghiệm là x  0, x  3.
Với x  0  y  1. Với 1
x  3  y   . 8  
Vậy hệ phương trình có hai nghiệm là   1 0;1 ,  3;     .  8
Tìm hệ số của số hạng chứa 8
x trong khai triển thành đa thức của 2c +
 + x ( − x) n 2 2 1 1    . Biết rằng 0 2 2 C + C + ... n + C = 2048. 2,0 2,0 2n 2n 2n ⊕ n Ta có (1− )2 0 1 2 3 2 1
= C − C + C − C + ... n + C 2n 2n 2n 2n 2n 0 2 2n 1 3 2n 1 C C ... C C C ... C − ⇔ + + + = + + + 0,5 0,5 2n 2n 2n 2n 2n 2n Mặt khác ta có ( n 1+ )2 0 1 2 3 2 1
= C + C + C + C + ... n + C 2n 2n 2n 2n 2n 2n Do đó n n− 2 0 2 2 1 3 2 1 0 2 2n 2n 1 C C ... C C C ... C C C ... C 2 − + + + = + + + = ⇒ + + + = 2n 2n 2n 2n 2n 2n 2n 2n 2 2 n 0,5 0,5
Kết hợp với giả thiết ta có 2n 1− 2n 1 − 11 2 = 2048 ⇔ 2 = 2 ⇔ n = 6. 8 k 8 ⊕ 8 k Ta có 2 1  + x (1− x) k 2
 = ∑C x (1− x) k 2k
 = ∑C x 1− x   . 8   8 ( ) 0,5 0,5 k =0 k =0 Hệ số của 8
x chỉ xuất hiện ở các số hạng ứng với k = 3 và k = 4 .
Từ đó ta có hệ số của 8 x là 3 2 4 0
C .C + C .C = 238. 0,5 0,5 8 3 8 4
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có A1;2. Gọi
M, N lần lượt là trung điểm của cạnh DC và AD , K là giao điểm của BM 2,0 3,0
với CN . Viết phương trình đường tròn ngoại tiếp tam giác BNK , biết BM
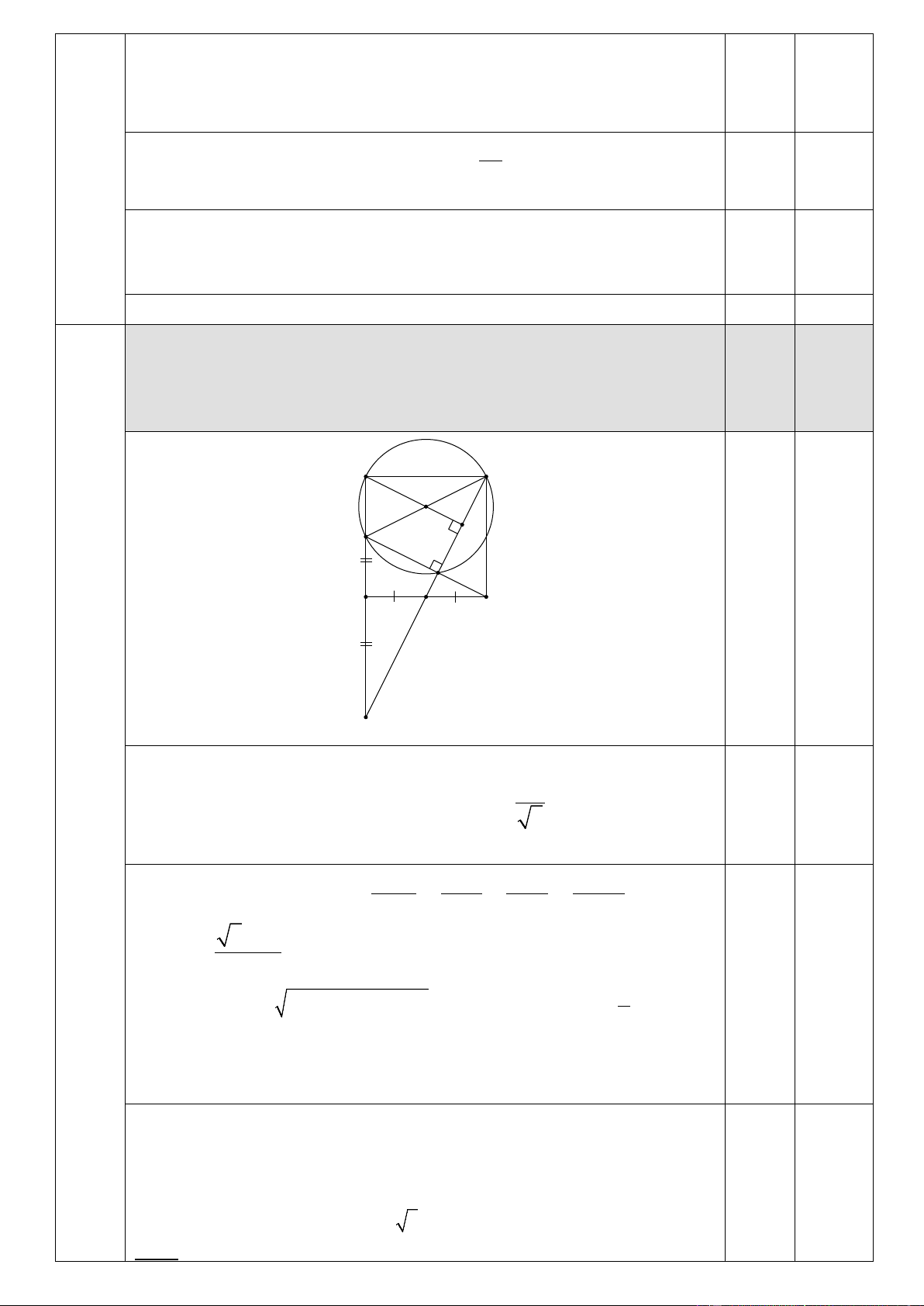
có phương trình 2x  y  8  0 và điểm B có hoành độ lớn hơn 2 . A B I H N K D M C E
Gọi E = BM ∩ AD ⇒ DM là đường trung bình của E
∆ AB ⇒ DA = DE. 3a
Dựng AH ⊥ BM tại H ⇒ AH  d A BM  8 ;  . 0,75 1,0 5   Ta có B  MC  CND 
 BMC  CND    0
BMC  DCN  90  BM  CN. 1 1 1 5 Trong tam giác vuông ABE:    2 2 2 2 AH AB AE 4 AB ⇒ 5.AH AB 
 4 , ta có B ∈ BM ⇒ B ( ;8 b − 2b). 2 0,75 1,0 Ta có 2 2 AB = 4 ⇔ (b + 1) + (6 − 2 ) b = 4 ⇔ b = 3 hoặc 7 b = . 5
Vì điểm B có hoành độ lớn hơn 2 nên chỉ nhận b = 3 ⇒ B (3; 2).
Phương trình AE : x + 1 = 0 . Ta có E = AE ∩ BM ⇒ E ( 1; − 10).
Mà D là trung điểm của AE ⇒ D ( 1;
− 6). Ta có N là trung điểm của AD ⇒ N ( 1;
− 4) ⇒ Trung điểm I của BN có tọa độ 1;3.
Do tứ giác ABKN nội tiếp nên đường tròn ngoại tiếp tam giác BNK là 0,5 1,0
đường tròn tâm I bán kính IA 
 BNK x  2  y  2 5 : 1 3  5.
Chú ý: Học sinh có thể sử dụng hệ thức lượng trong tam giác vuông để tính được AB = 4. U U
Cho đường tròn (O) đường kính AB , một đường thẳng d không có điểm
chung với đường tròn (O) và d vuông góc với AB kéo dài tại K ( B nằm
giữa A và K ). Gọi C là một điểm nằm trên đường tròn (O), (C khác A và 2,0
B ). Gọi D là giao điểm của AC và d , từ D kẻ tiếp tuyến DE với đường
tròn ( E là tiếp điểm và ,
E C nằm về hai phía của AB ). Gọi F là giao điểm
của EB và d , G là giao điểm của AF và (O), H là điểm đối xứng của G
qua AB . Chứng minh F, , C H thẳng hàng. A O H 3b G E B C d K D F
Gọi H là giao điểm của FC với (O). Để chứng minh bài toán ta cần 0,5
chứng minh H đối xứng với G qua AB.
Ta có AEKF là tứ giác nội tiếp ⇒  =  EAK EFK mà  1,0 =  ⇒  =  EAK DEF EFK DEF ⇒ D
∆ EF cân tại D ⇒ DE = DF. Ta có 2 2 = ⇒ = ⇒ ∆  ∆ ⇒  =  DE DC.DA DF DC.DA DCF DFA DCF DFA .
Mặt khác  =  =  ⇒  =  DCF ACH AGH DFA
HGA ⇒ GH / / FD 0,5
Mà FD ⊥ AB ⇒ GH ⊥ AB , Do AB là đường kính ⇒ G, H đối xứng nhau qua AB , (đpcm).
Cho hình chóp S.ABCD có đáy ABCD là hình thang với  =  0 A D = 90 ,
AB = AD = a, CD = 2 .
a Biết rằng hai mặt phẳng (SAC ) và (SBD) cùng
vuông góc với mặt phẳng đáy, góc giữa mặt phẳng (SBC) và mặt đáy bằng 3,0 4,0 0
45 . Tính theo a thể tích khối chóp S.ABCD và khoảng cách giữa hai
đường thẳng SD và BC. S 4 H E D C O A B F
Gọi O là giao điểm của AC và B .
D Khi đó, SO là giao tuyến của
hai mặt phẳng (SAC);(SBD) .
Mặt khác, do hai mặt phẳng (SAC);(SBD) cùng vuông góc với mặt đáy nên
SO ⊥ ( ABCD) . Gọi
E là trung điểm của CD ⇒ ABED là hình vuông cạnh a 0,5 1,0 Mặt khác, do 1 BE ⊥ C ; D BE = CD ⇒ B
∆ CD vuông cân tại . B 2
Do đó, BC ⊥ OB ⇒ BC ⊥ (SOB) ⇒ BC ⊥ SB
⇒ ((SBC) ( ABCD))  = (SB OB)  =  0 , , SBO = 45 . Ta có: 2 2 BD =
AD + AB = a 2. OB AB 1 1 a 2 2a 2 AB / /CD ⇒ = = ⇒ OB = BD = ;OD = . OD CD 2 3 3 3 (2a + a) 2 a 3a a 2 1,0 1,0 Ta có: 0 S = = ; SO = . OB tan 45 = ABCD 2 2 3 2 3 1 1 3a a 2 a 2 ⇒ V = S .SO = = . S . ABCD 3 ABCD 3 2 3 6
Gọi F là điểm đối xứng với B qua A ⇒ BCDF là hình bình hành 0
⇒ BC / /DF; F ∠ DB = DB ∠ C = 90 . Do đó
d ( BC SD) = d ( BC (SDF )) = d ( B (SDF )) 3 , , ,
= d (O,(SDF )). 0,5 2 Trong mặt phẳng (
SOD) dựng OH ⊥ S . D Khi đó, ta có: 1,0 OH  ⊥ SD 
⇒ OH ⊥ (SDF ) ⇒ d (O,(SDF )) = OH.Ta có: 1 1 1 = + OH  ⊥ FD 2 2 2 OH SO DO a 2 2a 2 S . O DO 2a 10 ⇒ OH = = =
⇒ d (BC SD) a 10 3 3 , = . 2 2 2 2 + 15 5 SO DO  a 2   2a 2    +   3 3     1,0
Chú ý: Kẻ BI  SD  BI là đoạn vuông góc chung của SD và BC. U U 1,0 a 2 .a 2 S . O BD a 10 Xét 3 S
 BD ta có BI.SD  S . O BD  BI    . SD a 10 5 3 Cho các số thực 6
x, y > 0 thỏa mãn 4 4 x + y + 4 = . Tìm giá trị nhỏ xy 2,0 2,0 nhất của biểu thức: 1 1 3 − 2xy P = + + . 2 2 1+ 2x 1+ 2 y 5 − x − y
 Theo BĐT AM-GM ta có: 4 4 2 2
x + y + 4 ≥ 2x y + 4 Do đó: 6 4 4 2 2 3 3
= x + y + 4 ≥ 2x y + 4 ⇔ 2x y + 4xy − 6 ≤ 0 xy 5 ⇔ ( xy − )( 2 2 2
1 x y + xy + 3) ≤ 0 ⇔ xy ≤ 1 0,5 0,5
 Ta luôn có bất đẳng thức phụ sau: 1 1 2 + ≥ , ∀ x, y > 0 . 1+ 2x 1+ 2 y 2 + xy Thật vậy ta có: 1 1 2 + ≥ 1+ 2x 1+ 2 y 2 + xy ⇔ +
xy + ( x + y) + xy ( x + y) 2 2 2 2
≥ 1+ 2x + 2y + 4xy ⇔ x y + y x +1 ≥ 3xy 0,5 0,5
(Điều này luôn đúng do 2 2 3 3 3
x y + y x +1 ≥ 3 x y = 3xy ). Vậy 1 1 3 − 2xy 2 3 − 2xy P = + + ≥ + (theo AM-GM). 2 2 1+ 2x 1+ 2 y 5 − x − y 2 + xy 5 − 2xy −  2 3 2t
Đặt t = xy,t ∈ (0;1] . Xét f (t) = + , t ∈ (0;1] 2 + t 5 − 2t 2 − 4 Ta có: f '(t) = − < ∀ ∈ 0,5 0,5 ( t 2 + t ) 0, (0;1] 2 (5− 2t)2
⇒ f (t) nghịch biến trên (0;1] nên P ≥ f (t) ≥ f (1) =1 2 2 Vậy x y = y x min P = 1 ⇔  ⇔ x = y = 1 xy = 1 0,5 0,5 u =  a 1
Cho a ≥ 1 . Xét dãy số (u ) xác định như sau:  ,∀n∈N *. RnR u = 2017 u u +  1 n+  1 n ( n )    1,0 1,0 2017 2017 2017  u u u Tìm  1 2 n  lim + + ... + .  u u u  2 3 n+ u + u + u +  1 2 3 n+1   u u u 1 2 n 
 Từ giả thiết u = 2017 u u
+1 ⇔ u − u = 2018 u
≥ 0,∀n∈N * . n+1 n ( n ) n+1 n n Mặt khác từ
u = a ≥ 1 và u = 2017 u u
+1 ⇒ u > 0,∀n∈N *. Do đó n+1 n ( n ) 1 n u − u = 2018 u
> 0,∀n∈N * ⇒ (u là dãy số tăng ⇒ u > ... > u > u = a ≥1. 0,25 0,25 n ) n+1 n n n 2 1  Ta có u = 2017 u u +1 ⇔ 2018 u = u − u . n+1 n ( n ) n n+1 n 2017 2018 Khi đó u u n = n un+1 u u + u + u u n n+1 n+1 n n+1 u n u − u u − u = n n n n 1 1 1 = 1 = − u u u + u u u u u n n+1 (+ n n+n ) + n n+1 n n+1 6 2017 2017 2017 Vậy u u u 1 + 2 + ... + n u u u 2 3 n+ u + u + u + 1 2 3 n+1 u u u 1 2 n 0,25 0,25       = 1 1 1 1 1 1 1 1 1 1  −  +  −  +... +  −        = − = −  u u u u u u u u a u 1 2   2 3   n n+1  1 n 1 + n 1 +
Ta đi xét 2 trường hợp sau:
 Trường hợp 1: Dãy (u bị chặn trên ⇒ (u có giới hạn. n ) n )
Giả sử giới hạn đó là a, lấy giới hạn 2 vế của giả thiết u = 2017 u u +1 n+1 n ( n )
ta có: a = a ( 2017 a + )
1 ⇔ a = 0 (mâu thuẫn với u > a ≥ 1, n ∀ ∈N * ). n 0,25 0,25
 Trường hợp 2: Dãy (u không bị chặn trên. Mà (u là dãy tăng n ) n )
⇒ lim u = +∞ ⇒ lim u = +∞ . n n 1 +    2017 2017 2017  Khi đó    u u u 1 1 1 1 2 n  lim + +... + = lim −  = . 0,25 0,25  u u u    2 3 n+ u + u + u + 1  a u a n+1   2 3 n+1   u u u 1 2 n  Hết U