


Preview text:
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 12 CẤP TRƯỜNG
TRƯỜNG THPT TRẦN HƯNG ĐẠO NĂM HỌC 2017 - 2018 MÔN THI: TOÁN (Đề thi có 01 trang)
Thời gian: 180 phút, không kể thời gian giao đề
Câu 1 (2,5 điểm).
a) Tìm tất cả các giá trị m để m 3 y
x m 2
x m 1 1 3
2 x đồng biến trên 2, 3 3 b) Cho hàm số 4 2
y x 2mx m 1 Cm , với m là tham số thực. Xác định tất cả các giá trị
của m để hàm số C có ba điểm cực trị đồng thời các điểm cực trị của đồ thị hàm số m
tạo thành một tam giác có một góc tù.
Câu 2 (2,0 điểm). a) Giải phương trình 2
3 sin 2x 3 1 2cos x
b) Cho A là tập hợp các số tự nhiên có 6 chữ số đôi một khác nhau lập được từ các chữ số 0,
2, 3, 5, 6, 8. Lấy ngẫu nhiên một số thuộc tập A . Tính xác suất để số lấy được có chữ số
0 và chữ số 5 không đứng cạnh nhau. 3 3 2 2
ìïx - y +6x -3y +14x-5y = -9
Câu 3 (1,5 điểm). Giải hệ phương trình ïí (x, y Î ) ï 2
ï 1- x - y = 2- y -1 ïî
Câu 4 (1,5 điểm). Trong mặt phẳng với hệ trục tọa độ Oxy , cho hình chữ nhật ABCD có (5
A ,7) , điểm C thuộc đường thẳng có phương trình d : x y 4 0 . Đường thẳng đi qua 1
D và trung điểm của đoạn AB có phương trình d : 3x 4y 23 0 . Tìm tọa độ của B và 2
C , biết điểm B có hoành độ dương.
Câu 5 (1,5 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a góc 0 BAD 60 ,
hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với điểm G là trọng tâm tam giác
BCD. Góc giữa SA và mặt phẳng (ABCD) bằng 0
60 . Tính thể tích khối chóp S.ABCD và khoảng
cách giữa hai đường thẳng DC và SA theo a.
Câu 6 (1,0 điểm). Cho các số thực dương x, y, z . Tìm giá trị lớn nhất của biểu thức: 1 2 S 2 2 2
x y z 1 x 1 y 1 z 1
---------------Hết----------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……….………..…….................…….….….; Số báo danh:……….....……….
TRƯỜNG THPT TRẦN HƯNG ĐẠO
ĐÁP ÁN KỲ THI CHỌN HSG CẤP TRƯỜNG (Đáp án có 05 trang) NĂM HỌC 2017 - 2018
MÔN THI: TOÁN KHỐI 12 I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài học sinh làm
theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
- Với bài hình học không gian nếu thí sinh không vẽ hình phần nào thì không cho điểm tương ứng với phần đó. II. ĐÁP ÁN: Câu Ý Nội dung trình bày Điểm 1 a 1,25
Hàm số đồng biến / 2, 2
y mx 2m
1 x 3m 2 0 x 2 (1) 0,25
m x 2 1 2 2 x 6 x
2 g x 2 x 6 m x 2 x 2 1 2 0,25 2 2
x 6x 3
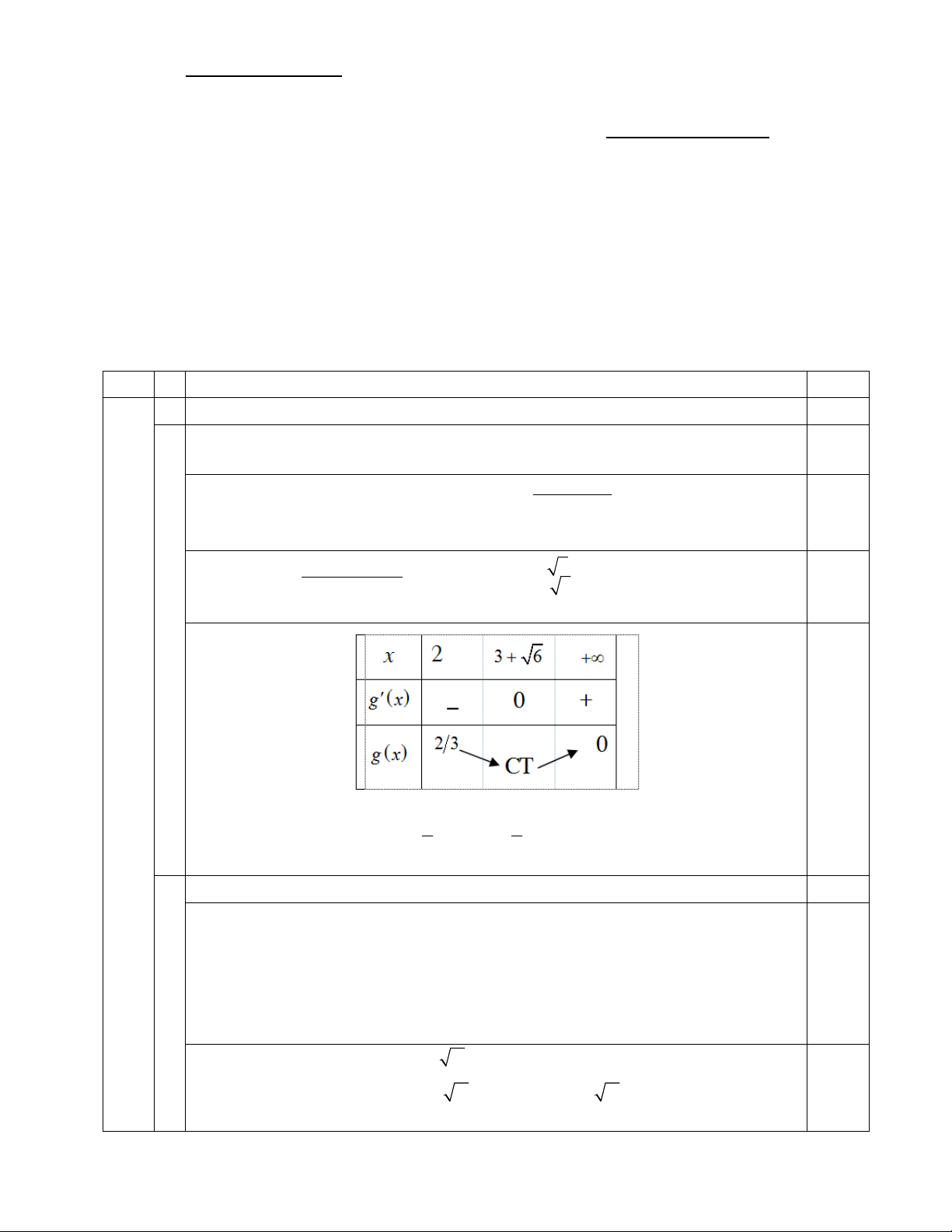
Ta có: g x 0 x 1
x 3 6 ; lim g x 0 2 2 0,25 (x 2x 3) x 2
x 3 6 x 0, 5 Từ BBT
g x g 2 Max 2 . Vậy 2 m x2 3 3 b 1,25
Tập xác định D Ta có 3
y x mx x 2 ' 4 4 4
x m. Khi đó hàm số C có 3 điểm cực trị khi và chỉ m 0,25
khi y ' 0 có 3 nghiệm phân biệt 2
x m 0 có 2 nghiệm phân biệt khác 0 m 0
Phương trình y ' 0 x 0, x m . Giả sử 3 điểm cực trị của đồ thị hàm số C m là , A ,
B C . Khi đó A m B 2
m m m C 2 0; 1 , ; 1 ,
m; m m 1 . 0,25 1 AB 2
m m AC 2 ; ;
m; m . Tam giác ABC cân tại A, nên nó sẽ có góc tù khi 0,5 0
90 AB; AC cos ; AB AC 0 4 AB AC m m 3
0 0 1
m 0 m 1 (Do m 0 ). 4 AB AC m m 0,25
Kết luận: 0 < m < 1. 2 a 1
Phương trình tương đương: 3 sin 2x 3 1 1 cos 2x . 0,25 1 3 3 cos 2x sin 2x . 0,25 2 2 2 3 cos 2x . 0,25 3 2 x k 12 k
x k 0,25 4
Vậy phương trình có nghiệm là x
k hoặc x k (k ) . 12 4 b 1 n( ) W = 5.5! 0,25
Gọi số cần tìm là a a a a a a (trong đó các a Î ). i {0,2,3,5,6, } 8 1 2 3 4 5 6 0,25
TH1: 5 và 0 đứng cạnh nhau ở vị trí a ,a có 4! số. 1 2
TH2: 5 và 0 đứng cạnh nhau ở vị trí còn lại có 4.2!4! số. 0,25
Vậy xác suất để số lấy được có chữ số 0 và chữ số 5 không đứng cạnh nhau là: 5.5!-(4!+ 4.2.4!) 16 0,25 P = = 5.5! 25 3 1,5 Điều kiện: 1
x 1;0 y 2 . Ta có 0,5
y 3 y x 3 (1) 1 2 1 2 2 x 2 2 Xét hàm số 3
f (t) t 2t, ta có 2
f '(t) 3t 2 0, t
f (t) đồng biến trên . 0,25
Vậy (1) f ( y 1) f (x 2) y x 1 Thế vào (2) ta được 2
1 x 1 x 1 x 1 0 (3) 2 t Đặt 2 2
t 1 x 1 x, t 0 1 x 2 0,5 2 t 2 t 0 (l) Khi đó 3 2
t 1 0 t 2t 0 2 t 2 Với 2
t 2 1 x 1 x 2 1 x 1 x 0 x 0
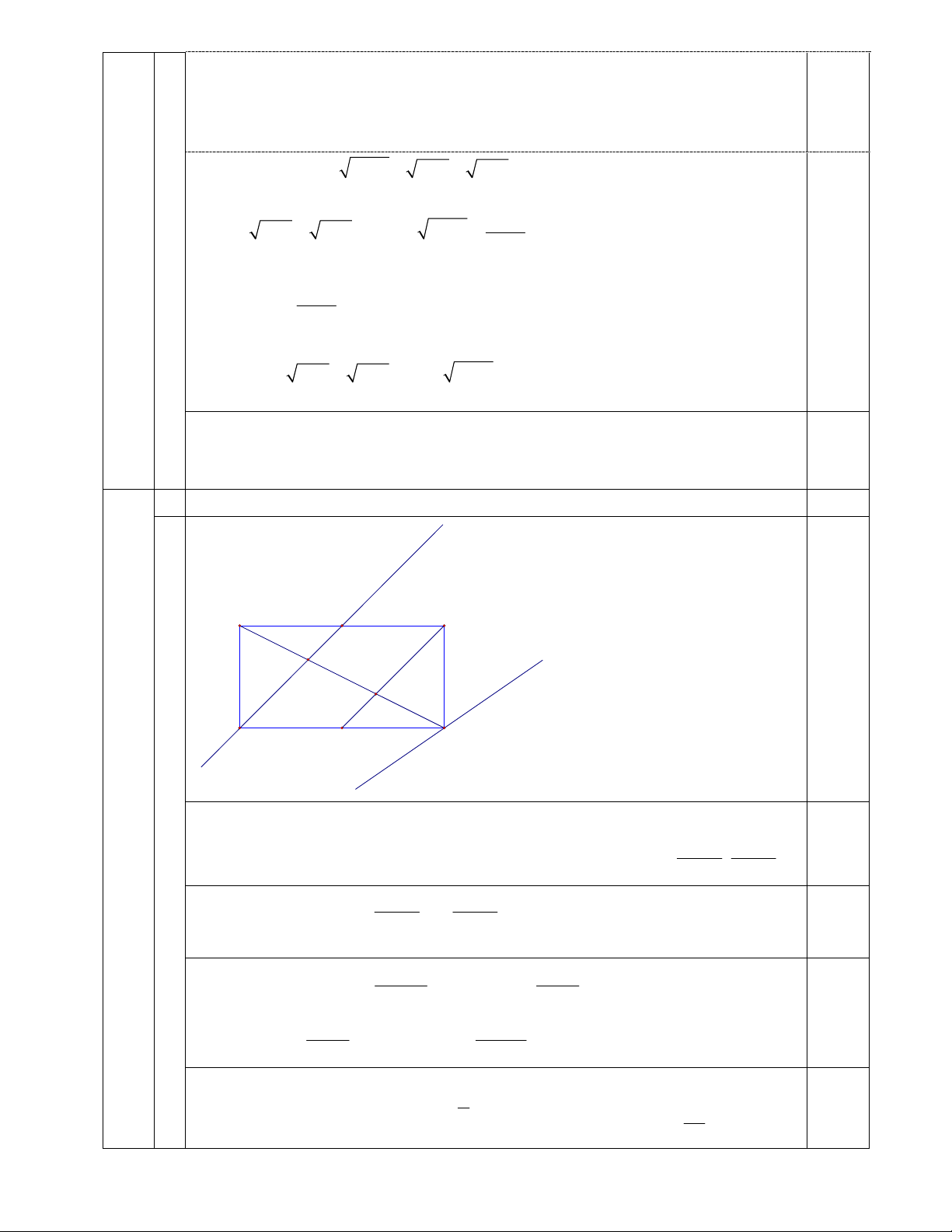
Với x 0 suy ra y 1. Vậy hệ có nghiệm duy nhất 0,25 y 1 4 1,5 d2: 3x - 4y - 23 = 0 A(5; -7) B M I D N C d1: x - y + 4 = 0 Gọi C ;
c c 4 d , M là trung điểm AB, I là giao điểm của AC và d 2 1 0,5
c 10 c 10
Ta có AIM đồng dạng CI
D CI 2AI CI 2IA I ; 3 3 c 10 c 10
Mà I d nên ta có: 3. 4.
23 0 c 1 0,25 2 3 3 Vậy C(1;5). 3t 23 3t 9
Ta có: M d M t; B 2t 5; 2 4 2 0,25
3t 5 3t 19 AB 2t 10;
, CB 2t 6; 2 2 t 1 1 0,5 Do . AB CB 0
4t 5t 3
3t 53t 19 0 29 4 t 5 3 B( 3 ; 3 ) (loai) 33 21 33 21 B ; B ; 5 5 5 5 5 1,5
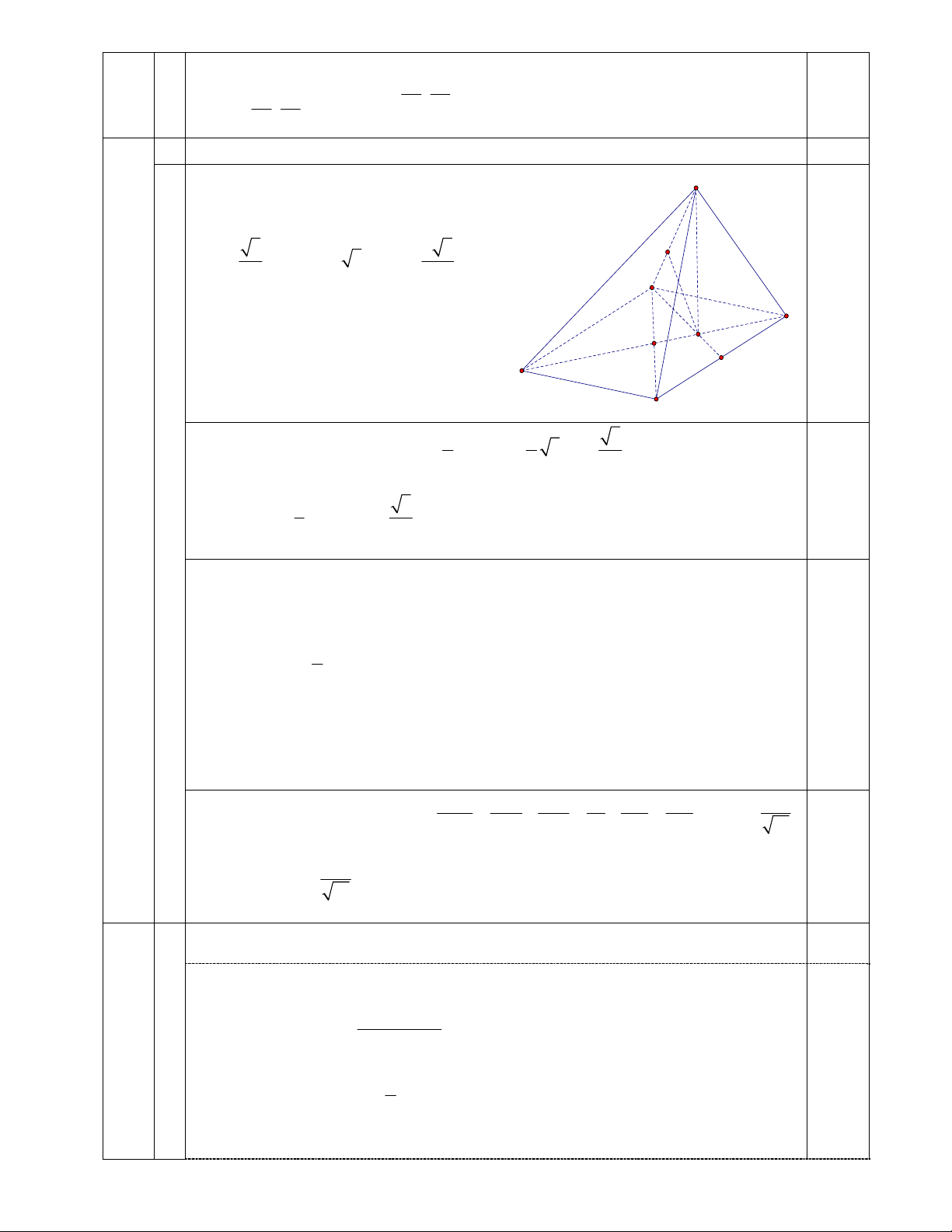
Gọi O là tâm của đáy. Theo bài ra ta có : S Góc 0 SAC 60 , 3 2 3 AO
a AC 3a, AG a H 2 3 B 0,5 Suy ra 0
SG AG.tan 60 2a C G O E A D 1 1 3 Diện tích hình thoi ABCD 2 S AC.BD 3 . a a a ABCD 2 2 2 0,25 1 3 Vậy 3 V S .SG a S .ABCD 3 ABCD 3
Gọi E BG CD
Ta có CD / / AB CD / /mp(SAB) d (CD, SA) d (CD, (SAB)) 3
d(E,(SAB)) d(G,(SAB)) 0,5 2
Do tam giác BDC đều nên BE CD BE AB . Do đó khi kẻ GH SB, H SB
Suy ra GH (SAB) d (G,(SAB)) GH 1 1 1 3 1 13 2a
Trong tam giác vuông SBG ta có GH 2 2 2 2 2 2 GH GB GS a 4a 4a 13 0,25 3a
Vậy d (CD, S ) A 13 6 1
Sử dụng BĐT cô-si cho 3 số dương ta có: 3
a b c a b c 3 1 1 1
, dấu bằng xảy ra khi và chỉ khi a b c 3 0,25 1
Mặt khác a b c 1 a b c 2 2 2 2
1 , dấu bằng xảy ra khi và chỉ khi 4
a b c 1 4 2 54
Đặt t x y z 1 1, ta có S f t 3 t 0,25 t 2 2 54 2 162 f (t) t , f '(t) ; f '(t) 0 t 4 0,25 t t 2 , 1 3 2 t t 24 1 1 Suy ra f
f (4) . Vậy ta có S
a b c 1 0,25 max 4 max 4
---------------Hết---------------- 5




