Đề Thi Chọn HSG Toán 12 Sở GD-ĐT Hưng Yên 2018-2019 Có Đáp Án Và Lời Giải

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12 HƯNG YÊN NĂM HỌC 2018-2019 MÔN THI: TOÁN
Thời gian làm bài: 180 phút, không kể thời gian phát đề Câu I (5,0 điểm) 1.Cho hàm số 2
y  2x  2  m x  4x  5 với m là tham số. Tìm các giá trị của m để hàm số có cực tiểu. 2.Cho hàm số 4 2
y  x  mx  2m  2C  với m là tham số. Gọi A là một điểm thuộc đồ thị C có
hoành độ bằng 1. Tìm các giá trị của m để tiếp tuyến của đồ thị C tại A cắt đường tròn T  2 2
: x  y  4 tại hai điểm phân biệt tạo thành một dây cung có độ dài nhỏ nhất. Câu II (4,0 điểm) 2 sin x  5  cos 2 x
1.Giải phương trình    5
 x 1  x  5 .  3    2 dx
2.Tính tích phân I  . 
x x 1  x 1 x. 1   Câu III(5,0 điểm)
1.Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a và 
ABC  60 . Gọi E , F lần lượt
là trung điểm của các cạnh SC , SD . Biết SA  SC  SD và mặt phẳng  ABEF  vuông góc
với mặt bên SCD , tính thể tích khối chóp S.ABCD theo a .
2.Cho tứ diện ABCD có độ dài các cạnh AB  3, AC  4 , AD  6 và các góc  
BAC  BAD  60 , 
CAD  90 . Tính khoảng cách giữa hai đường thẳng AB và CD .
Câu IV.(2,0 điểm) Cho đa thức f  x 4 3 2
 x  ax  bx  cx 1 với a; ;
b c là các số thực không âm.
Biết rằng phương trình f  x  0 có 4 nghiệm thực, chứng minh f   4 2018  2019 .  3 2
y  y  2y 1  ln  2
x 1  x  ln  2 y 1  y 
Câu V.(2,0 điểm)Giải hệ phương trình:  . 3 2
x  x  y  y 1 u  1 
Câu VI.(2,0 điểm)Cho dãy số được xác định như sau: 1  * u 
 1 2u u , n     n 1  n n 1 
1. Tìm số hạng thứ 10 của dãy số đã cho.
2. Chứng minh rằng u là số vô tỷ. 2019 Trang1
GIảI CHI TIếT Đề CHỌN HSG TỈNH Câu I (5,0 điểm) 1. Cho hàm số 2
y  2x  2  m x  4x  5 với m là tham số. Tìm các giá trị của m để hàm số có cực tiểu. 2. Cho hàm số 4 2
y  x  mx  2m  2C  với m là tham số. Gọi A là một điểm thuộc đồ thị C có
hoành độ bằng 1. Tìm các giá trị của m để tiếp tuyến của đồ thị C tại A cắt đường tròn T  2 2
: x  y  4 tại hai điểm phân biệt tạo thành một dây cung có độ dài nhỏ nhất. Lời giải 1. Xét 2
y  2x  2  m x  4x  5 TXĐ:  m  x  2 y  2  , x    . 2 x  4x  5
+) Hàm số có cực tiểu thì trước hết phương trình y '  0 có nghiệm. 2 2 x  4x  5
y '  0  m  (*) x  2   Đặ x x t g  x 2 2 4 5  x  2
2 x  2 x2 2
 2 x  4x  5 x  x   g ' x 2 4 5 2       x . x  2 0, 2 2
x 22 2x 4x 5 BBT: m  2
Từ bảng biến thiên ta có phương trình (*) có nghiệm   . m  2  x 22 2
x  4x  5  2 x  4x  5 m +) y '  m  , x   . 2 x  4x  5
 2x 4x5 2x 4x5
Với m  2  y '  0 : Hàm số không có cực tiểu. Với m  2
  y '  0 : Hàm số có cực tiểu. Vậy m  2
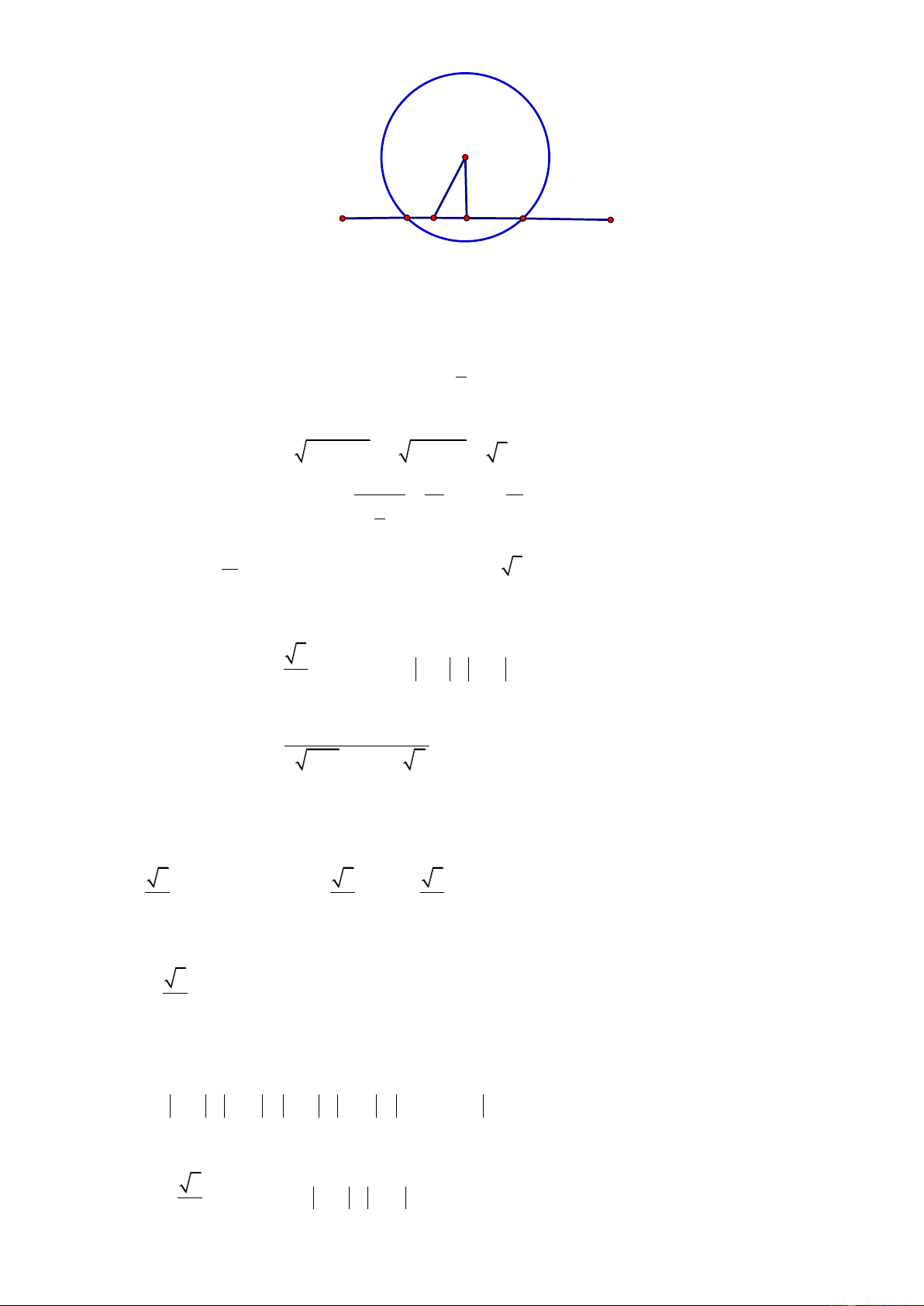
 thì hàm số có cực tiểu. 2. Trang2 O I H A M N Ta có ( A 1; m 1) .
Gọi d là tiếp tuyến của đồ thị C tại A . Phương trình đường thẳng d là:
y  4  2m x  
1  m 1  4  2m x  y  3m  5  0 .   Đườ 3
ng thẳng d luôn đi qua điểm cố định I ;1 
 nằm trong đường tròn.  2 
Do đó d luôn cắt đường tròn tại hai điểm M , N . Gọi H là trung điểm MN . Ta có: 2 2
MN  2MH  2 4  OH  2 4  OI  3 4  2m 1  11 MN
 H  I  OI  d    m  . min 3 1 4 2 11 Vậy với m 
thì MN đạt giá trị nhỏ nhất bằng 3 . 4 Câu II (4,0 điểm) 2 sin x  5  cos 2 x
1. Giải phương trình    5
 x 1  x  5 .  3    2 dx
2. Tính tích phân I  . 
x x 1  x 1 x. 1   Lời giải 1. Ta có: 2 sin x 0 5  5   5  2 0 
1;0  sin x 1      1. 3  3   3      cos 2 x 1 5  1; 1
  cos 2x 1 5  5  5. 2 sin x  5  Vậy cos2    5 x  6 
, dấu bằng xảy ra khi và chỉ khi 3    2 sin  x  0 
 sin x  0  x  k k  . cos 2x 1
Lại có x 1  x  5  1 x  x  5  1 x  x  5  6 , dấu bằng xảy ra khi và chỉ khi
1 xx 5  0  5   x 1. 2 sin x   x  k x    Do đó 5 cos 2  
 5 x  x 1  x  5    .    3    5   x 1 x  0 Trang3
Vậy phương trình có hai nghiệm là x   ; x  0. 2 2 dx dx 2. I    
x x 1  x 1 x    1   1 . x  x  1 . x x 1
2  x 1  x  2 dx  1 1  2 2    1 1 dx     dx  dx   . x x 1  x x 1  x x 1 1   1 1 1
 2 x 2 x 1 2  4 2  2 3  2. 1 Câu III (5,0 điểm)
1. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 2a và 
ABC  60 . Gọi E , F lần lượt
là trung điểm của các cạnh SC , SD . Biết SA  SC  SD và mặt phẳng  ABEF  vuông góc
với mặt bên SCD , tính thể tích khối chóp S.ABCD theo a .
2. Cho tứ diện ABCD có độ dài các cạnh AB  3, AC  4 , AD  6 và các góc  
BAC  BAD  60 , 
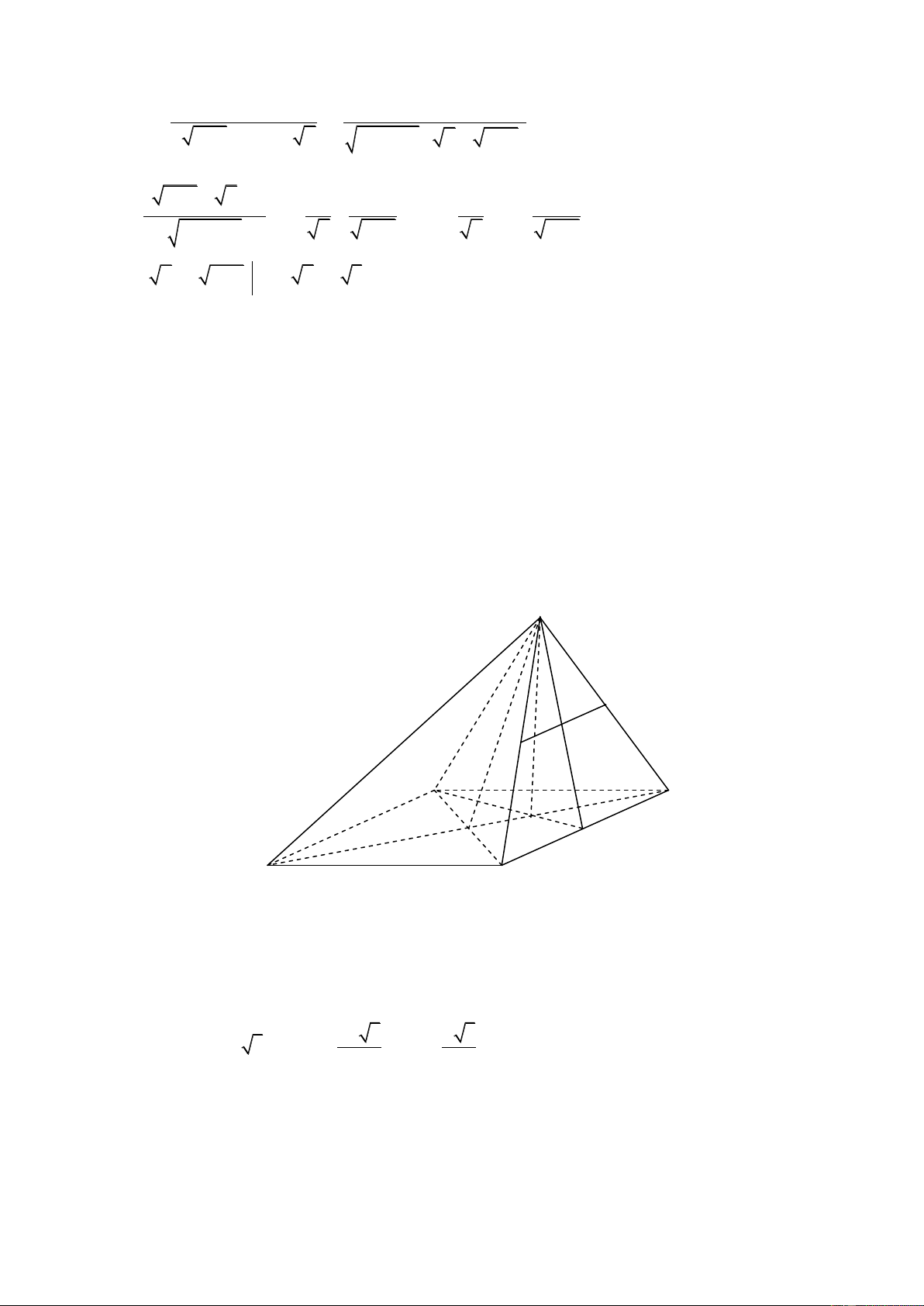
CAD  90 . Tính khoảng cách giữa hai đường thẳng AB và CD . Lời giải 1. S F E I A D O H M B C
Gọi M là trung điểm của CD , I là giao điểm của EF và SM , H là giao điểm của AM và DO .
Có ABCD là hình thoi cạnh 2a , 
ABC  60 nên A
 CD đều cạnh 2a . 2a 3 a 3      AM a 3 AH ; HM . 3 3
H là tâm đường tròn ngoại tiếp A  CD.
Có SA  SC  SD nên hình chiếu của S lên mặt
Có  ABEF   SCD theo giao tuyến EF
Mà SM  EF (Do SM  CD ; EF // CD ) Trang4
 SM   ABEF   SM  AI  A
 IM vuông tại I . S I A H K M
+) Gọi K là trung điểm của HM  IK là đường trung bình của S  HM .
IK  AM do SH  AM   Xé   t S H  AIM 2 IK
vuông tại I có IK  AM nên   2 IK  1 1
AK.KM  AH  HM . HM    2  2 a 15 a 15  IK   SH  6 3 1 1 a 15 Vậy V  SH .S  . 2a2sin60 S .ABCD 2. 3 ABCD 3 3
Gọi N là trung điểm của AD , M là điểm trên
Vì AB  3 , AC  4 , AD  6 Lại có  
BAC  BAD  60 ,  CAD  90 nên  B
 MN vuông tại B .
Gọi O là trung điểm của MN thì O là tâm
Lại có AB  AM  AN  3 Trang5  3 2
AO   BMN  và 2 2 AO  AN  ON  . 2 Vì B
 MN vuông tại B nên
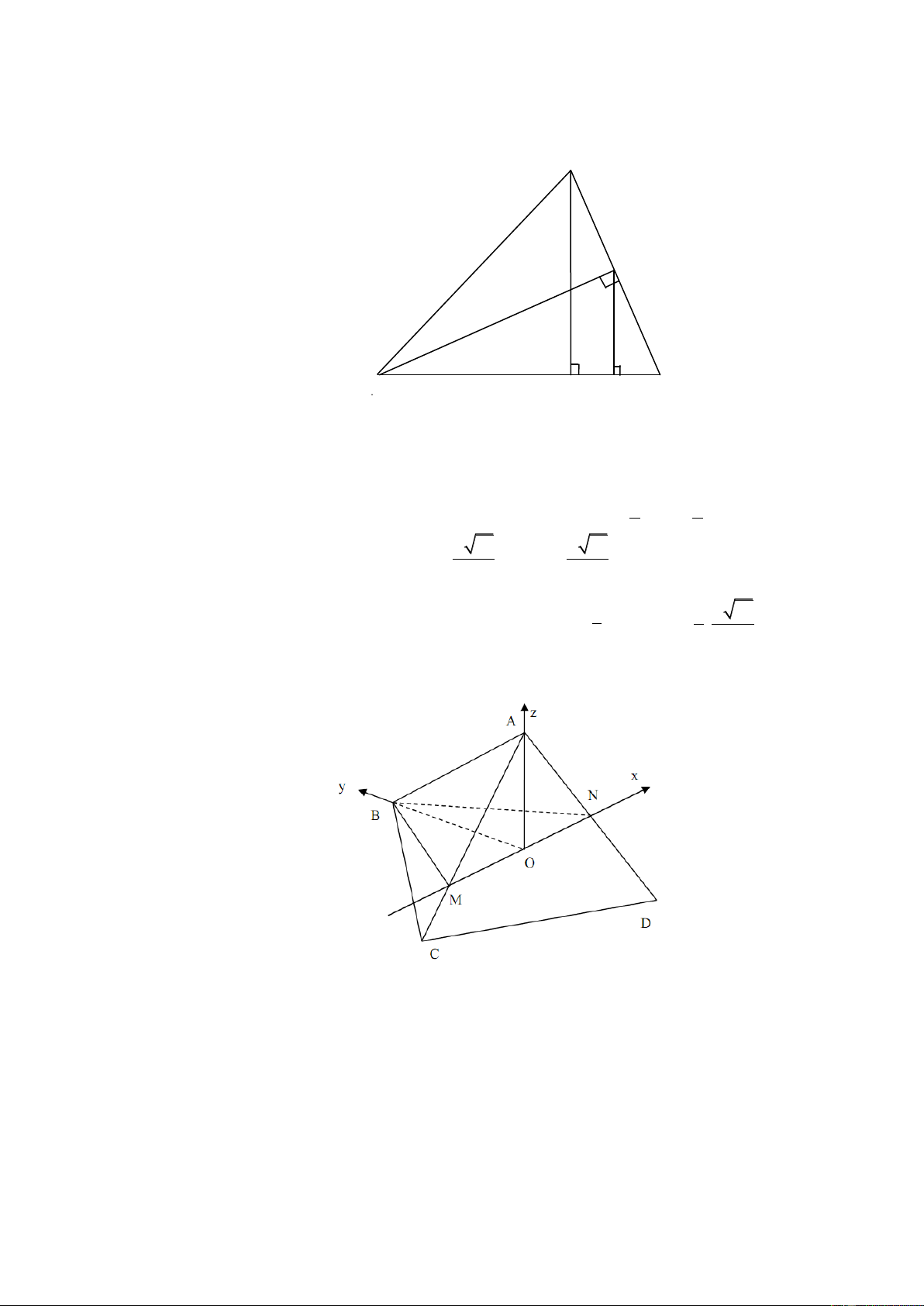
Đặt hệ trục toạ độ Oxyz như hình vẽ với:  3 2   3 2 
O0;0;0 , A 0;0;   , N  ;0;0    , 2   2  
+) Vì N là trung điểm của AD nên +) Có 
 CD  5 2;0; 2    
 AB,CD   3  ;15;15 . 3 2 3 2    Có AB   0; ;     2 2    Có AC   2  2;0; 2 2
  
 AB,CD.AC  6 2  30 2  36 2   .
   AB CD AC  
Áp dụng công thức d  AB CD , . ,    AB,CD  
 d  AB CD 36 2 4 102 ,   . 9  225  225 17
CâuIV.(2,0 điểm) Cho đa thức f  x 4 3 2
 x  ax  bx  cx 1 với a; ;
b c là các số thực không âm. Biết
rằng phương trình f  x  0 có 4 nghiệm thực, chứng minh f   4 2018  2019 . Lời giải
Nhận xét: Nếu x là nghiệm của phương trình f  x  0 thì x  0 (vì nếu x  0 thì 0 0 0
f  x  0 ). 0 
Gọi 4 nghiệm của phương trình f  x  0 là x ;  x ;  x ;  x với x  0, i  1;4 . 1 2 3 4 i
Khi đó f x  x  x x  x x  x
x  x ; f 0  1  x x x x  1. 1   2   3   4  1 2 3 4 4 4  
Ta có f 2018  2018  x   11...1 x  i  i   i 1  i 1   2018laà n  4  2019. x  4 4 2019 2019  2019 . x x x x  2019 . i 1 2 3 4 i 1 
Dấu “=” xảy ra  x  x  x  x  1 . 1 2 3 4 Trang6  3 2
y  y  2y 1  ln  2
x 1  x  ln  2 y 1  y 
Câu V.(2,0 điểm) Giải hệ phương trình:  . 3 2
x  x  y  y 1 Lời giải  3 2
y  y  2 y 1  ln 
 2x 1xln 2y 1 y  1  3 2
x  x  y  y 1  2 Cộng vế   1 và 2 ta có: 3 y  y 
 2x  x  2y   y 3 ln 1 ln 1  x  x 3
 y  y   2y   y 3
 x  x   2 ln 1 ln x 1  x 3
 y  y   2y   y 3
 x  x   2 ln 1 ln
x 1  x 3 (do  2
y   y 2 1
y 1  y  1 nên  2
y   y     2 ln 1 ln
y 1  y )
Xét hàm số f t  3
 t  t   2 ln
t 1  t  trên  . t 1  f t  2 t 1 1 2 2  3t 1  3t  1 2 2 t 1  t t 1   t f t  6t  t  3 2 1 t  0
f t   0   6 t  3 2 1  1  (phương trình t  3 2 6 1  1 vô nghiệm vì t  3 2 6 1  6  1, t    ) Bảng biến thiên: t  0  f t   0    f t  0
Từ bảng biến thiên ta có f t   0, t
   Hàm số f t đồng biến trên  .
Ta có: 3  f  x  f  y  y  x .
Thay y  x vào 2 ta có: 3 2 3 2
x  x  x  x 1  x  x  2x 1  0 4 Trang7 3 2       Đặ 1 1 1 1
t t  x  . Phương trình 4 trở thành: t   t   2 t  1  0       3  3   3   3  7 7 3  t  t   0 5 . 3 27 2 7 3t 3t 2 7 cos Với t  thì
 1, do đó tồn tại  0;  sao cho cos  hay t  3 2 7 2 7 3 2 7 cos Thay t  vào 5 ta có: 3 56 7 14 7 7 3 cos   cos   0 27 9 27 56 7 cos 3  3cos 14 7 7  .  cos   7 0 cos 3    27 4 9 27 14  1  7  k 2    arccos      3 14 3     k     1  7   k 2    arccos      3 14 3   
Do  0;  nên suy ra   7   arccos    14    2 7 1  7  1    x  y  cos  arccos        3 3 3 14    3     7   arccos     14 2 2 7 1  7    2  1     x  y  cos   arccos        3 3 3  3 14 3     3    7   arccos     14 2 2 7  1  7    2  1       x  y  cos  arccos         3 3 3   3 14 3     3   (Phương trình bậ 2 7
c ba có tối đa 3 nghiệm nên ta không cần xét trường hợp t  ) 3 u  1 
CâuVI.(2,0 điểm)
Cho dãy số được xác định như sau: 1  * u 
 1 2u u , n     n 1  n n 1 
1. Tìm số hạng thứ 10 của dãy số đã cho.
2. Chứng minh rằng u là số vô tỷ. 2019 Lời giải
1. Từ giả thiết dễ thấy * u  1, n   . n Trang8 Khi đó 2 2 2 u  1 2u u  u
1 2u u  u
 2u u 1  0  u  u  1 u n 1  n n 1  n 1  n n 1  n 1  n n 1  n 1  n n  Đặt u cot,     0; (do * u  1, n   ), khi đó n    4  n  2 2 cos 1 1 cos  2 2 u
 cot  1 cot   cot     cot . n 1  sin sin    2 2sin .cos 2 2    
Ta thấy u  1  cot nên u  cot  cot , u  cot
... , từ đó ta tìm được công thức tổng 1 4 2 3 3 4 8 2 2 
quát của dãy số là: u  cot . n n 1 2   Vậy u  cot . 10 11 2 2 u 1
2. Từ giả thiết ta viết lại n 1 u   , nên nếu u u hữu tỷ. n n 1  hữu tỷ thì n 2un 1    Do đó u  cot số hữu tỷ thì u
hữu tỷ….và u  cot
 1 2 hữu tỷ, vô lý. 2019 2020 2 2018 2 8  Vậy u  cot vô tỷ. 2019 2020 2 Trang9