SỞ GIÁO DỤC & ĐÀO TẠO BẮC GIANG ĐỀ THI CHỌN HỌC SINH GIỎI VĂN HÓA CẤP CỤM
CỤM THPT LẠNG GIANG NĂM HỌC 2016 - 2017
–––––––––––––––––––––
MÔN THI: TOÁN LỚP 12 PHỔ THÔNG ĐỀ CHÍNH THỨC Ngày thi: 19/02/2017
(Đề thi gồm 01 trang)
(Thời gian làm bài 180 phút, không kể thời gian giao đề)
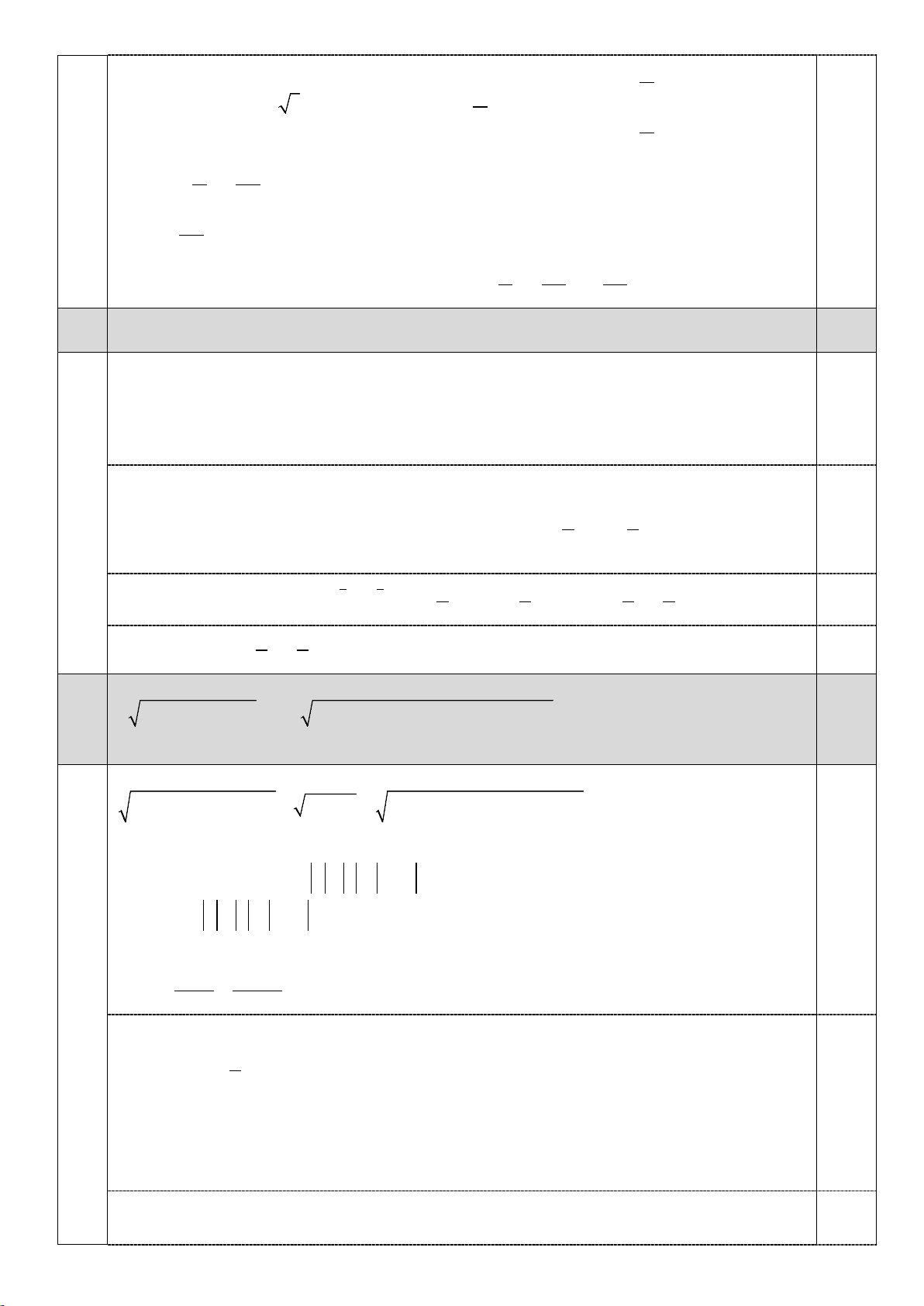
––––––––––––––––––––––– Câu 1 (2 điểm) x −
Tìm m để hàm số f ( x) 2 =
đồng biến trên khoảng (0;1). mx − 2 Câu 2 (2 điể 2x + 3
m) Cho hàm số y =
có đồ thị là đường cong (C ) và đường thẳng (d ) : y = 2 − x + m . x + 2
Tìm m để đường thẳng (d ) cắt đường cong (C ) tại hai điểm phân biệt ,
A B sao cho biểu thức 2017 2017 P = k + k
đạt giá trị nhỏ nhất với k = y ' x , k = y ' x . 1 ( A) 2 ( B ) 1 2
Câu 3 (2 điểm) Giải phương trình 3
2 3.sin x + (cos x +1)(6 cos x − 9) + 3sin 2 .
x sin x + 6 = 0 .
Câu 4 (2 điểm ) Cho a = log196 , b = log56 . Tính log 0.175 theo a, b.
Câu 5 (2 điểm) Giải hệ phương trình 2 2 2 2
 2x + 6xy +5y +5 = 2x + 6xy +5y +14x + 20y + 25  2 x+5 y 1 7
− = 6log (5x − 5y − 5) +1  7 Câu 6 (2 điểm) 3+ 2  1  1 Tính tích phân 2 I = 1− 14 − x − dx ∫   2 2  x  x 1
Câu 7 (1 điểm) Một hộp đựng 50 quả cầu được đánh số theo thứ tự từ 1 đến 50. Lấy ngẫu nhiên 3 quả cầu
từ hộp đó. Tính xác suất để tích 3 số ghi trên 3 quả cầu lấy được là một số chia hết cho 8.
Câu 8 (4 điểm) Cho hình lăng trụ ABC.A'B 'C ' có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông
góc hạ từ A' xuống ( ABC ) là trọng tâm của tam giác ABC . Mặt phẳng ( BCC ' B ') hợp với mặt phẳng đáy góc 45 . o
a) Tính thể tích khối lăng trụ ABC.A' B 'C '
b) Gọi I , J lần lượt là trung điểm của đoạn thẳng AB và CC ' . Tính khoảng cách giữa hai đường
thẳng AA' và IJ .
Câu 9 ( 2 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a . Điểm H nằm trên cạnh
AB thỏa mãn HB = 2HA , SH vuông góc với AB . Mặt phẳng (SAB) vuông góc với mặt phẳng chứa
đáy, SA hợp với đáy góc 60o .
a) Xác định tâm và bán kính của mặt cầu (S ) ngoại tiếp hình chóp S.ABCD .
b) Mặt phẳng ( P) đi qua trung điểm của SA và song song với mặt phẳng ( ABCD) , mặt phẳng ( P)
cắt mặt cầu (S ) theo giao tuyến là đường tròn (C ) . Tính bán kính đường tròn (C ) . Câu 10 (1 điểm)
Cho x, y, z là các số thực dương thỏa mãn + = ( 2 2 y z
x y + z ) .Tìm giá trị nhỏ nhất của biểu thức 1 1 1 4 P = + + + ( . x + )2 1 ( y + )2 1 (z + )2 1 (x + ) 1 ( y + ) 1 ( z + ) 1
––––––––– HẾT–––––––––
Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh…………………………………………..……Số báo danh……………………..
Giám thị 1 (Họ tên và chữ kí)………….…………………….……………………………………….
Giám thị 2 (Họ tên và chữ kí)………………….…………….………………………………………. HƯỚNG DẪN CHẤM Câu NỘI DUNG Điểm 1 x − 2
Tìm m để hàm số f ( x) 2 =
đồng biến trên khoảng (0;1). mx − 2 điểm
+ Điều kiện xác định của hàm số f (x) là mx ≠ 2. 0.5
+ Xét m = 0 không thỏa mãn bài toán. x − 2 0.5
+Xét m ≠ 0 hàm số trở thành 1 f (x) = . m 2 x − m 2 − + 2 1 2 − + 2m và f '(x) = . m = . 2 2 m  2   2  2  x − m   x −   m   m   2 0.5  ∉(0;1)
+ Để thỏa mãn bài toán ta có điều kiện m  2 − + 2m > 0.
+Rút ra được điều kiện là 1< m ≤ 2 . 0.5 2 2x + 3 2 Cho hàm số y =
có đồ thị là đường cong (C ) và đường thẳng (d ) : y = 2 − x + m . x + 2 điểm
Tìm m để đường thẳng (d ) cắt (C ) tại hai điểm phân biệt ,
A B sao cho biểu thức 2017 2017 P = k + k
đạt giá trị nhỏ nhất với k = y ' x , k = y ' x . 1 ( A) 2 ( B ) 1 2
+ Xét phương trình hoành độ giao điểm của đồ thị (C) và d: 0.25 2x + 3 x ≠ 2 − = 2
− x + m ⇔  x + 2 2
2x + (6 − m)x + 3 − 2m = 0 (1)
+Điều kiện để có hai giao điểm là phương trình ( )
1 có hai nghiệm phân biệt khác 2 − hay 0.25 ∆  ( ) > 0 2 1
m + 4m +12 > 0  ⇔  ⇔ m ∀ ∈  2.  ( 2 − )2 + (6 − m).( 2 − ) + 3− 2m ≠ 0  1 − ≠ 0 1 1 0.5
+ Giả sử các hoành độ giao điểm là x , x . Ta có k = , k = . 1 2 1 2 2 2 (x +1) (x +1) 1 2 1 1 Ta có k .k = = = 4 . 1 2
(x + 2)2 (x + 2)2 (x x + 2x + 2x + 4)2 1 2 1 2 1 2 2017 2017 2017 0.5
+ P = (k ) + (k ) ≥ 2. (k k ) 2018 = 2 . 1 2 1 2 1 1 0.5
+ Dấu bằng xảy ra khi 2 2 ⇔ =
⇔ (x + 2) = (x + 2) ⇒ m = 2. − 2 2 1 2 (x + 2) (x + 2) 1 2 3 Giải phương trình 3
2 3.sin x + (cos x +1)(6 cos x − 9) + 3sin 2 .
x sin x + 6 = 0 . 2 điểm
Phương trình tương đương 0.5 3 3 2
⇔ 2 3.sin x − 3(2cos x − 2cos x − cos x +1) = 0 2 ⇔ 2 3.sin .(
x 1− cos x)(1+ cos x) − 3(cos x −1)(2 cos x −1) = 0
⇔ 3(1− cos x) 2sin x(1+ cos x) + 3.cos 2x = 0 0.5   cos x = 1 ⇔ 
2sin x + sin 2x + 3.cos 2x = 0
Với cos x =1 ⇔ x = k.2π 0.5  π 0.5 2x + = −x + k.2π π  Với 3
2 sin x + sin 2x + 3.cos 2x = 0 ⇔ sin(2x + ) = sin(−x) ⇔  3 π
2x + = π + x + k.2π  3  π 2π x = − + k  9 3 ⇔  2π x = + k2π  3 Kết luận: π 2π 2π
phương trình có nghiệm x = k 2π ; x = − + k ; x = + k2π 9 3 3 4
Cho a = log196 , b = log 56 . Tính log 0.175 theo a, b. 2 điểm + Ta có 3 log 0.175 log 175.10 ( − = ) = log175 − 3 . 0.5
+ Giả sử tồn tại ba số , m ,
n p sao cho 175 10 .196 m .56 n p = 2 1 m 2 2 n 3 5 .7
(2.5) .(2 .7 ) .(2 .7) p ⇔ = 0 2 1 m+2n+3 p m 2 ⇔ 2 .5 .7 = 2 .5 .7 n+ p (*)
+ Vì 2, 5 và 7 là các số nguyên tố cùng nhau nên 0.5
m + 2n + 3p = 0  5 3 (*) ⇔ m = 2
⇔ m = 2, n = , p = − 4 2 2n + p =1  5 3 0.5 + Do đó − 5 3 5 3 2 4 2
log175 = log(10 .196 .56 ) = 2 + log196 − log 56 = 2 + a − b 4 2 4 2 + Vậy 5 3 0.5 log 0.175 = a − b −1 4 2 5 Giải hệ phương trình 2 2 2 2 2  điểm
2x + 6xy + 5 y + 5 = 2x + 6xy + 5 y +14x + 20 y + 25 ( )1  2 x+5 y 1 7
− = 6log (5x − 5y − 5) +1 2  7 ( )
Phương trình (1) tương đương 0.5
(x + y)2 +(x + y)2 + +
= (x + y + )2 + (x + y + )2 2 2 2 4 3 4 2 3 (*)    
Giả sử a = (x + y; x + 2y), b = (4;3) ⇒ a + b = (x + y + 4; x + 2y + 3) .    
Phương trình (*) có dạng a + b = a + b    
Ta luôn có a + b ≥ a + b . Do đó (*) xảy ra khi và chỉ khi  
a = ( x + y; x + 2 y), b = (4;3) cùng hướng.
Khi đó x + y x + 2y = ⇔ x = 5 − y 4 3
Thay vào phương trình (2) ta được x 1 7 − = 6 log 6x − 5 +1 0.5 7 ( ) Điều kiện: 5 x > 6 x 1
7 − = 6(t − ) + Đặt 1 1 t −1 = log
6x − 5 . Khi đó ta có hệ phương trình  7 ( ) t 1 7 − = 6x − 5
Trừ theo vế hai phương trình ta được x 1− t 1 7 6x 7 − + = + 6t (*)
Xét hàm số f (u) u 1 7 − =
+ 6u trên  . Ta dễ dàng thấy f (u) đồng biến trên  . 0.5 Khi đó (*) f ( x) f (t ) x t log (6x 5) x 1 − x 1 x 1 6x 5 7 7 − ⇔ = ⇔ = ⇔ − = − ⇔ − = ⇔ − 6x + 5 = 0 3 7 ( )
Xét hàm số g (x) x 1 7 − = − 6x + 5 trên  . 0.5 − Ta có g ( x) x 1 ' = 7 .ln 7 − 6 − g ( x) x 1 2 '' = 7 .ln 7 > 0 x ∀ ∈ 
Do g ''( x) > 0 x
∀ ∈  nên g '(x) là hàm số đồng biến trên  .
Do đó g '(x) = 0 có tối đa 1 nghiệm. Như thế phương trình g (x) = 0 có tối đa 2 nghiệm. Mặt khác g ( )
1 = g (2) = 0 , vì vậy phương trình (3) có đúng hai nghiệm x = 1; x = 2 .
Vậy hệ phương trình có hai nghiệm  1   2  1; −   và 2;−    5   5  6 3+ 2  1  1 2 Tính tích phân 2 I = 1− 14 − x − dx ∫   điểm 2 2  x  x 1 3 + 2 2  1   1  I = 16 − x + d x + ∫     0.5  x   x  1 Đặt 1  π π  π π 0.5 x +
= 4sin t với t ∈ − ; 
 . Đổi cận: x = 1⇒ t = , x = 3 + 2 ⇒ t = . x  2 2  6 3 π π 3 3 Ta có 2 I = 16 −16 sin t d ∫ (4sint) 2 = 16cos t dt ∫ 0.5 π π 6 6 π π 3 = ( π
8 + 8 cos 2t ) dt = (8t + 4sin 2t ) 3 4 = ∫ π . 0.5 π 3 6 6 7
Một hộp đựng 50 quả cầu được đánh số theo thứ tự từ 1 đến 50. Lấy ngẫu nhiên 3 quả cầu từ 1
hộp đó. Tính xác suất để tích 3 số ghi trên 3 quả cầu lấy được là một số chia hết cho 8. điểm Có 3
C cách lấy ra 3 quả cầu từ hộp đã cho. 50
Chia 50 quả cầu trong hộp thành 4 nhóm:
+ Nhóm I: gồm 25 quả cầu mang số lẻ 0.5
+ Nhóm II: gồm 13 quả cầu mang số chia hết cho 2 mà không chia hết cho 4.
+ Nhóm III: gồm 6 quả cầu mang số chia hết cho 4 mà không chia hết cho 8.
+ Nhóm IV: gồm 6 quả cầu mang số chia hết cho 8.
Để tích 3 số ghi trên 3 quả cầu lấy được là một số không chia hết cho 8 thì có 4 trường hợp sau xảy ra:
1) 1 quả thuộc nhóm I, 2 quả thuộc nhóm II: có 1 2
C .C cách lấy. 25 13
2) 2 quả thuộc nhóm I, 1 quả thuộc nhóm II: có 2 1 0.5
C .C cách lấy. 25 13
3) 2 quả thuộc nhóm I, 1 quả thuộc nhóm III: có 2 1
C .C cách lấy. 25 6
4) 3 quả thuộc nhóm I: có 3 C cách lấy. 25 1 2 2 1 2 1 3
Vậy xác suất cần tính là
C .C + C .C + C .C + C 193 25 13 25 13 25 6 25 1− = . 3 C 392 50 8
Cho hình lăng trụ ABC. ’ A ’
B C’ có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc 4 hạ từ ’
A xuống ( ABC ) là trọng tâm của tam giác ABC . Mặt phẳng ( BCC’ ’
B ) hợp với mặt điểm phẳng đáy góc 45 . o
a) Tính thể tích khối lăng trụ ABC. ’ A ’ B C’
b) Gọi I , J lần lượt là trung điểm của đoạn thẳng AB và CC’ . Tính khoảng cách giữa
hai đường thẳng A ’
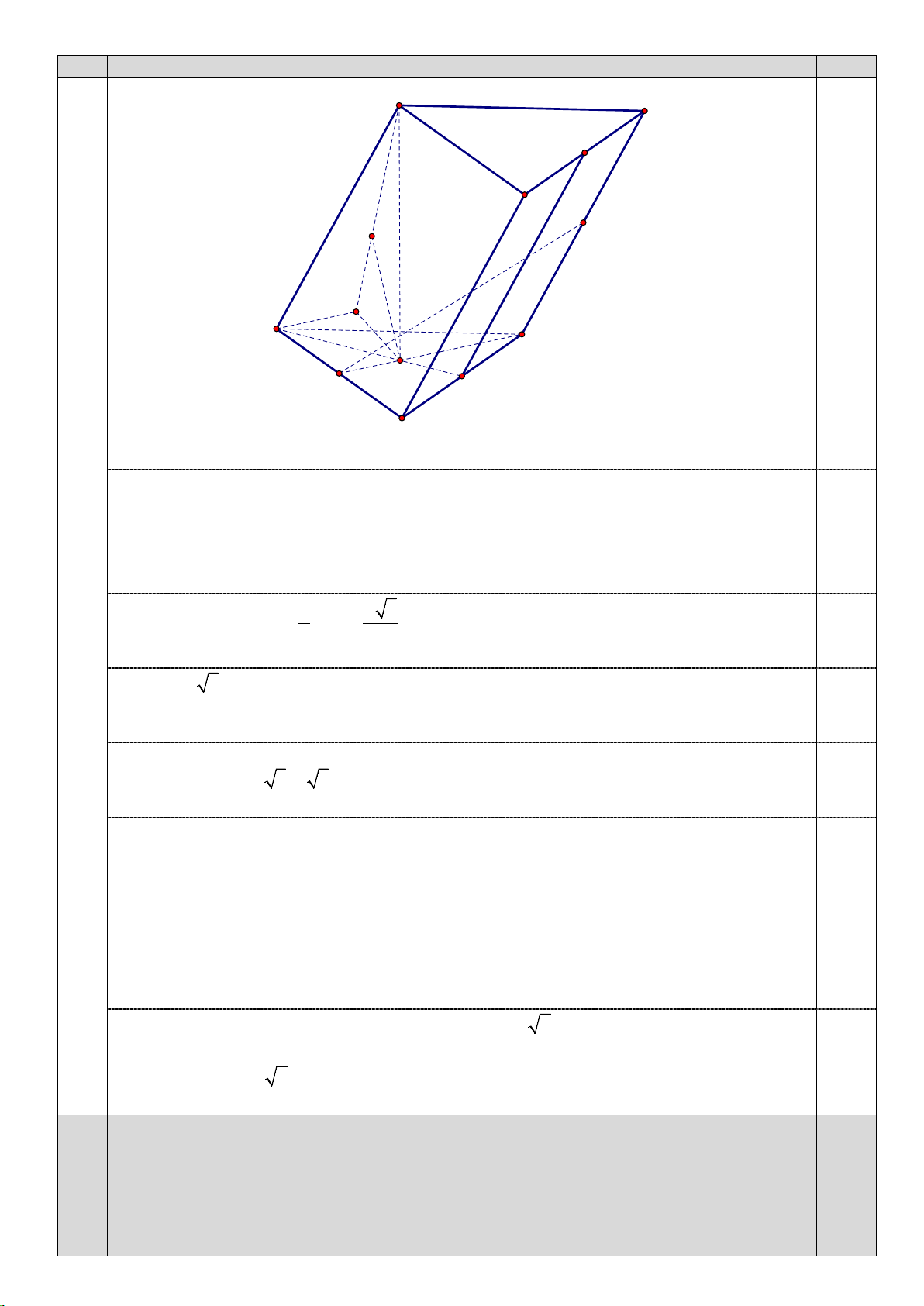
A và IJ . A' C' M' B' J K H A C G I M B
a) Gọi M, M’ lần lượt là trung điểm của BC, B’C’. 0,5
G là trọng tâm của tam giác ABC
Ta chứng minh được góc giũa hai mặt phẳng (BCC’ ’
B ) và ( ABC ) là góc giữa hai đường
thằng thẳng MM’ và AM hay là góc giữa A ’
A và AM bằng  ' 45o A AG = 0.5 Tính được 2 a 3
A 'G = AG = AM = 3 3 2 a 3 0.5 S =  (đvdt) ABC 4
Thể tích khối lăng trụ ABC.A’B’C’ là 2 3 a 3 a 3 a 0,5 V = S .A 'G = . =  (đvtt) ABC 4 3 4 b) 1 Kẻ Ax song song với CI
Kẻ GH vuông góc với Ax tại H
Kẻ GK vuông góc với A’H tại K Ta chứng minh được
( A' AH ) / /(C 'CI ) mà AA' ⊂ ( A' AH );IJ ⊂ (C 'CI )
Suy ra d ( AA', IJ ) = d (( A' AH ),(C 'CI )) = d (G,( A' AH )) = GK 1 Tính được a 1 1 1 a 7 GH = , = + ⇒ GK = 2 2 2 2 GK A 'G GH 7
Vậy d ( AA IJ ) a 7 ', = . 7 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a . Điểm H nằm trên cạnh
AB thỏa mãn HB = 2HA , SH vuông góc với AB . Mặt phẳng (SAB) vuông góc với mặt 2 điểm
phẳng chứa đáy, SA hợp với đáy góc 60o .
a) Xác định tâm và bán kính của mặt cầu (S ) ngoại tiếp hình chóp S.ABCD .
b) Mặt phẳng ( P) đi qua trung điểm của SA và song song với mặt phẳng ( ABCD) ,
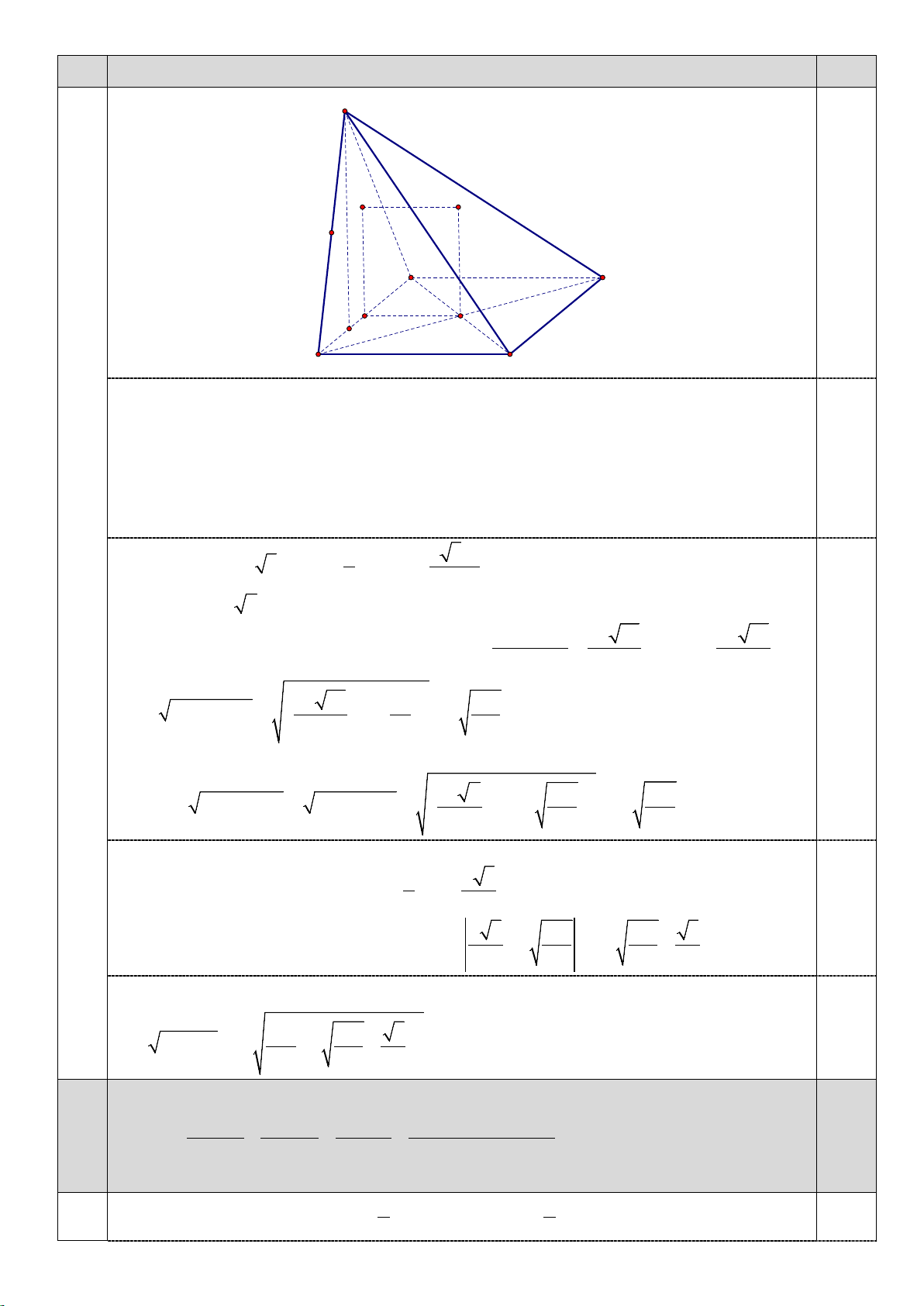
mặt phẳng ( P) cắt (S ) theo giao tuyến là đường tròn (C ) . Tính bán kính đường tròn (C ) . S K J M B C I O H A D a) 0.5
Gọi O là giao điểm của AC và BD
Gọi I là trung điểm của AB, K là tâm đường tròn ngoại tiếp tam giác SAB
Dựng (∆) đi qua O và vuông góc với mặt phẳng (ABCD)
Dựng (∆') đi qua K và vuông góc với (SAB)
(∆) cắt (∆') tại J. Suy ra J là tâm mặt cầu ngoại tiếp hình chóp S.ABCD 2 0.5 Tính được 1 3 3a
SH = a 3, S = A . B SH =  (đvdt) SAB 2 2
SA = 2a, SB = a 7
Bán kính đường tròn ngoại tiếp tam giác SAB . SA . SB AB 4a 21 4a 21 r = = ⇒ KA = 4S 3  3 ABC 2 2
 4a 21   3a  421 2 2 IK = AK − AI =   − = a     3    2  12
Bán kinh mặt cầu ngoại tiếp hình chóp S.ABCD là 2 2  3a 2   421  475 2 2 2 2 R = JA = AO + JO = AO + IK =   +  a      = a 2 12     12
b) Gọi M là trung điểm của SA 0.5
Khoảng cách từ M đến (ABCD) bằng 1 a 3 SH = 2 2  
Khoảng cách từ J đến mặt phẳng (P) bằng a 3 421 421 3 d = − a = a  −    2 12 12 2  
Bán kính đường tròn (C) là 0.5 2 475  421 3  2 2 r =
R − d = a −  −  1   12 12 2   10
Cho x, y, z là các số thực dương thỏa mãn + = ( 2 2 y z
x y + z ) .Tìm giá trị nhỏ nhất của biểu 1 điểm thức 1 1 1 4 P = + + + ( . x + )2 1 ( y + )2 1 (z + )2 1 (x + ) 1 ( y + ) 1 ( z + ) 1 Theo giả thiết 0.25
y + z = x ( y + z ) 1
≥ x( y + z)2 2 2 2 ⇒ y + z ≤ . 2 x Ta có: 2 1 1 2 8 8 2x + ≥ ≥ ≥ = ( . y + )2 1 (z + )2 1
( y + )1(z + )1 ( y + z + 2)2 2  2  (x + )2 1 + 2    x  2 1 4 4 x ( ≥ ≥ = . x + ) 1 ( y + ) 1 ( z + ) 1
(x + )1( y + z + 2)2 2 3 (   x + 1+ x) 2 ( )1 + 2    x  2 2 3 2 1 2x 4x
2x + 6x + x +1 0.5 Suy ra P ≥ + + = ( 1+ x)2 (1+ x)2 (1+ x)3 (1+ x)3 3 2 Xét hàm số + + + 91 f ( x) 2x 6x x 1 = (
với x > 0 tìm được giá trị nhỏ nhất của f ( x) là 0.25 1+ x)3 108 1 khi x = . 5
Vậy giá trị nhỏ nhất của 91 P là đạt được khi 1 x = , y = z = 5 . 108 5