TRƯỜNG THCS & THPT LONG THẠNH ĐỀ THI HỌC KỲ II – NĂM HỌC 2020 - 2021 TỔ TOÁN MÔN TOÁN 11
Thời gian làm bài : 90 Phút (không kể thời gian (Đề có 4 trang) giao đề) Ngày thi: 15/5/2021
Họ tên : ............................................................... Lớp : 11A... Mã đề 131
I. PHẦN TRẮC NGHIỆM (35 câu, 7.0 điểm; học sinh làm vào phiếu trả lời trắc nghiệm) 10n Câu 1: Tính lim 2n  3 10 A. 5 . B.  . C. 0. D.  . 3 Câu 2: Cho hàm số 7
y  x . Đẳng thức nào dưới đây đúng? A. 5 y  42x . B. 6 y  14x . C. 5 y  7x . D. 6 y  7x .
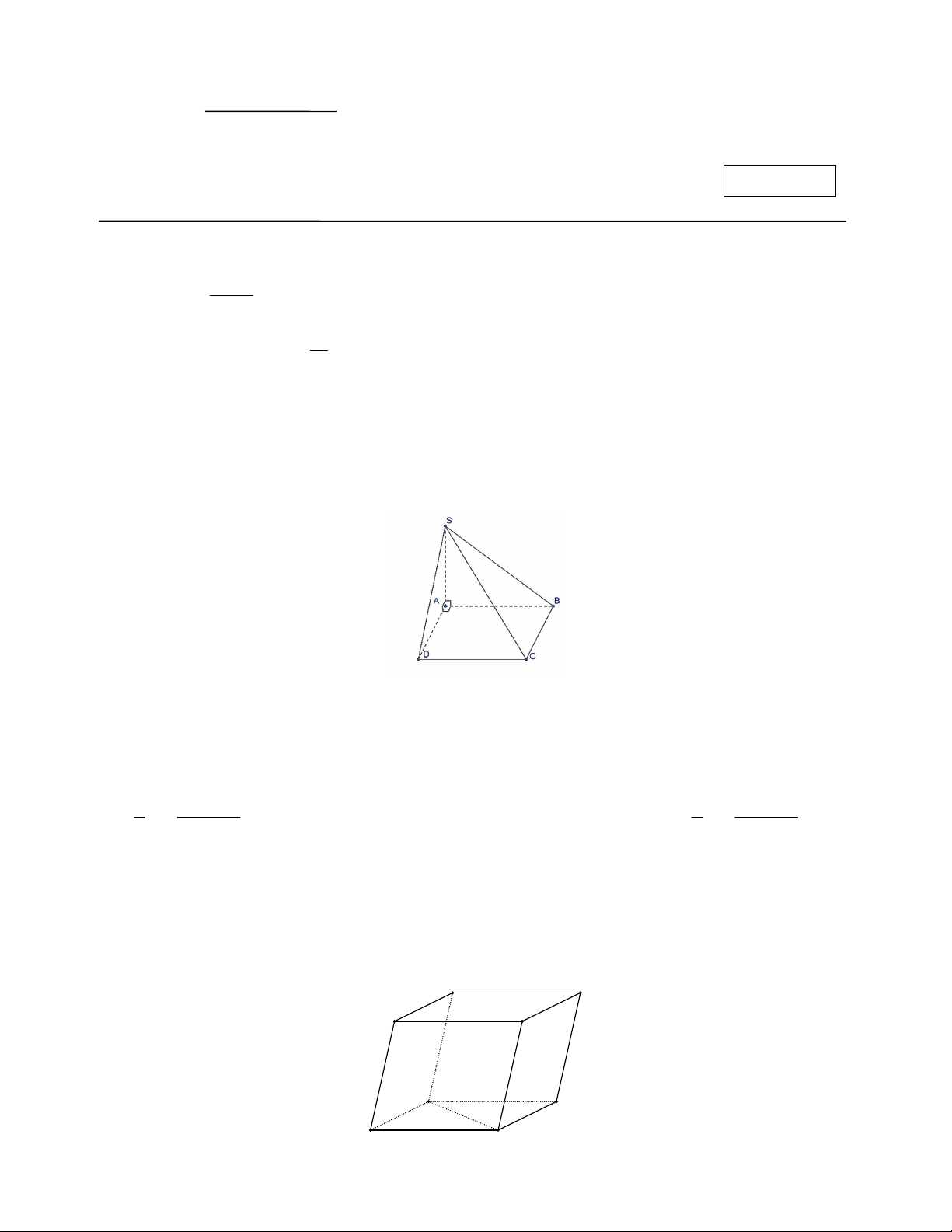
Câu 3: Cho hình chóp S.ABCD , có đáy ABCD là hình vuông, SA   ABCD . Khẳng định nào dưới đây là đúng?
A. SAB   ABCD . B. SAB  SAC . C. SAB  SCD . D. SAB  SBD .
Câu 4: Giả sử u  u  x , v  vx là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đẳng thức đúng là  u  u 'v  uv '  u   u 'v  uv ' A.    . B. (u ) v '  u 'v uv' . C. (u ) v '  u 'v uv' . D.  . 2    v  v  v  v
 
Câu 5: Trong không gian cho 3 điểm M , N, P phân biệt. Tính PM  MN .     A. PN . B. NM . C. MN . D. NP .
Câu 6: Trong hình hộp ABC . D  A  B C 
D có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào đúng? A' D' B' C' A D B C A. A'C  DD ' . B. A C  '  BB'. C. A C    AC . D. A'C '  BD . 1 – Mã đề 131
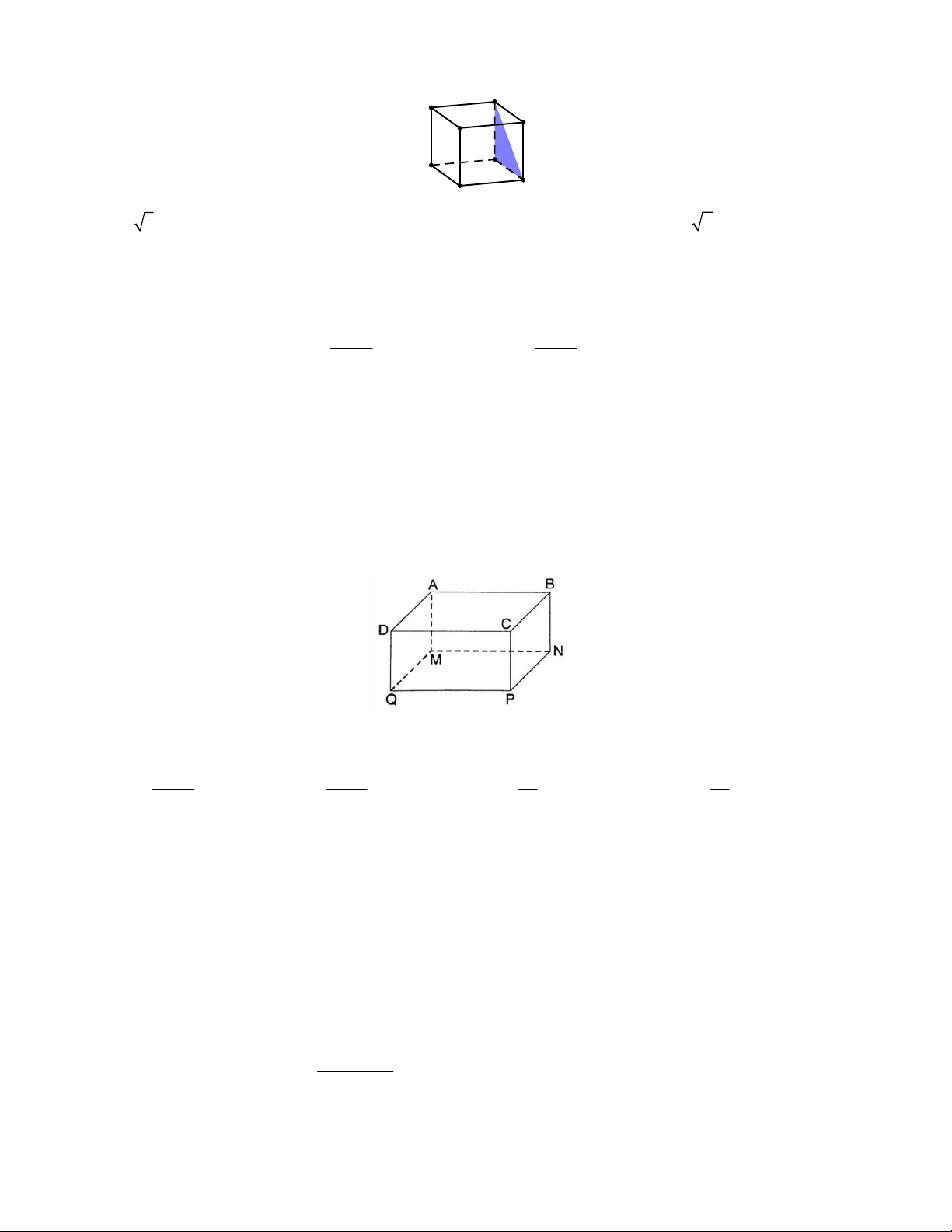
Câu 7: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng 7 cm. Tính khoảng cách từ điểm B đến mặt phẳng CD ’ D  . D' A' C' B' D A C B A. 7 3 cm. B. 7 cm. C. 14 cm. D. 7 2 cm. Câu 8: Tính 3
lim x ta được kết quả là x A. 3 . B.  . C. 0 . D.  .
Câu 9: Đạo hàm của hàm số y  cot x là 1 1 A. y  cos x . B. y  . C. y   . D. y  tan x. 2 sin x 2 sin x
Câu 10: Đạo hàm của hàm số y  sin x là A. y  cot x . B. y  sin x . C. y  tan x. D. y  cos x .
Câu 11: Trong quy tắc tính đạo hàm bằng định nghĩa tại điểm x của hàm số y  f (x) thì đại lượng 0 y bằng A. f (x  x
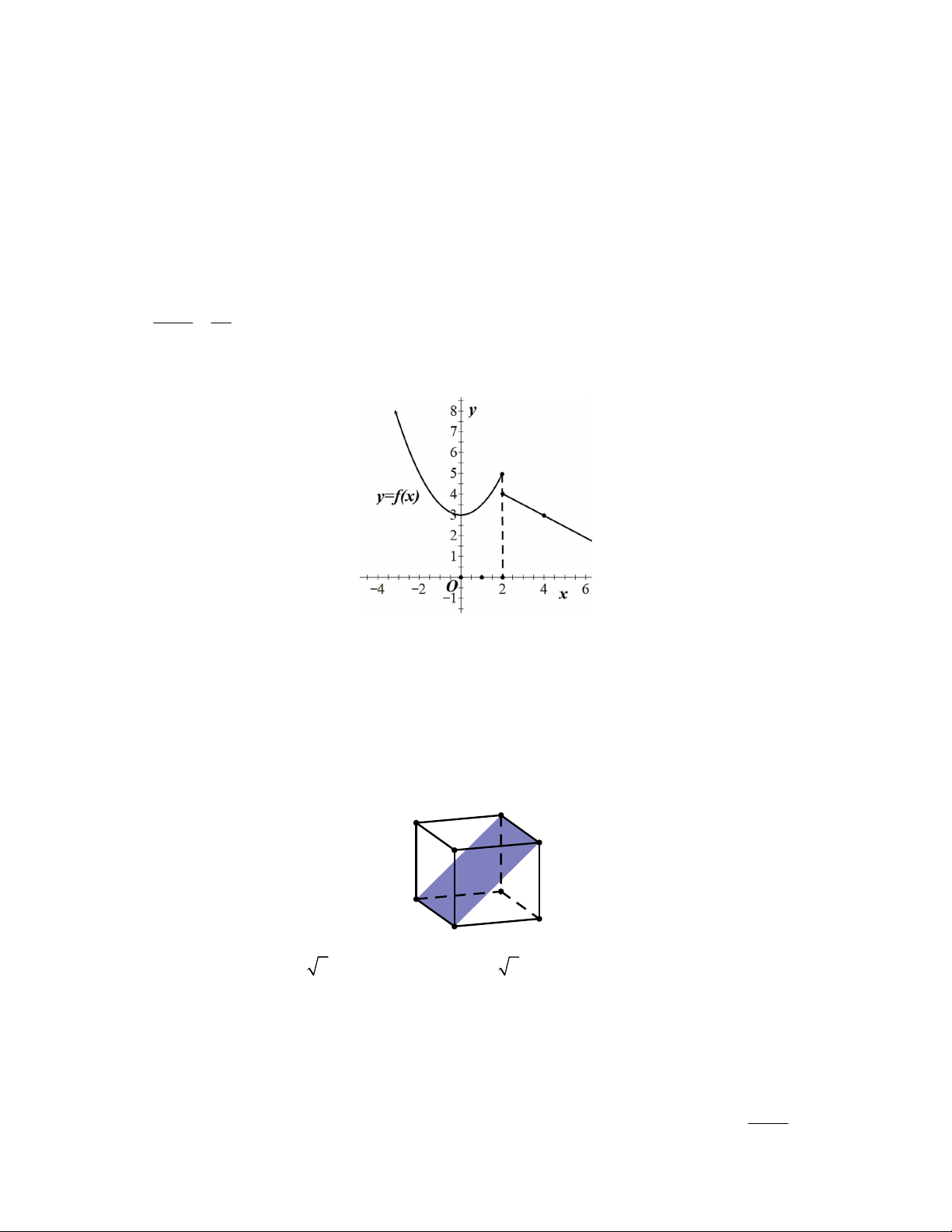
 )  f (x ) . B. f (x  x  )  f (x ). C. f (x  x  )  f (x ) . D. f (x  x  )  f (x ) . 0 0 0 0 0 0 0 0 Câu 12: Cho hình hộp ABC .
D MNPQ . Phép chiếu song song lên mặt phẳng MNPQ theo phương BM
biến điểm C thành điểm A. N . B. M . C. Q. D. P .
Câu 13: Hàm số nào liệt kê dưới đây liên tục trên  ? 1 1 4 3 A. y  . B. y  . C. y  . D. y  . 2 x  3 2 x  3 2 x 2 x
Câu 14: Tính đạo hàm của hàm số 2020 f (x)  x . A. 2021 f '(x)  2020x . B. 2020 f '(x)  2019x . C. f '(x)  2020x . D. 2019 f '(x)  2020x .
Câu 15: Tính vi phân d  2
x  7x  9 ta được kết quả là A. 2x  7dx . B.  x  7dx . C.  x  7 dx . D. 2x  7dx .
Câu 16: Cho đường thẳng  , mặt phẳng ( ) và 2 đường thẳng a,b phân biệt thuộc ( ) . Điều kiện để
đường thẳng  vuông góc với mặt phẳng ( ) là
A.   a,   b và a cắt b .
B.   a,   b và a //b .
C.   a,   b và // b .
D.   a,   b và  cắt b . 2   Câu 17: Tính giới hạn x 5x 6 I  lim . x2 x  2 A. I 1. B. I  5 . C. I  1  . D. I  0 .
Câu 18: Đạo hàm của hàm số y  c ( c là hằng số) là A. y'  y . B. y '  c . C. y' 1. D. y '  0 . 2 – Mã đề 131
Câu 19: Phương trình tiếp tuyến của đồ thị C  của hàm số y  f x tại điểm M x ; y là 0  0 0  A. y  f ' x x  x  y . B. y  y  f ' x x  x . 0  0  0  0   0  0 C. y  y  f ' x x  x . D. y  f ' x x  x  y . 0   0  0  0  0  0
Câu 20: Giả sử u  u x . Khi đó đẳng thức nào sau đây đúng? A.  n u  n 1  u  u  * . n    . B.  n u   n u  * . n    . C.  n u  n 1  n u   * . n   . D.  n u  n 1  n u  u  * . . n  .
Câu 21: Giả sử lim f x  L và lim g  x  M . Khi đó đẳng thức nào dưới đây là sai? x 0 x x 0 x A. lim  f
  x  g  x  L  M  . B. lim  f
  x g  x  L  M  . x  0 x x 0 x f  x L C. lim  M  . D. lim  f
  x  g  x  L  M  . xx g  x ,  0 0 M x 0 x
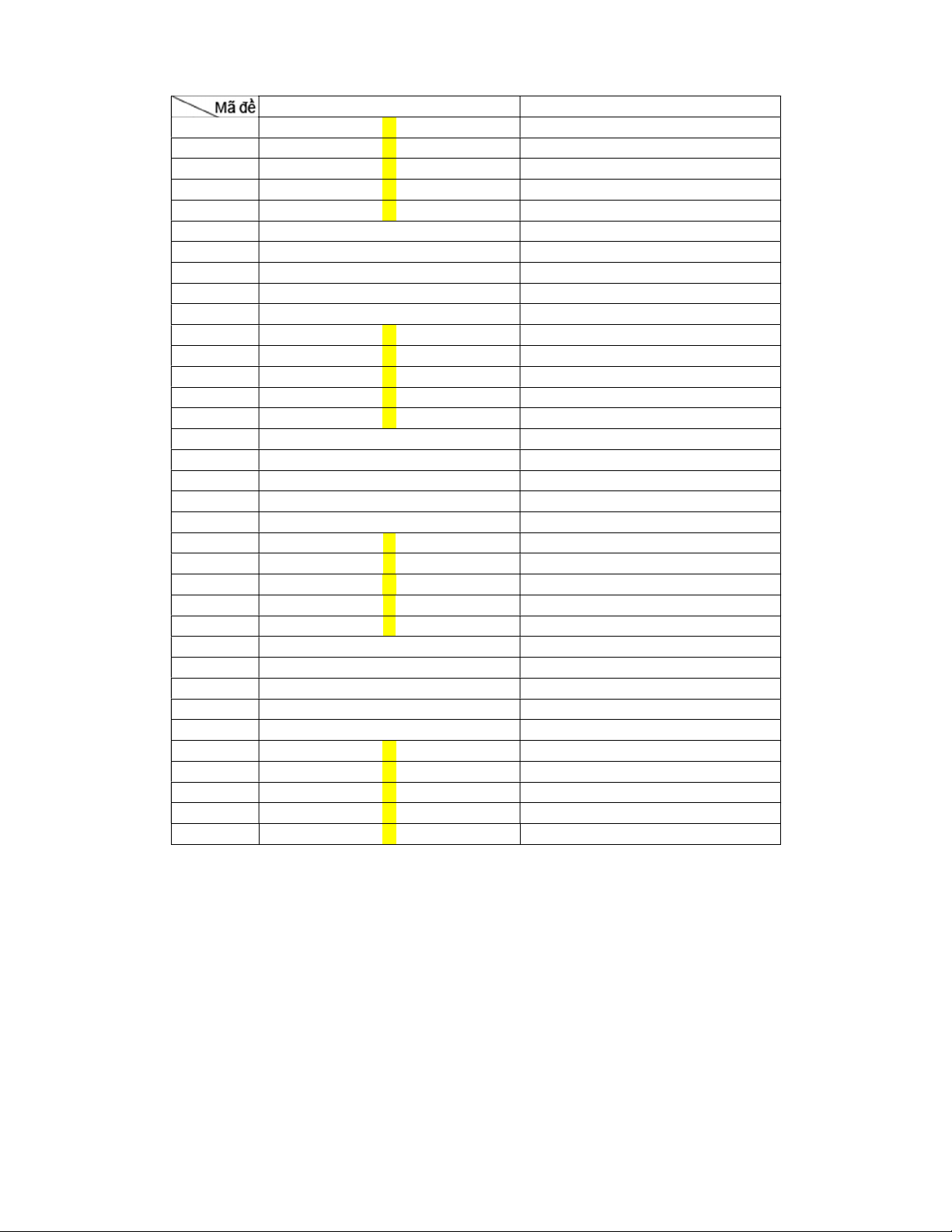
Câu 22: Cho hàm số y  f (x) có đồ thị trên  như hình vẽ bên. Hỏi hàm số bị gián đoạn tại điểm nào ? A. Tại điểm x  1
 . B. Tại điểm x  2 . C. Tại điểm x  2 . D. Tại điểm x  1. 0 0 0 0
Câu 23: Cho một vật chuyển động theo phương trình 3 2 2
S  t  mt 10t  m , trong đó t được tính bằng
giây, S được tính bằng mét và m là tham số thực. Biết tại thời điểm t  4s vận tốc của vật bị triệt tiêu.
Gọi a là gia tốc của vật tại thời điểm t  5s . Chọn khẳng định đúng trong các khẳng định sau A. a 30;40 . B. a 20;30 . C. a 0;10 . D. a 10;20 .
Câu 24: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng 8 cm. Tính khoảng cách giữa đường
thẳng A’B’ đến mặt phẳng  ABC ' D' . D' A' C' B' D A C B A. 4 cm. B. 4 2 cm. C. 8 2 cm. D. 8 cm.
Câu 25: Đạo hàm của hàm số y  sin3x là A. y  sin3x . B. y  3cos3x . C. y  cos3x . D. y  3sin3x .
Câu 26: Một vật chuyển động theo phương trình 2
S  t  9t 13 , trong đó t được tính bằng giây và S
được tính bằng mét. Tính vận tốc tức thời của chuyển động khi t  8s . A. 23 (m / s) . B. 25 (m / s) . C. 24 (m / s) . D. 149 (m / s) . 3x 1
Câu 27: Phương trình tiếp tuyến  tại điểm M( 2
 ;5) thuộc đồ thị C của hàm số y  là x 1 A.  : y  x  6 . B.  : y  x. C. : y  2x  9. D. : y  5x 3. 3 – Mã đề 131
Câu 28: Biết f (x), g(x) là các hàm số liên tục trên  . Tính đạo hàm của hàm số 1 2 4 h(x) f (     x )  g  a 
(với x  0, a là hằng số) . 3   x  3 1 3 1 A. h '(x) 2xf ' 2      x   g ' . B. h '(x) 2xf ' 2       x  3  g '  4a . 4  3    x  x  4 3 x  x  3 1 1 1 C. h '(x) 2xf ' 2       x  g ' . D. h '(x) 2xf ' 2       x  g ' . 4  3    x  x  6 3 x  x  2 2 2 2 1  2  3  ... n p Câu 29: Biết rằng lim
 (với q  0 và p là số hữu tỉ tối giản). Tính . p q . 3 7  2n q q A. 1  0. B. 6  . C. 3  . D. 1  00 . 4x  50
Câu 30: Cho hàm số f (x)  . Tính (2022) f
4 ta được kết quả là 2 x  25 4.2022! 2022 3.2022! 3.2022! A.  22  7  .2022! . B.  . C. 7  .2022! . D. 7  .2022! . 2023 9    3  2023 9 2023 9 3 x 11  x  59 m m Câu 31: Giới hạn lim 
( là phân số tối giản). Tính 2m  n bằng x 5  x  5 n n A. 59 . B. 57 . C. 60 . D. 58 .
Câu 32: Đạo hàm của hàm số 3 2
y  x  5x  6x 12 là A. 2 y '  x  2x  4 . B. 2 y '  7x  2x  4 . C. 2 y '  3x 10x  6 . D. 3 2 y '  x  3x  6x .
Câu 33: Đạo hàm cấp hai của hàm số y  cos5x là A. y  sin5x . B. y  5  sin5x. C. y  2  5cos5x . D. y 10cos5x . Câu 34: Tính  5 2 lim 4n  2n  7n  A.  . B. 4 . C. 7 . D.  .
Câu 35: Tính đạo hàm của hàm số 2 y  1 3x . 6  x 3  x 1 3  x A. y '  . B. y '  . C. y '  . D. y '  . 2 1 3x 2 2 1 3x 2 2 1 3x 2 1 3x
II. PHẦN TỰ LUẬN (3.0 điểm, học sinh trình bày bài giải vào giấy)
Câu 36. (1,0 điểm) Tính đạo hàm của các hàm số sau: a) 3 2 y  5x  2x  3x 1. x b) y  sin 2x  cos . 3 2x 1
Câu 37. (0,5 điểm) Viết phương trình tiếp tuyến  với đồ thị H  của hàm số y  tại x  2  . x 1 0
Câu 38. (1,5 điểm) Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a . Biết SB vuông góc với mặt
đáy và P là trung điểm của cạnh AC .
a) Chứng minh rằng AC  (SBP)
b) Gọi G là trọng tâm của tam giác ABC . Tính khoảng cách từ điểm G đến mặt phẳng (SAC)
biết góc tạo bởi (SAC) và mặt phẳng (ABC) bằng 0 60 . ---- HẾT ----
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm. 4 – Mã đề 131
ĐÁP ÁN TOÁN 11 – HỌC KỲ II Phần trắc nghiệm 131 1 A 2 A 3 A 4 C 5 A 6 D 7 B 8 B 9 C 10 D 11 D 12 C 13 A 14 D 15 A 16 A 17 C 18 D 19 A 20 D 21 B 22 B 23 D 24 B 25 B 26 B 27 C 28 C 29 B 30 D 31 D 32 C 33 C 34 D 35 D 5 – Mã đề 131
ĐÁP ÁN TOÁN 11 HỌC KỲ II – PHẦN TỰ LUẬN Đề 131
Câu 35. Tính đạo hàm của các hàm số sau: a) 3 2 y  5x  2x  3x 1. x b) y  sin 2x  cos . 3 Câu Nội dung Điểm a) 3 2 y  5x  2x  3x 1. y   3 x    2 5 2x   3x  1 0.25 2 y  15x  4x  3 0.25 x 1 b) y  sin 2x  cos 3      x  y sin 2x  cos   0.25  3  1  x 
y  2cos 2x  sin   0.25 3  3  2x 1
Câu 36. Viết phương trình tiếp tuyến  với đồ thị H  của hàm số y  tại x  2  . x 1 0 Câu Nội dung Điểm 2x 1
Viết phương trình tiếp tuyến  với đồ thị  H  của hàm số y  tại x  2  . x 1 0 x  Ta có x  2  thay vào H  2 1 : y  ta được y  5 . 0 x 1 0 3 y   x  2 1 0.25 2
Suy ra hệ số góc k  y 2    3
Phương trình tiếp tuyến  với  H  tại x  2  0 :  : y  y 2  x  2  5 0.25   : y  3x 11
Câu 37: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a . Biết SB vuông góc với mặt đáy và P
là trung điểm của cạnh AC .
a) Chứng minh rằng AC  (SBP)
b) Gọi G là trọng tâm của tam giác ABC . Tính khoảng cách từ điểm G đến mặt phẳng (SAC) biết góc
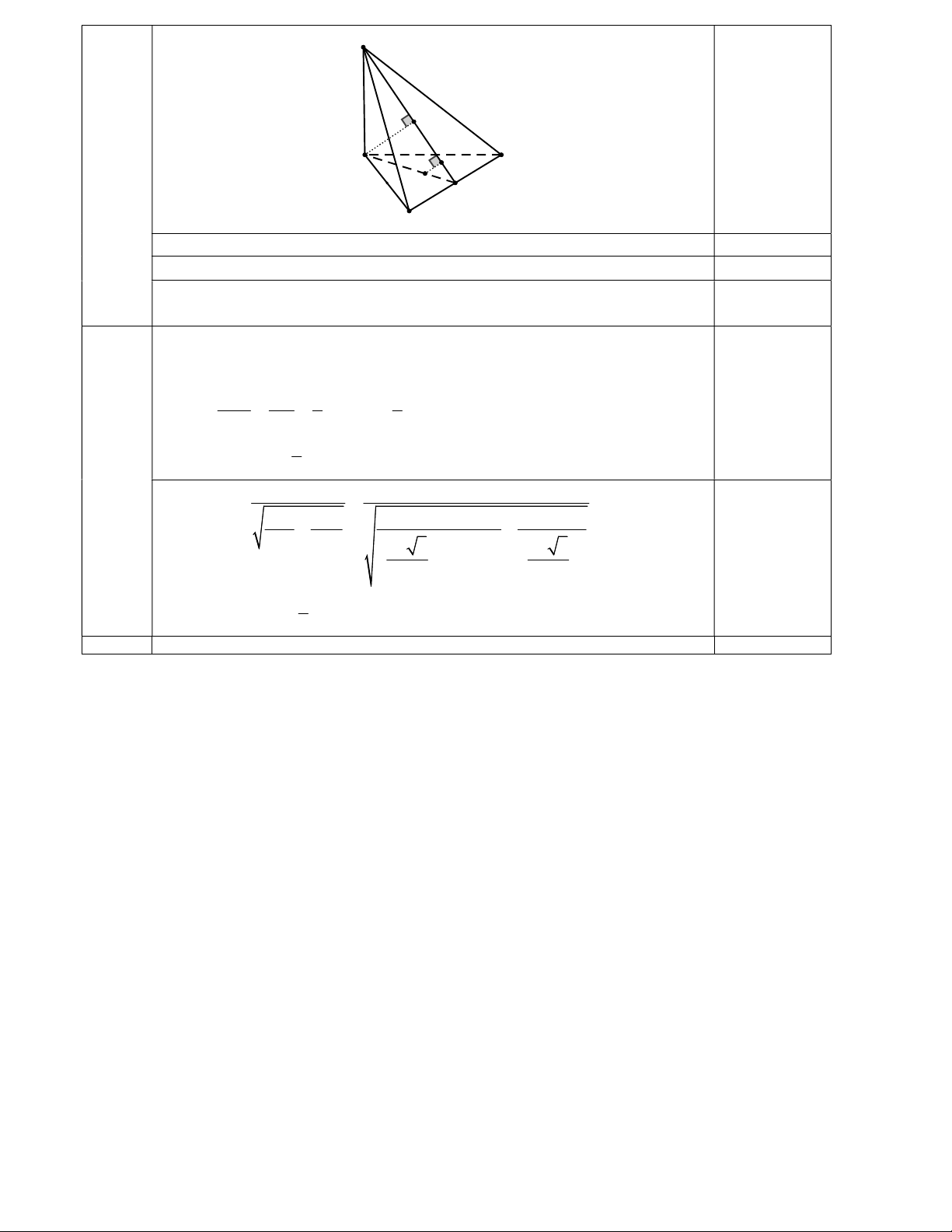
tạo bởi (SAC) và mặt phẳng (ABC) bằng 0 60 . Câu 3 Nội dung Thang điểm 6 – Mã đề 131 S H' 0.25 B H C 3a G P A
Ta có AC  BP (BP là đường trung tuyến A  BC đều) (1) 0.25
AC  SB (vì SB  ( ABC) ) (2) 0.25 SB  BP  B (3) 0.25
Từ (1), (2) và (3) suy ra AC  (SBP) Ta có BP  AC, SP  AC    SAC ABC   0 ( ), ( ) SPB  60 GH GP 1 1 Ta lại có    GH  BH ' BH ' BP 3 3  d G SAC  1 ,( )  d B,(SAC) 3 0.25 b 1 1 Ta có BH '    3a 1 1 1 1   2 2 2 2 SB BP  4a 3    0 4a 3  .tan 60    2 2     Vậy d G SAC  1 ,( )  .3a  a 3 0.25
Lưu ý: Nếu học sinh làm theo cách khác mà vẫn đúng thì giám khảo cho điểm tương ứng. 7 – Mã đề 131