SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II BẮC NINH NĂM HỌC: 2020 - 2021 Môn: Toán - Lớp 11 (Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Chọn phương án trả lời đúng cho các câu hỏi sau:
Câu 1. Nếu lim f x  5 thì lim 3x  4 f x   bằng bao nhiêu? x 0  x0 A. 17 . B. 1. C. 1. D. 2  0 . 3  x  4
Câu 2. Tính đạo hàm của hàm số sau y  . x  2   A. 2 11 5 10 y '  . B. y '  . C. y '  . D. y '  . 2 (x  2) 2 (x  2) 2 (x  2) 2 (x  2) Câu 3. Cho hàm số 2
f (x)  2x  4x  5 . Khẳng định nào dưới đây đúng? A. lim f (x)   . B. lim f (x)   . x x C. lim f (x)  2. D. lim f (x)  2  . x x 2  x 1  khi x  Câu 4. Tìm 1
m để hàm số f x   x 1
liên tục tại điểm x  1. 0 m  2 khi x  1  A. m  3 . B. m  0 . C. m  4 . D. m  1.
Câu 5. Hệ số góc của tiếp tuyến với đồ thị hàm số 3 2
y  x  4x 1 tại điểm có hoành độ bằng 1 là A. 5  . B. 5. C. 4. D. 4  .
Câu 6. Một chất điểm chuyển động thẳng xác định bởi công thức vt 2
 8t  3t , t tính bằng
giây, vt tính bằngm / s . Tính gia tốc của chất điểm khi vận tốc đạt 11 m / s . A. 20 . B.14 . C. 2 . D. 11.
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA  SC, SB  S .
D Khẳng định nào sau đây đúng? A. CD  AD . B. CD  (SBD). C. AB  (SAC) . D. SO  (ABC ) D Câu 8. Hàm số 2
y  cos 3x có đạo hàm là A. y '  6sin 6 . x B. y '  2cos3 . x C. y '  3  sin6 . x D. y '  3  sin3 . x
Câu 9. Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a . Gọi M là trung
điểm SA . Mặt phẳng MBD vuông góc với mặt phẳng nào dưới đây? A. SBC . B. SAC . C. SBD. D.  ABCD . 1 1
Câu 10. Cho hàm số f  x 3  x  m 2 2 x  2m  
3 x  2020 , m là tham số. Biết rằng tồn 3
tại giá trị m sao cho f x  0,x   . Khi đó m thuộc khoảng nào sau đây? 0 0 A. 0;2. B.  3  ;  1 . C. 3;6 . D.  4  ; 2 .
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA  (ABCD)
Khoảng cách từ điểm D đến mặt phẳng (SAC) bằng 2a 2 a 2 A. a 2 . B. a . C. . D. . 3 2 2  3      a Câu 12. Cho x x 2 3x 5 a lim   
( là phân số tối giản; , a b là số nguyên). Tính 2 x 1   x  3x  2  b   b tổng 2 2 P  a b . A. P  5. B. P  3. C. P  2 . D. P  2  . II. TỰ LUẬN (7,0 điểm) Câu 13. (3,0 điểm)
1) Tính các giới hạn sau: 2 x  7x 12 a) lim . b)    .   2 2 lim x x x 1 x  x 3  x  3
2) Tính đạo hàm của các hàm số sau: a) 4
y  x  2 x với x  0 . b) y  2cos x  3x .
Câu 14. (1,0 điểm) Cho hàm số 3
y  x  3x 1 có đồ thị là C. Viết phương trình tiếp tuyến
của C tại điểm có tung độ bằng 3 .
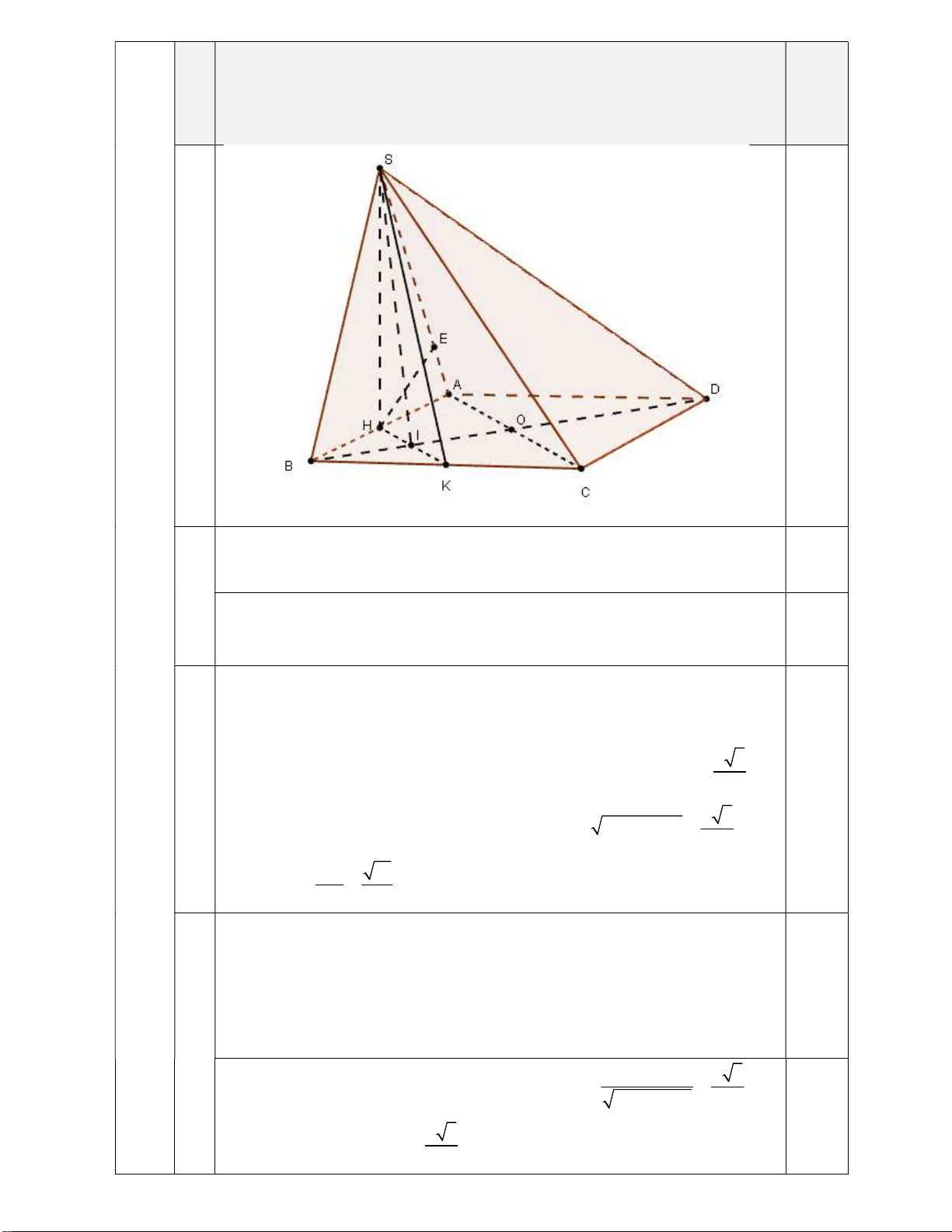
Câu 15. (2,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a .
Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
H , K lần lượt là trung điểm của AB, BC .
a) Chứng minh rằng SH   ABCD và SAD  SAB .
b) Gọi  là góc giữa đường thẳng SC và mặt phẳng  ABCD . Tính tan .
c) Tính khoảng cách từ K đến SAD.
Câu 16. (0,5 điểm) Cho hàm số 3 2
f (x)  ax  bx  cx  d a  0 có đồ thị là C. Biết C cắt
trục hoành tại 3 điểm phân biệt có hoành độ x , x , x . Tính giá trị biểu thức 1 2 3 1 1 1 D    . f ' x f ' x f ' x 1   2   3 ===== HẾT ===== 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
ĐỀ KIỂM TRA CUỐI HỌC KỲ II NĂM HỌC: 2020 - 2021 Môn: Toán - Lớp 11
(Hướng dẫn chấm có 03 trang)
I. TRẮC NGHIỆM (3,0 điểm) Câu 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. Đáp D A B B A B D C B A A A án II. TỰ LUẬN (7,0 điểm) Câu Ý Nội dung Điểm
1 1) Tính các giới hạn sau: 1,5 điểm 2 x  7x 12 x 3x 4 a) lim  lim  lim x  4  1  0,75 x 3  x 3  x3 x  3 x  3 1 1 x 1 1 x b) lim x  x  x     0,75 x  2 2 1 lim lim x 2 2 x  x  x 1 x 1 1 2 13 1  1 2 x x 1,5 2
2) Tính đạo hàm của các hàm số sau: điểm 1 a) 4 3
y  x  2 x  y '  4x  0,75 x
b) y  2 cos x  3x  y '  2sin x  3 . 0,75 Cho hàm số 3
y  x  3x 1 có đồ thị là C. Viết phương trình tiếp tuyến 1,0
của C tại điểm có tung độ bằng 3 điểm Ta có: 2 y  3x  3 . 0,25 14
Gọi M  x ; y là tiếp điểm 0 0  0,25 Với 3
y  3  x  3x  2  0  x  2, x  1 0 0 0 0 0
 x  1 y (1)  0 . Phương trình tiếp tuyến: y  3 0 0,5
 x  2  y (2)  9 . Phương trình tiếp tuyến: y  9(x  2)  3  9x 15. 0
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a .
Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với 2,5 15
đáy. Gọi H , K lần lượt là trung điểm của AB, BC . điểm
a) Chứng minh rằng SH   ABCD và SAD  SAB . 3
b) Gọi  là góc giữa đường thẳng SC và mặt phẳng  ABCD . Tính tan .
c) Tính khoảng cách từ K đến SAD. Theo Vì S
 AB là tam giác đều và H là trung điểm của AB  SH  AB 0,5
Vì SAB   ABCD theo giao tuyến AB nên SH   ABCD.
a) Ta có SH ABCD SH  AD. 0,5
Mà AB  AD , suy ra AD  SAB  SAD  SAB
Có SH   ABCD nên HC là hình chiếu của SC trên  ABCD . 0,5 Do đó SC, ABCD   SC,HC    SCH   . a 3
Xét  SAB là tam giác đều cạnh a và SH là đường cao nên SH  . b) 2 Tứ giác a 5
ABCD là hình vuông cạnh a nên 2 2 HC  BC  BH  0,25 2 Vậy SH 15 tan   . 0,25 HC 5
Vì BC / / AD  BC / / SAD  d K,SAD  d B,SAD  2d H,SAD
Trong mp SAB kẻ HE  SAE  SA 0,25
Có SAD  SAB  HE  SAD c)
Do đó d H,SAD  HE  d K,SAD  2HE .
Xét tam giác SHA có HE là đường cao nên SH.HA a 3 HE   2 2 SH  HA 4 0,25 Vậy d K SAD a 3 ,  2HE  . 2 4 Cho hàm số 3 2
f (x)  ax  bx  cx  d a  0 có đồ thị là C. Biết C cắt
trục hoành tại 3 điểm phân biệt có hoành độ x , x , x . Tính giá trị biểu 0,5 16 1 2 3 1 1 1 Điểm thức D    . f ' x f ' x f ' x 1   2   3 
Vì C cắt trục hoành tại 3 điểm phân biệt có hoành độ x , x , x . 1 2 3
 f (x)  ax  x x  x x  x . 1   2   3 
Suy ra f 'x  a x  x x  x  a x  x x  x  a x  x x  x . 2   3   1   3   1   2  f ' x  a x  x x  x 1   1 2  1 3 0,25
Do đó f 'x  a x  x x  x 2   2 1 2 3 f ' x  a x  x x  x 3   3 1 3 2 Vậy 1 1 1 D    f ' x f ' x f ' x 1   2   3  1 1 1 0,25     a  0 x  x x  x a x  x x  x a x  x x  x 1 2   1 3   2 1 2 3  3 1 3 2  5