Đề thi XS&TK 21 07 23
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút s Đề : 101 
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ……………… …
Số BD …………
Câu 1.(2 điểm): Cho 3 biến cố A, B, C có quan hệ độc lập. Biết P(A) = 0,9; P(B) = 0,8 và P(C) = 0,72. Đặt T = A + B + C. a) Tính xác suất P(T)? b) Tính P[(A + C)/T]?
Câu 2.(2 điểm): nhiên X:
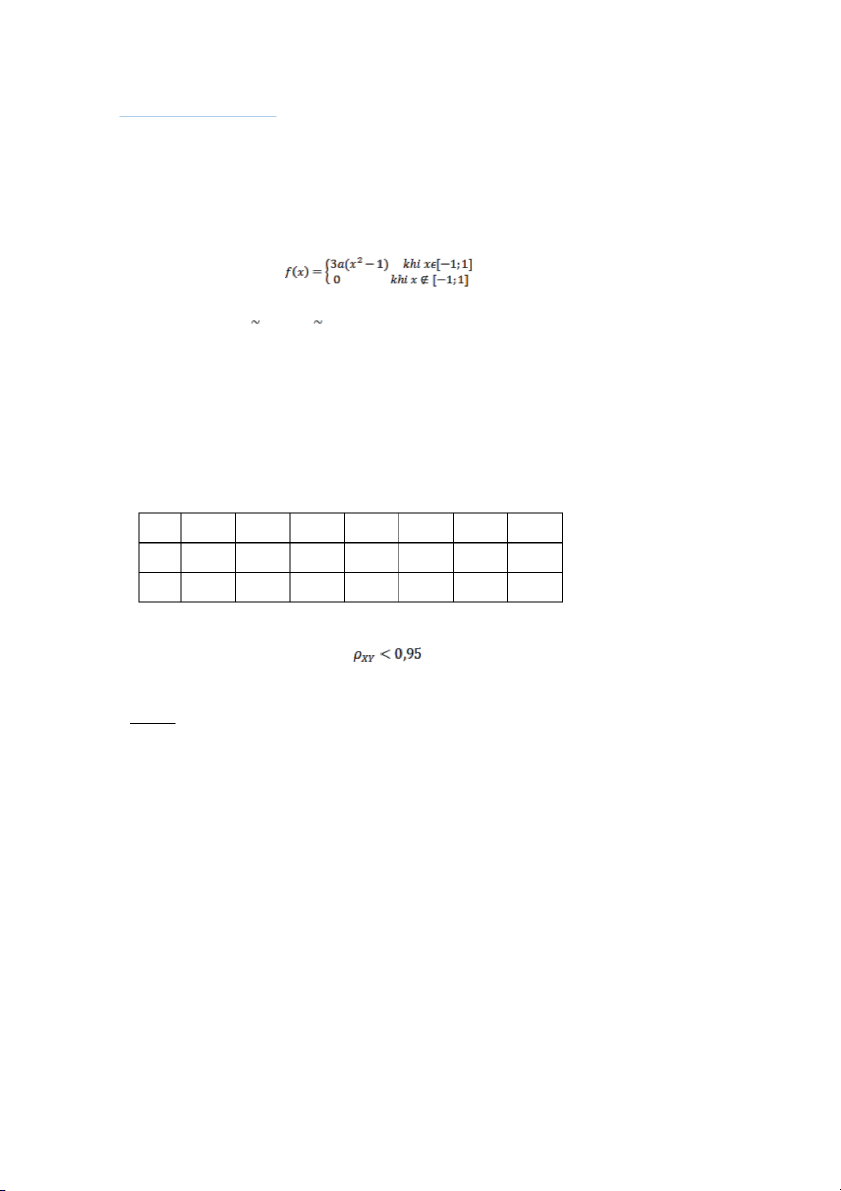
Cho hàm mật độ của biến ngẫu
a)Tìm a để f(x) là hàm mật độ.
b)Tính E(2022 2021X) và tìm ModX. –
Câu 3.( 1 điểm): Cho X N(5;4); Y H(25;10;15/25) và đặt T = 2X + 5Y – 7.medX.
a)Hãy tính giá trị của E(T)?
b)Xác định tập giá trị của đại lượng ngẫu nhiên Y?
Câu 4.( 3 điểm): Điều tra về mức chi tiêu của sinh viên tại Hà Nội ta có số liệu sau: cỡ mẫu 100 sinh
viên, mức chi tiêu trung bình 3,45 triệu/tháng, độ lệch chuẩn s’ = 0,92. Trong đó có 18 sinh viên có mức
chi tiêu tiết kiệm dưới 2 triệu/tháng.
1/. Hãy ước lượng mức chi tiêu trung bình của sinh viên tại Hà Nội với độ tin cậy 96%.
2/. Nếu dùng mẫu trên để ước lượng mức chi tiêu trung bình của sinh viên tại Hà Nội với sai số 0,15 triệu
thì độ tin cậy là bao nhiêu?
3/. Hãy ước lượng tỷ lệ sinh viên có mức chi tiêu tiết kiệm tại Hà Nội với độ tin cậy 92%. Câu 5 m): .(2 điể
Theo dõi trọng lượng y(kg) và s tháng tu ố i x(tháng) ổ của m t gi ộ ng l ố ợn trong một
trang trại chăn nuôi ta có bảng s ố liệu sau: xi 2,3 3,3 4,3 5,3 6,3 7,3 8,3 yi 32 40 50 62 73 86 97 ni 2 4 5 6 7 5 1 a) Lập phương trình i
hồ quy tuyến tính thực nghiệm, qua đó cho t biế nếu s ố tháng tu i ổ là 10 tháng thì tr ng c ọng lượ a l
ủ ợn ước tính qua hàm h i quy là bao nhiêu? ồ b) Với m cho r ức ý nghĩa 5%, có thể ằng không?
---------------------------------------------------------- ------------------------------ Hết -- -------------------- -
Ghi chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYT KHOA KHOA HC NG DN G
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút s Đề : 102 
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ……………… …
Số BD …………
Câu 1.(2 điểm): Cho 3 biến cố A, B, C có quan hệ độc lập. Biết P(A) = 0,9; P(B) = 0,8 và P(C) = 0,72. Đặt T = A + B + C. a) Tính xác suất P(T)?
b) Trong các giá trị P[(A + C)/T], P[(B + C)/T], P[(A + B)/T], tìm giá trị có xác suất nh nh ỏ ất?
Câu 2.(2 điểm):
Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm a để f(x) là hàm mật độ. b)Tính DX và tìm ModX.
Câu 3.( 1 điểm): Cho X N(5;9); Y B(10; 0,2) và đặt T = 2X + 5Y – 7.ModX.ModY.
a)Hãy tính giá trị của E(T)? b)Tính E(X2)?
Câu 4.( 3 điểm): Thời gian (giờ) để m t lo ộ ại sơn khô khi sơn ng l tườ à m t ch ộ  s quan tr ố ng ọ khi sản xuất
của công ty sơn Dulux. Để đánh giá m t
ộ mẫu sơn mới sản xuất, hãng tiến hành lấy mẫu với số liệu: cỡ
mẫu=36; trung bình mẫu là 1,538 giờ; độ lệch hiệu chnh là 0,129.
1. Kỹ sư ph trách nghiên c u
ứ mẫu sơn mới này cho rằng thời gian khô là khoảng 1,5 ). (giờ Hãy kết
luận với mức ý nghĩa 5%.
2. Hãy ước lượng thời gian sơn khô trung bình với độ tin cậy 97% .
3. Khi ước lượng thời gian khô trung bình với yêu u c
độ chính xác là 0,04 thì độ tin cậy bằng bao nhiêu?
Câu 5.(2 điểm): Để nghiên cứu về mối liên hệ giữa tuổi nghề X và năng suất lao động Y ở một phân
xưởng ta có mẫu số liệu như sau: xi (năm) 1,3 2,3 3,3 4,3 5,3 6,3 7,3 yi (kg/giờ) 5 6,5 7,5 9,5 11 13 14 ni ( ) số công nhân 2 4 6 8 7 5 3 a) Lập phương trình i
hồ quy tuyến tính thực nghiệm, qua đó cho t biế nếu tu i
ổ nghề là 6,5 năm
thì năng suất lao động ước tính qua hàm hồi quy là bao nhiêu?
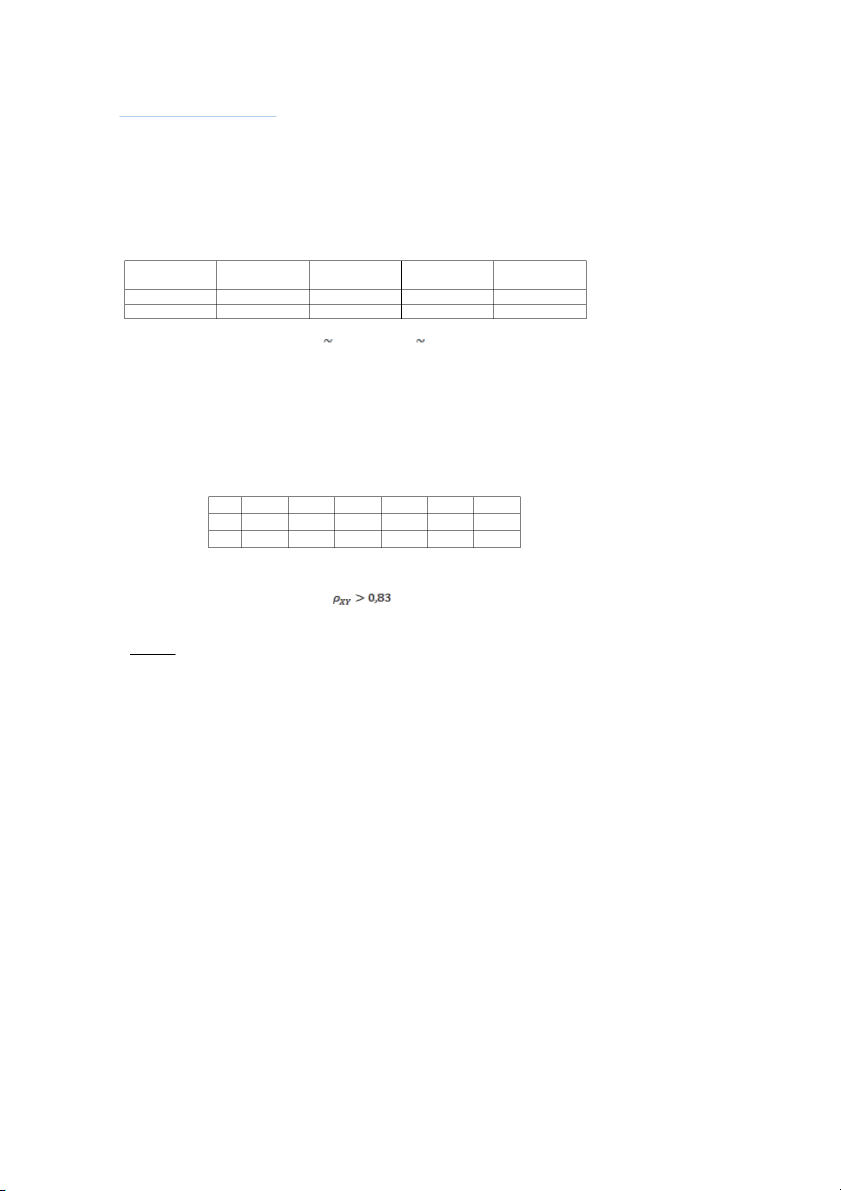
b) Hãy ước lượng hệ số tương quan ρxy với độ tin cậy 95%.
---------------------------------------------------------- ------------------------------ Hết -- -------------------- -
Ghi chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYT KHOA KHOA HC NG DN G
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút s Đề : 103 
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 điểm): Cho hai biến cố A và B độc lập nhau. Biết rằng P(A + B) = 0,83; P(A) = 0,5 và P(B) = a. a) Tìm giá trị c a a? ủ b) Cho biến c D = ố
A + B + C có P(D) = 0,85 và giả s
ử A, B, C độc lập hãy tính P(C )?
Câu 2.(2 điểm):
Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ.
b)Tính DX và P(X2 0,5 < 0)? –
Câu 3.( 1 điểm): Cho X N(5;9); Y B(10; 0,2) và đặt T = 2X + 5Y – 7.ModX.ModY.
a)Hãy tính giá trị của E(T)? b)Tính P(X > 4)?
Câu 4.( 3 điểm): . Số lượng khách hàng đến thăm quan và mua sắm ở cửa hàng qun áo Elise, Hà Nội là
biến ngẫu nhiên theo phân phối chuẩn. Điều tra số lượng khách hàng tại đây trong 70 ngày thu được kết
quả trung bình mỗi ngày có 126 khách và độ lệch hiệu chnh là 14,9782 khách, trong đó có 19 ngày đông
khách (tức là số khách đến trong ngày đó lớn hơn 135)
1. Hãy ước lượng số lượng khách trung bình đến cửa hàng với độ tin cậy 90%?
2. Khi ước lượng t lệ ngày đông khách, yêu cu độ chính xác 0,1
thì độ tin cậy là bao nhiêu?
3. Người quản lý cửa hàng báo cáo rằng trung bình mỗi ngày có khoảng 130 khách hàng đến thăm quan
và mua sắm; với mức ý nghĩa 5% hãy nhận xét về báo cáo đó?
Câu 5.(2 điểm): Để điều tra về mức thu nhập X (triệu/tháng) và nhu cu về một loại hàng hóa Y (kg/tháng
) của người dân thủ đô ta có số liệu như sau: xi (triệu/tháng) 4,3 5,3 6,3 7,3 8,3 9,3 10,3 yi (kg/tháng) 1,6 1,8 2,3 2,5 2,8 3,2 3,4 ni (người) 3 5 5 8 7 4 2 a) Lập phương trình i
hồ quy tuyến tính thực nghiệm, qua đó cho biết với mức thu nhập là 11
triệu/tháng thì nhu cu về m t
ộ loại hàng hóa Y của người dân thủ đô ước tính qua hàm hồi quy là bao nhiêu?
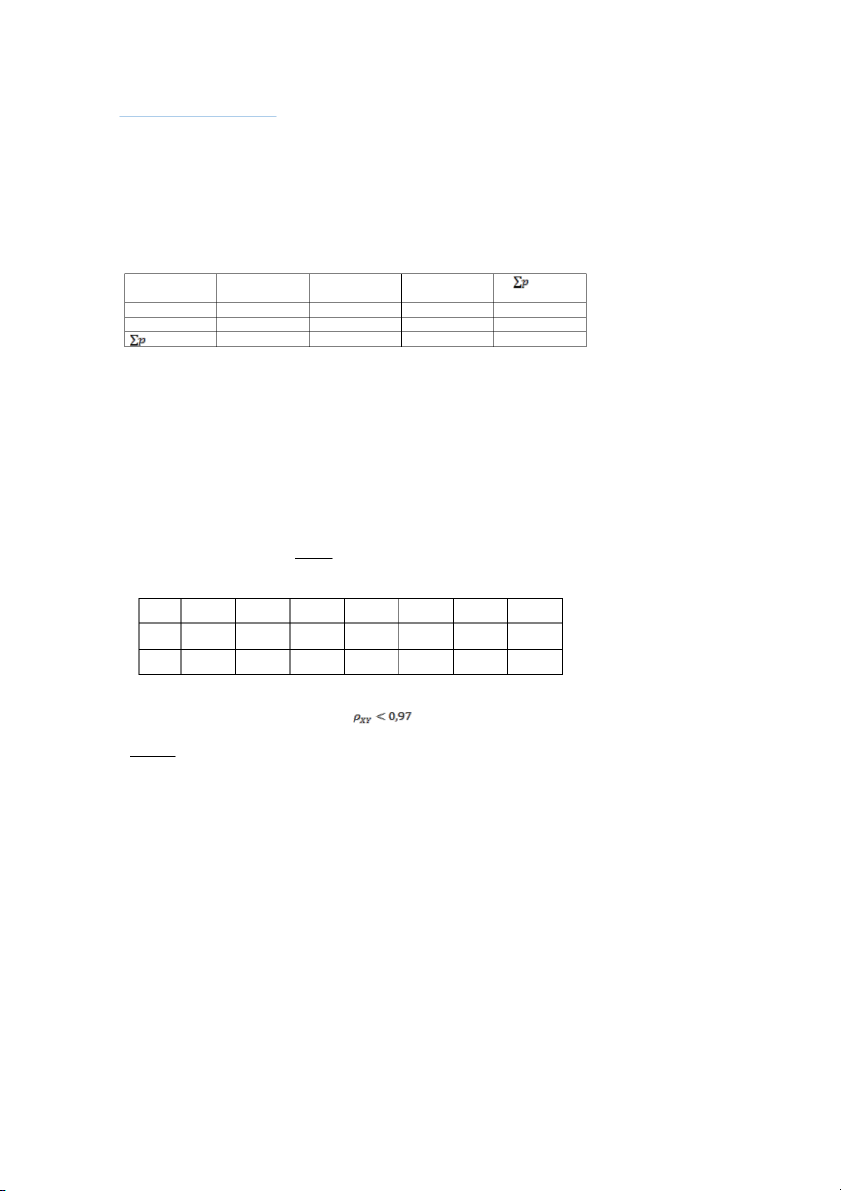
b) Hãy ước lượng hệ số tương quan ρxy với độ tin cậy 96%.
---------------------------------------------------------- ------------------------------ Hết -- -------------------- -
Ghi chú: Sinh viên đượ
c sử dụng bảng tra các giá trị tới hạn xác suất
DUYT KHOA KHOA HC NG DN G
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút s Đề : 104 
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ……………… …
Số BD …………
Câu 1.(2 điểm):
Cho hai biến cố A, B. Biết P(A + B) = 0,6; P(A) = 0,3; P(B) = 0,4. a) Tìm xác suất P(AB)? b) t C = Đặ
A + B, tính xác suất P(A|C)?
Câu 2.(2 điểm):
Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ. b)Tính E(5X3 + 4)?
Câu 3.( 1 điểm): Có 8 loại vắc-xin với xác suất sẽ được đưa vào sử dng trong tháng đều là 0,5. Gọi
X là số vắc-xin sẽ được đưa vào sử dng.
a)Tính trung bình có bao nhiêu vắc-xin sẽ được sử dng? b)Tính P(X > 1)?
Câu 4.( 3 điểm): Để khảo sát nhu cu sử dng thịt lợn của người dân trong một tháng, người ta điều tra
100 người thấy: nhu cu thịt lợn trung bình là 4,5 kg/tháng; độ lệch mẫu hiệu chnh là 2,13 kg và có 30
người có nhu cu thịt lợn cao.
1/. Hãy ước lượng tỷ lệ người có nhu cu sử dng thịt lợn cao với độ tin cậy 95%.
2/. Khi ước lượng nhu cu sử dng thịt lợn trung bình của người dân với độ chính xác là 0,35 và độ tin
cậy 99% thì cn khảo sát bao nhiêu người?
3/.Nếu tỷ lệ người có nhu cu sử dng thịt lợn cao là trên 20% thì cc quản lý thị trường sẽ can thiệp để
giảm giá thịt. Với mức ý nghĩa 1% hãy cho biết người dân có được giảm giá thịt hay không?
Câu 5.(2 điểm): Để khảo sát mối liên hệ giữa thời gian đọc sách X và thời gian sử dng Internet Y của
sinh viên trường ĐH Kinh tế-Kỹ thuật Công nghiệp , thu được mẫu số liệu như sau: xi(giờ) 1,55 1,8 1,8 2,3 2,3 2,55 2,8 3,3 yi( giờ ) 3 3 2,25 2,5 2 1,75 1,75 1 ni(sốsinh 4 2 6 6 4 6 2 5 viên)
a) Lập phương trình hồi quy tuyến tính mẫu, qua đó tính thời gian đọc sách ước lượng
qua hàm hồi quy mẫu khi thời gian sử dng Internet ở mức 2,5 giờ.
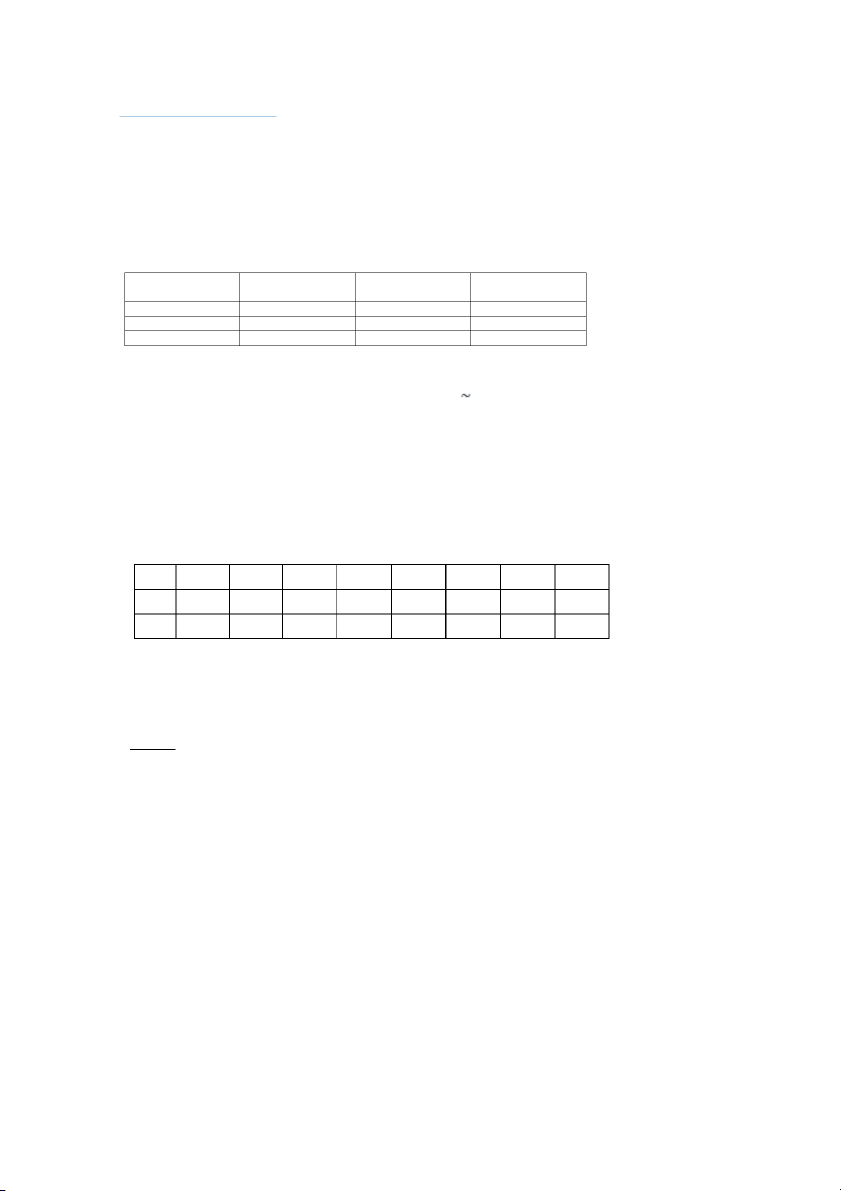
b) Hãy ước lượng hệ số tương quan ρxy với độ tin cậy 92%.
---------------------------------------------------------- ------------------------------ Hết -- -------------------- -
Ghi chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYT KHOA KHOA HC NG DN G
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề s: 105
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 điểm): Cho hai biến cố A, B. Biết P(A) = 0,3; P(B) = 0,5; P(A|B) = 0,2. a) Tìm xác suất P(AB)?
b) Tìm xác suất P(A + B + C) với C  A
Câu 2.(2 điểm):
Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau: Y -3 -2 2 3 X -3 a 2a 4a 4a 3 4a a 3a a
a)Tìm hệ số a từ bảng phân phối. b)Tính E(Y + 3) và D(2X2 - 1)?
Câu 3.( 1 điểm): Cho 2 biến độc lập: X N(8; 1,44) và Y B(10; 0,6); đặt Z = 5X – 2Y + 100. a)Hãy tính D(Z)?
b)Tính P(X < 9, Y = E(Y))?
Câu 4.( 3 điểm): Một doanh nghiệp dự định đưa một sản phẩm mới vào một thị trường có 10 triệu người
tiêu dùng. Điều tra ngẫu nhiên 1000 người tiêu dùng thì thấy có 0 người sẵn sàng mua sản phẩm đó. 35
1/. Với độ tin cậy 97% hãy ước lượng tỷ lệ khách hàng sẵn sàng mua sản phẩm đó.
2/. Khi ước lượng tỷ lệ khách hàng sẵn sàng mua sản phẩm đóvới sai số 5% và độ tin cậy 93% thì cn
điều tra bao nhiêu người tiêu dùng? 3/. Dựa vào kết quả ý
Hãy ước lượng số người tiêu dùng tiềm năng mua sản phẩm đó. 1/. Câu 5 m): .(2 điể Theo dõi độ dày c a m ủ t lo ộ
ại giấy và thời gian phân hủy ta được bảng s ố liệu sau: (bi dày X(mm) và th ết độ ời gian phân h y ủ Y(tháng)) X 1,6 3,6 10,6 16,6 26,6 36,6 Y 10 13 15 19 20 25 Ni 3 4 5 5 3 6 a). Lập phương trình h i ồ quy tuyến tính th c
ự nghiệm? và cho biết nếu đ
ộ dày của giấy là 30 mm thì
thời gian phân h y là bao nhiêu? ủ
b). Với mức ý nghĩa 5%, có thể cho rằng không?
----------------------------------------------------------
-------------------------------- Hết --------------------- Ghi chú: S
inh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYT KHOA KHOA HC NG DN G
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề s: 106
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 điểm): Cho hệ đy đủ 3 biến cố {A, B , C } với P(A) = 0,3; P(B) = 2P(A). Biết biến cố F
thỏa mãn: P(F/A) = 0,02; P(F/B) = 0,35; P(F/C) = 0,5. a) Tính xác suất P(F)?
b) Tính giá trị P[(A+B)|F] ?
Câu 2.(2 điểm):
Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau: Y -3 -2 2 3 X -3 a 2a 4a 4a 3 4a a 3a a
a)Tìm hệ số a từ bảng phân phối. b)Tính D(2Y3 6) và ModX? –
Câu 3.( 1 điểm): Một lớp học có 50 sinh viên trong đó có 20 nam. Lấy ngẫu nhiên ra 10 sinh viên để
tham gia hội sinh viên tình nguyện, gọi X là số sinh viên nữ có trong 10 sinh viên. Biết Y N(5; 9). a)Hãy tính E(X + 3DY 1)? – b)Tính P(Y2 5Y – 2 < 4)? –
Câu 4.( 3 điểm): Đo độ bền (kg/cm2) của một số con sợi ta có số liệu sau: cỡ mẫu 60 con sợi, độ bền
trung bình 3,34 kg/cm2, độ lệch chuẩn S’ = 0,351 kg/cm2, trong đó có 20 con sợi có độ bền trên 3,5 kg/cm2 được coi là loại A.
1/. Hãy ước lượng độ bền trung bình của các con sợi với độ tin cậy 94% .
2/. Hãy ước lượng tỷ lệ con sợi loại A với độ tin cậy 97% .
3/. Khi ước lượng tỷ lệ con sợi loại A 1
với độ chính xác 0, 14 thì độ tin cậy sẽ là bao nhiêu?
Câu 5.(2 điểm): Để điều tra về mức thu nhập X (triệu/tháng) và nhu cu về một loại hàng hóa Y (kg/tháng
) của người dân thủ đô ta có số liệu như sau:
xi (triệu/tháng) 4,6 5,6 6,6 7,6 8,6 9,6 10,6 yi (kg/tháng) 1,6 1,8 2,3 2,5 2,8 3,2 3,4 ni (người) 3 5 5 8 7 4 2 a) Lập phương trình h i
ồ quy tuyến tính thực nghiệm, qua đó cho t
biế với mức thu nhập là 11
triệu/tháng thì nhu cu về m t
ộ loại hàng hóa Y của người dân thủ đô ước tính qua hàm hồi quy là bao nhiêu? b) Với m cho r ức ý nghĩa 5%, có thể ằng không?
----------------------------------------------------------
-------------------------------- Hết ---------------------
Ghi chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYT KHOA KHOA HC NG DN G
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề s: 107
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 điểm): Cho hệ đy đủ ba biến cố {A, B, C} với P(A) = 2P(B) = P(C). Biết biến cố F
thỏa mãn: P(F|A) = m; P(F|B) = 2m và P(F|C) = 0,5.
a) Giả sử P(F) = 0,28 hãy tìm giá trị của m? b) Tính P(A + B)?
Câu 2.(2 điểm):
Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau: X 0 1 2 = P(Y) Y 2 0.05 0.4 4 0.2 = P(X) 0.2 0.5 1
a)Điền các giá trị còn thiếu vào bảng?
b)Tính MedZ với Z = X – 2Y?
Câu 3.( 1 điểm): Có 3 loại vắc-xin với xác suất sẽ được đưa vào sử dng trong tháng đều là 0,8. Gọi
X là số vắc-xin sẽ được đưa vào sử dng. a)Tính EX, DX? b)Tính E(X4) ?
Câu 4.( 3 điểm): Một khu rừng có diện tích rất lớn. Căn cứ vào kết quả điều tra ngẫu nhiên trên 31 ô,
mỗi ô có diện tích 0,1 ha ta tính được thể tích gỗ trung bình trên mỗi ô là 10,2 m3 và độ lệch hiệu chnh
là 1,45 m3. Giả thiết thể tích gỗ X tuân theo luật chuẩn.
1/. Hãy ước lượng thể tích gỗ trung bình của khu rừng đó với độ tin cậy 95%.
2/. Khi ước lượng thể tích gỗ trung bình của khu rừng với độ chính xác là 0,6 m3 thì độ tin cậy bằng bao nhiêu?
3/. Theo số liệu điều tra của năm trước thì thể tích gỗ trung bình của khu rừng đó là 15 m3. Vậy có thể
kết luận thể tích gỗ của khu rừng giảm đi với mức ý nghĩa 5% không? Câu 5 m): .(2 điể
Theo dõi trọng lượ và ng y(kg) s tháng tu ố i x(tháng) ổ của m t gi ộ ng l ố ợn trong một
trang trại chăn nuôi ta có bảng s ố liệu sau: xi 2,8 3,8 4,8 5,8 6,8 7,8 8,8 yi 32 40 50 62 73 86 97 ni 2 4 5 6 7 5 1 a) Lập phương trình i
hồ quy tuyến tính thực nghiệm, qua đó cho t biế nếu s ố tháng tu i ổ là 10 tháng thì tr ng c ọng lượ a l
ủ ợn ước tính qua hàm h i quy là bao nhiêu? ồ b) Với m cho r ức ý nghĩa 5%, có thể ằng không?
----------------------------------------------------------
-------------------------------- Hết ---------------------
Ghi chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất D Y
U T KHOA KHOA HC NG DN G
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề s: 108
(k 2 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 điểm): Cho hệ đy đủ ba biến cố {A, B, C} với P(A) = 0,3; P(B) = 2P(A). Biết biến cố
F thỏa mãn: P(F|A) = 0,02; P(F|B) = 0,35 và P(F|C) = 0,5. a) Tính xác suất P(F)?
b) Tính xác suất P(A + B + ABC)?
Câu 2.(2 điểm):
Cho biến nhẫu nhiên X và Y có bảng phân phối đồng thời như sau: Y -3 0 2 X -2 a 0,5a a 0 0,05 a 1,5a 1 0,15 0,1 0,2
a)Tìm hệ số a từ bảng phân phối? b)Tính E(3Y - 2) và P(Y = -3|X = 0) ?
Câu 3.( 1 điểm): Trong một lô 100 sản phẩm có 75 sản phẩm loại I. Lấy ngẫu nhiên 45 sản phẩm để
kiểm tra, gọi X là số sản phẩm loại I gặp được khi kiểm tra. Biết Y N(3;4).
a)Tính giá trị của E(4X – 3Y)?
b)Tính xác suất P(Y2 – 5Y + 4 < 0)?
Câu 4.( 3 điểm): Một doanh nghiệp dự định đưa một sản phẩm mới vào một thị trường có 3 triệu người
tiêu dùng. Điều tra ngẫu nhiên 2000 người tiêu dùng thì thấy có 800 người sẵn sàng mua sản phẩm đó.
1/. Với độ tin cậy 95% hãy ước lượng tỷ lệ khách hàng sẵn sàng mua sản phẩm đó.
2/. Khi ước lượng tỷ lệ khách hàng sẵn sàng mua sản phẩm đóvới sai số 3% thì độ tin cậy của ước lượng là bao nhiêu?
3/. Số lượng khách hàng tiềm năng mà doanh nghiệp hy vọng sẽ có được ở thị trường trên là bao nhiêu ?
Câu 5.(2 điểm): Khảo sát ch số chất lượng không khí y (đơn vị:AQI), và số lượng cây xanh trên
đu người x (m2/người) tại một số thành phố lớn khu vực Đông Nam Á, người ta thu được mẫu số liệu như sau: xi 60 55 42 35 28 20 11 5 yi 25 75 124 180 250 300 350 400 ni 3 5 2 6 4 3 5 2
Với biến BNN X về lượng cây xanh và Y ch số chất lượng không khí đều tuân theo luật chuẩn.
a) Lập phương trình hồi quy tuyến tính thực nghiệm, và cho biết khi khảo sát chất lượng không
khí ở thành phố nếu ch số chất lượng không khí là 380 (AQI) thì có lượng cây xanh trên đầu
người là bao nhiêu (m2/người)
b) Hãy ước lượng hệ số tương quan với độ tin cậy 91%.
----------------------------------------------------------
------------------------------------ Hết -----------------
Ghi chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYT KHOA KHOA HC NG DN G