BÀI TẬP CHƯƠNG 2
MÔ HÌNH HỒI QUY 2 BIẾN
Bài 1. Có số liệu về thu nhập (X) và chi tiêu (Y) của 10 hộ gia đình như sau:
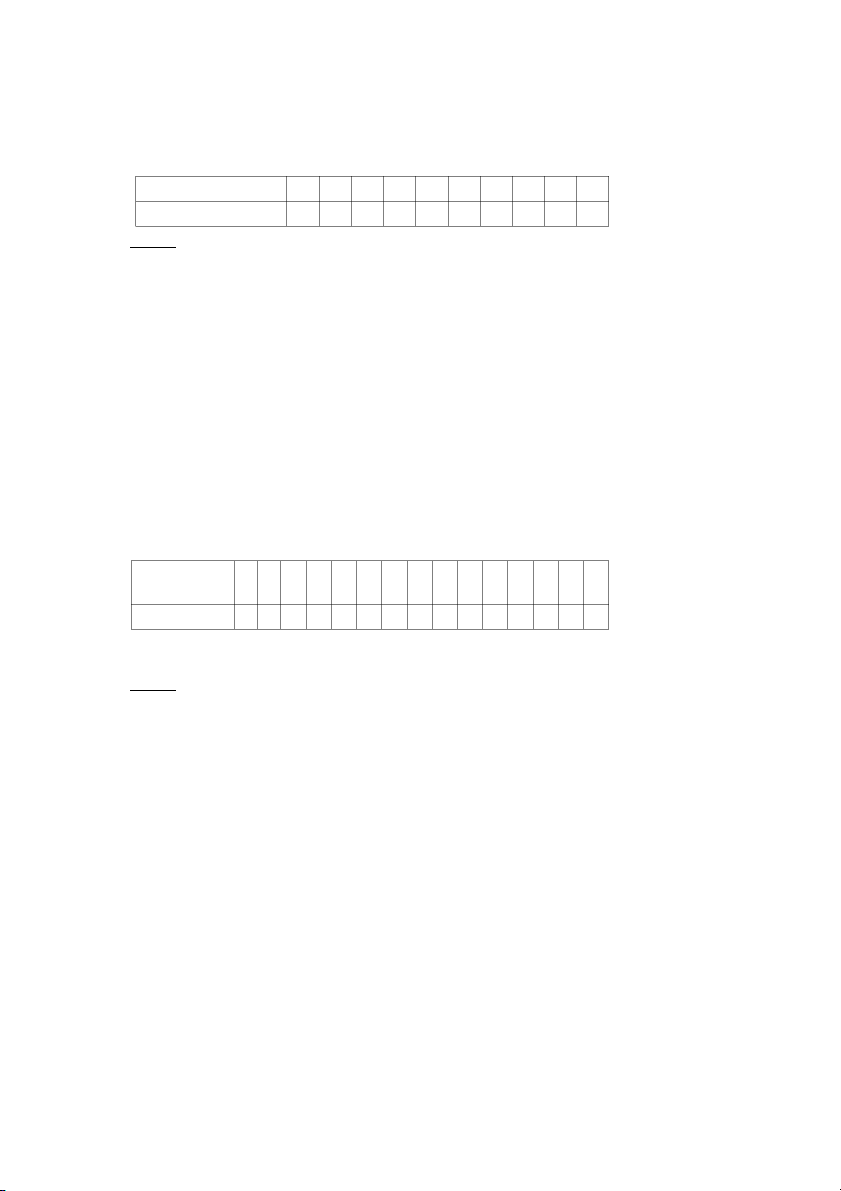
Thu nhập (triệu đồng) 8 9 10 11 12 15 15 16 17 20
Chi tiêu (triệu đồng) 7 8 9 8 10 12 11 13 12 15 Yêu cầu:
1. Xác định hàm hồi quy mẫu
2. Giải thích ý nghĩa kinh tế các hệ số ước lượng được.
3. Hệ số chặn trong mô hình có ý nghĩa thống kê không, với mức ý nghĩa 5%?
4. Với mức ý nghĩa 5%, hãy cho biết thu nhập có ảnh hưởng đến chi tiêu hay không?
5. Với mức ý nghĩa 5%, hãy cho biết khi thu nhập tăng thì chi tiêu có tăng hay không?
6. Khi không có thu nhập thì chi tiêu trung bình là bao nhiêu, với độ tin cậy 95%?
7. Khi thu nhập tăng 1 (triệu đồng) thì chi tiêu trung bình tăng trong khoảng nào, với độ tin cậy 95%?
8. Có thể cho rằng khi thu nhập tăng 1 (triệu đồng) thì chi tiêu trung bình tăng trên 0.6
(triệu đồng) hay không, với ứ m c ý nghĩa 5%?
9. Tính R2 và giải thích ý nghĩa kết quả nhận được.
10. Với mức thu nhập 21 (triệu đồng), hãy dự báo giá trị trung bình và giá trị cá biệt của
chi tiêu với hệ số tin cậy 95%.
Bài 2. Có số liệu về tuổi nghề (X) và năng suất lao động (Y) của 15 công nhân trong một doanh nghiệp như sau:
Tuổi nghề 2 2 5 7 9 9 10 12 12 14 15 15 17 18 18 (năm) NSLĐ (sp) 8
7 12 18 18 20 23 25 24 28 30 29 32 35 36
Các kiểm định được thực hiện với mức ý nghĩa 5%, các ước lượng được thực hiện với ộ đ tin cậy 90%. Yêu cầu:
1. Xác định hàm hồi quy mẫu
2. Giải thích ý nghĩa kinh tế các hệ số ước lượng được.
3. Hệ số chặn trong mô hình có ý nghĩa thống kê không?
4. Năng suất lao động có thực sự phụ thuộc vào tuổi nghề hay không?
5. Hãy cho biết khi tuổi nghề tăng thì năng suất lao ộ đ ng có tăng hay không?
6. Khi tuổi nghề bằng 0 thì năng suất lao động trung bình tối thiếu là bao nhiêu?
7. Khi tuổi nghề tăng 1 (năm) thì năng suất lao động trung bình tăng bao nhiêu?
8. Khi tuổi nghề tăng 1 (năm) thì năng suất lao động trung bình tăng tối thiểu bao nhiêu?
9. Tính R2 và giải thích ý nghĩa kết quả nhận được.
10. Với mức tuổi nghề là 20 (năm), hãy dự báo giá trị trung bình và giá trị cá biệt của năng
suất lao động với hệ số tin cậy 90%.
Bài 3. Cho biết số liệu về tiền lương trung bình 1 giờ (TL) và số năm được đào tạo (SN) như sau:
Quan sát Số năm được đào tạo
Lương trung bình một giờ (n) (SN - năm) (TL - USD) 1 6 4.4567 2 7 5.7700 3 8 5.9787 4 9 7.3317 5 10 7.3182 6 11 6.5844 7 12 7.8182 8 13 7.8351 9 14 11.0223 10 15 10.6738 11 16 10.8361 12 17 13.6150 13 18 13.5310
Từ số liệu trên, ta có kết quả hồi quy sau: L T ˆ SN = − 0 . 0 14453 + 7 . 0 24097 i i Se = (0.874624) (…)
t = (…) (10.40648) R2 = 0.9078 n = 13 Yêu cầu:
1. Hãy điền giá trị thích hợp vào chỗ t ố r ng (…)
2. Giải thích ý nghĩa của các hệ số ước lượng được.
3. Số năm đào tạo có ảnh hưởng đến tiền lương trung bình không?
4. Số năm đào tạo có tác động thuận chiều đến tiền lương trung bình không?
5. Đánh giá mức độ phù hợp của mô hình.
Bài 4. Một số liệu thống kê về lãi suất ngân hàng (X, % năm) và tổng vốn đầu tư (Y, tỉ
đồng) trên địa bàn tỉnh Bình Dương qua 10 năm liên tiếp như sau: Năm 1 2 3 4 5 6 7 8 9 10 Xi 7.0 6.5 6.5 6.0 6.0 6.0 5.5 5.5 5.0 4.5 Yi 29 32 31 34 32 35 40 43 48 50 Yêu cầu:
1. Hãy sử dụng phần mềm Eviews để thiết lập mô hình hồi quy tuyến tính mô tả quan hệ
giữa tổng vốn đầu tư và lãi suất ngân hàng.
2. Nêu ý nghĩa của các hệ số hồi quy ước lượng được.
3. Lãi suất ngân hàng có thực sự tác động đến tổng vốn đầu tư không với mức ý nghĩa 2%?
4. Đánh giá mức độ phù hợp của mô hình.
5. Dự báo tổng vốn đầu tư trung bình khi lãi suất là 4.8% năm với độ tin cậy 98%.
Bài 5. Cho bảng kết quả hồi quy sau, với Q là lượng hàng bán (sản phẩm), P là giá bán
(USD) của một cửa hàng trong 27 tháng. Các kiểm định với mức ý nghĩa 5%, các khoảng
tin cậy với độ tin cậy 95%. Dependent Variable: Q Method: Least Squares Sample: 1 27 Included observations: 27 Variable Coefficient Std. Error t-Statistic Prob C 2590.3 384.9544 6.7288 0.000 P -7.1461 0.12875 -5.5208 0.000 R-squared 0.95195 Mean dependent Var 1831.41 Adjusted R-squared 0.95002 S.D. dependent var 451.937 S.E. of regression 94.9031 F-statistic 495.29 Sum squared resid 225165 Prob(F-statistic) 0.000 Log likelihood -199.9393 Durbin-Watson stat 0.7079 Yêu cầu:
1. Viết hàm hồi quy mẫu.
2. Giải thích ý nghĩa các hệ số.
3. Các hệ số của mô hình có ý nghĩa thống kê không?
4. Hệ số xác định là bao nhiêu? Giá trị đó có ý nghĩa gì?
5. Sử dụng thống kê F đo độ phù hợp của hàm hồi qu y
6. Tìm ước lượng điểm cho phương sai sai số ngẫu nhiên.
7. Tổng bình phương phần dư là bao nhiêu?
8. TSS và ESS là bao nhiêu?
9. Tìm khoảng tin cậy cho hệ số chặn và hệ số góc của mô hình.
10. Khi giá bán giảm 1 USD thì lượng bán ra thay đổi trung bình như thế nào?
11. Khi giá bán tăng 1 USD thì lượng bán ra trung bình giảm tối đa bao nhiêu?
12. Có thể nói khi giá bán tăng 1 USD thì lượng bán trung bình giảm 10 (sp) được không?
13. Giá bán tăng 1 USD thì lượng bán trung bình giảm hơn 7 (sp) có đúng không?
14. Tìm một ước lượng điểm cho lượng sản phẩm bán ra khi giá bán là 105 USD.
15. Tìm lượng bán trung bình và cá biệt khi giá bán là 105 USD.
Bài 6. Cho bảng hồi quy sau với NS là năng suất thu hoạch (tạ/ha), TS là lượng thuốc trừ
sâu (tạ/ha) của một hợp tác xã trong năm 2012. Cho α = 5% Dependent Variable: NS Method: Least Squares Sample: 2012M01 2012M12 Included observations: 12 Variable Coefficient Std. Error t-Statistic Prob. C -14.00000 1.634848 -8.563488 0.0000 TS 7.848485 0.569181 13.78909 0.0000 R-squared 0.950035 Mean dependent var 7.583333 Adjusted R-squared 0.945038 S.D. dependent var 6.973434 S.E. of regression 1.634848 Akaike info criterion 3.971988 Sum squared resid 26.72727 Schwarz criterion 4.052806 Log likelihood -21.83193 Hannan-Quinn criter. 3.942067 F-statistic 190.1389 Durbin-Watson stat 0.932866 Prob(F-statistic) 0.000000 Yêu cầu:
1. Viết hàm hồi quy mẫu. Giải thích ý nghĩa các hệ số ước lượng được.
2. Năng suất thu hoạch có phụ thuộc vào lượng thuốc trừ sâu hay không?
3. Có thể nói rằng lượng thuốc trừ sâu tác động thuận chiều đến năng suất thu hoạch hay không?
4. Có thể nói rằng khi lượng thuốc trừ sâu tăng thêm 1 (tạ/ha) thì năng suất thu hoạch trung
bình tăng nhiều hơn 7.5 (tạ/ha) hay không?
5. Khi lượng thuốc trừ sâu tăng thêm 1 (tạ/ha) thì năng suất thu hoạch trung bình thay đổi trong khoảng nào?
6. Khi lượng thuốc trừ sâu tăng 1 (tạ/ha) thì năng suất thu hoạch trung bình tăng tối thiểu bao nhiêu?
7. Khi lượng thuốc trừ sâu tăng 1 (tạ/ha) thì năng suất thu hoạch trung bình tăng tối đa bao nhiêu?
8. Khi lượng thuốc trừ sâu bằng 0 thì năng suất thu hoạch trung bình là bao nhiêu?
9. Khi lượng thuốc trừ sâu bằng 0 thì năng suất thu hoạch trung bình tối đa là bao nhiêu?
10. Khi lượng thuốc trừ sâu bằng 0 thì năng suất thu hoạch trung bình tối thiểu là bao nhiêu?
11. Hệ số xác định là bao nhiêu? Giải thích ý nghĩa.
12. Kiểm định sự phù hợp của hàm hồi quy.
13. Tổng bình phương phần dư là bao nhiêu? 14. Tính TSS và ESS.
Bài 7. Cho bảng hồi quy sau với CT là chi tiêu (triệu đồng), TN là thu nhập (triệu đồng)
của 10 hộ gia đình. Cho α = 5% Dependent Variable: CT Method: Least Squares Sample: 1 10 Included observations: 10 Variable Coefficient Std. Error t-Statistic Prob. C -3.403587 0.753794 -4.515278 0.0020 TN 0.560538 0.052583 10.66004 0.0000 R-squared 0.934230 Mean dependent var 4.500000 Adjusted R-squared 0.926009 S.D. dependent var 1.581139 S.E. of regression 0.430090 F-statistic 113.6364 Sum squared resid 1.479821 Prob(F-statistic) 0.000005 Log likelihood -4.636064 Durbin-Watson stat 3.229311 Yêu cầu:
1. Viết hàm hồi quy mẫu
2. Giải thích ý nghĩa các hệ số ước lượng được.
3. Chi tiêu của các hộ gia đình có phụ thuộc vào thu nhập hay không?
4. Có thể nói rằng thu nhập tác động thuận chiều đến chi tiêu hay không?
5. Có thể nói rằng khi thu nhập tăng 1 triệu đồng thì chi tiêu trung bình tăng 0.5 tr ệ i u đồng hay không?
6. Khi thu nhập tăng 1 triệu đồng thì chi tiêu trung bình thay đổi trong khoảng nào?
7. Khi thu nhập tăng 1 triệu đồng thì chi tiêu trung bình tăng tối đa bao nhiêu?
8. Hệ số xác định là bao nhiêu? Giải thích ý nghĩa.
9. Kiểm định sự phù hợp của hàm hồi quy bằng kiểm định F.
10. Tổng bình phương phần dư là bao nhiêu? 11. Tính TSS và ESS.
Bài 8. Cho Q là sản lượng sản xuất ra (sản phẩm), L là lượng lao động (người ) và kết quả
hồi quy mô hình như sau với α = 5% Dependent Variable: Q Method: Least Squares Sample: 1 20 Included observations: 20 Variable Coefficient Std. Error t-Statistic Prob. C -255.5380 99.72089 2.562533 0.0196 L 6.068681 0.745640 8.138894 0.0000 R-squared 0.786329 Mean dependent var 551.9000 Adjusted R-squared 0.774458 S.D. dependent var 95.17900 S.E. of regression 45.20169 F-statistic 66.24160 Sum squared resid 36777.46 Prob(F-statistic) 0.000000 Yêu cầu:
1. Viết hàm hồi quy mẫu và cho biết dấu của các ước lượng hệ số có phù hợp với lý thuyết kinh tế không?
2. Hệ số chặn của mô hình có ý nghĩa thống kê không? Nếu mức ý nghĩa còn 1% thì kết luận thế nào?
3. Sản lượng có phụ thuộc vào lao động không? Nếu có thì lao động giải thích được bao
nhiêu % sự biến động của sản lượng?
4. Trong điều kiện các yếu tố khác không đổi, nếu tăng lao động thêm 1người thì sản lượng
trung bình thay đổi tối đa bao nhiêu?
5. Có thể cho rằng khi giảm lượng lao động đi 1 người thì sản lượng trung bình giảm chưa
đến 7 sản phẩm hay không?
6. Dự báo sản lượng trung bình khi lượng lao động là 150 người?
Bài 9. Cho số liệu về thu nhập TN (ngàn USD/tháng) và chi tiêu cho việc chăm sóc sức
khỏe CT (ngàn USD/tháng) của 51 cá nhân ở Mỹ. Ta có bảng kết quả hồi quy Eviews như sau: Dependent Variable: CT Method: Least Squares Sample: 1 51 Included observations: 51 Variable Coefficient Std. Error t-Statistic Prob. C 0.176496 0.467509 0.377525 0.7074 TN 0.141652 0.002875 49.27179 0.0000 R-squared 0.980216 Mean dependent var 15.06886 Adjusted R-squared 0.979812 S.D. dependent var 17.92664 S.E. of regression 2.547102 F-statistic 2427.709 Sum squared resid 317.8986 Prob(F-statistic) 0.000000 Yêu cầu:
Với mức ý nghĩa 5%, hãy trả lời các câu hỏi sau:
1. Viết hàm hồi quy mẫu và cho biết ý nghĩa của các hệ số hồi quy.
2. Tìm khoảng tin cậy cho hệ số chặn và hệ số góc trong mô hình hồi quy.
3. Thu nhập thay đổi có ảnh hưởng đến chi tiêu cho sức khỏe không?
4. Thu nhập có tác động thuận chiều đến chi tiêu cho sức khỏe không?
5. Trong điều kiện các yếu tố khác không đổi, khi thu nhập tăng thêm 1 ngàn USD/tháng
thì chi tiêu trung bình cho sức khỏe thay đổi trong khoảng nào?
6. Hệ số xác định của mô hìn
h là bao nhiêu? Giải thích ý nghĩa .
7. Kiểm định sự phù hợp của mô hình hồi quy.
8. Với mức thu nhập 100 nghìn USD, hãy dự báo giá trị trung bình và giá trị cá biệt của chi tiêu cho sức khỏe.
Bài 10. Cho số liệu 20 đại lý của một hãng thịt hộp tại 20 điểm trong cùng một tuần, với
PT là giá bán thịt hộp (nghìn đồng/hộp) và Q là lượng bán (hộp). Kết quả hồi quy như sau: Dependent Variable: Q Method: Least Squares Sample: 1 20 Included observations: 20 Variable Coefficient Std. Error t-Statistic Prob. C 486.7856 73.02756 6.665779 0.0000 PT -10.44716 2.857461 -3.656100 0.0018 R-squared 0.426150 Mean dependent var 221.9500 S.E. of regression 41.46273 F-statistic 13.36706 Sum squared resid 30944.85 Prob (F-statistic) 0.001807 Yêu cầu:
Với mức ý nghĩa 5%, hãy trả lời các câu hỏi sau:
1. Viết hàm hồi quy tổng thể, hàm hồi quy mẫu
2. Giải thích ý nghĩa của các hệ số hồi quy. Dấu của các ước lượng hệ số chặn và hệ số góc
có phù hợp với lý thuyết kinh tế không?
3. Hệ số xác định là bao nhiêu và cho biết điều gì? Các yếu tố khác giá bán thịt hộp giải
thích được bao nhiêu phần trăm sự biến động của lượng bán?
4. Ước lượng điểm lượng bán trung bình khi giá bán là 31 nghìn đồng.
MÔ HÌNH HỒI QUY ĐA BIẾN
Bài 1. Có số liệu thống kê về Y – Chi tiêu (triệu đồng), X2 – Tiền lương (triệu đồng), X3 –
Thu nhập khác (triệu đồng) của 10 hộ gia đình. Cho α = 5%. Y 10 11 12 13 14 15 16 17 17 17 X2 10 12 13 14 15 16 16 17 18 20 X3 2 0 3 4 4 6 8 9 4 2 Yêu cầu:
1. Trình bày cách xác định các chỉ tiêu thống kê theo phương pháp ma trận và viết hàm hồi quy mẫu.
2. Giải thích ý nghĩa của các hệ số ước lượng được.
3. Các hệ số có ý nghĩa thống kê không?
4. Tính R2 và giải thích ý nghĩa.
5. Kiểm định sự phù hợp của hàm hồi quy.
6. Kiểm định xem các hệ số có mang dấu dương hay không và giải thích ý nghĩa.
7. Khi tiền lương tăng 1 (triệu đồng), thu nhập khác không đổi thì chi tiêu thay đổi trong khoảng nào?
8. Khi thu nhập khác tăng 1 (triệu đồng), tiền lương không đổi thì chi tiêu trung bình thay đổi trong khoảng nào?
9. Nếu cả tiền lương và thu nhập khác cùng tăng 1 triệu thì chi tiêu trung bình thay đổi trong khoảng nào?
10. Dự báo chi tiêu trung bình của hộ có tiền lương là 20 (triệu đồng) và thu nhập khác là 10 (triệu đồng).
Bài 2. Có số liệu về CT – Chi tiêu theo TN – Thu nhập và S
N – số thành viên của 12 hộ
gia đình như sau, cho α = 5%. CT 10 12 13 14 15 16 17 17 17 18 19 20 TN 12 13 14 15 16 16 17 18 20 20 21 22 SN 2 2 2 3 3 3 4 4 4 5 5 5 Yêu cầu:
1. Lập bảng tính và sử dụng phương pháp bình phương bé nhất để thiết lập hàm hồi quy mẫu.
2. Cho biết kết quả hồi quy khi sử dụng phần mềm Eviews.
3. Giải thích ý nghĩa của các hệ số ước lượng được.
4. Hệ số chặn trong mô hình có ý nghĩa thống kê không?
5. Chi tiêu có phụ thuộc vào thu nhập không?
6. Số thành viên có ảnh hưởng đến chi tiêu của hộ gia đình không?
7. Hệ số xác định là bao nhiêu và cho biết điều gì?
8. Kiểm định sự phù hợp của hàm hồi quy.
Bài 3. Có kết quả hồi quy về doanh thu DT (triệu đồng), chi phí quảng cáo CP (triệu đồng),
tiền lương nhân viên tiếp thị TL (triệu đồng) của 12 công nhân trong doanh nghiệp, cho α = 5%. Dependent Variable: DT Method: Least Squares Sample: 1 12 Included observations: 12 Variable Coefficient Std. Error t-Statistic Prob. C 32.27726 6.253073 5.161823 0.0006 CP 2.505729 0.328573 7.626105 0.0000 TL 4.758693 0.410384 11.59572 0.0000 R-squared 0.975657 Mean dependent var 141.3333 Adjusted R-squared 0.970247 Durbin-Watson stat 2.527238 S.E. of regression 4.003151 F-statistic 180.3545 Sum squared resid 144.2269 Prob(F-statistic) 0.000000 Yêu cầu:
1. Viết hàm hồi quy mẫu. Giải thích ý nghĩa các hệ số ước lượng được.
2. Doanh thu có phụ thuộc vào chi phí quảng cáo hay không?
3. Tiền lương của nhân viên tiếp thị có ảnh hưởng đến doanh thu hay không?
4. Có thể nói rằng chi phí quảng cáo tác động thuận chiều đến doanh thu hay không?
5. Có thể nói rằng khi Tiền lương của nhân viên tiếp thị không đổi, nếu chi phí quảng cáo
tăng thêm 1 (triệu đồng) thì doanh thu trung bình tăng nhiều hơn 2.5 (tr ệ i u đồng) hay không?
6. Khi Tiền lương của nhân viên tiếp thị không đổi, nếu chi phí quảng cáo tăng thêm 1
(triệu đồng) thì doanh thu trung bình thay đổi trong khoảng nào?
7. Khi Tiền lương của nhân viên tiếp thị không đổi, nếu chi phí quảng cáo tăng 1 (triệu
đồng) thì doanh thu trung bình tăng tối đa bao nhiêu?
8. Các biến độc lập giải thích được bao nhiêu % sự biến động của biến phụ thuộc?
9. Kiểm định sự phù hợp của hàm hồi quy.
Bài 4. Tiến hành hồi quy được kết quả sau với LS, LK, LL là logarit cơ số tự nhiên của các biến tương ứng. Cho α = 5%. Dependent Variable: LS Method: Least Squares Sample: 1 20 Included observations: 20 Variable Coefficient Std. Error t-Statistic Prob INPT 2.8749 0.22746 12.6390 0.000 LK 0.52178 0.093498 5.5860 0.000 LL 0.68225 0.14080 4.8457 0.000 R-squared 0.78117 Mean dependent Var 4.5516 Adjusted R-squared 0.75543 S.D. dependent var 0.57067 S.E. of regression 0.28222 F-statistic 30.3438 Sum squared resid 1.3540 Prob(F-statistic) 0.000 Log likelihood -1.4523 Durbin-Watson stat 1.9602 βˆ Cov( β ˆ , ) = 0.0127 2 3 Yêu cầu:
1. Viết hàm hồi quy mẫu với các biến S, K, L. Giải thích ý nghĩa các hệ số ước lượng được.
2. Các biến độc lập giải thích được bao nhiêu phần trăm sự biến động của biến phụ thuộc?
3. Kiểm định sự phù hợp của hàm hồi quy.
4. Khi vốn không đổi, lao động tăng 1% thì sản lượng thay đổi trong khoảng nào?
5. Lao động không đổi, vốn giảm 1% thì sản lượng giảm tối đa bao nhiêu %?
6. Lao động không đổi, nếu vốn tăng bằng 1.2 lần so với trước thì sản lượng có tăng tương
ứng bằng 1.2 lần hay không?
7. Khi lao động không đổi, nếu vốn tăng lên t lần mà sản lượng tăng nhỏ hơn t lần thì ta
nói sản lượng tăng chậm hơn vốn, nếu sản lượng tăng lớn hơn t lần ta nói sản lượng tăng
nhanh hơn vốn và nếu sản lượng tăng đúng bằng t lần thì ta nói sản lượng tăng bằng vốn.
Theo kết quả hồi quy trên thì sản lương tăng nhanh, chậm hay bằng vốn?
8. Vốn không đổi, sản lượng có tăng bằng lao động hay không?
9. Có thể nói hiệu quả sản xuất không đổi theo quy mô không?
10. Có thể nói hiệu quả sản xuất tăng theo quy mô không?
11. Có thể nói tăng quy mô vốn đem lại kết quả ít hơn so với tăng quy mô lao động cùng tỷ lệ hay không?
Bài 5. Cho số liệu 20 đại lý của một hãng thịt hộp tại 20 điểm trong cùng một tuần, với PT
là giá bán thịt hộp (nghìn đồng/hộp), PC là giá bán cá hộp (nghìn đồng/hộp), Q là lượng bán (hộp).
Kết quả hồi quy như sau: Dependent Variable: Q Method: Least Squares Sample: 1 20 Included observations: 20 Variable Coefficient Std. Error t-Statistic Prob. C 302.7606 14.52326 20.84660 0.0000 PT -14.76790 0.517617 -28.53056 0.0000 PC 11.62597 0.473371 24.55997 0.0000 R-squared 0.984270 Mean dependent var 221.9500 S.E. of regression 0.982420 F-statistic 531.8780 Sum squared resid 848.2248 Prob(F-statistic) 0.000000
Hiệp phương sai ước lượng hai hệ số bằng -0.08 Yêu cầu:
Với mức ý nghĩa 5%, hãy trả lời các câu hỏi sau:
1. Viết hàm hồi quy tổng thể, hàm hồi quy mẫu và giải thích ý nghĩa của hệ số xác định.
2. Giải thích ý nghĩa của các hệ số góc. Dấu của các ước lượng hệ số chặn và hệ số góc có
phù hợp với lý thuyết kinh tế không?
3. Khi giá bán thịt hộp tăng, giá bán cá hộp không đổi thì lượng bán thịt hộp có giảm không?
4. Khi giá bán thịt hộp tăng 1 nghìn đồng/hộp, giá bán cá hộp không đổi thì lượng bán thịt
hộp trung bình giảm trong khoảng nào?
5. Khi giá bán cá hộp tăng 1 nghìn đồng/hộp, giá bán thịt hộp không đổi thì lượng bán thịt
hộp trung bình có tăng không? Nếu có thì tăng tối đa bao nhiêu?
6. Khi giá bán thịt hộp và giá bán cá hộp cùng tăng 1 nghìn đồng/hộp thì lượng bán thịt
hộp trung bình có thay đổi không? Nếu có thì thay đổi trong khoảng nào?
7. Có thể nói khi giá bán thịt hộp không đổi, nếu giá bán cá hộp tăng 1 nghìn đồng/hộp thì
lượng bán thịt hộp trung bình sẽ tăng hơn 10 hộp hay không?
8. Có thể nói khi giá bán cá hộp không đổi, nếu giá bán thịt hộp tăng 1 nghìn đồng/hộp thì
lượng bán thịt hộp trung bình sẽ giảm 10 hộp hay không?
9. Tìm ước lượng điểm lượng bán trung bình khi giá bán thịt hộp là 31 nghìn đồng và giá
bán cá hộp là 28 nghìn đồng.
10. Tìm ước lượng điểm sự thay đổi của lượng bán khi giá bán thịt hộp và giá bán cá hộp
cùng tăng thêm 1 nghìn đồng.
11. Tìm ước lượng điểm sự thay đổi của lượng bán khi giá bán thịt hộp giảm 2 nghìn đồng
và giá bán cá hộp tăng thêm 3 nghìn đồng.
12. Khi bỏ biến PC ra khỏi mô hình thì hệ số xác định là 0.426150. Bằng kiểm định F hãy
cho biết có nên bỏ biến PC hay không?
13. Khi thêm biến PH là giá của loại hàng hóa hoa quả đóng hộp thì hệ số xác định tăng
lên 0.986. Vậy có nên thêm biến PH vào mô hình không?
Bài 6. Cho kết quả ước lượng với 100 doanh nghiệp sản xuất chế biến. Y là sản lượng, K
là vốn, L là lao động; LY, LK, LL là logarit cơ số tự nhiên của các biến tương ứng. Cho α = 5%. Dependent Variable: LY Method: Least Squares Sample:1 100 Included observations: 100 Variable Coefficient Std. Error t-Statistic Prob C 0.416571 0.114175 3.648529 0.0004 LK 0.621661 0.014506 42.85566 0.0000 LL 0.476395 0.005883 80.97390 0.0000 R-squared 0.988628 Mean dependent Var 8.136574 Adjusted R-squared 0.988393 F-statistic 4216.348 Sum squared resid 0.204993 Prob(F-statistic) 0.000000 Yêu cầu:
1. Viết hàm hồi quy tổng thể, hồi quy mẫu với các biến Y, K, L.
2. Giải thích ý nghĩa của các hệ số ước lượng được.
3. Vốn tăng 1%, lao động không đổi thì sản lượng tăng trong khoảng nào?
4. Lao động tăng 1%, vốn không đổi thì sản lượng tăng trong khoảng nào?
5. Các biến độc lập giải thích được bao nhiêu phần trăm sự biến động của biến phụ thuộc?
7. Kiểm định sự phù hợp của hàm hồi quy.
8. Các hệ số có ý nghĩa thống kê không?
9. Dựa trên ước lượng điểm các hệ số, quá trình sản xuất có hiệu quả tăng, giảm hay không đổi theo quy mô.
Bài 7. Cho kết quả hồi quy với Z là lương (triệu đồng), X là doanh thu công ty (triệu đồng),
Y là số lao động (người). Với mức ý nghĩa 5% Dependent Variable: Z Method: Least Squares Sample: 1 372 Included observations: 372 Variable Coefficient Std. Error t-Statistic Prob C -61.53048 122.6508 -0.50167 0.6229 X 0.715687 0.006706 106.723 0.0000 Y -1.757382 0.463171 -3.794237 0.0002 R-squared 0.89749 Prob(F-statistic) 0.0000 Yêu cầu:
1. Viết hàm hồi quy mẫu và giải thích kết quả ước lượng được.
2. Với mức ý nghĩa 5%, mô hình có phù hợp không? Mô hình giải thích được bao nhiêu %
sự biến động của lương.
3. Với độ tin cậy 95%, nếu Y tăng thêm 1 đơn vị thì lương trung bình giảm trong khoảng nào?
4. Với mức ý nghĩa 5%, có thể cho rằng X tăng 1 đơn vị thì lương trung bình tăng nhiều
hơn 0.9 đơn vị hay không?
5. Có ý kiến cho rằng loại hình doanh nghiệp mà người lao động làm việc (DN liên doanh
và loại hình DN khác) có ảnh hưởng tới lương của người lao động. Hãy đề xuất cách mô
hình hóa để phân tích ý kiến này.
Bài 8. Cho kết quả hồi quy với GIP là tổng sản phẩm ngành công nghiệp, DI là đ ầu tư khu
vực trong nước, GE là chi tiêu chính phủ.
Số liệu của 52 nước đang phát triển, đơn vị tính triệu USD.
Với mức ý nghĩa 5% cho mọi kiểm định và khoảng tin cậy. Dependent Variable: GIP Method: Least Squares Sample: 1 52 Included observations: 52 Variable Coefficient Std. Error t-Statistic Prob C 5160.358 4141.907 1.245889 0.2187 DI 0.571653 0.068992 8.285835 0.0000 GE 0.682839 0.074374 9.181150 0.0002 R-squared 0.959679 F-statistic 583.1222 Prob (F-statistic) 0.000000 Yêu cầu:
1. Viết hàm hồi quy tổng thể và hàm hồi quy mẫu
2. Giải thích ý nghĩa kết quả ước lượng các hệ số và hệ số xác định.
3. Hàm hồi quy có phù hợp không?
4. Biến độc lập nào thực sự giải thích cho biến phụ thuộc.
5. Có thể nói cả hai biến độc lập đều tác động cùng chiều đến biến phụ thuộc không?
6. Khi đầu tư trong nước tăng 1 triệu USD, chi tiêu chính phủ không đổi thì GIP tăng trong khoảng nào?
7. Khi chi tiêu chính phủ tăng 1 triệu USD, đầu tư trong nước không đổi thì GIP có tăng hơn 0.5 triệu USD không?
8. Kiểm định ý kiến cho rằng tác động của DI và GE đến GIP là như nhau biết hiệp phương
sai ước lượng hai hệ số góc tương ứng xấp xỉ bằng 0.
9. Nếu thêm vào mô hình biến đầu tư trực tiếp nước ngoài FDI ta được kết quả sau: Dependent Variable: GIP Method: Least Squares Sample: 1 52 Included observations: 52 Variable Coefficient Std. Error t-Statistic Prob C 2200.373 3582.184 0.614255 0.5419 DI 0.516150 0.059942 8.610883 0.0000 GE 0.317418 0.103559 3.065095 0.0036 FDI 4.755274 1.067449 4.454594 0.0001 R-squared 0.971472 F-statistic 544.8594 Prob(F-statistic) 0.000000
a. Viết hàm hồi quy tổng thể và hàm hồi quy mẫu
b. Giải thích ý nghĩa kết quả ước lượng hệ số biến FDI.
c. Dùng kiểm định F để cho biết có nên thêm biến FDI vào mô hình hay không?
d. Khi các biến khác không đổi, FDI tăng 1 triệu USD thì GIP tăng tối thiểu bao nhiêu?
MÔ HÌNH HỒI QUY VỚI BIẾN GIẢ
Bài 1. Để phân tích mức thu nhập của người lao động phụ thuộc vào khu vực: Khu vực 1
(vùng sâu vùng xa), khu vực 2 (nông thôn), khu vực 3 (thành thị), người ta xây dựng mô hình như sau:
Yi = β1 + β2D2i + β3D3i + ui
Tiến hành lấy mẫu 20 lao động được kết quả như sau. Cho α = 5%.
Thu nhập (triệu đồng) Khu vực
Thu nhập (triệu đồng) Khu vực 5 1 14 3 4 1 16 3 5 1 16 3 8 2 15 3 9 2 10 2 12 3 9 2 13 3 3 1 15 3 4 1 6 1 4 1 8 2 7 2
D2i = 1 nếu người lao động thuộc khu vực 2.
D2i = 0 nếu người lao động không thuộc khu vực 2.
D3i = 1 nếu người lao động thuộc khu vực 3.
D3i = 0 nếu người lao động không thuộc khu vực 3.
Yi là thu nhập của lao động i. Yêu cầu:
1. Xác định hàm hồi quy mẫu.
2. Thu nhập trung bình khu vực 1 có khác khu vực 2 hay không?
3. Thu nhập trung bình khu vực 1 có khác khu vực 3 hay không?
4. Thu nhập trung bình khu vực 1 có thấp hơn khu vực 2 hay không?
5. Thu nhập trung bình khu vực 1 có thấp hơn khu vực 3 hay không?
6. Chênh lệch thu nhập trung bình khu vực 1 và khu vực 2 nằm trong khoảng nào?
7. Chênh lệch thu nhập trung bình khu vực 1 và khu vực 3 nằm trong khoảng nào?
Bài 2. Điều tra mẫu có kích thước n = 12, người ta thu được các số liệu sau: Y 60 61 63 65 67 70 70 73 77 78 80 85 X 4 4 5 5 6 6 7 8 7 8 9 9 Z 1 0 1 1 0 1 0 0 1 0 1 0
Trong đó: Y là thu nhập hàng năm của một giảng viên Đại học (triệu đồng); X là tuổi nghề
của giảng viên; Z = 1 nếu giảng viên thuộc một Trường Đại học ở phía Bắc và Z = 0 nếu
giảng viên thuộc một Trường Đại học ở phía Nam. Yêu cầu:
1. Bằng phương pháp bình phương bé nhất, xây dựng hàm hồi quy mẫu dạng tuyến tính.
2. Với mức ý nghĩa 2%, tuổi nghề có ảnh hưởng tới thu nhập của giáo viên không?
3. Xác định khoảng tin cậy 98% cho β3
4. Với mức ý nghĩa 5%, có thể nói cả hai yếu tố tuổi nghề và địa phương làm việc đều
không ảnh hưởng tới thu nhập của giảng viên hay không?
5. Với độ tin cậy 95%, dự báo giá trị trung bình củ a Y khi X = 8 và Z = 0.
Bài 3. Cho kết quả hồi quy với CS là tiêu dùng khu vực dân cư, GDP là tổng sản phẩm
quốc nội, Ln(CS), Ln(GDP) là logarit cơ số tự nhiên của các biến tương ứng, D92 là biến
giả nhận giá trị bằng 1 nếu quan sát từ năm 1992 về sau và bằng 0 trong các giai đoạn trước đó. Cho α = 5%. Dependent Variable: Ln(CS) Sample: 1976 2006 Included observations: 31 Variable Coefficient Std. Error t-Statistic Prob C 0.019662 0.115673 0.169976 0.8663 D92 1.006168 0.171370 5.871334 0.0000 Ln(GDP) 0.984527 0.013690 71.91794 0.0000 D92*Ln(GDP) -0.120398 0.018433 -6.531512 0.0000 R-squared 0.999401 F-statistic 15024.03 Durbin-Watson stat 1.058828 Prob(F-statistic) 0.000000
Hiệp phương sai hai ước lượng hệ số góc tương ứng với Ln(GDP) và D92*Ln(GDP) là nhỏ không đáng kể. Yêu cầu:
1. Viết hàm hồi quy mẫu ứng với các biến CS, GDP trong các giai đoạn từ năm 1992 về
sau và giai đoạn trước đó.
2. Giả sử GDP cùng bằng 1 thì tiêu dùng năm 2000 bằng tối đa bao nhiêu lần tiêu dùng năm 1990?
3. Nếu cùng mức tăng trưởng kinh tế thì mức tăng trưởng tiêu dùng hai giai đoạn có khác
nhau không? Nếu có thì giai đoạn nào tăng trưởng tiêu dùng nhanh hơn?
4. Vào năm 2000, nếu GDP tăng tr ởng ư
10% thì tiêu dùng dân cư tăng trong khoảng nào?
Bài 4. Nghiên cứu sự biến động của lượng gas bán ra Q (bình) phụ thuộc vào giá gas P
(1.000 đ/bình), có người cho rằng chất lượng gas là quan trọng. Người đó cho rằng trong
những tháng đại lý nhập bình gas mới thì lượng bán ra không giống với những tháng nhập
bình gas cũ, do đó đã hồi quy mô hình có các biến như sau:
D = 1 với những tháng nhập bình gas mới.
D = 0 với những tháng khác. DP = D*P. Cho α = 5%. Dependent Variable: Q Method: Least Squares Sample:97M1 99M3 Included observations: 27 Variable Coefficient Std. Error t-Statistic Prob