Đề thi cuối kỳ môn Giải tích 1 năm 2016 | Đại học Bách Khoa Hà Nội

ĐỀ THI CUỐI KÌ MÔN GIẢI TÍCH 1 – HỌC KÌ 20161 Đề 1 + 2
Câu 1. Tính các số thực a, thỏa mãn (1) ln(cos 3x) lim =1 x 0 ax →
Gợi ý: 2 +)  3 2  3x −9 ln(cos 3 ) = ln 1− sin x x x ;  2 x → 0 : 2 − sin ~ 2    2 2  −9 2 −  = +) 9x a  lim =1  2  x→ 0 2 ax a = 2  3 5 (1 +sin ) x 1 − (2) lim =1 x 0 ax → Câu 2. Tính 1  −  (1) x   f '(0) với e , x (0; ) f (x ) =  0, x  (− ;  0] 
Gợi ý: 1 1
f (x) − f (0) x L e 1 +) ' = = = = = + (0) lim lim lim x f lim 0 + + + 1 + 1 x→ 0 x→ 0 x→ 0 x→ 0 x − 0 x x x e e − +) f (x) f (0) f ' (0) = lim = 0 − x→ 0− x − 0 +) Vậy f '(0) = 0 1  −  (2) x 1
e − , x ( − ;  1)
f '(1) với f (x) =  0, x(1;+] 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 3. Tìm khai triển Maclaurin của
(1) f (x) = xsin x đến 6 x
Gợi ý: 3 5 4 6 +) x x 6 2 x x 7 sin x = x − +
+ 0(x )  f (x) = x sin x = x − + + 0(x ) 3! 5! 3! 5!
(2) f (x) = x cos x đến 5 x Câu 4. Tính (1) 2 sin x e sin(2 ) x dx 
Gợi ý: +) 2 2 2 2 sin x sin x sin x 2 sin = sin(2 ) = 2sin cos = (sin ) x I e x dx e x xdx e d x = e + C    (2) 2 cos x e sin(2 ) x dx 
Câu 5. Tính độ dài đường cong 3 x 1 (1) y = + , x1;  2 6 2x
Gợi ý: 3 2  x 1   x 1 
+) dy = y 'dx =  +  'dx =  −  dx 6 2x 2 2x     +) 2 2 2 2 2
dl = dx + dy = dx + ( y 'dx) = 1+ (y ') dx 2 2 2 2 2 2 2 2  x 1   x 1  +) 2 l = dl = 1 + ( y') dx = 1+ − dx = + dx      2   2 2 2  x 2 2x 1 1 1   1   2 2 1  1  17 2 = x + dx =   2  2  x  12 1 4 x 1 (2) y = + , x 1; 2 2   8 4x 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng + + (1) ( x 2)dx  4 2 x − x + 3 0
Gợi ý: + +) (x + 2)dx (x + 2) I = ;   0; x   0 4 2 x − x + 3 4 2 x − x + 3 0 x+ 2 1 1 +) Khi x → +: ~ ;  HT  I HT (TCSS) 4 2 3 x − x + 3 (x + 1) 3 (x +1) + (3x + 2) (2) dx  3 2 x + x + 4 0 Câu 7. Tính 3 (1) lim x 2 4
(x;y )→(0;0) x + y
Gợi ý: 3 x +)  x ; (  ; x ) y  (0;0) 2 4 x + y 3 +) x lim x = 0  lim = 0 2 4 (x ;y )→ (0;0)
(x ;y )→ (0;0) x + y 5 (2) y lim 4 2
(x;y )→(0;0) x + y
Câu 8. Tìm giá trị lớn nhất, nhỏ nhất của (1) 3 2
z = x + y + xy − 7x − 8y trong miền ở đó O(0;0), (6 A ;0), B(0;6)
Gợi ý: 3 CuuDuongThanCong.com
https://fb.com/tailieudientucntt z
 ' = 2x + y − 7 = 0   = x x 2 +) Điểm tới hạn     M (2;3) 1 z
 ' = 2y + x − 8= 0 y =  y  3 +) O(0;0), (6
A ;0)  Ox, B(0; 6)  Oy 7  7 2  ( ;
x y) OA  z = f (x) = x − 7 ,
x x  (0; 6); f '(x) = 0  x =  M ;0 2   2  2  2 ( ;
x y) OB  z = g( y) = y − 8 y, y  (0;6); g '( y) = 0  y = 4  M 0; 4 3 ( ) 5  5 7 2  ( ;
x y)  AB  z = h(x) = x − 5x −12; h'( x) = 0  x =  M ; 4   2  2 2 
+) max z = max (z0), (z ) A , ( z ) B , ( z M ), ( z M ), ( z M ), ( z M ) = 0 tại O(0;0) 1 2 3 4  (x ;y )
min z = minz(0), z( )
A , z(B), z(M ), z(M ), z(M ), z(M ) = −19 tại 1 2 3 4  M ,… ( 1 x ;y ) (2) 3 2
z = x + 2 y + 3xy −13x −18y trong miền
ở đó O(0;0), A(7;0), B(0;7) Câu 9. Hàm số
(1) z = z(u;v) khả vi trên , có ' ' z (1; 1 − ) = 2; z (1; 1 − ) = 3. Đặt 2 3
f (x) = z(x ; x ), u v tính f '(−1)
Gợi ý: +) 2 3 2 3 2
f '(x) = z ' (x ; x ).2x + z ' (x ;x ).3x u v
+)  f '(1) = z' (1; 1 − ).( 2 − ) + z' (1; 1 − ).3 = 2.( 2 − ) +3.3 = 5 u v
(2) z = z(u;v) khả vi trên , có ' '
z (1;1) = 3; z (1;1) = 4. Đặt 3 2
f (x) = z(x ; x ), tính u v f '(1) 4 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
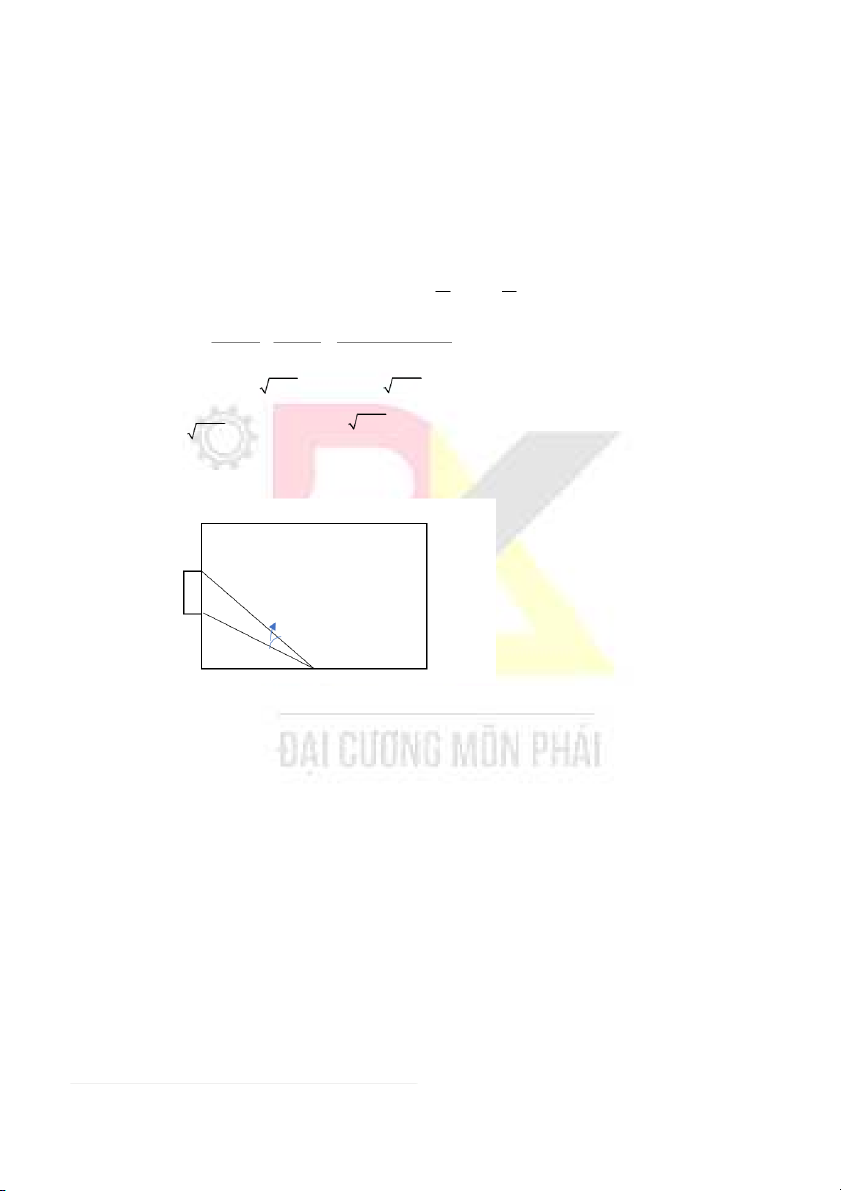
Câu 10. Một chiếc xe cứu hộ xuất phát từ góc của 1 hồ nước hình chữ nhật có các
cạnh dài a, cạnh rộng .
b Xe vừa có thể đi trên bờ hồ và đi trên mặt nước với vận tốc
tương ứng là 20m/s và 12m/s. Tính thời gian ít nhất để xe đi đến giao điểm 2 đường chéo của hồ (1) a =1600 ; m b = 600m
Gợi ý:
+) Có 2 lựa chọn đi trên bờ theo cạnh dài (hoặc cạnh ngắn) 1 đoạn rồi đi xuống nước
* TH1: Đi theo cạnh dài 1 đoạn x 2 2 (800− x) + 300
- Khi đó, thời gian đi tổng cộng t = f ( ) x =
( ) với x 0;80  1 s 0 12
f (0) = 71, 2(s); f (800) = 65(s) 1 ( − 500 − ) x f '(x) = +
= 0  x = 575  t(575) = 60(s) 2 2 20 12 (800 − x ) +300
- Vậy thời gian ngắn nhất trong TH1 là 60s
*TH2: Đi theo cạnh ngắn 1 đoạn y 2 2 (300 − y) + 800
- Khi đó, thời gian đi tổng cộng t = f (y) =
(s) với y  0;300 2 12
f (0) = 71, 2(s); f (300) = 81, 67(s) 1 ( − 300 − ) x f '(y) = +
= 0  x = 607,11 (loại) 2 2 20 12 (300− y ) +800
- Vậy thời gian ngắn nhất trong TH2 là 71,2s
+) Vậy thời gian ngắn nhất là 60s: đi bộ trên cạnh dài 1 đoạn 575m rồi đi xuống nước (2) a = 2000 ;
m b = 600m 5 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Đề 3 + 4
Câu 1. Tìm và phân loại điểm gián đoạn của hàm số  1 , x 9   (1) = 2 − log y  3 x 3,x   0;−9;  9
Gợi ý: +) 1 lim
= 0  y(0)  x = 0 là điểm gián đoạn có thể bỏ được
x→0 2 − log3 x +) 1 1 lim lim = +  x = 9
 là điểm gián đoạn loại 2 của hàm số x 9+ x 9 2 − log x − → → 2 − log 3 3 x  1 , x   8 (2)  = 3− log y  1 x 3,x   0;−8;  8 Câu 2. Tính 5 5 − (1) x sin(x ) lim 15 x →0 sin x
Gợi ý: 5 5 5 5 − − +) x sin(x ) x sin(x ) I = lim = lim 15 15 x →0 x →0 sin x x L L L − − +) Đặt 5 t sin t 1 cos t sin t cos t 1
t = x  I = lim = lim = lim = lim = 3 2 t → 0 t → 0 t → 0 t → 0 t 3t 6t 6 6 7 7 x − ln(1 + x ) (2) lim 14 x →0 tan x
Câu 3. Cho 3 số thực a,b,c thỏa mãn a +b+ c = 0. Chứng minh rằng: (1) PT 5 4
6ax + 5bx + c = 0 có ít nhất một nghiệm thuộc (0;1) Gợi ý:
+) Xét hàm số f (x) khả vi: 6 5
f (x) = ax + bx + c ; x x 0; 
1 ; f (0) = f (1) = 0 6 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
+) Theo định lý Rolle: x  (0; ) 5 4
1 : f '(x ) = 0  6ax + 5bx + c = 0 (đpcm!) 0 0 0 0 (2) PT 7 3
8ax + 3bx + c = 0 có ít nhất một nghiệm thuộc (0;1) Câu 4. Tính 3 (1) x dx  8 1+ x
Gợi ý: 3 4 x 1 d( x ) 1 +) 4 I = dx = = arctan(x ) +C  8  4 2 1+ x 4 1+ (x ) 4 4 (2) x dx  10 x −1
Câu 5. Tính diện tích mặt tròn xoay được tạo ra khi (1) Quay đường 2 y =
4x − x , x  1;2 quanh trục Ox một vòng Gợi ý: +) 2 2 2 dl = (d ) x + (d ) y = 1+ (y ') dx 2 +) 2
S = 2 y dl = 2 y 1 + ( y ') dx   1 2 2 2− x 4− 4 + +) 2 2 = 4 −  ' =  = 2 4 − . 1 x x y x x y S x x + dx  2 2 4 4x − x x − x 1 2 2 2 2 = 2
4x − x + 4 − 4x + x dx = 2 2dx = 4   1 1 (2) Quay đường 2
y = 8x − x , x  1; 2  quanh trục Ox một vòng 7 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng 1 (1) x xdx  1− cos 0 x
Gợi ý: 2 x 0+ → +) x x x x x 2
x →0 :1 −cos x ~ 0  ~ = ; x 0 2 2 1− cos x x x 2 1 1 +) 2 x xdx dx  HT →  HT (TCSS) 1− cos 0 x 0 x 1 ln(1+ x ) (2) dx  x sin 0 x
Câu 7. Tìm cực trị của hàm số (1) 1 3 2 y z = + y − 3 x x
Gợi ý:  −3 3y z ' = + = 0  x 4 2  x x x  = 1 +) Điểm tới hạn     M (1;1) 3 y =   1 2 z ' =3 y − = 0 y  x 12 6y 3 +) Lại có: z ' = − ;z ' ; z ' = 6y xx 5 3 xy 2 yy x x x
 z ' (M ) = 6;z ' (M ) = 3; z ' (M ) = 6 xx xy yy 2 2
  = 3 − 6  0. Vậy hàm số đạt cực tiểu tại M (1;1) ; z(1;1) = 1 − 1 3 (2) 3 x z = x − − 3 y y 8 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 8. Tính đạo hàm riêng  y a  rctan , x  0 (1) '
z (x ;y ) của hàm số z = y  x 0  , x =0
Gợi ý:  −  − +) 1 1 ' ( ; ) = . y z x y y = ; x  0 x 2  2  2 2  y 
 x  x + y +1    x  +) z( ; x 0) − z(0;0) z ' (0;0) = lim = 0 x x 0 → x − 0 arctan y
z (x; y) − z(0; y) ' (0; ) = lim = lim x z y
không tồn tại, y  0 x x 0 → x 0 x − 0 → x − 0  x a  rccot , y  0 (2) '
z (x ;y ) của hàm số z =  y y 0  , y =  0 Câu 9. Tìm (1) Hàm số z( ;
x y) thỏa mãn z ' = 2 x + , y z ' = 2 y + , x (  ; x ) y  x y
Gợi ý: 2 2 +) ' = 2 +  ( ; ) = (2 + ) x z x y z x y x y dx = + yx + ( C ) y  (1) x 2 +) '
z = 2y + x (2) y
+) (1)  z' = x +C'( ) y (3) y +) (2) và (3) 2
 C '(y) = 2y  C( y) = C '( y)dy = y + C  Vậy 2 2 z( ;
x y) = x + xy + y + C;C  (2) Hàm số z( ; x y) thỏa mãn ' '
z = 6x + 5y, z = 5x − 4y,(x; y) x y 9 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 10. Một sân bóng đá có biên ngang dài a (m), cầu môn rộng b (m). Bóng nằm
trên biên dọc, cách biên ngang x (m). Tính góc sút bóng vào cầu môn theo x, tìm x để góc sút lớn nhất (1) a = 69m; b = 7m
Gợi ý:
+) Từ hình vẽ, ta có góc sút: 38 31
 = f (x) = arctan − arctan ; x  0 x x 2 +) 3 − 8 31 7(1178 − x ) f '(x) = + = 2 2 2 2 2 2 2 2 x + 38 x + 31
(x + 38 )(x + 31 )
f '(0) = 0  x = 1178  34,3( )
m ; f ( 1178) = 0,1(rad )  − +) x 1178
x  1178  f '(x)  0    f =    0,1rad max max (2) a = 56m; b = 6m Góc sút x 10 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Đề 5 + 6 Câu 1. Cho hàm số (1) 2 2
z = ln(x + 3y ),( ; x y)  (0;0). Tính ' ' A = .
x z + y.z x y
Gợi ý: 2 6 +) x y z ' = ; z ' = x 2 2 x + 3y y 2 2 x + 3 y 2 2 +) 2 x 6 y
A = xz ' + yz' = + = 2 x y 2 2 2 2 x + 3y x + 3y (2) 4 4
z = ln(x + 5y ),( ; x y)  (0;0). Tính ' ' A = .
x z + y.z x y Câu 2. Tính (1) lim x  2 − arctan(2 ) x  x →+
Gợi ý: 4 − 2 L 2 +) =  −   − 2arctan 2x 4 1 +4 x lim 2 arctan(2 ) = lim = lim x I x x = lim =1 2 x→+ x→+ 1 x→+ 1 − x→+ 1+ 4x 2 x x (2) lim x ln x x →0
Câu 3. Xét tính lồi, lõm của đồ thị hàm số (1) = ( −1) x y x e
Gợi ý: +) ' x =  ' = ( 1 + ) x y xe y x
e  y' (0)  x = 1 −
 y '  0 : x  −1
+) Xét dấu của y' : 
 Vậy đồ thị lồi khi…; lõm khi…
y'  0 : x  1 −  (2) ( 1) x y x e− = + 11 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Câu 4. Tính (1) dx 
5cos x +12sin x +13
Gợi ý: 2 +) Đặt x 2dt 1− t 2t t = tan  dx = ;cos x = ;sin x = 2 2 2 2 1+ t 1+t 1+t +) dx 1 2dt dt I = = =   2 2  2
5cos x +12sin x +13 1−t 2t 1+t 4t +12t + 9 5 +12 +13 2 2 1+t 1+t dt −1 −1 = = +C = +C  2 (2t + 3) 2(2t + 3)   2 2 tan x +3    2  (2) dx 
12 cos x − 5sin x −13
Câu 5. Tính diện tích hình phẳng giới hạn bởi đường cong cho hệ tọa độ cực (1) r = 5 + 2cos
Gợi ý:
+) Áp dụng công thức diện tích hình phẳng trong tọa độ cực: 2 2 1 1  2 2 S = (5 + 2cos )  d = (25 +20cos  +4 cos )  d   2 2 0 0 cos 2 1 +) 2 cos  + = 2 2 1  1  S =
(27 + 20cos + 2 cos 2 )d = (27 + 20sin +sin 2 ) 2|       = 27  0 2 2 0 (2) r = 7 − 2cos 12 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng + +
(1) (sin x 2cosx)dx  2 x + 1 0
Gợi ý: sin x + 2cos x 3 +)  ;x 2 2 x +1 x +1 + + + +) 3
(sin x 2 cos x)dx dx  HT  2  HT (TCSS) x 1 + 2 x 1 + 0 0
+ (sin 2x − 3cosx) (2) dx  3 x +1 0
Câu 7. Tìm điểm gián đoạn của hàm số (1) 6 f (x) = lim , x 2 →+ 2 n n + x
Gợi ý: +) 6 x  1: lim = f (x) = 0; 2 →+ 2 n n + x 6 6 x  1: lim
= lim = f (x)= 3; 2 →+ 2 n n n + x →+ 2 6 6 x = 1: lim = lim = f (x) = 2 2 n 2 →+ 2+ x →+ 2+ 1 n n n
+) Vậy các điểm gián đoạn của f (x) là x = 1  arctan(nx) (2) f (x) = lim , x  2 n →+ 1+ x 13 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 8. Tìm cực trị của hàm số 4 3 (1) xy z = + − x y 12
Gợi ý:  −4 y z ' = − = 0  x 2  x 12 x = 4 − +) Điểm tới hạn:     M (−4; 3 − ) −3 x y = −3 z ' = − = 0  y 2  y 12  8 −1 6 −1 −2 +) z' = ; z ' = ; z ' =  z' (M) = ; z' (M ) = xx 3 xy yy 3 x 12 xx y 8 yy 9 2  1 −  2 1   = − .  0. 
Vậy z đạt cực đại tại z(M ) = 3 − tại M ( 4 − ; 3 − ) 12    9 8 2 3 (2) xy z = − + x y 6 Câu 9. (1) PT 3 3
x − y + 3xy −13 = 0 xác định hàm ẩn y = y(x). Viết phương trình tiếp
tuyến của đồ thị hàm ẩn này tại điểm ( A −1; −2)
Gợi ý: 2
F ' = 3x + 3y  F ' (−1;−2) = 3 − +) 3 3 
F (x; y) = x − y + 3xy− 13 x x     2
F ' = −3y + 3x F ' ( 1 − ; 2 − ) = 1 − 5   y  y F ' ( 1 − ; 2) − 1 −  y '( 1 − ) x = =  PTTT: 1 y = − x + a F ' ( 1 − ; 2) − 5 5 y +) Thay 1 11 ( ; x y) = ( 1 − ; 2 − )  2
− = − x −1+ a  a = −  PTTT: 1 11 y = − x − 5 5 5 5 (2) PT 3 3
x + 2y + 4xy − 7 = 0 xác định hàm ẩn y = y(x). Viết phương trình tiếp
tuyến của đồ thị hàm ẩn này tại điểm ( A 1;1) 14 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Câu 10.
(1) Gập 1 tấm tôn hình chữ nhật rộng 30cm, dài 3m thành 1 cái máng nước.
Gấp theo chiều dài mỗi bên tấm tôn 10cm, tính góc gập  để thể tích của máng lớn nhất
Gợi ý:
+) Máng là 1 lăng trụ đứng có chiều cao 3m. Chiều cao máng không đổi nên để máng
có thể tích lớn nhất thì diện tích đáy của máng phải lớn nhất  1   S = 2
.10 cos .sin  +10.10 sin  =10 cos .sin  +100 sin ; 0    day  2    2   +)  2 S(0) = 0; S =100(cm )  2   
+) S '( ) = (50sin2 1
+ 00sin )' =100(cos2 +cos ) ( )  1  cos =   = 2 S '( ) 0 cos 2 cos 0 2 cos  cos 1 0   =  + =  + − =  2 3 cos = 1 −   
+) Vậy thể tích máng lớn nhất tại  =  . 2 S = 75 3    129,9(cm ). 3  3  − 9 3 V 
=3.75 3.10 0,039(m ) max
(2) Gập 1 tấm tôn hình chữ nhật rộng 45cm, dài 4m thành 1 cái máng nước.
Gấp theo chiều dài mỗi bên tấm tôn 15cm, tính góc gập  để thể tích của máng lớn nhất 15 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Đề 7 + 8 Câu 1. Cho hàm số (1) 3 2
z = x + 2xy − .
y Tính vi phân dz(1; 2)
Gợi ý: 2 2 z
 ' =3x +2 y +) x   d (
z 1; 2) = z ' (1; 2)dx + z ' (1; 2)dy =11dx +7dy z ' = 4 xy 1 x y −  y (2) 2 3 5
z = x + 2xy − y . Tính vi phân dz(2;1) Câu 2. Tính 1  x x−5 (1)  lim  x →5  5 
Gợi ý: 1 1 5 − lim .ln x x +)  x  x 5 x 5 − 5 I = lim = e →   x →5  5 1 1 x 1  x −5  1 x −5 1 +) 5 I = lim .ln = lim .ln 1− = lim . =  = 1 I e   x 5 → x 5 → x→5 x − 5 5 x − 5  5  x − 5 5 5 1 −  + (2) x x 1 1 lim  x →1  2 
Câu 3. Tìm các tiệm cận của đồ thị hàm số ln (1) x y = x
Gợi ý: ln +) x lim y = lim
= −  x = 0 là TCĐ + + x →0 x →0 x 16 CuuDuongThanCong.com
https://fb.com/tailieudientucntt L +) ln x 1 lim y = lim = lim = 0  y = 0 là TCN x →+ x →+ x x →+ x +) Hàm số không có TCX (2) x y = x e − 1 Câu 4. Tính (x +1) (1) dx  2 x − 2x − 1
Gợi ý: + − +) (x 1)dx x 1 2 I = = dx + dx    2 2 2 x − 2x −1 x − 2 x 1 − x − 2x −1 2
1 d (x −1) − 2   d (x −1) 2 2 = + 2
= x − 2x −1 + 2ln x −1+ x − 2x −1 +C   2 2 2 (x −1) − 2 (x −1) − 2 (x + 1) (2) dx  2 2+ 2 x− x
Câu 5. Tính thể tích khối tròn xoay sinh ra khi quay miền giới hạn bởi các đường (1) 2
y = 0, y = x − 4x + 3 quanh trục Oy một vòng
Gợi ý:  x =1 +) Tìm cận: 2
x − 4x + 3 = 0  . 
Áp dụng CT tính thể tích khối tròn xoay: x =  3 3 3 3 16 2 3 2 V = 2 xy dx = 2 (
x −x + 4x − 3)dx = 2 (−x + 4x −3 ) x dx =    3 1 1 1 17 CuuDuongThanCong.com
https://fb.com/tailieudientucntt (2) 2
y = 0, y = x − 5x + 4 quanh trục Oy một vòng
Câu 6. Xét sự hội tụ, phân kì của tích phân suy rộng + (1) ln(1+ x)dx  x + 2 0
Gợi ý: +) ln(1 + ) x ln 2 x   1:   0 x + 2 x + 2 + + + +) ln 2 ln(1 ) x dx dx  PK   PK (TCSS) x + 2 x + 2 1 0 + + (2) ln(2 x)dx  2x + 1 0
Câu 7. Tìm các số thực a, để
(1) ( ) ln(3x 5 )x f x , ( g ) x ax = + =
là 2 vô cùng lớn tương đương khi x → +
Gợi ý: x x      +)   x x x 3 3 ln(3 + 5 )' = ln 5 1+ ' = x ln5+ ln 1     +      5x   5       3 x +) Khi  → + :
~ 0 ln(3x + 5x x ) ~x ln 5  5    a = ln 5
+) Để f (x) ~ g(x) khi x → +  xln 5 ~ ax    1 =  (2) ( ) ln(2x 3x f x ), g( ) x ax = + =
là 2 vô cùng lớn tương đương khi x → + 18 CuuDuongThanCong.com
https://fb.com/tailieudientucntt
Câu 8. Tìm cực trị của hàm số (1) 2 2
z = x + 3y − 5xy + 3x − y
Gợi ý: z
 ' =2x −5 y +3 =0 x = x 1 +) Điểm tới hạn     M (1;1) z
 ' = 6 y −5x 1 − = 0  y = y 1
+) z' = 2; z' = 5 − ; z' = 6 xx xy yy +) 2
 = 5 − 2.6  0. Vậy z không đạt cực trị tại M, z không có cực trị (2) 2 2
z = 2x + y − xy − 3x − y
Câu 9. Cho hàm số z = z( ; x y) khả vi trên và thỏa mãn (1) 2 z(t ; x ty) = t z( ; x y), (  ; x y)  . Tính ' ' T = . x z + . y z −2 z x y
Gợi ý:
+) Xét (x ; y ) 0 0
f (t ) = z(tx ;ty )  f '(t ) = x .z ' (tx ;ty ) + y .z ' (tx ;ty ) 0 0 0 x 0 0 0 y 0 0 2
f (t) = t z(x ; y )  f '(t) = 2t.z(x ; y ) 0 0 0 0 ' '
 x .z ' (tx ;ty )+ y .z ' (tx ;ty )= 2t .z (x ;y ) x.z + y.z − 2z = 0 0 x 0 0 0 y 0 0 0 0 x y (2) 3 z(t ; x ty) = t z( ; x y), (  ; x y)  . Tính ' ' T = . x z + . y z −3 z x y
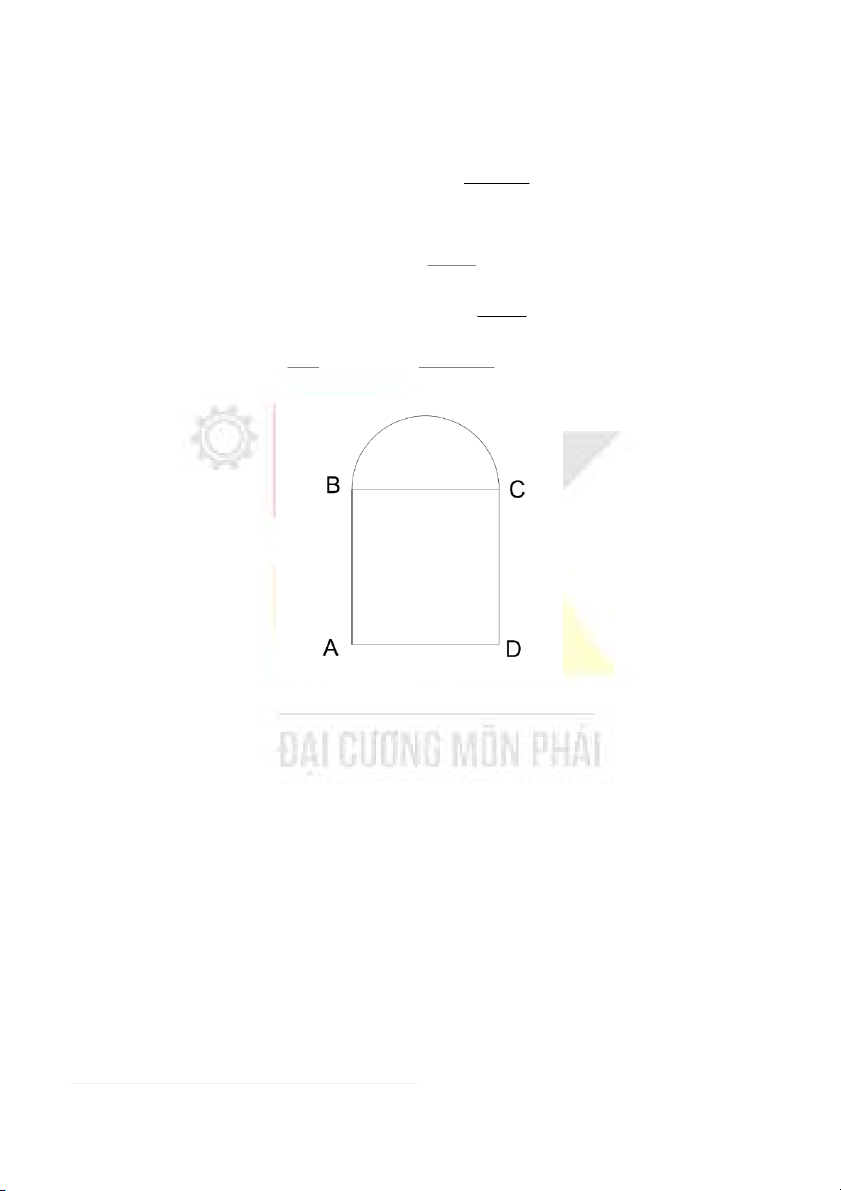
Câu 10. Một cửa sổ vòm kiểu Norman (gồm 1 hình chữ nhật ABCD và nửa hình tròn
đường kính BC ở phía trên) có chu vi là 5m. Tìm độ dài AB, AD để diện tích hình chữ
nhật ABCD lớn nhất .
Gợi ý:
+) Gọi bán kính đường tròn là x  AD = 2x 19 CuuDuongThanCong.com
https://fb.com/tailieudientucntt +) Chu vi vòm cửa là 5m 5 −x −2x
 2AB + AD + BC = 5  2AB + 2x + x = 5  AB = 2
+) Diện tích hình chữ nhật ABCD là: 2 S = A .
B AD = (5 − x −2 )
x x = 5x −( + 2)x 5
S '(x) = 5− 2( + 2)x  S '(x) = 0  x = = 0 x 2(2+  ) 5 S '( )
x  0  x  x . Vậy S đạt max tại = = 0 x 0 x 2(2 + ) 5 5− 2 −  +) Khi đó: x0 x0 2 AD = 2 x =  0,972 ; m AB = 1, 25m S 1,2156 0 max m 2 +  2 20 CuuDuongThanCong.com
https://fb.com/tailieudientucntt