

Preview text:
TRƯỜNG THPT THỦ ĐỨC
ĐỀ KIỂM TRA ĐÁNH GIÁ ĐỊNH KÌ GIỮA HỌC KỲ I
NĂM HỌC: 2022 – 2023 Môn: TOÁN KHỐI 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 60 phút. Không kể thời gian phát đề
Họ, tên thí sinh:……………………………………………
Số báo danh:………………………………………………
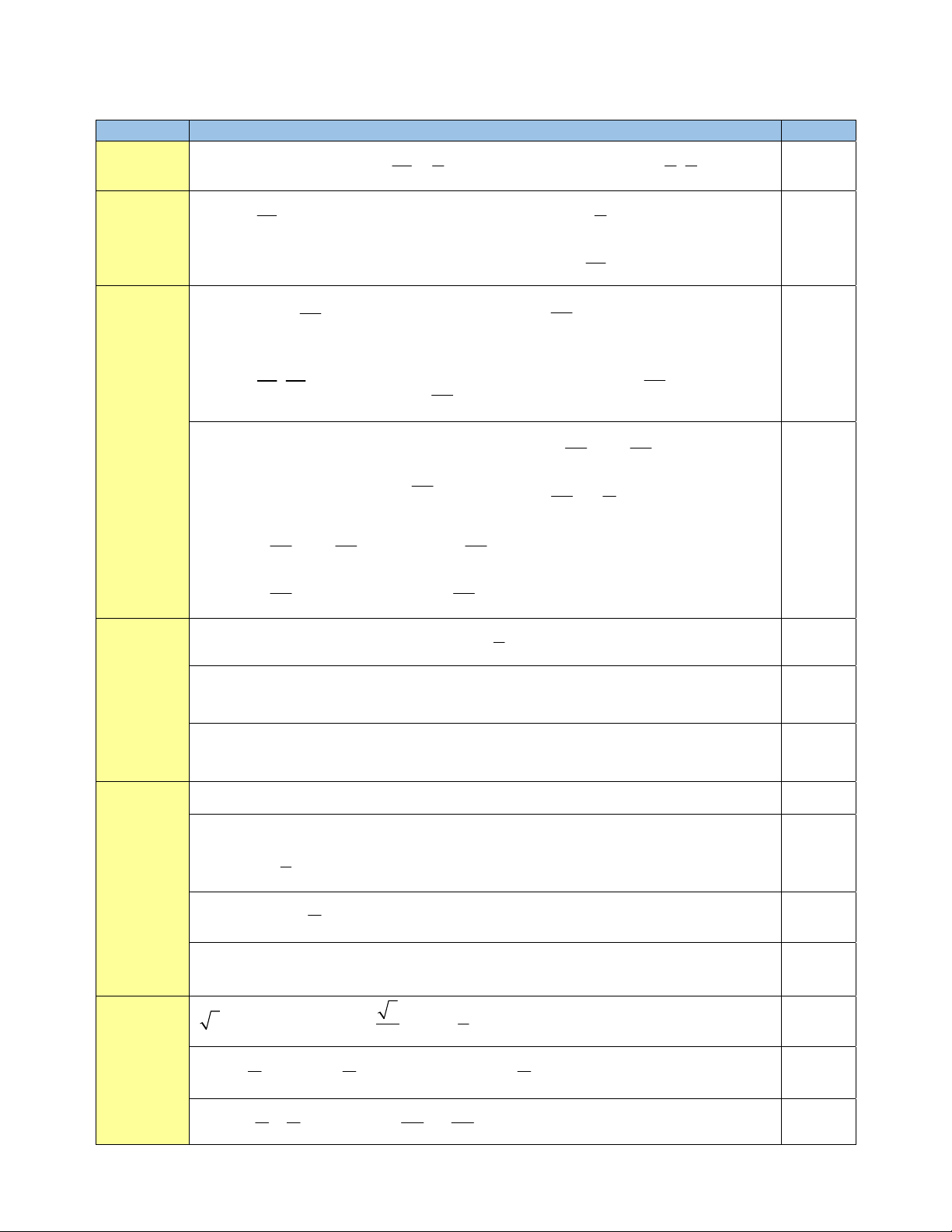
Câu 1. (2,5 điểm)
Cho hàm số y f x xác định trên và có bảng biến thiên như hình bên duới 5π π
a) Hãy mô tả chiều biến thiên của hàm số f x trên ; . 4 4 3π
b) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x trên ; π . 4 3 5π 3π
c) Tìm nghiệm của phương trình f x.sin x 1 2 f
x với x ; . 4 4 4
Câu 2. (3,5 điểm)
Giải các phương trình sau a) o
2 cos x 60 1 0 b) 2 2
2sin x cos x 5sin x 3
c) 3 sin 5x cos 5x 2 d) 2
8sin 2x 12 sin x cos x 3cos x 4
Câu 3. (1,0 điểm) 33 cos x 1
Gọi T là tập giá trị của hàm số y
. Hỏi trong T có bao nhiêu số nguyên dương? sin x 2
Câu 4. (2,0 điểm)
a) Từ các chữ số 0, 1, 2, 5, 8, 9 có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau sao
cho chữ số đầu tiên là số lẻ?
b) Danh sách đội tuyển quốc gia Việt Nam chuẩn bị tham dự AFF Mitsubishi Electric Cup 2022
vào tháng 12 năm 2022 có 31 cầu thủ gồm 3 thủ môn, 12 hậu vệ, 9 tiền vệ và 7 tiền đạo. Huấn luận viên
thường không tiết lộ danh sách 11 cầu thủ sẽ ra sân để thi đấu mà chỉ tiết lộ đội sẽ đá theo sơ đồ 3 – 4 – 3
(nghĩa là 3 hậu vệ, 4 tiền vệ, 3 tiền đạo và 1 thủ môn). Đối thủ đấu với đội tuyển Việt Nam đã có danh
sách tên và vị trí của 31 cầu thủ và rất muốn dự đoán đội hình, họ xét hết các khả năng có thể xảy ra. Hỏi
nếu đối thủ đã dự đoán được trước vị trí thủ môn thì có bao nhiêu đội hình có thể xảy ra?
Câu 5. (1,0 điểm)
Cáo Bắc Cực là loài động vật phổ biến ở vùng đồng hoang Bắc Cực. Giả sử
số lượng cáo ở Bắc Manitoba, Canada được biểu diễn theo hàm t f t 500sin
1000 trong đó t là thời gian, tính bằng tháng 1 t 12,t . 12
Hỏi vào thời điểm nào trong năm thì số lượng loài cáo đạt 1250 con?
------Hết------
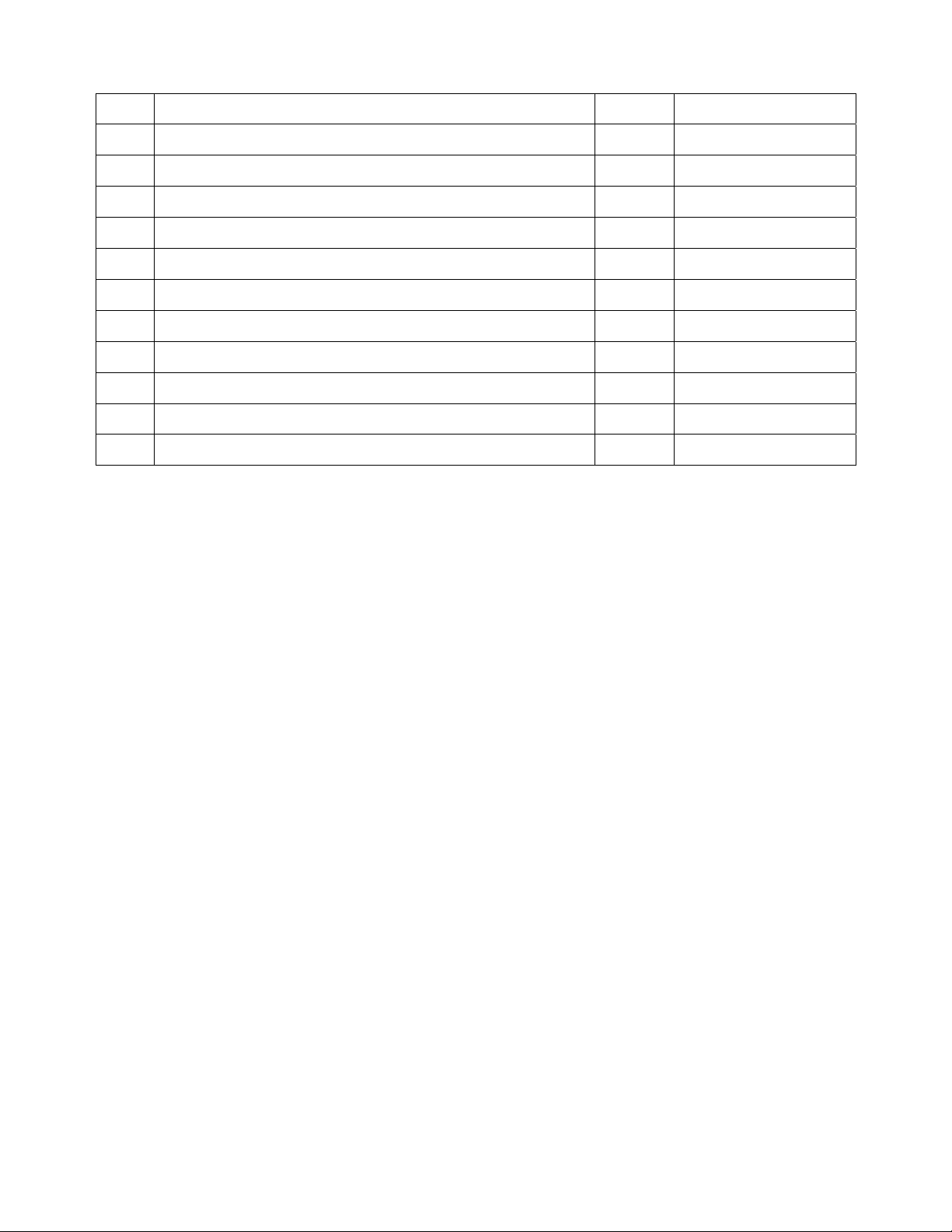
ĐÁP ÁN ĐỀ KIỂM TRA ĐÁNH GIÁ ĐỊNH KÌ GIỮA HKI MÔN TOÁN KHỐI 11
NĂM HỌC 2022 – 2023 (ĐỀ CHÍNH THỨC) Câu ĐÁP ÁN ĐIỂM 1a 5π π π π
Hàm số f x tăng trên ;
. Hàm số f x giảm trên ; . 0,5đx2 (1,0 điểm) 4 4 4 4 3π π Trên
; π , GTLN của hàm số f x là 3 khi x . 1b 4 4 0,5đx2 (1,0 điểm) 3π
GTNN của hàm số f x là 1 khi x . 4 f x 3 .sin x 1 2 f
x f x 3 . sin x 2 1 4 4
f x 1 0,25đ 5π 3π Trên ; , ta có 3 f x 3 . sin x 2 1 . 4 4 sin x 2 1 4 4 1c
f x 1 5 3 x x (0,5 điểm) Dấu bằng xảy ra khi 4 4 3 sin x 2 1 3 4 x k2 4 2 0,25đ 5 3 5 x x x 4 4 4 . 5 3 x
k2 k x 4 4 1 o
2 cos x 60 1 0 cos o
x 60 o x o cos 60 cos120 0,25đx2 2 o o o 2a x 60 120 k360 0,25đ (1,0 điểm) o o o
x 60 120 k360 o o
x 180 k360 k . 0,25đ o o
x 60 k360 2 2
2 sin x cos x 5sin x 3 2
3sin x 5sin x 2 0 0,25đ sin x 1 2 0,25đ sin x sin 2b 3 (1,0 điểm)
sin x 1 x k2 0,25đ 2
x k2
sin x sin k 0,25đ
x k2
3 sin 5x cos5x 3 1 2
sin 5x cos 5x 1 0,25đ 2 2 2c
cos sin 5x sin cos 5x 1 sin 5x 1 (1,0 điểm) 0,25đx2 6 6 6 5x 2 2 k2 x k k . 0,25đ 6 2 15 5 x x 2 cos 3 16sin
4 1 3sin x cos x 0
3cos x 8sin 2x 4 6sin 2x cos x 0 3cos x 4 2sin 2x 3cos x 4 0 0,25đ
3cos x 41 2sin 2x 0 4 2d 3cos x 4 0
cos x vn 3 (0,5 điểm) 1 2sin 2x 0 12sin2x 0 0,25đ 2x k2 x k 1 6 sin 2x 12 k . 2 5 5 2x k2 x k 6 12
Do sin x 2 0 nên hàm số xác định với mọi x .
Ta có y sin x 2 33 cos x 1 y sin x 33 cos x 1 2y . 0,25đ
Phương trình trên luôn có nghiệm với mọi x y y2 2 33 1 2 0,25đ 3a (1,0 điểm) 2
3y 4y 32 8
0 y 4 . 0,25đ 3 8 T ;4
. Vậy trong T có 4 số nguyên dương. 0,25đ 3
Gọi x abcd là số thỏa ycbt.
Do a lẻ a 1;5;
9 nên có a có 3 cách chọn. 0,25đ 4a
(1,0 điểm) bcd có 3 A cách chọn. 5 0,5đ Theo quy tắc nhân ta có 3
3.A 180 số thỏa ycbt. 0,25đ 5
Chọn 3 hậu vệ trong 12 hậu vệ: 3 C cách chọn 12 4b
Chọn 4 tiền vệ trong 9 tiền vệ: 4 C cách chọn 9 0,25đx4
(1,0 điểm) Chọn 3 tiền đạo trong 7 tiền đạo: 3 C cách chọn 7
Vậy theo quy tắc nhân số đội hình có thể xảy ra là 3 4 3
C .C .C 970200 . 12 9 7 t t ycbt 500sin 1000 1 1250 sin 0,25đ 12 12 2 t k2 12 6
t 2 24k 5 . 0,25đx2 t 5
t 10 24k (1,0 điểm) k2 12 6 t 2
Do 1 t 12,t . t 10 0,25đ
Vậy vào thời điểm tháng 2 hoặc tháng 10 thì số lượng loài cáo đạt 1250 con. MA TRẬN ĐỀ Bài Nội dung
Điểm Mức độ tư duy 1a Hàm số lượng giác 1,0 M1 1b Hàm số lượng giác 1,0 M1 1c Hàm số lượng giác 0,5 M3
2a Phương trình lượng giác 1,0 M1
2b Phương trình lượng giác 1,0 M2
2c Phương trình lượng giác 1,0 M2
2d Phương trình lượng giác 0,5 M3
3 Phương trình lượng giác 1,0 M2 4a Quy tắc đếm 1,0 M2 4b Hoán
vị, chỉnh hợp, tổ hợp 1,0 M2 5 Toán
thực tế ứng dụng hàm số lượng giác 1,0 M2




