

Preview text:
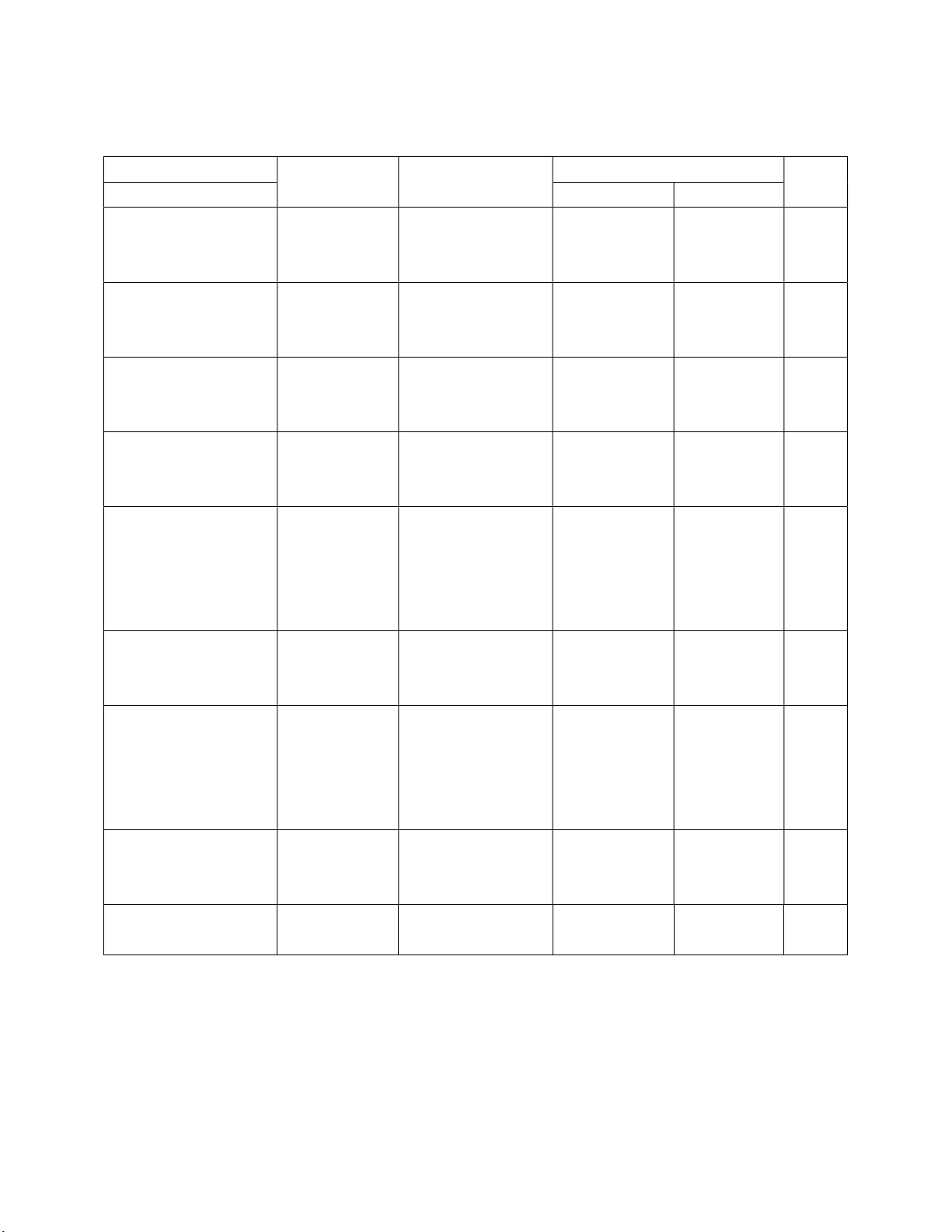
MA TRẬN ĐỀ THI Cấp độ Nhận biết Thông hiểu Vận dụng Tổng Nội dung
Cấp độ thấp Cấp độ cao 1. Thực hiên các Thực hiên các phép tính phép tính có chứa dấu căn bậc hai. Số ý Bài 1 Điểm 1,5đ 1,5đ Tỉ lệ 15% 2.Phương trình vô tỉ Giải phương Giải trình phương trình Số ý Bài 2 Bài 6 Điểm 2đ 0,5đ 2,5đ Tỉ lệ 20% 5% 3.Biểu thức, Biểu Tính giá trị Rút gọn, tìm biểu Tìm giá trị thức chứa căn thức biểu thức thức của x để bậc hai. biểu thức nhận gái trị nguyên Số ý Bài 3.a Bài 3.b Bài 3.c Điểm 0,5đ 1,0đ 0,5đ 2đ Tỉ lệ 5% 10% 5% 4. Hình học Một số hệ thức về Một số hệ Một số hệ cạnh và đường thức về cạnh thức về cao trong tam
và góc trong cạnh và góc giác vuông tam giác trong tam vuông giác vuông Số ý Bài 5. Bài 4. Bài 5. 4 đ Điểm 1. 1,25đ 2.a.1đ 1đ 3.0,75đ Tỉ lệ 22,5% 10% 7,5% Tổng 0,5đ 4,75đ 3đ 1,75đ 10đ 5% 47,5% 30% 17,5% 100%
TRƯỜNG THCS TÔ HIẾN THÀNH
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA KÌ I MÔN TOÁN 9 NĂM HỌC 2020 - 2021
Thời gian làm bài: 90 phút;
Bài 1. (1,5 điểm) Thực hiện phép tính:
a) 3 32 4 8 72 ; b) 2 2 5 2 ; 2 3 3 c) 4 2 3 3 1 3 1 Bài 2. (2,0 điểm) 7 x 2 x 24 Cho hai biểu thức A và B với x 0, x 9 . x 8 x 3 x 9
1) Tính giá trị của biểu thức A khi x 25. x 8 2) Chứng minh rằng B x 3
3) Tìm giá trị của x để biểu thức P .
A B có giá trị là số nguyên.
Bài 3. (2,0 điểm) Giải phương trình sau: 1 a) 9x 27 16x 48 x 3 6 b) 2 2x 1 x 4
Bài 4. (1,0 điểm) Một con mèo ở trên cành cây cao 6,5m. Để bắt mèo xuống cần
phải đặt một cái thang đạt độ cao đó, khi đó góc của thang với mặt đất là bao
nhiêu, biết chiếc thang dài 6,7m? (kết quả làm tròn đến độ).
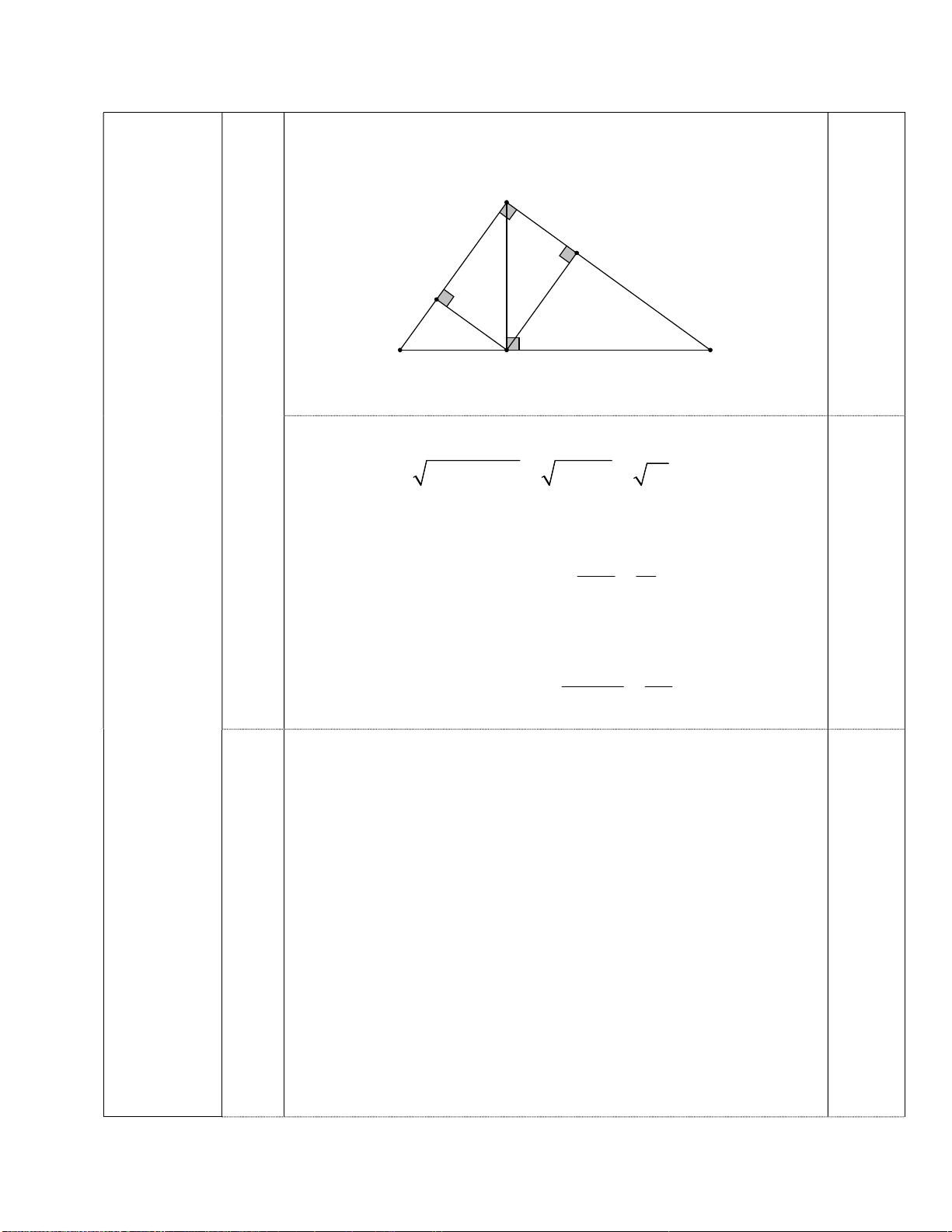
Bài 5. (3,0 điểm) Cho tam giác ABC vuông tại A có đường cao AH.
1) Cho biết AB = 3 cm, AC = 4 cm. Tính độ dài các đoạn BC, HB, HC, AH;
2) Vẽ HE vuông góc với AB tại E, HF vuông góc với AC tại F . a) Chứng minh 2 A . E EB EH ; b) Chứng minh: 2 A . E EB AF.FC AH . 3) Chứng minh: 3 BE B . C cos . B Bài 6. (0,5 điểm) Giải phương trình 2 x 3x 2 x 1. ======== HẾT ========
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
NĂM HỌC 2020 – 2021 | MÔN TOÁN 9 TT Đáp án Điểm Bài 1 a) Tính ra kết quả 10 2 0,5 (1,5 điểm) b) Tính ra kết quả 5 0,5 c) Tính ra kết quả 3 0,5 Bài 2 1) 7 0,5 Tính ra kết quả A = (2,5 điểm) 13 2) x 8 1 Rút gọn được B x 3 3) 7 x 8 7 Tìm được P x 8 x 3 x 3 Ta có: 7
x 0 x 0 x 3 0 0 P 0 (1) x 3
* Ta có: x 0 x 0 x 3 3 1 1 7 7 7 P (2) x 3 3 x 3 3 3 7 0,25 Từ (1) và (2) 0 P 3 Mà P Z P 1; 2
Với P 1 x 3 7 x 16 (tm) 7 1 Với P 2 x 3 x (tm) 2 4 1 Vậy x ;16 0,25 4 Bài 3 a) Tìm được đk x 3 0,25 (1,5 điểm) x = 1 (tm)=> kết luận 0,5 b) Tìm được đk x 2 0,25
x = 1 (ktm); x = 5 (tm)=> kết luận 0,5 Bài 4 - Vẽ được hình 1 (1,0 điểm) - Tính được: Xấp xỉ 0 76 1) 0,25 Vẽ hình đúng A F E B C H
Áp dụng định lí Pitago với tam giác vuông ABC ta có: 1 2 2 2 2
BC AB AC 3 4 25 5cm
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có: 2 2 AB 3 + 2 AB BC.HB HB 1,8cm BC 5 Bài 5
HC BC HB 5 1,8 3,2cm (3,0 điểm) A . B AC 3.4 + AH.BC A . B AC AH 2,4cm BC 5 2)
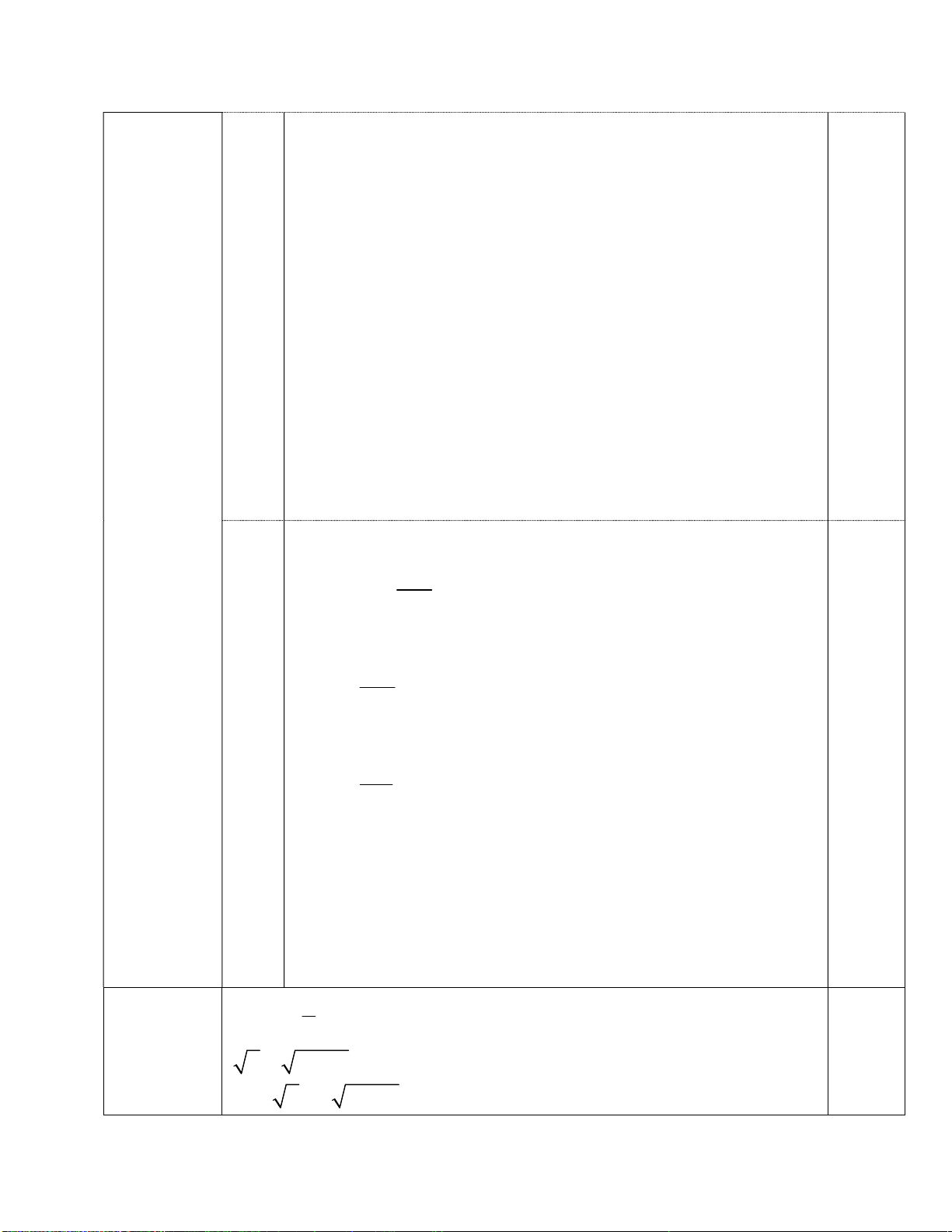
Tam giác AHBvuông tại H có HE là đường cao nên: 2 AE.AB AH 0.5
Tam giác AHC vuông tại H có HF là đường cao nên: 2 AF.AC = AH Do đó: A . E EB AF.FC A .
E (AB AE) AF.(AC AF) = 2 2 A . E AB AE AF.AC AF = 2 2 AH AH 2 2 AE AF (1)
Tứ giác AEHF có 90o AEH AFH EAF nên tứ giác
AEHF là hình chữ nhật do đó EF AH và 2 2 2 2 AE AF EF AH (2) 0.5 Từ (1) và (2) suy ra: 2 2 2 A .
E EB AF.FC 2.AH AH AH (đpcm) Cách khác:
Tam giác AHBvuông tại H có HE là đường cao nên: 2 AE.EB = EH
Tam giác AHC vuông tại H có HF là đường cao nên: 2 AF.FC = FH
Chứng minh tứ giác AEHF là hình chữ nhật. Suy ra: AH EF Mà 2 2 2
EH FH EF .Suy ra đpcm 3) Tam giác BEH vuông tại E 0,75 BE nên cos B BE BH.cos B (3) BH
Tam giác AHBvuông tại H nên BH cos B BH A . B cos B (4) AB
Tam giác ABC vuông tại A nên AB cos B AB BC.cos B (5) BC
Từ (3); (4) và (5) suy ra: BE H . B cos B A . B cos B.cos B
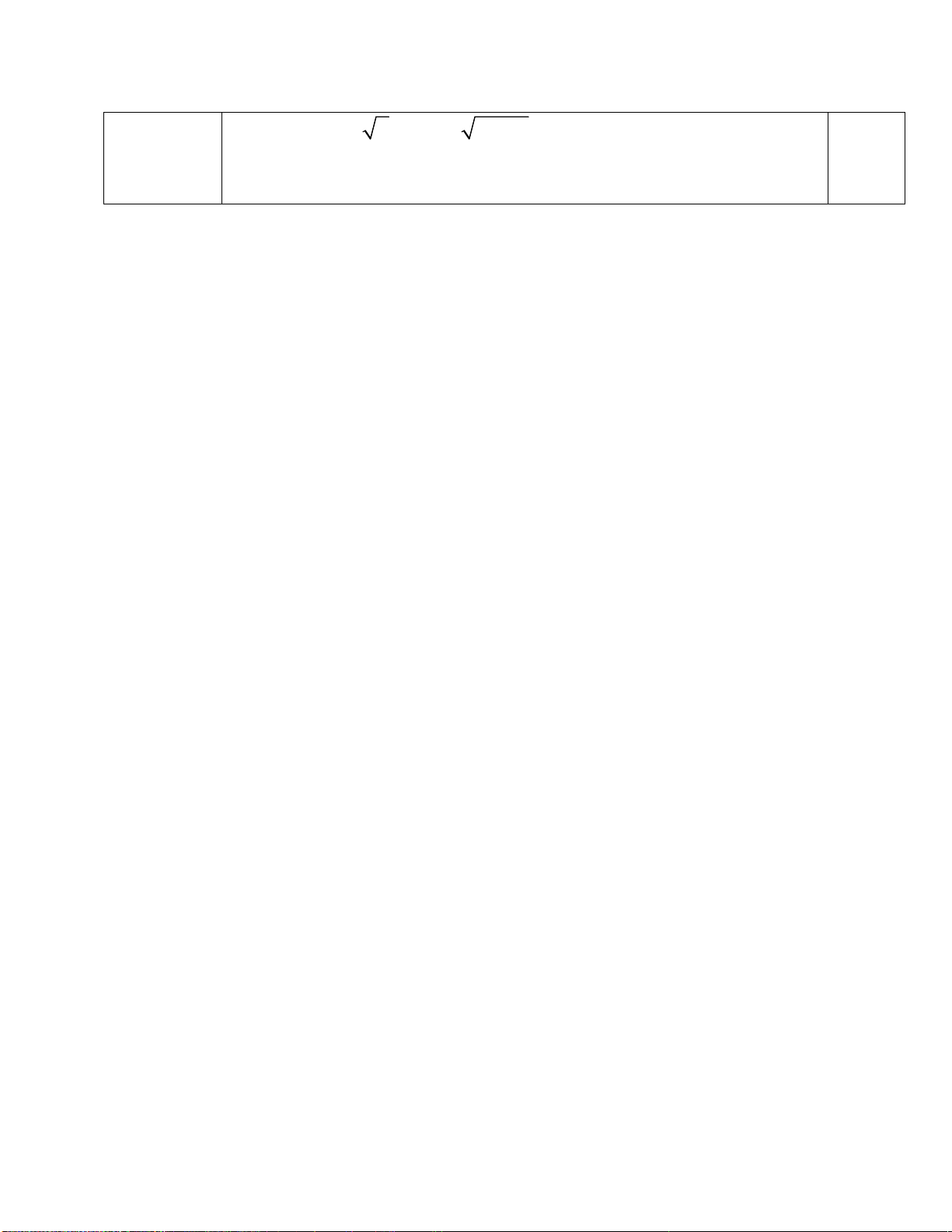
BC.cosB.cosB.cosB Hay 3 BE B . C cos B (đpcm) 2 ĐK x Bài 6 3 (0,5 điểm) 2 x 3x 2 x 1 2
2 x 2 3x 2 2x 2 2 2 2
2(x 1) ( x 1) ( 3x 2 1) 0 0,25
Lập luận dẫn đến x 1(TMĐK). 0,25 Vậy x 1.
- Học sinh làm cách khác đúng cho điểm tương đương.
- Điểm toàn bài làm tròn đến 0,5.