Đề thi giữa học kì 1 môn Toán 11 năm 2023 - 2024 sách Kết nối tri thức với cuộc sống | đề 2

Đề thi giữa kì 1 Toán 11 Kết nối tri thức năm 2023 - 2024 mang đến 11 đề thi giữa kì 1 có ma trận, đáp án hướng dẫn giải chi tiết, chính xác. Thông qua đề thi giữa kì 1 Toán 11 quý thầy cô có thêm nhiều tài liệu tham khảo để ra đề thi cho các em học sinh của mình.

32 16 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Sách: Kết nối tri thức

Thông tin:

17 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
TRƯỜNG THPT
ĐỀ CHÍNH THỨC
(Đề có 05 trang)
ĐỀ KIỂM TRA GIỮA KÌ I NĂM HỌC 2023 - 2024
MÔN: TOÁN - LỚP: 11 (SÁCH KNTT)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh: ....................................................................... Số báo danh: ...................
I. PHẦN TRẮC NGHIỆM (7,0 điểm).
Câu 1: Cung có số đo
250
thì có số đo theo đơn vị là radian là
A.
35
18
. B.
25
18
. C.
25
12
. D.
25
9
.
Câu 2: Cho góc
thỏa mãn
. Khẳng định nào sau đây đúng?
A.
sin 0
. B.
cot 0
. C.
sin 0
. D.
cos 0
.
Câu 3: Khẳng định nào sau đây đúng?
A.
22
sin cos 1

+=
. B.
22
sin cos 0

+=
.
C.
22
sin cos 2

+=
. D.
22
sin cos 1

+ = −
.
Câu 4:
sin2a
bằng
A.
2sin .cosaa
. B.
sina
. C.
cosa
. D.
cos2a
.
Câu 5: Chu kỳ tuần hoàn của hàm số
sinyx=
là
A.
2k
()k
. B.
2
. C.
. D.
2
.
Câu 6: Tập giá trị của hàm số
cos2023yx=
là
A.
1;1−
. B.
( 1;1)−
. C.
2023;2023−
. D.
11
;
22

−


.
Câu 7: Nghiệm của phương trình
tan 1x =
là
A.
,
4
x k k
= +
. B.
3
,
4
x k k
= +
.
C.
,x k k
=
. D.
,
2
x k k
= +
.
Câu 8: Cho dãy số
( )
n
u
xác định bởi
21
n
un=−
với
1n
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Câu 9: Dãy số nào sau đây là dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6;4;2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Câu 10: Cho cấp số cộng
( )
n
u
với
1
3u =
và
2
5.u =
Công sai của cấp số cộng đã cho bằng
Trang 2
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 11: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
2
1
n
un=+
. B.
2
1
3
n
u
n
=−
. C.
sin
n
u n n=+
. D.
2
sin
n
un=
.
Câu 12: Cho
a
,
b
,
c
là ba số hạng liên tip của một cấp số cộng. Đẳng thc nào sau đây đúng?
A.
2
b ac=
. B.
2b a c=+
. C.
2a b c+=
. D.
2b c a+=
.
Câu 13: Dãy số nào sau đây là cấp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x
.
Câu 14: Cho cấp số cộng
( )
n
u
bit
6
48u =
và
11
83u =
. Tìm cặp
( )
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
( )
13; 7
. D.
( )
13; 7−−
.
Câu 15: Cho cấp số nhân với và công bội . Tìm giá trị của bit số hạng tổng quát
.
A. . B. . C. . D. .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kt quả sau:
Nhóm
Chiều cao (cm)
Số học sinh
1
)
150;152
5
2
)
152;154
18
3
)
154;156
40
4
)
156;158
26
5
)
158;160
8
6
)
160;162
3
100N =
Giá trị đại diện của nhóm th tư là
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm cha mốt của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
( )
n
u
1
3u =
2=−q
n
1536=−
n
u
8=n
9n =
257n =
10n =
Trang 3
Nhóm cha trung vị của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
T phân vị th nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8,6
.
Câu 21: Bit
4
sin
5
−
=
và
3
2


. Giá trị
cos
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
D.
9
.
5
Câu 22: Giá trị của biểu thc
sin
34
A


=+


là
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Câu 23: Hàm số nào sau đây là hàm số lẻ?
A.
2cosyx=−
. B.
2
2sin 2yx= − +
. C.
2sinyx=−
. D.
2cos 2yx= − +
.
Câu 24: Tập nghiệm của phương trình
cos 1x =−
là
A.
2 | .
2
S k k

= +

B.
2 | .
2
S k k

= − +

C.
2 | .S k k
=
D.
2 | .S k k

= +
Câu 25: Cho dãy số
1 1 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng liền trước nó). Công thc tổng
quát của dãy số đã cho là
Trang 4
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Câu 26: Cho cấp số cộng
( )
n
u
có
1
2; 5ud= = −
. Số hạng th
20
của cấp số cộng là
A.
93−
. B.
10
. C.
93
. D.
23
.
Câu 27: Cho cấp số nhân
( )
n
x
có
2
3x =−
và
4
27.x =−
Tính số hạng đầu
1
x
và công bội
q
của cấp số
nhân.
A.
1
1, 3xq= − = −
hoặc
1
1, 3.xq==
B.
1
1, 3xq= − =
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq= − =
D.
1
3, 1xq==
hoặc
1
3, 1.xq= − = −
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi
bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Doanh thu
)
5;7
)
7;9
)
9;11
)
11;13
)
13;15
Số ngày
2
7
7
3
1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Nhóm cha trung vị là
A.
)
30;45
. B.
)
15;30
. C.
)
45;60
. D.
)
60;75
.
Câu 31: Một chic phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi
hàm số
( )
5sin
5
h t t

=


, trong đó
( )
ht
là độ cao tính bằng cetimét trên mực nước biển trung
bình tại thời điểm
t
giây. Nu chic phao đang ở đỉnh của sóng thì trong bao lâu chic phao lại
ở vị trí đỉnh của cơn sóng tip theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
33
sin 3
42
x

−=


bằng
Trang 5
A.
.
9
B.
.
6
−
C.
.
6
D.
.
9
−
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng th nhất trồng
1
cây, hàng
th hai trồng
2
cây, hàng th ba trồng
3
cây, …, c tip tục trồng như th cho đn khi ht số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Câu 34: Một cấp số nhân có số hạng đầu
1
3u =
, công bội
2q =
. Bit
765
n
S =
. Tìm
n
.
A.
8n =
. B.
9n =
. C.
6n =
. D.
7n =
.
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đn nơi làm việc của các nhân viên một
công ty như sau:
Thời gian
)
15;20
)
20;25
)
25;30
)
30;35
)
35;40
)
40;45
)
45;50
Số nhân viên
7
14
25
37
21
14
10
T phân vị th nhất
1
Q
và t phân vị th ba
3
Q
của mẫu số liệu ghép nhóm này là
A.
13
1360 800
,
37 21
QQ==
. B.
13
1360 3280
,
37 83
QQ==
.
C.
13
136 3280
,
5 83
QQ==
. D.
13
136 800
,
5 21
QQ==
.
II. PHẦN TỰ LUẬN (3,0 điểm).
Câu 36: (1,0 điểm)
a. Giải phương trình
cot 3
3
x

+=


.
b. Cho
2
sin
3
=
, tính giá trị của biểu thc
(1 3cos )(1 3cos )P

= − +
.
Câu 37: (1,0 điểm)
Giải phương trình
cos3 sin2 0xx−=
.
Câu 38: (1,0 điểm) Giải phương trình
sin cos
3
xx

=+


.
Câu 39: (0,5 điểm) Một công ty khoan ging đưa ra định mc giá như sau: Giá từ mét khoan đầu tiên là
100000
đồng và kể từ mét khoan th hai, giá mỗi mét tăng thêm
30000
đồng so với giá của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan ging này để khoan ging
sâu
20
mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan ging, gia
đình đó phải thanh toán cho cơ sở khoan ging số tiền bằng bao nhiêu?
-------------- HẾT --------------
Trang 6
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM (7,0 điểm).
BẢNG ĐÁP ÁN
1.B
2.A
3.A
4.A
5.D
6.C
7.A
8.A
9.A
10.A
11.D
12.B
13.C
14.C
15.D
16.B
17.A
18.A
19.B
20.C
21.A
22.B
23.C
24.D
25.B
26.A
27.B
28.C
29.B
30.A
31.B
32.C
33.A
34.A
35.D
ĐÁP ÁN CHI TIẾT
Câu 1: Cung có số đo
250
thì có số đo theo đơn vị là radian là
A.
35
18
. B.
25
18
. C.
25
12
. D.
25
9
.
Lời giải
Chọn B
Số đo theo đơn vị là radian là
0
0
250 . 25.
18
180

=
.
Câu 2: Cho góc
thỏa mãn
0
2

. Khẳng định nào sau đây đúng?
A.
sin 0
. B.
cot 0
. C.
sin 0
. D.
cos 0
.
Lời giải
Chọn A
Câu 3: Khẳng định nào sau đây đúng?
A.
22
sin cos 1

+=
. B.
22
sin cos 0

+=
.
C.
22
sin cos 2

+=
. D.
22
sin cos 1

+ = −
.
Lời giải
Chọn A
Câu 4:
sin2a
bằng
A.
2sin .cosaa
. B.
sina
. C.
cosa
. D.
cos2a
.
Lời giải
Chọn A
Câu 5: Chu kỳ tuần hoàn của hàm số
sinyx=
là
A.
2k
()k
. B.
2
. C.
. D.
2
.
Lời giải
Chọn D
Câu 6: Tập giá trị của hàm số
cos2023yx=
là
A.
1;1−
. B.
( 1;1)−
. C.
2023;2023−
. D.
11
;
22

−


.
Trang 7
Lời giải
Chọn C
Câu 7: Nghiệm của phương trình
tan 1x =
là
A.
,
4
x k k
= +
. B.
3
,
4
x k k
= +
.
C.
,x k k
=
. D.
,
2
x k k
= +
.
Lời giải
Chọn A
Ta có
tan 1 ,
4
x x k k
= = +
Câu 8: Cho dãy số
( )
n
u
xác định bởi
21
n
un=−
với
1n
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Lời giải
Chọn A
Ta có:
1
2.1 1 1u = − =
Câu 9: Dãy số nào sau đây là dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6;4;2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Lời giải
Chọn A
Câu 10: Cho cấp số cộng
( )
n
u
với
1
3u =
và
2
5.u =
Công sai của cấp số cộng đã cho bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Chọn A
Công sai của cấp số cộng
21
5 3 2d u u= − = − =
.
Câu 11: Trong các dãy số
()
n
u
sau, dãy số nào bị chặn?
A.
2
1
n
un=+
. B.
2
1
3
n
u
n
=−
. C.
sin
n
u n n=+
. D.
2
sin
n
un=
.
Lời giải
Chọn D
Với mọi
*
,Nn
ta có
2
1 sin 1 0 sin 1nn−
nên dãy số đã cho bị chặn.
Phân tích phương án nhiu:
A. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
B. Sai do dãy số này bị chặn trên nhưng không bị chặn dưới.
C. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
Trang 8
Câu 12: Cho
a
,
b
,
c
là ba số hạng liên tip của một cấp số cộng. Đẳng thc nào sau đây đúng?
A.
2
b ac=
. B.
2b a c=+
. C.
2a b c+=
. D.
2b c a+=
.
Lời giải
Chọn B
Phân tích phương án nhiu:
A: Sai vì nhớ nhầm của cấp số nhân.
B, C: Sai vì không phân biệt th tự của các số hạng của cấp số cộng.
Câu 13: Dãy số nào sau đây là cấp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x
.
Lời giải
Chọn C
6 3.2=
,
12 6.2=
,
24 12.2=
.
Phân tích phương án nhiu:
A. Sai do thay
21
:2uu=−
nhưng
43
:2uu=
.
B. Sai do học sinh lầm tưởng đây là cấp số nhân với công bội
11q =
.
D. Sai do dãy số trên là cấp số cộng, không phải cấp số nhân.
Câu 14: Cho cấp số cộng
( )
n
u
bit
6
48u =
và
11
83u =
. Tìm cặp
( )
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
( )
13; 7
. D.
( )
13; 7−−
.
Lời giải
Chọn C
Ta có:
6
11
48
83
u
u
=
=
1
1
5 48
10 83
ud
ud
+=
+=
1
13
7
u
d
=
=
.
Phân tích phương án nhiu:
A. Sai vì đặt nhầm th tự của yêu cầu bài toán.
B. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình và đặt nhầm th tự
của yêu cầu bài toán.
D. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình.
Câu 15: Cho cấp số nhân với và công bội . Tìm giá trị của bit số hạng tổng quát
?
A. . B. . C. . D. .
Lời giải
Chọn D
.
( )
n
u
1
3u =
2=−q
n
1536=−
n
u
8=n
9n =
257n =
10n =
11
1
1536 . 1536 3.( 2) 1536
−−
= − = − − = −
nn
n
u u q
Trang 9
.
Phân tích phương án nhiu:
A. Sai do tính .
B. Sai do nhầm công thc số hạng tổng quát .
C. Sai do tính .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kt quả sau:
Nhóm
Chiều cao (cm)
Số học sinh
1
)
150;152
5
2
)
152;154
18
3
)
154;156
40
4
)
156;158
26
5
)
158;160
8
6
)
160;162
3
100N =
Giá trị đại diện của nhóm th tư là
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Lời giải
Chọn B
Giá trị đại diện của nhóm th tư là
156 158
157
2
+
=
.
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm cha mốt của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Lời giải
Chọn A
Mốt
0
M
cha trong nhóm
[40;60)
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm cha trung vị của mẫu số liệu trên là
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
( )
9
1
( 2) 512 2 10
−
− = − = − =
n
n
( )
1
2 512
−
− = −
n
( )
( )
2
512 2 512:( 2) 256
2
−
= − − = − − =
−
n
n
8n=
( )
1
. 1536 2 512 9
n
n
u q n= − − = − =
( )
1
512
2 512 1 256 257
2
−
−
− = − − = = =
−
n
nn
Trang 10
Lời giải
Chọn A
Ta có:
42n =
Nên trung vị của mẫu số liệu trên là
21 22
2
2
xx
Q
+
=
Mà
)
21 22
, 40;60xx
Vậy nhóm cha trung vị của mẫu số liệu trên là
nhóm
[40;60)
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Lời giải
Chọn B
Bảng tần số ghép nhóm theo giá trị đại diện là
Số trung bình:
2.6 7.8 7.10 3.12 1.14
9,4
20
x
+ + + +
==
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
T phân vị th nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8,6
.
Lời giải
Chọn C
Gọi
1 2 20
, ,...,x x x
là doanh thu bán hàng trong 20 ngày xp theo th tự không giảm.
Khi đó:
)
12
, 5;7xx
,
)
39
,..., 7; 9xx
,,
)
9 16
,..., 9; 11xx
)
17 19
,..., 11; 13xx
,
)
20
13; 15x
Do đó, t phân vị th nhất
của mẫu số liệu thuộc nhóm
)
7;9
1
20, 7, 2, 7, 9
m m m
n n C u u
+
= = = = =
Trang 11
1
1.20
2
4
7 ( )
7
89 7 7,86Q −=+
−
Câu 21: Bit
4
sin
5
−
=
và
3
2


. Giá trị
cos
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
D.
9
.
5
Lời giải
Chọn A
Vì
3π
πα
2

nên
cosα0
. Mặt khác
22
sin α cos α 1+=
ta có
2
cosα 1 sin α= − −
2
1
43
55

= − − − = −


.
Câu 22: Giá trị của biểu thc
sin
34
A


=+


là
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Lời giải
Chọn B
Ta có
3 2 2 1 6 2
sin sin cos sin cos . . .
3 4 3 4 4 3 2 2 2 2 4
A
+

= + = + = + =


Câu 23: Hàm số nào sau đây là hàm số lẻ?
A.
2cosyx=−
. B.
2
2sin 2yx= − +
. C.
2sinyx=−
. D.
2cos 2yx= − +
.
Lời giải
Chọn C
Tập xác định của hàm số
( )
2siny f x x= = −
là
D =
.
Do đó, nu
x
thuộc tập xác định
D
thì
x−
cũng thuộc tập xác định
D
.
Ta có
( ) ( )
2sin( ) sinf x x x f x− = − − = = −
. Vậy
2sinyx=−
là hàm số lẻ.
Câu 24: Tập nghiệm của phương trình
cos 1x =−
là
A.
2 | .
2
S k k

= +

B.
2 | .
2
S k k

= − +

C.
2 | .S k k
=
D.
2 | .S k k

= +
Lời giải
Chọn D
Ta có
cos 1 2 ,x x k k

= − = +
.
Trang 12
Câu 25: Cho dãy số
1 1 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng liền trước nó). Công thc tổng
quát của dãy số đã cho là
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Lời giải
Chọn D
Câu 26: Cho cấp số cộng
( )
n
u
có
1
2; 5ud= = −
. Số hạng th
20
của cấp số cộng là
A.
93−
. B.
10
. C.
93
. D.
23
.
Lời giải
Chọn D
20 1
19 2 19( 5) 93u u d= + = + − = −
.
Câu 27: Cho cấp số nhân
( )
n
x
có
2
3x =−
và
4
27.x =−
Tính số hạng đầu
1
x
và công bội
q
của cấp số
nhân.
A.
1
1, 3xq= − = −
hoặc
1
1, 3.xq==
B.
1
1, 3xq= − =
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq= − =
D.
1
3, 1xq==
hoặc
1
3, 1.xq= − = −
Lời giải
Chọn B
2
21
3
4 1 1
1
9
3 3 3
3
27. 27. 1.
.
q
x x q q
x x q x
x
q
=
= − = − =


= − = − =
=−


Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi
bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
Lời giải
Chọn C
Theo bảng thống kê, giá trị lớn nhất là 60 thuộc lớp
)
6,5;8
nên giá trị đại diện là
6,5 8
7,25
2
+
=
.
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Trang 13
Doanh thu
)
5;7
)
7;9
)
9;11
)
11;13
)
13;15
Số ngày
2
7
7
3
1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Lời giải
Chọn B
Số trung bình của mẫu số liệu trên là:
6.2 8.7 10.7 12.3 14.1
9,4
20
x
+ + + +
==
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép
nhóm sau:
Nhóm cha trung vị là
A.
)
30;45
. B.
)
15;30
. C.
)
45;60
. D.
)
60;75
.
Lời giải
Chọn A
Cỡ mẫu:
9 5 15 14 7 50n = + + + + =
.
Gọi
1 50
,...,xx
là thời gian khảo sát tập thể dục trong ngày của 50 học sinh khối 11 và giả sử dãy
này đã được sắp xp theo th tự tăng dần. Khi đó, trung vị là
25 26
2
xx+
. Do hai giá trị
25 26
,xx
thuộc nhóm
)
30;45
.
Câu 31: Một chic phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa
bởi hàm số
( )
5sin
5
h t t

=


, trong đó
( )
ht
là độ cao tính bằng cetimét trên mực nước biển
trung bình tại thời điểm
t
giây. Nu chic phao đang ở đỉnh của sóng thì trong bao lâu chic
phao lại ở vị trí đỉnh của cơn sóng tip theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm
số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Lời giải
Chọn B
Ta có mô hình hóa chiều cao của sóng nước là hàm hàm số
( )
5sin
5
h t t

=


nên để chic phao
ở vị trí đỉnh ở hai lần liên tip thì cách nhau một chu kì của sóng
( )
2
10
5
Ts
==
.
Trang 14
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình
33
sin 3
42
x

−=


bằng:
A.
.
9
B.
.
6
−
C.
.
6
D.
.
9
−
Lời giải
Chọn C
Ta có
3
32
3 3 3
43
sin 3 sin 3 sin
3
4 2 4 3
32
43
xk
xx
xk



− = +
− = − =
− = − +
.
( )
13 2
13
32
36 3
12
.
17 17 2
32
12 36 3
xk
xk
kZ
x k x k

=+
=+
= + = +
TH1. Với
min
max
13 13
00
13 2
24 36
.
13 11
36 3
01
24 36
Cho
x k k x
xk
x k k x

− = → =
= + ⎯⎯→
− = − → = −
TH2. Với
min
max
17 17
00
17 2
24 36
.
17 7
36 3
01
24 36
Cho
x k k x
xk
x k k x

− = → =
= + ⎯⎯→
− = − → = −
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là
7
36
x
=−
và nghiệm dương nhỏ nhất là
13
.
36
x
=
Khi đó tổng hai nghiệm bằng
13 7
.
36 36 6
−=
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam giác như sau: hàng th nhất trồng
1
cây, hàng
th hai trồng
2
cây, hàng th ba trồng
3
cây, …, c tip tục trồng như th cho đn khi ht số
cây. Số hàng cây được trồng là
A.
77
. B.
79
. C.
76
. D.
78
.
Lời giải
Chọn A
Gọi số cây ở hàng th
n
là
n
u
.
Ta có:
1
1u =
,
2
2u =
,
3
3u =
, … và
1 2 3
... 3003
n
S u u u u= + + + + =
.
Nhận xét dãy số
( )
n
u
là cấp số cộng có
1
1u =
, công sai
1d =
.
Trang 15
Khi đó
( )
1
21
2
n u n d
S
+−


=
3003=
( )
2.1 1 1
3003
2
nn+−


=
( )
1 6006nn + =
2
6006 0nn + − =
77
78
n
n
=
=−
77n=
(vì
n
).
Câu 34: Một cấp số nhân có số hạng đầu
1
3u =
, công bội
2q =
. Bit
765
n
S =
. Tìm
n
?
A.
8n =
. B.
9n =
. C.
6n =
. D.
7n =
.
Lời giải
Chọn A
Áp dụng công thc của cấp số nhân ta có:
( ) ( )
1
1 3. 1 2
765
1 1 2
nn
n
uq
S
q
−−
= = =
−−
8n=
.
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đn nơi làm việc của các nhân viên một
công ty như sau:
Thời gian
)
15;20
)
20;25
)
25;30
)
30;35
)
35;40
)
40;45
)
45;50
Số nhân viên
7
14
25
37
21
14
10
T phân vị th nhất
1
Q
và t phân vị th ba
3
Q
của mẫu số liệu ghép nhóm này là
A.
13
1360 800
,
37 21
QQ==
. B.
13
1360 3280
,
37 83
QQ==
.
C.
13
136 3280
,
5 83
QQ==
. D.
13
136 800
,
5 21
QQ==
.
Lời giải
Chọn D
Cỡ mẫu là
128n =
.
T phân vị th nhất
1
Q
là
32 33
2
xx+
. Do
32 33
,xx
đều thuộc nhóm
[25;30)
nên nhóm này cha
1
Q
.
Do đó,
213 3 4 3
3; 25; 25; 21, 5p a m m am a= = = = − =+
và ta có
1
21
136
4
25
8
5
5
12
25
Q
−
= + =
Với t phân vị th ba
3
Q
là
96 97
2
xx+
. Do
96 97
,xx
đều thuộc nhóm
[35;40)
nên nhóm này cha
3
Q
.
Do đó,
125 5 4 6 53
5; 35; 21; 7 14 25 37 83; 5p a m m m m m a a= = = + + + = + + + = − =
và ta có
3
3.128
83
800
4
35 5
21 21
Q
−
= + =
.
Trang 16
II. PHẦN TỰ LUẬN (3,0 điểm).
Câu
Đp n
Biểu điểm
36a
Giải phương trình
cot 3
3
x

+=


.
0.5
cot 3
3 3 6
x x k

+ = + = +


0.25
6
xk
= − +
()k
.
0.25
36b
Cho
2
sin
3
=
, tính giá trị của biểu thức
(1 3cos )(1 3cos )P

= − +
.
0.5
( )
2
2
(1 3cos )(1 3cos ) 1 3cos 1 9cosP
= − + = − = −
.
0.25
2
sin
3
=
,
2 2 2
5
sin cos 1 cos
9
+ = =
.
5
1 9. 4
9
P = − = −
.
0.25
37
Giải phương trình
cos3 sin2 0xx−=
.
1.0
cos3 sin2 0 cos3 sin2 cos3 cos 2
2
x x x x x x

− = = = −


0.25
3 2 2
2
x x k

= − +


0.25
52
2
2
2
xk
xk
=+
= − +
0.25
2
10 5
()
2
2
xk
k
xk

=+

= − +
0.25
38
Giải phương trình
sin cos
3
xx

=+


1.0
sin cos
3
cos cos
23
xx
xx


=+


− = +
0,25
( )
2
23
2
23
x x k
k
x x k


− = + +

− = − − +
0,25
22
6
xk
− = − +
( )
k
0,25
12
xk
= −
( )
k
.
0,25
Trang 17
39
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu
tiên là
100000
đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm
30000
đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng
với cơ sở khoan giếng này để khoan giếng sâu
20
mét lấy nước dùng cho sinh
hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh
toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
0.5
Giá tiền mỗi mét khoan ging lập thành một cấp số cộng với
1
100000u =
(số tiền mét khoan đầu tiên),
21
30000uu=+
(số tiền mét khoan th hai),
3 2 1
30000 2.30000u u u= + = +
(số tiền mét khoan th ba)
…
20 19 1
30000 19.30000u u u= + = +
(số tiền mét khoan th 20),
và công sai
30000d =
.
0,25
Tổng chi phí cần phải thanh toán là
20 1 2 3 20
...S u u u u= + + + +
20(2.10000 19.30000)
2
+
=
7700000=
.
0,25
-------------- HẾT --------------
| 1/17
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT
ĐỀ KIỂM TRA GIỮA KÌ I NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC
MÔN: TOÁN - LỚP: 11 (SÁCH KNTT) (Đề có 05 trang)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ và tên thí sinh: ....................................................................... Số báo danh: ...................
I. PHẦN TRẮC NGHIỆM (7,0 điểm).
Câu 1: Cung có số đo 250 thì có số đo theo đơn vị là radian là 35 25 25 25 A. . B. . C. . D. . 18 18 12 9 
Câu 2: Cho góc  thỏa mãn 0   
. Khẳng định nào sau đây đúng? 2 A. sin  0 . B. cot  0 .
C. sin  0 .
D. cos  0 .
Câu 3: Khẳng định nào sau đây đúng? A. 2 2 sin  + cos  = 1. B. 2 2 sin  + cos  = 0 . C. 2 2 sin  + cos  = 2 . D. 2 2 sin  + cos  = 1 − .
Câu 4: sin 2a bằng A. 2sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a .
Câu 5: Chu kỳ tuần hoàn của hàm số y = sin x là
A. k 2 (k  ) . B. . C.  . D. 2 . 2
Câu 6: Tập giá trị của hàm số y = cos 2023x là  1 1  A.  1 − ;  1 . B. ( 1 − ;1) . C.  2 − 023;202  3 . D. − ;   .  2 2
Câu 7: Nghiệm của phương trình tan x =1 là  3 A. x =
+ k , k  . B. x =
+ k , k  . 4 4 
C. x = k , k  . D. x = + k ,k  . 2
Câu 8: Cho dãy số (u xác định bởi u = 2n −1 với n 1. Số hạng u bằng n ) n 1 A. 1. B. 2 . C. 3. D. 4 .
Câu 9: Dãy số nào sau đây là dãy tăng? A. 1;3;5; 7;9 . B. 10;8;6; 4; 2 . C. 1;5;3; 7;9 . D. 1;1;1;1;1 .
Câu 10: Cho cấp số cộng (u với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 Trang 1 A. 2 . B. 4 . C. 6 . D. 8 .
Câu 11: Trong các dãy số (u ) sau, dãy số nào bị chặn? n 2 A. 2 u = n +1. B. u = 1− .
C. u = n + sin n . D. 2 u = sin n . n n 3n n n
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a .
Câu 13: Dãy số nào sau đây là cấp số nhân? A. 1, 2 − , 4 , 8 , 16 − .
B. 2 , 22 , 222 , 22222 . C. 3 , 6 , 12 , 24 .
D. x , 2x , 3x , 4x với x  0 .
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7 − ; 1 − 3) . C. (13; 7) . D. ( 1 − 3; − 7) .
Câu 15: Cho cấp số nhân (u u = 3 q = 2 − n ) với và công bội
. Tìm giá trị của n biết số hạng tổng quát 1 = 1536 − . n u A. n = 8 . B. n = 9 . C. n = 257 . D. n = 10 .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 150;152) 5 2 152;154) 18 3 154;156) 40 4 156;158) 26 5 158;160) 8 6 160;162) 3 N = 100
Giá trị đại diện của nhóm thứ tư là A. 156, 5 . B. 157 . C. 157, 5 . D. 158 .
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) .
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Trang 2
Nhóm chứa trung vị của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) .
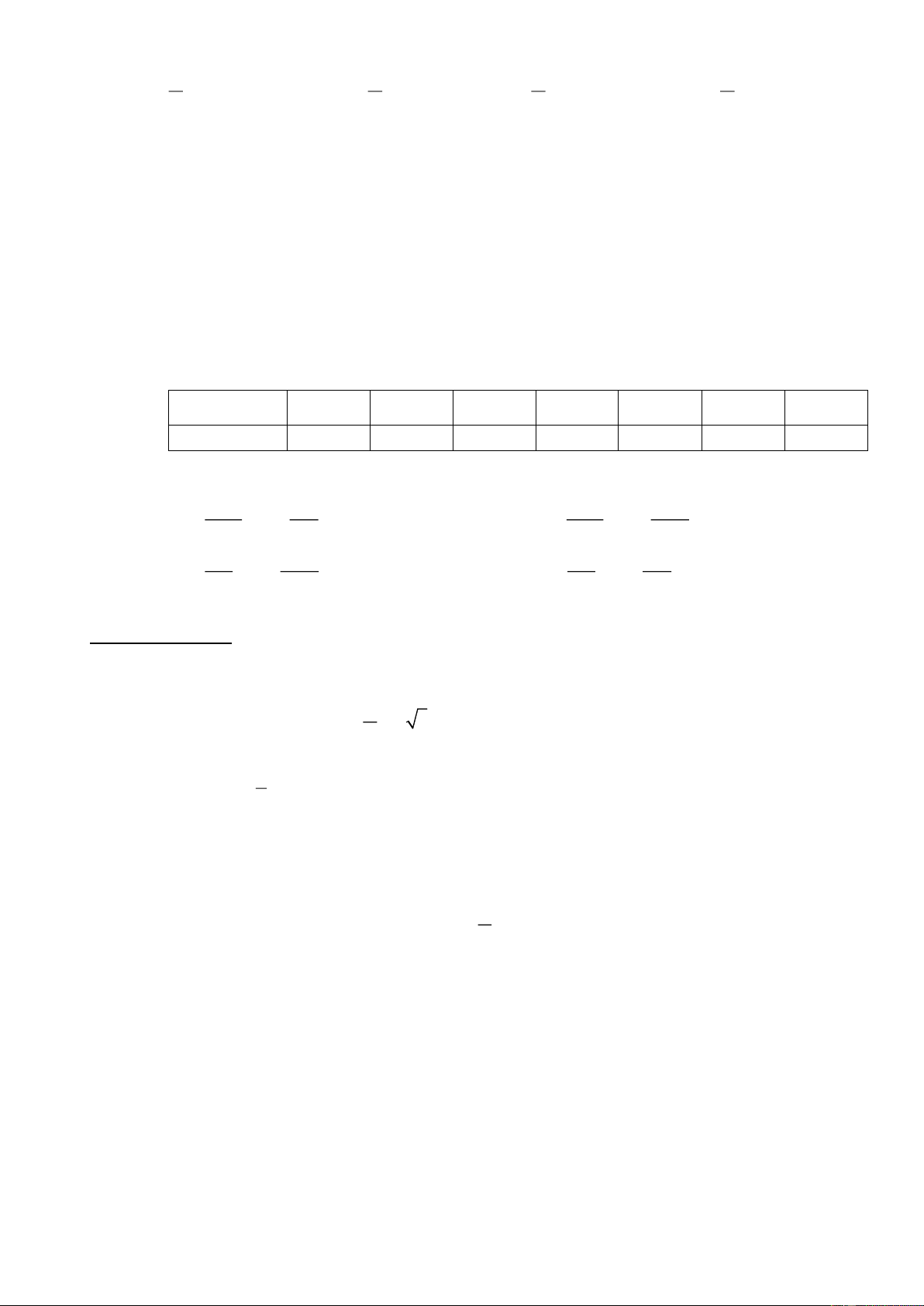
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) .
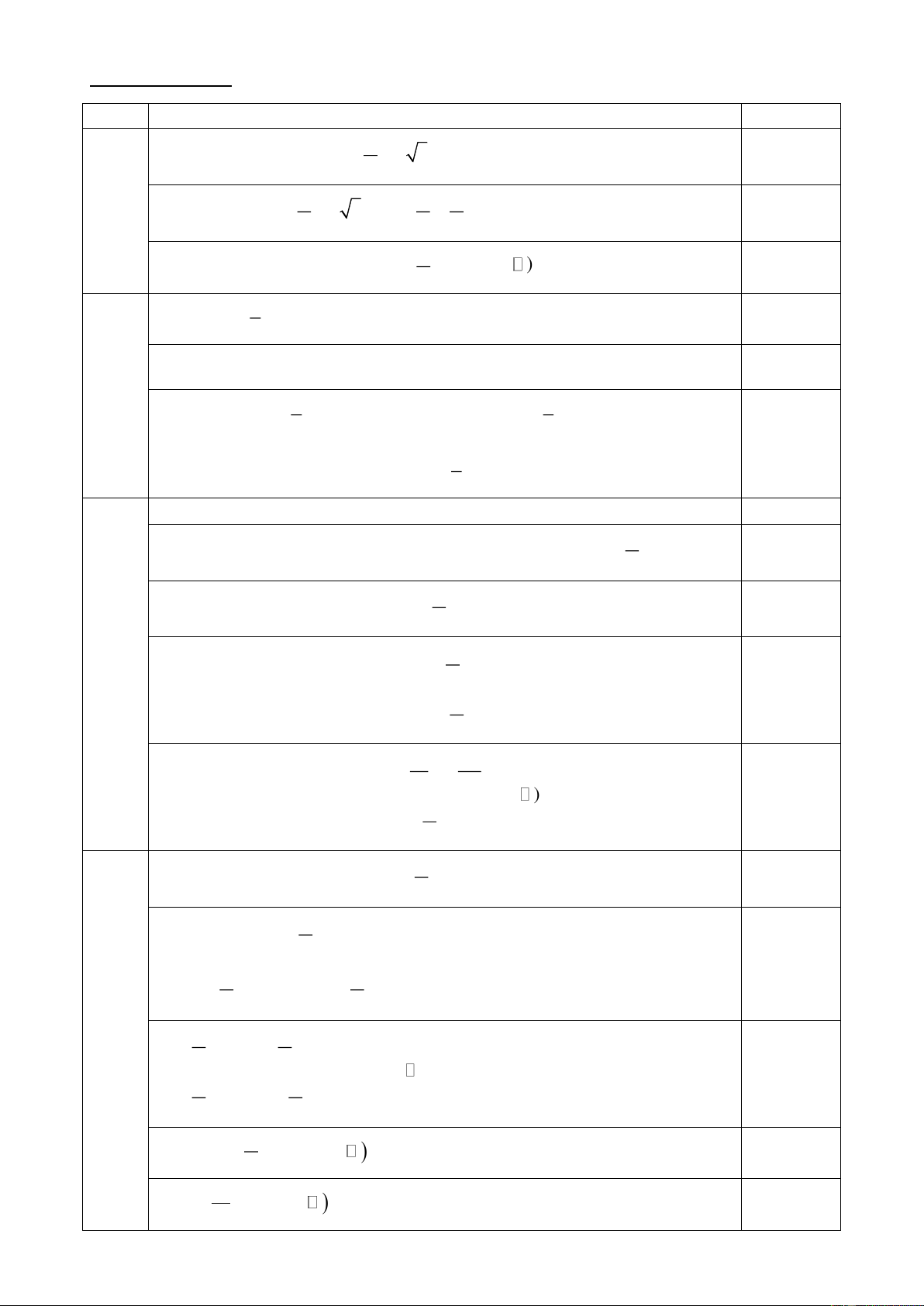
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7, 6 . C. 8 . D. 8, 6 .  Câu 21: 4 Biết sin − = và 3     . Giá trị cos bằng 5 2 3 3 3 9 A. − . B. . C.  . D. . 5 5 5 5    
Câu 22: Giá trị của biểu thức A = sin +   là  3 4  6 − 2 6 + 2 − 6 + 2 − 6 − 2 A. . B. . C. . D. . 4 4 4 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2. C. y = 2 − sin x . D. y = 2 − cos x + 2 .
Câu 24: Tập nghiệm của phương trình cos x = 1 − là     
A. S =  + k2 | k  . B. S = −
+ k2 |k  .  2   2 
C. S = k2 |k  .
D. S =  + k2 | k  . Câu 25: Cho dãy số 1 1 1 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là Trang 3 nn 1 − n 1   1  1 (− ) 1 A. u = . B. u = . C. u = . D. u = . n      − 3  n  3  n 3n n n 1 3
Câu 26: Cho cấp số cộng (u có u = 2; d = 5
− . Số hạng thứ 20 của cấp số cộng là n ) 1 A. 93 − . B. 10 . C. 93 . D. 23.
Câu 27: Cho cấp số nhân ( x có x = 3 − và x = 27. −
Tính số hạng đầu x và công bội q của cấp số n ) 2 4 1 nhân. A. x = 1 − ,q = 3
− hoặc x =1,q = 3. B. x = 1
− ,q = 3 hoặc x =1,q = 3 − . 1 1 1 1
C. x = 3, q = 1
− hoặc x = 3 − ,q =1.
D. x = 3, q = 1 hoặc x = 3 − ,q = 1 − . 1 1 1 1
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6, 5 . B. 7, 5 . C. 7, 25 . D. 8 .
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng): Doanh thu 5;7) 7;9) 9;1 )1 11;13) 13;15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) .
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. 30;45) . B. 15;30) . C. 45;60) . D. 60;75) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi   
hàm số h(t) = 5sin t
 , trong đó h(t ) là độ cao tính bằng cetimét trên mực nước biển trung  5 
bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc phao lại
ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5 giây. B. 10 giây. C. 2, 5 giây. D. 20 giây.   
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3 3 sin 3x − =   bằng  4  2 Trang 4     A. . B. − . C. . D. − . 9 6 6 9
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 .
Câu 34: Một cấp số nhân có số hạng đầu u = 3, công bội q = 2 . Biết S = 765 . Tìm n . 1 n A. n = 8 . B. n = 9 . C. n = 6 . D. n = 7 .
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
15;20) 20;25) 25;30) 30;35) 35;40) 40;45) 45;50) Số nhân viên 7 14 25 37 21 14 10
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 1360 800 1360 3280 A. Q = , Q = . B. Q = ,Q = . 1 3 37 21 1 3 37 83 136 3280 136 800 C. Q = , Q = . D. Q = , Q = . 1 3 5 83 1 3 5 21
II. PHẦN TỰ LUẬN (3,0 điểm). Câu 36: (1,0 điểm)   
a. Giải phương trình cot x + = 3   .  3  2 b. Cho sin  =
, tính giá trị của biểu thức P = (1− 3cos)(1+ 3cos) . 3 Câu 37: (1,0 điểm)
Giải phương trình cos3x − sin 2x = 0 .   
Câu 38: (1,0 điểm) Giải phương trình sin x = cos x +   .  3 
Câu 39: (0,5 điểm) Một công ty khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là
100000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30000 đồng so với giá của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng
sâu 20 mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia
đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
-------------- HẾT -------------- Trang 5
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM (7,0 điểm). BẢNG ĐÁP ÁN 1.B 2.A 3.A 4.A 5.D 6.C 7.A 8.A 9.A 10.A 11.D 12.B 13.C 14.C 15.D 16.B 17.A 18.A 19.B 20.C 21.A 22.B 23.C 24.D 25.B 26.A 27.B 28.C 29.B 30.A 31.B 32.C 33.A 34.A 35.D ĐÁP ÁN CHI TIẾT
Câu 1: Cung có số đo 250 thì có số đo theo đơn vị là radian là 35 25 25 25 A. . B. . C. . D. . 18 18 12 9 Lời giải Chọn B 0 250 . 25.
Số đo theo đơn vị là radian là = . 0 180 18 
Câu 2: Cho góc  thỏa mãn 0   
. Khẳng định nào sau đây đúng? 2 A. sin  0 . B. cot  0 .
C. sin  0 .
D. cos  0 . Lời giải Chọn A
Câu 3: Khẳng định nào sau đây đúng? A. 2 2 sin  + cos  = 1. B. 2 2 sin  + cos  = 0 . C. 2 2 sin  + cos  = 2 . D. 2 2 sin  + cos  = 1 − . Lời giải Chọn A Câu 4: sin 2a bằng A. 2sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a . Lời giải Chọn A
Câu 5: Chu kỳ tuần hoàn của hàm số y = sin x là
A. k 2 (k  ) . B. . C.  . D. 2 . 2 Lời giải Chọn D
Câu 6: Tập giá trị của hàm số y = cos 2023x là  1 1  A.  1 − ;  1 . B. ( 1 − ;1) . C.  2 − 023;202  3 . D. − ;   .  2 2 Trang 6 Lời giải Chọn C
Câu 7: Nghiệm của phương trình tan x =1 là  3 A. x =
+ k , k  . B. x =
+ k , k  . 4 4 
C. x = k , k  . D. x = + k ,k  . 2 Lời giải Chọn A
Ta có tan x = 1  x = + k , k  4
Câu 8: Cho dãy số (u xác định bởi u = 2n −1 với n 1. Số hạng u bằng n ) n 1 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn A
Ta có: u = 2.1−1 = 1 1
Câu 9: Dãy số nào sau đây là dãy tăng? A. 1;3;5; 7;9 . B. 10;8;6; 4; 2 . C. 1;5;3; 7;9 . D. 1;1;1;1;1 . Lời giải Chọn A
Câu 10: Cho cấp số cộng (u với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 4 . C. 6 . D. 8 . Lời giải Chọn A
Công sai của cấp số cộng d = u − u = 5 − 3 = 2 . 2 1
Câu 11: Trong các dãy số (u ) sau, dãy số nào bị chặn? n 2 A. 2 u = n +1. B. u = 1− .
C. u = n + sin n . D. 2 u = sin n . n n 3n n n Lời giải Chọn D Với mọi * n  N , ta có 2 1
−  sin n 1 0  sin n 1 nên dãy số đã cho bị chặn.
Phân tích phương án nhiễu:
A. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
B. Sai do dãy số này bị chặn trên nhưng không bị chặn dưới.
C. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên. Trang 7
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a . Lời giải Chọn B
Phân tích phương án nhiễu:
A: Sai vì nhớ nhầm của cấp số nhân.
B, C: Sai vì không phân biệt thứ tự của các số hạng của cấp số cộng.
Câu 13: Dãy số nào sau đây là cấp số nhân? A. 1, 2 − , 4 , 8 , 16 − .
B. 2 , 22 , 222 , 22222 . C. 3 , 6 , 12 , 24 .
D. x , 2x , 3x , 4x với x  0 . Lời giải Chọn C
6 = 3.2 , 12 = 6.2 , 24 = 12.2 .
Phân tích phương án nhiễu:
A. Sai do thay u : u = 2
− nhưng u :u = 2. 2 1 4 3
B. Sai do học sinh lầm tưởng đây là cấp số nhân với công bội q = 11 .
D. Sai do dãy số trên là cấp số cộng, không phải cấp số nhân.
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7 − ; 1 − 3) . C. (13; 7) . D. ( 1 − 3; − 7) . Lời giải Chọn C u  = 48 u  + 5d = 48 u  =13 Ta có: 6  1   1   . u = 83  u +10d = 83  d = 7 11 1
Phân tích phương án nhiễu:
A. Sai vì đặt nhầm thứ tự của yêu cầu bài toán.
B. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình và đặt nhầm thứ tự của yêu cầu bài toán.
D. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình.
Câu 15: Cho cấp số nhân (u u = 3 q = − n ) với và công bội
2 . Tìm giá trị của n biết số hạng tổng quát 1 = 1536 − ? n u A. n = 8 . B. n = 9 . C. n = 257 . D. n = 10 . Lời giải Chọn D n 1 − n 1 − u = 1 − 536  u .q = 1 − 536  3.( 2 − ) = 1 − 536 . n 1 Trang 8 n 1 −  ( 2 − ) = 5 − 12 = ( 2 − )9  n =10 .
Phân tích phương án nhiễu: ( n 2 − ) n− n
A. Sai do tính (− ) 1 2 = 5 − 12  = 51 − 2  ( 2 − ) = 51 − 2 : ( 2) − = 256  n = 8. 2 − n
B. Sai do nhầm công thức số hạng tổng quát . n u q = 15 − 36  2 − = 51 − 2  n = 9 1 ( ) . n− −
C. Sai do tính (− ) 1 512 2 = 5 − 12  n −1 = = 256  n = 257 . 2 −
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 150;152) 5 2 152;154) 18 3 154;156) 40 4 156;158) 26 5 158;160) 8 6 160;162) 3 N = 100
Giá trị đại diện của nhóm thứ tư là A. 156, 5 . B. 157 . C. 157, 5 . D. 158 . Lời giải Chọn B +
Giá trị đại diện của nhóm thứ tư là 156 158 = 157 . 2
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Chọn A
Mốt M chứa trong nhóm [40; 60) 0
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) . Trang 9 Lời giải Chọn A Ta có: n = 42 + Nên trung vị x x
của mẫu số liệu trên là 21 22 Q = 2 2
Mà x , x  40;60 21 22  )
Vậy nhóm chứa trung vị của mẫu số liệu trên là nhóm [40; 60)
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) . Lời giải Chọn B
Bảng tần số ghép nhóm theo giá trị đại diện là + + + + Số trung bình: 2.6 7.8 7.10 3.12 1.14 x = = 9, 4 20
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7, 6 . C. 8 . D. 8, 6 . Lời giải Chọn C
Gọi x , x ,..., x là doanh thu bán hàng trong 20 ngày xếp theo thứ tự không giảm. 1 2 20
Khi đó: x , x  5;7 , x ,..., x  7; 9 ,, x ,..., x  9; 11 x ,..., x  11; 13 , x  13; 15 20  ) 17 19  ) 9 16  ) 3 9  ) 1 2  )
Do đó, tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm 7;9)
n = 20, n = 7,C = 2,u = 7,u = 9 m m m 1 + Trang 10 1.20 − 2 4 Q = 7 + (9 − 7)  7,86  8 1 7  Câu 21: 4 Biết sin − = và 3     . Giá trị cos bằng 5 2 3 3 3 9 A. − . B. . C.  . D. . 5 5 5 5 Lời giải Chọn A Vì 3π π  α 
nên cosα  0 . Mặt khác 2 2 sin α + cos α = 1 ta có 2 cosα = − 1− sin α 2 2  4  3 = − 1− − = −   .  5  5    
Câu 22: Giá trị của biểu thức A = sin +   là  3 4  6 − 2 6 + 2 − 6 + 2 − 6 − 2 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn B         + Ta có 3 2 2 1 6 2 A = sin + = sin cos + sin cos = . + . = .    3 4  3 4 4 3 2 2 2 2 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2. C. y = 2 − sin x . D. y = 2 − cos x + 2 . Lời giải Chọn C
Tập xác định của hàm số y = f ( x) = 2
− sin x là D = .
Do đó, nếu x thuộc tập xác định D thì −x cũng thuộc tập xác định D .
Ta có f (−x) = 2
− sin(−x) = sin x = − f (x). Vậy y = 2
− sin x là hàm số lẻ.
Câu 24: Tập nghiệm của phương trình cos x = 1 − là     
A. S =  + k2 | k  . B. S = −
+ k2 |k  .  2   2 
C. S = k2 |k  .
D. S =  + k2 | k  . Lời giải Chọn D Ta có cos x = 1
−  x =  + k2,k  . Trang 11 Câu 25: 1 1 1 Cho dãy số 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là nn 1 − n 1   1  1 (− )1 A. u = . B. u = . C. u = . D. u = . n      3  n  3  n − 3n n n 1 3 Lời giải Chọn D
Câu 26: Cho cấp số cộng (u có u = 2; d = 5
− . Số hạng thứ 20 của cấp số cộng là n ) 1 A. 93 − . B. 10 . C. 93 . D. 23. Lời giải Chọn D
u = u +19d = 2 +19( 5 − ) = 9 − 3. 20 1
Câu 27: Cho cấp số nhân ( x có x = 3 − và x = 27. −
Tính số hạng đầu x và công bội q của cấp số n ) 2 4 1 nhân. A. x = 1 − ,q = 3
− hoặc x =1,q = 3. B. x = 1
− ,q = 3 hoặc x =1,q = 3 − . 1 1 1 1
C. x = 3, q = 1
− hoặc x = 3 − ,q =1.
D. x = 3, q = 1 hoặc x = 3 − ,q = 1 − . 1 1 1 1 Lời giải Chọn B 2   q = 9  x = 3 −  x q = 3 −   q = 3  2 1      3   3 x = 2 − 7. x q = 2 − 7. x = − . x = 1.     4 1 1 1   q
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6, 5 . B. 7, 5 . C. 7, 25 . D. 8 . Lời giải Chọn C
Theo bảng thống kê, giá trị lớn nhất là 60 thuộc lớp 6,5;8) nên giá trị đại diện là 6, 5 + 8 = 7, 25. 2
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng): Trang 12 Doanh thu 5;7) 7;9) 9;1 )1 11;13) 13;15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13) . D. 13; 15) . Lời giải Chọn B 6.2 + 8.7 +10.7 +12.3 +14.1
Số trung bình của mẫu số liệu trên là: x = = 9,4 20
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. 30;45) . B. 15;30) . C. 45;60) . D. 60;75) . Lời giải Chọn A
Cỡ mẫu: n = 9 + 5 +15 +14 + 7 = 50 .
Gọi x ,..., x là thời gian khảo sát tập thể dục trong ngày của 50 học sinh khối 11 và giả sử dãy 1 50 x + x
này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là 25
26 . Do hai giá trị x , x 2 25 26 thuộc nhóm 30; 45) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa   
bởi hàm số h (t ) = 5sin t
 , trong đó h(t ) là độ cao tính bằng cetimét trên mực nước biển  5 
trung bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc
phao lại ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5 giây. B. 10 giây. C. 2, 5 giây. D. 20 giây. Lời giải Chọn B   
Ta có mô hình hóa chiều cao của sóng nước là hàm hàm số h(t) = 5sin t   nên để chiếc phao  5   ở 2
vị trí đỉnh ở hai lần liên tiếp thì cách nhau một chu kì của sóng T = =10(s)  . 5 Trang 13   
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3 3 sin 3x − =    4  2 bằng:     A. . B. − . C. . D. − . 9 6 6 9 Lời giải Chọn C  3  3x − = + k2         Ta có 3 3 3 4 3 sin 3x − =  sin 3x − = sin       .  4  2  4  3 3    3x − =  − + k2  4 3  13  13 2 3x = + k2 x = + k   12 36 3     (k Z ). 17 17    2 3x = + k2 x = + k  12  36 3  13 13
x  0  k  −  k = 0 → x =  min 13 2 Cho 24 36 TH1. Với x = + k ⎯⎯→  . 36 3 13 11  
x  0  k  −  k = −1→ x = − max  24 36  17 17
x  0  k  −  k = 0 → x =  min 17 2 Cho 24 36 TH2. Với x = + k ⎯⎯→  . 36 3 17 7  
x  0  k  −  k = −1→ x = − max  24 36 
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là 7 x = −
và nghiệm dương nhỏ nhất là 36 13 13 7  x =
. Khi đó tổng hai nghiệm bằng − = . 36 36 36 6
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 . Lời giải Chọn A
Gọi số cây ở hàng thứ n là u . n
Ta có: u =1, u = 2 , u = 3, … và S = u + u + u +...+ u = 3003 . 1 2 3 1 2 3 n
Nhận xét dãy số (u là cấp số cộng có u = 1, công sai d =1. n ) 1 Trang 14
n 2u + n −1 d   n 2.1+  (n − ) 1 1 1 ( ) Khi đó   S = = 3003  = 3003 2 2  =  n n (n + ) 1 = 6006 2
n + n − 6006 = 77 0  
n = 77 (vì n ). n = 78 −
Câu 34: Một cấp số nhân có số hạng đầu u = 3, công bội q = 2 . Biết S = 765 . Tìm n ? 1 n A. n = 8 . B. n = 9 . C. n = 6 . D. n = 7 . Lời giải Chọn A u 1 n − q 3. 1− 2n 1 ( ) ( )
Áp dụng công thức của cấp số nhân ta có: S = = = 765  n = . n 1− q 1− 8 2
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
15;20) 20;25) 25;30) 30;35) 35;40) 40;45) 45;50) Số nhân viên 7 14 25 37 21 14 10
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 1360 800 1360 3280 A. Q = , Q = . B. Q = , Q = . 1 3 37 21 1 3 37 83 136 3280 136 800 C. Q = , Q = . D. Q = , Q = . 1 3 5 83 1 3 5 21 Lời giải Chọn D
Cỡ mẫu là n = 128 . x + x
Tứ phân vị thứ nhất Q là 32
33 . Do x , x đều thuộc nhóm [25;30) nên nhóm này chứa 1 2 32 33 Q . 1
Do đó, p = 3;a = 25;m = 25;m + m = 21, a − a = 5 và ta có 3 3 1 2 4 3 8 12 − 21 136 4 Q = 25 + 5 = 1 25 5 x + x
Với tứ phân vị thứ ba Q là 96
97 . Do x , x đều thuộc nhóm [35; 40) nên nhóm này chứa 3 2 96 97 Q . 3
Do đó, p = 5;a = 35;m = 21;m + m + m + m = 7 +14 + 25 + 37 = 83;a − a = 5 và ta có 5 5 1 2 3 4 6 5 3.128 −83 800 4 Q = 35 + 5 = . 3 21 21 Trang 15
II. PHẦN TỰ LUẬN (3,0 điểm). Câu Đáp án Biểu điểm    0.5
Giải phương trình cot x + = 3   .  3       0.25 36a cot x +
= 3  x + = + k    3  3 6   0.25 x = −
+ k (k  ) . 6 2 0.5 Cho sin  =
, tính giá trị của biểu thức P = (1− 3cos)(1+ 3cos) . 3 P = −  +  = − (  )2 2 (1 3cos )(1 3cos ) 1 3cos =1− 9cos  . 0.25 36b 2 5 0.25 sin  = , 2 2 2
sin  + cos  = 1  cos  = . 3 9 5 P = 1− 9. = 4 − . 9
Giải phương trình cos3x −sin 2x = 0 . 1.0    0.25
cos3x − sin 2x = 0  cos3x = sin 2x  cos3x = cos − 2x    2      0.25 3x =  − 2x + k2    2    0.25 5x = + k2 37  2   
x = − + k2  2   2 0.25 x = + k  10 5   (k  ) 
x = − + k2  2    1.0
Giải phương trình sin x = cos x +    3     sin x = cos x +    3  0,25        cos − x = cos x +      2   3    38
− x = x + + k2  2 3   (k  )   0,25
 − x = −x − + k2  2 3   2
− x = − + k2 (k  ) 0,25 6   x =
− k (k  ) . 0,25 12 Trang 16
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu
tiên là 100000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30000
đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng 0.5
với cơ sở khoan giếng này để khoan giếng sâu 20 mét lấy nước dùng cho sinh
hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh
toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
Giá tiền mỗi mét khoan giếng lập thành một cấp số cộng với
u = 100000 (số tiền mét khoan đầu tiên), 1 39
u = u + 30000 (số tiền mét khoan thứ hai), 2 1
u = u + 30000 = u + 2.30000 (số tiền mét khoan thứ ba) 0,25 3 2 1 …
u = u + 30000 = u +19.30000 (số tiền mét khoan thứ 20), 20 19 1
và công sai d = 30000 .
Tổng chi phí cần phải thanh toán là 20(2.10000 +19.30000)
S = u + u + u + ... + u = = 7700000 . 0,25 20 1 2 3 20 2
-------------- HẾT -------------- Trang 17