Đề thi giữa học kì 1 môn Toán 11 năm 2023 - 2024 sách Kết nối tri thức với cuộc sống | đề 5

Đề thi giữa kì 1 Toán 11 Kết nối tri thức năm 2023 - 2024 mang đến 11 đề thi giữa kì 1 có ma trận, đáp án hướng dẫn giải chi tiết, chính xác. Thông qua đề thi giữa kì 1 Toán 11 quý thầy cô có thêm nhiều tài liệu tham khảo để ra đề thi cho các em học sinh của mình.

54 27 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 11

Môn: Toán 11

Sách: Kết nối tri thức

Thông tin:

54 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
ĐỀ 5
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 đim).
Câu 1. Gi tr no sau đây mang du dương?
A.
0
cos120
B.
0
sin120
C.
0
tan120
. D.
0
cot120
.
Câu 2. Trong mặt phẳng cho ba tia
,,Ou Ov Ox
. Trong cc mnh đ sau, mnh đ no đng?
A.
.
B.
.
C.
.
D.
.
Câu 3. Trong cc khẳng đnh sau, khẳng đnh no đng?
A.
( )
cos cos cos sin sin .a b a b a b+ = −
B.
( )
cos cos cos sin sin .a b a b a b+ = +
C.
( )
cos cos sin sin cos .a b a b a b+ = +
D.
( )
cos sin cos cos sin .a b a a b b+ = +
Câu 4. Trong cc khẳng đnh sau, khẳng đnh no sai?
A.
22
sin2 cos sina a a=−
B.
cos2 2sinaa=
C.
2
cos2 2cos 1.aa=−
D.
2
cos2 1 2sin .aa=−
Câu 5. Đồ th dưới đây l đồ th của hm số no?
A.
1 sin2yx=+
. B.
cosyx=
. C.
sinyx=−
. D.
cosyx=−
.
Câu 6. Trong cc hm số sau, hm số no l hm số chẵn?
A.
tan .yx=
B.
cot .yx=
C.
sin .yx=
D.
cos .yx=
Câu 7. Điu kin có nghim của phương trình
sin xm=
l
A.
1m
. B.
1m
. C.
1m
. D.
1m
.
Câu 8. Cho dãy số
( )
n
u
, biết
2
n
un=+
. Ba số hạng đầu tiên của dãy số lần lượt l
A.
3;4;5.
B.
0;1;2.
C.
2;3;4.
D.
1;2;3.
Câu 9. Trong cc dãy số sau dãy số no l dãy số hữu hạn
A.
2345
1 1 1 1 1
, , , , ....
3 3 3 3 3
B.
5,10,15,20,25....
C.
8,15,22,29,36.
D.
2,0,4,6,8,...
Câu 10. Cho cp số cộng
( )
n
u
, biết
12
2, 8uu==
. Công sai của cp số cộng l
A.
6d =
. B.
16d =
. C.
10d =
. D.
4d =
.
Câu 11. Cho cp số cộng
( )
n
u
, biết
1
2u =
v công sai
3d =
. Khẳng đnh no sau đây đng?
A.
2
5.u =
B.
2
2.u =
C.
2
6.u =
D.
2
3.u =
Câu 12. Cho cp số cộng
( )
n
u
. Gọi
n
S
l tổng của
n
số hạng đầu của cp số cộng. Khẳng đnh đng l
A.
( )
1
1
2
n
nn
S nu d
−
=+
. B.
( )
1
1
2
n
nu n n
Sd
+−
=
.
C.
( )
1
1
n
S nu n n d= + −
. D.
( )
1
1
2
n
n
S nu d
−
=+
.
Câu 13. Dãy số no sau đây không phải l cp số nhân?
A.
1; 3;9; 27;54−−
. B.
1;2;4;8;16
. C.
1; 1;1; 1;1−−
. D.
1; 2;4; 8;16−−
.
Câu 14. Cho cp số nhân
( )
n
u
với
1
81u =
v
4
3u =
. Tìm công bội
q
?
A.
1
3
1
3
−
. B.
1
3
−
. C.
3
. D.
3−
.
Câu 15. Cho cp số nhân
( )
n
u
với
1
2u =
v công bội
3q =
. Gi tr của
2
u
bằng
A.
6
. B.
9
. C.
8
. D.
2
3
.
Câu 16. Trong mẫu số liu ghép nhóm, độ di mỗi nhóm
)
;ab
được tính như thế no?
A.
.ba−
B.
.
2
ab+
C.
.ab+
D.
..ab
Câu 17. Cc gi tr xut hin nhiu nht trong mẫu số liu được gọi l
A. mốt. B. số trung bình.
C. số trung v. D. tứ phân v.
Câu 18. Trong mẫu số liu ghép nhóm, gi tr đại din của nhóm
)
;ab
được tính như thế no?
A.
.
2
ab+
B.
.ba−
C.
.ab+
D.
..ab
Câu 19. Trong cc khẳng đnh sau, khẳng đnh no l đng?
A. Số trung v l
( )
( )
11
1
...
2
p
e p p p
p
n
mm
M a a a
m
+
+
− + +
= + −
.
B. Số trung v b ảnh hưởng bởi cc gi tr qu lớn hay qu bé.
C. Số trung v luôn l một số liu no đó của mẫu.
D. Số trung v chính l số trung bình.
Câu 20. Đo chiu cao (tính bằng
cm
) của
500
học sinh trong một trường THPT ta thu được kết quả như
sau:
Chiu cao
)
150;154
)
154;158
)
158;162
)
162;166
)
166;170
Số học sinh
25
50
200
175
50
Mẫu số liu ghép nhóm đã cho có tt cả bao nhiêu nhóm?
A.
5
. B.
6
. C.
7
. D.
12
.
Câu 21. Biết
1
sin
3
=
v
.
2


. Gi tr
cos
bằng
A.
22
.
3
−
B.
23
.
3
−
C.
32
.
2
−
D.
33
.
2
−
Câu 22. Biết
1
sin
4
=
. Gi tr
cos2
bằng
A.
7
.
8
B.
8
.
7
C.
7
.
8
−
D.
8
.
7
−
Câu 23. Tập gi tr của hm số
2sinyx=
l
A.
1;1 .−
B.
0;2 .
C.
2;2 .−
D.
2;2 .−
Câu 24. Tập nghim của phương trình
cos 0x =
l
A.
2 | .
2
S k k

= +

B.
|.
2
S k k

= +

C.
2 | .S k k
=
D.
2 | .
2
S k k

= − +

Câu 25. Xét tính tăng giảm của dãy số
1 1 1 1
; ; ; .
2345
− − − −
A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng không giảm D. Dãy số vừa tăng vừa giảm
Câu 26. Cho một cp số cộng có cc số hạng lần lượt l
1,6,11, .x
Khi đó gi tr của
x
l
A. 5 . B. 18. C. 17. D. 16.
Câu 27. Cho cp số nhân có cc số hạng lần lượt l 1; 4; 16; 64. Gọi
n
S
l tổng của n số hạng đầu tiên của
cp số nhân đó. Mnh đ no sau đây đng?
A.
41
3
n
n
S
−
=
. B.
( )
1
14
2
n
n
n
S
−
+
=
. C.
1
4
n
n
S
−
=
. D.
( )
4 4 1
3
n
n
S
−
=
.
Câu 28. Bảng số liu ghép nhóm sau cho biết chiu cao
( )
cm
của 45 học sinh lớp
11A
.
Mẫu số liu ghép nhóm ny có số mốt l
A.
2
. B.
1
. C.
0
. D.
3
.
Câu 29. Cơ cu dân số Vit Nam năm
2020
theo độ tuổi được cho trong bảng sau:
(Theo:http://ourwoldindata.org)
Chọn
85
l gi tr đại din cho nhóm trên
65
tuổi. Tính tuổi trung bình của người Vit Nam năm
2020
.
A.
36,17
. B.
34,82
. C.
35,6
. D.
37,12
.
Câu 30. Khảo st chiu cao (cm) của 52 học sinh khối 11 thu được mẫu số liu ghép nhóm sau:
Nhóm chứa trung v l
A.
)
165;170
. B.
)
160;165
. C.
)
170;175
. D.
)
175;180
.
Câu 31. Tập xc đinh của hm số
sin cosy x x=+
l
A.
.
B.
\ | .kk
C.
\ | .k
D.
\ 2 | .kk
Câu 32. Phương trình
2cos 3x =−
có bao nhiêu nghim thuộc tập
;3

−
A. 4. B. 3. C. 2. D. 1.
Câu 33. Cho dãy số
( )
n
u
xc đnh bởi
2 2 2 2
1 1 1 1
...
1 2 3
n
u
n
= + + + +
. Chọn mnh đ đng?
A. Dãy số
( )
n
u
b chặn.
B. Dãy số
( )
n
u
b chặn trên, nhưng không b chặn dưới.
C. Dãy số
( )
n
u
b chặn dưới, nhưng không b chặn trên.
D. Dãy số
( )
n
u
không b chặn.
Câu 34. Gọi
1 11 111 ... 111...1S = + + + +
(
n
số
1
) thì
S
nhận gi tr no sau đây?
A.
1 10 1
10
99
n
Sn


−
=−




. B.
10 1
10
81
n
S

−
=


.
C.
10 1
10
81
n
Sn

−
=−


. D.
10 1
81
n
S
−
=
.
Câu 35. Khảo st vận tốc (dặm/h;
1
dặm
1,609km=
) của
300
xe ô tô chạy trên con đường
A
thu được
mẫu số liu ghép nhóm như sau:
Nhóm chứa tứ phân v thứ nht l
A.
)
32,5 ;37,5
. B.
)
27,5 ;32,5
. C.
)
37,5 ;42,5
. D.
)
42,5 ;47,5
.
II. PHẦN TỰ LUẬN
(3 đim).
Câu 36
(1 đim).
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liu trên?
Câu 37
(1 đim).
a) Tìm tập xc đnh của hm số sau:
22
sin
sin cos
=
−
x
y
xx
.
b) Giải phương trình
( )
sin cos 1x
=
.
Câu 38 (1 đim). Người ta trồng
2145
cây theo hình một tam gic như sau: hng thứ nht có
1
cây, hng
thứ hai có
2
cây, hng thứ ba có 3 cây,… Hỏi có tt cả bao nhiêu hng cây?
……………… HT ………………
ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng.
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
B
A
A
B
B
D
C
A
C
A
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
A
A
A
A
A
A
A
A
A
A
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
A
A
D
B
B
D
A
A
A
A
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
A
A
A
A
A
II. PHẦN TỰ LUẬN
Câu
Đp n
Biu đim
36
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liu trên?
Tần số lớn nht l
16
nên nhóm chứa mốt l nhóm
)
50,5;55,5
v
3j =
0,25
Ta có
3 4 4 3
50,5; 55,5 5u u h u u= = = − =
0,25
Tần số:
2 3 4
7; 16; 4n n n= = =
.
0,25
( ) ( )
( ) ( )
1
2
3
11
3
3
2 3 4
jj
oj
j j j j
n
n
M u h u h
n
n
n
n
n
n n
n
n
n
−
−+
−
−
= + = +
− + −
− + −
0
16 7
50,5 .5 52,6
(16 7) ) (16 4
M
−
= + =
−−+
0,25
37
a) Tìm tập xc đnh của hm số sau:
22
sin
sin cos
=
−
x
y
xx
.
Điu kin xc đnh của hm số
l
22
sin cos 0 cos2 0 2 ;
2 4 2
− − + +
k
x x x x k x k
.
0,25
Vậy tập xc đnh của hm số l
\;
42


= +


k
Dk
0,25
b) Giải phương trnh
( )
sin cos 1x
=
.
( )
sin cos 1 cos 2 ,
2
x x k k
= = +
1
cos 2 ,
2
x k k = +
0,25
Vì
1 cos 1x−
nên
1 3 1
1 2 1
2 4 4
kk− + −
.
Do
0kk =
suy ra
1
cos 2 ,
23
x x m m
= = +
.
0,25
38
Người ta trồng
2145
cây theo hình một tam gic như sau: hng thứ nht có
1
cây,
hng thứ hai có
2
cây, hng thứ ba có 3 cây,… Hỏi có tt cả bao nhiêu hng
cây?
Gọi số hng cây l
n
, hng thứ
n
có
n
cây.
0,25
Ta có
1 2 3 ... 2145n+ + + + =
0,25
( )
1
2145
2
nn+
=
.
0,25
65n=
0,25
======
ĐỀ 6
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 đim):
Câu 1. Cho
thuộc góc phần tư III của đường tròn lượng gic. Khẳng đnh no dưới đây đng?
A.
sin 0; 0cos


. B.
sin 0; 0cos


.
C.
sin 0; 0cos


. D.
sin 0; 0cos


.
Câu 2. Một chiếc đồng hồ có kim chỉ giờ
OG
chỉ số
9
v kim pht
OP
chỉ số
12
. Số đo của góc lượng
gic
( )
,OG OP
l
A.
00
90 360 ,kk− +
. B.
00
270 360 ,kk− +
.
C.
00
270 360 ,kk+
. D.
00
90 360 ,kk+
.
Câu 3. Trên đường tròn lượng gic, cho điểm
( )
;M x y
v
( )
,sđ OA OM
=
. Khẳng đnh no dưới đây
đng?
A.
sin y
=
. B.
sin xy
=−
. C.
cos y
=
. D.
cos xy
=+
.
Câu 4.
cot
6
bằng
A.
0
. B.
1
3
. C.
3
. D.
1
.
Câu 5. Cho tam gic
ABC
. Khẳng đnh no dưới đây đng?
A.
( )
cos cosA B C+=
. B.
( )
cos sinA B C+=
.
C.
( )
cos sinA B C+ = −
. D.
( )
cos cosA B C+ = −
.
Câu 6. Cho góc
thỏa
4
cos
5
=
v
0
2

. Gi tr của
sin2
bằng
A.
12
25
−
. B.
24
25
. C.
24
25
−
. D.
12
25
.
Câu 7. Đường cong trong hình bên l đồ th của hm số no dưới đây?
A.
tanyx=
. B.
cosyx=
. C.
cotyx=
. D.
sinyx=
.
Câu 8. Hm số no dưới đây l hm số chẵn?
A.
cosyx=
. B.
tanyx=
. C.
cotyx=
. D.
sinyx=
.
Câu 9. Hm số
3sin 2yx=
tuần hon với chu kì
A.
6T
=
. B.
3T
=
. C.
T
=
. D.
2T
=
.
Câu 10. Tập gi tr của hm số
2sin 3yx=+
l
A.
1;1−
. B.
1;5
. C.
4; 8
. D.
( )
1;5
.
Câu 11. Nghim của phương trình
cos 1x =
l
A.
,x k k
=
. B.
2,x k k
=
.
C.
,
2
x k k
= +
. D.
2,x k k

= +
.
Câu 12. Nghim của phương trình
3tan 1x =
l
A.
2,
6
x k k
= +
. B.
,
4
x k k
= +
.
C.
,
3
x k k
= +
. D.
,
6
x k k
= +
.
Câu 13. Nghim của phương trình
2cos 1 0x −=
l
A.
2,
4
x k k
= +
. B.
2,
3
x k k
= +
.
C.
,
4
x k k
= +
. D.
,
3
x k k
= +
.
Câu 14. Dãy số no dưới đây l dãy số tăng?
A.
2, 4, 3
B.
1 1 1
,,
4 3 2
. C.
3, 3, 3
D.
1 1 1
,,
2 3 4
.
Câu 15. Trong cc dãy số
( )
n
u
dưới đây, dãy số no b chặn dưới?
A.
2
n
un=−
. B.
12
n
un=−
. C.
1
1
n
u
n
=
+
. D.
1
2
n
n
u =
.
Câu 16. Cho dãy số
( )
n
u
xc đnh bởi h thức truy hồi
( )
1
1
1
2
3
nn
u
n
u u n
−
=−
=+
. Gi tr của
3
u
bằng
A.
1
. B.
3
. C.
2
. D.
0
.
Câu 17. Dãy số no dưới đây không l cp số cộng?
A.
1, 2, 4, 8
B.
1, 2, 3, 4
. C.
1, 0, 1, 2−−
. D.
1,1,1,1
.
Câu 18. Cho cp số cộng
2, 3,8,...−
. Công sai của cp số cộng đã cho bằng
A.
1
. B.
5−
. C.
5
. D.
1−
.
Câu 19. Cho cp số cộng
( )
n
u
với số hạng tổng qut
21
n
un=−
. Số hạng thứ tư của cp số cộng đã cho
bằng
A.
7
. B.
3
. C.
4
. D.
5
.
Câu 20. Cho cp số cộng
( )
n
u
với
1
0u =
v công sai
4d =
. Số hạng thứ my của cp số cộng đã cho
bằng
20
?
A. Số hạng thứ
8
. B. Số hạng thứ
5
. C. Số hạng thứ
7
. D. Số hạng thứ
6
.
Câu 21. Cho cp số cộng
( )
n
u
được xc đnh bởi công thức:
( )
1
1
2
2
3
nn
u
n
uu
−
=
=−
. Số hạng tổng qut của
cp số cộng đã cho l
A.
1
n
un=+
. B.
53
n
un=−
. C.
31
n
un=−
. D.
53
n
un=−
.
Câu 22. Dãy số
( )
n
u
được cho bởi công thức no dưới đây l một cp số nhân?
A.
2 n+
. B.
1
1
1
nn
u
u nu
+
=
=
. C.
2
n
un=
. D.
1
1
1
2
nn
u
uu
+
=
=
.
Câu 23. Ba số hạng no dưới đây theo thứ tự đó lập thnh một cp số nhân?
A.
1, 3, 5
. B.
3, 5, 9
. C.
1, 3, 9
. D.
1, 5, 9
.
Câu 24. Cho cp số nhân
( )
n
u
với
1
2u =
v công bội
1
2
q =
. Bốn số hạng đầu của cp số nhân đã cho l
A.
1
,1, 2, 4
2
. B.
2,1,1,1
. C.
5 9 13
2, , ,
2 2 2
. D.
11
2,1, ,
24
.
Câu 25. Cho cp số nhân
( )
n
u
với
1
5u =−
v công bội
3q =
. Gi tr của
5
u
bằng
A.
1875
. B.
405−
. C.
15−
. D.
7
.
Câu 26. Cho cp số nhân
3, 12, 48,...−
. Số hạng tổng qut của cp số nhân đã cho l
A.
( )
1
3. 4
n
n
u
+
=−
. B.
( )
34
n
n
u =−
. C.
( )
1
3. 4
n
n
u
−
=−
. D.
( )
1
3. 4
n
n
u
−
=
.
Câu 27. Độ di của nhóm
)
1;20
bằng
A.
19.
B.
20.
C.
18.
D.
17.
Câu 28. Thống kê v nhit độ tại một đa điểm trong
30
ngy, ta có bảng số liu sau:
Nhit độ
( )
0
C
)
18; 22
)
22; 25
)
25; 28
)
28; 31
)
31; 34
Số ngy
3
6
10
5
6
Số ngy có nhit độ thp hơn
0
25 C
l
A.
10
. B.
9
. C.
19
. D.
3
.
Câu 29. Thống kê số lỗi chính tả trong bi kiểm tra giữa HKI môn Ngữ Văn của học sinh khối 11 thu
được kết quả ở bảng sau:
Số lỗi
)
1; 3
)
3; 5
)
5; 7
)
7; 9
)
9;11
Số bi
122
75
14
5
2
Khẳng đnh no dưới đây đng?
A. Có
5
bi kiểm tra sai
7
lỗi chính tả.
B. Có
5
bi kiểm tra sai
8
lỗi chính tả.
C. Có
5
bi kiểm tra sai từ
7
đến
8
lỗi chính tả.
D. Có
5
bi kiểm tra sai từ
7
đến
9
lỗi chính tả.
Câu 30. Một công ty xây dựng khảo st khch hng xem họ có nhu cầu mua nh ở mức gi no. Kết quả
khảo st được ghi lại ở bảng sau:
Mức gi
(triu đồng/
2
m
)
)
10;14
)
14;18
)
18; 22
)
22; 26
)
26; 30
Tần số
54
78
120
45
12
Mức gi thuộc nhóm no dưới đây l phù hợp với đa số khch hng được khảo st?
A.
)
14;18
. B.
)
26; 30
. C.
)
18; 22
. D.
)
10;14
.
Câu 31. Điu tra v điểm kiểm tra giữa HKI của
36
học sinh lớp 11A ta được kết quả sau:
Điểm
)
0; 2
)
2; 4
)
4; 6
)
6;8
)
8;10
Tần số
1
5
9
14
7
Điểm trung bình của
36
học sinh trên gần nht với số no dưới đây?
A.
6,4
. B.
6,2
. C.
6,0
. D.
6,6
.
Câu 32. Doanh thu (triu đồng) bn hng trong 20 ngy được lựa chọn ngẫu nhiên của một cửa
hng được ghi lại ở bảng sau:
Doanh thu
)
5; 7
)
7; 9
)
9;11
)
11;13
)
13;15
Số ngy
2
7
7
3
1
Trung v của mẫu số liu trên thuộc nhóm no dưới đây?
A.
)
9;11
.
B.
)
7; 9
.
C.
)
11;13
.
D.
)
13;15
.
Câu 33. Phỏng vn một số học sinh khối 11 v thời gian (giờ) ngủ của một buổi tối thu được kết
quả sau:
Thời gian
)
4; 5
)
5; 6
)
6; 7
)
7;8
)
8; 9
Số học
sinh
10
18
23
20
15
Nhóm chứa tứ phân v thứ nht của mẫu số liu trên l
A.
)
5; 6
.
B.
)
7;8
.
C.
)
4; 5
.
D.
)
6; 7
.
Câu 34. Thời gian (pht) truy bi trước mỗi buổi học của một số học sinh trong một tuần được ghi lại ở
bảng sau:
Thời gian
)
9,5;12,5
)
12,5;15,5
)
15,5;18,5
)
18,5; 21,5
)
21,5; 24,5
Số học sinh
3
12
15
24
2
Trung v của mẫu số liu trên bằng
A.
16,2
. B.
18,1
. C.
15
. D.
9
.
Câu 35. Người ta ghi lại tuổi thọ của một số con muỗi ci trong phòng thí nghim cho kết quả như sau:
Tuổi thọ (ngy)
)
0; 20
)
20; 40
)
40; 60
)
60; 80
)
80;100
Số lượng
5
12
23
31
29
Muỗi ci có tuổi thọ khoảng bao nhiêu ngy l nhiu nht?
A.
80
ngy. B.
66
ngy. C.
76
ngy. D.
90
ngy.
II. TỰ LUẬN
(3,0 đim)
Bài 1
(1,0 đim).
Cho góc
thỏa
4
cos
5
=−
v
3
2


. Tính
tan
4

−


.
Bài 2 (1.0 đim). Giải phương trình
sin4 cos3 cos 0x x x+ − =
.
Bài 3 (0.5 đim). Trong một đợt quyên góp để ủng hộ học sinh vùng khó khăn. 40 học sinh lớp 11 của
trường THPT X thực hin kế hoạch quyên góp như sau: Ngy đầu tiên mỗi bạn quyên góp 2000 đồng, từ
ngy thứ hai trở đi mỗi bạn quyên góp hơn ngy lin trước l 500 đồng. Hỏi sau bao nhiêu ngy thì số tin
quyên góp được l 9800000 đồng.
Bài 4 (0.5 đim). Đầu mùa thu hoạch sầu riêng, ông A đã bn cho người thứ nht nửa số sầu riêng thu
hoạch được v tặng thêm 1 quả, bn cho người thứ hai nửa số sầu riêng còn lại v tặng thêm 1 quả. Ông cứ
tiếp tục cch bn như trên thì đến người thứ bảy số sầu riêng của ông được bn hết. Tính số sầu riêng m
ông A thu hoạch được.
………………Ht……………….
ĐÁP ÁN
I. TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
B
A
A
C
D
B
B
A
C
B
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
B
D
B
B
A
D
A
C
A
D
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
B
D
C
D
B
C
A
B
C
C
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
B
A
A
B
C
II. TỰ LUẬN
Bài
Đp n
Đi
m
1
(1,0đ)
Cho góc
thỏa
4
cos
5
=−
và
3
2


. Tính
tan
4

−


.
2
3
sin 1 cos
5

= − =
0,25
33
sin
25
= −
0,25
sin
1
tan 1
cos
tan
sin
4 1 tan
1
cos

−
−

− = =

+

+
0,25
1
7
=−
0,25
2
(1,0đ)
Giải phương trnh
sin4 cos3 cos 0x x x+ − =
.
Phương trình đã cho tương đương
2sin2 cos2 2sin2 sin 0x x x x−=
0,25
( )
( )
sin2 0 1
sin2 (cos2 sin ) 0
cos2 sin 2
x
x x x
xx
=
− =
=
0,25
( )
1
2
k
x
=
0,25
( )
2
63
2 cos2 cos
2
2
2
k
x
xx
xk

=+

= −


= − +
. Nghim PT:
2
63
2
k
x
k
x

=+
=
0,25
3
(0,5đ)
Trong một đợt quyên góp để ủng hộ học sinh vùng khó khăn. 40 học sinh lớp 11
của trường THPT X thực hiện kế hoạch quyên góp như sau: Ngày đầu tiên mỗi
bạn quyên góp 2000 đồng, từ ngày thứ hai trở đi mỗi bạn quyên góp hơn ngày
liền trước là 500 đồng. Hỏi sau bao nhiêu ngày th số tiền quyên góp được là
9800000 đồng.
Số tin mỗi học sinh quyên góp theo từng ngy lập thnh một cp số cộng
với số hạng đầu
1
2000u =
v công sai
d 500=
Do đó tổng số tin m 40 học sinh quyên góp được sau
n
ngy l
0,25
Theo giả thiết ta có:
22
10000 70000 9800000 7 980 0n n n n+ = + − =
( )
28
35
n
nL
=
=−
Vậy số ngy cần quyên góp l 28 ngy
0,25
4
(0,5đ)
Đầu mùa thu hoạch sầu riêng, ông A đã bán cho người thứ nhất nửa số sầu riêng
thu hoạch được và tặng thêm 1 quả, bán cho người thứ hai nửa số sầu riêng còn
lại và tặng thêm 1 quả. Ông cứ tiếp tục cách bán như trên th đến người thứ bảy
số sầu riêng của ông được bán hết. Tính số sầu riêng mà ông A thu hoạch được.
Gọi
x
l số quả sầu riêng m ông A thu hoạch được
Khi đó số quả sầu riêng m người thứ nht mua v được tặng l:
12
1
22
x
x
+
+=
Số quả sầu riêng m người thứ hai mua v được tặng l:
2
1 2 2
1
2 2 2
xx
x
++

− + =


...
Số quả sầu riêng m người thứ bảy mua v được tặng l:
7
2
2
x +
0,25
Khi đó:
( )
2 7 2 7
2 2 2 1 1 1
... 2 ...
2 2 2 2 2 2
x x x
x x x
+ + +

+ + + = + + + + =


( ) ( )
7
1
1
1 127
2
2 . 2 254
1
2 128
1
2
x x x x x

−


+ = + = =
−
0,25
ĐỀ 7
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 đim - gồm 35 câu: từ câu 1 đến câu 35).
Câu 1: Gi tr của bằng
A. B. C. D.
Câu 2: Số đo theo đơn v rađian của góc
315
l
A.
7
2
. B.
7
4
. C.
2
7
D.
4
7
.
Câu 3: Cho bốn cung (trên một đường tròn đnh hướng):
5 25 19
, , ,
6 3 3 6
= − = = =
, Cc cung
có điểm cuối trùng nhau l
A.
v
;
v
. B.
,,
. C.
,,
.
D.
v
;
v
.
Câu 4: Một bnh xe có
72
răng. Số đo góc m bnh xe đã quay được khi di chuyển
10
răng l:
A.
0
60
. B.
0
30
. C.
0
40
. D.
0
50
.
Câu 5: Biết
tan 2
=
v
180 270

. Gi tr
cos sin

+
bằng
A.
35
5
−
. B.
1– 5
. C.
35
2
. D.
51
2
−
.
Câu 6: Trong cc công thức sau, công thức no sai?
A.
22
cos 2 cos – sin .a a a=
. B.
22
cos2 cos sin .a a a=+
.
C.
2
cos 2 2cos –1.aa=
D.
2
cos 2 1– 2sin .aa=
Câu 7: Biết
1
sin
2
x =
thì
cos2x
có gi tr l :
A.
0
. B.
1
. C.
1
2
−
. D.
1
2
.
Câu 8: Rt gọn
( ) ( )
sin cos cos sinM x y y x y y= + − +
?
A.
cosMx=
. B.
sinMx=
. C.
( )
sin 2M x y=+
. D.
( )
cos 2M x y=+
.
Câu 9: Tập xc đnh của hm số
sinyx=
l
A.
\
2
D

=


. B.
\ 2 ,
2
D k k

= +


.C.
D =
. D.
\
2
D

=


.
Câu 10: Cho hm số
( )
y f x=
có đồ th như hình vẽ.
Đồ th hm số
( )
y f x=
l đồ th của hm số no dưới đây?
A.
tanyx=
. B.
sinyx=
. C.
cosyx=
. D.
cotyx=
.
Câu 11: Tập xc đnh của hm số
sin5 cos cot2y x x x= + +
l
A.
\,
2
D k k

= +


. B.
\ 2 ,
2
D k k

= +


.
C.
\,D k k
=
. D.
\,
2
D k k

=


.
Câu 12: Nghim của phương trình
tan 1x =
l:
A.
( )
4
x k k
= +
B.
( )
2
3
x k k
= +
C.
( )
2
4
x k k
= +
D.
( )
5
2
6
x k k
= +
Câu 13: Nghim của phương trình
1
cos
2
x =-
l:
A.
2
2
3
xk
p
p= ± +
B.
6
xk
p
p= ± +
C.
2
3
xk
p
p= ± +
D.
2
6
xk
p
p= ± +
Câu 14: Tìm tt cả cc nghim của phương trình
sin 1
6
x

+=


.
A.
3
xk
=+
( )
k
. B.
2
6
xk
= − +
( )
k
.
C.
2
3
xk
=+
( )
k
. D.
5
2
6
xk
=+
( )
k
.
Câu 15: Nghim của phương trình
tan3 tanxx=
l
A.
,.
2
k
xk
=
B.
,x k k
=
. C.
2 , .x k k
=
D.
,.
6
k
xk
=
Câu 16: Dãy số no dưới đây l dãy số nguyên tố nhỏ hơn
10
theo thứ tự tăng dần?
A.
0
,
1
,
2
,
3
,
5
,
7
. B.
1
,
2
,
3
,
5
,
7
. C.
2
,
3
,
5
,
7
. D.
1
,
3
,
5
,
7
.
Câu 17: Cho dãy số
( )
,
n
u
biết
2
n
n
n
u =
. Chọn đp n đng.
A.
4
1
4
u =
. B.
5
1
16
u =
. C.
5
1
32
u =
. D.
3
1
8
u =
.
Câu 18: Cho dãy số có cc số hạng đầu l
1 2 3 4
0; ; ; ; ;...
2 3 4 5
.Số hạng tổng qut của dãy số ny l:
A.
1
n
n
u
n
+
=
. B.
1
n
n
u
n
=
+
. C.
1
n
n
u
n
−
=
. D.
2
1
n
nn
u
n
−
=
+
.
Câu 19: Dãy số no sau đây không phải l cp số cộng?
A.
2;5;8;11;14...
B.
2;4;8;10;14...
C.
1;2;3;4;5;6...
D.
15;10;5;0; 5;...−
Câu 20: Cho cp số cộng
( )
n
u
có số hạng đầu
1
1
,
2
u =−
công sai
1
.
2
d =
Năm số hạng liên tiếp đầu tiên
của cp số cộng l:
A.
11
;0;1; ;1.
22
−
B.
111
;0; ;0; .
222
−
C.
1 3 5
;1; ;2; .
2 2 2
D.
1 1 3
;0; ;1; .
2 2 2
−
Câu 21: Cho cp số cộng
( )
n
u
có số hạng đầu
1
5u =−
v công sai
3d =
. Số 100 l số hạng thứ my của
cp số cộng?
A. 15. B. 20. C. 35. D. 36.
Câu 22: Cho dãy số
( )
n
u
l một cp số nhân có số hạng đầu
1
u
v công bội
q
. Đẳng thức no sau đây
đúng?
A.
( )
1
1
n
u u n q= + −
,
( )
2n
. B.
1
1
n
n
u u q
−
=
,
( )
2n
.
C.
( )
1
1
.
n
n
u q u
−
=
,
( )
2n
. D.
1
1
n
n
u
u
q
−
=
,
( )
2k
.
Câu 23: Cho cp số nhân
( )
n
u
với công bội
1q
. Đặt
12
...
nn
S u u u= + + +
. Khẳng đnh no sau đây
đng?
A.
( )
1
1
1
n
n
uq
S
q
−
=
−
. B.
( )
1
1
1
1
n
n
uq
S
q
−
−
=
−
. C.
( )
1
1
n
n
S u q=−
. D.
( )
1
1
1
n
n
uq
S
q
−
=
−
.
Câu 24: Cho dãy số
( )
n
u
l một cp số nhân với
1
1
;2
2
uq= = −
. Năm số hạng đầu tiên của CSN l
A.
1
;1;2;4;8
2
. B.
1
; 1;2; 4;8
2
−−
. C.
1 1 1 1 1
; ; ; ;
2 4 8 16 32
−−
. D.
1 1 1 1 1
; ; ; ;
2 4 8 16 32
.
Câu 25: Cho cp số nhân
( )
n
u
biết
2
2u =−
v
5
54u =
. Tìm tổng 10 số hạng đầu tiên của cp số nhân
A.
10
10
2
. 1 3
3
4
S

−

=
. B.
10
10
2
. 1 3
3
4
S

+

=
. C.
10
10
2
. 1 3
3
2
S

−−

=
. D.
10
10
2
. 1 3
3
2
S

−

=
−
.
Câu 26: Trong không gian, cho 3 điểm phân bit không thẳng hng. Khí đó có bao nhiêu mặt phẳng đi
qua ba điểm đó?
A. 1 B. 0 C. 2 D. Vô số
Câu 27: Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) v (SBC) l đường thẳng
A. SA B. SD C. SB D. AC
Câu 28: Cho hình chóp S.ABCD, gọi O l giao điểm của AC v BD. Giao tuyến của hai mặt phẳng (SAD)
v (SBC) l đường thẳng
A. SA B. SB C. SC D. SO
Câu 29: Cho tứ din ABCD có M, N lần lượt l cc điểm thuộc cạnh BC v BD sao cho MN không song
song CD. Gọi K l giao điểm của MN v (ACD). Khẳng đnh no sau đây đng?
A. K l giao của CM v DN B. K l giao MN v AC
C. K l giao của MN v AD D. K l giao của MN v CD
Câu 30: Cho hình chóp S.ABCD có đy lhình bình hnh. M, N lần lượt l trung điểm của BC v SD.
Giao tuyến của hai mặt phẳng (AMN) v (SCD) l
A. đường thẳng NI với I l giao điểm giữa SC v MN
B. đường thẳng NI với I l giao điểm giữa SC v AM
C. đường thẳng NI với I l giao điểm giữa CD v AM
D. đường thẳng NI với I l giao điểm giữa CD v MN
Câu 31: Trong cc mnh đ sau, mnh đ no đng?
A. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân bit thì chéo nhau.
B. Hai đường thẳng không có điểm chung thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng phân bit không song song thì chéo nhau.
Câu 32: Cho hình chóp
.S ABCD
có đy
ABCD
l hình thoi. Trong cc cặp đường thẳng sau, cặp đường
thẳng no cắt nhau?
A.
AB
v
CD
. B.
AC
v BD C.
SB
v
CD
. D.
SD
v
BC
.
Câu 33: Cho hình chóp
.S ABCD
có đy
ABCD
l hình bình hnh. Gọi
M
,
N
,
P
,
Q
lần lượt l trug
điểm của cc cạnh bên
SA
,
SB
,
SC
,
SD
(
H
.4.27). Tứ gic
MNPQ
l hình gì?
A. Tứ gic
MNPQ
l hình bình hnh. B. Tứ gic
MNPQ
l hình vuông.
C. Tứ gic
MNPQ
l hình chữ nhật. D. Tứ gic
MNPQ
l hình thoi.
Câu 34: Cho hình chóp
.S ABCD
có đy
ABCD
l hình thang cạnh đy AB. Gọi
d
l giao tuyến của hai
mặt phẳng
( )
SAB
v
( )
.SCD
Khẳng đnh no sau đây đng?
A.
d
qua
S
v song song với
.BC
B.
d
qua
S
v song song với
AD
C.
d
qua
S
v song song với
.AB
D.
d
qua
S
v song song với
.BD
Câu 35: Cho hình chóp
.S ABCD
có đy
ABCD
l hình thang, đy lớn l
CD
. Gọi
M
l trung điểm của
SA
,
N
l giao điểm của cạnh
SB
v mặt phẳng
( )
MCD
. Mnh đ no sau đây đng?
A.
MN
v
SD
cắt nhau. B.
//MN CD
.
C.
MN
v
SC
cắt nhau. D.
MN
v
CD
chéo nhau.
II. PHẦN TỰ LUẬN (3 đim - gồm 04 câu: từ câu 36 đến câu 39).
Câu 36 (1,5 đim):
a) Cho
1
os
3
c
=−
với
2


. Tính
sin2
b) Giải phương trình lượng gic sau:
sin2 2cos sin 1
0
tan 3
x x x
x
+ − −
=
+
Câu 37 (0,5 đim): Cho cp số cộng
( )
n
u
có
1 5 3
16
10
7
u u u
uu
+ − =
+=
. Tìm số hạng đầu
1
u
v công sai d của cp
số cộng đó.
Câu 38 (1,5 đim): Cho hình chóp S.ABCD có đy l hình thang
( )
/ / ,AB CD AB CD
.
a) Tìm giao tuyến của mặt phẳng
( )
SAC
v
( )
SBD
;
( )
SAB
v
( )
SCD
.
b) Gọi M l một điểm nằm trên cạnh SA sao cho
4SA SM=
.
Tìm giao điểm I của đường thẳng BM v mặt phẳng
( )
SCD
.
--------------------------- HT ---------------------------
HƯỚNG DẪN CHẤM
I. PHẦN TRẮC NGHIỆM
BẢNG ĐÁP ÁN
1.B
2.B
3.A
4.D
5.A
6.B
7.D
8.B
9.C
10.B
11.D
12.A
13.A
14.C
15.B
16.C
17.A
18.C
19.B
20.D
21.D
22.B
23.A
24.B
25.A
26.A
27.C
28.D
29.D
30.C
31.C
32.B
33.A
34.C
35.B
II. PHẦN TỰ LUẬN
Câu 36
a) Vì
2


sin 0

1 2 2
sin 1
93
= − =
sin2
=
2 2 1 4 2
2sin . 2.( ).
3 3 9
c


= − = −


os
0,25
0,25
b) Điu kin:
( )
cos 0
*
tan 3
x
x
−
sin2 2cos sin 1 0 2sin cos sin 2cos 1 0
sin 1
2
2
(2cos 1)(sin 1) 0
1
cos
2
2
3
Pt x x x x x x x
x
xk
x x k
x
xk
+ − − = − + − =
=−
= − +
− + =
=
= +
Z
Kết hợp điu kin (*)=>Nghim của phương trình l
2
3
xk
=+
0,25
0,25
0,25
0,25
Câu 37
Ta có
( ) ( )
( )
1 1 1
1 5 3
16
11
1
1
1
4 2 10
10
7
57
2 10
36
.
2 5 7
13
u u d u d
u u u
uu
u u d
ud
u
ud
d
+ + − + =
+ − =

+=
+ + =
+=
=


+=
=−
0,25
0,25
Câu 38
a) Trong mp(ABCD) gọi
O AC BD=
Ta có
( ) ( )
SAC SBD SO=
có
( ) ( )
( ) ( )
//
;
S SAB SCD
AB CD
AB SAB CD SCD


( ) ( ) ( )
, / / ,/ /SAB SCD S AB CD =
0,5
0,25
0,25
b) Gọi
( )
BM I BM SCD I = =
0,5
ĐỀ 8
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
PHẦN 1. TRẮC NGHIỆM (35 CÂU – 7.0 ĐIỂM))
Câu 1: (NB) Cho
2


, tìm pht biểu đúng trong cc pht biểu sau:
A.
sin 0.x
B.
cos 0.x
C.
tan 0.x
D.
cot 0.x
Câu 2: (NB) Đổi số đo của góc
5
4
=
sang đơn v độ.
A.
0
45 .
=
B.
0
135 .
=
C.
0
225 .
=
D.
0
45 .
=−
Câu 3: (TH) Cho M l điểm biểu diễn góc lượng gic có tia đầu OA v tia cuối OM (như hình vẽ).
Số đo góc lượng gic đó l
A.
3
.
4
B.
3
k 2 .
4
+
C.
5
.
4
D.
5
k 2 .
4
+
Câu 4: (NB) Công thức no sau đây l đng?
A.
22
cos2 cos sin .a a a=−
B.
cos2 cos sin .a a a=−
C.
22
cos2 cos sin .a a a=+
D.
cos2 2cos .aa=
.
Câu 5: (NB) Biết
1
sin
2
a =−
gi tr của
sin( )a
−
l
A.
1
sin( ) .
2
a
−=
B.
1
sin( ) .
2
a
− = −
C.
3
sin( ) .
2
a
−=
D.
3
sin( ) .
2
a
− = −
Câu 6: (TH) Tính
cos .
12
A.
26
cos .
12 4
+
=
B.
26
cos .
12 4
−
=
C.
62
cos .
12 4
−
=
D.
1
cos .
12 8
=
Câu 7: (TH) Biết
tan 2a =
v
0
2
a

Tính
cos .a
A.
5
cos .
5
a =
B.
5
cos .
5
a =−
C.
3
cos .
3
a =
D.
1
cos .
2
a =
Câu 8: (NB) Trong cc hm số sau, hm số no l hm số chẵn?
A.
sin .yx=
B.
cos .yx=
C.
tan .yx=
D.
cot .yx=
Câu 9: (TH) Hm số
cos3yx=
tuần hon với chu kỳ bằng bao nhiêu?
A.
2T π=
. B.
2
3
π
T =
. C.
6T π=
. D.
3T π=
.
Câu 10: (NB) Phương trình
cos cos
3
x
=
có nghim l
A.
2
2,
3
x k k
= +
. B.
,
3
x k k
= +
.
C.
2,
3
x k k
= +
. D.
2,
3
x k k
= +
.
Câu 11: (NB) Phương trình
sinx = -1
có một nghim l gía tr no sau đây?
A.
x = -
p
4
. B.
x = -
p
6
. C.
x = -
p
2
. D.
x = -
p
3
.
Câu 12: (NB) Phương trình
tan 1x =−
có nghim l
A.
x = -
p
4
. B.
4
xk
= − +
. C.
4
xk
=+
. D.
2
xk
=+
.
Câu 13: (TH) Nghim của phương trình
2sin 1 0x −=
được biểu diễn trên đường tròn lượng gic ở hình
bên có thể l những điểm no?
A. Điểm
E
, điểm
D
. B. Điểm
C
, điểm
F
. C. Điểm
D
, điểm
C
. D. Điểm
E
, điểm
F
.
Câu 14: (TH) Phương trình
2
sin(2 )
42
x
−=
có nghim l
A.
2
4
3
2
4
xk
xk
=+
=+
. B.
4
2
xk
xk
=+
=+
. C.
4
xk
xk
=+
=
. D.
2
4
2
4
xk
xk
=+
= − +
.
Câu 15: (TH) Phương trình
cot3 3 0x−=
có nghim l
A.
18
xk
=+
. B.
18 3
k
x

=+
. C.
93
k
x

=+
. D.
2
xk
=+
.
Câu 16: (NB) Cho dãy số
( )
n
u
cho bởi công thức tổng qut
2*
3 4 ,
n
u n n= +
. Khi đó
5
u
bằng
A.
103
. B.
23
. C.
503
. D.
97−
.
Câu 17: (TH) Cho dãy số
1
1
4
nn
u
u u n
+
=
=+
. Năm số hạng đầu của dãy số l
O
x
y
A
B
A
B
E
D
C
F
A.
4,5,6,7,8.
. B.
4,16,32,64,128.
. C.
4,6,9,13,18.
. D.
4,5,7,10,14.
Câu 18: (NB) Dãy số no sau đây l một cp số cộng?
A.
4,5,6,7,8.
. B.
4,6,10,16,26.
. C.
4,6,2,8,4.
. D.
4,5,7,10,14.
Câu 19: (NB) Cho cp số cộng
( )
n
u
với công sai d. Công thức tính số hạng tổng qut
n
u
l
A.
1n
u u d=+
. B.
1n
u u nd=+
. C.
1
( 1)
n
u u n d= − −
. D.
1
( 1)
n
u u n d= + −
.
Câu 20: (TH) Cho cp số cộng 3,1,-1,-3,-5. Tìm công sai của cp số cộng đó.
A.
2d =
. B.
2d =−
. C.
3d =
. D.
5d =
.
Câu 21: (TH) Cho cp số cộng
( )
n
u
cho bởi công thức tổng qut
*
2 1,
n
u n n= +
Tính tổng 10 số
hạng đầu của cp số cộng đó
A.
10
12S =
. B.
10
24S =
. C.
10
21S =
. D.
10
2S =
.
Câu 22: (NB) Dãy số no sau đây l một cp số nhân?
A.
4,5,6,7,8.
. B.
4,6,8,10,12.
. C.
4,8,16,32,64.
D.
4,5,7,10,14.
Câu 23: (NB) Cho cp số nhân
( )
n
u
với công bội q. Công thức tính số hạng tổng qut
n
u
l
A.
1
1
n
n
u u q
−
=
. B.
1
n
n
u u q=
. C.
1
1
n
n
u u q
−
=+
. D.
1
( 1)
n
u u n d= + −
.
Câu 24: (TH) Cho cp số nhân
11
3,1, , ,...
39
. Tìm số hạng thứ 5 của cp số nhân đó.
A.
5
1
27
u =
. B.
5
1
9
u =
. C.
5
3u =
. D.
5
1
3
u =
.
Câu 25: (TH) Cho cp số nhân
( )
n
u
với
2q =
v
1
3u =−
Tính tổng 5 số hạng đầu của cp số nhân đó
A.
5
48S =−
. B.
5
96S =−
. C.
5
486S =−
. D.
5
162S =
.
Câu 26: (NB) Cho hình vẽ sau :
A
S
C
B
M
N
Số điểm chung của đường thẳng MN v mặt phẳng (SAB) l
A.
0
. B.
1
. C.
2
. D. vô số.
Câu 27: (NB) Cho tứ din ABCD .Tìm giao tuyến của hai mặt phẳng (ABC) v (ABD).
A. CD. B. AB. C. AD. D. AC.
Câu 28: (TH)Cho 4 điểm
, , ,A B C D
không cùng nằm trên một mặt phẳng. Trên
,AB AD
lần lượt ly 2
điểm
,MN
sao cho
MN
cắt
BD
tại
I
. Điểm
I
không thuộc mặt phẳng no sau đây?
A.
( )
ABD
. B.
( )
BCD
. C.
( )
CMN
. D.
( )
ACD
.
Câu 29: (NB) Cho đường thẳng a nằm trên mp (P) đường thẳng b cắt (P) tại O v O không thuộc a.
V trí tương đối của
a
v
b
l
A. chéo nhau. B. cắt nhau. C. song song nhau. D. trùng nhau.
Câu 30: (NB) Cho hình chóp
.S ABCD
có đy
ABCD
l hình bình hnh. Gọi
, , ,I J E F
lần lượt l
trung điểm
,SA
,SB
,SC
SD
. Trong cc đường thẳng sau, đường thẳng no không song song với
IJ
?
A.
EF
. B.
DC
. C.
AD
. D.
AB
.
Câu 31: (TH) Cho hình chóp S.ABCD có đy lhình bình hnh. Gọi M, N,I lần lượt l trung điểm SD,
SA,AB. Gọi G l trọng tâm tam gic SAB, K l giao điểm của GM với mp(ABCD). K l giao điểm của
GM với đường thẳng no sau đây:
A.
AB
. B. NI. C.
BC
. D.
DI
.
Câu 32: (NB) Cho tứ din
ABCD
.
M
,
N
lần lượt l trung điểm
BC
,
BD
. Đường thẳng
MN
song song
với mặt phẳng
A.
( .)BCD
B.
( )
.ACD
C.
( )
.ABC
D.
( )
.ABD
Câu 33: (NB) Cho hình chóp
.S ABCD
, đy
ABCD
l hình bình hnh. Giao tuyến của hai mặt phẳng
( )
SAD
v
( )
SBC
l đường thẳng song song với đường thẳng no sau đây?
D
A
B
C
S
A.
BD
. B.
DC
. C.
AD
. D.
AC
.
Câu 34: (TH) Cho tứ din
ABCD
. Gọi
M
,
N
lần lượt l trọng tâm cc tam gic
ABC
v
ABD
. Xét
cc khẳng đnh sau:
( )
1
( )
//MN BCD
.
( )
2
( )
//MN ACD
.
( )
3
( )
//MN ABD
.
Những khẳng đnh đng l
A. Chỉ có
( )
1
đng. B.
( )
1
v
( )
2
. C.
( )
2
v
( )
3
. D.
( )
1
v
( )
3
.
Câu 35: (TH) Cho hình chóp
.S ABCD
có đy
ABCD
l hình chữ nhật. Gọi
M
,
N
theo thứ tự l trọng
tâm
SAB
v
SCD
. Khi đó
MN
song song với mặt phẳng
A.
()SAC
. B.
()SBD
. C.
()SAB
. D.
()ABCD
.
PHẦN 2. TỰ LUẬN (3 ĐIỂM)
Bài 1. (1,0đ) (VD)
Giải phương trình
s n5x cosxi =
.
Bài 2. (0,5đ) (VDC)
Tin công khoan giếng ở hai cơ sở được tính như sau:
- Cơ sở A: Gi của mét khoan đầu tiên l 50.000 đồng v kể từ mét khoan thứ hai, gi của mỗi
mét sau tăng thêm 10000 đồng so với gi của mét khoan ngay trước.
- Cơ sở B: Gi của mét khoan đầu tiên l 50.000 đồng v kể từ mét khoan thứ hai, gi của mỗi
mét sau tăng thêm 8% gi của mét khoan ngay trước.
Một người muốn khoan hai ci giếng gồm một ci sâu 20 mét, một ci sâu 30 mét ở hai đa điểm
khc nhau. Hỏi người y nên chọn cơ sở khoan giếng no cho từng giếng để chi phí khoan hai
giếng l ít nht. Biết cht lượng v thời gian khoan giếng của hai cơ sở l như nhau.
Bài 3. (1,5đ) Cho hình chóp
.S ABCD
có đy
ABCD
l hình bình hnh. Gọi
M
,
P
lần lượt l trung điểm
của cc cạnh
SA
v
SC
. Điểm
N
thuộc cạnh
SB
sao cho
2
3
SN
SB
=
. Gọi
Q
l giao điểm của
cạnh
SD
v mặt phẳng
( )
MNP
.
a) (1,0đ) (VD) Xc đnh giao tuyến của 2 mặt phẳng (MNP) v (ABCD)
b) (0,5) (VDC) Tính tỷ số
SQ
SD
.
ĐỀ 9
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 đim):
Câu 1: Cho
l góc lượng gic, trong cc khẳng đnh sau khẳng đnh no đng?
A.
sin( ) .cos
−=
B.
sin( ) sin .
− = −
C.
sin( ) sin .
−=
D.
sin( ) .cos
− = −
Câu 2: Cho
thuộc góc phần tư thứ nht của đường tròn lượng gic. Hãy chọn kết quả đng trong cc
kết quả sau đây.
A.
sin 0; 0.cos


B.
sin 0; 0.cos


C.
sin 0; 0.cos


D.
sin 0; 0.cos


Câu 3: Gi tr của
15
sin( )
6
bằng
A.
1
2
. B.
1
. C.
3
2
. D.
3
2
−
.
Câu 4: Một chiếc đồng hồ, có kim chỉ giờ
OG
chỉ số
9
v kim pht
OP
chỉ số
12
. Số đo của góc
lượng gic
( )
,OG OP
l
A.
2,
2
kk
p
p+΢
. B.
00
270 360 , .kk- + Î ¢
C.
00
270 360 ,kk+΢
. D.
9
2,
10
kk
p
p+΢
.
Câu 5: Trong cc khẳng đnh sau, khẳng đnh đnh no đng?
A.
( )
sin sin cos cos sina b a b a b− = −
. B.
( )
sin sin cos cos sina b a b a b− = +
.
C.
( )
sin cos cos sin sina b a b a b− = −
. D.
( )
sin sin sin cos cosa b a b a b− = −
.
Câu 6: Trong cc khẳng đnh sau, khẳng đnh đnh no sai?
A.
sin2 2sin cos .a a a=
B.
22
cos2 cos sin .a a a=−
C.
2
cos2 2cos 1.aa=+
D.
2
cos2 1 2sin .aa=−
Câu 7: Biết
4
cos
5
=−
v
3
22


. Gi tr
sin2
bằng
A.
24
.
5
−
B.
2
.
5
C.
24
.
25
−
D.
8
.
25
−
Câu 8: Cho
l góc lượng gic, trong cc khẳng đnh sau khẳng đnh no sai?
A. Tập xc đnh của hm số
sin
l . B. Tập xc đnh của hm số
cos
l .
C. Tập xc đnh của hm số cotan l
{ +k | }
2
k
.
D. Tập xc đnh của hm số tan l
{ +k | }
2
k
.
Câu 9: Đường cong trong hình vẽ l đồ th của hm số no dưới đây?
A.
tanyx=
. B.
sinyx=
. C.
cotyx=
. D.
cosyx=
.
Câu 10: Hm số no sau đây l một hm số chẵn?
A.
cosy x x=−
. B.
cos 1yx=+
. C.
2
siny x x=+
.D.
sin2yx=
.
Câu 11: Tập gi tr của hm số
1 sinyx=−
l
A.
1;1 .−
B.
0;2 .
C.
1;2 .−
D.
1;3 .
Câu 12: Nghim của phương trình
cos 0x =
l
A.
,.
2
x k k
p
p= + Î ¢
B.
,.
6
x k k
p
p= ± + Î ¢
C.
2 , .
3
x k k
p
p= + Î ¢
D.
,.
6
x k k
p
p= + Î ¢
Câu 13: Chọn khẳng đnh đng trong cc khẳng đnh sau
A. Phương trình
cos xm=
có nghim khi v chỉ khi
| | 1m
.
B. Phương trình
cos xm=
có nghim khi v chỉ khi
| | 1m
.
C. Phương trình
cos xm=
có nghim khi v chỉ khi
1m
.
D. Phương trình
cos xm=
có nghim khi v chỉ khi
1m
.
Câu 14: Nghim của phương trình
tan 1x =−
l
A.
( )
4
x k k
= − +
.
B.
( )
2
3
x k k
= +
.
C.
( )
2
4
x k k
= +
.
D.
( )
5
2
6
x k k
= +
.
Câu 15: Tìm tt cả cc nghim của phương trình
sin sinx
3
x

+=


.
A.
3
xk
=+
( )
k
. B.
2
6
xk
= − +
( )
k
.
C.
2
3
xk
=+
( )
k
. D.
5
2
6
xk
=+
( )
k
.
Câu 16: Dãy số
()
n
u
,
*n
được gọi l dãy số tăng khi
A.
1
.
nn
uu
+
B.
1
.
nn
uu
+
C.
1
.
nn
uu
+
D.
1
.
nn
uu
+
Câu 17: Dãy số no dưới đây l dãy cc số nguyên chia hết cho
3
v sắp xếp theo thứ tự tăng dần?
A.
9
,
3
,
15
,
0
. B.
1
,
2
,
3
,
5
,
7
. C.
0
,
3
,
6
,
9
. D.
1
,
3
,
5
,
7
.
Câu 18: Khẳng đnh no sau đây l sai?
A. Một dãy số tăng thì b chặn dưới. B. Một dãy số giảm thì b chặn trên.
C. Một dãy số b chặn thì phải tăng hoặc giảm. D. Một dãy số không đổi thì b chặn.
Câu 19: Cho dãy số
( )
,*
n
un
biết
1
n
n
u
n
=
+
. Tính
5
u
.
A.
5
5
6
u =
. B.
5
1
5
u =
. C.
5
1
6
u =
. D.
5
16
25
u =
.
Câu 20: Cho dãy số
( )
,*
n
un
có 5 số hạng đầu l
1 1 3 1 5
; ; ; ; ;...
2 2 8 4 32
Số hạng tổng qut của dãy số
( )
n
u
l
A.
1
2
n
n
n
u
−
=
. B.
2
n
n
u
n
=
+
. C.
2
n
n
n
u =
. D.
1
1
n
u
n
=
+
.
Câu 21: Cho cp số cộng
( )
n
u
với công sai
d
có công thức truy hồi l
A.
1nn
u u d
−
=+
, với
2.n
B.
1nn
u u d
−
=−
, với
2.n
C.
1
.
nn
u u d
−
=
, với
2.n
D.
1nn
u u d
+
=+
, với
2.n
.
Câu 22: Dãy số no sau đây l cp số cộng?
A.
2;5;8;11;14...
B.
2;4;8;12;14...
C.
1;3;5;7...−
D.
2;4;8;16;...
Câu 23: Cho cp số cộng
( )
n
u
với công sai
d
. Chọn khẳng đnh đng.
A.
51
4u u d=+
. B.
51
4u u d=−
. C.
51
5u u d=+
. D.
51
5u u d=+
.
Câu 24: Cho cp số cộng
( )
n
u
, biết
1
2u =
v công sai
3d =−
. Khẳng đnh no sau đây đng?
A.
3
4.u =−
B.
3
4.u =
C.
3
1.u =−
D.
3
1.u =
Câu 25: Cho cp số cộng
( )
n
u
có số hạng đầu
1
5u =−
v công sai
3d =
. Số 94 l số hạng thứ my của
cp số cộng?
A. 33. B. 20. C. 35. D. 34.
Câu 26: Cho dãy số
( )
n
u
l một cp số nhân có số hạng đầu
1
u
v công bội
q
. Đẳng thức no sau đây
đng?
A.
( )
1
1
n
u u n q= + −
,
( )
2n
. B.
1
1
n
n
u u q
−
=
,
( )
2n
.
C.
( )
1
1
.
n
n
u q u
−
=
,
( )
2n
. D.
1
1
n
n
u
u
q
−
=
,
( )
2n
.
Câu 27: Cho cp số nhân
( )
n
u
, biết
1
3u =
v công bội
2q =−
. Khẳng đnh no sau đây đng?
A.
5
48.u =
B.
5
48.u =−
C.
5
96.u =−
D.
5
96.u =
Câu 28: Cho dãy số
( )
n
u
l một cp số nhân có số hạng đầu
1
u
v công bội
q
. Tổng của
n
số hạng đầu
có công thức l
A.
( )
1
1
1
n
n
uq
S
q
−
=
−
. B.
( )
1
1
1
1
n
n
uq
S
q
−
−
=
−
. C.
( )
1
1
1
1
n
n
uq
S
q
−
−
=
−
. D.
( )
1
1
1
1
n
n
uq
S
q
−
+
=
+
.
Câu 29: Cho dãy số
( )
n
u
l một cp số nhân với
16
1
; 16
2
uu= = −
. Công bội của CSN l
A.
2q =−
. B.
2q =
. C.
1
4
q =
. D.
1
4
q =−
.
Câu 30: Tìm
x
để cc số
2; 8; ; 128x
theo thứ tự đó lập thnh một cp số nhân.
A.
14.x =
B.
32.x =
C.
64.x =
D.
68.x =
Câu 31: Trong mẫu số liu ghép nhóm, độ di của nhóm
)
1;10
bằng bao nhiêu?
A. 8. B. 5. C. 10. D. 9.
Câu 32: Mẫu số liu cho dưới dạng bảng tần số của cc nhóm số liu được gọi l
A. Mẫu số liu bảng. B. Mẫu số liu ghép nhóm.
C. Số trung v. D. Mốt.
Câu 33: Kết quả khảo st cân nặng của 25 quả to ở lô hng B được cho ở bảng sau:
Cân nặng (g)
[150;155)
[155;160)
[160;165)
[165;170)
[170;175)
Số quả to ở lô hng
B
1
3
7
10
4
Mẫu số liu ny có bao nhiêu nhóm?
A.
5.
B.
6.
C.
7.
D.
25.
Câu 34: Trong hoạt động Ngy chủ nhật xanh, đon thanh niên lớp 11A1 tiến hnh trồng cây. Kết quả sau
hoạt động được ghi lại ở bảng sau:
Số cây
)
1;8
)
8;15
)
15;22
)
22;29
)
29;36
Số học sinh
7
15
6
10
3
Hãy tìm số trung bình của mẫu số liu ghép nhóm trên.
A. 16,3. B. 15,5. C. 16,2. D. 26.
Câu 35: Chiu cao của học sinh khối lớp 11 của trường THPT Đơn Dương, ta được mẫu số liu sau:
Chiu cao (cm)
Số học sinh
[150;152)
20
[152;154)
35
[154;156)
45
[156;158)
60
[158;160)
30
[160;162)
15
Tần số của nhóm
)
156;158
bằng bao nhiêu?
A.
15.
B.
60.
C.
45.
D.
30.
II. PHẦN TỰ LUẬN
(3 đim):
Bài 1
(1,0 điểm).
Giải phương trình lượng gic
sin2 cos 0xx+=
.
Bài 2 (1,5 điểm).
A(0.5 điểm) Cho cp số cộng
( )
n
u
có
1 5 3
16
10
7
u u u
uu
+ = +
=−
. Tìm số hạng đầu
1
u
v công sai d của cp số cộng
đó.
b)
(1,0 điểm)
Giả sử rằng một tế bo ung thư cứ sau một giờ sẽ nhân đôi một lần. Hỏi nếu ban đầu có 8 tế
bo ung thư thì sau một ngy đêm số tế bo sẽ l bao nhiêu?
Bài 3 (0.5 điểm). Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết
quả như bảng bên. Tìm tứ phân v thứ ba cho mẫu số liu ghép nhóm
………………Ht……………….
HƯỚNG DẪN CHẤM
I. PHẦN TRẮC NGHIỆM
BẢNG ĐÁP ÁN
1.C
2.C
3.B
4.A
5.A
6.C
7.C
8.C
9.B
10.B
11.B
12.A
13.A
14.A
15.A
16.A
17.C
18.D
19.A
20.C
21.A
22.A
23.A
24.A
25.D
26.B
27.A
28.A
29.A
30.B
31.D
32.B
33.A
34.A
35.B
II. PHẦN TỰ LUẬN
Câu 1
- Biến đổi
cos (2sin 1) 0xx+=
- Biến đổi
cos 0
2sin 1 0
x
pt
x
=
+=
- Giải đng nghim phương trình
cos 0
2
x x k
= = +
- Giải đng nghim phương trình
2
6
2sin 1 0
7
2
6
xk
x
xk
= − +
+ =
=+
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Câu 2a
Ta có
( ) ( )
( )
1 1 1
1 5 3
16
11
1
1
1
4 2 10
10
7
57
2 10
36
.
2 5 7
13
u u d u d
u u u
uu
u u d
ud
u
ud
d
+ + − + =
+ = +

=−
+ + =
+=
=


+=
=−
0,25 đ
0,25 đ
Câu 2b
- Một ngy đêm có 24 giờ nên số lần nhân đôi của TBUT l 24
- Sau 24 lần nhân đôi thì một TBUT sẽ được l
24
2 16.777.216=
- Vậy 8 TBUT sau một ngy đêm ta có số TBUT l 134.217.728
0,25đ
0,5đ
0,25đ
Câu 3
Tứ phân v thứ ba
3
Q
l
150 151
2
xx+
. Do
150 151
,xx
đu thuộc nhóm [170;175)
nên tứ phân v thứ ba thuộc nhóm [170;175). Do đó
5 5 1 2 3 4 6 5
5; 170; 41; 18 28 35 43 124; 5p a m m m m m a a= = = + + + = + + + = − =
3
600
124
4
170 5 173.17
41
Q
−
= + =
0,25đ
0,25đ
ĐỀ 10
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 đim).
Câu 1: Trên đường tròn lượng gic gốc
A
, biết góc lượng gic
( )
,OA OM
có số đo bằng
0
410
, điểm
M
nằm ở góc phần tư thứ my?
A.
I
. B.
III
. C.
II
. D.
IV
.
Câu 2: Đường tròn lượng gic có bn kính bằng:
A.
2
. B.
1
. C.
2
. D.
.
Câu 3: Khi quy đổi
1
o
ra đơn v radian, ta được kết quả l
A.
rad.
B.
180
rad.
C.
rad.
180
D.
rad.
360
Câu 4: Mnh đ no sau đây sai?
A.
sin( ) sin .
+=
B.
cot( ) cot .
+=
C.
( )
cos cos
+ = −
. D.
tan( ) tan .
+=
Câu 5: Cho
4
sin ,
52
=
. Tính
cos
.
A.
3
cos
5
=−
. B.
1
cos
5
=
. C.
3
cos
5
=
. D.
1
cos
5
=
.
Câu 6: Trong cc công thức dưới đây, công thức no đúng?
A.
cos cos 2cos cos .
22
a b a b
ab
+−
−=
B.
cos cos 2sin sin .
22
a b a b
ab
+−
−=
C.
cos cos 2cos cos .
22
a b a b
ab
+−
− = −
D.
cos cos 2sin sin .
22
a b a b
ab
+−
− = −
Câu 7: Trong cc công thức dưới đây, công thức no đúng?
A.
( )
cos sin .cos cos .sina b a b a b+ = −
. B.
( )
cos sin .cos cos .sina b a b a b+ = +
.
C.
( )
cos cos .cos sin .sina b a b a b+ = +
. D.
( )
cos cos .cos sin .sina b a b a b+ = −
.
Câu 8: Cho
1
cos =
3
. Tính
cos2
.
A.
7
cos2
9
=
. B.
1
cos2
3
=
. C.
7
cos2
9
=−
. D.
2
cos2
3
=
.
Câu 9: Rt gọn biểu thức
sin sin
33
T x x

= + − −
ta được kết quả l
A.
3cosTx=
. B.
sinTx=
. C.
3
2
. D.
sin2Tx=
.
Câu 10: Tập xc đnh hm số
sinyx=
l:
A.
[ 1;1].D =−
B.
.D =
C.
\ , .D k k
=
D.
\ , .
2
D k k

=


Câu 11: Mnh đ no sau đây l đúng?
A. Hm số
sinyx=
l hm số chẵn. B. Hm số
cosyx=
l hm số chẵn.
C. Hm số
tanyx=
l hm số chẵn. D. Hm số
cotyx=
l hm số chẵn.
Câu 12:
Cho hm số
()y f x=
có đồ th như hình bên dưới. Mnh đ no sau đây l
đúng
?
A.
Hm số đồng biến trên
3
;.
22


−−


B.
Hm số đồng biến trên
3
;.
22




C. Hm số đồng biến trên
;.
22


−


D. Hm số đồng biến trên
;0 .
2

−


Câu 13: Hm số
sin 2
4
yx

=−


đồng biến trên khoảng no trong cc khoảng sau đây?
A.
3
;
88


−


. B.
3
;
44


−


. C.
;
22


−


. D.
;
44


−


.
Câu 14: Phương trình no sau đây có nghim?
A.
1
sin .
2
x =
B.
sin 2.x =−
C.
2 sin 2.x =
D.
cos 2.x =
Câu 15: Phương trình
sin sinx
=
có tập nghim l:
A.
2 | .S k k
= +
B.
|.S k k
= +
C.
2 ; 2 | .S k k k

= + +−
D.
2 ; 2 | .S k k k

= + +−
Câu 16: Phương trình
cos2 1x =
có nghim l:
A.
,x k k
=
. B.
2,
2
x k k
= +
. C.
,
2
k
xk
=
. D.
2,
4
x k k
= +
.
Câu 17: Tìm tổng nghim dương bé nht v nghim âm lớn nht của phương trình
( )
sin cos 2xx=
.
A.
3
−
. B.
0
. C.
4
. D.
2
3
.
Câu 18: Cho dãy số (
n
u
) với
( 5)
n
n
u =−
. Mnh đ no sau đây đúng?
A.
4
625u =−
. B.
4
20u =
. C.
4
625u =
. D.
4
20u =−
.
Câu 19: Cho dãy số
()
n
u
. Mnh đ no sau đây đúng?
A. Nếu
*
1
,
nn
u u n
+
thì
()
n
u
l dãy số giảm.
B. Nếu
*
1
,
nn
u u n
+
thì
()
n
u
l dãy số giảm.
C. Nếu
*
1
,
nn
u u n
+
thì
()
n
u
l dãy số giảm.
D. Nếu
*
1
,
nn
u u n
+
thì
()
n
u
l dãy số giảm.
Câu 20: Trong cc dãy số
( )
n
u
cho bởi số hạng tổng qut
n
u
sau, dãy số no l dãy số tăng?
A.
1
.
2
n
n
u =
B.
1
.
n
u
n
=
C.
5
.
31
n
n
u
n
+
=
+
D.
21
.
1
n
n
u
n
−
=
+
Câu 21: Cho cp số cộng
( )
n
u
có
1
3u =
v công sai
2d =
. Số hạng tổng qut của cp số cộng
( )
n
u
l:
A.
32
n
un=+
. B.
32
n
un=−
. C.
22
n
un=−
. D.
21
n
un=+
.
Câu 22: Cp số cộng
( )
n
u
có số hạng đầu
1
u
v công sai
d
thì tổng
n
số hạng đầu của cp số cộng
( )
n
u
được xc đnh
bởi công thức
A.
1
( 1)
2
n
nn
S nu d
+
=+
. B.
1
( 1)
2
n
nn
S nu d
+
=−
.
C.
1
( 1)
2
n
nn
S nu d
−
=−
. D.
1
( 1)
2
n
nn
S nu d
−
=+
.
Câu 23: Cho dãy số
( )
n
u
l một cp số cộng với công sai
d
, ta có công thức truy hồi
A.
*
1
.,
nn
u u d n
+
=
. B.
*
1
,
nn
u u d n
+
= +
.
C.
*
1
,
n
n
u
un
d
+
=
. D.
*
1
,
nn
u u d n
+
= −
.
Câu 24: Tìm
x
để ba số thực
1; ; 5x
theo thứ tự lập thnh một cp số cộng.
A.
1x =
. B.
0x =
. C.
2x =
. D.
3x =
.
Câu 25: Tìm tổng
S
của
100
số nguyên dương đầu tiên v đu chia
5
dư
1
.
A.
24353
. B.
25100
. C.
50200
. D.
5001
.
Câu 26: Cho cp số nhân
( )
n
u
có công bội
.q
Mnh đ no sau đây đúng?
A.
1
1
. ( 2)
n
n
u u q n
−
=
. B.
1
1
. ( 2)
n
n
u u q n
+
=
. C.
1
. ( 2)
n
n
u u q n=
. D.
( 2)
n
n
u q n=
.
Câu 27: Trong cc dãy số sau, dãy số no không phải l một cp số nhân?
A.
2; 4; 8; 16;
B.
1; 1; 1; 1; −−
C.
2 2 2 2
1 ; 2 ; 3 ; 4 ;
D.
( )
3 5 7
; ; ; ; 0 .a a a a a
Câu 28: Cho cp số nhân
( )
n
u
với
1
2u =−
v
5.q =−
Viết bốn số hạng đầu tiên của cp số nhân
( )
n
u
.
A.
2; 10; 50; 250.−−
B.
2; 10; 50; 250.−−
C.
2; 10; 50; 250.− − − −
D.
2; 10; 50; 250.−
Câu 29: Cho cp số nhân
( )
n
u
có cc số hạng lần lượt l
3; 9; 27; 81; ...
. Tìm số hạng tổng qut
n
u
của
cp số nhân
( )
n
u
.
A.
1
3.
n
n
u
−
=
B.
3.
n
n
u =
C.
1
3.
n
n
u
+
=
D.
3 3 .
n
n
u =+
Câu 30: Bc Bình gửi tiết kim
500
triu đồng kì hạn
1
thng với lãi sut
6%
một năm theo hình thức lãi
sut kép. Nếu sau đng một năm bc Bình mới đến ngân hng rt tin thì số tin lãi Bc Bình có
được gần nht với số no sau đây.
A.
63,58
(triu đồng). B.
60,15
triu đồng. C.
60
triu đồng. D.
62,58
triu đồng.
Câu 31: Khảo st thời gian tập thể dục trong ngy của một số học sinh khối 11 thu được mẫu số liu ghép
nhóm sau:
Thời gian (pht)
)
0;20
)
20;40
)
40;60
)
60;80
)
80;100
Số học sinh
5
9
12
10
6
Gi tr đại din của nhóm
[20;40)
l
A. 10. B. 20. C. 30. D. 40.
Câu 32: Tuổi thọ (năm) của 50 bình ắc quy ô tô thu được mẫu số liu ghép nhóm sau:
Tuổi thọ (năm)
)
2;2,5
)
2,5;3
)
3;3,5
)
3,5;4
)
4;4,5
)
4,5;5
Tần số
4
9
14
11
7
5
Mẫu số liu ghép nhóm ny có số mốt bằng
A. 14. B. 9. C. 7. D. 5.
Câu 33: Cho mẫu số liu ghép nhóm v thời gian (pht) đi từ nh đến nơi lm vic của cc nhân viên một
công ty như sau:
Thời gian
)
15;20
)
20;25
)
25;30
)
30;35
)
35;40
)
40;45
)
45;50
Số nhân viên
6
14
25
37
21
13
9
Có bao nhiêu nhân viên có thời gian đi từ nh đến nơi lm vic l từ 15 pht đến dưới 20
pht?
A. 6. B. 9. C. 14. D. 13.
Câu 34: Cho mẫu số liu ghép nhóm sau:
Nhóm
)
12
;aa
.
)
1
;
ii
aa
+
.
)
1
;
kk
aa
+
Tần số
1
m
.
i
m
.
k
m
Với
12
...
k
n m m m= + + +
l cỡ mẫu v
1
2
ii
i
aa
x
+
+
=
(
1,...ik=
) l gi tr đại din của nhóm
)
1
;
ii
aa
+
. Khi đó công thức tính số trung bình cộng của mẫu số liu ghép nhóm trên l:
A.
11 kk
x
mx
n
mx
=
++
. B.
( ) ( )
11 kk
m x m x
x
n
=
.
C.
11 kk
m x m x
x
n
−−
=
. D.
11 kk
m x m x
x
n
++
=
Câu 35: Khảo st thời gian tập thể dục trong ngy của một số học sinh khối 11 thu được mẫu số liu ghép
nhóm sau:
Thời gian (pht)
)
0;20
)
20;40
)
40;60
)
60;80
)
80;100
Số học sinh
5
9
12
10
6
Nhóm chứa trung v l
A.
[0;200)
. B.
[20;40)
. C.
[40;60)
. D.
[60;80)
.
II. PHẦN TỰ LUẬN
(3 đim).
Bài 1. (1,0 điểm).
a) Tìm tập xc đnh của hm số.
1
1 cos
y
x
=
+
.
b) Cho dãy số
( )
,
n
u
biết
1
1
n
u
n
=
+
. Viết ba số hạng đầu tiên của dãy số
( )
n
u
.
Bài 2. (1 điểm). Tìm m để phương trình để
2
2sin 3sin 5 0
2
x
xm+ − =
luôn có nghim.
Bài 3. (1 điểm). Một đa gic có chu vi l
158cm
, độ di cc cạnh của nó lập thnh một cp số
cộng. Biết cạnh lớn nht có độ di l
44cm
. Tìm số cạnh của đa gic đó?
……………… HT ………………
ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng.
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Câu 9
Câu 10
A
B
C
A
A
D
D
C
B
B
Câu 11
Câu 12
Câu 13
Câu 14
Câu 15
Câu 16
Câu 17
Câu 18
Câu 19
Câu 20
B
D
A
A
D
A
A
C
C
D
Câu 21
Câu 22
Câu 23
Câu 24
Câu 25
Câu 26
Câu 27
Câu 28
Câu 29
Câu 30
D
D
B
D
A
A
C
B
B
A
Câu 31
Câu 32
Câu 33
Câu 34
Câu 35
C
A
A
D
C
II. PHẦN TỰ LUẬN
Câu
Nội dung
Đim
1
a. Tìm tập xc đnh của hm số
1
1 cos
y
x
=
+
.
Điu kin xc đnh của hm số l:
cos 1x −
0,25
hay
2xk

+
(
k
).
Tập xc đnh của hm số
1
1 cos
y
x
=
+
l
\ 2 |D k k

= +
0,25
b. Cho dãy số
( )
,
n
u
biết
1
1
n
u
n
=
+
. Viết ba số hạng đầu tiên của dãy số
( )
n
u
.
1
1
2
u =
0,25
0,25
Vậy ba số hạng đầu tiên của dãy số
( )
n
u
l:
111
; ; .
234
2
Tìm m để phương trình để
2
2sin 3sin 5 0
2
x
xm+ − =
luôn có nghim.
2
2sin 3sin 5 0
2
3sin cos 5 1 0
x
xm
x x m
+ − =
− − + =
0.25
2sin 5 1 0
6
xm

− − + =


0.25
Hay
51
sin
62
m
x
−

−=


M
1 sin 1
6
x

− −


0.25
Nên để phương trình trên luôn có nghim khi
51
11
2
m −
−
13
55
m −
0.25
3
Một đa gic có chu vi l
158cm
, độ di cc cạnh của nó lập thnh một cp số cộng. Biết cạnh lớn
nht có độ di l
44cm
. Tìm số cạnh của đa gic đó?
Giả sử đa gic có
n
cạnh (
,3nn
).
Gọi độ di cc cạnh của đa gic l
1 2 3
, , ,...,
n
u u u u
theo thứ tự lập thnh cp số cộng v
cạnh lớn nht có độ di l nên
1 2 3
0 ... 44
n
u u u u cm =
.
0,25
Vì đa gic có chu vi l
158cm
nên
( )
1
1 2 3
...
2
n
nn
u u n
S u u u u
+
= + + + + =
hay
( )
1
44
158
2
un+
=
suy ra
1
316
44
n
u
=
+
0,25
M
n
nên
1
44u +
l ước nguyên dương của
316
hay
1
44 2; 4; 79; 158; 316u +
0.25
1
44u +
2
4
79
158
316
1
u
1
0u
(loại)
1
0u
(loại
)
1
35u =
1
114u =
(không thỏa
mãn vì
44
n
u cm=
)
1
272u =
(không thỏa
mãn vì
44
n
u cm=
)
Vậy đa gic đã cho có
316
4
79
n ==
cạnh.
0.25
ĐỀ 11
ĐỀ KIỂM TRA GIỮA HỌC KÌ I
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7,0 đim).
Câu 1: Cung có số đo
250
thì có số đo theo đơn v l radian l
A.
35
18
. B.
25
18
. C.
25
12
. D.
25
9
.
Câu 2: Cho góc
thỏa mãn
0
2

. Khẳng đnh no sau đây đng?
A.
sin 0
. B.
cot 0
. C.
sin 0
. D.
cos 0
.
Câu 3: Khẳng đnh no sau đây đng?
A.
22
sin cos 1

+=
. B.
22
sin cos 0

+=
.
C.
22
sin cos 2

+=
. D.
22
sin cos 1

+ = −
.
Câu 4:
sin2a
bằng
A.
2sin .cosaa
. B.
sina
. C.
cosa
. D.
cos2a
.
Câu 5: Chu kỳ tuần hon của hm số
sinyx=
l
A.
2k
()k
. B.
2
. C.
. D.
2
.
Câu 6: Tập gi tr của hm số
cos2023yx=
l
A.
1;1−
. B.
( 1;1)−
. C.
2023;2023−
. D.
11
;
22

−


.
Câu 7: Nghim của phương trình
tan 1x =
l
A.
,
4
x k k
= +
. B.
3
,
4
x k k
= +
.
C.
,x k k
=
. D.
,
2
x k k
= +
.
Câu 8: Cho dãy số
( )
n
u
xc đnh bởi
21
n
un=−
với
1n
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Câu 9: Dãy số no sau đây l dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6;4;2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Câu 10: Cho cp số cộng
( )
n
u
với
1
3u =
v
2
5.u =
Công sai của cp số cộng đã cho bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Câu 11: Trong cc dãy số
()
n
u
sau, dãy số no b chặn?
A.
2
1
n
un=+
. B.
2
1
3
n
u
n
=−
. C.
sin
n
u n n=+
. D.
2
sin
n
un=
.
Câu 12: Cho
a
,
b
,
c
l ba số hạng liên tiếp của một cp số cộng. Đẳng thức no sau đây đng?
A.
2
b ac=
. B.
2b a c=+
. C.
2a b c+=
. D.
2b c a+=
.
Câu 13: Dãy số no sau đây l cp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x
.
Câu 14: Cho cp số cộng
( )
n
u
biết
6
48u =
v
11
83u =
. Tìm cặp
( )
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
( )
13; 7
. D.
( )
13; 7−−
.
Câu 15: Cho cp số nhân
( )
n
u
với
1
3u =
v công bội
2=−q
. Tìm gi tr của
n
biết số hạng tổng qut
1536=−
n
u
.
A.
8=n
. B.
9n =
. C.
257n =
. D.
10n =
.
Câu 16: Điu tra v chiu cao của học sinh khối lớp 11, ta có kết quả sau:
Nhóm
Chiu cao (cm)
Số học sinh
1
)
150;152
5
2
)
152;154
18
3
)
154;156
40
4
)
156;158
26
5
)
158;160
8
6
)
160;162
3
100N =
Gi tr đại din của nhóm thứ tư l
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Câu 17: Khảo st thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liu trên l
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 18: Khảo st thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liu ghép nhóm sau:
Nhóm chứa trung v của mẫu số liu trên l
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Câu 19: Doanh thu bn hng trong 20 ngy được lựa chọn ngẫu nhiên của một của hng được ghi lại
ở bảng sau (đơn v: triu đồng):
Số trung bình của mẫu số liu trên thuộc khoảng no trong cc khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Câu 20: Doanh thu bn hng trong 20 ngy được lựa chọn ngẫu nhiên của một của hng được ghi lại
ở bảng sau (đơn v: triu đồng):
Tứ phân v thứ nht của mẫu số liu gần nht với gi tr no trong cc gi tr dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8,6
.
Câu 21: Biết
4
sin
5
−
=
v
3
2


. Gi tr
cos
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
D.
9
.
5
Câu 22: Gi tr của biểu thức
sin
34
A


=+


l
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Câu 23: Hm số no sau đây l hm số lẻ?
A.
2cosyx=−
. B.
2
2sin 2yx= − +
. C.
2sinyx=−
. D.
2cos 2yx= − +
.
Câu 24: Tập nghim của phương trình
cos 1x =−
l
A.
2 | .
2
S k k

= +

B.
2 | .
2
S k k

= − +

C.
2 | .S k k
=
D.
2 | .S k k

= +
Câu 25: Cho dãy số
1 1 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng lin trước nó). Công thức tổng
qut của dãy số đã cho l
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Câu 26: Cho cp số cộng
( )
n
u
có
1
2; 5ud= = −
. Số hạng thứ
20
của cp số cộng l
A.
93−
. B.
10
. C.
93
. D.
23
.
Câu 27: Cho cp số nhân
( )
n
x
có
2
3x =−
v
4
27.x =−
Tính số hạng đầu
1
x
v công bội
q
của cp số
nhân.
A.
1
1, 3xq= − = −
hoặc
1
1, 3.xq==
B.
1
1, 3xq= − =
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq= − =
D.
1
3, 1xq==
hoặc
1
3, 1.xq= − = −
Câu 28: Theo số liu thông kê điểm Giữa học kì I môn ton khối 10 của một trường THPT được cho bởi
bảng số liu sau:
Điểm no đại din cho nhiu học sinh đạt được nht?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
Câu 29: Doanh thu bn hng trong 20 ngy được lựa chọn ngẫu nhiên của một của hng được ghi lại
ở bảng sau (đơn v: triu đồng):
Doanh thu
)
5;7
)
7;9
)
9;11
)
11;13
)
13;15
Số ngy
2
7
7
3
1
Số trung bình của mẫu số liu trên thuộc khoảng no trong cc khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Câu 30: Khảo st thời gian tập thể dục trong ngy của một số học sinh khối 11 thu được mẫu số liu ghép
nhóm sau:
Nhóm chứa trung v l
A.
)
30;45
. B.
)
15;30
. C.
)
45;60
. D.
)
60;75
.
Câu 31: Một chiếc phao được thả cố đnh trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi
hm số
( )
5sin
5
h t t

=


, trong đó
( )
ht
l độ cao tính bằng cetimét trên mực nước biển trung
bình tại thời điểm
t
giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc phao lại ở
v trí đỉnh của cơn sóng tiếp theo (giả sử cc cơn sóng đu mô hình hóa bởi cùng hm số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Câu 32: Tổng nghim âm lớn nht v nghim dương nhỏ nht của phương trình
33
sin 3
42
x

−=


bằng
A.
.
9
B.
.
6
−
C.
.
6
D.
.
9
−
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam gic như sau: hng thứ nht trồng
1
cây, hng
thứ hai trồng
2
cây, hng thứ ba trồng
3
cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hng cây được trồng l
A.
77
. B.
79
. C.
76
. D.
78
.
Câu 34: Một cp số nhân có số hạng đầu
1
3u =
, công bội
2q =
. Biết
765
n
S =
. Tìm
n
.
A.
8n =
. B.
9n =
. C.
6n =
. D.
7n =
.
Câu 35: Cho mẫu số liu ghép nhóm v thời gian (pht) đi từ nh đến nơi lm vic của cc nhân viên một
công ty như sau:
Thời gian
)
15;20
)
20;25
)
25;30
)
30;35
)
35;40
)
40;45
)
45;50
Số nhân
viên
7
14
25
37
21
14
10
Tứ phân v thứ nht
1
Q
v tứ phân v thứ ba
3
Q
của mẫu số liu ghép nhóm ny l
A.
13
1360 800
,
37 21
QQ==
. B.
13
1360 3280
,
37 83
QQ==
.
C.
13
136 3280
,
5 83
QQ==
. D.
13
136 800
,
5 21
QQ==
.
II. PHẦN TỰ LUẬN (3,0 đim).
Câu 36: (1,0 đim)
a. Giải phương trình
cot 3
3
x

+=


.
b. Cho
2
sin
3
=
, tính gi tr của biểu thức
(1 3cos )(1 3cos )P

= − +
.
Câu 37: (1,0 đim)
Giải phương trình
cos3 sin2 0xx−=
.
Câu 38: (1,0 đim) Giải phương trình
sin cos
3
xx

=+


.
Câu 39: (0,5 đim) Một công ty khoan giếng đưa ra đnh mức gi như sau: Gi từ mét khoan đầu tiên l
100000
đồng v kể từ mét khoan thứ hai, gi mỗi mét tăng thêm
30000
đồng so với gi của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng ny để khoan giếng
sâu
20
mét ly nước dùng cho sinh hoạt gia đình. Hỏi sau khi hon thnh vic khoan giếng, gia
đình đó phải thanh ton cho cơ sở khoan giếng số tin bằng bao nhiêu?
-------------- HT --------------
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM (7,0 đim).
BẢNG ĐÁP ÁN
1.B
2.A
3.A
4.A
5.D
6.C
7.A
8.A
9.A
10.A
11.D
12.B
13.C
14.C
15.D
16.B
17.A
18.A
19.B
20.C
21.A
22.B
23.C
24.D
25.B
26.A
27.B
28.C
29.B
30.A
31.B
32.C
33.A
34.A
35.D
ĐÁP ÁN CHI TIT
Câu 1: Cung có số đo
250
thì có số đo theo đơn v l radian l
A.
35
18
. B.
25
18
. C.
25
12
. D.
25
9
.
Lời giải
Chọn B
Số đo theo đơn v l radian l
0
0
250 . 25.
18
180

=
.
Câu 2: Cho góc
thỏa mãn
0
2

. Khẳng đnh no sau đây đng?
A.
sin 0
. B.
cot 0
. C.
sin 0
. D.
cos 0
.
Lời giải
Chọn A
Câu 3: Khẳng đnh no sau đây đng?
A.
22
sin cos 1

+=
. B.
22
sin cos 0

+=
.
C.
22
sin cos 2

+=
. D.
22
sin cos 1

+ = −
.
Lời giải
Chọn A
Câu 4:
sin2a
bằng
A.
2sin .cosaa
. B.
sina
. C.
cosa
. D.
cos2a
.
Lời giải
Chọn A
Câu 5: Chu kỳ tuần hon của hm số
sinyx=
l
A.
2k
()k
. B.
2
. C.
. D.
2
.
Lời giải
Chọn D
Câu 6: Tập gi tr của hm số
cos2023yx=
l
A.
1;1−
. B.
( 1;1)−
. C.
2023;2023−
. D.
11
;
22

−


.
Lời giải
Chọn C
Câu 7: Nghim của phương trình
tan 1x =
l
A.
,
4
x k k
= +
. B.
3
,
4
x k k
= +
.
C.
,x k k
=
. D.
,
2
x k k
= +
.
Lời giải
Chọn A
Ta có
tan 1 ,
4
x x k k
= = +
Câu 8: Cho dãy số
( )
n
u
xc đnh bởi
21
n
un=−
với
1n
. Số hạng
1
u
bằng
A.
1.
B.
2
. C.
3.
D.
4
.
Lời giải
Chọn A
Ta có:
1
2.1 1 1u = − =
Câu 9: Dãy số no sau đây l dãy tăng?
A.
1;3;5;7;9
. B.
10;8;6;4;2
. C.
1;5;3;7;9
. D.
1;1;1;1;1
.
Lời giải
Chọn A
Câu 10: Cho cp số cộng
( )
n
u
với
1
3u =
v
2
5.u =
Công sai của cp số cộng đã cho bằng
A.
2
. B.
4
. C.
6
. D.
8
.
Lời giải
Chọn A
Công sai của cp số cộng
21
5 3 2d u u= − = − =
.
Câu 11: Trong cc dãy số
()
n
u
sau, dãy số no b chặn?
A.
2
1
n
un=+
. B.
2
1
3
n
u
n
=−
. C.
sin
n
u n n=+
. D.
2
sin
n
un=
.
Lời giải
Chọn D
Với mọi
*
,Nn
ta có
2
1 sin 1 0 sin 1nn−
nên dãy số đã cho b chặn.
Phân tích phương án nhiu:
A. Sai do dãy số ny b chặn dưới nhưng không b chặn trên.
B. Sai do dãy số ny b chặn trên nhưng không b chặn dưới.
C. Sai do dãy số ny b chặn dưới nhưng không b chặn trên.
Câu 12: Cho
a
,
b
,
c
l ba số hạng liên tiếp của một cp số cộng. Đẳng thức no sau đây đng?
A.
2
b ac=
. B.
2b a c=+
. C.
2a b c+=
. D.
2b c a+=
.
Lời giải
Chọn B
Phân tích phương án nhiu:
A: Sai vì nhớ nhầm của cp số nhân.
B, C: Sai vì không phân bit thứ tự của cc số hạng của cp số cộng.
Câu 13: Dãy số no sau đây l cp số nhân?
A.
1
,
2−
,
4
,
8
,
16−
. B.
2
,
22
,
222
,
22222
.
C.
3
,
6
,
12
,
24
. D.
x
,
2x
,
3x
,
4x
với
0x
.
Lời giải
Chọn C
6 3.2=
,
12 6.2=
,
24 12.2=
.
Phân tích phương án nhiu:
A. Sai do thay
21
:2uu=−
nhưng
43
:2uu=
.
B. Sai do học sinh lầm tưởng đây l cp số nhân với công bội
11q =
.
D. Sai do dãy số trên l cp số cộng, không phải cp số nhân.
Câu 14: Cho cp số cộng
( )
n
u
biết
6
48u =
v
11
83u =
. Tìm cặp
( )
1
; ud
.
A.
( )
7;13
. B.
( )
7; 13−−
. C.
( )
13; 7
. D.
( )
13; 7−−
.
Lời giải
Chọn C
Ta có:
6
11
48
83
u
u
=
=
1
1
5 48
10 83
ud
ud
+=
+=
1
13
7
u
d
=
=
.
Phân tích phương án nhiu:
A. Sai vì đặt nhầm thứ tự của yêu cầu bi ton.
B. Sai vì sử dụng my tính giải h nhập sai h số tự do trong phương trình v đặt nhầm thứ tự
của yêu cầu bi ton.
D. Sai vì sử dụng my tính giải h nhập sai h số tự do trong phương trình.
Câu 15: Cho cp số nhân
( )
n
u
với
1
3u =
v công bội
2=−q
. Tìm gi tr của
n
biết số hạng tổng qut
1536=−
n
u
?
A.
8=n
. B.
9n =
. C.
257n =
. D.
10n =
.
Lời giải
Chọn D
11
1
1536 . 1536 3.( 2) 1536
−−
= − = − − = −
nn
n
u u q
.
( )
9
1
( 2) 512 2 10
−
− = − = − =
n
n
.
Phân tích phương án nhiu:
A. Sai do tính
( )
1
2 512
−
− = −
n
( )
( )
2
512 2 512:( 2) 256
2
−
= − − = − − =
−
n
n
8n=
.
B. Sai do nhầm công thức số hạng tổng qut
( )
1
. 1536 2 512 9
n
n
u q n= − − = − =
.
C. Sai do tính
( )
1
512
2 512 1 256 257
2
−
−
− = − − = = =
−
n
nn
.
Câu 16: Điu tra v chiu cao của học sinh khối lớp 11, ta có kết quả sau:
Nhóm
Chiu cao (cm)
Số học sinh
1
)
150;152
5
2
)
152;154
18
3
)
154;156
40
4
)
156;158
26
5
)
158;160
8
6
)
160;162
3
100N =
Gi tr đại din của nhóm thứ tư l
A.
156,5
. B.
157
. C.
157,5
. D.
158
.
Lời giải
Chọn B
Gi tr đại din của nhóm thứ tư l
156 158
157
2
+
=
.
Câu 17: Khảo st thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liu trên l
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Lời giải
Chọn A
Mốt
0
M
chứa trong nhóm
[40;60)
Câu 18: Khảo st thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liu ghép nhóm sau:
Nhóm chứa trung v của mẫu số liu trên l
A.
[40;60)
.
B.
[20;40)
.
C.
[60;80)
.
D.
[80;100)
.
Lời giải
Chọn A
Ta có:
42n =
Nên trung v của mẫu số liu trên l
21 22
2
2
xx
Q
+
=
M
)
21 22
, 40;60xx
Vậy nhóm chứa trung v của mẫu số liu trên l
nhóm
[40;60)
Câu 19: Doanh thu bn hng trong 20 ngy được lựa chọn ngẫu nhiên của một của hng được ghi lại
ở bảng sau (đơn v: triu đồng):
Số trung bình của mẫu số liu trên thuộc khoảng no trong cc khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Lời giải
Chọn B
Bảng tần số ghép nhóm theo gi tr đại din l
Số trung bình:
2.6 7.8 7.10 3.12 1.14
9,4
20
x
+ + + +
==
Câu 20: Doanh thu bn hng trong 20 ngy được lựa chọn ngẫu nhiên của một của hng được ghi lại
ở bảng sau (đơn v: triu đồng):
Tứ phân v thứ nht của mẫu số liu gần nht với gi tr no trong cc gi tr dưới đây?
A.
7
.
B.
7,6
.
C.
8
.
D.
8,6
.
Lời giải
Chọn C
Gọi
1 2 20
, ,...,x x x
l doanh thu bn hng trong 20 ngy xếp theo thứ tự không giảm.
Khi đó:
)
12
, 5;7xx
,
)
39
,..., 7; 9xx
,,
)
9 16
,..., 9; 11xx
)
17 19
,..., 11; 13xx
,
)
20
13; 15x
Do đó, tứ phân v thứ nht
của mẫu số liu thuộc nhóm
)
7;9
1
20, 7, 2, 7, 9
m m m
n n C u u
+
= = = = =
1
1.20
2
4
7 ( )
7
89 7 7,86Q −=+
−
Câu 21: Biết
4
sin
5
−
=
v
3
2


. Gi tr
cos
bằng
A.
3
.
5
−
B.
3
.
5
C.
3
.
5
D.
9
.
5
Lời giải
Chọn A
Vì
3π
πα
2

nên
cosα0
. Mặt khc
22
sin α cos α 1+=
ta có
2
cosα 1 sin α= − −
2
1
43
55

= − − − = −


.
Câu 22: Gi tr của biểu thức
sin
34
A


=+


l
A.
62
.
4
−
B.
62
.
4
+
C.
62
.
4
−+
D.
62
.
4
−−
Lời giải
Chọn B
Ta có
3 2 2 1 6 2
sin sin cos sin cos . . .
3 4 3 4 4 3 2 2 2 2 4
A
+

= + = + = + =


Câu 23: Hm số no sau đây l hm số lẻ?
A.
2cosyx=−
. B.
2
2sin 2yx= − +
. C.
2sinyx=−
. D.
2cos 2yx= − +
.
Lời giải
Chọn C
Tập xc đnh của hm số
( )
2siny f x x= = −
l
D =
.
Do đó, nếu
x
thuộc tập xc đnh
D
thì
x−
cũng thuộc tập xc đnh
D
.
Ta có
( ) ( )
2sin( ) sinf x x x f x− = − − = = −
. Vậy
2sinyx=−
l hm số lẻ.
Câu 24: Tập nghim của phương trình
cos 1x =−
l
A.
2 | .
2
S k k

= +

B.
2 | .
2
S k k

= − +

C.
2 | .S k k
=
D.
2 | .S k k

= +
Lời giải
Chọn D
Ta có
cos 1 2 ,x x k k

= − = +
.
Câu 25: Cho dãy số
1 1 1
1, , , ,...
3 9 27
(số hạng sau bằng một phần ba số hạng lin trước nó). Công thức tổng
qut của dãy số đã cho l
A.
1
3
n
n
u

=


. B.
1
1
3
n
n
u
−

=


. C.
1
3
n
u
n
=
. D.
( )
1
1
3
n
n
n
u
−
−
=
.
Lời giải
Chọn D
Câu 26: Cho cp số cộng
( )
n
u
có
1
2; 5ud= = −
. Số hạng thứ
20
của cp số cộng l
A.
93−
. B.
10
. C.
93
. D.
23
.
Lời giải
Chọn D
20 1
19 2 19( 5) 93u u d= + = + − = −
.
Câu 27: Cho cp số nhân
( )
n
x
có
2
3x =−
v
4
27.x =−
Tính số hạng đầu
1
x
v công bội
q
của cp số
nhân.
A.
1
1, 3xq= − = −
hoặc
1
1, 3.xq==
B.
1
1, 3xq= − =
hoặc
1
1, 3.xq= = −
C.
1
3, 1xq= = −
hoặc
1
3, 1.xq= − =
D.
1
3, 1xq==
hoặc
1
3, 1.xq= − = −
Lời giải
Chọn B
2
21
3
4 1 1
1
9
3 3 3
3
27. 27. 1.
.
q
x x q q
x x q x
x
q
=
= − = − =


= − = − =
=−


Câu 28: Theo số liu thông kê điểm Giữa học kì I môn ton khối 10 của một trường THPT được cho bởi
bảng số liu sau:
Điểm no đại din cho nhiu học sinh đạt được nht?
A.
6,5
. B.
7,5
. C.
7,25
. D.
8
.
Lời giải
Chọn C
Theo bảng thống kê, gi tr lớn nht l 60 thuộc lớp
)
6,5;8
nên gi tr đại din l
6,5 8
7,25
2
+
=
.
Câu 29: Doanh thu bn hng trong 20 ngy được lựa chọn ngẫu nhiên của một của hng được ghi lại
ở bảng sau (đơn v: triu đồng):
Doanh thu
)
5;7
)
7;9
)
9;11
)
11;13
)
13;15
Số ngy
2
7
7
3
1
Số trung bình của mẫu số liu trên thuộc khoảng no trong cc khoảng dưới đây?
A.
)
7; 9
.
B.
)
9; 11
.
C.
)
11; 13
.
D.
)
13; 15
.
Lời giải
Chọn B
Số trung bình của mẫu số liu trên l:
6.2 8.7 10.7 12.3 14.1
9,4
20
x
+ + + +
==
Câu 30: Khảo st thời gian tập thể dục trong ngy của một số học sinh khối 11 thu được mẫu số liu ghép
nhóm sau:
Nhóm chứa trung v l
A.
)
30;45
. B.
)
15;30
. C.
)
45;60
. D.
)
60;75
.
Lời giải
Chọn A
Cỡ mẫu:
9 5 15 14 7 50n = + + + + =
.
Gọi
1 50
,...,xx
l thời gian khảo st tập thể dục trong ngy của 50 học sinh khối 11 v giả sử dãy
ny đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung v l
25 26
2
xx+
. Do hai gi tr
25 26
,xx
thuộc nhóm
)
30;45
.
Câu 31: Một chiếc phao được thả cố đnh trên biển dùng để đo độ cao của sóng biển được mô hình hóa
bởi hm số
( )
5sin
5
h t t

=


, trong đó
( )
ht
l độ cao tính bằng cetimét trên mực nước biển
trung bình tại thời điểm
t
giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc
phao lại ở v trí đỉnh của cơn sóng tiếp theo (giả sử cc cơn sóng đu mô hình hóa bởi cùng hm
số).
A.
5
giây. B.
10
giây. C.
2,5
giây. D.
20
giây.
Lời giải
Chọn B
Ta có mô hình hóa chiu cao của sóng nước l hm hm số
( )
5sin
5
h t t

=


nên để chiếc phao
ở v trí đỉnh ở hai lần liên tiếp thì cch nhau một chu kì của sóng
( )
2
10
5
Ts
==
.
Câu 32: Tổng nghim âm lớn nht v nghim dương nhỏ nht của phương trình
33
sin 3
42
x

−=


bằng:
A.
.
9
B.
.
6
−
C.
.
6
D.
.
9
−
Lời giải
Chọn C
Ta có
3
32
3 3 3
43
sin 3 sin 3 sin
3
4 2 4 3
32
43
xk
xx
xk



− = +
− = − =
− = − +
.
( )
13 2
13
32
36 3
12
.
17 17 2
32
12 36 3
xk
xk
kZ
x k x k

=+
=+
= + = +
TH1. Với
min
max
13 13
00
13 2
24 36
.
13 11
36 3
01
24 36
Cho
x k k x
xk
x k k x

− = → =
= + ⎯⎯→
− = − → = −
TH2. Với
min
max
17 17
00
17 2
24 36
.
17 7
36 3
01
24 36
Cho
x k k x
xk
x k k x

− = → =
= + ⎯⎯→
− = − → = −
So snh bốn nghim ta được nghim âm lớn nht l
7
36
x
=−
v nghim dương nhỏ nht l
13
.
36
x
=
Khi đó tổng hai nghim bằng
13 7
.
36 36 6
−=
Câu 33: Người ta trồng
3003
cây theo dạng một hình tam gic như sau: hng thứ nht trồng
1
cây, hng
thứ hai trồng
2
cây, hng thứ ba trồng
3
cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hng cây được trồng l
A.
77
. B.
79
. C.
76
. D.
78
.
Lời giải
Chọn A
Gọi số cây ở hng thứ
n
l
n
u
.
Ta có:
1
1u =
,
2
2u =
,
3
3u =
, … v
1 2 3
... 3003
n
S u u u u= + + + + =
.
Nhận xét dãy số
( )
n
u
l cp số cộng có
1
1u =
, công sai
1d =
.
Khi đó
( )
1
21
2
n u n d
S
+−


=
3003=
( )
2.1 1 1
3003
2
nn+−


=
( )
1 6006nn + =
2
6006 0nn + − =
77
78
n
n
=
=−
77n=
(vì
n
).
Câu 34: Một cp số nhân có số hạng đầu
1
3u =
, công bội
2q =
. Biết
765
n
S =
. Tìm
n
?
A.
8n =
. B.
9n =
. C.
6n =
. D.
7n =
.
Lời giải
Chọn A
Áp dụng công thức của cp số nhân ta có:
( ) ( )
1
1 3. 1 2
765
1 1 2
nn
n
uq
S
q
−−
= = =
−−
8n=
.
Câu 35: Cho mẫu số liu ghép nhóm v thời gian (pht) đi từ nh đến nơi lm vic của cc nhân viên một
công ty như sau:
Thời gian
)
15;20
)
20;25
)
25;30
)
30;35
)
35;40
)
40;45
)
45;50
Số nhân
viên
7
14
25
37
21
14
10
Tứ phân v thứ nht
1
Q
v tứ phân v thứ ba
3
Q
của mẫu số liu ghép nhóm ny l
A.
13
1360 800
,
37 21
QQ==
. B.
13
1360 3280
,
37 83
QQ==
.
C.
13
136 3280
,
5 83
QQ==
. D.
13
136 800
,
5 21
QQ==
.
Lời giải
Chọn D
Cỡ mẫu l
128n =
.
Tứ phân v thứ nht
1
Q
l
32 33
2
xx+
. Do
32 33
,xx
đu thuộc nhóm
[25;30)
nên nhóm ny chứa
1
Q
.
Do đó,
213 3 4 3
3; 25; 25; 21, 5p a m m am a= = = = − =+
v ta có
1
21
136
4
25
8
5
5
12
25
Q
−
= + =
Với tứ phân v thứ ba
3
Q
l
96 97
2
xx+
. Do
96 97
,xx
đu thuộc nhóm
[35;40)
nên nhóm ny chứa
3
Q
.
Do đó,
125 5 4 6 53
5; 35; 21; 7 14 25 37 83; 5p a m m m m m a a= = = + + + = + + + = − =
v ta có
3
3.128
83
800
4
35 5
21 21
Q
−
= + =
.
II. PHẦN TỰ LUẬN (3,0 đim).
Câu
Đp n
Biu
đim
36a
Giải phương trnh
cot 3
3
x

+=


.
0.5
cot 3
3 3 6
x x k

+ = + = +


0.25
6
xk
= − +
()k
.
0.25
36b
Cho
2
sin
3
=
, tính giá trị của biểu thức
(1 3cos )(1 3cos )P

= − +
.
0.5
( )
2
2
(1 3cos )(1 3cos ) 1 3cos 1 9cosP
= − + = − = −
.
0.25
2
sin
3
=
,
2 2 2
5
sin cos 1 cos
9
+ = =
.
5
1 9. 4
9
P = − = −
.
0.25
37
Giải phương trnh
cos3 sin2 0xx−=
.
1.0
cos3 sin2 0 cos3 sin 2 cos3 cos 2
2
x x x x x x

− = = = −


0.25
3 2 2
2
x x k

= − +


0.25
52
2
2
2
xk
xk
=+
= − +
0.25
2
10 5
()
2
2
xk
k
xk

=+

= − +
0.25
38
Giải phương trnh
sin cos
3
xx

=+


1.0
sin cos
3
cos cos
23
xx
xx


=+


− = +
0,25
( )
2
23
2
23
x x k
k
x x k


− = + +

− = − − +
0,25
22
6
xk
− = − +
( )
k
0,25
12
xk
= −
( )
k
.
0,25
39
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét
khoan đầu tiên là
100000
đồng và kể từ mét khoan thứ hai, giá
mỗi mét tăng thêm
30000
đồng so với giá của mét khoan ngay
trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này
để khoan giếng sâu
20
mét lấy nước dùng cho sinh hoạt gia đnh.
Hỏi sau khi hoàn thành việc khoan giếng, gia đnh đó phải thanh
toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
0.5
Gi tin mỗi mét khoan giếng lập thnh một cp số cộng với
1
100000u =
(số tin mét khoan đầu tiên),
21
30000uu=+
(số tin mét khoan thứ hai),
3 2 1
30000 2.30000u u u= + = +
(số tin mét khoan thứ ba)
…
20 19 1
30000 19.30000u u u= + = +
(số tin mét khoan thứ 20),
v công sai
30000d =
.
0,25
Tổng chi phí cần phải thanh ton l
20 1 2 3 20
...S u u u u= + + + +
20(2.10000 19.30000)
2
+
=
7700000=
.
0,25
| 1/54
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


ĐỀ KIỂM TRA GIỮA HỌC KÌ I ĐỀ 5
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1. Giá trị nào sau đây mang dấu dương? A. 0 cos120 B. 0 sin120 C. 0 tan120 . D. 0 cot120 .
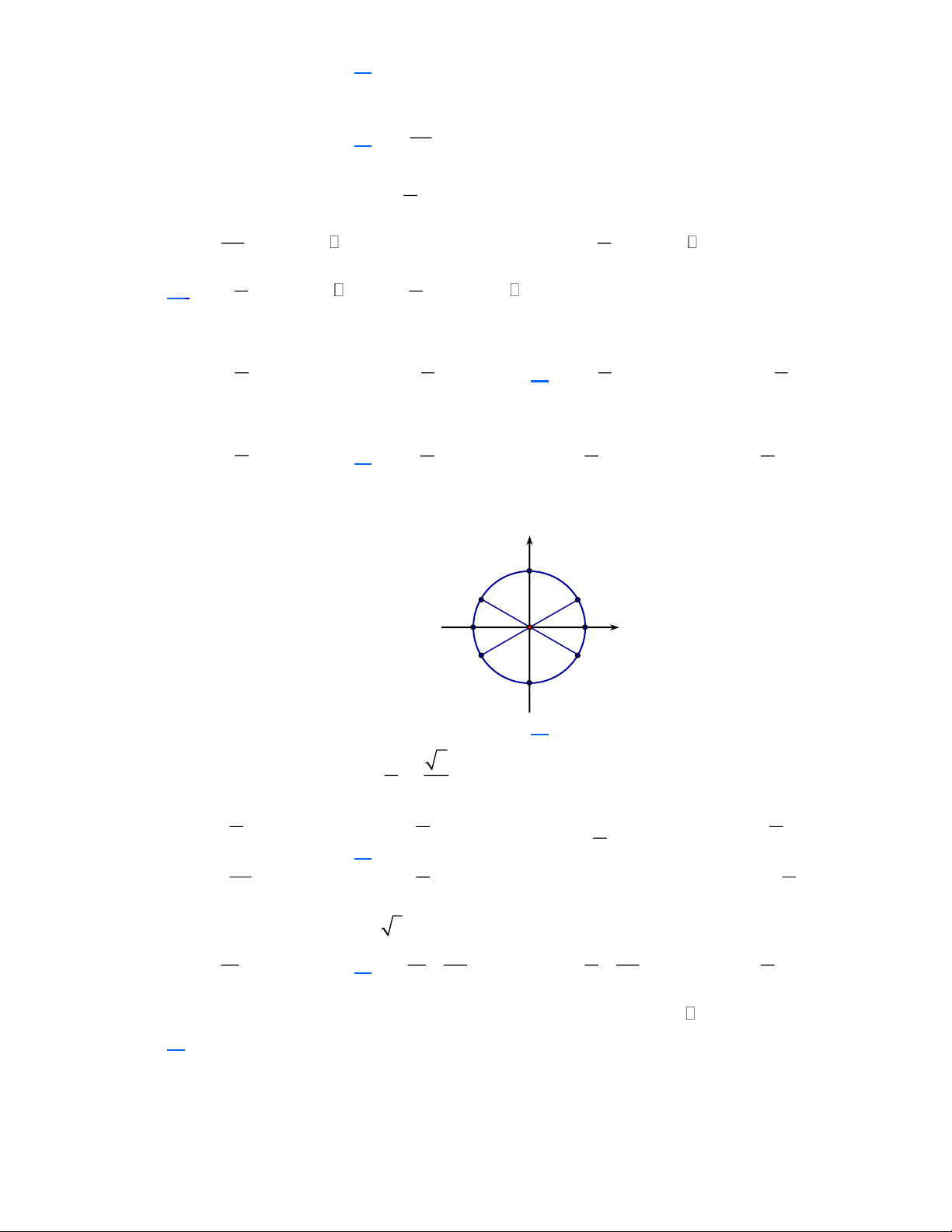
Câu 2. Trong mặt phẳng cho ba tia Ou,O ,
v Ox . Trong các mệnh đề sau, mệnh đề nào đúng?
A. sñ (O ,
u Ov) = sñ(O ,
u Ox) + sñ(O , x Ov) + k  2 ,k Z .
B. sñ (O ,
u Ov) = sñ(O ,
u Ov) + sñ(O , x Ou) + k  2 ,k Z .
C. sñ (O ,
u Ov) = sñ(O ,
v Ox) + sñ(O , x Ou) + k  2 ,k Z .
D. sñ (O ,
u Ov) = sñ(O ,
v Ox) + sñ(O , u Ox) + k  2 ,k Z .
Câu 3. Trong các khẳng định sau, khẳng định nào đúng?
A. cos (a + b) = cos a cos b − sin a sin . b
B. cos (a + b) = cos a cosb + sin a sin . b
C. cos (a + b) = cos a sin b + sin a cos . b
D. cos (a + b) = sin a cos a + cosbsin . b
Câu 4. Trong các khẳng định sau, khẳng định nào sai? A. 2 2
sin 2a = cos a − sin a
B. cos 2a = 2sin a C. 2
cos 2a = 2 cos a −1. D. 2 cos 2a = 1− 2sin . a
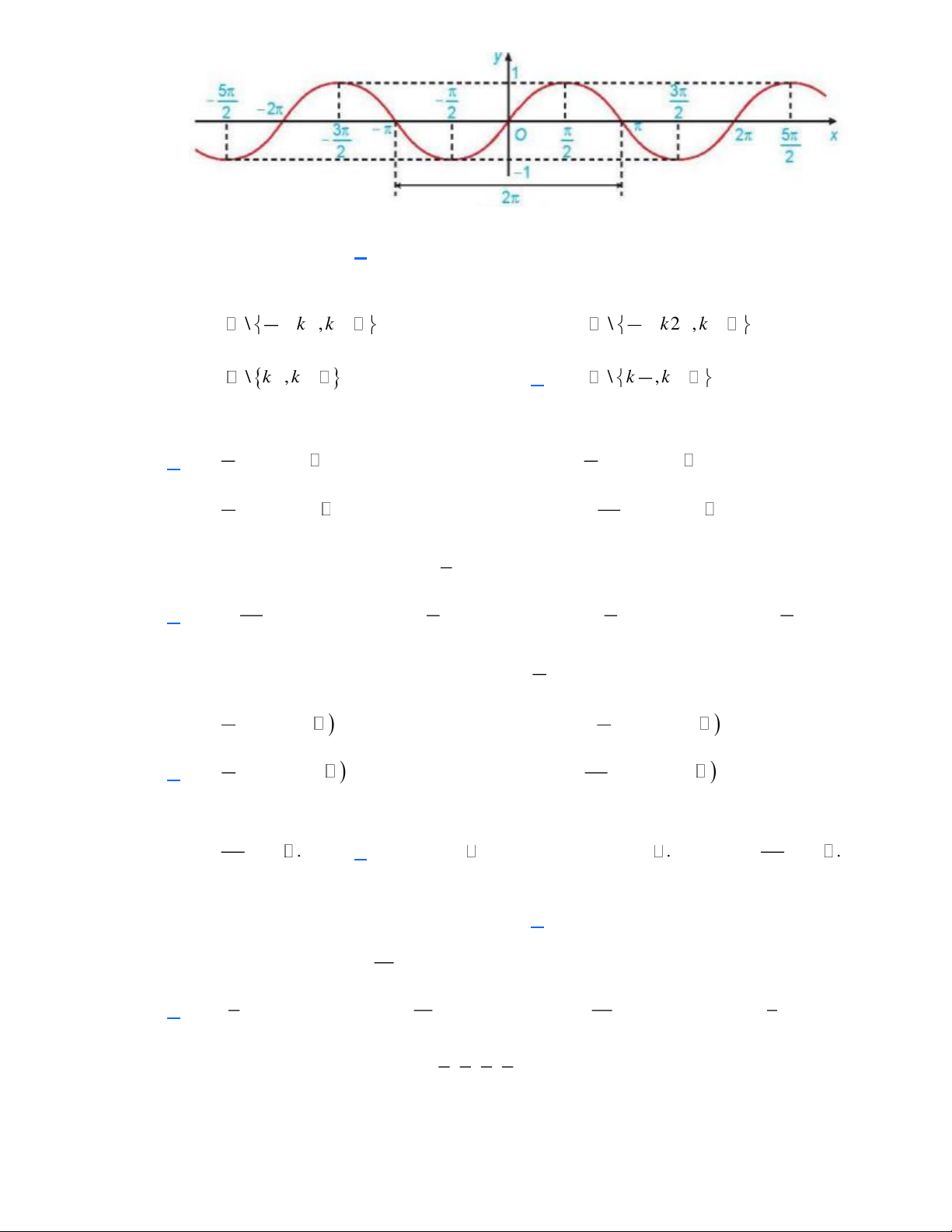
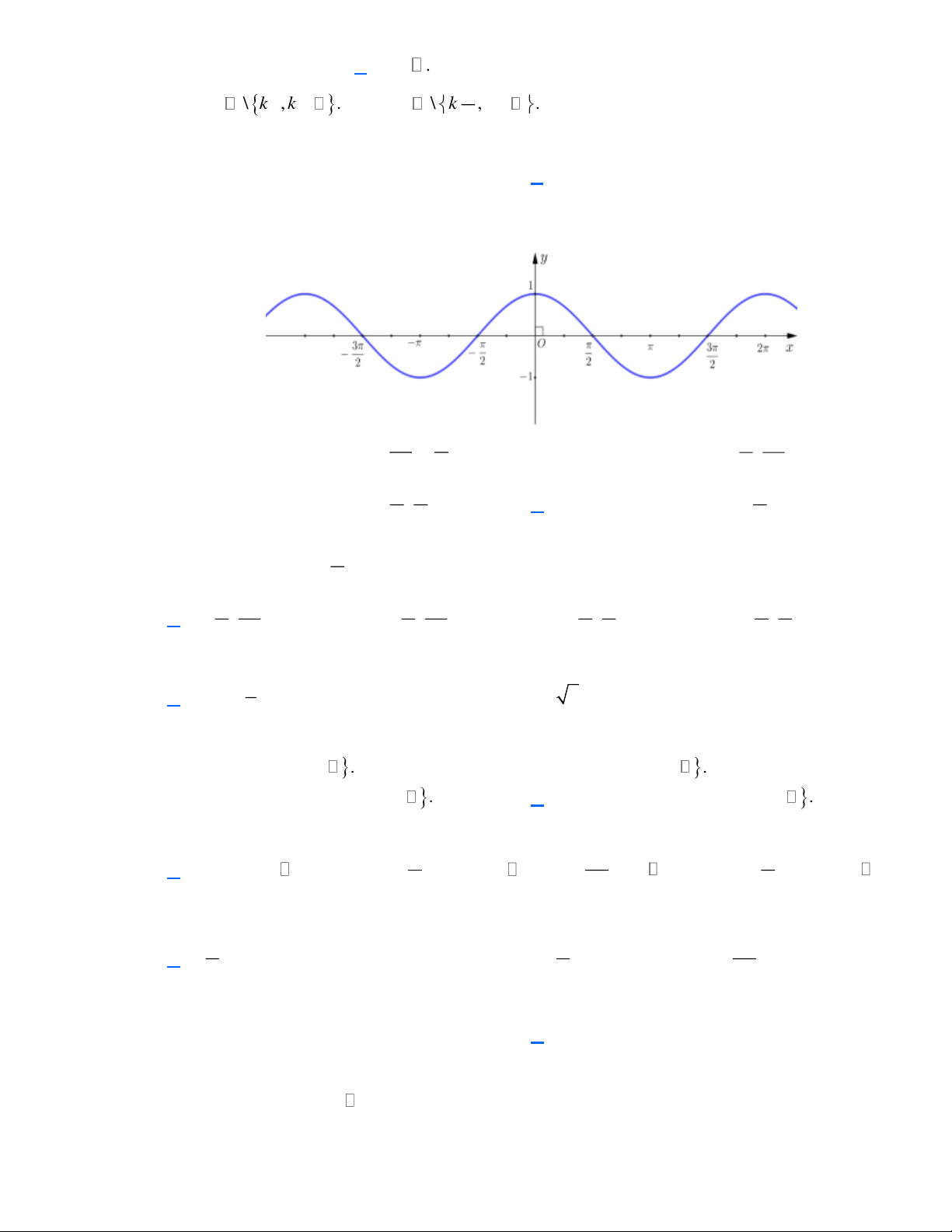
Câu 5. Đồ thị dưới đây là đồ thị của hàm số nào?
A. y = 1+ sin 2x .
B. y = cos x . C. y = − sin x . D. y = −cos x .
Câu 6. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y = tan . x B. y = cot . x C. y = sin . x D. y = cos . x
Câu 7. Điều kiện có nghiệm của phương trình sin x = m là A. m  1. B. m  1. C. m  1. D. m  1.
Câu 8. Cho dãy số (u , biết u = n + 2. Ba số hạng đầu tiên của dãy số lần lượt là n ) n A. 3; 4;5. B. 0;1; 2. C. 2;3; 4. D. 1; 2;3.
Câu 9. Trong các dãy số sau dãy số nào là dãy số hữu hạn 1 1 1 1 1 A. , , , ,
.... B. 5,10,15, 20, 25.... 2 3 4 5 3 3 3 3 3
C. 8,15, 22, 29,36. D. 2, 0, 4, 6,8,...
Câu 10. Cho cấp số cộng (u , biết u = 2,u = 8. Công sai của cấp số cộng là n ) 1 2 A. d = 6 . B. d = 16 . C. d = 10 . D. d = 4 .
Câu 11. Cho cấp số cộng (u , biết u = 2 và công sai d = 3. Khẳng định nào sau đây đúng? n ) 1 A. u = 5. B. u = 2. C. u = 6. D. u = 3. 2 2 2 2
Câu 12. Cho cấp số cộng (u . Gọi S là tổng của n số hạng đầu của cấp số cộng. Khẳng định đúng là n ) n n (n − ) 1 nu + n n −1 1 ( )
A. S = nu + d . B. S = d . n 1 2 n 2 (n− )1
C. S = nu + n n −1 d .
D. S = nu + d . n 1 ( ) n 1 2
Câu 13. Dãy số nào sau đây không phải là cấp số nhân?
A. 1; − 3;9; − 27;54 . B. 1; 2; 4;8;16 . C. 1; −1;1; −1;1.
D. 1; − 2; 4; − 8;16 .
Câu 14. Cho cấp số nhân (u với và . Tìm công bội n ) u = 81 u = 3 1 q ? 4 1 1 1 A. − . B. − . C. 3 . D. 3 − . 3 3 3
Câu 15. Cho cấp số nhân (u với u = 2 và công bội q = 3. Giá trị của u bằng n ) 1 2 2 A. 6 . B. 9 . C. 8 . D. . 3
Câu 16. Trong mẫu số liệu ghép nhóm, độ dài mỗi nhóm a;b) được tính như thế nào? a + b A. b − . a B. . C. a + . b D. . a . b 2
Câu 17. Các giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là A. mốt. B. số trung bình. C. số trung vị. D. tứ phân vị.
Câu 18. Trong mẫu số liệu ghép nhóm, giá trị đại diện của nhóm a;b) được tính như thế nào? a + b A. . B. b − . a C. a + . b D. . a . b 2
Câu 19. Trong các khẳng định sau, khẳng định nào là đúng?
n −(m +...+ m 1 1 + )
A. Số trung vị là 2 p M = a + a − a . e p ( p 1+ p) mp
B. Số trung vị bị ảnh hưởng bởi các giá trị quá lớn hay quá bé.
C. Số trung vị luôn là một số liệu nào đó của mẫu.
D. Số trung vị chính là số trung bình.
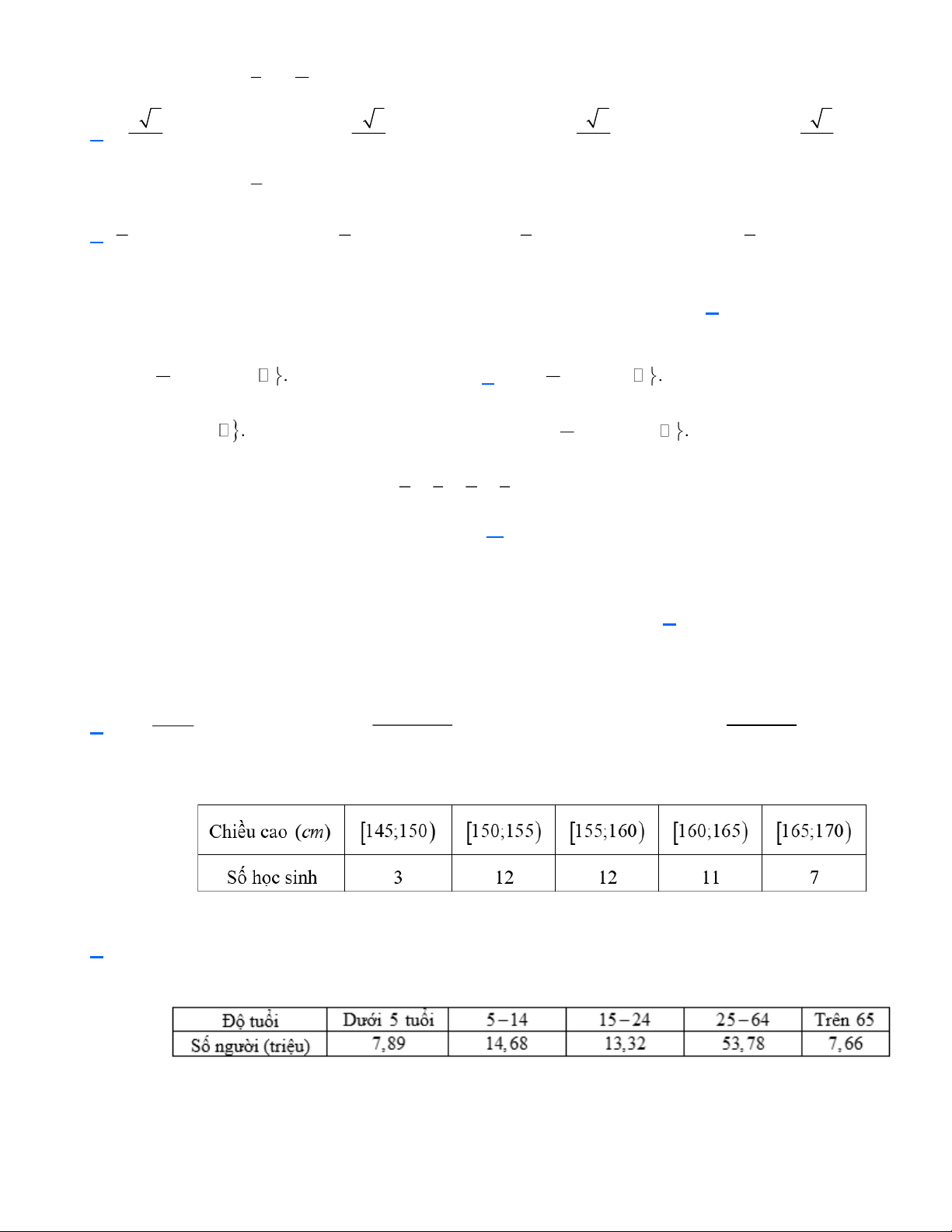
Câu 20. Đo chiều cao (tính bằng cm ) của 500 học sinh trong một trường THPT ta thu được kết quả như sau: 150;154) Chiều cao 154;158) 158;162) 162;166) 166;170) Số học sinh 25 50 200 175 50
Mẫu số liệu ghép nhóm đã cho có tất cả bao nhiêu nhóm? A. 5 .
B. 6 . C. 7 . D. 12 .  Câu 21. 1 Biết sin  = và
   . . Giá trị cos bằng 3 2 2 2 2 3 3 2 3 3 A. − . B. − . C. − . D. − . 3 3 2 2 Câu 22. 1 Biết sin  = . Giá trị cos 2 bằng 4 7 8 7 8 A. . B. . C. − . D. − . 8 7 8 7
Câu 23. Tập giá trị của hàm số y = 2sin x là A.  1 − ;  1 . B. 0; 2. C.  2 − ;  2 . D.  2 − ;2.
Câu 24. Tập nghiệm của phương trình cos x = 0 là    
A. S =  + k2 | k  .
B. S =  + k |k  .  2   2    
C. S = k2 |k  .
D. S = − + k2 | k  .  2  1 1 1 1
Câu 25. Xét tính tăng giảm của dãy số − ;− ;− ;− . 2 3 4 5 A. Dãy số tăng B. Dãy số giảm
C. Dãy số không tăng không giảm
D. Dãy số vừa tăng vừa giảm
Câu 26. Cho một cấp số cộng có các số hạng lần lượt là1,6,11, .
x Khi đó giá trị của x là A. 5 . B. 18. C. 17. D. 16.
Câu 27. Cho cấp số nhân có các số hạng lần lượt là 1; 4; 16; 64. Gọi S là tổng của n số hạng đầu tiên của n
cấp số nhân đó. Mệnh đề nào sau đây đúng? n ( n 1 1 4 − + ) 4 (4n − ) 4n −1 1 A. S = . B. S = . C. 1 S 4n− = . D. S = . n n n 3 2 n 3
Câu 28. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 45 học sinh lớp 11A .
Mẫu số liệu ghép nhóm này có số mốt là A. 2 . B. 1. C. 0 . D. 3 .
Câu 29. Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau:
(Theo:http://ourwoldindata.org)
Chọn 85 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020 . A. 36,17 . B. 34,82 . C. 35, 6 . D. 37,12 .
Câu 30. Khảo sát chiều cao (cm) của 52 học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là
A. 165;170) . B. 160;165) . C. 170;175) . D. 175;180) .
Câu 31. Tập xác đinh của hàm số y = sin x + cos x là A. . B.
\ k |k  . C. \  |k  . D.
\ k2 |k  .
Câu 32. Phương trình 2cos x = − 3 có bao nhiêu nghiệm thuộc tập   − ;3  A. 4. B. 3. C. 2. D. 1. 1 1 1 1
Câu 33. Cho dãy số (u xác định bởi u = + + +...+
. Chọn mệnh đề đúng? n ) n 2 2 2 2 1 2 3 n
A. Dãy số (u bị chặn. n )
B. Dãy số (u bị chặn trên, nhưng không bị chặn dưới. n )
C. Dãy số (u bị chặn dưới, nhưng không bị chặn trên. n )
D. Dãy số (u không bị chặn. n )
Câu 34. Gọi S =1+11+111+...+111...1 ( n số 1 ) thì S nhận giá trị nào sau đây? 1  10n −1  10n −1 A. S = 10    − n . B. S = 10  . 9   9    81  10n −1 10n −1 C. S = 10  − n . D. S = .  81  81
Câu 35. Khảo sát vận tốc (dặm/h; 1 dặm = 1,609km ) của 300 xe ô tô chạy trên con đường A thu được
mẫu số liệu ghép nhóm như sau:
Nhóm chứa tứ phân vị thứ nhất là A. 32,5 ;37,5) . B. 27,5 ;32,5) . C. 37,5 ; 42,5) . D. 42,5 ;47,5) .
II. PHẦN TỰ LUẬN (3 điểm).
Câu 36 (1 điểm). Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liệu trên?
Câu 37 (1 điểm). sin x
a) Tìm tập xác định của hàm số sau: y = . 2 2 sin x − cos x
b) Giải phương trình sin ( cos x) = 1.
Câu 38 (1 điểm). Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây, hàng
thứ hai có 2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
……………… HẾT ……………… ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng. Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 B A A B B D C A C A
Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 A A A A A A A A A A
Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 A A D B B D A A A A
Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 A A A A A II. PHẦN TỰ LUẬN Câu Đáp án Biểu điểm 36
Đo cân nặng của một số học sinh lớp 11D cho trong bảng sau:
Tính mốt của mẫu số liệu trên? Tần số lớn nhất là 0,25
16 nên nhóm chứa mốt là nhóm 50,5;55,5) và j = 3
Ta có u = 50,5;u = 55,5  h = u −u = 5 0,25 3 4 4 3 = = = Tần số: n 7; n 16; n 4 2 3 4 . 0,25 n − n − 0,25 j j 1 − n n M = u + h = u +  h o j ( 3 3 n − n + n − n n − n + n − n j j 1 − ) ( j j 1+) 2 ( 3 2) ( 3 4) 16 − 7 M = 50,5 + .5 = 52, 6 0 (16 − 7) + (16 − ) 4 37 sin x
a) Tìm tập xác định của hàm số sau: y = . 2 2 sin x − cos x Điều kiện xác định của hàm số 0,25   k 2 2
sin x − cos x  0  − cos 2x  0  2x
+ k  x  + ; k  là 2 4 2 .   k0,25
Vậy tập xác định của hàm số là D = \  + ; k    4 2 
b) Giải phương trình sin ( cos x) =1.
sin ( cos x) = 1   cos x = + k2 ,k  1
 cos x = + 2k, k 0,25 2 2 Vì 0,25 1
−  cos x 1 nên 1 3 1 1
−  + 2k 1  −  k  . 2 4 4 1 
Do k   k = 0 suy ra cos x =
x =  + m2 ,m . 2 3 38
Người ta trồng 2145 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây,
hàng thứ hai có 2 cây, hàng thứ ba có 3 cây,… Hỏi có tất cả bao nhiêu hàng cây?
Gọi số hàng cây là n , hàng thứ n có n cây. 0,25
Ta có 1+ 2 +3+...+ n = 2145 0,25 n (n + ) 1  = 0,25 2145 . 2  n = 65 0,25 ======
ĐỀ KIỂM TRA GIỮA HỌC KÌ I ĐỀ 6
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm):
Câu 1. Cho  thuộc góc phần tư III của đường tròn lượng giác. Khẳng định nào dưới đây đúng?
A. sin  0; cos  0 .
B. sin  0; cos  0 .
C. sin  0; cos  0 . D. sin  0; cos  0 .
Câu 2. Một chiếc đồng hồ có kim chỉ giờ OG chỉ số 9 và kim phút OP chỉ số 12 . Số đo của góc lượng
giác (OG,OP) là A. 0 0 9
− 0 + k360 , k  . B. 0 0
−270 + k360 , k  . C. 0 0
270 + k360 , k  . D. 0 0
90 + k360 , k  .
Câu 3. Trên đường tròn lượng giác, cho điểm M ( ;
x y) và sđ (O ,
A OM ) =  . Khẳng định nào dưới đây đúng? A. sin = y .
B. sin = x − y . C. cos = y .
D. cos = x + y .  Câu 4. cot bằng 6 1 A. 0 . B. . C. 3 . D. 1. 3
Câu 5. Cho tam giác ABC . Khẳng định nào dưới đây đúng?
A. cos ( A + B) = cosC . B. cos( A + B) = sin C .
C. cos ( A + B) = −sin C . D. cos( A + B) = −cosC . 4 
Câu 6. Cho góc  thỏa cos = và 0   
. Giá trị của sin 2 bằng 5 2 12 24 24 12 A. − . B. . C. − . D. . 25 25 25 25
Câu 7. Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A. y = tan x .
B. y = cos x .
C. y = cot x .
D. y = sin x .
Câu 8. Hàm số nào dưới đây là hàm số chẵn?
A. y = cos x .
B. y = tan x .
C. y = cot x .
D. y = sin x .
Câu 9. Hàm số y = 3sin 2x tuần hoàn với chu kì
A. T = 6 .
B. T = 3 .
C. T =  . D. T = 2 .
Câu 10. Tập giá trị của hàm số y = 2sin x + 3 là A.  1 − ;  1 . B. 1;5. C. 4; 8. D. (1;5) .
Câu 11. Nghiệm của phương trình cos x = 1 là
A. x = k , k  .
B. x = k 2 , k  . C. x =
+ k , k  . D. x =  + k2, k  . 2
Câu 12. Nghiệm của phương trình 3 tan x = 1 là   A. x =
+ k2 , k  . B. x =
+ k , k  . 6 4   C. x =
+ k , k  . D. x =
+ k , k  . 3 6
Câu 13. Nghiệm của phương trình 2cos x −1 = 0 là   A. x = 
+ k2 , k  . B. x =  + k2 , k  . 4 3   C. x = 
+ k , k  . D. x =  + k , k  . 4 3
Câu 14. Dãy số nào dưới đây là dãy số tăng? 1 1 1 1 1 1 A. 2, 4, 3 B. , , . C. 3, 3, 3 D. , , . 4 3 2 2 3 4
Câu 15. Trong các dãy số (u dưới đây, dãy số nào bị chặn dưới? n ) 1 1
A. u = n − 2 .
B. u = 1− 2n . C. u = u = . n n n n + . D. 1 n 2n u  = 1 −
Câu 16. Cho dãy số (u xác định bởi hệ thức truy hồi 1 
(n  2). Giá trị của u bằng n ) u = 3u + n  3 n n 1 − A. 1. B. 3 . C. 2 . D. 0 .
Câu 17. Dãy số nào dưới đây không là cấp số cộng? A. 1, 2, 4, 8 B. 1, 2, 3, 4 . C. 1, 0, −1, − 2 . D. 1, 1, 1, 1.
Câu 18. Cho cấp số cộng 2
− , 3, 8,.... Công sai của cấp số cộng đã cho bằng A. 1. B. 5 − . C. 5 . D. 1 − .
Câu 19. Cho cấp số cộng (u với số hạng tổng quát u = 2n −1. Số hạng thứ tư của cấp số cộng đã cho n ) n bằng A. 7 . B. 3 . C. 4 . D. 5 .
Câu 20. Cho cấp số cộng (u với u = 0 và công sai d = 4 . Số hạng thứ mấy của cấp số cộng đã cho n ) 1 bằng 20 ?
A. Số hạng thứ 8 .
B. Số hạng thứ 5 .
C. Số hạng thứ 7 .
D. Số hạng thứ 6 . u  = 2
Câu 21. Cho cấp số cộng (u được xác định bởi công thức: 1 
(n  2). Số hạng tổng quát của n ) u = u − 3  n n 1 −
cấp số cộng đã cho là
A. u = n +1.
B. u = 5 − 3n .
C. u = 3n −1.
D. u = 5n − 3 . n n n n
Câu 22. Dãy số (u được cho bởi công thức nào dưới đây là một cấp số nhân? n ) u  = 1 u  = 1 A. 2 + n . B. 1  .
C. u = 2n . D. 1  . u = nun u = 2u n 1 + nn 1+ n
Câu 23. Ba số hạng nào dưới đây theo thứ tự đó lập thành một cấp số nhân? A. 1, 3, 5 . B. 3, 5, 9 . C. 1, 3, 9 . D. 1, 5, 9 . 1
Câu 24. Cho cấp số nhân (u với u = 2 và công bội q = . Bốn số hạng đầu của cấp số nhân đã cho là n ) 1 2 1 5 9 13 1 1 A. , 1, 2, 4 . B. 2, 1, 1, 1. C. 2, , , . D. 2, 1, , . 2 2 2 2 2 4
Câu 25. Cho cấp số nhân (u với u = 5
− và công bội q = 3. Giá trị của u bằng n ) 1 5 A. 1875 . B. 405 − . C. 15 − . D. 7 .
Câu 26. Cho cấp số nhân 3, −12, 48,.... Số hạng tổng quát của cấp số nhân đã cho là n+ n n− n− A. u = − . B. u = 3 − . C. u = − . D. u = . n ( ) 1 3. 4 n ( ) 1 3. 4 n ( 4) n ( ) 1 3. 4
Câu 27. Độ dài của nhóm 1;20) bằng A. 19. B. 20. C. 18. D. 17.
Câu 28. Thống kê về nhiệt độ tại một địa điểm trong 30 ngày, ta có bảng số liệu sau: Nhiệt độ (
18; 22) 22; 25) 25; 28) 28; 3 )1 31; 34) 0 C ) Số ngày 3 6 10 5 6
Số ngày có nhiệt độ thấp hơn 0 25 C là A. 10 . B. 9 . C. 19 . D. 3 .
Câu 29. Thống kê số lỗi chính tả trong bài kiểm tra giữa HKI môn Ngữ Văn của học sinh khối 11 thu
được kết quả ở bảng sau: Số lỗi 1; 3) 3; 5) 5; 7) 7; 9) 9;1 )1 Số bài 122 75 14 5 2
Khẳng định nào dưới đây đúng?
A. Có 5 bài kiểm tra sai 7 lỗi chính tả.
B. Có 5 bài kiểm tra sai 8 lỗi chính tả.
C. Có 5 bài kiểm tra sai từ 7 đến 8 lỗi chính tả.
D. Có 5 bài kiểm tra sai từ 7 đến 9 lỗi chính tả.
Câu 30. Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào. Kết quả
khảo sát được ghi lại ở bảng sau: Mức giá
10;14) 14;18) 18; 22) 22; 26) 26; 30) (triệu đồng/ 2 m ) Tần số 54 78 120 45 12
Mức giá thuộc nhóm nào dưới đây là phù hợp với đa số khách hàng được khảo sát? A. 14; 18) .
B. 26; 30) . C. 18; 22) . D. 10; 14) .
Câu 31. Điều tra về điểm kiểm tra giữa HKI của 36 học sinh lớp 11A ta được kết quả sau: Điểm
0; 2) 2; 4) 4; 6) 6;8) 8;10) Tần số 1 5 9 14 7
Điểm trung bình của 36 học sinh trên gần nhất với số nào dưới đây? A. 6, 4 . B. 6, 2 . C. 6, 0 . D. 6, 6 .
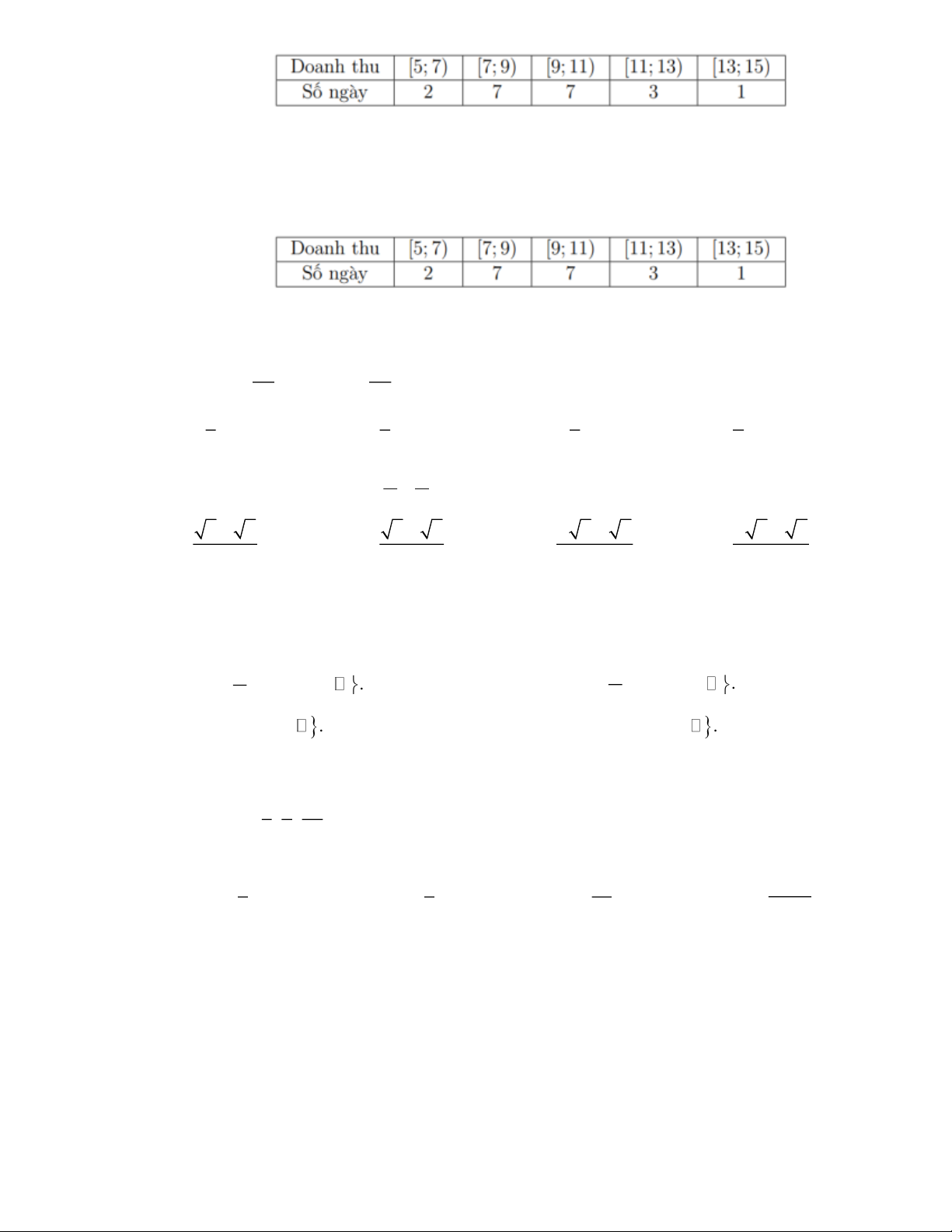
Câu 32. Doanh thu (triệu đồng) bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa
hàng được ghi lại ở bảng sau: Doanh thu
5; 7) 7; 9) 9;1 )1 11;13) 13;15) Số ngày 2 7 7 3 1
Trung vị của mẫu số liệu trên thuộc nhóm nào dưới đây? A. 9; 1 ) 1 . B. 7; 9) . C. 11; 13). D. 13; 15) .
Câu 33. Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối thu được kết quả sau:
Thời gian 4; 5) 5; 6) 6; 7) 7; 8) 8; 9) Số học 10 18 23 20 15 sinh
Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu trên là A. 5; 6) . B. 7; 8) . C. 4; 5) . D. 6; 7) .
Câu 34. Thời gian (phút) truy bài trước mỗi buổi học của một số học sinh trong một tuần được ghi lại ở bảng sau: Thời gian 9,5;12,5) 12,5;15,5) 15,5;18,5) 18,5; 21,5) 21,5; 24,5) Số học sinh 3 12 15 24 2
Trung vị của mẫu số liệu trên bằng A. 16, 2 . B. 18,1 . C. 15 . D. 9 .
Câu 35. Người ta ghi lại tuổi thọ của một số con muỗi cái trong phòng thí nghiệm cho kết quả như sau: Tuổi thọ (ngày) 0; 20)
20; 40) 40; 60) 60;80) 80;100) Số lượng 5 12 23 31 29
Muỗi cái có tuổi thọ khoảng bao nhiêu ngày là nhiều nhất? A. 80 ngày. B. 66 ngày. C. 76 ngày. D. 90 ngày.
II. TỰ LUẬN (3,0 điểm)    
Bài 1 (1,0 điểm). Cho góc  thỏa 4 cos = − và 3     . Tính tan  −   . 5 2  4 
Bài 2 (1.0 điểm). Giải phương trình sin 4x + cos3x − cos x = 0 .
Bài 3 (0.5 điểm). Trong một đợt quyên góp để ủng hộ học sinh vùng khó khăn. 40 học sinh lớp 11 của
trường THPT X thực hiện kế hoạch quyên góp như sau: Ngày đầu tiên mỗi bạn quyên góp 2000 đồng, từ
ngày thứ hai trở đi mỗi bạn quyên góp hơn ngày liền trước là 500 đồng. Hỏi sau bao nhiêu ngày thì số tiền
quyên góp được là 9800000 đồng.
Bài 4 (0.5 điểm). Đầu mùa thu hoạch sầu riêng, ông A đã bán cho người thứ nhất nửa số sầu riêng thu
hoạch được và tặng thêm 1 quả, bán cho người thứ hai nửa số sầu riêng còn lại và tặng thêm 1 quả. Ông cứ
tiếp tục cách bán như trên thì đến người thứ bảy số sầu riêng của ông được bán hết. Tính số sầu riêng mà ông A thu hoạch được.
………………Hết………………. ĐÁP ÁN
I. TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 B A A C D B B A C B
Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 B D B B A D A C A D
Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 B D C D B C A B C C
Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 B A A B C II. TỰ LUẬN Bài Đáp án Điể m    
Cho góc thỏa 4 cos = − và 3     . Tính tan  −   . 5 2  4  3 2
sin =  1− cos  =  5 0,25 3 3       = − 1 sin 2 5 0,25 (1,0đ) sin − 1    tan −1 cos tan  − = =   0,25  4  1+ tan sin 1+ cos 1 = − 7 0,25
Giải phương trình sin 4x + cos3x − cos x = 0 .
Phương trình đã cho tương đương 2sin 2xcos2x − 2sin 2xsin x = 0 0,25 sin 2x = 0 ( ) 1  − = 
sin 2x(cos 2x sin x) 0 
cos 2x = sin x  (2) 0,25 2 (1,0đ) k 0,25 ( )1  x = 2   k2   k2 x = +  x = +  ( )    6 3 6 3 0,25 2  cos 2x = cos − x     . Nghiệm PT:   2    k  x = − + k2  x =  2  2
Trong một đợt quyên góp để ủng hộ học sinh vùng khó khăn. 40 học sinh lớp 11
của trường THPT X thực hiện kế hoạch quyên góp như sau: Ngày đầu tiên mỗi
bạn quyên góp 2000 đồng, từ ngày thứ hai trở đi mỗi bạn quyên góp hơn ngày
liền trước là 500 đồng. Hỏi sau bao nhiêu ngày thì số tiền quyên góp được là 9800000 đồng.
Số tiền mỗi học sinh quyên góp theo từng ngày lập thành một cấp số cộng 3
với số hạng đầu u = 2000 và công sai d = 500 (0,5đ) 1
Do đó tổng số tiền mà 40 học sinh quyên góp được sau n ngày là 0,25 n  +  (n − ) 2 40. 2.2000
1 500 = 10000n + 70000n  2 Theo giả thiết ta có: 2 2
10000n + 70000n = 9800000  n + 7n − 980 = 0 n = 28   n = 35 −  (L) 0,25
Vậy số ngày cần quyên góp là 28 ngày
Đầu mùa thu hoạch sầu riêng, ông A đã bán cho người thứ nhất nửa số sầu riêng
thu hoạch được và tặng thêm 1 quả, bán cho người thứ hai nửa số sầu riêng còn
lại và tặng thêm 1 quả. Ông cứ tiếp tục cách bán như trên thì đến người thứ bảy
số sầu riêng của ông được bán hết. Tính số sầu riêng mà ông A thu hoạch được.
Gọi x là số quả sầu riêng mà ông A thu hoạch được
Khi đó số quả sầu riêng mà người thứ nhất mua và được tặng là: 1 x + 2 + = x 1 2 2 0,25 4
Số quả sầu riêng mà người thứ hai mua và được tặng là: (0,5đ) 1  x + 2  x + 2 x − +1 =   2 2  2  2 ... x + 2
Số quả sầu riêng mà người thứ bảy mua và được tặng là: 7 2 + + + Khi đó x 2 x 2 x 2  1 1 1  : + + ... + = x x + 2 + + ...+ = x   2 7 ( ) 2 7 2 2 2  2 2 2  7  1  0,25 1−   (    x + 2) 1 2 127 . = x
(x + 2) = x x = 254 2 1 128 1− 2
ĐỀ KIỂM TRA GIỮA HỌC KÌ I ĐỀ 7
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm - gồm 35 câu: từ câu 1 đến câu 35).
Câu 1: Giá trị của bằng A. B. C. D.
Câu 2: Số đo theo đơn vị rađian của góc 315 là 7 7 2 4 A. . B. . C. D. . 2 4 7 7     Câu 3: 5 25 19
Cho bốn cung (trên một đường tròn định hướng): = − ,  = , = , = , Các cung 6 3 3 6
có điểm cuối trùng nhau là
A.  và  ;  và  .
B.  ,  , . C.  , , .  D. và  ;  và  .
Câu 4: Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là: A. 0 60 . B. 0 30 . C. 0 40 . D. 0 50 . Câu 5:   Biết tan = 2 và 180
 270 . Giá trị cos +sin bằng 3 5 3 5 5 −1 A. − . B. 1– 5 . C. . D. . 5 2 2
Câu 6: Trong các công thức sau, công thức nào sai? A. 2 2
cos 2a = cos a – sin . a . B. 2 2
cos 2a = cos a + sin . a . C. 2
cos 2a = 2cos a –1. D. 2 cos 2a = 1– 2sin . a 1
Câu 7: Biết sin x = thì cos 2x có giá trị là : 2 1 1 A. 0 . B. 1. C. − . D. . 2 2
M = sin ( x + y)cos y − cos( x + y) Câu 8: sin y Rút gọn ?
A. M = cos x .
B. M = sin x .
C. M = sin ( x + 2y) . D. M = cos( x + 2y) .
Câu 9: Tập xác định của hàm số y = sin x là        A. D = \   . B. D =
\  + k2 , k   .C. D = . D. D = \   .  2   2   2 
Câu 10: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Đồ thị hàm số y = f (x) là đồ thị của hàm số nào dưới đây?
A. y = tan x .
B. y = sin x .
C. y = cos x .
D. y = cot x .
Câu 11: Tập xác định của hàm số y = sin 5x + cos x + cot 2x là     A. D =
\  + k , k   . B. D =
\  + k2 , k   .  2   2     C. D =
\ k , k   . D. D = \ k , k   .  2 
Câu 12: Nghiệm của phương trình tan x =1 là:   A. x = + k (k  ) x = + k2 k 4 B. ( ) 3  5 C. x =
+ k2 (k  ) x =  + k2 k 4 D. ( ) 6
Câu 13: Nghiệm của phương trình 1 cos x = - là: 2 2p p p p A. x = ± + k2p B. x = ± + kp C. x = ± + k2p D. x = ± + k2p 3 6 3 6   
Câu 14: Tìm tất cả các nghiệm của phương trình sin x + =1   .  6    A. x =
+ k (k  ) . B. x = −
+ k2 (k  ) . 3 6  5 C. x =
+ k2 (k  ) . D. x =
+ k2 (k  ) . 3 6
Câu 15: Nghiệm của phương trình tan 3x = tan x là kkA. x = , k  .
B. x = k , k .
C. x = k 2 , k  . D. x = , k  . 2 6
Câu 16: Dãy số nào dưới đây là dãy số nguyên tố nhỏ hơn 10 theo thứ tự tăng dần?
A. 0 , 1, 2 , 3 , 5 , 7 .
B. 1, 2 , 3 , 5 , 7 .
C. 2 , 3 , 5 , 7 . D. 1, 3 , 5 , 7 . Câu 17: n
Cho dãy số (u ), n biết u = . Chọn đáp án đúng. n 2n 1 1 1 1 A. u = . B. u = . C. u = . D. u = . 4 4 5 16 5 32 3 8
Câu 18: Cho dãy số có các số hạng đầu là 1 2 3 4
0; ; ; ; ;... .Số hạng tổng quát của dãy số này là: 2 3 4 5 n +1 n n −1 2 n − n A. u = . B. u = . C. u = . D. u = . n n n n +1 n n n n +1
Câu 19: Dãy số nào sau đây không phải là cấp số cộng? A. 2;5;8;11;14...
B. 2; 4;8;10;14... C. 1; 2;3; 4;5; 6... D. 15;10;5; 0; 5 − ;... 1 1
Câu 20: Cho cấp số cộng (u có số hạng đầu u = − , công sai d = . Năm số hạng liên tiếp đầu tiên n ) 1 2 2
của cấp số cộng là: 1 1 1 1 1 1 3 5 1 1 3
A. − ; 0;1; ;1.
B. − ; 0; ; 0; . C. ;1; ; 2; . D. − ; 0; ;1; . 2 2 2 2 2 2 2 2 2 2 2
Câu 21: Cho cấp số cộng (u có số hạng đầu u = 5
− và công sai d = 3. Số 100 là số hạng thứ mấy của n ) 1 cấp số cộng? A. 15. B. 20. C. 35. D. 36.
Câu 22: Cho dãy số (u là một cấp số nhân có số hạng đầu u và công bội q . Đẳng thức nào sau đây n ) 1 đúng?
A. u = u + n −1 q , (n  2) . B. n 1 u u q − = , (n  2) . n 1 ( ) n 1 n− u C. u = . q u , (n  2) . D. 1 u = , (k  2) . n ( ) 1 1 n n 1 q −
Câu 23: Cho cấp số nhân (u với công bội q  1. Đặt S = u + u +...+ u . Khẳng định nào sau đây n ) n 1 2 n đúng? u 1 n − q u ( n 1 1 q − − u 1− q 1 ( ) 1 ) 1 ( ) A. S = S = S = u 1 n − q . D. S = n 1− . B. q n 1− . C. n 1 ( ) q n 1 n − . q 1
Câu 24: Cho dãy số (u là một cấp số nhân với u = ;q = 2
− . Năm số hạng đầu tiên của CSN là n ) 1 2 1 1 1 1 1 1 1 1 1 1 1 1 A. ;1; 2; 4;8 .
B. ; −1; 2; − 4;8 . C. ; − ; ; − ; . D. ; ; ; ; . 2 2 2 4 8 16 32 2 4 8 16 32
Câu 25: Cho cấp số nhân (u biết u = 2
− và u = 54 . Tìm tổng 10 số hạng đầu tiên của cấp số nhân n ) 2 5 2 2 2 2 10 . 1  − 3    10 . 1  + 3    10 − . 1  − 3    10 . 1  − 3    A. 3 S = . B. 3 S = . C. 3 S = . D. 3 S = . 10 4 10 4 10 2 10 2 −
Câu 26: Trong không gian, cho 3 điểm phân biệt không thẳng hàng. Khí đó có bao nhiêu mặt phẳng đi qua ba điểm đó? A. 1 B. 0 C. 2 D. Vô số
Câu 27: Cho hình chóp S.ABCD. Giao tuyến của hai mặt phẳng (SAB) và (SBC) là đường thẳng A. SA B. SD C. SB D. AC
Câu 28: Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Giao tuyến của hai mặt phẳng (SAD)
và (SBC) là đường thẳng A. SA B. SB C. SC D. SO
Câu 29: Cho tứ diện ABCD có M, N lần lượt là các điểm thuộc cạnh BC và BD sao cho MN không song
song CD. Gọi K là giao điểm của MN và (ACD). Khẳng định nào sau đây đúng?
A. K là giao của CM và DN
B. K là giao MN và AC
C. K là giao của MN và AD
D. K là giao của MN và CD
Câu 30: Cho hình chóp S.ABCD có đáy là hình bình hành. M, N lần lượt là trung điểm của BC và SD.
Giao tuyến của hai mặt phẳng (AMN) và (SCD) là
A. đường thẳng NI với I là giao điểm giữa SC và MN
B. đường thẳng NI với I là giao điểm giữa SC và AM
C. đường thẳng NI với I là giao điểm giữa CD và AM
D. đường thẳng NI với I là giao điểm giữa CD và MN
Câu 31: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng lần lượt nằm trên hai mặt phẳng phân biệt thì chéo nhau.
B. Hai đường thẳng không có điểm chung thì chéo nhau.
C. Hai đường thẳng chéo nhau thì không có điểm chung.
D. Hai đường thẳng phân biệt không song song thì chéo nhau.
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Trong các cặp đường thẳng sau, cặp đường thẳng nào cắt nhau?
A. AB và CD .
B. AC và BD
C. SB và CD .
D. SD và BC .
Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N , P , Q lần lượt là trug
điểm của các cạnh bên SA , SB , SC , SD ( H .4.27). Tứ giác MNPQ là hình gì?
A. Tứ giác MNPQ là hình bình hành.
B. Tứ giác MNPQ là hình vuông.
C. Tứ giác MNPQ là hình chữ nhật.
D. Tứ giác MNPQ là hình thoi.
Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình thang cạnh đáy AB. Gọi d là giao tuyến của hai
mặt phẳng (SAB)và (SCD). Khẳng định nào sau đây đúng?
A. d qua S và song song với BC.
B. d qua S và song song với AD
C. d qua S và song song với AB.
D. d qua S và song song với BD.
Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là CD . Gọi M là trung điểm của
SA , N là giao điểm của cạnh SB và mặt phẳng (MCD) . Mệnh đề nào sau đây đúng?
A. MN và SD cắt nhau.
B. MN / /CD .
C. MN và SC cắt nhau.
D. MN và CD chéo nhau.
II. PHẦN TỰ LUẬN (3 điểm - gồm 04 câu: từ câu 36 đến câu 39).
Câu 36 (1,5 điểm): 1  a) Cho os c  = − với
    . Tính sin 2 3 2 x + x − x −
b) Giải phương trình lượng giác sau: sin 2 2 cos sin 1 = 0 tan x + 3 u  + u −u =10
Câu 37 (0,5 điểm): Cho cấp số cộng (u có 1 5 3 
. Tìm số hạng đầu u và công sai d của cấp n ) u + u = 7  1 1 6 số cộng đó.
Câu 38 (1,5 điểm): Cho hình chóp S.ABCD có đáy là hình thang ( AB / /C , D AB CD) .
a) Tìm giao tuyến của mặt phẳng (SAC) và (SBD); (SAB) và (SCD) .
b) Gọi M là một điểm nằm trên cạnh SA sao cho SA = 4SM .
Tìm giao điểm I của đường thẳng BM và mặt phẳng (SCD) .
--------------------------- HẾT --------------------------- HƯỚNG DẪN CHẤM
I. PHẦN TRẮC NGHIỆM BẢNG ĐÁP ÁN 1.B 2.B 3.A 4.D 5.A 6.B 7.D 8.B 9.C 10.B 11.D 12.A 13.A 14.C 15.B 16.C 17.A 18.C 19.B 20.D 21.D 22.B 23.A 24.B 25.A 26.A 27.C 28.D 29.D 30.C 31.C 32.B 33.A 34.C 35.B II. PHẦN TỰ LUẬN Câu 36  1 2 2 a) Vì
     sin  0 sin = 1− = 0,25 2 9 3 2 2 1 4 2 sin2 = 2sin.c    os = 2.( ). − = −   0,25 3  3  9 cos x  0
b) Điều kiện:  (*) 0,25 tan x  − 3
Pt  sin 2x + 2 cos x − sin x −1 = 0  2sin x cos x − sin x + 2 cos x −1 = 0 0,25   sin x = 1 − x = − + k2   0,25 2 
(2 cos x −1)(sin x +1) = 0  1   k   Z cos x =    x =  + k2 2    3 0,25
Kết hợp điều kiện (*)=>Nghiệm của phương trình là x = + k2 3 Câu 37 u
 + u − u =10 u
 + u + 4d − u + 2d =10  0,25 1 5 3 1 ( 1 ) ( 1 )    u + u = 7  u  + u + 5d = 7 1 6  1 ( 1 ) Ta có u  + 2d =10 u  = 36 1 1     . 0,25 2u + 5d = 7  d = 13 − 1 Câu 38
a) Trong mp(ABCD) gọi O = AC BD 0,5
Ta có (SAC) (SBD) = SO 0,25 0,25
S  (SAB)  (SCD)  có AB / /CD
AB  (SAB); CD   (SCD)
 (SAB) (SCD) = (S , / / A , B / / CD)
b) Gọi BM   = I BM  (SCD) = I 0,5
ĐỀ KIỂM TRA GIỮA HỌC KÌ I ĐỀ 8
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
PHẦN 1. TRẮC NGHIỆM (35 CÂU – 7.0 ĐIỂM)) Câu 1: (NB) Cho
    , tìm phát biểu đúng trong các phát biểu sau: 2
A. sin x  0.
B. cos x  0.
C. tan x  0.
D. cot x  0.
Câu 2: (NB) Đổi số đo của góc 5  = sang đơn vị độ. 4 A. 0  = 45 . B. 0  =135 . C. 0  = 225 . D. 0  = 4 − 5 .
Câu 3: (TH) Cho M là điểm biểu diễn góc lượng giác có tia đầu OA và tia cuối OM (như hình vẽ).
Số đo góc lượng giác đó là 3 3 5 5 A. . B. + k 2. C. . D. + k 2. 4 4 4 4
Câu 4: (NB) Công thức nào sau đây là đúng? A. 2 2
cos 2a = cos a − sin . a
B. cos 2a = cos a − sin . a C. 2 2
cos 2a = cos a + sin . a
D. cos 2a = 2cos . a . Câu 5: 1
(NB) Biết sin a = −
giá trị của sin( − a) là 2 1 1 3 3
A. sin( − a) = .
B. sin( − a) = − .
C. sin( − a) = .
D. sin( − a) = − . 2 2 2 2  Câu 6: (TH) Tính cos . 12  2 + 6  2 − 6  6 − 2  1 A. cos = . B. cos = . C. cos = . D. cos = . 12 4 12 4 12 4 12 8 
Câu 7: (TH) Biết tan a = 2 và 0  a  Tính cos . a 2 5 5 3 1 A. cos a = . B. cos a = − . C. cos a = . D. cos a = . 5 5 3 2
Câu 8: (NB) Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y = sin x.
B. y = cos x.
C. y = tan x.
D. y = cot x.
Câu 9: (TH) Hàm số y = cos3x tuần hoàn với chu kỳ bằng bao nhiêu? 2π
A. T = 2π . B. T = .
C. T = 6π .
D. T = 3π . 3 
Câu 10: (NB) Phương trình cos x = cos có nghiệm là 3 2  A. x =
+ k2 , k  . B. x = 
+ k , k  . 3 3   C. x = 
+ k2 , k  . D. x = + k2 , k  . 3 3
Câu 11: (NB) Phương trình sinx = -1 có một nghiệm là gía trị nào sau đây? p A. x = - . B. x = - p . C. x = - p . D. x = - p . 4 6 2 3
Câu 12: (NB) Phương trình tan x = 1 − có nghiệm là p    A. x = - . B. x = − + k . C. x = + k . D. x = + k . 4 4 4 2
Câu 13: (TH) Nghiệm của phương trình 2sin x −1 = 0 được biểu diễn trên đường tròn lượng giác ở hình
bên có thể là những điểm nào? y B D C AO x A E F B
A. Điểm E , điểm D .
B. Điểm C , điểm F . C. Điểm D , điểm C . D. Điểm E , điểm F . 
Câu 14: (TH) Phương trình 2 sin(2x − ) = có nghiệm là 4 2       x = + k2  x = + k    x = + k2  4 4 x = + k  4 A.  . B.  . C. 4 . D.  . 3       x = + k2 = +   =  = − +   x k x k x k 2  4  2  4
Câu 15: (TH) Phương trình cot 3x − 3 = 0 có nghiệm là   k  k  A. x = + k . B. x = + . C. x = + . D. x = + k . 18 18 3 9 3 2
Câu 16: (NB) Cho dãy số (u cho bởi công thức tổng quát 2 *
u = 3 + 4n , n
. Khi đó u bằng n ) n 5 A. 103 . B. 23. C. 503 . D. 97 − . u  = 4 Câu 1
17: (TH) Cho dãy số 
. Năm số hạng đầu của dãy số là u = u + nn 1+ n 4, 5, 6, 7,8. 4,16,32, 64,128.
4, 6, 9,13,18. . D. 4, 5, 7,10,14. A. . B. . C.
Câu 18: (NB) Dãy số nào sau đây là một cấp số cộng? 4, 5, 6, 7,8. 4, 6,10,16, 26. 4, 6, 2,8, 4.. D. 4,5, 7,10,14. A. . B. . C.
Câu 19: (NB) Cho cấp số cộng (u với công sai d. Công thức tính số hạng tổng quát u là n ) n
A. u = u + d .
B. u = u + nd .
C. u = u − (n −1)d .
D. u = u + (n −1)d . n 1 n 1 n 1 n 1
Câu 20: (TH) Cho cấp số cộng 3,1,-1,-3,-5. Tìm công sai của cấp số cộng đó. A. d = 2 . B. d = 2 − .
C. d = 3 . D. d = 5 .
Câu 21: (TH) Cho cấp số cộng (u cho bởi công thức tổng quát *
u = 2n +1, n  Tính tổng 10 số n ) n
hạng đầu của cấp số cộng đó A. S = 12 . B. S = 24 .
C. S = 21. D. S = 2 . 10 10 10 10
Câu 22: (NB) Dãy số nào sau đây là một cấp số nhân? 4, 5, 6, 7,8. 4, 6,8,10,12. 4,8,16,32, 64. D. 4,5, 7,10,14. A. . B. . C.
Câu 23: (NB) Cho cấp số nhân (u với công bội q. Công thức tính số hạng tổng quát u là n ) n A. n 1 u u q − = . B. n
u = u q . C. n 1 u u q − = + .
D. u = u + (n −1)d . n 1 n 1 n 1 n 1 1 1
Câu 24: (TH) Cho cấp số nhân 3,1, , ,... . Tìm số hạng thứ 5 của cấp số nhân đó. 3 9 1 1 1 A. u = . B. u = .
C. u = 3. D. u = . 5 27 5 9 5 5 3
Câu 25: (TH) Cho cấp số nhân (u với q = 2 và u = 3
− Tính tổng 5 số hạng đầu của cấp số nhân đó n ) 1 A. S = 48 − . B. S = 96 − . C. S = 486 − . D. S = 162 . 5 5 5 5
Câu 26: (NB) Cho hình vẽ sau : S M A C N B
Số điểm chung của đường thẳng MN và mặt phẳng (SAB) là A. 0 . B. 1. C. 2 . D. vô số.
Câu 27: (NB) Cho tứ diện ABCD .Tìm giao tuyến của hai mặt phẳng (ABC) và (ABD). A. CD. B. AB. C. AD. D. AC.
Câu 28: (TH)Cho 4 điểm ,
A B, C, D không cùng nằm trên một mặt phẳng. Trên AB, AD lần lượt lấy 2
điểm M , N sao cho MN cắt BD tại I . Điểm I không thuộc mặt phẳng nào sau đây? A. ( ABD) . B. ( BCD) . C. (CMN ) . D. ( ACD) .
Câu 29: (NB) Cho đường thẳng a nằm trên mp (P) đường thẳng b cắt (P) tại O và O không thuộc a.
Vị trí tương đối của a và b là A. chéo nhau. B. cắt nhau. C. song song nhau. D. trùng nhau.
Câu 30: (NB) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm ,
SA SB, SC, SD . Trong các đường thẳng sau, đường thẳng nào không song song với IJ ? A. EF . B. DC . C. AD . D. AB .
Câu 31: (TH) Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N,I lần lượt là trung điểm SD,
SA,AB. Gọi G là trọng tâm tam giác SAB, K là giao điểm của GM với mp(ABCD). K là giao điểm của
GM với đường thẳng nào sau đây: A. AB . B. NI. C. BC . D. DI .
Câu 32: (NB) Cho tứ diện ABCD . M , N lần lượt là trung điểm BC , BD . Đường thẳng MN song song với mặt phẳng A. (BCD . ) B. ( ACD). C. ( ABC).
D. ( ABD).
Câu 33: (NB) Cho hình chóp S.ABCD , đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng
(SAD) và (SBC) là đường thẳng song song với đường thẳng nào sau đây? S A D B C A. BD . B. DC . C. AD . D. AC .
Câu 34: (TH) Cho tứ diện ABCD . Gọi M , N lần lượt là trọng tâm các tam giác ABC và ABD . Xét các khẳng định sau:
( )1 MN //(BCD).
(2) MN //(ACD). (3) MN //(ABD).
Những khẳng định đúng là A. Chỉ có ( ) 1 đúng. B. ( ) 1 và (2) . C. (2) và (3) . D. ( ) 1 và (3) .
Câu 35: (TH) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Gọi M , N theo thứ tự là trọng tâm SAB và SCD
. Khi đó MN song song với mặt phẳng A. (SAC) . B. (SBD) . C. (SAB) . D. ( ABCD) .
PHẦN 2. TỰ LUẬN (3 ĐIỂM) Bài 1. (1,0đ) (VD)
Giải phương trình s i n 5 x = cosx .
Bài 2. (0,5đ) (VDC)
Tiền công khoan giếng ở hai cơ sở được tính như sau:
- Cơ sở A: Giá của mét khoan đầu tiên là 50.000 đồng và kể từ mét khoan thứ hai, giá của mỗi
mét sau tăng thêm 10000 đồng so với giá của mét khoan ngay trước.
- Cơ sở B: Giá của mét khoan đầu tiên là 50.000 đồng và kể từ mét khoan thứ hai, giá của mỗi
mét sau tăng thêm 8% giá của mét khoan ngay trước.
Một người muốn khoan hai cái giếng gồm một cái sâu 20 mét, một cái sâu 30 mét ở hai địa điểm
khác nhau. Hỏi người ấy nên chọn cơ sở khoan giếng nào cho từng giếng để chi phí khoan hai
giếng là ít nhất. Biết chất lượng và thời gian khoan giếng của hai cơ sở là như nhau.
Bài 3. (1,5đ) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , P lần lượt là trung điểm SN 2
của các cạnh SA và SC . Điểm N thuộc cạnh SB sao cho
= . Gọi Q là giao điểm của SB 3
cạnh SD và mặt phẳng (MNP) .
a) (1,0đ) (VD) Xác định giao tuyến của 2 mặt phẳng (MNP) và (ABCD) SQ
b) (0,5) (VDC) Tính tỷ số . SD
ĐỀ KIỂM TRA GIỮA HỌC KÌ I ĐỀ 9
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm):
Câu 1: Cho  là góc lượng giác, trong các khẳng định sau khẳng định nào đúng?
A. sin( − ) = cos. B. sin( − ) = − sin.
C. sin( − ) = sin. D. sin( − ) = −cos.
Câu 2: Cho  thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
A. sin  0; cos  0.B. sin  0; cos  0. C. sin  0; cos  0.D. sin  0; cos  0. 15 sin( )
Câu 3: Giá trị của 6 bằng 1 3 3 A. . B. 1. C. . D. − . 2 2 2
Câu 4: Một chiếc đồng hồ, có kim chỉ giờ OG chỉ số 9 và kim phút OP chỉ số12 . Số đo của góc
lượng giác (OG,OP ) là p 0 0 A.
+ k2p, k Î ¢
- 270 + k360 , k Î ¢ . 2 . B. 9p C. 0 0
270 + k360 , k Î ¢ . D.
+ k2p, k Î ¢ 10 .
Câu 5: Trong các khẳng định sau, khẳng định định nào đúng?
A. sin (a − b) = sin a cosb − cos a sin b .
B. sin (a − b) = sin a cosb + cos a sin b .
C. sin (a − b) = cos a cosb − sin a sin b .
D. sin (a − b) = sin a sin b − cos a cosb .
Câu 6: Trong các khẳng định sau, khẳng định định nào sai?
A. sin 2a = 2sin a cos . a B. 2 2
cos 2a = cos a − sin . a C. 2
cos 2a = 2 cos a +1. D. 2 cos 2a = 1− 2sin . a 4  3 cos = −    Câu 7: Biết 5 và 2
2 . Giá trị sin 2 bằng 24 2 24 −8 A. − . B. . C. − . D. . 5 5 25 25
Câu 8: Cho  là góc lượng giác, trong các khẳng định sau khẳng định nào sai?
A. Tập xác định của hàm số sin là .
B. Tập xác định của hàm số cos là . 
C. Tập xác định của hàm số cotan là { +k | k  }. 2 
D. Tập xác định của hàm số tan là { +k | k  }. 2
Câu 9: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A. y = tan x .
B. y = sin x .
C. y = cot x .
D. y = cos x .
Câu 10: Hàm số nào sau đây là một hàm số chẵn?
A. y = cos x − x .
B. y = cos x +1. C. 2
y = sin x + x .D. y = sin 2x .
Câu 11: Tập giá trị của hàm số y = 1− sin x là A.  1 − ;  1 . B. 0; 2. C.  1 − ;2. D. 1;  3 .
Câu 12: Nghiệm của phương trình cos x = 0 là p p A. x =
+ kp, k Î ¢ . B. x = ± + kp, k Î ¢ . 2 6 p p C. x =
+ k2p, k Î ¢ . D. x = + kp, k Î ¢ . 3 6
Câu 13: Chọn khẳng định đúng trong các khẳng định sau
A. Phương trình cos x = m có nghiệm khi và chỉ khi | m | 1 .
B. Phương trình cos x = m có nghiệm khi và chỉ khi | m | 1 .
C. Phương trình cos x = m có nghiệm khi và chỉ khi m  1.
D. Phương trình cos x = m có nghiệm khi và chỉ khi m  1.
Câu 14: Nghiệm của phương trình tan x = 1 − là   A. x = −
+ k (k  ) . x = + k2 k  . 4 B. ( ) 3  5 C. x =
+ k2 (k  ) . x =  + k2 k  . 4 D. ( ) 6   
Câu 15: Tìm tất cả các nghiệm của phương trình sin x + = sinx   .  3    A. x =
+ k (k  ) . B. x = − + k2 (k  ) . 3 6  5 C. x =
+ k2 (k  ) . D. x =
+ k2 (k  ) . 3 6
Câu 16: Dãy số (u ) , n
  * được gọi là dãy số tăng khi n A. uu . B. uu . C. uu . D. uu . n 1 + n n 1 + n n 1 + n n 1 + n
Câu 17: Dãy số nào dưới đây là dãy các số nguyên chia hết cho 3 và sắp xếp theo thứ tự tăng dần?
A. 9 , 3 , 15 , 0 .
B. 1, 2 , 3 , 5 , 7 .
C. 0 , 3 , 6 , 9 . D. 1, 3 , 5 , 7 .
Câu 18: Khẳng định nào sau đây là sai?
A. Một dãy số tăng thì bị chặn dưới.
B. Một dãy số giảm thì bị chặn trên.
C. Một dãy số bị chặn thì phải tăng hoặc giảm. D. Một dãy số không đổi thì bị chặn. Câu 19: n
Cho dãy số (u ), n  * biết u = . Tính u . n n n +1 5 5 1 1 16 A. u = . B. u = . C. u = . D. u = . 5 6 5 5 5 6 5 25
Câu 20: Cho dãy số (u ),n * có 5 số hạng đầu là 1 1 3 1 5 ; ; ; ;
;... Số hạng tổng quát của dãy số n 2 2 8 4 32 (u là n ) n −1 n n 1 A. u = . B. u = . C. u = . D. u = n n 2n n n + 2 n 2n n + . 1
Câu 21: Cho cấp số cộng (u với công sai d có công thức truy hồi là n ) A. u = u
+ d , với n  2. B. u = u
− d , với n  2. n n 1 − n n 1 −
C. u = u .d , với n  2. D. u = u
+ d , với n  2.. n n 1 − n n 1 +
Câu 22: Dãy số nào sau đây là cấp số cộng? A. 2;5;8;11;14... B. 2; 4;8;12;14... C. 1 − ;3;5;7... D. 2; 4;8;16;...
Câu 23: Cho cấp số cộng (u với công sai d . Chọn khẳng định đúng. n )
A. u = u + 4d .
B. u = u − 4d .
C. u = u + 5d .
D. u = 5u + d . 5 1 5 1 5 1 5 1
Câu 24: Cho cấp số cộng (u , biết u = 2 và công sai d = 3
− . Khẳng định nào sau đây đúng? n ) 1 A. u = − 4. B. u = 4. C. u =−1. D. u =1. 3 3 3 3
Câu 25: Cho cấp số cộng (u có số hạng đầu u = 5
− và công sai d = 3. Số 94 là số hạng thứ mấy của n ) 1 cấp số cộng? A. 33. B. 20. C. 35. D. 34.
Câu 26: Cho dãy số (u là một cấp số nhân có số hạng đầu u và công bội q . Đẳng thức nào sau đây n ) 1 đúng?
A. u = u + n −1 q , (n  2) . B. n 1 u u q − = , (n  2) . n 1 ( ) n 1 n− u C. u = . q u , (n  2) . D. 1 u = , (n  2) . n ( ) 1 1 n n 1 q −
Câu 27: Cho cấp số nhân (u , biết u = 3 và công bội q = 2
− . Khẳng định nào sau đây đúng? n ) 1 A. u = 48. B. u = − 48. C. u =− 96. D. u =96. 5 5 5 5
Câu 28: Cho dãy số (u là một cấp số nhân có số hạng đầu u và công bội q . Tổng của n số hạng đầu n ) 1 có công thức là u 1 n − q u ( n 1 1 q − − u ( n 1 1 q − − u ( n 1 1 q − + 1 ) 1 ) 1 ) 1 ( ) A. S = S = S = S = n 1− . B. q n 1− . C. q n q − . D. 1 n 1+ . q Câu 29: 1
Cho dãy số (u là một cấp số nhân với u = ;u = 1
− 6 . Công bội của CSN là n ) 1 6 2 1 1 A. q = 2 − .
B. q = 2 . C. q = . D. q = − . 4 4
Câu 30: Tìm x để các số 2; 8; x; 128 theo thứ tự đó lập thành một cấp số nhân. A. x = 14. B. x = 32. C. x = 64. D. x = 68.
Câu 31: Trong mẫu số liệu ghép nhóm, độ dài của nhóm 1;10) bằng bao nhiêu? A. 8. B. 5. C. 10. D. 9.
Câu 32: Mẫu số liệu cho dưới dạng bảng tần số của các nhóm số liệu được gọi là
A. Mẫu số liệu bảng.
B. Mẫu số liệu ghép nhóm. C. Số trung vị. D. Mốt.
Câu 33: Kết quả khảo sát cân nặng của 25 quả táo ở lô hàng B được cho ở bảng sau: Cân nặng (g) [150;155) [155;160) [160;165) [165;170) [170;175)
Số quả táo ở lô hàng 1 3 7 10 4 B
Mẫu số liệu này có bao nhiêu nhóm? A. 5. B. 6. C. 7. D. 25.
Câu 34: Trong hoạt động Ngày chủ nhật xanh, đoàn thanh niên lớp 11A1 tiến hành trồng cây. Kết quả sau
hoạt động được ghi lại ở bảng sau: Số cây
1;8) 8;15) 15;22) 22;29) 29;36) Số học sinh 7 15 6 10 3
Hãy tìm số trung bình của mẫu số liệu ghép nhóm trên. A. 16,3. B. 15,5. C. 16,2. D. 26.
Câu 35: Chiều cao của học sinh khối lớp 11 của trường THPT Đơn Dương, ta được mẫu số liệu sau: Chiều cao (cm) Số học sinh [150;152) 20 [152;154) 35 [154;156) 45 [156;158) 60 [158;160) 30 [160;162) 15
Tần số của nhóm 156;158) bằng bao nhiêu? A. 15. B. 60. C. 45. D. 30.
II. PHẦN TỰ LUẬN (3 điểm):
Bài 1 (1,0 điểm).
Giải phương trình lượng giác sin2x + cos x = 0 .
Bài 2 (1,5 điểm). u  + u =10 + u
A(0.5 điểm) Cho cấp số cộng (u có 1 5 3 
. Tìm số hạng đầu u và công sai d của cấp số cộng n ) u = 7 − u  1 1 6 đó.
b) (1,0 điểm) Giả sử rằng một tế bào ung thư cứ sau một giờ sẽ nhân đôi một lần. Hỏi nếu ban đầu có 8 tế
bào ung thư thì sau một ngày đêm số tế bào sẽ là bao nhiêu?
Bài 3 (0.5 điểm). Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết
quả như bảng bên. Tìm tứ phân vị thứ ba cho mẫu số liệu ghép nhóm
………………Hết………………. HƯỚNG DẪN CHẤM
I. PHẦN TRẮC NGHIỆM BẢNG ĐÁP ÁN 1.C 2.C 3.B 4.A 5.A 6.C 7.C 8.C 9.B 10.B 11.B 12.A 13.A 14.A 15.A 16.A 17.C 18.D 19.A 20.C 21.A 22.A 23.A 24.A 25.D 26.B 27.A 28.A 29.A 30.B 31.D 32.B 33.A 34.A 35.B II. PHẦN TỰ LUẬN Câu 1 = 0,25 đ -
Biến đổi cos x(2sin x +1) 0 cos x = 0 0,25 đ pt 2 sin x +1 = 0 - Biến đổi 0,25 đ -
Giải đúng nghiệm phương trình cos x = 0  x = + k 2 0,25 đ x = − + k2 6 -
Giải đúng nghiệm phương trình 2sin x +1 = 0  7 x = + k2 6 Câu 2a u  + u =10 + u u
 + u + 4d − u + 2d =10  1 5 3 1 ( 1 ) ( 1 )    0,25 đ u = 7 − uu  + u + 5d = 7 1 6  1 ( 1 ) Ta có u  + 2d =10 u  = 36 1 1     . 0,25 đ 2u + 5d = 7  d = 13 − 1 Câu 2b -
Một ngày đêm có 24 giờ nên số lần nhân đôi của TBUT là 24 0,25đ -
Sau 24 lần nhân đôi thì một TBUT sẽ được là 24 2 = 16.777.216 0,5đ -
Vậy 8 TBUT sau một ngày đêm ta có số TBUT là 134.217.728 0,25đ Câu 3 x + x
Tứ phân vị thứ ba Q là 150
151 . Do x , x đều thuộc nhóm [170;175) 3 2 150 151
nên tứ phân vị thứ ba thuộc nhóm [170;175). Do đó 0,25đ
p = 5; a = 170; m = 41; m + m + m + m = 18 + 28 + 35 + 43 = 124; a − a = 5 5 5 1 2 3 4 6 5 0,25đ 600 −124 4 Q = 170 + 5 =173.17 3 41
ĐỀ KIỂM TRA GIỮA HỌC KÌ I ĐỀ 10
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7 điểm).
Câu 1: Trên đường tròn lượng giác gốc A , biết góc lượng giác (O ,
A OM ) có số đo bằng 0 410 , điểm
M nằm ở góc phần tư thứ mấy? A. I . B. III . C. II . D. IV .
Câu 2: Đường tròn lượng giác có bán kính bằng:  A. 2 . B. 1. C. . D.  . 2
Câu 3: Khi quy đổi 1o ra đơn vị radian, ta được kết quả là 180   A.  rad. B. rad.  C. rad. D. rad. 180 360
Câu 4: Mệnh đề nào sau đây sai?
A. sin( +  ) = sin.
B. cot( +  ) = cot.
C. cos ( + ) = − cos .
D. tan( +  ) = tan.  Câu 5: 4 Cho sin = ,
    . Tính cos . 5 2 3 1 3 1 A. cos = − . B. cos = . C. cos = . D. cos = . 5 5 5 5
Câu 6: Trong các công thức dưới đây, công thức nào đúng? a + b a − b a + b a − b
A. cos a − cos b = 2 cos cos .
B. cos a − cos b = 2sin sin . 2 2 2 2 a + b a − b a + b a − b
C. cos a − cos b = 2 − cos cos .
D. cos a − cos b = 2 − sin sin . 2 2 2 2
Câu 7: Trong các công thức dưới đây, công thức nào đúng?
A. cos (a + b) = sin .
a cos b − cos .
a sin b .
B. cos (a + b) = sin . a cos b + cos . a sin b .
C. cos (a + b) = cos . a cos b + sin .
a sin b .
D. cos (a + b) = cos .
a cos b − sin . a sin b . Câu 8: 1 Cho cos = . Tính cos2 . 3 7 1 7 2 A. cos2 = . B. cos2 = . C. cos2 = − . D. cos2 = . 9 3 9 3      Câu 9:
Rút gọn biểu thức T = sin + x − sin − x   
 ta được kết quả là  3   3  3
A. T = 3 cos x .
B. T = sin x . C. .
D. T = sin 2x . 2 Câu 10:
Tập xác định hàm số y = sin x là:
A. D = [ −1;1]. B. D = .    C. D =
\ k , k  . D. D = \ k , k  .  2 
Câu 11: Mệnh đề nào sau đây là đúng?
A. Hàm số y = sin x là hàm số chẵn.
B. Hàm số y = cos x là hàm số chẵn.
C. Hàm số y = tan x là hàm số = chẵn. D. Hàm số y
cot x là hàm số chẵn.
Câu 12: Cho hàm số y = f (x) có đồ thị như hình bên dưới. Mệnh đề nào sau đây là đúng?        
A. Hàm số đồng biến trên 3 − ; − .  
B. Hàm số đồng biến trên 3 ; .    2 2   2 2        
C. Hàm số đồng biến trên − ; .  
D. Hàm số đồng biến trên − ; 0 .    2 2   2    Câu 13:
Hàm số y = sin 2x − 
 đồng biến trên khoảng nào trong các khoảng sau đây?  4    3    3          A. − ;   . B. − ;   . C. − ;   . D. − ;   .  8 8   4 4   2 2   4 4  Câu 14:
Phương trình nào sau đây có nghiệm? 1 A. sin x = . B. sin x = 2 − .
C. 2 sin x = 2. D. cos x = 2. 2 Câu 15:
Phương trình sin x = sin có tập nghiệm là:
A. S =  + k2 | k  .
B. S =  + k | k  .
C. S =  + k2 ; 
− + k2 | k  .
D. S =  + k2 ; − + k2 | k  . Câu 16:
Phương trình cos 2x = 1 có nghiệm là:  k 
A. x = k , k  . B. x =
+ k2 , k  . C. x = , k  . D. x =
+ k2 , k  . 2 2 4
Câu 17: Tìm tổng nghiệm dương bé nhất và nghiệm âm lớn nhất của phương trình sin x = cos(2x) .   2 A. − . B. 0 . C. . D. . 3 4 3 Câu 18:
Cho dãy số ( u ) với u = ( 5
− )n . Mệnh đề nào sau đây đúng? n n A. u = 625 − .
B. u = 20 .
C. u = 625 . D. u = 20 − . 4 4 4 4 Câu 19:
Cho dãy số (u ) . Mệnh đề nào sau đây đúng? n A. Nếu * uu , n  
thì (u ) là dãy số giảm. n 1 + n n B. Nếu * uu , n  
thì (u ) là dãy số giảm. n 1 + n n C. Nếu * uu , n  
thì (u ) là dãy số giảm. n 1 + n n D. Nếu * uu , n  
thì (u ) là dãy số giảm. n 1 + n n
Câu 20: Trong các dãy số (u cho bởi số hạng tổng quát u sau, dãy số nào là dãy số tăng? n ) n 1 1 n + 5 2n −1 A. u = . B. u = . C. u = . u = . n 2n n n n 3n + D. 1 n n + 1 Câu 21:
Cho cấp số cộng (u
có u = 3 và công sai d = 2 . Số hạng tổng quát của cấp số cộng (u là: n ) n ) 1
A. u = 3n + 2 .
B. u = 3n − 2 .
C. u = 2n − 2 .
D. u = 2n +1. n n n n Câu 22: Cấp số cộng (u
có số hạng đầu u và công sai d u được xác định n )
thì tổng n số hạng đầu của cấp số cộng ( n ) 1 bởi công thức n(n +1) n(n +1)
A. S = nu +
d . B. S = nu − d . n 1 2 n 1 2 n(n −1) n(n −1)
C. S = nu −
d . D. S = nu + d . n 1 2 n 1 2 Câu 23: Cho dãy số (u
là một cấp số cộng với công sai d , ta có công thức truy hồi n ) A. * u
= u .d, n . B. * u
= u + d, n . n 1 + n n 1 + n u C. n * u = , n  . D. * u
= u − d, n . n 1 + + d n 1 n Câu 24:
Tìm x để ba số thực 1; ;
x 5 theo thứ tự lập thành một cấp số cộng.
A. x = 1.
B. x = 0 .
C. x = 2 .
D. x = 3 .
Câu 25: Tìm tổng S của 100 số nguyên dương đầu tiên và đều chia 5 dư 1. A. 24353. B. 25100 . C. 50200 . D. 5001.
Câu 26: Cho cấp số nhân (u có công bội .
q Mệnh đề nào sau đây đúng? n ) A. n 1 u u .q − = (n  2) . B. n 1 u u .q + =
(n  2) . C. u = u . n
q (n  2) . D. n
u = q (n  2) . n 1 n 1 n 1 n
Câu 27: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân? A. 2; 4; 8; 16; B. 1; −1; 1; −1; C. 2 2 2 2 1 ; 2 ; 3 ; 4 ; D. 3 5 7 ;
a a ; a ; a ; (a  0).
Câu 28: Cho cấp số nhân (u với u = 2 − và q = 5.
− Viết bốn số hạng đầu tiên của cấp số nhân (u . n ) n ) 1 A. 2
− ; 10; 50; − 250. B. 2 − ; 10; − 50; 250. C. 2
− ; −10; − 50; − 250. D. 2 − ; 10; 50; 250.
Câu 29: Cho cấp số nhân (u có các số hạng lần lượt là 3; 9; 27; 81; .... Tìm số hạng tổng quát u của n ) n cấp số nhân (u . n ) A. n 1 u 3 − = . B. u = 3 . n C. n 1 u 3 + = . D. u = 3 + 3 . n n n n n
Câu 30: Bác Bình gửi tiết kiệm 500 triệu đồng kì hạn 1 tháng với lãi suất 6% một năm theo hình thức lãi
suất kép. Nếu sau đúng một năm bác Bình mới đến ngân hàng rút tiền thì số tiền lãi Bác Bình có
được gần nhất với số nào sau đây.
A. 63, 58 (triệu đồng).
B. 60,15 triệu đồng.
C. 60 triệu đồng.
D. 62, 58 triệu đồng.
Câu 31: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
0;20) 20;40) 40;60) 60;80) 80;100) Số học sinh 5 9 12 10 6
Giá trị đại diện của nhóm [20;40) là A. 10. B. 20. C. 30. D. 40.
Câu 32: Tuổi thọ (năm) của 50 bình ắc quy ô tô thu được mẫu số liệu ghép nhóm sau: Tuổi thọ (năm)
2;2,5) 2,5;3) 3;3,5) 3,5;4) 4;4,5) 4,5;5) Tần số 4 9 14 11 7 5
Mẫu số liệu ghép nhóm này có số mốt bằng A. 14. B. 9. C. 7. D. 5.
Câu 33: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
15;20) 20;25) 25;30) 30;35) 35;40) 40;45) 45;50) Số nhân viên 6 14 25 37 21 13 9
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 phút đến dưới 20 phút? A. 6. B. 9. C. 14. D. 13.
Câu 34: Cho mẫu số liệu ghép nhóm sau: Nhóm a ;a . a ;a . a ;a k k 1 + ) i i 1 + ) 1 2 ) Tần số m . m . m 1 i k a + a
Với n = m + m + ... + m là cỡ mẫu và i i 1 x + =
( i = 1,...k ) là giá trị đại diện của nhóm 1 2 k i 2
a ;a . Khi đó công thức tính số trung bình cộng của mẫu số liệu ghép nhóm trên là: i i 1 + ) n (m x m x 1 1 ) ( k k ) A. x = . B. x = . m x ++ m x n 1 1 k k
m x −− m x m x ++ m x C. 1 1 k k x = . D. 1 1 k k x = n n
Câu 35: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Thời gian (phút)
0;20) 20;40) 40;60) 60;80) 80;100) Số học sinh 5 9 12 10 6 Nhóm chứa trung vị là A. [0; 200) . B. [20; 40) . C. [40; 60) . D. [60;80) .
II. PHẦN TỰ LUẬN (3 điểm).
Bài 1. (1,0 điểm). 1
a) Tìm tập xác định của hàm số. y = 1+ . cos x 1
b) Cho dãy số (u ), biết u = u . n n
n + . Viết ba số hạng đầu tiên của dãy số ( n ) 1 x
Bài 2. (1 điểm). Tìm m để phương trình để 2 2sin
+ 3 sin x − 5m = 0 luôn có nghiệm. 2
Bài 3. (1 điểm). Một đa giác có chu vi là 158cm , độ dài các cạnh của nó lập thành một cấp số
cộng. Biết cạnh lớn nhất có độ dài là 44cm . Tìm số cạnh của đa giác đó?
……………… HẾT ……………… ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM: 0,2 điểm / 1 câu trả lời đúng. Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 A B C A A D D C B B
Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16 Câu 17 Câu 18 Câu 19 Câu 20 B D A A D A A C C D
Câu 21 Câu 22 Câu 23 Câu 24 Câu 25 Câu 26 Câu 27 Câu 28 Câu 29 Câu 30 D D B D A A C B B A
Câu 31 Câu 32 Câu 33 Câu 34 Câu 35 C A A D C II. PHẦN TỰ LUẬN Câu Nội dung Điểm 1
a. Tìm tập xác định của hàm số y = 1+ . cos x
Điều kiện xác định của hàm số là: cos x  1 − 0,25
hay x   + k2 ( k  ). 1
Tập xác định của hàm số y = D =
\  + k 2 | k 0,25 1+ là   cos x 1
b. Cho dãy số (u ), biết u = u . n n n 1
n + . Viết ba số hạng đầu tiên của dãy số ( ) 1 1 u = 1 2 0,25 0,25 1 1 1
Vậy ba số hạng đầu tiên của dãy số (u là: ; ; . n ) 2 3 4 x
Tìm m để phương trình để 2 2sin
+ 3 sin x − 5m = 0 luôn có nghiệm. 2 x 2 2sin
+ 3 sin x − 5m = 0 2 0.25
 3 sin x − cos x − 5m +1 = 0    2  2sin x − − 5m +1 = 0    6  0.25    5m −1 Hay sin x − =    6  2    0.25 Mà 1 −  sin x − 1    6  5m −1
Nên để phương trình trên luôn có nghiệm khi 1 −  1 2 0.25 1 3  −  m  5 5 3
Một đa giác có chu vi là 158cm , độ dài các cạnh của nó lập thành một cấp số cộng. Biết cạnh lớn
nhất có độ dài là 44cm . Tìm số cạnh của đa giác đó?
Giả sử đa giác có n cạnh ( n  , n  3 ).
Gọi độ dài các cạnh của đa giác là u ,u ,u ,...,u theo thứ tự lập thành cấp số cộng và 1 2 3 n 0,25
cạnh lớn nhất có độ dài là nên 0  u u u ...u = 44cm . 1 2 3 n (u +u n 0,25 1 n )
Vì đa giác có chu vi là 158cm nên S = u + u +u +...+u = n 1 2 3 n 2 (u + 44 n 1 ) 316 hay 158 = suy ra n = 2 u + 44 1
Mà n  nên u + 44 là ước nguyên dương của 316 hay u + 44 2; 4; 79; 158; 316 0.25 1   1 u + 44 2 4 79 158 316 0.25 1 u u  0 u  0 (loại u = 35 u = 114 (không thỏa u = 272 (không thỏa 1 1 1 1 1 1 (loại) )
mãn vì u = 44cm )
mãn vì u = 44cm ) n n 316
Vậy đa giác đã cho có n = = 4 cạnh. 79
ĐỀ KIỂM TRA GIỮA HỌC KÌ I ĐỀ 11
MÔN: TOÁN - KHỐI LỚP 11 - KNTT
Thời gian làm bài: 90 phút (không tính thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (7,0 điểm).
Câu 1: Cung có số đo 250 thì có số đo theo đơn vị là radian là 35 25 25 25 A. . B. . C. . D. . 18 18 12 9 
Câu 2: Cho góc  thỏa mãn 0   
. Khẳng định nào sau đây đúng? 2 A. sin  0 . B. cot  0 .
C. sin  0 .
D. cos  0 .
Câu 3: Khẳng định nào sau đây đúng? A. 2 2 sin  + cos  = 1. B. 2 2 sin  + cos  = 0 . C. 2 2 sin  + cos  = 2 . D. 2 2 sin  + cos  = 1 − .
Câu 4: sin 2a bằng A. 2sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a .
Câu 5: Chu kỳ tuần hoàn của hàm số y = sin x là
A. k 2 (k  ) . B. . C.  . D. 2 . 2
Câu 6: Tập giá trị của hàm số y = cos 2023x là  1 1  A.  1 − ;  1 . B. ( 1 − ;1) . C.  2 − 023;202  3 . D. − ;   .  2 2
Câu 7: Nghiệm của phương trình tan x =1 là  3 A. x =
+ k , k  . B. x =
+ k , k  . 4 4 
C. x = k , k  . D. x = + k ,k  . 2
Câu 8: Cho dãy số (u xác định bởi u = 2n −1 với n 1. Số hạng u bằng n ) n 1 A. 1. B. 2 . C. 3. D. 4 .
Câu 9: Dãy số nào sau đây là dãy tăng? A. 1;3;5; 7;9 . B. 10;8;6; 4; 2 . C. 1;5;3; 7;9 . D. 1;1;1;1;1 .
Câu 10: Cho cấp số cộng (u với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 4 . C. 6 . D. 8 .
Câu 11: Trong các dãy số (u ) sau, dãy số nào bị chặn? n 2 A. 2 u = n +1. B. u = 1− .
C. u = n + sin n . D. 2 u = sin n . n n 3n n n
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a .
Câu 13: Dãy số nào sau đây là cấp số nhân? A. 1, 2 − , 4 , 8 , 16 − .
B. 2 , 22 , 222 , 22222 . C. 3 , 6 , 12 , 24 .
D. x , 2x , 3x , 4x với x  0 .
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7 − ; 1 − 3) . C. (13; 7) . D. ( 1 − 3; − 7) .
Câu 15: Cho cấp số nhân (u u = 3 q = − n ) với và công bội . Tìm giá trị của 1 2
n biết số hạng tổng quát = 1536 − n u . A. n = 8 . B. n = 9 . C. n = 257 . D. n = 10 .
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 150;152) 5 2 152;154) 18 3 154;156) 40 4 156;158) 26 5 158;160) 8 6 160;162) 3 N = 100
Giá trị đại diện của nhóm thứ tư là A. 156, 5 . B. 157 . C. 157, 5 . D. 158 .
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) .
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) .
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13). D. 13; 15) .
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7, 6 . C. 8 . D. 8, 6 .  Câu 21: 4 Biết sin − = và 3     . Giá trị cos bằng 5 2 3 3 3 9 A. − . B. . C.  . D. . 5 5 5 5    
Câu 22: Giá trị của biểu thức A = sin +   là  3 4  6 − 2 6 + 2 − 6 + 2 − 6 − 2 A. . B. . C. . D. . 4 4 4 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2. C. y = 2 − sin x . D. y = 2 − cos x + 2 .
Câu 24: Tập nghiệm của phương trình cos x = 1 − là     
A. S =  + k2 | k  . B. S = −
+ k2 |k  .  2   2 
C. S = k2 |k  .
D. S =  + k2 | k  . Câu 25: 1 1 1 Cho dãy số 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là nn 1 − n 1   1  1 (− ) 1 A. u = . B. u = . C. u = . D. u = . n      3  n  3  n 3n n n 1 3 −
Câu 26: Cho cấp số cộng (u có u = 2; d = 5
− . Số hạng thứ 20 của cấp số cộng là n ) 1 A. 93 − . B. 10 . C. 93 . D. 23.
Câu 27: Cho cấp số nhân ( x có x = 3 − và x = 27. −
Tính số hạng đầu x và công bội q của cấp số n ) 2 4 1 nhân. A. x = 1 − ,q = 3
− hoặc x =1,q = 3. B. x = 1
− ,q = 3 hoặc x =1,q = 3 − . 1 1 1 1
C. x = 3, q = 1
− hoặc x = 3 − ,q =1.
D. x = 3, q = 1 hoặc x = 3 − ,q = 1 − . 1 1 1 1
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6, 5 . B. 7, 5 . C. 7, 25 . D. 8 .
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng): Doanh thu 5;7) 7;9) 9;1 )1 11;13) 13;15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13). D. 13; 15) .
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. 30;45) . B. 15;30) . C. 45;60) . D. 60;75) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa bởi   
hàm số h(t) = 5sin t
 , trong đó h(t ) là độ cao tính bằng cetimét trên mực nước biển trung  5 
bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc phao lại ở
vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5 giây. B. 10 giây. C. 2, 5 giây. D. 20 giây.   
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3 3 sin 3x − =   bằng  4  2     A. . B. − . C. . D. − . 9 6 6 9
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 .
Câu 34: Một cấp số nhân có số hạng đầu u = 3, công bội q = 2 . Biết S = 765 . Tìm n . 1 n A. n = 8 . B. n = 9 . C. n = 6 . D. n = 7 .
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
15;20) 20;25) 25;30) 30;35) 35;40) 40;45) 45;50) Số nhân 7 14 25 37 21 14 10 viên
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 1360 800 1360 3280 A. Q = ,Q = . B. Q = ,Q = . 1 3 37 21 1 3 37 83 136 3280 136 800 C. Q = ,Q = . D. Q = , Q = . 1 3 5 83 1 3 5 21
II. PHẦN TỰ LUẬN (3,0 điểm).
Câu 36: (1,0 điểm)   
a. Giải phương trình cot x + = 3   .  3  2 b. Cho sin  =
, tính giá trị của biểu thức P = (1− 3cos)(1+ 3cos) . 3 Câu 37: (1,0 điểm)
Giải phương trình cos3x − sin 2x = 0 .   
Câu 38: (1,0 điểm) Giải phương trình sin x = cos x +   .  3 
Câu 39: (0,5 điểm) Một công ty khoan giếng đưa ra định mức giá như sau: Giá từ mét khoan đầu tiên là
100000 đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm 30000 đồng so với giá của mét
khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng
sâu 20 mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia
đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
-------------- HẾT --------------
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM (7,0 điểm). BẢNG ĐÁP ÁN 1.B 2.A 3.A 4.A 5.D 6.C 7.A 8.A 9.A 10.A 11.D 12.B 13.C 14.C 15.D 16.B 17.A 18.A 19.B 20.C 21.A 22.B 23.C 24.D 25.B 26.A 27.B 28.C 29.B 30.A 31.B 32.C 33.A 34.A 35.D ĐÁP ÁN CHI TIẾT
Câu 1: Cung có số đo 250 thì có số đo theo đơn vị là radian là 35 25 25 25 A. . B. . C. . D. . 18 18 12 9 Lời giải Chọn B 0 250 . 25.
Số đo theo đơn vị là radian là = . 0 180 18 
Câu 2: Cho góc  thỏa mãn 0   
. Khẳng định nào sau đây đúng? 2 A. sin  0 . B. cot  0 .
C. sin  0 .
D. cos  0 . Lời giải Chọn A
Câu 3: Khẳng định nào sau đây đúng? A. 2 2 sin  + cos  = 1. B. 2 2 sin  + cos  = 0 . C. 2 2 sin  + cos  = 2 . D. 2 2 sin  + cos  = 1 − . Lời giải Chọn A Câu 4: sin 2a bằng A. 2sin .
a cos a . B. sin a .
C. cos a .
D. cos 2a . Lời giải Chọn A
Câu 5: Chu kỳ tuần hoàn của hàm số y = sin x là
A. k 2 (k  ) . B. . C.  . D. 2 . 2 Lời giải Chọn D
Câu 6: Tập giá trị của hàm số y = cos 2023x là  1 1  A.  1 − ;  1 . B. ( 1 − ;1) . C.  2 − 023;202  3 . D. − ;   .  2 2 Lời giải Chọn C
Câu 7: Nghiệm của phương trình tan x =1 là  3 A. x =
+ k , k  . B. x =
+ k , k  . 4 4 
C. x = k , k  . D. x = + k ,k  . 2 Lời giải Chọn A
Ta có tan x = 1  x = + k , k  4
Câu 8: Cho dãy số (u xác định bởi u = 2n −1 với n 1. Số hạng u bằng n ) n 1 A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn A
Ta có: u = 2.1−1 = 1 1
Câu 9: Dãy số nào sau đây là dãy tăng? A. 1;3;5; 7;9 . B. 10;8;6; 4; 2 . C. 1;5;3; 7;9 . D. 1;1;1;1;1 . Lời giải Chọn A
Câu 10: Cho cấp số cộng (u với u = 3 và u = 5. Công sai của cấp số cộng đã cho bằng n ) 1 2 A. 2 . B. 4 . C. 6 . D. 8 . Lời giải Chọn A
Công sai của cấp số cộng d = u − u = 5 − 3 = 2 . 2 1
Câu 11: Trong các dãy số (u ) sau, dãy số nào bị chặn? n 2 A. 2 u = n +1. B. u = 1− .
C. u = n + sin n . D. 2 u = sin n . n n 3n n n Lời giải Chọn D Với mọi * n  N , ta có 2 1
−  sin n 1 0  sin n 1 nên dãy số đã cho bị chặn.
Phân tích phương án nhiễu:
A. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
B. Sai do dãy số này bị chặn trên nhưng không bị chặn dưới.
C. Sai do dãy số này bị chặn dưới nhưng không bị chặn trên.
Câu 12: Cho a , b , c là ba số hạng liên tiếp của một cấp số cộng. Đẳng thức nào sau đây đúng? A. 2 b = ac .
B. 2b = a + c .
C. a + b = 2c .
D. b + c = 2a . Lời giải Chọn B
Phân tích phương án nhiễu:
A: Sai vì nhớ nhầm của cấp số nhân.
B, C: Sai vì không phân biệt thứ tự của các số hạng của cấp số cộng.
Câu 13: Dãy số nào sau đây là cấp số nhân? A. 1, 2 − , 4 , 8 , 16 − .
B. 2 , 22 , 222 , 22222 . C. 3 , 6 , 12 , 24 .
D. x , 2x , 3x , 4x với x  0 . Lời giải Chọn C
6 = 3.2 , 12 = 6.2 , 24 = 12.2 .
Phân tích phương án nhiễu:
A. Sai do thay u : u = 2
− nhưng u :u = 2. 2 1 4 3
B. Sai do học sinh lầm tưởng đây là cấp số nhân với công bội q = 11 .
D. Sai do dãy số trên là cấp số cộng, không phải cấp số nhân.
Câu 14: Cho cấp số cộng (u biết u = 48 và u = 83 . Tìm cặp (u ; d . 1 ) n ) 6 11 A. (7;13) . B. ( 7 − ; 1 − 3) . C. (13; 7) . D. ( 1 − 3; − 7) . Lời giải Chọn C u  = 48 u  + 5d = 48 u  =13 Ta có: 6  1   1   . u = 83  u +10d = 83  d = 7 11 1
Phân tích phương án nhiễu:
A. Sai vì đặt nhầm thứ tự của yêu cầu bài toán.
B. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình và đặt nhầm thứ tự
của yêu cầu bài toán.
D. Sai vì sử dụng máy tính giải hệ nhập sai hệ số tự do trong phương trình.
Câu 15: Cho cấp số nhân (u với u = 3 và công bội q = − . Tìm giá trị của n ) 1 2
n biết số hạng tổng quát = 1536 − n u ? A. n = 8 . B. n = 9 . C. n = 257 . D. n = 10 . Lời giải Chọn D n 1 − n 1 − u = 1 − 536  u q = −  − = − n 1. 1536 3.( 2) 1536 . n 1 −  ( 2 − ) = 5 − 12 = ( 2 − )9  n =10 .
Phân tích phương án nhiễu: ( n 2 − ) n− n
A. Sai do tính (− ) 1 2 = 5 − 12  = 51 − 2  ( 2 − ) = 51 − 2 : ( 2) − = 256  n = 8. 2 − n
B. Sai do nhầm công thức số hạng tổng quát . n u q = 15 − 36  2 − = 51 − 2  n = 9 . 1 ( ) n− −
C. Sai do tính (− ) 1 512 2 = 5 − 12  n −1 = = 256  n = 257 . 2 −
Câu 16: Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau: Nhóm Chiều cao (cm) Số học sinh 1 150;152) 5 2 152;154) 18 3 154;156) 40 4 156;158) 26 5 158;160) 8 6 160;162) 3 N = 100
Giá trị đại diện của nhóm thứ tư là A. 156, 5 . B. 157 . C. 157, 5 . D. 158 . Lời giải Chọn B +
Giá trị đại diện của nhóm thứ tư là 156 158 = 157 . 2
Câu 17: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa mốt của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Chọn A
Mốt M chứa trong nhóm [40; 60) 0
Câu 18: Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Nhóm chứa trung vị của mẫu số liệu trên là A. [40; 60) . B. [20; 40) . C. [60;80) . D. [80;100) . Lời giải Chọn A Ta có: n = 42 + Nên trung vị x x
của mẫu số liệu trên là 21 22 Q = 2 2
Mà x , x  40;60 21 22  )
Vậy nhóm chứa trung vị của mẫu số liệu trên là nhóm [40; 60)
Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13). D. 13; 15) . Lời giải Chọn B
Bảng tần số ghép nhóm theo giá trị đại diện là + + + + Số trung bình: 2.6 7.8 7.10 3.12 1.14 x = = 9, 4 20
Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng):
Tứ phân vị thứ nhất của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây? A. 7 . B. 7, 6 . C. 8 . D. 8, 6 . Lời giải Chọn C
Gọi x , x ,..., x là doanh thu bán hàng trong 20 ngày xếp theo thứ tự không giảm. 1 2 20
Khi đó: x , x  5;7 , x ,..., x  7; 9 ,, x ,..., x  9; 11 x ,..., x  11; 13 , x  13; 15 20  ) 17 19  ) 9 16  ) 3 9  ) 1 2  )
Do đó, tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm 7;9)
n = 20, n = 7,C = 2,u = 7,u = 9 m m m 1 + 1.20 − 2 4 Q = 7 + (9 − 7)  7,86  8 1 7  Câu 21: 4 Biết sin − = và 3     . Giá trị cos bằng 5 2 3 3 3 9 A. − . B. . C.  . D. . 5 5 5 5 Lời giải Chọn A Vì 3π π  α 
nên cosα  0 . Mặt khác 2 2 sin α + cos α = 1 ta có 2 cosα = − 1− sin α 2 2  4  3 = − 1− − = −   .  5  5    
Câu 22: Giá trị của biểu thức A = sin +   là  3 4  6 − 2 6 + 2 − 6 + 2 − 6 − 2 A. . B. . C. . D. . 4 4 4 4 Lời giải Chọn B         + Ta có 3 2 2 1 6 2 A = sin + = sin cos + sin cos = . + . = .    3 4  3 4 4 3 2 2 2 2 4
Câu 23: Hàm số nào sau đây là hàm số lẻ? A. y = 2 − cos x . B. 2 y = 2
− sin x + 2. C. y = 2 − sin x . D. y = 2 − cos x + 2 . Lời giải Chọn C
Tập xác định của hàm số y = f ( x) = 2
− sin x là D = .
Do đó, nếu x thuộc tập xác định D thì −x cũng thuộc tập xác định D .
Ta có f (−x) = 2
− sin(−x) = sin x = − f (x). Vậy y = 2
− sin x là hàm số lẻ.
Câu 24: Tập nghiệm của phương trình cos x = 1 − là     
A. S =  + k2 | k  . B. S = −
+ k2 |k  .  2   2 
C. S = k2 |k  .
D. S =  + k2 | k  . Lời giải Chọn D Ta có cos x = 1
−  x =  + k2,k  . Câu 25: 1 1 1 Cho dãy số 1, , ,
,... (số hạng sau bằng một phần ba số hạng liền trước nó). Công thức tổng 3 9 27
quát của dãy số đã cho là nn 1 − n 1   1  1 (− ) 1 A. u = . B. u = . C. u = . D. u = . n      3  n  3  n 3n n n 1 3 − Lời giải Chọn D
Câu 26: Cho cấp số cộng (u có u = 2; d = 5
− . Số hạng thứ 20 của cấp số cộng là n ) 1 A. 93 − . B. 10 . C. 93 . D. 23. Lời giải Chọn D
u = u +19d = 2 +19( 5 − ) = 9 − 3. 20 1
Câu 27: Cho cấp số nhân ( x có x = 3 − và x = 27. −
Tính số hạng đầu x và công bội q của cấp số n ) 2 4 1 nhân. A. x = 1 − ,q = 3
− hoặc x =1,q = 3. B. x = 1
− ,q = 3 hoặc x =1,q = 3 − . 1 1 1 1
C. x = 3, q = 1
− hoặc x = 3 − ,q =1.
D. x = 3, q = 1 hoặc x = 3 − ,q = 1 − . 1 1 1 1 Lời giải Chọn B 2   q = 9  x = 3 −  x q = 3 −   q = 3  2 1      3   3 x = 2 − 7. x q = 2 − 7. x = − . x = 1.     4 1 1 1   q
Câu 28: Theo số liệu thông kê điểm Giữa học kì I môn toán khối 10 của một trường THPT được cho bởi bảng số liệu sau:
Điểm nào đại diện cho nhiều học sinh đạt được nhất? A. 6, 5 . B. 7, 5 . C. 7, 25 . D. 8 . Lời giải Chọn C
Theo bảng thống kê, giá trị lớn nhất là 60 thuộc lớp 6,5;8) nên giá trị đại diện là 6, 5 + 8 = 7, 25. 2
Câu 29: Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại
ở bảng sau (đơn vị: triệu đồng): Doanh thu 5;7) 7;9) 9;1 )1 11;13) 13;15) Số ngày 2 7 7 3 1
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây? A. 7; 9) . B. 9; 1 ) 1 . C. 11; 13). D. 13; 15) . Lời giải Chọn B 6.2 + 8.7 +10.7 +12.3 +14.1
Số trung bình của mẫu số liệu trên là: x = = 9,4 20
Câu 30: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau: Nhóm chứa trung vị là A. 30;45) . B. 15;30) . C. 45;60) . D. 60;75) . Lời giải Chọn A
Cỡ mẫu: n = 9 + 5 +15 +14 + 7 = 50 .
Gọi x ,..., x là thời gian khảo sát tập thể dục trong ngày của 50 học sinh khối 11 và giả sử dãy 1 50 x + x
này đã được sắp xếp theo thứ tự tăng dần. Khi đó, trung vị là 25
26 . Do hai giá trị x , x 2 25 26 thuộc nhóm 30; 45) .
Câu 31: Một chiếc phao được thả cố định trên biển dùng để đo độ cao của sóng biển được mô hình hóa   
bởi hàm số h (t ) = 5sin t
 , trong đó h(t ) là độ cao tính bằng cetimét trên mực nước biển  5 
trung bình tại thời điểm t giây. Nếu chiếc phao đang ở đỉnh của sóng thì trong bao lâu chiếc
phao lại ở vị trí đỉnh của cơn sóng tiếp theo (giả sử các cơn sóng đều mô hình hóa bởi cùng hàm số). A. 5 giây. B. 10 giây. C. 2, 5 giây. D. 20 giây. Lời giải Chọn B   
Ta có mô hình hóa chiều cao của sóng nước là hàm hàm số h(t) = 5sin t   nên để chiếc phao  5   ở 2
vị trí đỉnh ở hai lần liên tiếp thì cách nhau một chu kì của sóng T = =10(s)  . 5   
Câu 32: Tổng nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình 3 3 sin 3x − =    4  2 bằng:     A. . B. − . C. . D. − . 9 6 6 9 Lời giải Chọn C  3  3x − = + k2         Ta có 3 3 3 4 3 sin 3x − =  sin 3x − = sin       .  4  2  4  3 3    3x − =  − + k2  4 3  13  13 2 3x = + k2 x = + k   12 36 3     (k Z ). 17 17    2 3x = + k2 x = + k  12  36 3  13 13
x  0  k  −  k = 0 → x =  min 13 2 Cho 24 36 TH1. Với x = + k ⎯⎯→  . 36 3 13 11  
x  0  k  −  k = −1→ x = − max  24 36  17 17
x  0  k  −  k = 0 → x =  min 17 2 Cho 24 36 TH2. Với x = + k ⎯⎯→  . 36 3 17 7  
x  0  k  −  k = −1→ x = − max  24 36 
So sánh bốn nghiệm ta được nghiệm âm lớn nhất là 7 x = −
và nghiệm dương nhỏ nhất là 36 13 13 7  x =
. Khi đó tổng hai nghiệm bằng − = . 36 36 36 6
Câu 33: Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng
thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, …, cứ tiếp tục trồng như thế cho đến khi hết số
cây. Số hàng cây được trồng là A. 77 . B. 79 . C. 76 . D. 78 . Lời giải Chọn A
Gọi số cây ở hàng thứ n là u . n
Ta có: u =1, u = 2 , u = 3, … và S = u + u + u +...+ u = 3003 . 1 2 3 1 2 3 n
Nhận xét dãy số (u là cấp số cộng có u = 1, công sai d =1. n ) 1
n 2u + n −1 d   n 2.1+  (n − )11 1 ( ) Khi đó   S = = 3003  = 3003 2 2  =  n n (n + ) 1 = 6006 2
n + n − 6006 = 77 0  
n = 77 (vì n ). n = 78 −
Câu 34: Một cấp số nhân có số hạng đầu u = 3, công bội q = 2 . Biết S = 765 . Tìm n ? 1 n A. n = 8 . B. n = 9 . C. n = 6 . D. n = 7 . Lời giải Chọn A u 1 n − q 3. 1− 2n 1 ( ) ( )
Áp dụng công thức của cấp số nhân ta có: S = = = 765  n = . n 1− q 1− 8 2
Câu 35: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau: Thời gian
15;20) 20;25) 25;30) 30;35) 35;40) 40;45) 45;50) Số nhân 7 14 25 37 21 14 10 viên
Tứ phân vị thứ nhất Q và tứ phân vị thứ ba Q của mẫu số liệu ghép nhóm này là 1 3 1360 800 1360 3280 A. Q = , Q = . B. Q = , Q = . 1 3 37 21 1 3 37 83 136 3280 136 800 C. Q = , Q = . D. Q = , Q = . 1 3 5 83 1 3 5 21 Lời giải Chọn D
Cỡ mẫu là n = 128 . x + x
Tứ phân vị thứ nhất Q là 32
33 . Do x , x đều thuộc nhóm [25;30) nên nhóm này chứa 1 2 32 33 Q . 1
Do đó, p = 3;a = 25;m = 25;m + m = 21, a − a = 5 và ta có 3 3 1 2 4 3 8 12 − 21 136 4 Q = 25 + 5 = 1 25 5 x + x
Với tứ phân vị thứ ba Q là 96
97 . Do x , x đều thuộc nhóm [35; 40) nên nhóm này chứa 3 2 96 97 Q . 3
Do đó, p = 5;a = 35;m = 21;m + m + m + m = 7 +14 + 25 + 37 = 83;a − a = 5 và ta có 5 5 1 2 3 4 6 5 3.128 −83 800 4 Q = 35 + 5 = . 3 21 21
II. PHẦN TỰ LUẬN (3,0 điểm). Câu Đáp án Biểu điểm    0.5
Giải phương trình cot x + = 3   .  3       0.25 36a cot x +
= 3  x + = + k    3  3 6 
x = − + k (k  ) . 0.25 6 2
Cho sin = , tính giá trị của biểu thức P = (1− 3cos)(1+ 3cos) . 0.5 3 P = −  +  = − (  )2 2 (1 3cos )(1 3cos ) 1 3cos =1− 9cos  . 0.25 36b 2 5 0.25 sin  = , 2 2 2
sin  + cos  = 1  cos  = . 3 9 5 P = 1− 9. = 4 − . 9
Giải phương trình cos3x −sin 2x = 0. 1.0    0.25
cos3x − sin 2x = 0  cos3x = sin 2x  cos3x = cos − 2x    2      0.25 3x =  − 2x + k2    2    0.25 5x = + k2 37  2   
x = − + k2  2   2 0.25 x = + k  10 5   (k  ) 
x = − + k2  2    1.0 38
Giải phương trình sin x = cos x +    3     sin x = cos x +    3  0,25        cos − x = cos x +      2   3   
− x = x + + k2  2 3   (k  )   0,25
 − x = −x − + k2  2 3   2
− x = − + k2 (k  ) 0,25 6   x =
− k (k  ) . 0,25 12
Một cơ sở khoan giếng đưa ra định mức giá như sau: Giá từ mét
khoan đầu tiên là 100000 đồng và kể từ mét khoan thứ hai, giá
mỗi mét tăng thêm 30000 đồng so với giá của mét khoan ngay
trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này 0.5
để khoan giếng sâu 20 mét lấy nước dùng cho sinh hoạt gia đình.
Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh
toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
Giá tiền mỗi mét khoan giếng lập thành một cấp số cộng với
u = 100000 (số tiền mét khoan đầu tiên), 39 1
u = u + 30000 (số tiền mét khoan thứ hai), 2 1
u = u + 30000 = u + 2.30000 (số tiền mét khoan thứ ba) 0,25 3 2 1 …
u = u + 30000 = u +19.30000 (số tiền mét khoan thứ 20), 20 19 1
và công sai d = 30000 .
Tổng chi phí cần phải thanh toán là 20(2.10000 +19.30000) S
= u + u + u +...+ u = = 7700000 . 0,25 20 1 2 3 20 2