Đề thi giữa học kỳ 1 Toán 9 năm 2020 – 2021 trường THCS Bế Văn Đàn – Hà Nội

Đề thi giữa học kỳ 1 Toán 9 năm 2020 – 2021 trường THCS Bế Văn Đàn – Hà Nội gồm 01 trang với 04 bài toán dạng tự luận, thời gian làm bài 90 phút. Mời bạn đọc đón xem.

38 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 9

Môn: Toán 9

Thông tin:

5 trang 9 tháng trước

Tác giả:

Profile Hà Việt Anh
UB
ND QUẬN ĐỐNG ĐA
TRƯỜNG THCS BẾ VĂN ĐÀN
----------
THCS.TOANMATH.com
Bài 1: (2,5 điểm) Cho hai biểu thức
25
3
xx
A
x

và
2 9 32 1
5 6 23
x xx
B
xx x x



với
0, 4, 9xxx
a) Tính giá trị của
A
khi
16.x
b) Rút gọn biểu thức
B
c) Biết rằng
:P AB
. Tìm giá trị nhỏ nhất của
P
Bài 2: (3,0 điểm) Giải các phương trình sau:
a)
52x
b)
2
6 95xx 
c)
d)
22
4 4 4 12 9xx x x 
Bài 3: ( 3,5 điểm) Cho tam giác
ABC
vuông tại
A
(
AB AC
), đường cao
AH
(
H BC
). Vẽ
phân giác
AD
của góc
BAH
(
D BH
). Cho
M
là trung điểm của
BA
.
a) Cho
3AC cm
;
4AB cm
. Hãy giải tam giác
ABC
?. Làm tròn đến độ
b) Tính diện tích tam giác
AHC
c) Chứng minh rằng:
DH HC
DB AC
d) Gọi
E
là giao điểm của
DM
và
AH
. Chứng minnh:
A C DEC
SS
E
Bài 4: (1,0 điểm)
Một con thuyền ở địa điểm
F
di chuyển từ
bờ sông
b
sang bờ sông
a
với vận tốc trung
bình là
6
km/h, vượt qua khúc sông nước
chảy mạnh trong
5
phút. Biết đường đi của
con thuyền là
FG
, tạo với bờ sông một góc
60
.
a) Tính
FG
b) Tính chiều rộng của khúc sông (làm tròn
đến mét)
HẾT
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT
Bài 1: a) Ta có
16x
(thỏa mãn điều kiện), thay vào biểu thức
A
ta có:
16 2 16 5 29
29
1
16 3
A


Vậy khi
16x
thì
29A
b) Ta có:

 



2 9 32 1
5 6 23
2 9 32 1
23
23
2 9 3 32 1 2
23
29 9232
23
21
21
3
23 23
x xx
B
xx x x
x xx
xx
xx
x xx xx
xx
x x xx
xx
xx
xx x
x
xx xx














 
Vậy
1
3
x
B
x
,
0, 4, 9xxx
c) Ta có
2
14
25 1 25 4
:: 1
33 1 1 1
x
xx x xx
P AB x
xx x x x

 


Do
0 0 10xxx 
Áp dụng bất đẳng thức Cô si cho 2 số dương
1x
và
4
1x
ta có:
44
1 21 4
11
Px x
xx


Dấu bằng xảy ra
4
1 12 1 1
1
x x xx
x
 
(thỏa mãn điều
kiện)
Vậy
min 4P
khi
1x
UB
ND QUẬN ĐỐNG ĐA
TRƯỜNG THCS BẾ VĂN ĐÀN
----------
THCS.TOANMATH.com
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Bài 2: a)
52x
.
Điều kiện xác định
5x
Ta có:
52 54 9xxx
(thỏa mãn
5x
)
Vậy tập nghiệm của phương trình là
9S
.
b)
2
6 95xx 
Ta có:
2
2
35 8
6 95 3 5 35
35 2
xx
xx x x
xx



  

 

Vậy tập nghiệm của phương trình là
8; 2S 
.
c)
Ta có:
2
2
1
10
2
4 41 1 21 121 1
21 1
21 1
0
x
x
x
xx x x x x x
xx
xx
x
nhaän
nhaän


  






Vậy tập nghiệm của phương trình là
2;0S
.
d)
22
4 4 4 12 9xx x x 
Ta có:
22
22
44 4 129 2 23 223xx x x x x x x  
1
22 3 1
5
2 2335
3
x
xx x
x xx
x







Vậy tập nghiệm của phương trình là
5
1;
3
S







.
Bài 3:
a) Xét
ABC
vuông tại
A
(gt) có:
2
1
G
H
M
A
C
B
D
E
222
AB AC BC
(định lí Pytago)
22 2
43BC
2
25BC
5BC
(cm)
Ta có:
3
sin 37
5
AC
BB
BC

90BC
53C
b) Áp dụng hệ thức lượng vào
ABC
vuông tại
A
, đường cao
AH
ta có:
..AH BC AB AC
. 4.3
2,4
5
AB AC
AH
BC

(cm)
Lại có:
2
2
39
. 1,
8
5
AC CH BC CH
BC

(cm)
Diện tích tam giác
AHC
là:
2
11
. . .2,4.1,8 2,16
22
HC AH c
m
c) Xét
ABH
có phân giác
AD
(giả thuyết)
DH AH
DB AB

(tính chất phân giác trong tam giác)
AHB CHA”
(g-g)
AH HC
AB AC

(hai góc tương ứng)
DH HC AH
DB AC AB



(đpcm)
d) Kẻ
HG AB//
Xét
ABD
có
ADC
là góc ngoài
2
ADC ABD A 
Mà
1
DAC A HAC
Lại có
ABD HAC
ADC DAC
ACD
cân tại
C
(dhnb)
AC DC
(tính chất)
DH HC HC
DB AC DC

(1)
Xét
AEM
, có
GH AB//
EH HG
EA AM

(định lí Ta lét)
Vì
M
là trung điểm của
AB
(gt)
AM BM
EH HG
EA BM

Xét
DGH
, có
//GH AB
DH HG
DB BM

(định lí Ta lét)
EH DH
EA DB

(2)
Từ
(1); (2) . .
HC HE
HC AE DC HE
DC AE

Ta có
1
.
2
ACE
S CH AE
,
1
.
2
DEC
S EH DC
.
1
.
ACE
DEC
S
CH AE
S EH DC

Vậy
A C DEC
SS
E
Bài 4:
a)
FG
là quãng đường đi được của thuyền.
5
6. 0,5 500
60
FG k
m m
.
b) Gọi
GH
là chiều rộng của khúc sông.
Xét
GHF
vuông tại H, áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có:
3
.sin 500.sin60 500. 250 3 433
2
GH FG GFB 
m.
Vậy, chiều rộng của khúc sông xấp xỉ
433
m.
HẾT
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

UBND QUẬN ĐỐNG ĐA
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS BẾ VĂN ĐÀN NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Bài 1:
(2,5 điểm) Cho hai biểu thức x  2 x  5 2 x 9 x  3 2 x 1 A  và B   
với x  0, x  4, x  9 x 3 x 5 x  6 x  2 3 x
a) Tính giá trị của A khi x 16.
b) Rút gọn biểu thức B
c) Biết rằng P A : B . Tìm giá trị nhỏ nhất của P Bài 2:
(3,0 điểm) Giải các phương trình sau: a) x 5  2 b) 2
x  6x  9  5 c) 2
4x  4x 1  x 1 d) 2 2
x  4x  4  4x 12x  9 Bài 3:
( 3,5 điểm) Cho tam giác ABC vuông tại A ( AB AC ), đường cao AH ( H BC ). Vẽ
phân giác AD của góc BAH ( D BH ). Cho M là trung điểm của BA .
a) Cho AC  3cm ; AB  4cm . Hãy giải tam giác ABC ?. Làm tròn đến độ
b) Tính diện tích tam giác AHC DH HC c) Chứng minh rằng:  DB AC
d) Gọi E là giao điểm của DM và AH . Chứng minnh: SS AC E DEC Bài 4: (1,0 điểm)
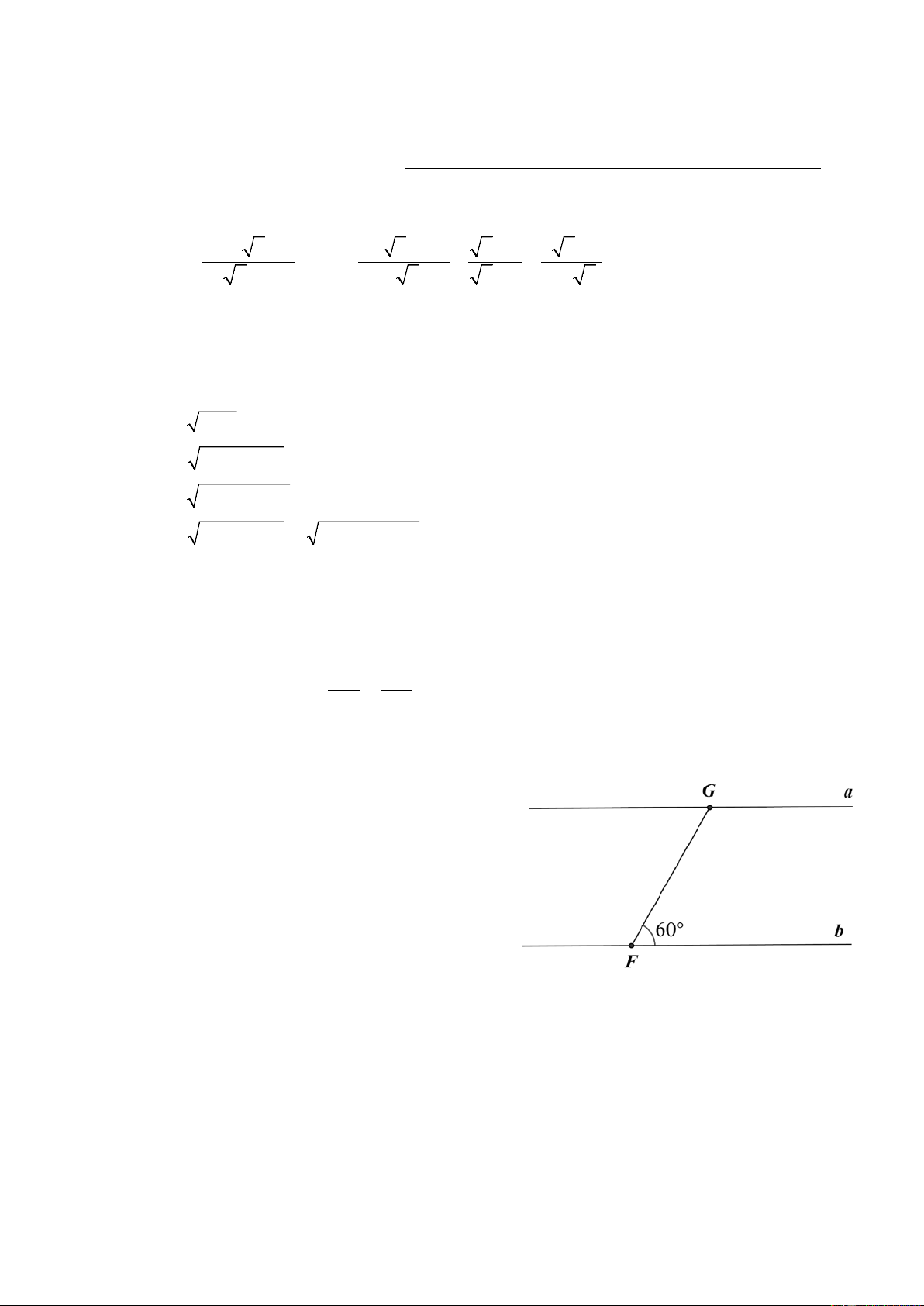
Một con thuyền ở địa điểm F di chuyển từ
bờ sông b sang bờ sông a với vận tốc trung
bình là 6 km/h, vượt qua khúc sông nước
chảy mạnh trong 5 phút. Biết đường đi của
con thuyền là FG , tạo với bờ sông một góc 60 . a) Tính FG
b) Tính chiều rộng của khúc sông (làm tròn đến mét) HẾT
UBND QUẬN ĐỐNG ĐA
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS BẾ VĂN ĐÀN NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT Bài 1:
a) Ta có x  16 (thỏa mãn điều kiện), thay vào biểu thức A ta có: 16  2 16  5 29 A    29 16 3 1
Vậy khi x 16 thì A  29 b) Ta có: 2 x 9 x  3 2 x 1 B    x 5 x  6 x  2 3 x 2 x 9 x  3 2 x 1     x   2  x   3 x  2 x 3
2 x 9 x   3  x   3 2 x   1  x   2 
x  2 x  3
2 x 9 x  9  2x 3 x  2 
x  2 x  3
x  2 x x x    1 2 x 1     x   2  x   3
x  2 x  3 x 3 x 1 Vậy B
, x  0, x  4, x  9 x 3 c) Ta có       x x x x x x  2 1  4 2 5 1 2 5 4
P A : B  :    x 1 x 3 x 3 x 1 x 1 x 1
Do x  0  x  0  x 1 0 4
Áp dụng bất đẳng thức Cô si cho 2 số dương x 1và ta có: x 1 4 P x     x   4 1 2 1  4 x 1 x 1 4
Dấu bằng xảy ra  x 1
x 1 2  x 1  x 1(thỏa mãn điều x 1 kiện)
Vậy min P  4 khi x 1 Bài 2: a) x 5  2 .
Điều kiện xác định x  5
Ta có: x 5  2  x 5  4  x  9 (thỏa mãn x  5 )
Vậy tập nghiệm của phương trình là S    9 . b) 2
x  6x  9  5 x3  5 x  8
Ta có: x  6x  9  5  x  2 2 3
 5  x3  5     x3  5 x  2  
Vậy tập nghiệm của phương trình là S  8;  2 . c) 2
4x  4x 1  x 1 Ta có:      x 1 x 1 0      
4x  4x 1  x 1  2x  2 2 1
x 1  2x1  x 1  2x1 x 1   x   2nhaän      
2x 1 x 1  x   0  nhaän 
Vậy tập nghiệm của phương trình là S  2;  0 . d) 2 2
x  4x  4  4x 12x  9 2 2 Ta có: 2 2
x  4x  4  4x 12x  9  x  2  2x   3
x2  2x3 x 1
x2  2x3 x  1        5
x2  2x 3 3x  5 x     3    
Vậy tập nghiệm của phương trình là 5 S  1  ;   .  3   Bài 3: E B G D M H 2 1 A C a) Xét A
BC vuông tại A (gt) có: 2 2 2
AB AC BC (định lí Pytago) 2 2 2  4 3  BC 2  BC  25  BC  5 (cm) AC 3 Ta có:  sin B    B  37 BC 5  
B C  90   C  53
b) Áp dụng hệ thức lượng vào A
BC vuông tại A , đường cao AH ta có:
AH.BC A . B AC A . B AC 4.3  AH    2, 4 (cm) BC 5 2 3 9 Lại có: 2
AC CH.BC CH   1,8 (cm) BC 5
Diện tích tam giác AHC là: 1 1
.HC.AH  .2, 4.1,8  2,16 2 cm  2 2 c) Xét A
BH có phân giác AD (giả thuyết) DH AH  
(tính chất phân giác trong tam giác) DB AB AHB ” CHA (g-g) AH HC   (hai góc tương ứng) AB AC DH HC AH         (đpcm) DB AC  AB  d) Kẻ HG // AB Xét ABD có  ADC là góc ngoài   
ADC ABD A2 Mà   
DAC A HAC 1 Lại có   ABD HAC  
ADC DAC A
CD cân tại C (dhnb)
AC DC (tính chất) DH HC HC    (1) DB AC DC EH HG Xét A
EM , có GH // AB   (định lí Ta lét) EA AM EH HG
Vì M là trung điểm của AB (gt)  AM BM   EA BM DH HG Xét DGH
, có GH / / AB   (định lí Ta lét) DB BM EH DH   (2) EA DB HC HE Từ (1);(2)  
HC.AE DC.HE DC AE 1 1 Ta có S
CH.AE , SEH.DC ACE 2 DEC 2 S CH .AE ACE   1 S EH .DC DEC Vậy SS AC E DEC Bài 4: 5
a) FG là quãng đường đi được của thuyền. FG  6.
 0,5km  500 m . 60
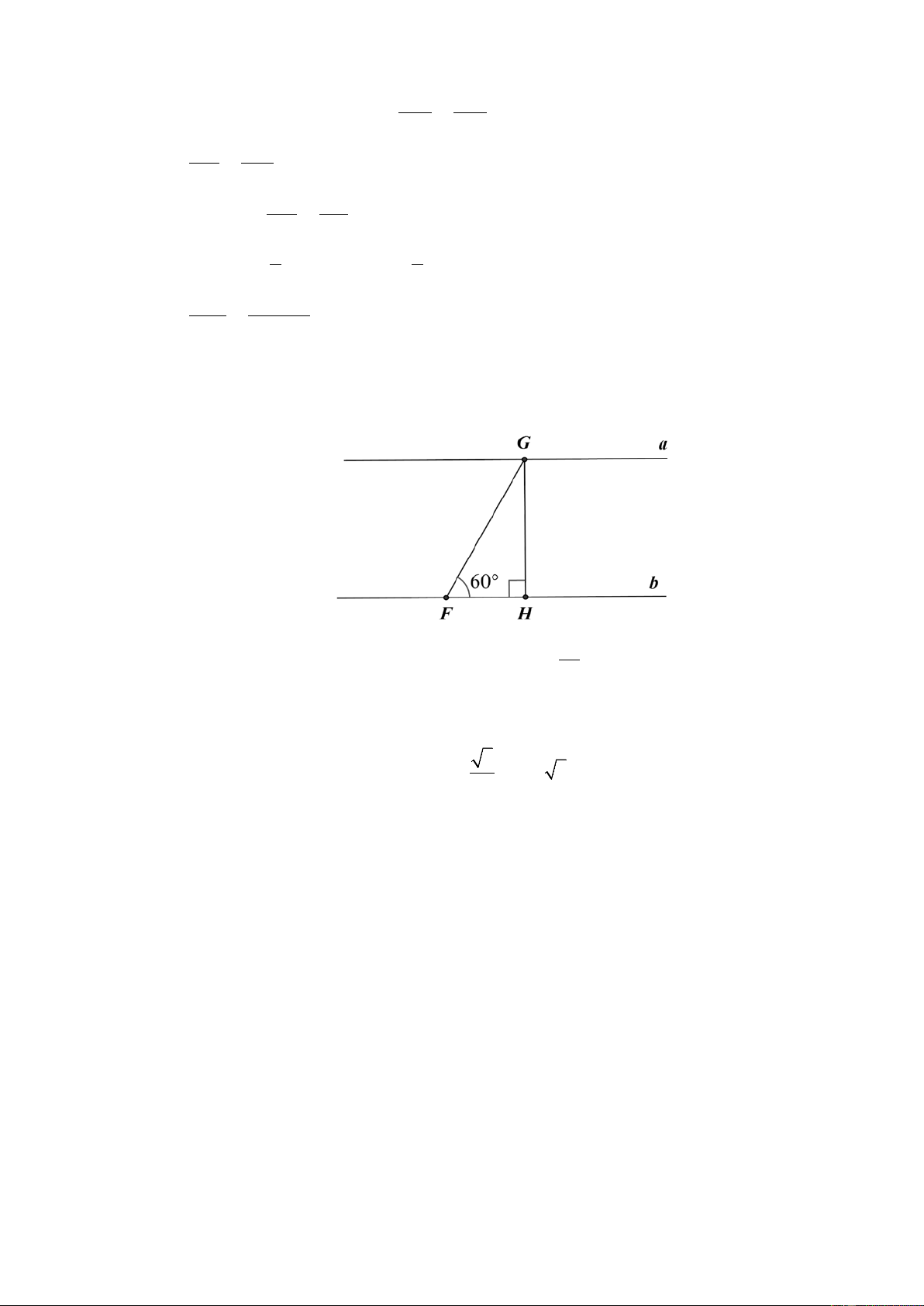
b) Gọi GH là chiều rộng của khúc sông. Xét GHF
vuông tại H, áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có:  3 GH F .
G sin GFB  500.sin 60  500.  250 3  433 m. 2
Vậy, chiều rộng của khúc sông xấp xỉ 433 m.  HẾT