




Preview text:
UBND QUẬN TÂY HỒ
KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THCS PHÚ THƯỢNG
Năm học: 2023 - 2024 Môn: Toán 9
Thời gian làm bài: 90 phút
Bài 1: (2 điểm) Cho biểu thức x + 2 + + A = và x x 14 5 B = −
với x ≥ 0; x ≠ 4 x +1 x − 4 x − 2
1) Tính giá trị biểu thức A khi x =16 . 2) Chứng minh rằng x − 2 B = . x + 2 3) Cho M = .
A B . Tìm giá trị nhỏ nhất của M.
Bài 2: (2 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một ca nô chạy xuôi dòng 63km và ngược dòng 30km hết tất cả 5giờ. Nếu
cũng trên khúc sông đó, ca nô chạy xuôi dòng 42 km và ngược dòng 45 km hết tất
cả 5giờ. Tính vận tốc thực của ca nô và vận tốc của dòng nước. Bài 3: (2 điểm) 4 2x + = 4 y −1
1) Giải hệ phương trình : 8 5 x − =1 y − 1 2) Cho hàm số 2
y = x có đồ thị là parabol (P) và đường thẳng (d): y = 5x − 4 a) Vẽ đồ thị hàm số 2
y = x trên mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán. Bài 4 (3,5 điểm)
1) Một con thuyền ở địa điểm D di chuyển từ bờ sông a sang bờ sông b với vận tốc
trung bình là 2 km/h, vượt qua khúc sông nước chảy mạnh trong 20 phút. Biết đường
đi con thuyền là DE , tạo với bờ sông một góc 60o. Tính chiều rộng khúc sông.
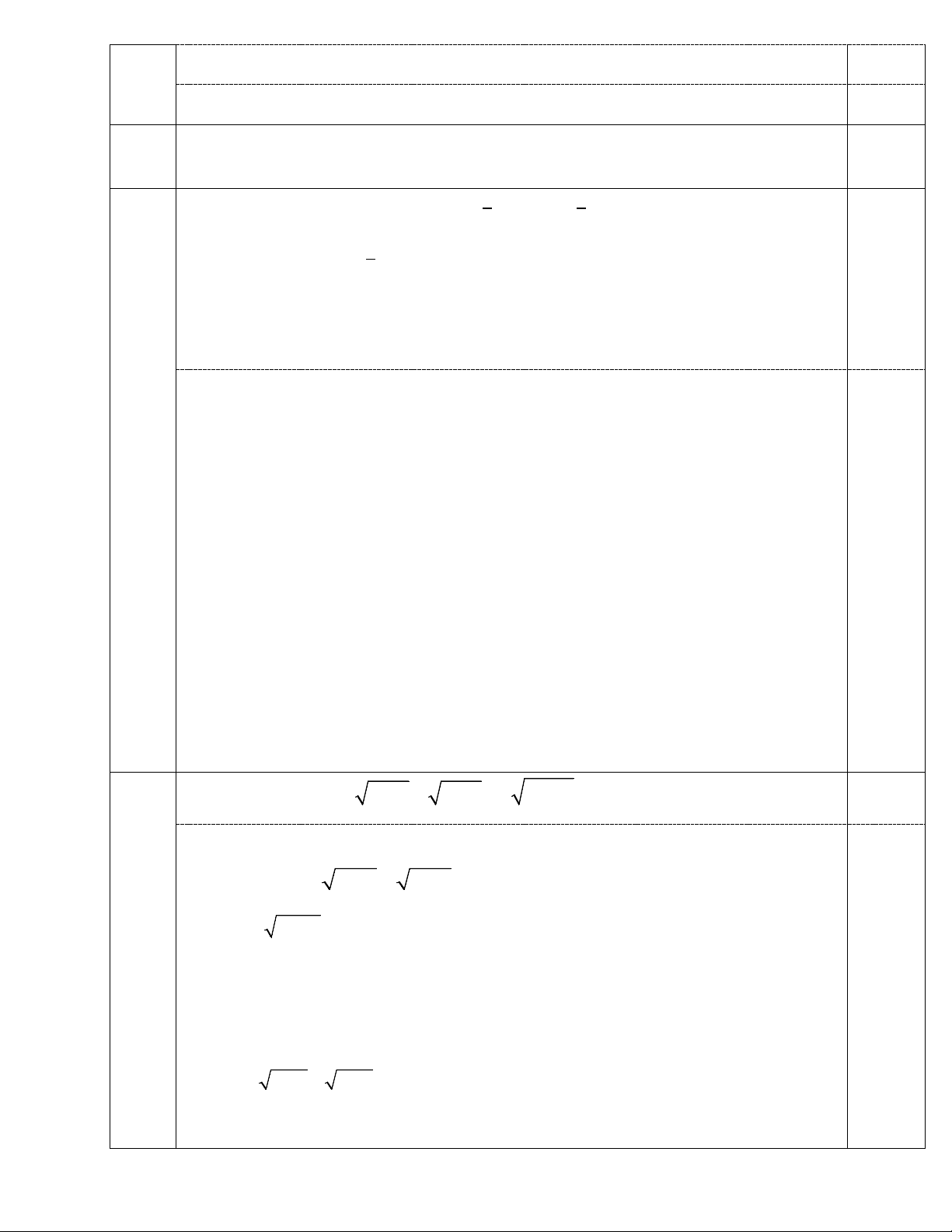
2) Cho đường tròn (O, R), BC là dây không đi qua tâm. Các tiếp tuyến của đường
tròn tâm O tại B và C cắt nhau ở điểm A. Lấy M thuộc cung nhỏ BC. Kẻ MI, MK,
MH lần lượt vuông góc với BC, AB, AC. Chứng minh rằng:
a, Tứ giác BIMK nội tiếp đường tròn.
b, Chứng minh: 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � và MH.MK = MI2.
c, Gọi BM cắt KI tại E, CM cắt IH tại F. Chứng minh: FE // BC và FE là tiếp tuyến
của đường tròn ngoại tiếp tam giác MHF
Bài 5: (0,5 điểm) Giải phương trình: 2
x + 2 + x − 2 + 2 x − 4 = 2(3− x) ________Hết________
TRƯỜNG THCS PHÚ THƯỢNG HƯỚNG DẪN CHẤM
ĐỀ KIỂM TRA GIỮA HỌC KỲ 2 MÔN TOÁN 9 Năm học 2023 - 2024 BÀI ĐÁP ÁN ĐIỂM
I.1 Thay x =16 (thỏa mãn điều kiện) vào A ta có: 0,25 16 2 A + = 16 +1 6 A = 0,25 5 I.2 x + x +14 5 B = − x − 4 x − 2 5 x x ( x + + + 2 14 ) 0,25 B = ( −
x − 2)( x + 2) ( x − 2)( x + 2) x − 4 x + 4 B = ( 0,25 x − 2)( x + 2) 2 ( x − 2) B = ( 0,25 x − 2)( x + 2) x − 2 B = 0,25 x + 2 I.3 P = . A B x + 2 x − 2 P = . x +1 x + 2 x − 2 P = x +1 3 P =1− x +1
Với mọi x thuộc ĐKXĐ ta có: 0,25 x ≥ 0 ⇒ x +1≥1 3 ⇒ ≤ 3 x +1 3 ⇒1− ≥1− 3 0,25 x +1 ⇒ P ≥ 2 −
Vậy giá trị nhỏ nhất của P = 2 − khi x = 0
II Gọi vận tốc thực của ca nô là x (km/h)
Gọi vận tốc của dòng nước là y (km/h; x > y > 0 )
Vận tốc ca nô đi xuôi dòng là x + y (km/h)
Vận tốc ca nô đi ngược dòng là x − y (km/h) Trường hợp 1:
Thời gian ca nô đi xuôi dòng là 63 (h) x + y
Thời gian ca nô đi ngược dòng là 30 (km) x − y
Vì ca nô chạy xuôi dòng 63km và ngược dòng 30km hết tất cả 5giờ nên ta có phương trình: 63 30 + = 5
x + y x − y Trường hợp 1:
Thời gian ca nô đi xuôi dòng là 63 (h) x + y
Thời gian ca nô đi ngược dòng là 30 (km) x − y
Vì ca nô chạy xuôi dòng 63km và ngược dòng 30km hết tất cả 5giờ nên ta có phương trình: 63 30 + = 5 (1)
x + y x − y Trường hợp 2:
Thời gian ca nô đi xuôi dòng là 42 (h) x + y
Thời gian ca nô đi ngược dòng là 45 (km) x − y
Vì ca nô chạy xuôi dòng 42 km và ngược dòng 45 km hết tất cả 5giờ nên ta có phương trình: 42 45 + = 5 (2)
x + y x − y 63 30 + = 5
Từ (1), (2) ta có hệ phương trình: x + y x − y 42 45 + = 5
x + y x − y 189 90 + = 15 105 = 5 x + y = 21
x + y x − y x + y ⇔ ⇔ ⇔ 42 45 84 90 + = 5 + = 10 42 45 + = 5 − 21 x y
x + y x − y
x + y x − y x + y = 21 x = x = 18 x = 18 ⇔ 2 36 ⇔ ⇔ ⇔ (thoả mãn) x − y = 15 x − y = 15 18 − y = 15 y = 3
Vậy vận tốc của ca nô là 18km/h; vận tốc của dòng nước là 3(km/h) ĐKXĐ: y > 1 0,25 4 8 2x + = 4 4x + = 8 y 1 − y −1 0,75 <=> III.1 8 8 5 x 1 5 − = x − = 1 y −1 y − 1 9 x = 9 x = 1 4 <=> <=> 4 2x + = 4 2x + = 4 a = 2 Giải hpt tìm được y 1 − y − 1 b = 2 x = 1 <=> (TM ) y = 5 0,25
Vậy hệ phương trình đã cho có 1 nghiệm duy nhất x =1 y = 5 III.1
Gọi H là hình chiếu của E lên a ⇒ EH ⊥ a 1 2 DE = 2. = (km) 3 3 60o EH Sin = 0,25 2 3 o 2 3 EH = Sin60 . = (km) 3 3 0,25 Vậy khúc sông rộng 3 km 3 III.2 a) *Vẽ đúng (P) 0,5 2a
* Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình 0,5 x2 = 5x – 4 ⇔ x2 - 5x + 4 = 0 ⇔ x2 - 4x – x + 4 = 0 ⇔ (x – 4)( x – 1) = 0 x = 1 ⇔ x = 4 Với x = 1 thì y = 1 Với x = 4 thì y = 16
Kết luận: Tọa độ giao điểm của 2 đồ thị là A(1; 1) ; B(4; 16) IV C Hình vẽ H đúng đến câu 1 O A I M 0,25 K B 1
Chứng minh được tứ giác BKMI nội tiếp 0,75 2
Chứng minh rằng: MI2 = MH. MK
Chứng minh tứ giác CMHI nội tiếp 0,25
Chứng minh được: 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 �- 0,25
- Chứng minh được: ΔMIH ~ΔMKI (g - g) 0,25 => MI2 = MH. MK 0,25 3
Gọi BM cắt KI tại E, CM cắt IH tại F. Chứng minh: FE // BC và FE là tiếp
tuyến của đường tròn ngoại tiếp tam giác MHF
Cm được: 𝑀𝑀𝑀𝑀𝐸𝐸
� = 𝑀𝑀𝑀𝑀𝑀𝑀
� + 𝑀𝑀𝑀𝑀𝑀𝑀 =
� 1 𝑠𝑠đ𝑀𝑀𝑀𝑀 + 1 𝑠𝑠đ 𝑀𝑀𝑀𝑀 0,25 2 2
𝑀𝑀𝑀𝑀𝐸𝐸
� = 1 𝑠𝑠đ 𝑀𝑀𝑀𝑀 2
=>𝑀𝑀𝑀𝑀𝐸𝐸
� + 𝑀𝑀𝑀𝑀𝐸𝐸 � = 1800
Từ đó chứng minh tứ giác EIFM nội tiếp được => 𝑀𝑀𝑀𝑀𝐸𝐸 � = 𝑀𝑀𝑀𝑀𝐸𝐸 � 0,25 Mà 𝑀𝑀𝑀𝑀𝐸𝐸 � = 𝑀𝑀𝑀𝑀𝑀𝑀
� => 𝑀𝑀𝑀𝑀𝐸𝐸 � = 𝑀𝑀𝑀𝑀𝑀𝑀 �
hai góc ở vị trí đồng vị => EF//BC
- Kẻ Fx là tiếp tuyến của đường tròn ngoại tiếp tam giác MFH
=> 𝑀𝑀𝐸𝐸𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝐸𝐸 � Mà 𝑀𝑀𝑀𝑀𝐸𝐸
� = 𝑀𝑀𝑀𝑀𝑀𝑀 � (do tg MHCI nội tiếp) 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝐸𝐸𝑀𝑀 � (hai góc đồng vị)
Nên => 𝑀𝑀𝐸𝐸𝑀𝑀 � = 𝑀𝑀𝐸𝐸𝑀𝑀 � => Fx trùng FE
=> FE là tiếp tuyến của đường tròn ngoại tiếp tam giác MFH V Giải phương trình: 2
x + 2 + x − 2 + 2 x − 4 = 2(3− x) (1) 0,25 ĐKXĐ: x ≥ 2 0,25
Đặt ẩn phụ: t = x + 2 + x − 2(t ≥ 0) 2 2
t = 2x + 2 x − 4 PT (1) t = 2(TM ) 2
t + t = 6 2t + t − 6 = 0 <=> t = 3( − KTM ) Trả lại biến cũ:
t = 2 <=> x + 2 + x − 2 = 2 x =2 (TMĐK)
Vậy phương trình có nghiệm: S = {2} Lưu ý:
- Học sinh làm theo cách khác đúng, cho điểm tương đương.
- Bài hình: Học sinh vẽ sai hình từ câu nào, cho 0 điểm từ câu đó.




